0 引言
中国的黄土面积约为63万km2[1],是世界上黄土分布最广的国家之一。当前黄土地区地质灾害频发仍未得到较好的解决,严重威胁黄土地区人民的生产生活安全。研究[2-5]表明大部分黄土滑坡的发生与地下水位的变化密切相关。通过控制地下水位可以减少滑坡发生,现阶段控制地下水位的措施主要有地表排水沟、水平排水孔、地下排水隧洞3种方式,其中,地表排水沟排水效果不佳,水平排水孔缺乏长期稳定性,地下排水隧洞虽效率较高,但施工周期长,费用高,以上缺点严重制约了排水措施的实施。虹吸排水作为一种免动力并能排出坡体深部地下水的有效技术,其施工参数确定方法较为完备[6-7],已在多处滑坡体中应用,并取得了良好的效果[8-9]。吴梦萍等[10]建立了边坡虹吸排水间距的最优范围,并认为其主要与土体渗透系数和水位降深有关;任珊珊[11]对排水孔的布位设置、孔间距及倾斜角度对排水效果的影响做了详细研究,揭示了其对边坡地下水渗流场的影响规律。但关于虹吸排水技术目前所得出的结论均是在土质各向同性的基础上建立的,对于黄土地区土质竖向渗透系数显著大于水平向渗透系数情况下的虹吸排水技术鲜见报道。本文考虑在虹吸排水稳定时,将复杂的Neuman方程简化,结合流量与影响半径的关系,求解出各向异性情况下的降落漏斗影响半径计算表达式,并利用拦截比的概念,求解出一种各向异性情况下的边坡虹吸排水孔间距解析解。将该结论应用于黑方台黄土地区进行求解分析,利用数值模拟对该地区进行虹吸排水模拟,以验证理论分析结果的可行性,为实际工程的应用奠定基础。
1 边坡虹吸排水最优排水孔间距解析解推导 1.1 考虑各向异性降落漏斗影响半径确定在缺乏实测数据时,工程实践中常按式(1)的经验公式来进行潜水含水层降水影响半径的计算。但在各向异性条件下,水平和竖向渗透系数不同,计算结果存在较大误差。
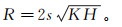 (1)
(1) 式中:R为降落漏斗的影响半径,m;s为水位降深,m;K为渗透系数,m/s;H为含水层厚度,m。
土体的各向异性是一个极为复杂的性质,以往对土体各向异性的考虑大多较为繁琐,所以在实际工程应用中,总会假设土体为各向同性,这在某些特殊的情况下将会造成降落漏斗影响半径存在较大误差。本研究将竖向渗透系数(Kz)与水平渗透系数(Kr)的比值定义为土体的各向异性系数(k), 即k=Kz/Kr,k表示土体的各向异性程度。
Neuman[12-13]曾计算出了各向异性土体的水位降深解,如式(2)所示。
 (2)
(2) 式中:r为地下水位线上任意一点距离排水孔中心在水平方向的距离,m;z为不同的高程观测点,m;t为时间,s;Q为排水孔涌水量,m3/d;T为导水系数,T=KrH,m2/s;J0(x)为零阶第一类贝塞尔函数;x为积分变量;ω0和ωn为中间变量;n为正整数。假设此时排水孔的降水已经趋于稳定,即时间t→∞,ω0(x)和ωn(x)分别按式(3)(4)取值。
 (3)
(3) 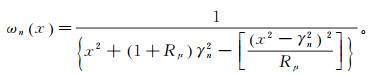 (4)
(4) 式中:Rμ为给水度之比,Rμ=μe/μd, μe为弹性给水度,μd为重力给水度;γ0和γn为求解过程中隐式方程的根,选取李凤玲等[14]对Neuman解中隐式方程的近似解。
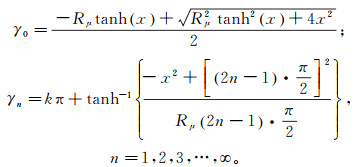
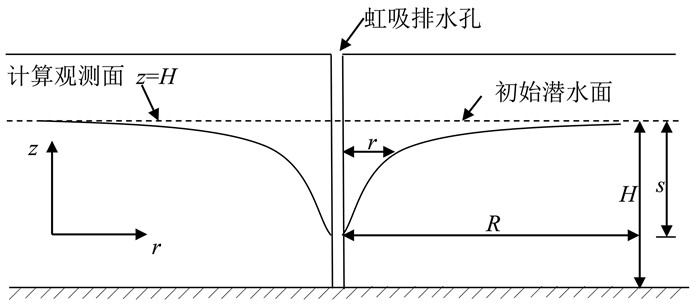
为了计算不同降深下所对应的影响半径,首先令式(2)中r=R,如图 1所示。本次计算中选取潜水层表面,即z=H作为计算观测面。根据以上假定,并利用Matlab将以上各参数代入Neuman降深方程(2)式,化简后可得式(5):
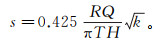 (5)
(5)
|
| 图 1 单孔虹吸排水示意图 Fig. 1 Schematic diagram of single-hole siphon drainage |
|
|
根据(5)式可反算出影响半径R的值:
 (6)
(6) 可知排水井的影响半径不仅与水平渗透系数有关,还与土体各项异性程度有关,在其他参数不变的情况下,地下水位的影响半径与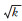
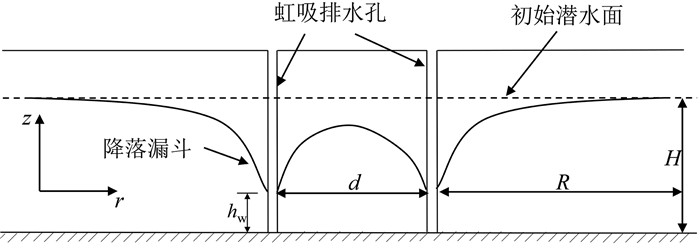
在实际的虹吸排水工程中,一般设置各排水孔间距小于单井抽水的影响半径,从而各排水孔彼此间的降深相互影响,使其排水效果在叠加的作用下进一步增大[15],叠加的实际情况如图 2所示。一般来讲,为了使水位降低明显,虹吸排水钻孔间距越小效果越好,不过涉及经济和可行性的因素,需要确定排水孔间距的最优解。
|
| d.虹吸排水孔间距,m。 图 2 多孔情况下虹吸排水地下水位示意 Fig. 2 Underground water level diagram of siphon drainage under porous conditions |
|
|
考虑各向异性条件,对边坡虹吸排水孔间距进行优化。
排水孔的涌水量可近似为[16]
 (7)
(7) 式中:rw为排水孔半径,m。
将方程(6)与方程(7)联立即可求出相应的流量以及影响半径。此时采用设置拦截比来进行优化设计,假设水力梯度i不变,且在相同的土质中各向渗透系数恒定,则
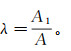 (8)
(8) 式中:λ为拦截比;A1为虹吸管排走的流量所对应的过水断面面积;A为总流量所对应的过水断面面积。
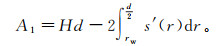 (9)
(9) 式中, s′(r)为井流曲线。s′(r) 引用Dupuit井流方程[16]计算:
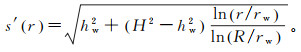 (10)
(10) 式中:hw为排水孔水深,m。
根据以上推导,令
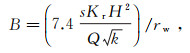
可得
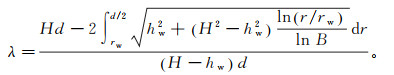 (11)
(11) 式(11)在考虑各向异性的情况下,建立了拦截比λ与排水孔间距d的关系。对于实际工程,在确定拦截比的情况下可以根据该公式来进行合理的虹吸排水孔间距设计。
在实际的工程应用中,一般设定排走50%的水量,即可达到大大提高斜坡稳定性的目的,基于此可求得虹吸排水孔最优间距关系式:
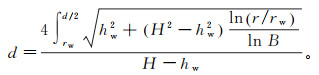 (12)
(12) 甘肃省永靖县黑方台是在黄河Ⅳ级阶地上再次堆积第四系更新统风积黄土而形成的黄土台塬,包括面积较大的黑台和面积较小的方台(图 3、4)。20世纪60年代,刘家峡、八盘峡移民于此,为满足居民的生产生活需要,建成了提水灌溉工程。原本属于旱台的黑方台,在常年大面积灌溉的作用下,台缘处频发滑坡灾害。据不完全统计,该地平均每年发生3~5次滑坡,近30年来累计已发生滑坡100余次,且滑坡规模和频率越来越高,成为近年来甘肃省滑坡灾害最为频繁和严重的地段[17-19]。

|
| a. 研究区位置;b. 黑方台地形图;c. 研究区鸟瞰图。 图 3 黑方台位置及地貌特征 Fig. 3 Location and geomorphic features of Heifangtai area |
|
|
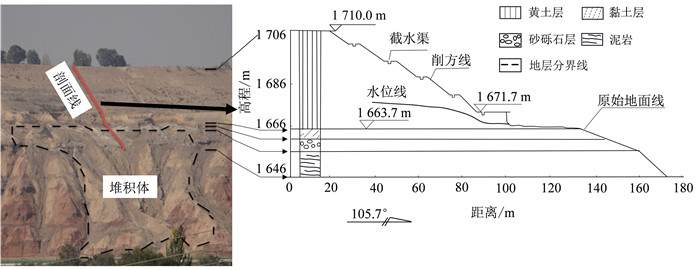
|
| 图 4 黑方台黄土地区剖面图 Fig. 4 Profile of Heifangtai loess area |
|
|
潘攀[20]曾将虹吸排水技术应用到该黄土地区进行滑坡防治的过程中,但其未充分考虑黄土各向异性程度,从而导致虹吸排水间距的确定出现一定的误差,未达到最优的排水效果。
虹吸排水应用位置如图 5所示。该地区上覆风积黄土,以粉粒为主,成分均匀,疏松多孔,具较强湿陷性,坡脚处局部分布全新统已滑塌黄土;中间夹中更新统冲积物,其上部为具有水平层理的浅棕红色薄层粉质黏土、土黄色薄层砂土,下部为砂砾石层,其顶部常有厚1.0~1.3 m的中细砂层,局部夹有青灰色透镜状疏松砂层;下为白垩统河口群,岩性以棕红色、紫红色厚层-块状粉砂质泥岩为主,夹紫灰、紫红色薄层至巨厚层的中细粒砂岩和少量棕红色薄层泥质粉砂岩,偶夹绿灰色薄层粉砂岩。梁燕等[21]对黑方台黄土的各向异性进行了详细的研究,选取各项计算参数如表 1所示。将参数代入式(12)确定最优间距。

|
| 图 5 黑方台地区坡体虹吸排水位置 Fig. 5 Location of slope siphon drainage in Heifangtai area |
|
|
| 竖向渗透系数/(10-7m/s) | 水平渗透系数/(10-7m/s) | 渗透系数之比 | 井径/m | 潜水层厚度/m |
| 21.20 | 3.42 | 6.2 | 0.1 | 20 |
在实际工程中,斜孔排水的效果往往优于竖直孔排水,因此在排水点处将斜孔投影为竖直孔所得计算结果更为安全有效。在拦截比为50%的情况下,计算得影响半径R约为1.0 m,最优排水间距为0.4 m。
2.2 数值模拟与定量分析对比验证 2.2.1 模型建立基于以上理论分析,利用abaqus有限元分析软件采用以点带孔的方法验证0.4 m孔间距排水的有效性,并借助geo-seep计算结果,定量对比其排水量差异。依据研究区域实际地形,建立三维模型如图 6所示,为减小边界效应,设定模型总宽36 m,整个坡体的网格间距设置为4.5 m,排水孔周围网格间距加密为0.1 m,模型的具体形状、尺寸、坡体两端的实际水位情况以及虹吸排水孔的位置布设情况如图 7所示,图 6中5个台阶地的高度均为6 m。
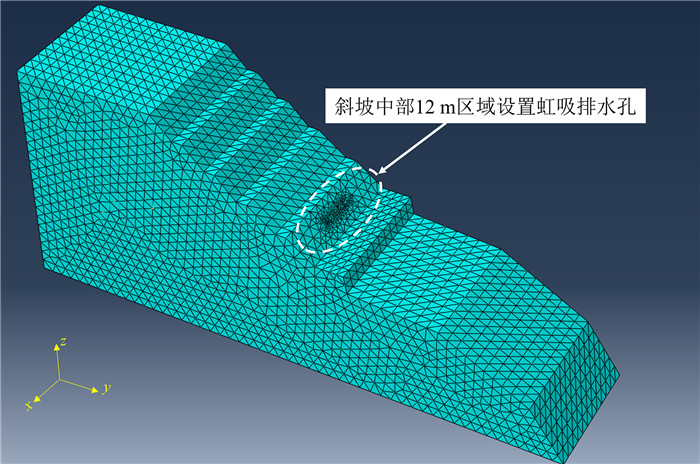
|
| 图 6 研究区三维有限元边坡渗流模型 Fig. 6 3D finite element slope seepage model in the study area |
|
|

|
| 图 7 研究区边坡渗流场计算模型及各排水间距的模拟水位 Fig. 7 Calculation model of seepage field of slope and comparison of water level after drainage at different drain spacing in the study area |
|
|
模拟水位如图 7所示,提取数值模拟结果中汇水量数据发现,在坡体中设置0.4 m间距虹吸排水孔时,钻孔总汇水量为8.7×10-7 m3/s,坡体后部的总流量为17.5×10-7 m3/s,此时坡体排水的拦截比为49.7%,与理论公式中所设定为50%的拦截比基本一致。
在一定的范围内,虹吸排水孔间距越小,数量越多,排水效果越好。但由于群井效应,孔间距减小后会导致单孔排水量降低,减弱坡体整体排水效果。假定在坡宽12 m的间距范围内进行虹吸排水,利用geo-seep进行虹吸排水孔汇水量计算,定义土体竖向渗透系数以及水平渗透系数分别21.20×10-7 m/s和3.42×10-7 m/s,最终绘制出虹吸排水单孔排水量与虹吸排水间距的关系如图 8a所示。忽略次要因素的影响,将单孔汇水量与相应孔数量相乘得到坡体虹吸排水总体汇水量,如图 8b所示。

|
| 图 8 研究区虹吸排水孔间距与单孔汇水量(a)和总体汇水量(b)的关系 Fig. 8 Relationship between the spacing of siphon drainage holes and the amount of single hole drainage (a) and the total amount of drainage (b) in the study area |
|
|
由图 8可知,0.2,0.3,0.4 m间距的虹吸排水情况处于一个水平,超过0.4 m总汇水量将会减小,排水效果变差。当虹吸排水孔间距超过影响半径1.0 m时,尽管单孔排水量继续增加,但总汇水量却急剧下降,故大于影响半径的孔间距是不宜选取的。
在确保其他模拟参数不变的情况下,将土体设置为各向同性,渗透系数取较大数值,发现0.4 m间距下其汇水量为各向异性时的1.60倍,且此时2.0 m排水孔间距的汇水量与各向异性情况下0.4 m孔内汇水量仅相差2%;另保留其他参数不变,渗透系数取较小值,计算发现此时0.4 m间距下其汇水量为各向异性时的0.26倍,说明仅靠减小间距,汇水量不能达到各向异性时的汇水量。
利用geo-studio运用Morgenstern-price方法对坡体进行稳定性分析,如图 9所示,初始状态下坡体稳定性系数为1.068,此时边坡处于临界状态;0.4 m孔间距虹吸排水处理后的稳定性系数为1.182,其远高于初始状态,此时边坡满足稳定性要求。另外,根据图 9可以看到最优间距排水后水位降至坡脚阶地以下,避免了水流侵蚀阶地所导致的流滑破坏[22],满足工程要求。
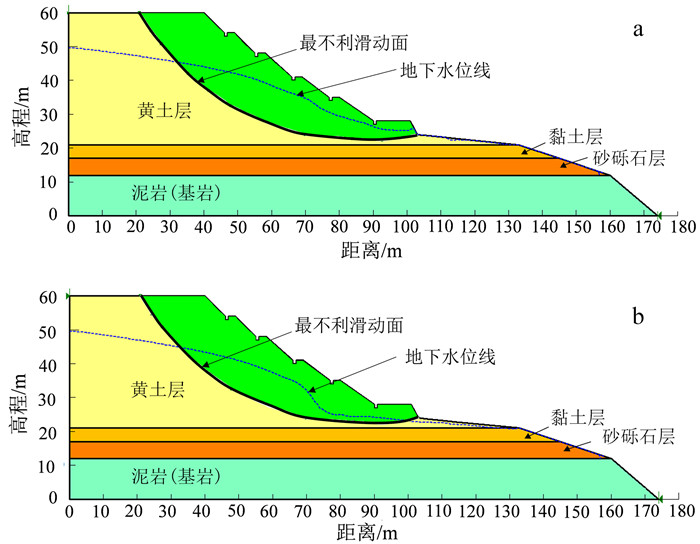
|
| a. 初始水位情况下,稳定性系数为1.068;b. 最优间距排水后,稳定性系数为1.182。 图 9 研究区坡体稳定性分析 Fig. 9 Slope stability analysis in the study area |
|
|
数值模拟及定量分析结果证明了理论公式的正确性,故对于实际工程而言,本文所得的理论公式能为黄土等各向异性土质地区虹吸排水工程中孔间距的确定提供依据。
3 结论1) 验证了各向异性程度是一个不容忽视的影响因素,随着各向异性系数的不断增大,排水孔最优间距逐渐减小。基于Neuman渗流理论,考虑了排水孔间距受降深、渗透系数,以及各向异性程度的影响作用,引用拦截比的概念,推导出一种针对各向异性土质的虹吸排水孔间距理论解。
2) 将虹吸排水孔间距理论解应用至黑方台实际工程,计算出在该地区的最优间距为0.4 m,利用数值模拟验证了该间距下坡体虹吸排水拦截比为49.7%,与理论计算的差值仅为0.3%。
3) 若虹吸排水孔间距大于其单孔降落漏斗半径时,坡体的排水效果会大大减弱。分析结果充分验证了0.4 m间距下,坡体的地下水位以及稳定性均符合工程要求,且与其他间距相比更为有效合理,对于工程的适用性更好。
| [1] |
徐张建, 林在贯, 张茂省. 中国黄土与黄土滑坡[J]. 岩石力学与工程学报, 2007, 26(7): 1297-1312. Xu Zhangjian, Lin Zaiguan, Zhang Maosheng. Loess in China and Loess Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(7): 1297-1312. DOI:10.3321/j.issn:1000-6915.2007.07.001 |
| [2] |
Xu L, Dai F C, Gong Q M, et al. Irrigation-Induced Loess Flow Failure in Heifangtai Platform, North-West China[J]. Environmental Earth Sciences, 2012, 66(6): 1707-1713. DOI:10.1007/s12665-011-0950-y |
| [3] |
Deng L, Fan W, Yin Y, et al. Case Study of a Collapse Investigation of Loess Sites Covered by Very Thick Loess-Paleosol Interbedded Strata[J]. International Journal of Geomechanics, 2018, 18(11): 05018009. DOI:10.1061/(ASCE)GM.1943-5622.0001160 |
| [4] |
王家鼎, 惠泱河. 黑方台台缘灌溉水诱发黄土滑坡群的系统分析[J]. 水土保持通报, 2001, 21(3): 10-12. Wang Jiading, Hui Yanghe. System Analysis of Heifangtai Loess Landslide in Crows Induced by Irrigated Water[J]. Bulletin of Soil and Water Conservation, 2001, 21(3): 10-12. DOI:10.3969/j.issn.1000-288X.2001.03.003 |
| [5] |
陈永珍, 吴斌, 杨帆, 等. 充气截排水渗流与变形耦合数值模拟[J]. 吉林大学学报(地球科学版), 2019, 49(2): 485-492. Chen Yongzhen, Wu Bin, Yang Fan, et al. Coupled Numerical Simulation of Seepage and Deformation of Interceptingand Drainaging Water with Compressed Air[J]. Journal of Jilin University(Earth Science Edition), 2019, 49(2): 485-492. |
| [6] |
熊晓亮, 孙红月, 张世华, 等. 高扬程虹吸保障条件分析与合理管径选择数值模拟[J]. 吉林大学学报(地球科学版), 2014, 44(5): 1595-1601. Xiong Xiaoliang, Sun Hongyue, Zhang Shihua, et al. Analysis of Condition of Ensuring High-Lift Siphon Drainage and Numerical Simulation of Choice of Optimum Diameter[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(5): 1595-1601. |
| [7] |
吴纲, 谢威, 严鑫, 等. 虹吸水流作用下的土柱运动特性及虹吸管道防淤堵措施[J]. 吉林大学学报(地球科学版), 2019, 49(5): 1398-1404. Wu Gang, Xie Wei, Yan Xin, et al. Motion Characteristics of Clay Column Under Action of Siphon Flow and Anti-Clogging Measures[J]. Journal of Jilin University(Earth Science Edition), 2019, 49(5): 1398-1404. |
| [8] |
尚岳全, 蔡岳良, 魏振磊, 等. 滑坡虹吸排水方法[J]. 工程地质学报, 2015, 23(4): 706-711. Shang Yuequan, Cai Yueliang, Wei Zhenlei, et al. Siphon Drainage Method for Landslide Prevention[J]. Journal of Engineering Geology, 2015, 23(4): 706-711. |
| [9] |
Sun H, Wang D, Shang Y, et al. An Improved Siphon Drainage Method for Slope Stabilization[J]. Journal of Mountain Science, 2019, 16(3): 701-713. DOI:10.1007/s11629-018-5171-3 |
| [10] |
吴梦萍, 孙红月, 梅成. 边坡虹吸排水孔间距研究[J]. 自然灾害学报, 2017, 26(2): 40-46. Wu Mengping, Sun Hongyue, Mei Cheng. Analysis of Slope Siphon Drainage Hole Spacing[J]. Journal of Natural Disasters, 2017, 26(2): 40-46. |
| [11] |
任姗姗. 边坡高扬程虹吸排水效果与影响因素研究[D]. 杭州: 浙江大学, 2014: 56. Ren Shanshan. Research on the Effect and Influencing Factors of Slope High-Lift Siphon Drainage[D]. Hangzhou: Zhejiang University, 2014: 56. |
| [12] |
Neuman P S. Theory Flow in Unconfined Aquifers Considering Delayed Response the Water Table[J]. Water Resources Research, 1972, 4(8): 1030-1044. |
| [13] |
Neuman P S. Aquifers Considering Delayed Gravity Response[J]. Water Resources Research, 1974, 2(10): 303-312. |
| [14] |
李凤玲, 朝伦巴根, 高瑞忠. 基于Nueman理论获取潜水含水层系统参数的简化方法[J]. 工程勘察, 2008(4): 33-37. Li Fengling, Chaolun Bagen, Gao Ruizhong. A Simplified Method to Obtain the Parameters of Underwater Aquifer System Based on Nueman Theory[J]. Geotechnical Investigation & Surveying, 2008(4): 33-37. |
| [15] |
宫志强, 田西昭, 刘伟江, 等. 抽出-处理技术抽出污染地下水: 抽出效率及抽出终点[J]. 吉林大学学报(地球科学版), 2020, 50(4): 1139-1150. Gong Zhiqiang, Tian Xizhao, Liu Weijiang, et al. Pumping Treatment Technology to Pump out Contaminated Groundwater: Extraction Efficiency and Extraction Endpoint[J]. Journal of Jilin University(Earth Science Edition), 2020, 50(4): 1139-1150. |
| [16] |
陈崇希. 地下水动力学[M]. 武汉: 中国地质大学出版社, 2011. Chen Chongxi. Underground Water Dynamics[M]. Wuhan: China University of Geosciences Press, 2011. |
| [17] |
Zhang F, Wang G. Effect of Irrigation-Induced Densification on the Post-Failure Behavior of Loess Flowslides Occurring on the Heifangtai Area, Gansu, China[J]. Engineering Geology, 2018, 236: 111-118. DOI:10.1016/j.enggeo.2017.07.010 |
| [18] |
Wen B, Yan Y. Influence of Structure on Shear Characteristics of the Unsaturated Loess in Lanzhou, China[J]. Engineering Geology, 2014, 168: 46-58. DOI:10.1016/j.enggeo.2013.10.023 |
| [19] |
Xu L, Dai F C, Tu X B, et al. Occurrence of Landsliding on Slopes Where Flowsliding Had Previously Occurred: An Investigation in a Loess Platform, North-West China[J]. Catena, 2013, 104: 195-209. DOI:10.1016/j.catena.2012.11.010 |
| [20] |
潘攀. 黑方台滑坡机理及防治对策研究[D]. 杭州: 浙江大学, 2017: 144. Pan Pan. Study on Mechanism and Treatment of Landslide in Heifangtai[D] Hangzhou: Zhejiang University, 2017: 144. |
| [21] |
梁燕, 邢鲜丽, 李同录, 等. 晚更新世黄土渗透性的各向异性及其机制研究[J]. 岩土力学, 2012, 33(5): 1313-1318. Liang Yan, Xing Xianli, Li Tonglu, et al. Study of the Anisotropic Permeability and Mechanism of Q3 Loess[J]. Rock and Soil Mechanics, 2012, 33(5): 1313-1318. DOI:10.3969/j.issn.1000-7598.2012.05.006 |
| [22] |
Pan P, Shang Y, Lue Q, et al. Periodic Recurrence and Scale-Expansion Mechanism of Loess Landslides Caused by Groundwater Seepage and Erosion[J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 1143-1155. DOI:10.1007/s10064-017-1090-8 |



