2. 数学与交叉科学广东普通高校重点实验室(广州大学), 广州 510006
2. Key Laboratory of Mathematics and Interdisciplinary Sciences of Guangdong Higher Education Institutes (Guangzhou University), Guangdong 510006, China
0 引言
成矿元素是成矿系统中最基本的单元,利用其时空分布信息不仅有利于了解地质作用过程产生的物质分异和就位机制,而且可以直接圈定成矿物质富集区,厘定分布范围和边界,为找矿提供直接信息[1-3]。因此,剖析成矿元素分布是研究矿床成因、矿化富集和赋存规律的有效途径之一。由于地质作用过程的长期性,矿化过程往往呈多期次性。成矿事件形成于特定的地质构造环境,不同的成矿期对应于不同成矿事件,而每一次成矿事件都会形成与其相对应的地球化学响应,导致复杂的成矿元素品位变化。从非线性和复杂性理论角度看,成矿过程是一种奇异性地质过程,可在较短的时间或空间范围内发生能量的巨量释放或物质的超常富集和堆积,表现为元素品位空间分布具有自相似嵌套结构,传统的时间序列和统计方法已经无法有效提取隐藏的非线性动力学的相关信息[4-12]。
多重分形是非线性理论的一个重要分支,指在分形结构上由多个标度指数所组成的集合,其谱函数可以描述分形结构上不同的局域条件或分形结构在演化过程中不同层次所导致的特殊结构行为与特征[13]。传统计算多重分形谱函数的方法是配分函数法,但该方法对受趋势影响的非平稳数据的计算结果会出现不正确的现象。多重分形去趋势移动均值(multifractal detrended moving average,MFDMA) 法是有效刻画非平稳序列分形结构的新方法,它是通过去除移动窗口的平均值趋势后进行拟合计算。该方法比配分函数法更为稳健[14],已在金融、环境和物理等领域有较好的应用[15-19]。
斑岩型铜矿床中地质过程及其形成的地质现象是复杂的,在空间上的分布具有明显的不均一性,即便是各种条件相近的斑岩型铜矿床,其矿化的类型、强度、矿化分带特征也均有不同,甚至有些斑岩体中成矿元素品位很高却不能形成矿体。随着斑岩型多金属矿的发现和开采,以及现代分析测试技术的进步,斑岩型矿床成矿复杂性的相关研究越来越深入,对岩浆-成矿作用过程及含矿斑岩的动力学背景的探索也越来越重视[20-22]。
本研究将运用MFDMA法,研究云南普朗斑岩型铜矿床4号勘探线多钻孔Cu元素品位序列的多重分形特征,并探索其对矿化强度的指示作用,为进一步建立区域成矿预测和资源潜力评价模型提供理论支持。
1 理论与方法 1.1 MFDMA算法步骤令长度为N的序列为{xi} (i=1, 2, …, N),多重分形去趋势移动均值法的主要步骤如下[23]。
第1步,计算累积和y(i),构造新的序列:
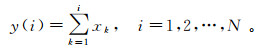 (1)
(1) 第2步,在尺度为s的移动窗口中,计算第i个移动窗口的平均函数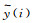
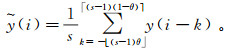 (2)
(2) 式中: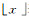
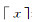
第3步,计算残差序列ε(i):
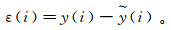 (3)
(3) 第4步,把得到的残差序列根据相等的长度s划分为Ns=int(N/s)(int(·)取整数)个不重叠的区间,再将序列反向分割一次,得到2Ns个区间段。定义第v个子区间的局部波动变量Fv(s):
 (4)
(4) 这里εv(i)=ε(l+i),l=(v-1)s。
第5步,计算q (q为整数)阶全局波动函数Fq(s):
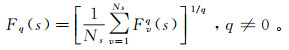 (5)
(5) 当q=0时,
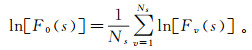 (6)
(6) 第6步, 根据不同的划分长度s,波动函数Fq(s)与s若具有幂律关系,则
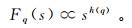 (7)
(7) 式中,h(q)是广义Hurst指数,可通过最小二乘法拟合得到其估计值。h(q)与多重分形质量指数τ(q)相关,可表示为
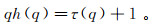 (8)
(8) 根据Legendre变化,得到奇异指数α(q)以及谱函数f(α)满足:
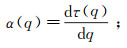 (9)
(9) 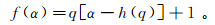 (10)
(10) 多重分形谱α~f(α)形状呈钩或钟罩状,序列不同分布结构的多重分形谱曲线呈不同的形状,对应着不同的物理意义。多重分形谱也称奇异谱,其谱高差为
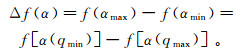 (11)
(11) 多重分形强度可以h(q)的极差表示:
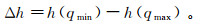 (12)
(12) 多重分形谱宽度及其左右分支可定义为:
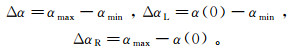 (13)
(13) 式中:α(0)是对应q=0的特殊值;αmax、αmin分别为α(q)的最大值和最小值;qmax、qmin分别为q的最大值和最小值;Δh、Δα及ΔαL和ΔαR分别反映总体及最大、最小测度子集多重分形的强度,值越大分布越不均匀;多重分形谱高差Δf(α)反映最大、最小测度子集数目间的比例,其物理意义是对分形结构上非均质性的量度[13-14]。
1.2 算法检验与参数选择在MFDMA法中θ是确定如何划分子区间位置的参数。利用de Wijs模型,对不同位置参数所估计的广义Hurst指数与其理论值的误差和谱图进行对比分析,探索适合地质数据的位置参数。de Wijs模型是H.J.de Wijs在20世纪50年代研究岩石中矿物分布时提出的,亦称为矿化富集模型。该模型蕴含着多重分形特征,已成为模拟成矿元素或矿物富集分布的经典模型[24]。其一维迭代公式为
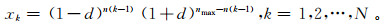 (14)
(14) 式中:n(k)表示数值k在二进制中取1的个数;N=nmax;d(0<d<1)为富集参数。此迭代过程不断重复,使分割的两个子集一个不断相对贫化,而另一个相对富集,d值越大指示相对贫化或富集的程度越高。
令hth(q)表示de Wijs模型Hurst指数的理论值,则MFDMA法估计的广义Hurst指数h(q)与hth(q)的误差记为
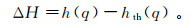 (15)
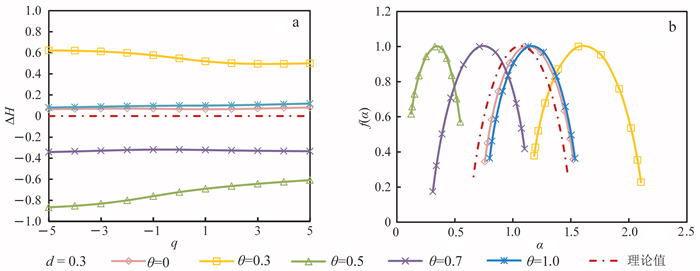
(15) 图 1是de Wijs模型不同位置参数的ΔH和多重谱分形曲线,其中d=0.3,θ为0、0.3、0.5、0.7、1.0,数据容量N=212,尺度范围[5,N/4],q为-5~5,步长0.5。从图 1a中可以看出,θ= 0时ΔH绝对值最小且最接近零,其次为θ=1.0,而θ为0.3,0.5,0.7时误差更大;图 1b中也是θ=0时的谱图最接近理论值,即θ=0时计算结果更可靠,称θ=0时为后向移动平均法(backward detrended moving average,BDMA)。下面的实例分析中我们均选择位置参数θ=0进行计算。
|
| 图 1 不同位置参数的de Wijs序列MFDMA法估计值与理论值对比(a)和多重分形谱(b) Fig. 1 Comparison of estimated value and theoretical value of de Wijs sequence with different position parameters base on MFDMA(a) and the multifractal spectra(b) |
|
|
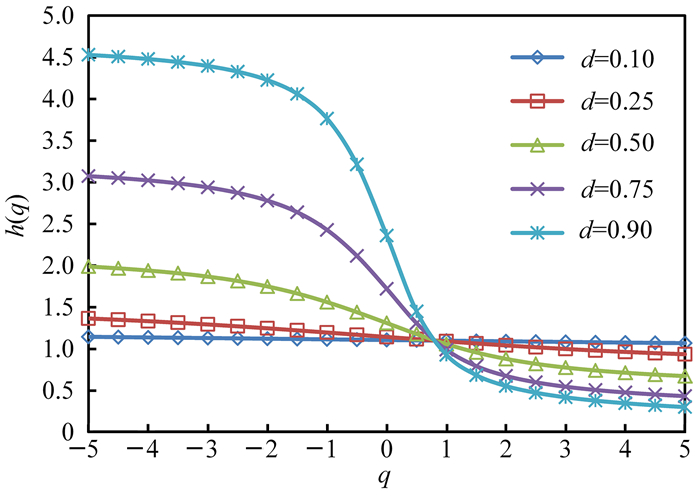
图 2是θ= 0,d为0.10、0.25、0.50、0.75、0.90时h(q)随q变化的曲线,以此检验模型MFDMA法对不同富集参数多重特征识别的有效性。可见不同富集参数de Wijs模型的h(q)对q存在依赖性,且随d的增加h(q)对q的依赖性增强,亦即富集参数增大使奇异性增大。这与地质中成矿元素或矿物富集意义一致,表明MFDMA法能有效识别不同富集参数de Wijs模型的多重分形特征。因此,该方法适用于成矿元素或矿物富集的地质数据。
|
| 图 2 不同富集参数的de Wijs序列h(q)曲线 Fig. 2 h(q) of de Wijs sequences with different enrichment parameters |
|
|
云南普朗矿床是中甸弧内近年发现的规模最大的斑岩型铜矿床,目前已探明普朗铜矿区内铜资源储量达650万t,属义敦-中甸印支期斑岩成矿带,构造上位于义敦岛弧带。其南北断续延伸500余km,介于西侧中咱-中甸陆块与东侧甘孜-理塘蛇绿构造混杂带之间,主要为晚三叠世火山-沉积岩系和印支晚期—燕山期花岗岩基。成矿作用发生于普朗复式斑岩体内,矿化与蚀变相伴生长,同时,由蚀变带中心向外铜矿化逐渐减弱,且斑岩体从中心向外,依次出现钾硅化带—靠外侧的绢英岩化带—外缘的青磐岩化带,矿化呈现出“面型”—“线型”—“稀疏细脉或星点状” [25-30]。
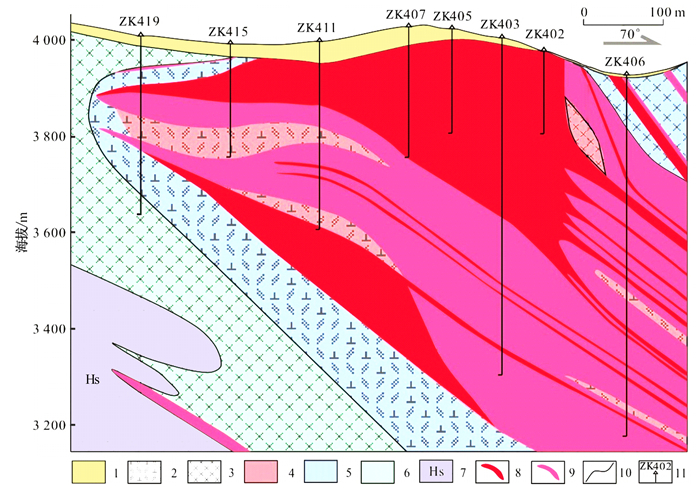
普朗铜矿床的成矿元素Cu品位数据源于云南省地质调查局,采用示波极谱法和碘氟法在云南省地矿局第三地质大队实验室完成测定。本文选取普朗铜矿床4号勘探线上8个钻孔(ZK402、ZK403、ZK405、ZK406、ZK407、ZK411、ZK415、ZK419)的Cu元素为分析对象,采样位置见表 1。ZK402、ZK403、ZK405、ZK407及ZK411位于钾化带中,ZK406与ZK415位于钾化带与绢英岩化带的过渡部位,ZK419主体位于绢英岩化带与青磐岩化带的过渡部位,并且在钻孔的深部揭露了角岩(图 3)。不同蚀变带中,Cu元素品位的分布存在一定的差异性,Cu的边界品位为0.4%,根据元素品位大于边界品位的比例,将钻孔矿化强度分布由弱到强分为3个等级:(Ⅰ)弱矿化区元素品位大于边界品位的比例小于20%,且矿体难以圈定;(Ⅱ)中等矿化区元素品位大于边界品位的比例介于20%~50%之间,矿化区域间断出现;(Ⅲ)强矿化区元素品位大于边界品位的比例大于50%,矿体部分连续。据此4号勘探线上的8个钻孔可分为:ZK406、ZK411、ZK415、ZK419属于弱矿化孔(记为等级Ⅰ),ZK407属于中等矿化孔(记为等级Ⅱ),ZK402、ZK403及ZK405属于强矿化孔(记为等级Ⅲ)。
| 钻孔编号 | [起点: 间距: 终点]/m | 样本数 | 均值/% | 标准差/% | 极差/% | JB统计量 | ADF统计量 | 矿化等级 |
| ZK402 | [3: 1.5: 171] | 113 | 0.594 | 0.207 | 1.100 | 25.93* | -3.401** | Ⅲ |
| ZK 403 | [20: 2: 630] | 306 | 0.532 | 0.324 | 1.150 | 35.42* | -3.170** | Ⅲ |
| ZK 405 | [25:1.5:217] | 129 | 0.696 | 0.231 | 1.260 | 12.41* | -3.028** | Ⅲ |
| ZK 406 | [7: 2: 751] | 373 | 0.270 | 0.156 | 1.990 | 2 47.98* | -6.992 | Ⅰ |
| ZK 407 | [44: 2: 254] | 106 | 0.339 | 0.170 | 0.810 | 43.01* | -3.728 | Ⅱ |
| ZK 411 | [42: 2: 394] | 177 | 0.235 | 0.103 | 0.601 | 34.87* | -7.739 | Ⅰ |
| ZK 415 | [26:1.5:191] | 111 | 0.293 | 0.258 | 0.894 | 15.78* | -3.771 | Ⅰ |
| ZK 419 | [23: 2: 367] | 172 | 0.120 | 0.114 | 0.798 | 504.27* | -7.185 | Ⅰ |
| 注:*表示在5%的水平下具有显著性;* *表示在1%的水平下具有显著性。 | ||||||||
|
| 1. 第四系;2. 石英二长斑岩;3. 石英闪长斑岩;4. 钾化带;5. 绢英岩化带;6. 青磐岩化带;7. 角岩;8. 高品位矿体;9. 低品位矿体;10. 地质界线;11. 钻孔及孔号。据脚注①修编。 图 3 普朗铜矿床4号勘探线的地质剖面图 Fig. 3 Vertical cross-section along exploration Line 4 in Pulang porphyry copper deposit |
|
|
① 云南地质调查局. 云南省迪庆普朗铜矿区勘探地质报告. 昆明:云南地质调查局,2009.
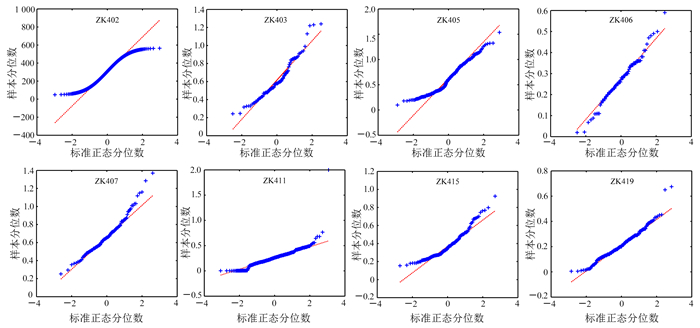
2.2 数据统计分析与检验采用Jarque Beratest (JB test) 和Augmented Dickey-Fuller (ADF) 检验研究区Cu元素钻孔数据的正态性和平稳性,基本统计与检验结果见表 1。在5%的显著水平下,JB统计量均大于对应的临界值5.82,表明Cu元素品位分布拒绝了零假设。图 4是样本分位数与标准正态分位数对比双分位数图,可以看出散点两端都偏离虚实线,结合JB检验和双分位数图可得出云南普朗铜矿床4号勘探线钻孔品位均呈非正态分布。此外,通过平稳性检验,钻孔ZK402、ZK403、ZK405的ADF统计量值均大于1%显著性的临界值-3.49,表明ZK402、ZK403、ZK405品位为非平稳序列,其余钻孔Cu品位的ADF统计量小于临界值,即为平稳序列。因此,基于正态分布假设和平稳序列的传统统计方法就难以准确描述其非线性的复杂特征。
|
| 图 4 样本分位数与标准正态分布分位数对比 Fig. 4 Quantiles of sample data versus standard normal quantiles |
|
|
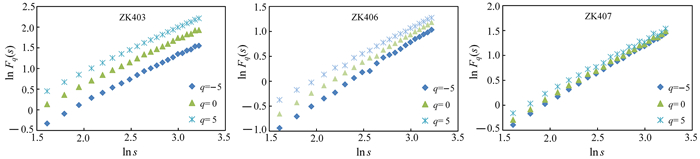
根据公式(1)-(6)计算波动函数Fq(s),其中q=-5~5,步长为0.5。图 5分别是q=-5,0,5时,ZK403、ZK406、ZK407对应的Fq(s)与s的双对数函数图,可以看出ln Fq(s)与ln s具有明显线性相关性,且相关程度较高,其他钻孔也有类似结果。由公式(7),利用最小二乘法估计其斜率,即可得到广义Hurst指数h(q)。
|
| 图 5 ln Fq(s)与ln s散点图 Fig. 5 The ln-ln plot of the fluctuation function Fq(s) versus s for various values of q |
|
|
由公式(8)-(13)计算相应的多重分形参数,其结果见表 2。其中:Δh和Δα是反映多重分形强度的指标,其分形参数值越大可表示多重分形强度越大;ΔαL对应q < 0,ΔαR对应q>0的情况;Δf的大小和符号反映了谱函数的高差及左、右侧开口的分布模式,可指示元素高品位值部分比低品位值部分在不同级次子区域上的平均密度变化差异;W反映多重谱对称性,当W=1时,多重谱图呈钟罩状。可以看到,Δh和Δα均不为零,表明所有钻孔Cu元素品位序列存在多重分形性,但其强度的大小有差异,且W=ΔαR/ΔαL≠1,表示多重谱图为非对称状;强矿化钻孔ZK402、ZK403、ZK405的对应值ΔαL < ΔαR,W>1,Δf>0,而中弱矿钻孔ZK406、ZK407、ZK411、ZK415、ZK419的ΔαL>ΔαR,且W < 1,Δf < 0,表明强矿化钻孔的高品位局部聚集,随着矿化程度的减小多重分形谱图由左钩转变为右钩,即地球化学模式以富集为主转向贫化;a(0)对应奇异谱的峰值,值越大代表分割子集越少,强矿化和弱矿化的a(0)值大于中等矿化,表明中等矿化钻孔元素序列的分布非均匀性大于强矿化和弱矿化钻孔。
| 钻孔号 | Δh | Δα | ΔαL | ΔαR | α(0) | Δf | W | 〈Δhshuf(q)〉 | 矿化等级 |
| ZK402 | 0.082 7 | 0.154 2 | 0.055 9 | 0.098 3 | 1.123 8 | 0.093 8 | 1.760 0 | 0.017 5(0.004 4) | Ⅲ |
| ZK403 | 0.075 5 | 0.122 6 | 0.032 3 | 0.090 3 | 1.112 9 | 0.117 9 | 2.793 2 | 0.048 8(0.005 5) | Ⅲ |
| ZK405 | 0.073 5 | 0.144 3 | 0.060 4 | 0.083 9 | 1.105 3 | 0.039 9 | 1.389 1 | 0.040 5(0.008 4) | Ⅲ |
| ZK406 | 0.207 6 | 0.425 3 | 0.240 9 | 0.184 3 | 1.127 9 | -0.329 8 | 0.765 1 | 0.127 8(0.015 9) | Ⅰ |
| ZK407 | 0.093 4 | 0.174 4 | 0.107 7 | 0.066 7 | 1.085 5 | -0.166 7 | 0.618 7 | 0.041 4(0.005 4) | Ⅱ |
| ZK411 | 0.111 6 | 0.220 4 | 0.110 9 | 0.109 4 | 1.121 6 | -0.054 0 | 0.986 4 | 0.044 0(0.008 0) | Ⅰ |
| ZK415 | 0.115 3 | 0.218 8 | 0.122 2 | 0.096 6 | 1.100 1 | -0.123 6 | 0.790 2 | 0.088 1(0.013 1) | Ⅰ |
| ZK419 | 0.485 8 | 0.715 8 | 0.359 1 | 0.356 7 | 1.213 9 | -0.239 2 | 0.968 3 | 0.345 0(0.057 7) | Ⅰ |
| 注:Δhshuf=h(-5)-h(5);〈Δhshuf(q)〉为hshuf(q)的均值,其后括号内的值对应标准差;W=ΔαR/ΔαL。 | |||||||||
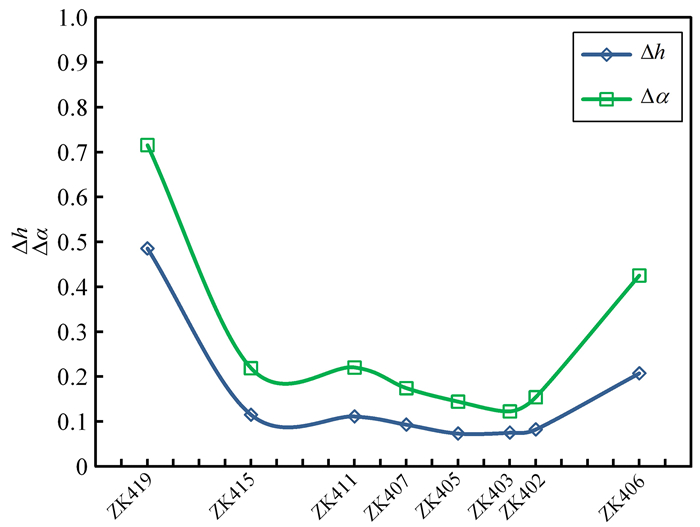
图 6是4号勘探线剖面上按钻孔位置从左到右(ZK419—ZK406)对应Δh和Δα的变化图,从钾化带—绢英岩化带,Δh和Δα整体呈一致的波浪变化趋势,在其内侧(ZK403/ZK405)达到波谷,在外侧与角岩化/青磐岩化带又缓慢增大,ZK419最大,ZK406次之,反映在钾化带与绢英岩化带中,高品位分布相对集中,利于成矿。
|
| 图 6 多重分形参数随钻孔位置变化曲线 Fig. 6 Variation curve of multifractal parameters with borehole location |
|
|
引起成矿元素品位序列的多重分形原因一般有两种:一种是由概率密度函数或厚尾产生的,称为分布多重分形;另一种是由序列的长相关性产生的多重分形,称为相关多重分形[31]。重排前、后的广义Hurst指数分别记为horig(q)和hshuf(q)。对这两种多重分形的区分,可采用数据随机重排前、后广义Hurst指数的变化来识别。如果属纯分布多重分形,则重排后序列的密度分布没有改变,即有horig(q) =hshuf(q);如果属纯相关多重分形,重排后序列的长相关性被毁坏,则有hshuf(q)≈0.5,呈接近完全随机状态。
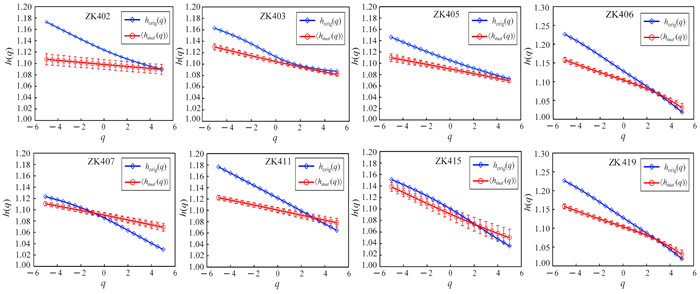
对8个钻孔Cu元素品位序列随机重排20次,图 7是重排前后的广义Hurst指数曲线对比分析,〈hshuf(q)〉是20次重排后hshuf(q)的均值,可以看出所有钻孔的horig(q)和〈hshuf(q)〉均随q的变化单调减少。其中:ZK415的horig(q)与〈hshuf(q)〉最为接近,ZK402、ZK403、ZK405的〈hshuf(q)〉 < horig(q),ZK406、ZK407、ZK411、ZK415、ZK419的〈hshuf(q)〉与horig(q)呈现前段减小后段增大的剪刀叉状,但总体hshuf(q)曲线变得更平缓,且多重谱宽度Δhshuf(q)明显变小(表 2);两条曲线没有完全重叠,表明Cu元素品位的多重分形是由分布概率密度和长相关性共同引起,其多重分形结构主要归于长相关性,其次是概率密度或厚尾。
|
| 图 7 Cu元素的horig(q)与〈Δhshuf(q)〉比较 Fig. 7 Comparison of horig(q) and〈Δhshuf(q)〉of Cu |
|
|
1) 通过矿化富集模型验证了MFDMA法是识别成矿元素多重分形结构的有效方法之一,且当位置参数θ= 0时,计算结果具有较高的可靠性,为进一步地质数据的应用提供了理论依据。
2) 研究发现云南普朗斑岩型铜矿4号勘探线多钻孔的Cu元素品位的分布具有明显多重分形特征,其多重强度和谱函数存在差异,多重分形强度随矿化强度等级减弱而增加。根据剖面上钻孔位置从左到右分析可知,在钾化带—绢英岩化带内侧钻孔多重分形强度低于外侧与角岩化/青磐岩化带,表明在其内侧强矿化钻孔Cu元素品位分布相对均匀聚集,而在外侧与角岩化/青磐岩化带中、弱矿化钻孔Cu元素高品位分布相对分散,显示多重分形特征对矿化强度有指示意义。
3) 利用数据重排技术分析普朗Cu元素品位的多重分形结构来源是由分布概率密度和相关性共同引起,其多重结构主要贡献归于长相关性,其次是分布概率密度或厚尾,这可能是由斑岩型铜矿的硫化、蚀变叠加等控制因素的作用所致。
对研究区成矿元素的多重分形特征及来源与矿化强度指示意义的讨论,有助于查明构造环境对斑岩矿床成矿元素分布特征的影响,揭示成矿元素在成矿系统形成和演化过程中离散与聚集的机制以及时空分布格局,对认识和理解超大型斑岩铜矿成矿体系的复杂现象和形成机理具有较重要科学意义。
致谢: 对提供基础数据的云南省地质调查局表示感谢!
| [1] |
Richards J P, Spell T, Rameh E A, et al. High Sr/Y Magmas Reflect Arcmaturity, High Magmatic Water Content, and Porphyry Cu±Mo±Au Potential: Examples from the Tethyan Arcs of Central and Eastern Iran and Western Pakistan[J]. Economic Geology, 2012, 107(2): 295-332. DOI:10.2113/econgeo.107.2.295 |
| [2] |
赵鹏大. 定量地学方法及应用[M]. 北京: 高等教育出版社, 2004: 1-10. Zhao Pengda. Quantitative Geologic Method and Its Application[M]. Beijing: Higher Education Press, 2004: 1-10. |
| [3] |
成秋明. 地质异常的奇异性度量与隐伏源致矿异常识别[J]. 地球科学: 中国地质大学学报, 2011, 36(2): 307-316. Cheng Qiuming. Singularity Modeling of Geo-Anomalies and Recognition of Anomalies Caused by Buried Sources Earth[J]. Earth Science: Journal of China University of Geosciences, 2011, 36(2): 307-316. |
| [4] |
Cheng Qiuming, Agterberg Frits. Singularity Analysis of Ore-Mineral and Toxic Trace Elements in Stream Sediments[J]. Computers & Geosciences, 2009, 35: 234-244. |
| [5] |
Cheng Qiuming. Multifractal Modelling and Spectrum Analysis: Methods and Applications to Gamma Ray Spectrometer Data from Southwestern Nova Scotia, Canada[J]. Science in China: Series D: Earth Sciences, 2006, 49(3): 283-294. DOI:10.1007/s11430-006-0283-y |
| [6] |
万丽, 刘欢, 杨林, 等. 成矿元素巨量聚集的混沌机制: 斑岩型和构造蚀变岩型矿床例析[J]. 岩石学报, 2015, 31(11): 3455-3465. Wan Li, Liu Huan, Yang Lin, et al. Chaotic Mechanisms of the Ore-Forming Element Accumulation: Case Study of Porphyry and Disseminated-Veinlet Gold Deposits[J]. Acta Petrologica Sinica, 2015, 31(11): 3455-3465. |
| [7] |
Wan Li, Zhu Yongqian, Deng Xiaocheng. Multifractal Characteristics of Gold Grades Series in the Dayingezhuang Deposit, Jiaodong Gold Province, China[J]. Earth Science Informatics, 2015, 8(4): 843-851. DOI:10.1007/s12145-015-0218-2 |
| [8] |
万丽, 邓小成, 王庆飞, 等. MF-DFA方法与成矿元素分布特征: 以山东大尹格庄金矿为例[J]. 中国矿业大学学报, 2012, 41(1): 133-138. Wan Li, Deng Xiaocheng, Wang Qingfei, et al. Method of MF-DFA and Distribution Characteristics of Metallogenic Elements: Examplefrom the Dayingezhuang Gold Deposit, China[J]. Journal of China University of Mining Technolgy, 2012, 41(1): 133-138. |
| [9] |
万丽, 胡序懿, 邓小成. 成矿元素含量序列的近似熵分析及矿化识别[J]. 中国矿业大学学报, 2014, 43(2): 345-350. Wan Li, Hu Xuyi, Deng Xiaocheng. Approximate Entropy Analysis of Metallogenic Element Content Sequences and Identification of Mineral Intensity: A Case Study of Dayingezhuang Gold Deposit[J]. Journal of China University of Mining and Technology, 2014, 43(2): 345-350. |
| [10] |
Deng Jun, Wang Qingfei, Wan Li, et al. Random Difference of the Trace Element Distribution in Skarn and Marbles from Shizishan Orefield, Anhui Province, China[J]. Journal of China University of Geosciences, 2008, 19(4): 319-326. DOI:10.1016/S1002-0705(08)60064-3 |
| [11] |
Deng Jun, Wang Qingfei, Wan Li, et al. Self-Similar Fractal Analysis of Gold Mineralization of Dayingezhuang Disseminated-Veinlet Deposit in Jiaodong Gold Province, China[J]. Journal of Geochemical Exploration, 2009, 102(2): 95-102. DOI:10.1016/j.gexplo.2009.03.003 |
| [12] |
李忠潭, 薛林福, 冉祥金, 等. 基于卷积神经网络的智能找矿预测方法: 以甘肃龙首山地区铜矿为例[J]. 吉林大学学报(地球科学版), 2021, 51. Li Zhongtan, Xue Linfu, Ran Xiangjin, et al. Intelligent Prospect Prediction Method Based on Convolutional Neural Network: A Case Study of Copper Deposits in the Longshoushan Area, Gansu Province[J]. Journal of Jilin University (Earth Science Edition), 2021, 51. DOI:10.13278/j.cnki.jjuese.20210081 |
| [13] |
Turcotte D L. Fractals and Chaos in Geology and Geophysics[M]. Cambridge: Cambridge University Press, 1997: 100-113.
|
| [14] |
Schumann A Y, Kantelhardt J W. Multifractal Moving Average Analysis and Test of Multifractal Model with Tuned Correlations[J]. Physica A: Statistical Mechanics and Its Applications, 2011, 390(14): 2637-2654. DOI:10.1016/j.physa.2011.03.002 |
| [15] |
Xiong Gang, Zhang Shuning, Zhao Huichang. Multifractal Spectrum Distribution Based on Detrending Moving Average[J]. Chaos, Solitons & Fractals, 2014, 65: 97-110. |
| [16] |
Chen Feier, Tian Kang, Ding Xiaoxu, et al. Finite-Size Effect and the Components of Multifractality in Transport Economics Volatility Based on Multifractal Detrending Mmoving Average Method[J]. Physica A, 2016, 462: 1058-1066. DOI:10.1016/j.physa.2016.06.101 |
| [17] |
Zhang Chen, Ni Zhiwei, Ni Liping, et al. Asymmetric Multifractal Detrending Moving Average Analysis in Time Series of PM2.5 Concentration[J]. Physica A, 2016, 457: 322-330. DOI:10.1016/j.physa.2016.03.072 |
| [18] |
Mali Provash, Mukhopadhyay Amitanha, Singh Gurmukh. Multifractal Detrended Mmoving Average Analysis of Particle Density Functions in Relativistic Nuclear Collisions[J]. Physica A, 2016, 450: 323-332. DOI:10.1016/j.physa.2016.01.023 |
| [19] |
张佳佳, 王建, 李研, 等. 黑龙江多宝山-铜山斑岩铜(钼)矿床绿帘石矿物成分特征及其成矿指示意义[J]. 世界地质, 2019, 38(2): 362-377. Zhang Jiajia, Wang Jian, Li Yan, et al. Mineral Composition of Epidote in Duobaoshan-Tongshan Porphyry Cu-Mo Deposit, Heilongjiang and Its Implications for Mineralization[J]. Global Geology, 2019, 38(2): 362-377. DOI:10.3969/j.issn.1004-5589.2019.02.005 |
| [20] |
侯增谦, 杨志明. 中国大陆环境典型斑岩型矿床成矿规律和找矿模型研究进展[J]. 矿床地质, 2012, 31(4): 645-646. Hou Zengqian, Yang Zhiming. Progress in Metallogenic Regularity and Prospecting Models of Typical Porphyry Deposits in Chinese Mainland[J]. Minreal Deposits, 2012, 31(4): 645-646. DOI:10.3969/j.issn.0258-7106.2012.04.001 |
| [21] |
Sun Weidong, Huang Ruifan, Li He, et al. Porphyry Deposits and Oxidized Magmas[J]. Ore Geology Reviews, 2014, 65: 97-131. |
| [22] |
Liang Huaying, Sun Weidong, Su Wenchao, et al. Porphyry Copper-Gold Mineralization at Yulong, China, Promoted by Decreasing Redox Potential During Magnetite Alteration[J]. Economic Geology, 2009, 104: 587-596. DOI:10.2113/gsecongeo.104.4.587 |
| [23] |
Gu Gaofeng, Zhou Weixing. Detrending Moving Average Algorithm for Multifractals[J]. Physical Review E, 2010, 82(1): 011136. DOI:10.1103/PhysRevE.82.011136 |
| [24] |
Agterberg Frits. New Applications of the Model of de Wijs in Regional Geochemistry[J]. Mathemtical Geology, 2007, 39(1): 1-25. DOI:10.1007/s11004-006-9063-7 |
| [25] |
Deng Jun, Wang Qingfei, Li Gongjian, et al. Tethys Tectonic Eevolution and Its Bearing on the Distribution of Important Mineral Deposits in the Sanjiang Region, SW China[J]. Gondwana Research, 2014, 26(2): 419-437. DOI:10.1016/j.gr.2013.08.002 |
| [26] |
Deng Jun, Wang Qingfei, Li Gongjian, et al. Cenozoic Tectono-Magmatic and Metallogenic Processes in the Sanjiang Region, Southwestern China[J]. Earth-Science Reviews, 2014, 138: 268-299. DOI:10.1016/j.earscirev.2014.05.015 |
| [27] |
Deng Jun, Wang Qingfei, Li Gongjian, et al. Structural Control and Genesis of the Oligocene Zhenyuan Orogenic Gold Deposit, SW China[J]. Ore Geology Reviews, 2015, 65: 42-54. DOI:10.1016/j.oregeorev.2014.08.002 |
| [28] |
李文昌, 曾普胜. 云南普朗超大型斑岩铜矿特征及成矿模型[J]. 成都理工大学学报(自然科学版), 2007, 34(4): 436-446. Li Wenchang, Zeng Pusheng. Characteristics and Metallogenic Model of Pulang Superlarge Porphyry Copper Deposit in Yunnan, China[J]. Journal of Chengdu University of Technology (Sciencec & Technology Edition), 2007, 34(4): 436-446. DOI:10.3969/j.issn.1671-9727.2007.04.011 |
| [29] |
李文昌, 刘学龙, 曾普胜, 等. 云南普朗斑岩型铜矿成矿岩体的基本特征[J]. 中国地质, 2011, 38(2): 403-414. Li Wenchang, Liu Xuelong, Zeng Pusheng, et al. The Characteristics of Metallogenic Rock in the Pulang Porphyry Copper Deposit in Yunnan, China[J]. Grology in China, 2011, 38(2): 403-414. DOI:10.3969/j.issn.1000-3657.2011.02.015 |
| [30] |
胡清华, 张世权, 尹静, 等. 中甸普朗斑岩型铜矿床围岩蚀变初步研究[J]. 矿物岩石地球化学通报, 2010, 29(2): 192-201. Hu Qinghua, Zhang Shiquan, Yin Jing, et al. A Study of Wall-Rock Alteration in the Zhongdian Pulang Porphyry Copper Deposit[J]. Bulletin of Minearlogy, Petrology and Geochemistry, 2010, 29(2): 192-201. DOI:10.3969/j.issn.1007-2802.2010.02.012 |
| [31] |
Kantelhardt Jan W, Zschiegner Stephan A, Koscielny-Bunde E, et al. Multifractal Detrended Fluctuation Analysis of Nonstationary Time Series[J]. Physica A, 2002, 316: 87-114. DOI:10.1016/S0378-4371(02)01383-3 |


