2. 中国地质大学(北京)信息工程学院, 北京 100083;
3. 中国石油长庆油田分公司第五采气厂, 西安 750006
2. School of Information Engineering, China University of Geosciences, Beijing 100083, China;
3. Fifth Gas Production Plant of PetroChina Changqing Oilfield Company, Xi'an 750006, China
0 引言
岩性识别是储层评价的重要工作之一,也是油藏描述、实时钻井监控及储层参数求解的基础。传统的岩性识别方法主要有岩屑录井、钻井取心及测井资料解释等技术,对录井质量的依赖程度较高[1],识别精度与效率低,泛化能力差。随着测井技术与计算机技术的迅速发展,将测井资料与计算机技术相结合来开展岩性研究已成为岩性识别的有效手段[2]。
梯度提升决策树(gradient boosting decision tree,GBDT)是一个基于决策树的集成学习框架,其首先通过不断在先前模型损失函数梯度下降的方向上构建新的模型,使得决策模型不断改进,然后将所有树的结论进行累加作为最终的预测输出[3]。针对GBDT算法训练速度慢、时间复杂度高和难以并行化等缺点,XGBoost算法和LightGBM算法对其进行了相应改进。
XGBoost算法的改进措施:自动利用CPU的多线程进行并行运算,提高了结点分裂的效率;损失函数采用二阶泰勒展开,具有准确率高、不易过拟合和可扩展性等特点[4];与GBDT算法相比,XGBoost算法不仅支持分类与回归树(classifi-cation and regression tree,CART)作为基分类器,还支持线性分类器;在损失函数中加入了正则项以控制模型的复杂度,提高了模型的泛化能力。
LightGBM算法采用了带深度限制的Leaf-wise叶子生长策略、histogram优化算法以及直方图作差加速等技术,具有更快的训练速度和更低的计算代价,而且支持并行学习,可以快速地处理海量数据。
在苏里格气田苏东41-33区块测井数据上使用XGBoost算法和LightGBM算法进行测试,并与K近邻分类器(K-nearest neighbor,KNN)、朴素贝叶斯和支持向量机等传统机器学习算法所得结果进行对比,以观察该方法对识别精度和效率的影响。
1 算法原理 1.1 集成学习和GBDT集成学习是一种联合多个学习器进行协同决策的机器学习方法。集成学习的思想是使用一定的规则生成多个弱分类器,并采用某种集成策略进行组合,最后综合判断得出预测结果。
Boosting算法是集成学习中最具代表性的方法之一,其核心思想[5]是:在建模过程中不断地改变错分样本的权值,以便后续分类器更加关注上一轮分类器难以区分的样本;增加误差率低的弱分类器的权值,使其在表决中起较大的作用。
GBDT算法是斯坦福大学教授Friedman[6]于2001年提出的一种决策树与Boosting方法相结合的算法。它将当前模型的损失函数负梯度值作为残差的近似值拟合回归树[6-7],并通过加法模型将各次迭代生成的回归树线性进行组合得到最终的分类器。GBDT算法的预测精度高、鲁棒性强,可以灵活处理各种类型的数据,并在一定程度上避免了过拟合问题。
假设Τ={(x1, y1), (x2, y2), …, (xN, yN)}为输入训练数据集,x={x1,x2,…, xN}为样本属性集合,y={y1,y2,…, yN}为样本标记集合,N为样本数目;f(x)为目标函数, L为损失函数, 则梯度提升(gradient boosting)算法的具体流程如下。
1) 对f(x)进行初始化:
 (1)
(1) 式中: c为常数项; yi为y中的一个元素。
2) 对m=1, 2, …, M(M为决策树的棵数),循环进行步骤①②③:
① 计算样本i的残差rmi,
 (2)
(2) 式中,fm-1(x)为第m-1棵决策树。
② 对rmi拟合1棵回归树,得到第m棵树第j个节点的叶子节点区域Rmj, j=1, 2, …, J(J为叶子结点的数目)。
③ 计算Rmj上固定的输出值cmj,
 (3)
(3) 3) 更新回归树:
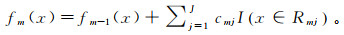 (4)
(4) 式中,I(x)为指示函数。
4) 得到最终的分类模型:
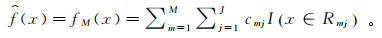 (5)
(5) XGBoost算法是针对梯度提升决策树算法GBDT的改进型集成学习算法[8],它采用了GBDT的回归树生成算法和梯度提升思想,并在很多方面进行了改进。
对于样本属性集合x={x1,x2,…, xN}和样本标记集合y={y1,y2,…, yN},XGBoost算法使用前向分布算法,学习到包含K棵回归树的加法模型
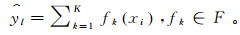 (6)
(6) 式中:K为回归树的棵数;f为回归树模型;F对应回归树组成的函数空间[9]。
带正则项的目标函数计算公式为:
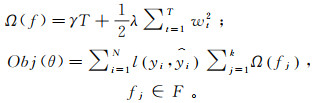 (7)
(7) 式中:T为叶子结点的数目;wt为第t个叶子结点的权重;γ和λ为正则化系数;目标函数Obj(θ)为损失值与正则项乘积的累加和,θ为函数的参数;l(yi, ŷi)为预测值与真实值之间的误差;∑j=1kΩ (fj)由前k棵树的正则项相加而来的。由于XGBoost又是前向分布算法,所以ŷi(t)可以写成
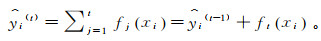 (8)
(8) 在进行第t次迭代时,将前t-1次迭代的正则项看成一个常数,通过泰勒公式近似目标函数,进行二阶泰勒展开,因此目标函数可以改写为
 (9)
(9) 式中: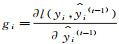
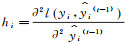
由于在第t次迭代时,l(yi, ŷi(t-1))是一个常数,因此
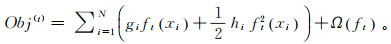 (10)
(10) 所以,目标函数只依赖于前t-1棵树组成的学习模型预测误差的一阶导数和二阶导数。
每个叶子节点j上的样本集合Ij={i|q(xi=j)},即
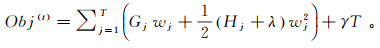 (11)
(11) 式中:Gj=∑i∈Ijgi;Hj=∑i∈Ijhi。对目标函数进行优化,计算第t次迭代时使得目标函数最小的叶子节点的权重w,对w进行求导,使导数为0,得
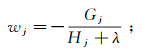
代入目标函数得
 (12)
(12) XGBoost算法在进行节点分裂时,从根节点开始,递归地选择树结构的最优特征,将目标函数值下降最大的点作为切分点,假设IL和IR是分割后左节点和右节点的样本集合,信息增益G如下:
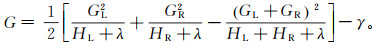 (14)
(14) 式中:GL和GR为分裂后左子节点和右子节点目标函数的二阶导数之和;HL和HR为分裂后左子节点和右子节点目标函数的一阶导数之和。每次选择信息增益下降最大的点作为切分点,对树进行分裂。
XGBoost算法的主要优势有:
1) XGBoost算法对损失函数进行二阶泰勒展开,同时用到了一阶和二阶导数信息,在一定程度上提高了预测精度。
2) XGBoost算法除了以CART树作为基学习器,还支持线性分类器。
3) 损失函数中加入了正则项,以控制模型的复杂度,提高泛化能力。
4) XGBoost算法对数据做了预排序并将其保存为block结构,使得各个特征的增益计算可以开多线程进行,充分利用了多核CPU的并行计算优势,提高了分类的精度和速度。
5) XGBoost算法还可以通过统计得到特征变量的重要性及排序,这为高维数据的数据降维提供了一种新的思路。
1.3 LightGBM算法LightGBM算法是一个基于决策树算法的梯度提升框架[9],具有更快的训练效率、更低的内存占用率和更高的预测准确率,而且支持高效的并行训练,可以快速地处理规模庞大的数据。
如图 1所示,LightGBM算法采用了直方图优化算法,其基本思想是先把连续的浮点型数据划分到n个互相独立的区间内,同时构造一个宽度为n的直方图。
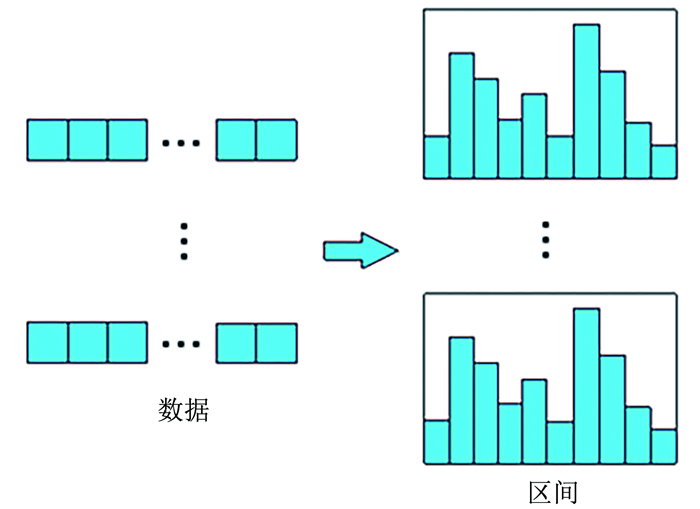
|
| 图 1 直方图优化 Fig. 1 Histogram optimization |
|
|
直方图的每个区间内包含了两类信息,分别是每个区间中的样本梯度之和与每个区间中的样本数量。
在数据遍历时,把离散后的值作为索引在直方图的每个区间中累积统计量,然后在离散值上遍历寻找最优的分割点[10]。在计算代价上,XGBoost算法的预排序策略需要在每遍历一个特征值时就计算一次分裂增益,而采用直方图优化算法则只需计算n次,可以减小储存成本和计算成本。
大多数GBDT工具使用Level-wise (按层生长) 的决策树生长策略,但并非所有的结点在分裂后都会产生预期的信息增益,将全部结点进行分裂会导致更高的计算成本和时间复杂度。
LightGBM算法采用了一种带深度限制的Leaf-wise的叶子生长策略,在每次分裂前遍历所有叶子结点,选择其中信息增益最大的结点进行生长。但是Leaf-wise策略可能会生成较高的树,可以通过控制树的高度和每个叶子结点的最小数目来减少过拟合。在分裂次数相同的情况下,Leaf-wise策略的预测精度更高,收敛速度更快。
此外,LightGBM算法还采用了直方图作差技术进一步提升运行效率。一个叶子的直方图可以由其父结点和兄弟结点的直方图作差得到。在每次结点分裂时,只需计算具有较少样本的子结点的直方图,通过作差的方式即可获得其兄弟结点的直方图,在速度上可以提升一倍。
2 实验数据及环境 2.1 实验数据如图 2所示,研究区为苏里格气田苏东41-33区块,位于鄂尔多斯盆地苏里格中区与东区的交界处,该地区碳酸盐岩储层受岩溶古地貌、沉积、成岩等因素影响,普遍具有渗透率低、非均质性强、砂体分布连续性差等特点[11]。
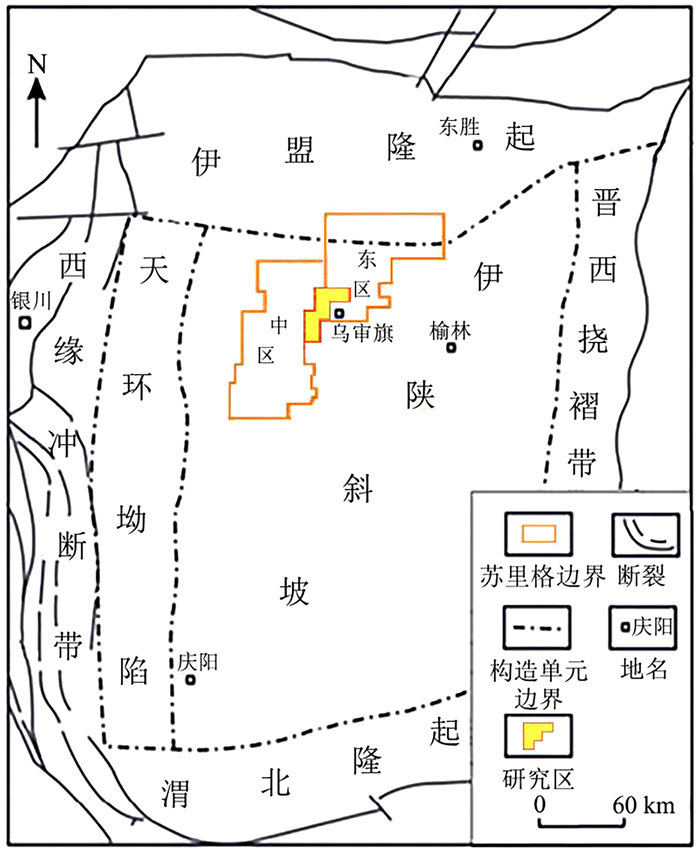
|
| 图 2 鄂尔多斯盆地区域构造及研究区地理位置图 Fig. 2 Ordos basin regional structure and location map of the study area |
|
|
根据测井和录井参数资料分析,该地区主要发育石灰岩、白云质灰岩、泥质灰岩、白云岩、灰质白云岩、泥质白云岩等6种岩石类型。研究区碳酸盐岩储层岩性成分的复杂性和各向异性给岩性解释带来很大困难,因此针对复杂碳酸盐岩进行的岩性识别是研究区储层评价的关键。
对原始的测井资料进行离散化处理。使用隔点取样的方法将连续的测井曲线转化为离散的样本点。即先在深度上每间隔0.1 m选取该点的各项测井参数生成一个样本,然后组成实验数据集。选取该区块下49-13、42-12、44-7号井的测井资料生成训练数据,共计3 122个样本;选取70-06号井的测井资料生成测试数据,共计1 095个样本。训练样本与测试样本的数目比例约为3∶1。
针对研究区块储层特征,以测井资料中已知岩性地层的数据为基础,根据行业标准优选出6个岩性区分度较好的属性特征,分别是声波时差(AC)、自然伽马(GR)、补偿中子(CNL)、密度(DEN)、光电吸收截面指数(PE)和深侧向电阻率(RLLD)。实验使用优选出的6种属性特征进行岩性识别。在数据预处理方面,由于RLLD的属性值过大,因此其值取关于10的对数。
2.2 实验环境机器配置:处理器为2.3 GHz的Intel Core i5-8300H CPU,内存为8 GB,显示适配器为NVIDIA GeForce GTX 1050 Ti。
软件环境:64位Windows 10操作系统,开发平台为Python 3.7+JetBrains PyCharm。
2.3 测井岩性识别交会图交会图法是一种常用的测井资料解释技术[12],通过把测井数据在平面图上两两交会,反映出不同类型的岩性在属性变量空间上的分布区域、形态[13],直观展现了不同属性组合的特征空间对于测井数据岩性的区分能力。
如图 3所示,将不同岩性的6种测井属性值进行交会,分析岩性与测井属性的变化规律。GR和RLLD的特征组合明显区分出了含泥质岩和其他岩性[14],体现了泥质岩性GR值较高的特点;AC和CNL的特征组合对灰岩和白云岩有一定的区分度,但在部分岩性上的重叠区域较多;依据PE和DEN构建的特征空间,将灰岩和白云岩映射在不同区域,具有较好的岩性区分度。
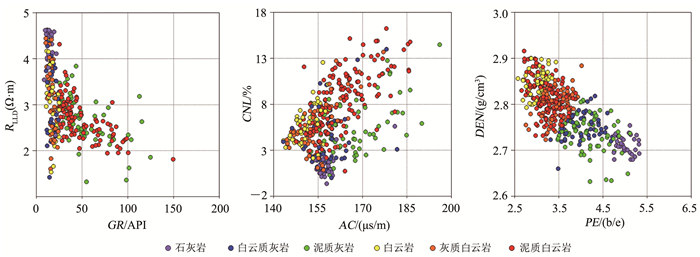
|
| 图 3 测井变量交会图 Fig. 3 Intersection diagram of logging variable |
|
|
首先,对XGBoost算法和LightGBM算法进行参数寻优,确定最优参数组合。由于两种算法都是由若干棵决策树组成的,因此分类正确率与决策树的棵数呈正相关关系。为了提高效率,在其他参数保持不变的情况下,寻找使正确率达到收敛的最优迭代次数。
实验发现, XGBoost算法和LightGBM算法的岩性识别正确率分别在200次和1 000次迭代后不再发生明显变化,基本趋于稳定[15]。因此,固定XGBoost算法和LightGBM算法的迭代次数分别为200和1 000次,尝试采用不同的树的高度,并观察树的高度对分类精度的影响。当树的高度值分别为1、3、5、7时,随着迭代次数的增加,两种算法的分类正确率变化曲线如图 4所示。当树的高度的值为1时,由于树的结构过于简单,两种算法分类正确率曲线收敛的速度较慢,振荡幅度较大。在迭代初期,两种算法的分类正确率较低;随着树的高度值的增加,两种算法分类正确率增长的速度加快,说明预测准确性增高,模型更快达到收敛。由图 4可见,当树的高度的值设置为7时,两种算法的分类性能最优。
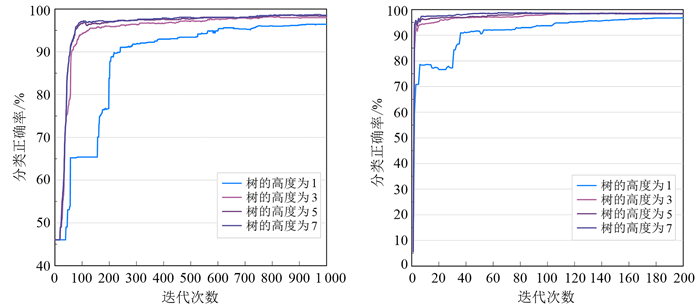
|
| a.XGBoost算法;b.LightGBM算法。 图 4 不同树高度时两种算法的分类正确率 Fig. 4 Classification accuracy of the two algorithms at different tree heights |
|
|
在确定了最优的迭代次数和树的高度之后,采用网格搜索(Grid SearchCV)的方法[16],在指定的参数调整范围内,按步长依次调整两种算法的其他参数。使用调整后的参数训练分类器,确定在测试集上效果最优的参数组合作为最终的参数取值。XGBoost算法与LightGBM算法的主要参数、调整范围及步长如表 1和表 2所示。
| 参数 | 调整范围 | 最优值 | 步长 |
| 迭代次数 | 1~200 | 200 | 1 |
| 树的高度 | 1~7 | 7 | 2 |
| 学习率 | 0.05~0.50 | 0.05 | 0.05 |
| 训练样本占整体样本数目的比例 | 0.50~0.90 | 0.85 | 0.05 |
| 每次迭代时选取的特征比例 | 0.50~0.90 | 0.85 | 0.05 |
| 最小叶子节点样本权重之和 | 1~5 | 3 | 2 |
| 权重的L2正则项 | 0~5 | 1 | 1 |
| 参数 | 调整范围 | 最优值 | 步长 |
| 迭代次数 | 1~1 000 | 1 000 | 1 |
| 树的高度 | 1~7 | 7 | 2 |
| 学习率 | 0.01~0.10 | 0.01 | 0.01 |
| 每棵树的叶子数目 | 32~256 | 256 | 32 |
| 每次迭代选用的数据比例 | 0.6~1.0 | 0.8 | 0.05 |
| 每次迭代随机选取的特征比例 | 0.6~1.0 | 0.8 | 0.05 |
| L1正则化系数 | 0~0.3 | 0.1 | 0.05 |
| L2正则化系数 | 0~0.3 | 0.1 | 0.05 |
当学习率的值减小时,模型的预测准确性升高,但模型收敛所需的时间也随之增加。在XGBoost算法和LightGBM算法中,适当缩减训练样本所占的比例和每次迭代选取的特征比例,可以有效地减少过拟合。在XGBoost算法中,最小叶子节点样本权重之和的值过小时,就会出现一个叶子结点仅包含单个样本的情况,很容易过拟合。同时,对正则项中的惩罚系数lambda进行调整,也可以有效减少过拟合。
通过参数调整之后,确定XGBoost算法的最优参数组合,见表 1,LightGBM算法的最优参数组合见表 2。
3.2 特征重要性排序使用XGBoost和LightGBM建模过程中的信息增益指标作为特征变量的重要性得分,用于描述每个特征变量对模型的贡献程度。进行特征变量的重要性排序,有利于判断哪些特征变量对岩性识别的影响更为显著[17]。
图 5为基于XGBoost和LightGBM算法得出的特征重要性排序。两种算法得出的结果一致,特征变量的重要性得分由高到低依次为:PE、DEN、GR、AC、CNL、RLLD。由图 5可知,PE、DEN和GR的特征重要性得分排在前3位,对岩性识别的影响比较显著。当只使用这3个特征进行建模时,两种算法的岩性识别准确率均达到了98.26%,与基于全波段得到的准确率相差不大。因此,移除一些重要性得分较低的特征,可以在最大限度地保持分类精度的同时,缩减数据规模,提高岩性识别的效率。
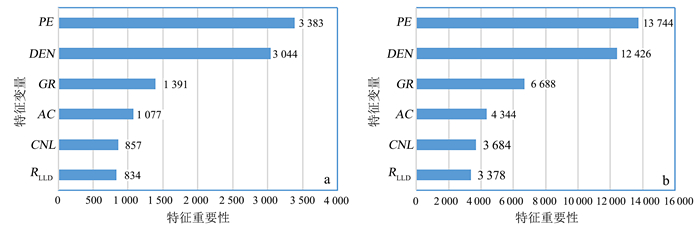
|
| a.XGBoost算法;b.LightGBM算法。 图 5 两种算法的特征重要性 Fig. 5 Feature importance of two algorithms |
|
|
图 6是基于XGBoost算法和LightGBM算法得到的70-06号井的岩性识别结果。与钻录井岩心得到的结果进行对比,发现两种算法识别结果与测井、录井的岩性解释结论几乎一致,仅存在极少的误判现象,岩性识别准确率较高。
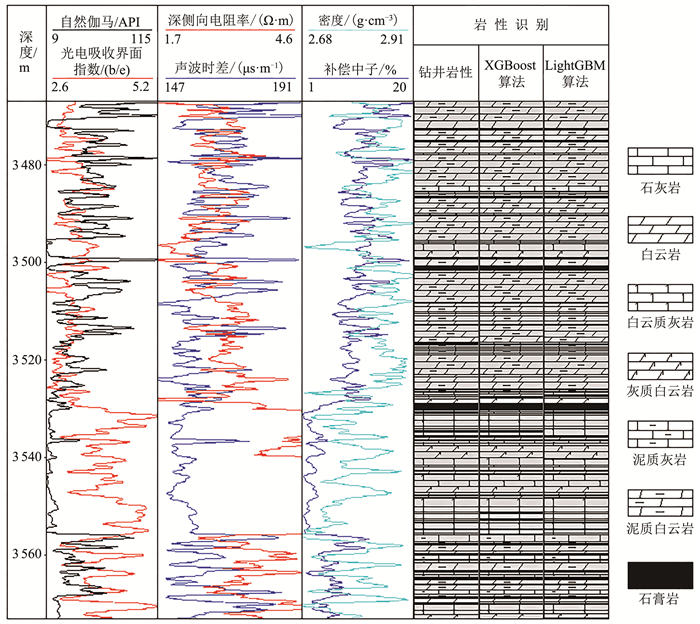
|
| 图 6 研究区70-06号井岩性识别结果 Fig. 6 Lithology identification results of Well 70-06 in the study area |
|
|
为评价XGBoost算法和LightGBM算法的预测性能,同时采用传统机器学习算法(如KNN、朴素贝叶斯和支持向量机等)和GBDT算法进行预测,并将预测结果与基于XGBoost和LightGBM模型的预测结果在预测精度和时间代价等指标上进行比较。不同模型的预测结果对比如表 3所示。
| 模型名称 | KNN | 朴素贝叶斯 | 决策树 | 支持向量机 | 随机森林 | GBDT | XGBoost | LightGBM |
| 识别准确率/% | 78.45 | 74.43 | 79.54 | 78.72 | 96.80 | 79.73 | 98.90 | 98.72 |
| 训练耗时/s | 0.01 | 0.01 | 0.01 | 0.32 | 0.05 | 1.61 | 1.82 | 2.68 |
| 预测耗时/s | 0.04 | 0.01 | 0.01 | 0.03 | 0.01 | 0.01 | 0.01 | 0.10 |
从表 3可以看出:基于KNN、朴素贝叶斯和支持向量机等传统算法的岩性识别准确率均较低,分别为78.45%、74.43%和78.72%;采用GBDT算法的识别准确率为79.73%,仅略高于KNN等算法;而基于XGBoost算法和LightGBM算法的识别准确率分别达到了98.90%和98.72%,远高于传统算法。
在预测精度上,GBDT算法的优化效果不明显,并未达到预期的效果;而XGBoost算法和LightGBM算法在识别准确率上有了较大幅度的提升,取得了良好的识别效果。在时间代价上,XGBoost算法和LightGBM算法需要迭代地构造决策树作为基学习器,并将其进行线性组合成最终分类模型,因此在训练和建模过程上耗时较多。但是XGBoost算法和LightGBM算法采取了并行运算和直方图作差加速等措施,因此并不会造成太大的时间代价,基本可以在提升分类精度的同时,保证模型的运行效率。
4 实验结果分析在分类过程中,当各类别的样本数量分布不均衡,即某些类别的样本数远小于其他类别时,将会严重影响模型的分类精度。在实验数据集中,泥质含量较高的泥质白云岩和泥质灰岩的样本数目占总体的52.88%,而石灰岩所占的比例仅有5.66%。样本分布的不均衡,给岩性识别造成了一定的困难。
如表 4所示,计算得出每种岩性基于不同算法的召回率[18],对不同模型得出的岩性识别结果进行分析。基于KNN和支持向量机等传统机器学习算法,白云岩和灰质白云岩的召回率只有42.00%和67.00%左右,白云质灰岩的召回率也仅有78.00%左右。实验结果表明,对于这种样本分布不均衡的数据,传统算法表现出一定的局限性,识别效果较差。
| % | |||||||||||||||||||||||||||||
| 岩性类型 | KNN | 朴素贝叶斯 | 决策树 | 支持向量机 | 随机森林 | GBDT | XGBoost | LightGBM | |||||||||||||||||||||
| 石灰岩 | 96.77 | 80.65 | 100.00 | 91.94 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||||||||||||
| 白云质灰岩 | 80.49 | 62.20 | 83.54 | 77.44 | 93.29 | 92.68 | 98.78 | 98.78 | |||||||||||||||||||||
| 泥质灰岩 | 96.00 | 92.00 | 98.67 | 97.33 | 100.00 | 100.00 | 100.00 | 100.00 | |||||||||||||||||||||
| 白云岩 | 42.86 | 55.00 | 39.29 | 40.71 | 91.43 | 94.29 | 94.29 | 93.57 | |||||||||||||||||||||
| 灰质白云岩 | 68.00 | 60.00 | 61.33 | 66.67 | 97.33 | 99.33 | 99.33 | 98.00 | |||||||||||||||||||||
| 泥质白云岩 | 85.91 | 84.72 | 89.29 | 88.89 | 99.60 | 99.80 | 99.80 | 100.00 | |||||||||||||||||||||
从表 5可以看出,XGBoost算法和LightGBM算法对白云岩的召回率分别达到了94.29%和93.57%,对灰质白云岩的召回率分别达到了99.33%和98.00%。相比传统机器学习算法,几乎每种岩性的识别准确率都有了显著提升[19],LightGBM算法在泥质含量较高的石灰岩、泥质灰岩和泥质白云岩上的识别准确率达到了100.00%。
| 岩性类型 | 样本数目 | 召回率/% | |||||
| 石灰岩 | 白云质灰岩 | 泥质灰岩 | 白云岩 | 灰质白云岩 | 泥质白云岩 | ||
| 62 | 164 | 75 | 140 | 150 | 504 | ||
| 石灰岩 | 62/62 | 0/0 | 0/0 | 0/0 | 0/0 | 0/0 | 100.00/100.00 |
| 白云质灰岩 | 0/0 | 162/162 | 0/0 | 0/0 | 2/2 | 0/0 | 98.78/98.78 |
| 泥质灰岩 | 0/0 | 0/0 | 75/75 | 0/0 | 0/0 | 0/0 | 100.00/100.00 |
| 白云岩 | 0/0 | 0/0 | 0/0 | 132/131 | 8/9 | 0/0 | 94.29/93.57 |
| 灰质白云岩 | 0/0 | 1/3 | 0/0 | 0/0 | 149/147 | 0/0 | 99.33/98.00 |
| 泥质白云岩 | 0/0 | 0/0 | 0/0 | 0/0 | 1/0 | 503/504 | 99.80/100.00 |
| 准确率/% | 100.00/100.00 | 99.39/98.18 | 100.00/100.00 | 100.00/100.00 | 93.12/93.04 | 100.00/100.00 | 98.90/98.72 |
| 注:表中分式代表XGBoost算法/LightGBM算法。 | |||||||
以上结果表明,本文所提出的梯度提升模型对于分类器具有一定的优化作用[20],提高了岩性识别的准确性,即使在不均衡数据上也可以取得较好的识别效果。
5 结语1) XGBoost算法和LightGBM算法的识别准确率和迭代次数呈正相关关系,需要确定使得算法收敛的最小迭代次数,以提高识别效率。适当减小训练的样本比例和特征比例,可以有效地减少过拟合。
2) 在建模过程中,根据信息增益进行特征变量重要性排序,通过移除重要性得分较低的特征变量,可以实现数据降维。
3) 与常用的机器学习算法相比,XGBoost算法和LightGBM算法在样本分布不均衡的数据上也可以取得较好的预测效果,是一种有效的复杂岩性识别方法。
| [1] |
马峥, 张春雷, 高世臣. 主成分分析与模糊识别在岩性识别中的应用[J]. 岩性油气藏, 2017, 29(5): 127-133. Ma Zheng, Zhang Chunlei, Gao Shichen. Lithology Identification Based on Principal Component Analysis and Fuzzy Recognition[J]. Lithologic Reservoirs, 2017, 29(5): 127-133. DOI:10.3969/j.issn.1673-8926.2017.05.015 |
| [2] |
叶涛, 韦阿娟, 黄志, 等. 基于主成分分析法与Bayes判别法组合应用的火山岩岩性定量识别: 以渤海海域中生界为例[J]. 吉林大学学报(地球科学版), 2019, 49(3): 873-880. Ye Tao, Wei Ajuan, Huang Zhi, et al. Quantitative Identification of Volcanic Lithology Based on Comprehensive Principal Component Analysis and Bayes Discriminant Method: A Case Study of Mesozoic in Bohai Bay[J]. Journal of Jilin University(Earth Science Edition), 2019, 49(3): 873-880. |
| [3] |
韩启迪, 张小桐, 申维. 基于梯度提升决策树(GBDT)算法的岩性识别技术[J]. 矿物岩石地球化学通报, 2018, 37(6): 1173-1180. Han Qidi, Zhang Xiaotong, Shen Wei. Lithology Identification Technology Based on Gradient Boosting Decision Tree (GBDT) Algorithm[J]. Bulletin of Mineralogy, Petrology and Geochemistry, 2018, 37(6): 1173-1180. |
| [4] |
叶倩怡, 饶泓, 姬名书. 基于Xgboost的商业销售预测[J]. 南昌大学学报(理科版), 2017, 41(3): 275-281. Ye Qianyi, Rao Hong, Ji Mingshu. Sales Prediction of Stores Based on Xgboost Algorithm[J]. Journal of Nanchang University (Natural Science), 2017, 41(3): 275-281. DOI:10.3969/j.issn.1006-0464.2017.03.015 |
| [5] |
曹莹, 苗启广, 刘家辰, 等. AdaBoost算法研究进展与展望[J]. 自动化学报, 2013, 39(6): 745-758. Cao Ying, Miao Qiguang, Liu Jiachen, et al. Advance and Prospects of Ada Boost Algorithm[J]. Acta Automatica Sinica, 2013, 39(6): 745-758. |
| [6] |
Friedman J H. Greedy Function Approximation: Gradient Boosting Machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. DOI:10.1214/aos/1013203450 |
| [7] |
王华勇, 杨超, 唐华. 基于LightGBM改进的GBDT短期负荷预测研究[J]. 自动化仪表, 2018, 39(9): 76-78, 82. Wang Huayong, Yang Chao, Tang Hua. Research on the Short-Term Load Forecasting Using Improved GBDT Based on LightGBM[J]. Process Automation Instrumentation, 2018, 39(9): 76-78, 82. |
| [8] |
Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Francisco: ACM, 2016: 785-794.
|
| [9] |
Ke G, Meng Q, Finley T, et al. Lightgbm: A Highly Efficient Gradient Boosting Decision Tree[C]//31st Conference on Neural Information Processing Systems(NIPS 2017). Long Beach: Advances in Neural Information Processing Systems, 2017: 3146-3154.
|
| [10] |
马晓君, 沙靖岚, 牛雪琪. 基于LightGBM算法的P2P项目信用评级模型的设计及应用[J]. 数量经济技术经济研究, 2018, 35(5): 144-60. Ma Xiaojun, Sha Jinglan, Niu Xueqi. An Empirical Study on the Credit Rating of P2P Projects Based on LightGBM Algorithm[J]. The Journal of Quantitative & Technical Economics, 2018, 35(5): 144-60. |
| [11] |
袁照威, 段正军, 张春雨, 等. 基于马尔科夫概率模型的碳酸盐岩储集层测井岩性解释[J]. 新疆石油地质, 2017, 38(1): 96-102. Yuan Zhaowei, Duan Zhengjun, Zhang Chunyu, et al. Interpretation of Logging Lithology in Carbonate Reservoirs Based on Markov Chain Probability Model[J]. Xinjiang Petroleum Geology, 2017, 38(1): 96-102. |
| [12] |
张涛, 莫修文. 基于交会图与模糊聚类算法的复杂岩性识别[J]. 吉林大学学报(地球科学版), 2007, 37(1): 109-113. Zhang Tao, Mo Xiuwen. Complex Lithologic Identification Based on Cross Plot and Fuzzy Clustering Algorithm[J]. Journal of Jilin University(Earth Science Edition), 2007, 37(1): 109-113. |
| [13] |
王振洲, 张春雷, 高世臣. 利用决策树方法识别复杂碳酸盐岩岩性: 以苏里格气田苏东41-33区块为例[J]. 油气地质与采收率, 2017, 24(6): 25-33. Wang Zhenzhou, Zhang Chunlei, Gao Shichen. Lithology Identification of Complex Carbonate Rocks Based on Decision Tree Method: An Example from Block Sudong 41-33 in Sulige Gas Field[J]. Petroleum Geology and Recovery Efficiency, 2017, 24(6): 25-33. DOI:10.3969/j.issn.1009-9603.2017.06.004 |
| [14] |
江凯, 王守东, 胡永静, 等. 基于Boosting Tree算法的测井岩性识别模型[J]. 测井技术, 2018, 42(4): 395-400. Jiang Kai, Wang Shoudong, Hu Yongjing, et al. Lithology Identification Model by Well Logging Based on Boosting Tree Algorithm[J]. Well Logging Technology, 2018, 42(4): 395-400. |
| [15] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. Yan Xingyu, Gu Hanming, Xiao Yifei, et al. XGBoost Algorithm Applied in the Interpretation of Tight-Sand Gas Reservoir on Well Logging Data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [16] |
李大中, 王超, 李颖宇. 基于XGBoost算法的风机叶片结冰状态评测[J]. 电力科学与工程, 2019, 35(9): 43-48. Li Dazhong, Wang Chao, Li Yingyu. Evaluation of Fan Blade Icing Based on XGBoost Algorithm[J]. Electric Power Science and Engineering, 2019, 35(9): 43-48. |
| [17] |
蒋晋文, 刘伟光. XGBoost算法在制造业质量预测中的应用[J]. 智能计算机与应用, 2017, 7(6): 58-60. Jiang Jinwen, Liu Weiguang. Application of XGBoost Algorithm in Manufacturing Quality Prediction[J]. Intelligent Computer and Applications, 2017, 7(6): 58-60. |
| [18] |
仲鸿儒, 成育红, 林孟雄, 等. 基于SOM和模糊识别的复杂碳酸盐岩岩性识别[J]. 岩性油气藏, 2019, 31(5): 84-91. Zhong Hongru, Cheng Yuhong, Lin Mengxiong, et al. Lithology Identification of Complex Carbonate Based on SOM and Fuzzy Recognition[J]. Lithologic Reservoirs, 2019, 31(5): 84-91. |
| [19] |
钟仪华, 李榕. 基于主成分分析的最小二乘支持向量机岩性识别方法[J]. 测井技术, 2009, 33(5): 425-429. Zhong Yihua, Li Rong. Application of Principal Component Analysis and Least Square Support Vector Machine to Lithology Identification[J]. Well Logging Technology, 2009, 33(5): 425-429. DOI:10.3969/j.issn.1004-1338.2009.05.005 |
| [20] |
单敬福, 陈欣欣, 赵忠军, 等. 利用BP神经网络法对致密砂岩气藏储集层复杂岩性的识别[J]. 地球物理学进展, 2015, 30(3): 1257-1263. Shan Jingfu, Chen Xinxin, Zhao Zhongjun, et al. Identification of Complex Lithology for Tight Sandstone Gas Reservoirs Based on BP Neural Net[J]. Progress in Geophysics, 2015, 30(3): 1257-1263. |


