2. 吉林大学地球探测科学与技术学院, 长春 130026
2. College of GeoExploration Science and Techonology, Jilin University, Changchun 130026, China
0 引言
鄂尔多斯盆地上古生界煤系烃源岩地层之上发育大型砂岩致密气藏,储层物性受成岩作用改造强烈,成岩过程中早期压实作用和矿物胶结作用是造成砂岩储层致密化的主要成因[1]。储层的孔隙空间以溶蚀颗粒孔、溶蚀粒间孔以及胶结物溶孔等次生孔隙为主,还包含少量原生残余粒间孔。此外,致密砂岩中还发育少量微裂缝。致密砂岩储层的孔渗特征与溶蚀孔和微裂缝发育程度有关[2]。由于低孔低渗的致密砂岩储层孔隙结构复杂,难以应用常规岩石物理理论进行有效描述。因此,针对复杂孔隙结构进行岩石物理建模,研究孔隙结构对储层弹性和力学特征影响的岩石物理机制,有助于致密砂岩气储层的精细地震描述。
国外关于致密砂岩储层岩石物理的研究中:Tutuncu等[3]的研究发现致密砂岩颗粒间低纵横比微裂隙的存在导致致密砂岩纵、横波速度对压力变化比普通砂岩更为敏感;Smith等[4]的研究认为,需要引入低纵横比的孔隙或微裂缝来解释致密砂岩气储层中复杂的速度与孔隙度关系;Ruiz等[5]根据实验室测量结果,认为岩石基质中低纵横比软孔隙的存在有助于解释致密砂岩的弹性特征,并且在岩石物理建模过程中引入两种不同纵横比的孔隙模拟致密砂岩的孔隙结构,应用于北美致密砂岩储层弹性参数的预测。
国内学者针对致密砂岩储层进行了系统的岩石物理研究:Yin等[6]应用等效介质理论与岩石物理实验测量,发现存在致密砂岩中微裂缝微观结构主导岩石弹性性质变化的情况;周枫等[7]在岩石薄片分析基础上,按纵横比划分致密砂岩的孔隙结构并进行岩石物理建模,研究孔隙结构参数与岩石弹性性质的定量关系;印兴耀等[8]在Biot相洽理论中考虑致密砂岩中孔隙和裂隙共存的情况,并应用岩石骨架泊松比构建流体因子进行储层含气性识别;杨志芳等[9]应用修正的White模型建立含气饱和度定量预测模板,并应用于致密砂岩气储层含气饱和度的定量地震预测;赖锦等[10]通过岩心观察、薄片分析、电镜扫描等方法研究了致密砂岩气储层孔隙结构特征及其成因机理。邓继新等[11]基于孔隙弹性介质和喷射流理论,研究了致密砂岩双孔隙模型中孔隙分布特征对速度频散的影响;王璞等[12]在岩石物理模型中考虑了致密砂岩储层中的孔隙和固体颗粒形状,通过横波速度预测进行模型的适用性分析;姜仁等[13]应用Brie和Xu-White模型进行致密砂岩储层岩石物理建模,在此基础上研究通过地震属性进行含气饱和度预测的方法;刘倩等[14]针对致密砂岩低孔低渗特征,利用Raymer公式引入不连通孔隙,通过岩石物理模型研究其对岩石弹性模量和流体响应特征的影响;印兴耀等[15]基于Hudson理论和各向异性Gassmann理论提出了一种各向异性的致密孔隙裂隙储层岩石物理模型,研究了弹性参数随裂隙参数变化的敏感性;王大兴[16]通过致密砂岩的实验室岩心测量孔隙度、含水饱和度与纵横波速度、泊松比等参数的关系,在此基础上建立岩石物理模型用于储层含气性的地震预测;贾凌云等[17]研究了Krief模型、Nur模型及Pride-Lee模型等应用于致密砂岩储层的适用性并给出优化方法;郭梦秋等[18]研究了致密砂岩孔隙结构的非均质性对弹性性质的影响;何润发等[19]应用Biot-Rayleigh理论研究致密砂岩储层的双重孔隙结构,在此基础上建立岩石物理模板预测致密砂岩储层的孔隙度与裂隙含量。
本文针对致密砂岩气储层的复杂孔隙结构进行岩石物理建模,在岩石物理模型中分别以孔隙纵横比、软孔比例等参数表征孔隙结构,应用等效介质理论计算孔隙结构参数与弹性性质的定量关系。通过井中岩石物理反演与横波速度预测,对比不同孔隙结构表征方式在研究区的适用性。在明确孔隙结构表征方式的基础上,计算致密砂岩干岩石骨架弹性模量并与传统计算方法对比。计算结果可用于致密砂岩储层干岩石骨架孔隙结构特征分析,也可为岩石物理流体替换模型、频散衰减模型等提供骨架弹性模量参数。
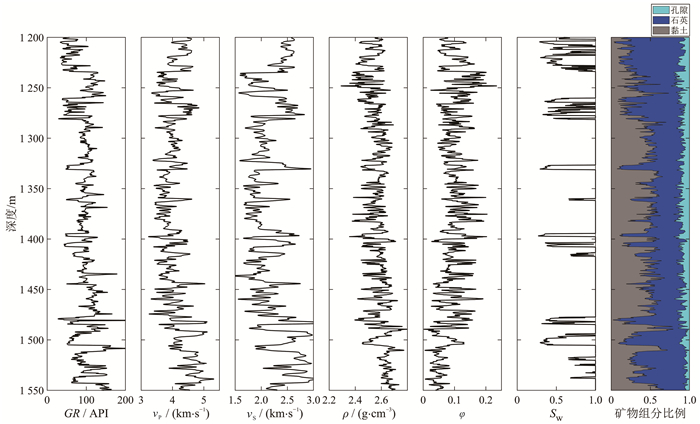
1 致密砂岩气储层测井数据图 1为研究区测井数据。砂泥岩互层的地层结构中,砂岩层段石英体积分数一般大于70%,泥岩层段黏土矿物体积分数一般大于50%。砂岩地层孔隙度一般低于10%。与泥岩相比,砂岩的纵、横波速度较高、密度较低。
|
| GR. 自然伽马;vP. 纵波速度;vS. 横波速度;ρ. 密度;φ. 孔隙度;Sw. 含水饱和度。 图 1 研究区测井数据 Fig. 1 Logging data of study area |
|
|
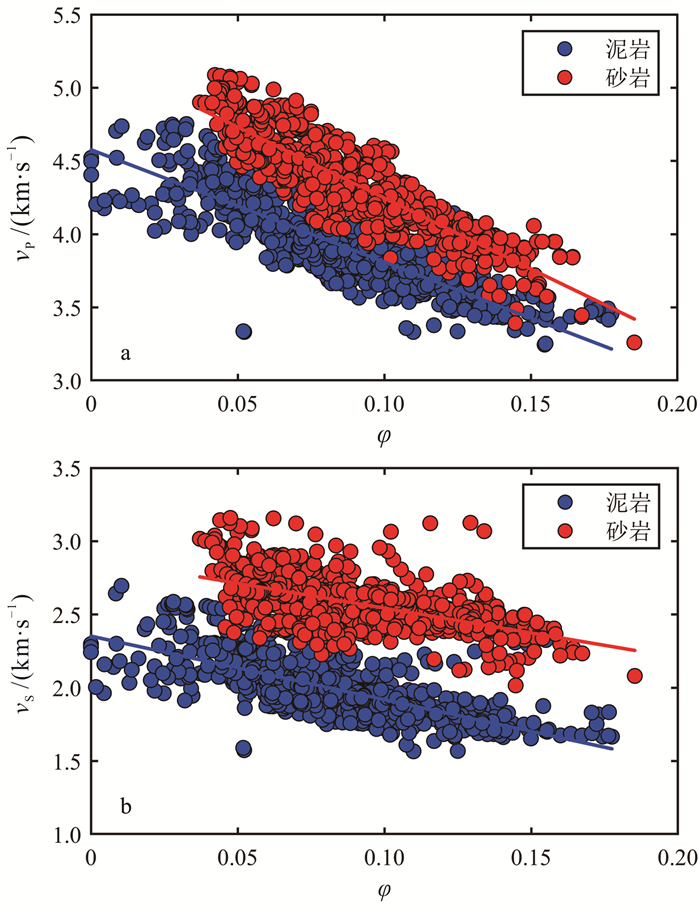
图 2为图 1测井数据中砂岩、泥岩层段的纵波速度、横波速度分别与孔隙度的交会图。由图 2可以观察到,速度随孔隙度增加而降低,但是数据点较分散,不呈简单线性关系,说明砂岩和泥岩的速度-孔隙度关系复杂,孔隙度不是决定速度的唯一因素,速度还与孔隙结构,以及黏土矿物组分体积分数等有关。Smith等[4]与Ruiz等[5]的研究发现,对于致密砂岩,孔隙结构(孔隙形态的变化)和孔隙度(孔隙空间的大小)共同影响其弹性模量及声学速度。因此,有必要建立致密砂岩储层岩石物理模型,定量研究孔隙结构对储层弹性和力学特征的影响。
|
| a. 纵波速度与孔隙度; b. 横波速度与孔隙度。 图 2 速度-孔隙度关系交会图 Fig. 2 Cross plot of velocity and porosity |
|
|
针对储层微观孔隙结构的岩石物理研究,逄硕等[20]提出基于岩石物理模型的孔隙结构参数反演和速度预测方法;张冰等[21]研究了储层裂缝属性及各向异性参数的岩石物理反演方法;李博南等[22]探讨了基于岩石物理模型的储层微观孔隙特征分析方法。
如图 3所示,本文以两种模型描述致密砂岩的微观孔隙结构。图 3a为单一孔隙纵横比模型,所有孔隙具有相同的以孔隙纵横比参数α表示的几何形态;图 3b为双孔隙模型,岩石的总孔隙空间等效为两部分的组合,即孔隙度为φstiff的高纵横比孔隙(硬孔隙)与孔隙度为φsoft的低纵横比微裂隙(软孔隙),总孔隙度为φtotal = φstiff+ φsoft。模型中,假设硬孔隙为球形孔隙,纵横比αstiff=1;软孔隙纵横比αsoft= 0.01。以总孔隙空间中的软孔比例fsoft = φsoft / φtotal表征双孔隙模型中的孔隙结构特征。

|
| a. 单一孔隙纵横比模型;b. 双孔隙模型。 图 3 致密砂岩气储层岩石物理模型示意图 Fig. 3 Schematic diagram of petrophysical model of tight sandstone gas reservoir |
|
|
图 4为与图 3对应的岩石物理建模流程。图 4a所示的单一孔隙纵横比模型中,首先应用HSB (Hashin-Strikman bounds) 岩石物理界限理论,计算由石英和黏土矿物组成的固体基质弹性模量,之后应用SCA (self-consistent approximation)自相容近似理论,将具有特定纵横比的孔隙填充到固体基质中,计算得到致密砂岩弹性参数。图 4b所示的双孔隙模型中,在由HSB理论计算固体基质弹性模量的基础上,应用SCA理论计算与软、硬孔形态和比例有关的致密砂岩的弹性参数。岩石物理模型所用的组分参数如表 1所示。

|
| a. 单一孔隙纵横比模型;b. 双孔隙模型。 图 4 致密砂岩气储层岩石物理建模流程图 Fig. 4 Flow chart of rock physical modeling of tight sandstone gas reservoir |
|
|
| 组分 | 体积模量/ GPa |
剪切模量/ GPa |
密度/ (g·cm-3) |
| 石英 | 37.000 | 44 | 2.65 |
| 黏土 | 21.000 | 7 | 2.60 |
| 水 | 2.500 | - | 1.00 |
| 气 | 0.063 | - | 0.11 |
根据Berryman [23]的研究,图 4中岩石物理建模所用的多相介质SCA理论为:
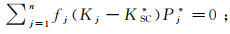 (1)
(1)  (2)
(2) 式中:角标j表示第j相组分;n为组成岩石组分的种类数,包括固体矿物与孔隙流体;fj为固体、流体各组分的体积分数;Kj和μj分别为其体积模量和剪切模量;KSC*和μ*SC分别为基于自相容近似方法计算的的等效体积模量和剪切模量;Pi*为与体积模量有关的几何因子;Qi*为与剪切模量有关的几何因子。
在公式(1)和(2)中,若第n相为孔隙流体相,则fn=φtotal。对于软、硬孔组成的双孔隙模型,有fn=φtotal=φstiff+φsoft。
图 4所示模型中,由气和水组成的流体混合物的体积模量Kf由Wood理论[24]计算:
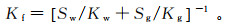 (3)
(3) 式中:Kw和Kg分别为水和气的体积模量;Sw和Sg分别为含水和含气的饱和度。
气水混合物的密度为
 (4)
(4) 式中,ρw和ρg分别为水和气的密度。
2.2 岩石物理正演分析在上述岩石物理建模的基础上,引入孔隙结构参数分析图 2中致密砂岩的速度-孔隙度关系。如图 2所示的数据,致密砂岩纵、横波速度随孔隙度迅速降低,并且速度-孔隙度关系呈复杂的非线性形态。
图 5为应用图 4a中单一孔隙纵横比模型计算的致密砂岩层纵、横波速度在不同孔隙纵横比情况下随孔隙度的变化。可以观察到,速度与孔隙度的复杂关系可通过引入纵横比解释。在相同孔隙度下,较低的孔隙纵横比对应更为狭长的孔隙,比高纵横比球形孔隙更能显著降低岩石的弹性模量和速度。如图 5所示,致密砂岩的纵波速度-孔隙度关系主要分布在纵横比0.05~0.20之间,集中于0.10周围,而横波的速度-孔隙度关系对应的纵横比范围稍大。

|
| a. 纵波速度与孔隙度的关系;b. 横波速度与孔隙度的关系。 图 5 致密砂岩单一孔隙纵横比模型岩石物理正演分析 Fig. 5 Rock physical analysis using the single pore aspect ratio model of tight sandstone |
|
|
图 6为应用图 4b中双孔隙模型计算的致密砂岩纵、横波速度在不同软孔比例情况下随孔隙度的变化。从图 6可以看到,软孔比例参数可以解释速度-孔隙度的复杂关系。在相同孔隙度情况下,较高的软孔比例对应较低的纵、横波速度。数据分布情况显示,速度-孔隙度数据主要集中在软孔比例0.05~0.20之间,且横波数据对应的软孔比例范围稍大。
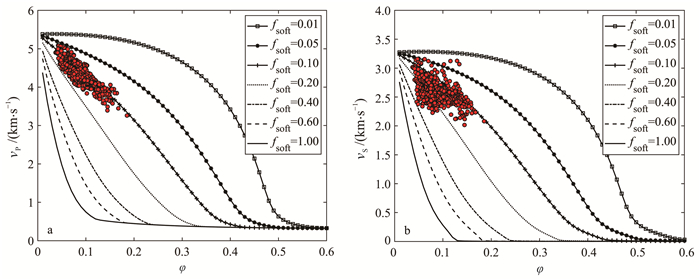
|
| a. 纵波速度与孔隙度的关系;b. 横波速度与孔隙度的关系。 图 6 致密砂岩双孔隙模型岩石物理正演分析 Fig. 6 Rock physical analysis using dual-porosity model of tight sandstone |
|
|
上述分析表明,致密砂岩储层速度与孔隙度和孔隙形态有关,以纵横比、软孔比例等描述的孔隙结构能够解释致密砂岩复杂的速度-孔隙度关系。
3 孔隙结构反演及横波速度预测图 5和图 6的岩石物理正演分析表明,孔隙空间的大小(孔隙度)和孔隙结构(纵横比或软孔比例等)共同影响致密砂岩储层的速度。在如图 1所示的测井数据中,当孔隙度及矿物组分、含水饱和度等参数已知时,可基于本文的岩石物理模型设计反演流程,计算孔隙纵横比、软孔比例等孔隙结构参数。
图 7为基于单一孔隙纵横比模型的岩石物理反演流程,图 8为基于双孔隙模型的反演流程。上述反演流程的基本思路: 在目标函数中通过岩石物理正演迭代,寻找使得计算的纵波速度与井中实测的纵波速度达到最佳拟合时对应的孔隙纵横比、软孔比例等参数。反演过程同时输出横波速度,在缺少井中横波实测数据的情况下可作为对横波速度的估计。
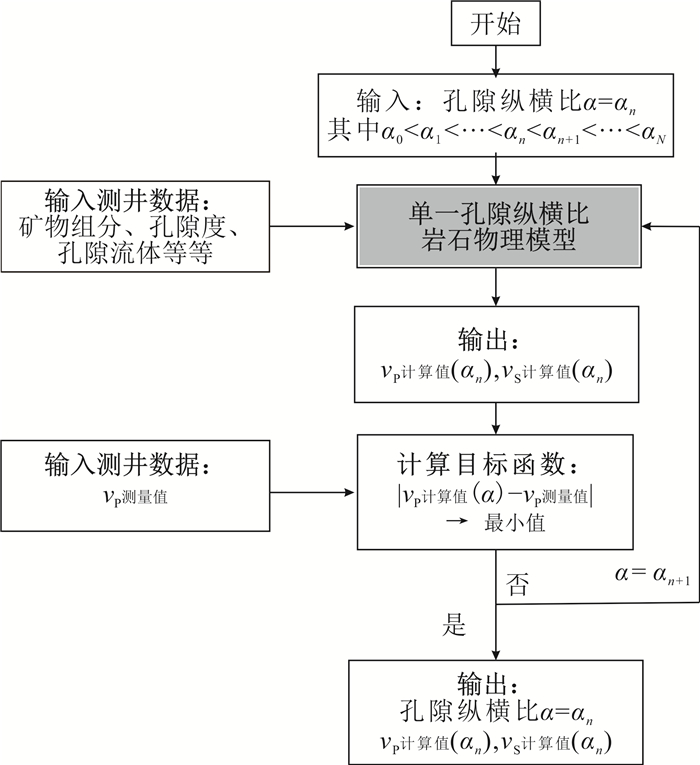
|
| 图 7 基于单一孔隙纵横比模型的岩石物理反演及横波速度预测流程图 Fig. 7 Flow chart of rock physics inversion and vS prediction using the single pore aspect ratio model |
|
|

|
| 图 8 基于双孔隙模型软孔比例反演及横波速度预测流程图 Fig. 8 Flow chart of rock physics inversion and vS prediction using the dual-porosity model |
|
|
图 9为图 7反演流程对应的计算结果。可以观察到,通过寻找孔隙纵横比的最优值,可以使得计算的纵波速度与实测值达到较高的吻合度,因此孔隙纵横比的变化可以解释致密砂岩气储层在矿物、孔隙度和孔隙流体等已知的情况下纵波速度的变化。同时,预测的横波速度曲线与实测曲线也具有较好的一致性,二者相关系数为0.91。图 10为图 8反演流程对应的计算结果,与图 9相比,纵波速度的拟合程度更高,横波速度预测结果精度也更高,相关系数为0.94。

|
| a. 孔隙纵横比;b. 纵波速度;c. 横波速度。 图 9 基于单一孔隙纵横比模型的岩石物理反演及横波速度预测结果 Fig. 9 Rock physics inversion and vS prediction using the single pore aspect ratio model |
|
|
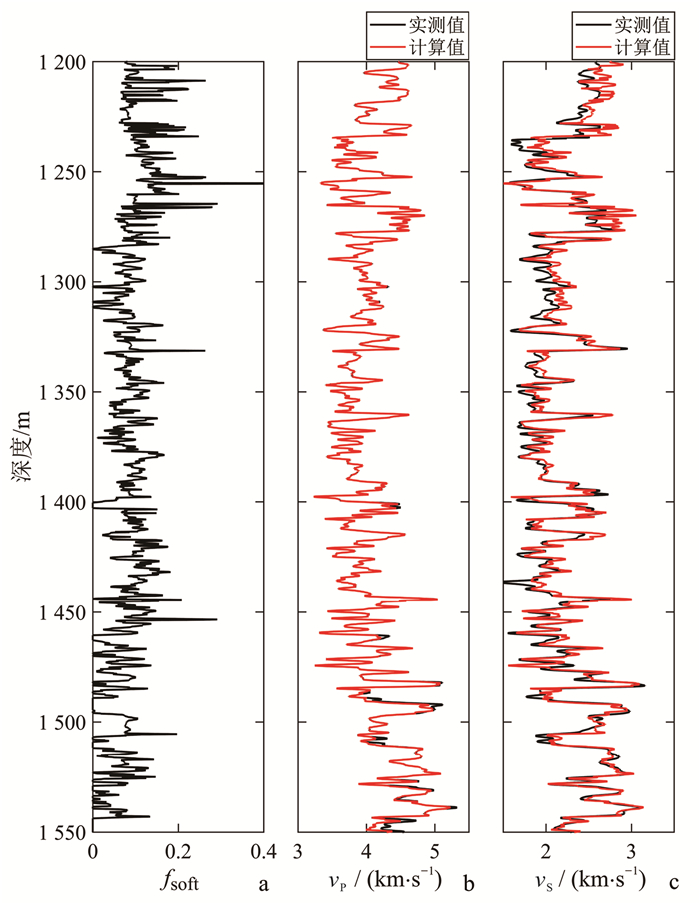
|
| a. 软孔比例;b. 纵波速度;c. 横波速度。 图 10 基于双孔隙模型的岩石物理反演及横波速度预测结果 Fig. 10 Rock physics inversion and vS prediction using the dual-porosity model |
|
|
对比图 9与图 10,由于双孔隙模型比单一纵横比模型在拟合纵波速度、预测横波速度方面具有更高的精度,因此在该研究区的岩石物理模型中,将微观孔隙结构等效为软、硬孔的组合更为合理。同时,图 10中软孔比例在测井层段的变化表明了孔隙结构的空间分布具有非均匀性。
4 致密砂岩地层骨架弹性模量预测 4.1 岩石骨架弹性模量预测方法在应用Gassmann流体替换理论[25]、Biot理论[26]以及BISQ(Biot/Squirt)理论[27-28]等研究孔弹介质的等效弹性模量时,岩石骨架的弹性模量都是关键的输入参数。岩石骨架的弹性模量受矿物、孔隙度和孔隙结构等因素的影响[29]。虽然岩石骨架的弹性模量可通过实验室对岩心测量获取,但是其井中原位估计较为困难。
Krief等[30]建立了干岩石骨架模量随孔隙度变化的非线性关系:
 (5)
(5) 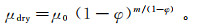 (6)
(6) 式中:岩性参数m为经验参数;Kdry和μdry为干岩石骨架的体积模量和剪切模量;K0和μ0为岩石基质的体积模量和剪切模量。
Pride等[31]在干岩石骨架经验公式中引入了固结系数,之后Lee[32]对该公式中的剪切模量做了修正:
 (7)
(7) 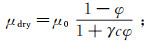 (8)
(8)  (9)
(9) 式中:c为固结系数,表示岩石的固结程度; γ为固结系数c的函数。
上述经验公式需要针对特定研究区数据确定经验参数,并且没有充分考虑致密储层复杂的矿物组分及孔隙结构等因素,存在一定的局限性。
本文提出一种基于岩石物理模型的岩石骨架弹性模量预测方法。即在如图 10a所示双孔隙岩石物理反演的基础上,将孔隙填充物体积模量和剪切模量设为零,得到如图 11所示的致密砂岩地层岩石骨架弹性模量和密度。其中:Ksat为饱和岩石体积模量;μsat为饱和岩石剪切模量;ρsat为饱和岩石密度;ρdry为干岩石骨架密度。与经验公式相比,该方法充分考虑了矿物组成、孔隙度与孔隙结构等因素。
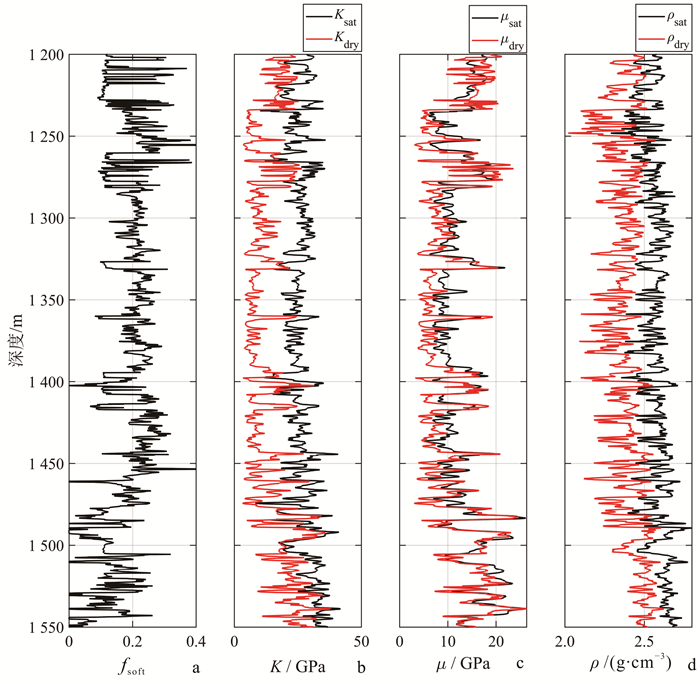
|
| a. 软孔比例;b.体积模量;c. 剪切模量;d. 密度。 图 11 应用双孔隙模型计算的干岩石骨架弹性模量 Fig. 11 Elastic modulus of dry rock skeleton calculated by the dual-pore model |
|
|
图 12和图 13展示了图 10中计算得到的致密砂岩骨架模量随孔隙度的变化规律,并与公式(5)至(9)中Krief和Pride经验公式的预测结果进行了对比。可以观察到,致密砂岩地层岩石骨架模量与孔隙度的关系复杂,不能由简单的经验关系描述。图 12中体积模量随孔隙度的离散分布对应Krief理论中经验参数m的取值范围为3~7,而剪切模量随孔隙度的数据更为离散,Krief模型不能提供较好的预测。同样,图 13中Pride经验公式也无法对致密砂岩骨架弹性模量与孔隙度关系给出较好预测结果。
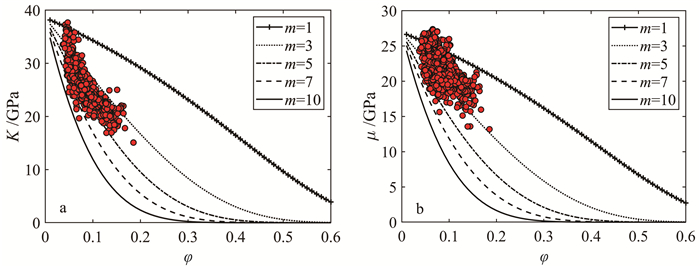
|
| a. 体积模量与孔隙度的关系;b. 剪切模量与孔隙度的关系。 图 12 应用双孔隙模型计算的干岩石骨架弹性模量与Krief理论对比 Fig. 12 Relationship between the elastic modulus of dry rock skeleton calculated by the dual-pore model and Krief's experience |
|
|
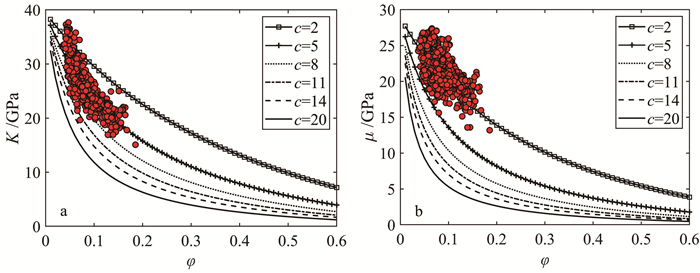
|
| a. 体积模量与孔隙度的关系;b. 剪切模量与孔隙度的关系。 图 13 应用双孔隙模型计算的干岩石骨架弹性模量与Pride理论对比 Fig. 13 Relationship between the elastic modulus of dry rock skeleton calculated by the dual-pore model and Pride's experience |
|
|
因此,与传统Krief和Pride经验公式相比,本文计算干岩石骨架弹性模量的方法充分考虑了矿物组成、孔隙度以及孔隙结构等因素的影响,对具有非均质孔隙结构的致密砂岩储层具有适用性。
4.2 岩石骨架模量与物性参数关系分析图 14为测井数据中砂岩层段饱和岩石的纵波速度vPsat与孔隙度的交会图。图 15为由图 11中干岩石骨架弹性模量和密度计算的砂岩层段岩石骨架纵波速度vPdry与孔隙度交会图。对比图 14与图 15,可以观察到当排除了孔隙流体的影响,砂岩地层岩石骨架纵波速度-孔隙度关系的数据较分散,纵波速度与孔隙度的关系更为复杂。
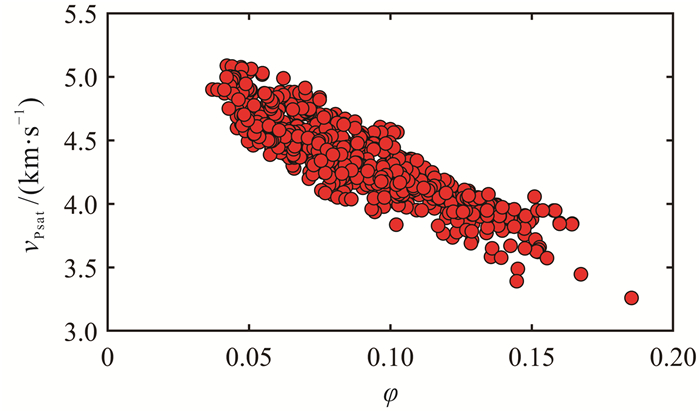
|
| 图 14 流体饱和的致密砂岩纵波速度与孔隙度交会图 Fig. 14 Cross plot of vP and porosity for saturated tight sandstone |
|
|
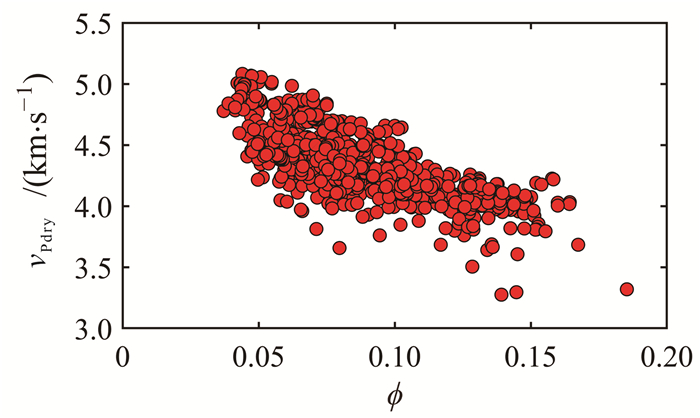
|
| 图 15 致密砂岩干岩石骨架纵波速度与孔隙度交会图 Fig. 15 Cross plot of vP and porosity for dry rock skeleton of tight sandstone |
|
|
由图 16可以观察到, 软孔比例的增加能够显著降低致密砂岩骨架的纵波速度,这一趋势与图 6中双孔隙模型的正演分析一致。由图 17可以发现,图 16中软孔比例较少(即较多的球形孔隙)的砂岩具有较高的含气饱和度,说明致密砂岩中的球形孔隙为致密气提供了主要的赋存空间。

|
| 图 16 以软孔比例为色标的致密砂岩干岩石骨架纵波速度与孔隙度交会图 Fig. 16 Cross plot of vP and porosity for dry rock skeleton of tight sandstone color-coded by the soft pore ratio fsoft |
|
|

|
| 图 17 以含气饱和度为色标的致密砂岩干岩石骨架纵波速度与孔隙度交会图 Fig. 17 Cross plot of vP and porosity for dry rock skeleton of tight sandstone color-coded by gas saturation Sg |
|
|
基于Biot-Gassmann理论[25, 33], 饱和岩石与干岩石骨架体积模量关系如下:
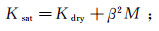 (10)
(10) 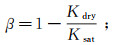 (11)
(11) 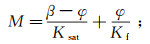 (12)
(12) 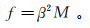 (13)
(13) 式中:β为描述流体饱和地层性质的Biot系数;M为描述固体相和流体相的耦合模量;f为Gassmann方程的混合流体项,描述孔隙度、孔隙流体及岩石骨架基质的共同影响;Kf为孔隙流体等效模量。
Han等[34]简化了混合流体项,将矿物、孔隙度与孔隙流体的影响进行分离,表达为:
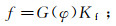 (14)
(14) 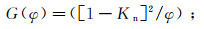 (15)
(15)  (16)
(16) 式中:Kn为归一化模量;G(φ)为岩石骨架孔隙函数。
在致密砂岩地层岩石骨架基础上,根据公式(11)-(16)计算得到的各参数曲线如图 18所示,可为致密砂岩地层进一步的岩石物理分析提供依据。
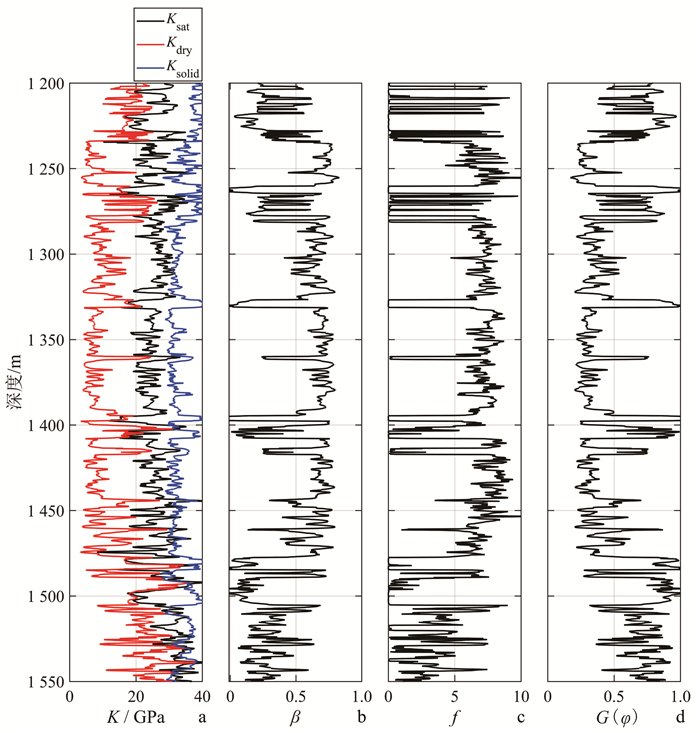
|
| a. 饱和岩石、干岩石及基质的体积模量;b. Biot系数;c. 混合流体项;d. 岩石骨架孔隙函数。Ksolid为岩石基质体积模量。 图 18 以岩石骨架模量为基础计算的各参数曲线 Fig. 18 Calculated curves based on dry frame modulus |
|
|
致密砂岩储层具有低孔低渗、孔隙结构复杂和非均质强的特点,其速度-孔隙度关系复杂,孔隙结构与孔隙度共同影响其弹性性质。本文研究了致密砂岩微观孔隙结构的岩石物理建模技术及应用方法,研究结论如下:
1) 在岩石物理模型中比较了两种孔隙结构的表征方式,计算结果表明基于双孔隙模型的横波速度预测精度高于单一孔隙纵横比模型,说明将孔隙空间等效为软、硬孔组合的双孔隙模型更适用于描述研究区致密砂岩储层的微观孔隙结构。反演的软孔比例能够反映孔隙结构的非均匀分布。
2) 应用双孔隙岩石物理模型计算致密砂岩储层井中岩石骨架的弹性模量,与传统Krief及Pride等经验公式相比,考虑了矿物基质、孔隙度和孔隙结构等微观物性因素,理论上更具有严谨性,能够反映岩石骨架模量与孔隙度的复杂关系。
3) 致密砂岩地层岩石骨架弹性性质与物性参数的关系分析发现,当排除了孔隙流体的影响,岩石骨架纵波速度-孔隙度的关系更为复杂,并且孔隙结构中软孔比例的增加能够显著降低致密砂岩骨架的纵波速度,说明微裂隙的存在能够显著影响致密砂岩的弹性性质。同时,较低的软孔比例(即较多的球形孔隙)对应较高的含气饱和度,说明致密砂岩储层中球形孔隙是致密气的主要赋存空间。
4) 通过本文方法计算的致密砂岩地层骨架弹性模量,可进一步计算用于地层评价的Biot系数、Gassmann流体混合参数,以及岩石骨架孔隙函数,也可为Gassmann流体替换理论、Biot和BISQ等孔隙弹性介质理论提供岩石骨架模量的关键参数。
| [1] |
惠学智, 许有为, 吕娜娜, 等. 鄂尔多斯盆地华庆地区长8段成岩主控因素及其对储层的影响[J]. 世界地质, 2019, 38(4): 1012-1020. Hui Xuezhi, Xu Youwei, Lyu Nana, et al. Major Controlling Factors of Diagenesis and Their Influences on Chang-8 Section Reservoir, Huaqing Area, Ordos Basin[J]. Global Geology, 2019, 38(4): 1012-1020. DOI:10.3969/j.issn.1004-5589.2019.04.012 |
| [2] |
刘喜杰, 马遵敬, 韩冬, 等. 鄂尔多斯盆地东缘临兴区块致密砂岩优质储层形成的主控因素[J]. 天然气地球科学, 2018, 29(4): 481-490. Liu Xijie, Ma Zunjing, Han Dong, et al. Research on the Main Factors of High Quality Tight Sand Stone Reservoir in Linxing Block, Ordos Basin[J]. Natural Gas Geoscience, 2018, 29(4): 481-490. DOI:10.11764/j.issn.1672-1926.2018.02.002 |
| [3] |
Tutuncu A N, Podio A L, Sharma M M. An Experimental Investigation of Factors Influencing Compressional-and Shear-Wave Velocities and Attenuations in Tight Gas Sandstones[J]. Geophysics, 1994, 59(1): 77-86. DOI:10.1190/1.1443536 |
| [4] |
Smith T M, Sayers C M, Sondergeld C H. Rock Properties in Low-Porosity/Low-Permeability Sandstones[J]. Leading Edge, 2009, 28(1): 48-59. DOI:10.1190/1.3064146 |
| [5] |
Ruiz F, Cheng A. A Rock Physics Model for Tight Gas Sand[J]. Leading Edge, 2010, 29(12): 1484-1489. DOI:10.1190/1.3525364 |
| [6] |
Yin H, Zhao J, Tang G, et al. Pressure and Fluid Effect on Frequency-Dependent Elastic Moduli in Fully Saturated Tight Sandstone[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(11): 8925-8942. DOI:10.1002/2017JB014244 |
| [7] |
周枫, 徐鸣洁, 马中高. 等效孔隙结构模型在鄂尔多斯致密含气砂岩中的应用[J]. 高校地质学报, 2013, 19(4): 588-593. Zhou Feng, Xu Mingjie, Ma Zhonggao, et al. Application of Effective Porosity Model to Tight Gas Sands in Ordos Basin[J]. Geological of China Universities, 2013, 19(4): 588-593. DOI:10.3969/j.issn.1006-7493.2013.04.004 |
| [8] |
印兴耀, 刘欣欣, 曹丹平. 基于Biot相洽理论的致密砂岩弹性参数计算方法[J]. 石油物探, 2013, 52(5): 445-451. Yin Xingyao, Liu Xinxin, Cao Danping. Elastic Parameters Calculation for Tight Sand Reservoir Based on Biot-Consistent Theory[J]. Geological Prospecting for Petroleum, 2013, 52(5): 445-451. DOI:10.3969/j.issn.1000-1441.2013.05.001 |
| [9] |
杨志芳, 曹宏, 姚逢昌, 等. 复杂孔隙结构储层地震岩石物理分析及应用[J]. 中国石油勘探, 2014, 19(3): 50-56. Yang Zhifang, Cao Hong, Yao Fengchang, et al. Seismic Rock Physical Analysis of Complex Porous Reservoir and Its Application[J]. China Petroleum Exploration, 2014, 19(3): 50-56. DOI:10.3969/j.issn.1672-7703.2014.03.006 |
| [10] |
赖锦, 王贵文, 罗官幸, 等. 基于岩石物理相约束的致密砂岩气储层渗透率解释建模[J]. 地球物理学进展, 2014, 29(3): 1173-1182. Lai Jin, Wang Guiwen, Luo Guanxing, et al. A Fine Logging Interpretation Model of Permeability Confined by Petrophysical Facies of Tight Gas Sandstone Reservoirs[J]. Progress in Geophysics, 2014, 29(3): 1173-1182. DOI:10.6038/pg20140323 |
| [11] |
邓继新, 周浩, 王欢, 等. 基于储层砂岩微观孔隙结构特征的弹性波频散响应分析[J]. 地球物理学报, 2015, 58(9): 3389-3400. Deng Jixin, Zhou Hao, Wang Huan, et al. The Influence of Pore Structure in Reservoir Sandstone on Dispersion Properties of Elastic Waves[J]. Chinese Journal of Geophysics, 2015, 58(9): 3389-3400. |
| [12] |
王璞, 吴国忱. 基于自相容近似的致密储层岩石物理建模[J]. 地球物理学进展, 2015, 30(5): 2233-2238. Wang Pu, Wu Guochen. The Rock Physics Modeling for Tight Reservoir Based on the Self-Consistent Approximation[J]. Progress in Geophysics, 2015, 30(5): 2233-2238. |
| [13] |
姜仁, 曾庆才, 黄家强, 等. 基于岩石物理分析的致密砂岩流体检测方法研究[J]. 科学技术与工程, 2015, 15(1): 163-167. Jiang Ren, Zeng Qingcai, Huang Jiaqiang, et al. Tight Gas Saturation Detection by Most Sensitive AVO Attributes with Rock Physics Analysis[J]. Science Technology and Engineering, 2015, 15(1): 163-167. DOI:10.3969/j.issn.1671-1815.2015.01.030 |
| [14] |
刘倩, 印兴耀, 李超. 含不连通孔隙的致密砂岩储层岩石弹性模量预测方法[J]. 石油物探, 2015, 54(6): 635-642. Liu Qian, Yin Xingyao, Li Chao. Rock Elastic Modulus Estimation for Tight Sandstone Reservoirs with Disconnected Pores[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 635-642. DOI:10.3969/j.issn.1000-1441.2015.06.001 |
| [15] |
印兴耀, 刘倩. 致密储层各向异性地震岩石物理建模及应用[J]. 中国石油大学学报(自然科学版), 2016, 40(2): 52-58. Yin Xingyao, Liu Qian. Anisotropic Rock Physical Modeling of Tight Sandstone and Applications[J]. Journal of China University of Petroleum (Edition of Natural Science), 2016, 40(2): 52-58. DOI:10.3969/j.issn.1673-5005.2016.02.006 |
| [16] |
王大兴. 致密砂岩气储层的岩石物理模型研究[J]. 地球物理学报, 2016, 59(12): 4603-4622. Wang Daxing. Study on Rock Physics Model of Gas Reservoirs in Tight Sandstone[J]. Chinese Journal of Geophysics, 2016, 59(12): 4603-4622. DOI:10.6038/cjg20161222 |
| [17] |
贾凌云, 李琳, 王千遥, 等. 致密砂岩储层岩石物理模型的优化建立[J]. 地球科学进展, 2018, 33(4): 416-424. Jia Lingyun, Li Lin, Wang Qianyao, et al. Optimization of the Rock Physical Model in Tight Sandstone Reservoir[J]. Advances in Earth Science, 2018, 33(4): 416-424. DOI:10.11867/j.issn.1001-8166.2018.04.0416 |
| [18] |
郭梦秋, 巴晶, 马汝鹏, 等. 含流体致密砂岩的纵波频散及衰减: 基于双重双重孔隙结构模型描述的特征分析[J]. 地球物理学报, 2018, 61(3): 1053-1068. Guo Mengqiu, Ba Jing, Ma Rupeng, et al. P-Wave Velocity Dispersion and Attenuation in Fluid-Saturated Tight Sandstones: Characteristics Analysis Based on a Double Double-Porosity Structure Model Description[J]. Chinese Journal of Geophysics, 2018, 61(3): 1053-1068. DOI:10.6038/cjg2018L0678 |
| [19] |
何润发, 巴晶, 陈天胜, 等. 致密砂岩气藏裂隙-孔隙型弹性岩石物理模板研究: 以川西坳陷A区为例[J]. 地球物理学进展, 2020, 35(1): 116-123. He Runfa, Ba Jing, Chen Tiansheng, et al. A Study on Fracture-Pore Elastic Rock Physics Template of Tight Sandstone Gas Reservoirs: A Case Study of Area A in West Sichuan Depression[J]. Progress in Geophysics, 2020, 35(1): 116-123. |
| [20] |
逄硕, 刘财, 郭智奇, 等. 基于岩石物理模型的页岩孔隙结构反演及横波速度预测[J]. 吉林大学学报(地球科学版), 2017, 47(2): 606-615. Pang Shuo, Liu Cai, Guo Zhiqi, et al. Estimation of Pore-Shape and Shear Wave Velocity Based on Rock-Physics Modelling in Shale[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 606-615. DOI:10.13278/j.cnki.jjuese.201702304 |
| [21] |
张冰, 郭智奇, 徐聪, 等. 基于岩石物理模型的页岩储层裂缝属性及各向异性参数反演[J]. 吉林大学学报(地球科学版), 2018, 48(4): 1244-1252. Zhang Bing, Guo Zhiqi, Xu Cong, et al. Fracture Properties and Anisotropic Parameters Inversion of Shales Based on Rock Physics Model[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(4): 1244-1252. DOI:10.13278/j.cnki.jjuese.20170285 |
| [22] |
李博南, 曲寿利, 沈珲. 基于岩石物理模型的碳酸盐岩储层微观孔隙特征分析方法[J]. 吉林大学学报(地球科学版), 2020, 50(1): 285-293. Li Bonan, Qu Shouli, Shen Hui. Microscopic Characterization Method of Carbonate Reservoirs Based on Rock Physics Model[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(1): 285-293. DOI:10.13278/j.cnki.jjuese.20190001 |
| [23] |
Berryman J G. Mixture Theories for Rock Properties[M]. Washington, DC: American Geophysical Union, 1995: 205-228. DOI:10.1029/RF003p0205
|
| [24] |
Wood A B, Lindsay R B. A Textbook of Sound[J]. Physics Today, 1956, 9(11): 37. DOI:10.1063/1.3059819 |
| [25] |
Gassmann F. Uber die Elastizitat Poroser Medien[J]. Vier Der Natur Gesellschaft in Zurich, 1951, 96: 1-23. |
| [26] |
Bi ot, Maurice A. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low Frequency Range. Ⅱ. Higher Frequency Range[J]. The Journal of the Acoustical Society of America, 1955, 28(182): 168-191. |
| [27] |
Dvorkin J, Nur A. Dynamic Poroelasticity: A Unified Model with the Squirt and the Biot Mechanisms[J]. Geophysics, 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [28] |
Dvorkin J, Nolen-Hoeksema R, Nur A. The Squirt-Flow Mechanism: Macroscopic Description[J]. Geophysics, 1994, 59(3): 428-438. DOI:10.1190/1.1443605 |
| [29] |
Yan X F, Yao F C, Cao H, et al. Analyzing the Mid-Low Porosity Sandstone Dry Frame in Central Sichuan Based on Effective Medium Theory[J]. Applied Geophysics, 2011, 18(3): 163-170. DOI:10.1007/s11770-011-0293-1 |
| [30] |
Krief M, Garat J, Stellingwerff J, et al. A Petrophysical Interpretation Using the Velocities of P and S Waves (Full-Waveform Sonic)[J]. Log Analyst, 1990, 31: 355-369. |
| [31] |
Pride S R, Berryman J G, Harris J M. Seismic Attenuation Due to Wave-Induced Flow[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B1). DOI:10.1029/2003JB002639 |
| [32] |
Lee M W. A Simple Method of Predicting S-Wave Velocity[J]. Geophysics, 2006, 71(6): F161-F164. DOI:10.1190/1.2357833 |
| [33] |
Biot M A. General Theory of Three-Dimensional Consolidation[J]. Journal of Applied Physics, 1941, 12(2): 155-164. DOI:10.1063/1.1712886 |
| [34] |
Han D H, Batzle M. Gain Function and Hydrocarbon Indicators[J]. SEG Technical Program Expanded Abstracts, 2003, 22(1): 1695. DOI:10.1190/1.1817633 |


