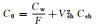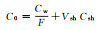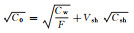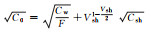0 引言
阿尔奇公式[1]提出以后,根据电阻率测井和孔隙度测井计算纯地层含水饱和度的方法得到广泛应用。阿尔奇公式的核心是计算出100%含水时岩石的电导率C0,通过与含油气时的岩石电导率Ct比较,计算出含水饱和度,因此C0是关键参数。但阿尔奇公式只适用于孔隙结构较为简单的纯砂岩地层,此时C0与地层水电导率Cw为线性关系。对于含泥质的地层,Patnode等[2]发现地层电导率和地层水电导率不满足线性关系。实验表明,地层水矿化度较低时,具有相同有效孔隙度的泥质砂岩的电导率比纯砂岩的电导率高,岩石表现出附加导电性Cex。黏土的存在使岩石的电导率关系(C0-Cw关系)复杂。C0是计算含水饱和度的重要依据,如果不能正确考虑泥质对电导率的影响,就无法得到正确的饱和度值。
解释泥质砂岩电性特征的导电模型大体上可以分成两类[3-4]:①泥质体积分数和分布形式的导电模型[5-7],主要描述孔隙度、泥质体积分数等对岩石电性的影响,因为与非电法测井方法(中子、密度、伽马射线和声波测井)有很好的相关性所以被用于测井分析中。但当地层水矿化度变化范围较大时,与岩心数据相差较大。这些公式都是通过统计数据得到的经验公式,只能在特定情况下使用。②电化学作用的导电模型[8-11],主要描述孔隙度和黏土阳离子交换能力等对岩石电性的影响,它们在不同地层水矿化度条件下与实验数据有很好的一致性,但因为阳离子交换能力的值通常难以得到,导致在实际测井中较难应用。
泥质砂岩具有复杂的组成成分与孔隙结构,基于实验室岩石电性测量难以控制变量,即难以定量分析岩石导电机理[12]。数字岩心技术可以将岩石数字化,较好地表征岩石孔隙结构[13-14]。近年来,许多学者通过数字岩心技术建立岩石模型,模拟计算岩石电性和弹性特征等[15-19]。本文在贝雷砂岩数字岩心的基础上,建立含黏土的数字岩心,考虑随地层水矿化度变化的黏土电导率变化,并利用有限元方法计算饱和水岩石的电导率,将结果与不同泥质砂岩导电模型的计算结果对比,评价经典泥质砂岩导电模型的适用条件。
1 理论基础 1.1 阿尔奇公式阿尔奇[1]1942年发现了均匀纯砂岩电阻率、孔隙度和含水饱和度之间的线性关系:
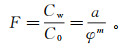 (1)
(1) 式中:F为地层因素;Cw为地层水电导率;a是岩性系数,通常取1;φ是岩石孔隙度;m是胶结指数。从此根据测井方法估计含水饱和度成为储层评价的一个重要手段。
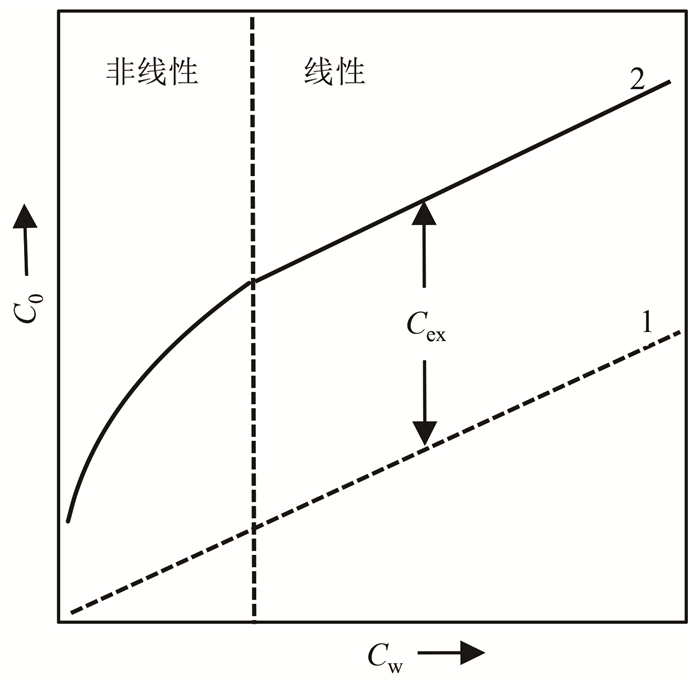
1.2 泥质砂岩导电模型图 1表示纯砂岩和泥质砂岩电导率C0随地层水电导率Cw变化的关系[3]。在Cw很低时,Cex随Cw增大而增加;当Cw达到某一数值后,Cex不随Cw变化。泥质是黏土矿物与其他细颗粒的混合物,泥质与岩石骨架的导电性差异主要在于黏土矿物,因此下文用黏土来代表泥质。围绕黏土附加导电性的问题,测井解释研究者先后针对地层饱和度求解问题提出了多种导电模型,其中经典的导电模型有:Hossin公式、Simandoux公式、Doll公式、Waxman-Smith公式(简称W-S公式)和Indonesia公式。表 1列出了这5种导电模型的公式和适用情况。
|
| 虚线1表示纯砂岩电导率与地层水电导率的关系;实线2表示泥质砂岩电导率与地层水电导率的关系。 图 1 含水泥质砂岩电导率与地层水电导率之间关系示意图 Fig. 1 Schematic diagram of the relationship between the brine-saturated rock conductivity and the brine conductivity |
|
|
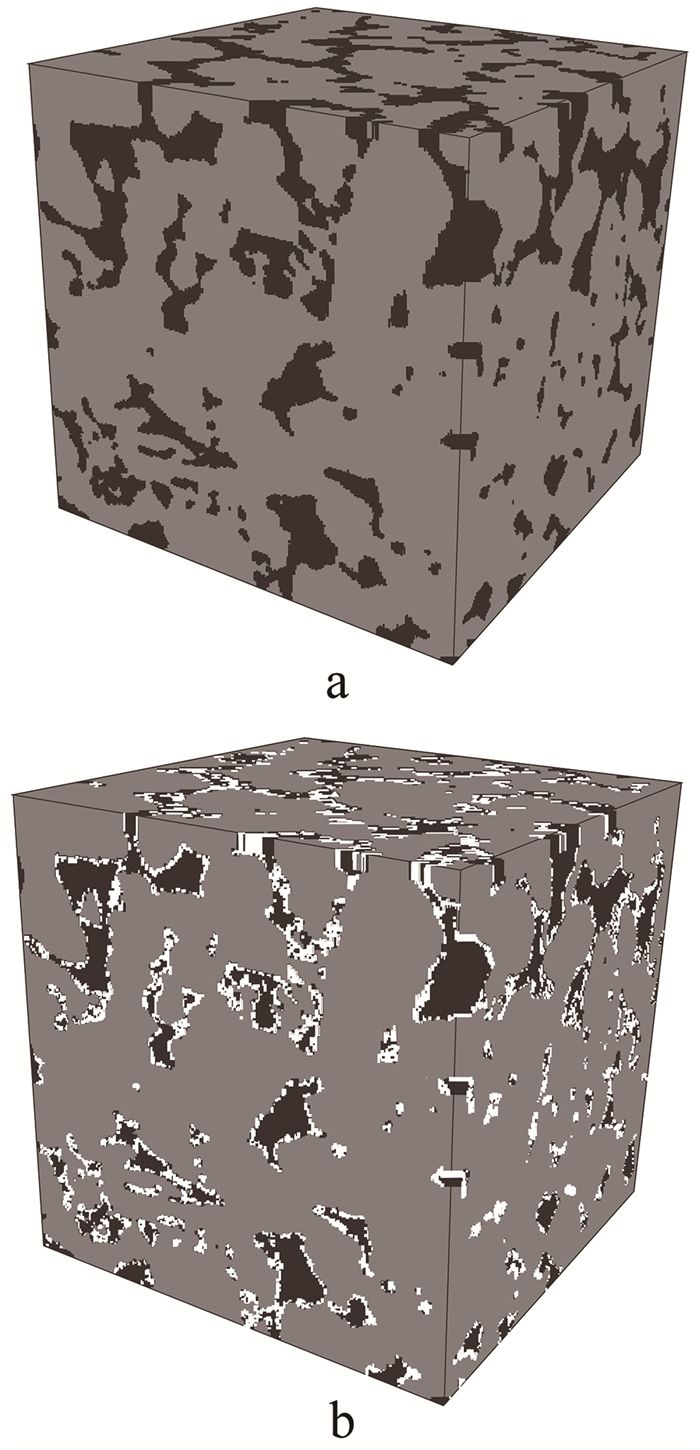
本文选择分辨率为5.35 μm/体素的贝雷砂岩的二值化图像[20],图像大小为200像素× 200像素×200像素(图 2a)。该岩石的孔隙度是19.62%。基于贝雷砂岩的数字岩心,添加黏土(在孔隙壁上沉积的黏土和将与孔隙壁连接的骨架蚀变为黏土,建立不同孔隙度和黏土体积分数的泥质砂岩)。图 2b是构建的含黏土砂岩。
|
| a. 贝雷砂岩的数字岩心;b. 含黏土砂岩的数字岩心(1.07 mm×1.07 mm×1.07 mm)。灰色代表岩石骨架,黑色代表孔隙空间,白色代表黏土矿物。 图 2 三维数字岩心 Fig. 2 Three-dimensional digital cores |
|
|
Garboczi[21]提出有限元方法(FEM)计算数字岩心的电性特征。有限元结果与实验数据显示出了很好的一致性。FEM基于线性导电性问题中的变分原理,并且通过能量最小原理利用共轭梯度法解拉普拉斯方程。在岩心的两端施加外部电场,三维数字岩心的每个像素代表一个结构单元,每个结构单元有8个节点。每个单元的能量可以表示为节点电压的函数:
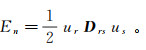 (2)
(2) 式中: n为每个体素的编号;ur和us分别为第n个体素上节点r和节点s的电压,r和s的变化范围为1~8;Drs是体素的刚度矩阵,表示能量与电压的关系。各体素能量的总和就是整个三维数字岩心的能量。根据能量最小原则,当能量对于电压的梯度为零时,可以确定每个体素上最终的能量分布:
 (3)
(3) 式中,um为一个体素中第m个节点的电压。
3 岩石电学特性数值模拟结果本文利用200像素×200像素×200像素的数字岩心图像来模拟泥质砂岩的电学性质,每个体素分别代表不同的岩石组分。假设岩石的骨架中不含导电矿物,即骨架不导电,设置骨架的电导率Cma为0.000 01 S/m。当岩石100%含水时,地层水矿化度对含黏土砂岩的电导率有重要影响。因此,本文设置了36个地层水电导率Cw(0.05~28.00 S/m)。对于黏土的电导率Cex,借助Waxman等[10]提出的经验公式来计算:
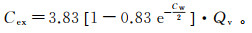 (4)
(4) 黏土电导率随地层水电导率的变化而变化。施加外加电场,采用有限元方法计算数字岩心饱和水情况下的电压分布,进而得到饱和水岩石的电导率C0。
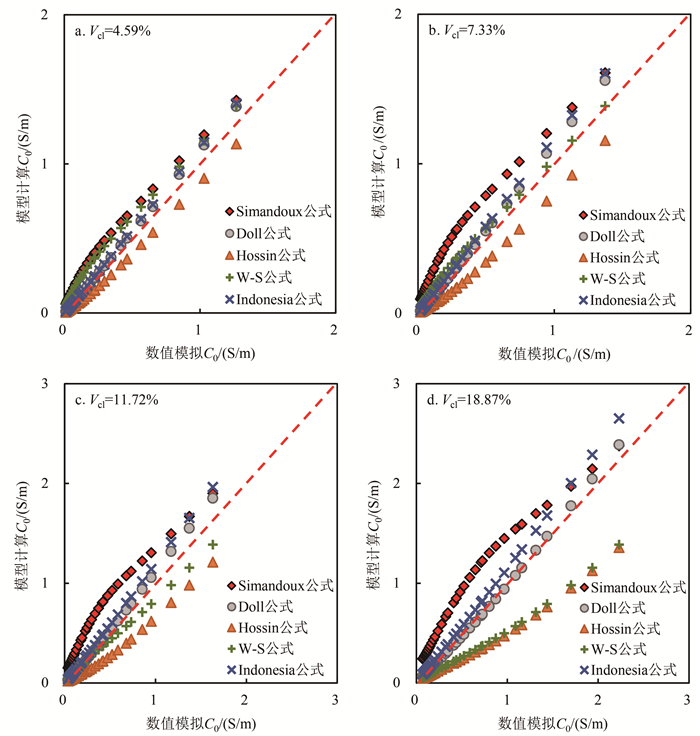
3.1 不同黏土体积分数表 2是构建不同黏土体积分数的数字岩心参数表。岩石的孔隙度均为19.62%,4块数字岩心的黏土体积分数逐渐增加,分别为4.59%、7.33%、11.72%和18.87%。设定岩心中黏土的Qv为1.74 mmol/mL,并根据公式(4)计算相应的黏土电导率。利用有限元方法计算得到饱和水岩心的电导率C0。与此同时,用表 1中传统的经验模型分别计算岩心的饱和水电导率C0。图 3是数字岩心模拟C0与模型计算C0交会图。可以看出,随着地层水电导率Cw的增加,计算误差增大。Indonesia公式和Doll公式的计算结果与数值模拟结果相关性较好,尤其是在低矿化度区间,Simandoux公式的计算结果与数值模拟结果相关性较差。Hossin公式的计算结果小于数值模拟结果,仅在黏土体积分数很低时(Vcl=4.59%)的计算结果与数值模拟结果相关性较好,随着黏土体积分数的增加,计算误差明显增大。黏土体积分数较大时(大于12%),W-S公式的误差较大。
| 编号 | φ/% | Vma/% | Vcl/% | Qv/(mmol/mL) | Cw/(S/m) |
| A1 | 19.62 | 75.79 | 4.59 | 1.74 | 0.05~28.00 |
| A2 | 19.62 | 73.05 | 7.33 | 1.74 | 0.05~28.00 |
| A3 | 19.62 | 68.66 | 11.72 | 1.74 | 0.05~28.00 |
| A4 | 19.62 | 61.51 | 18.87 | 1.74 | 0.05~28.00 |
| 注:Vc1为黏土体积分数;Vma为骨架体积分数。 | |||||
|
| 图 3 不同黏土体积分数的数字岩心数值模拟C0与模型计算C0交会图 Fig. 3 Relationship between numerical simulation results and equation calculation results with different clay volume |
|
|
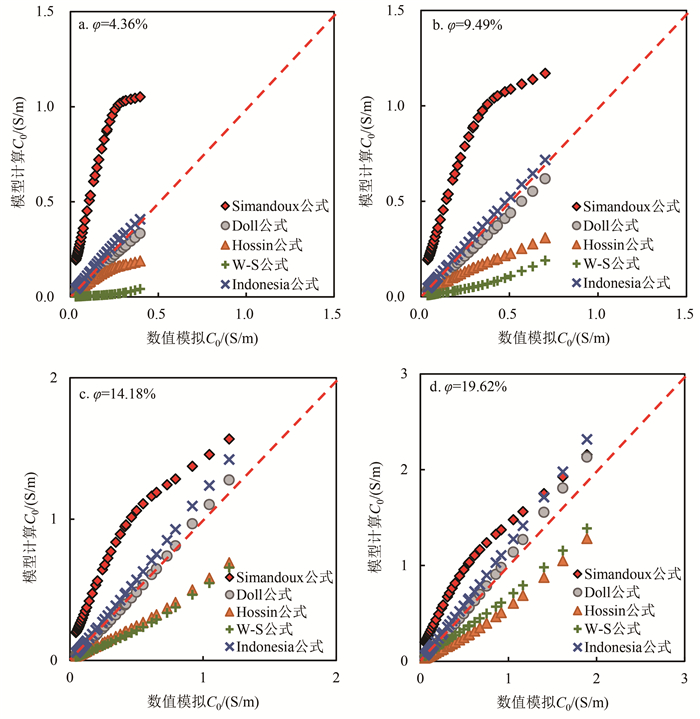
表 3是构建的不同孔隙度的数字岩心参数表。4块岩石的黏土体积分数均约为15%,孔隙度逐渐增大,分别为4.36%、9.49%、14.18%和19.62%。设定岩心中黏土的Qv为1.74 mmol/mL,并根据公式(4)计算相应的黏土电导率。利用有限元方法计算得到饱和水岩心的电导率C0。与此同时,我们用传统的经验模型分别计算岩心的饱和水电导率C0。图 4是数字岩心数值模拟C0与模型计算C0交会图。可以看出,随着地层水矿化度的增加,即地层水电导率Cw的增加,5个模型的计算误差增大。Indonesia公式和Doll公式的计算结果与数值模拟结果相关性较好。Simandoux公式和W-S公式的计算结果与数值模拟结果相关性较差。Hossin公式的计算结果小于数值模拟结果,仅在孔隙度很低时(φ=4.36%)且地层水矿化度较小时的计算结果与数值模拟结果相关性较好。
| 编号 | φ/% | Vma/% | Vcl/% | Qv/(mmol/mL) | Cw/(S/m) |
| B1 | 4.36 | 80.37 | 15.27 | 1.74 | 0.05~28.00 |
| B2 | 9.49 | 75.26 | 15.25 | 1.74 | 0.05~28.00 |
| B3 | 14.18 | 70.28 | 15.54 | 1.74 | 0.05~28.00 |
| B4 | 19.62 | 64.84 | 15.54 | 1.74 | 0.05~28.00 |
|
| 图 4 不同孔隙度的数字岩心数值模拟C0与模型计算C0交会图 Fig. 4 The relationship between numerical simulation results and equation calculation results with different porosity |
|
|
表 4是构建的不同阳离子交换容量Qv的数字岩心参数表。4块岩石的孔隙度均为19.62%,黏土体积分数均为15.54%。设定4块岩心中黏土的Qv分别为0.18、0.45、1.74和5.35 mmol/mL。并根据公式(4)计算相应的黏土电导率。利用有限元方法计算得到饱和水岩心的电导率C0。与此同时,我们用传统的经验模型分别计算岩心的饱和水电导率C0。图 5是数字岩心数值模拟C0与模型计算C0交会图。可以看出,随着地层水矿化度的增加,所有模型计算误差增大。从图 5a可以看出,当Qv很小时,5个模型的计算结果均接近数值模拟的结果。随着Qv的增大,Indonesia公式和Doll公式的计算结果与数值模拟结果相关性仍然较好。Simandoux公式的计算结果大于数值模拟结果。Hossin公式和W-S公式的计算结果小于数值模拟结果。
| 编号 | φ/% | Vma/% | Vcl/% | Qv/(mmol/mL) | Cw/(S/m) |
| C1 | 19.62 | 64.84 | 15.54 | 0.18 | 0.05~28.00 |
| C2 | 19.62 | 64.84 | 15.54 | 0.45 | 0.05~28.00 |
| C3 | 19.62 | 64.84 | 15.54 | 1.74 | 0.05~28.00 |
| C4 | 19.62 | 64.84 | 15.54 | 5.35 | 0.05~28.00 |

|
| 图 5 不同阳离子交换容量的数字岩心数值模拟C0与模型计算C0交会图 Fig. 5 The relationship between numerical simulation results and equation calculation results with different Qv |
|
|
1) 与数值模拟C0相比,Simandoux公式计算C0偏大,Hossin公式计算C0偏小,W-S公式计算C0普遍偏小。Doll公式和Indonesia公式计算C0与数值模拟C0接近,基本适用于不同孔隙度及黏土体积分数和阳离子交换容量的情况。
2) 黏土体积分数越小,黏土的阳离子交换容量越小,岩石孔隙度越大,5个公式计算的C0越接近数值模拟C0。
3) 随着地层水矿化度的增加,5个公式计算的C0与数值模拟C0的误差增大。
| [1] |
Archie G E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics[J]. Petroleum Technology, 1942, 146(1): 54-62. |
| [2] |
Patnode H W, Wyllie M R J. The Presence of Conductive Solids in Reservoir Rock as a Factor in Electric Log Interpretation[J]. Journal of Petroleum Technology, 1950, 2(2): 47-52. DOI:10.2118/950047-G |
| [3] |
李舟波, 潘保芝, 范晓敏. 地球物理测井数据处理与综合解释[M]. 北京: 地质出版社, 2008. Li Zhoubo, Pan Baozhi, Fan Xiaomin. Data Processing and Comprehensive Interpretation of Geophysical Logging Data[M]. Beijing: Geological Publishing House, 2008. |
| [4] |
Tenchov G. Improvement of an Equation for the Electrical Conductivity of Water Saturated Shaly Sands Using the Dual Water Model[J]. Dokladi na Bolgarskata Akademiya na Naukite, 1992, 45(11): 47-49. |
| [5] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 东营: 石油大学出版社, 2002. Yong Shihe, Zhang Chaomo. Logging Data Processing and Comprehensive Interpretation[M]. Dongying: China University of Petroleum Press, 2002. |
| [6] |
Simandoux P. Dielectric Measurements in Porous Media and Application to Shaly Formation[J]. Revue de L'Institut Français du Pétrole, 1963, 18: 193-215. |
| [7] |
Poupon A, Leveaux J. Evaluation of Water Saturations in Shaly Formation[J]. The Log Analyst, 1971, XII(4): 3-8. |
| [8] |
Winsauer W O, McCardell W M. Ionic Double-Layer Conductivity in Reservoir Rock[J]. Journal of Petroleum Technology, 1953, 5(5): 129-134. DOI:10.2118/953129-G |
| [9] |
Hill H I, Milbum J D. Effect of Clay and Water Salinity on Electrochemical Behavior of Reservoir Rocks[J]. Transactions of the AIME, 1956, 207: 65-72. DOI:10.2118/532-G |
| [10] |
Waxman M H, Smits L J M. Electrical Conductivities in Oil-Bearing Shaly Sands[J]. Society of Petroleum Engineers Journal, 1968, 8(2): 107-122. DOI:10.2118/1863-A |
| [11] |
Clavier C, Coates G, Dumanoir J. Theoretical and Experimental Bases for the Dual-Water Model for the Interpretation of Shaly Sands[J]. Society of Petroleum Engineers Journal, 1984, 24(2): 153-168. DOI:10.2118/6859-PA |
| [12] |
张丽华, 潘保芝, 王云梅, 等. 砂岩中绿泥石包膜与岩石润湿性及岩电参数的关系研究[J]. 石油物探, 2020, 59(4): 647-654. Zhang Lihua, Pan Baozhi, Wang Yunmei, et al. Relationship Between Pore-Lining Chlorite and Wettability of Rocks, and Rock Electrical Parameters of Sandstone[J]. Geophysical Prospecting for Petroleum, 2020, 59(4): 647-654. DOI:10.3969/j.issn.1000-1441.2020.04.015 |
| [13] |
李易霖, 张云峰, 丛琳, 等. X-CT扫描成像技术在致密砂岩微观孔隙结构表征中的应用: 以大安油田扶余油层为例[J]. 吉林大学学报(地球科学版), 2016, 46(2): 379-387. Li Yilin, Zhang Yunfeng, Cong Lin, et al. Application of X-CT Scanning Technique in the Characterization of Micro Pore Structure of Tight Sandstone Reservoir: Taking the Fuyu Oil Layer in Daan Oilfield as an Example[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 379-387. DOI:10.13278/j.cnki.jjuese.201602107 |
| [14] |
林承焰, 王杨, 杨山, 等. 基于CT的数字岩心三维建模[J]. 吉林大学学报(地球科学版), 2018, 48(1): 307-317. Lin Chengyan, Wang Yang, Yang Shan, et al. 3D Modeling of Digital Core Based on X-Ray Computed Tomography[J]. Journal of Jilin University(Earth Science Edition), 2018, 48(1): 307-317. DOI:10.13278/j.cnki.jjuese.20160305 |
| [15] |
Arns C H, Knackstedt M A, Pinczewski M V, et al. Accurate Estimation of Transport Properties from Microtomographic Images[J]. Geophysical Research Letters, 2001, 28(17): 3361-3364. DOI:10.1029/2001GL012987 |
| [16] |
Knackstedt M A, Arns C H, Pinczewskiz W V, et al. Computation of Linear Elastic Properties from Microtomographic Images: Methodology and Agreement Between Theory and Experiment[J]. Geophysics, 2002, 67(5): 1396-1405. DOI:10.1190/1.1512785 |
| [17] |
Liu X, Sun J, Wang H. Numerical Simulation of Rock Electrical Properties Based on Digital Cores[J]. Applied Geophysics, 2009, 6(1): 1-7. DOI:10.1007/s11770-009-0001-6 |
| [18] |
Yue W Z, Tao G, Chai X Y, et al. Digital Core Approach to the Effects of Clay on the Electrical Properties of Saturated Rocks Using Lattice Gas Automation[J]. Applied Geophysics, 2011, 8(1): 11-17. DOI:10.1007/s11770-010-0267-8 |
| [19] |
杨坤, 王付勇, 曾繁超, 等. 基于数字岩心分形特征的渗透率预测方法[J]. 吉林大学学报(地球科学版), 2020, 50(4): 1003-1011. Yang Kun, Wang Fuyong, Zeng Fanchao, et al. Permeability Prediction Based on Fractal Characteristics of Digital Rock[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(4): 1003-1011. |
| [20] |
Fan Y F, Pan B Z, Guo Y H, et al. Effects of Clay Minerals and Pore-Water Conductivity on Saturation Exponent of Clay-Bearing Sandstones Based on Digital Rock[J]. Petrophysics, 2020, 61(4): 352-362. |
| [21] |
Garboczi E J. Finite Element and Finite Difference Programs for Computing the Linear Electric and Elastic Properties of Digital Images of Random Materials[R]. Gaithersburg: National Institute of Standards and Technology Internal, 1998.
|