0 引言
地震断层滑动时会产生多普勒效应[1-4],卓钰如等[1]和Douglas等[2]用地震P波初至频率在地震断层周围的分布规律证实了多普勒效应在地震发生过程中的存在。上述方法在理论上清晰、准确,对于断层滑动速度较大的地震,在不同的方位P波初至的频率差异大,多普勒效应明显,容易判断多普勒效应的存在。如果地震断层滑动速度非常小,多普勒效应导致的处于不同方位的地震波P波初至差异不大,不易识别;如果进一步考虑到地震记录仪器的误差和P波拾取工作人员的能力差异,用该方法确定多普勒效应存在局限性。Ge Jin等[3]研究了汶川地震记录,用拐角频率确定了多普勒效应的存在。他们确定了汶川地震断层滑动左前方的拐角频率为0.054 Hz,而左后方的拐角频率为0.050 Hz,断层滑动破裂前方的拐角频率略大于后方;还确定了地震断层滑动右前方的拐角频率为0.082 Hz,而右后方的拐角频率为0.072 Hz,也是前方略大于后方。如果拐角频率准确,这种方法用于判断多普勒效应是否存在是可行的,但问题是拐角频率的确定有一定的人为因素。刘瑞丰等[4]在研究汶川地震记录后,从三方面证实地震过程中存在多普勒效应:第一,用面波震级在空间不同的分布来证实多普勒效应的存在,他们认为多普勒效应使得断层破裂传播前方振动加强、后方振动减弱,表现出来的就是前方测定的面波震级偏大,后方测定的偏小;第二,用地震烈度的空间分布判定多普勒效应的存在,他们认为多普勒效应使得断层破裂传播前方地震烈度衰减慢,后方衰减快;第三,用破裂的方向性效应确定多普勒效应的存在,他们认为多普勒效应使得在地震断层破裂传播方向上的能量快速聚集,同时在相反方向的能量迅速降低,因此地震动幅值在空间有规律的分布证实了多普勒效应的存在。上述用多普勒效应解释地震动方向性效应的观点已存在多年,自1966年美国Parkfield地震第一次记录到断层破裂的方向性效应以来[5],陆陆续续记录到了地震断层破裂的方向性效应。比如,1979年美国Imperial Valley地震[6]、1992年美国Landers地震[7]和1999年中国台湾集集地震[8],此外还有多次大地震都记录到了地震动的方向性效应[9-14]。并且有很多学者都用地震动的方向性效应证实多普勒效应的存在,或者用多普勒效应解释地震动的方向性效应[1, 10]。
面波震级和地震烈度都与地震动振幅有关,所以无论是用面波震级空间分布、还是用地震烈度空间分布判定多普勒效应,本质上都是用地震动振幅强弱的空间分布,即都用地震动的方向性效应证实多普勒效应的存在,都认为多普勒效应使得在断层破裂前方的地震动加强。这是不正确的,因为多普勒效应是在运动物体前方接收到波的频率增大,注意是频率增大,而不是振幅增大,简单认为多普勒效应使能量聚集是概念不清的表现。恰恰相反,如果考虑到地震波的高频衰减作用,仅仅由于地震波频率的增大,不仅不会导致地震波传播过程中振幅的加强,反而会导致高频振幅的迅速衰减,当然低频地震波幅值也会衰减,但衰减得慢。另外,有部分学者认为用多普勒效应可以确定断层的破裂传播速度[1],这是混淆了地震断层滑动速度与断层破裂传播速度的区别,断层破裂传播时可以不滑动,类似于用剪刀剪布,剪得快,破裂传播得快,但布没有滑动,破裂传播不会产生多普勒效应,只有断层滑动,即产生位错时才会出现多普勒效应。
利用地震断层滑动过程中产生的多普勒效应可以确定地震过程中断层的滑动速度[15-17],可以确定地震破裂面[11]。对地震过程中多普勒效应的研究是地震工程的一项基础工作,有助于加强对地震工程概念的深入理解, 有助于地震工作者在重视地震动幅值研究的前提下,开始重视对地震动频率空间分布的研究。为使确定多普勒效应是否存在的方法更明确,本论文提出用小波变换确定地震中的多普勒效应。
1 多普勒效应导致的地震时地震波频率空间分布具有波动性物质的波源和观察者之间发生相对运动时,观察者接收到波的频率与发出频率不同的现象,称为多普勒效应,表示为[17-18]
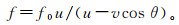 (1)
(1) 式中:f是观察者接收到的频率;f0是断层发出的频率;u是地震波的传播速度;v是断层滑动速度,也就是波源的速度;θ是断层上的波源和观察者连线与断层上的波源滑动方向的夹角,称之为方位角。地震断层滑动时,在不同的方位观察者接收到的地震波频率不同。
从式(1)可以看出:如果观察者位于断层滑动的前方,即-90° < θ < 90°,接收到地震波的频率高于实际频率;如果观察者位于断层滑动的后方,即90° < θ < 270°,接收到地震波的频率低于实际频率;如果观察者位于断层滑动破裂的垂直方向,即θ=90°或270°,接收到的地震波频率等于实际频率。
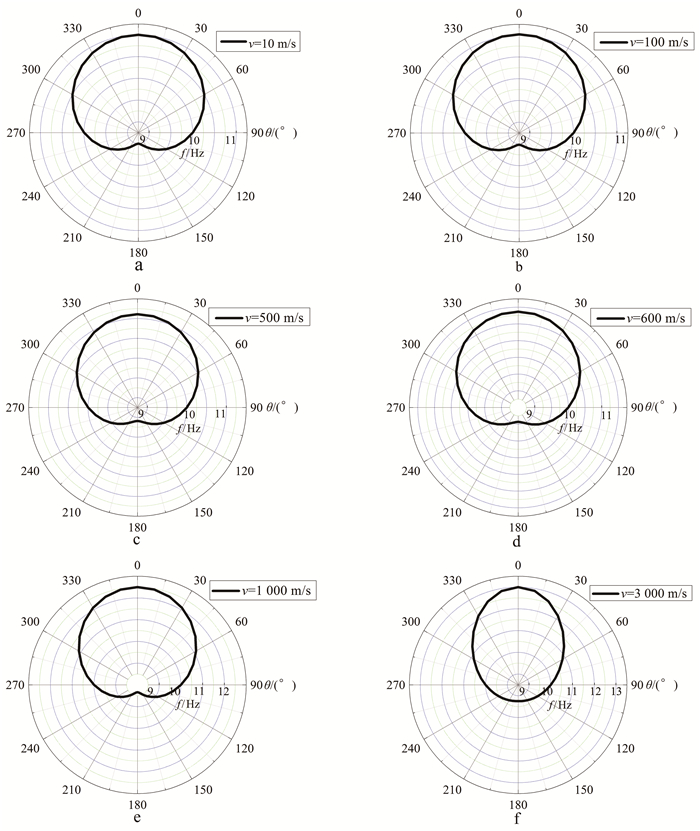
为了进一步说明在多普勒效应作用下,断层滑动时产生的地震波频率在空间的分布规律,假定式(1)中u=5 000 m/s,f0=10 Hz,在图 1中绘制了地震波频率随空间方位角的变化。从图 1可以看出:在断层滑动的垂直方向,接收到的地震波频率等于断层发出的实际频率;在断层滑动的前方,接收到的地震波频率高于断层发出的实际频率;在断层滑动的后方,接收到的频率低于断层发出的实际频率。反过来,如果地震断层周围有上述频率分布,说明地震时存在着多普勒效应。从图 1还可以看出,地震断层滑动速度越大,地震断层滑动前方接收到的地震波频率越高,地震断层滑动后方接收到的地震波频率越低,说明断层滑动速度越大,多普勒效应越明显,越容易被观测到。
|
| u=5 000 m/s; f0=10 Hz。 图 1 多普勒效应导致的频率空间分布 Fig. 1 Spatial distributions of frequencies caused by Doppler effect |
|
|
傅里叶变换处理随时间稳定不变的信号具有良好效果,但对于类似于地震记录的非平稳信号,由于傅里叶变换是对整个信号的全局变换,不具有“时间-频率”的局部化分析能力,使得傅里叶变换对非平稳信号处理很难捕捉到细节变化。短时傅里叶变换虽然提高了对信号时间的定位能力,但其滑动窗函数在运算过程中固定不变,这导致其不具备自适应能力。
Morlet于1974年提出小波变换的理论,它继承了短时傅里叶变换的局部化思想,并克服了傅里叶变换窗口大小不能随波频率变化的缺点,提供了可以随频率改变的“时间-频率”窗口,简称“时-频”窗口,使得小波变换能对时间域和频率域进行局部化分析,而不是像傅里叶变换只能进行全局分析[19]。小波变换通过伸缩平移运算对信号进行多尺度细化,最终达到在信号高频处进行时间细化处理、在信号低频处进行频率细化处理,并逐步适应时频信号高质量分析的要求,可以突出体现信号的所有细节,解决了傅里叶变换仅考虑信号全局变化、不具有全局分析能力、不能很好分析类似地震等非平稳信号的缺点。
采用下式对地震信号进行小波分析:
 (2)
(2) 式中:ψ(t)为复Morlet小波;t为地震记录时刻;带宽F取为2;中心频率E取为1。由小波基通过平移和伸缩产生小波函数,得到
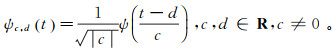 (3)
(3) 式中:c为尺度因子,c=2j, j=0, 1, …;d为平移因子,d=0.005c,限制在采样时间内。对以时间t为自变量的地震加速度信号f(t)做以式(3)为小波函数的小波变换,得到以时间和地震信号周期为自变量的小波谱:
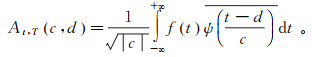 (4)
(4) 式中:At, T c, d简称为小波谱;T为地震信号周期。
选择地震台站0~5 s最初时段的地震记录,用公式(4)对地震记录进行小波变换。选择最初时段分析的优点是该时段没有反射波和折射波的干扰,也不存在波形转换的问题,同时该时段断层速度变化规律比较强。小波变换取周期为0~1 s范围,而不是取某频率范围,因为从理论上讲,周期0~1 s包含了所有的高频,而一个再大的频率数值也不能包括所有的高频,而包含所有高频才可能捕捉到多普勒效应。
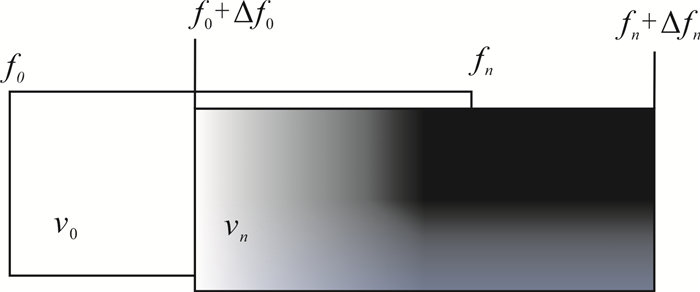
由于多普勒效应的存在,位于前方台站接收到的地震波频率会增大,而位于后方台站接收到的地震波频率会降低。假定台站位于断层滑动破裂前方,断层滑动速度最初为v0,其发出地震波被台站接收到的频率范围为f0~fn,如图 2所示。以后断层滑动速度不断增加:当断层滑动速度增至vn时,接收到的频率范围变为[f0+Δf0, fn+Δfn](Δf0为f0的增量,Δfn为fn的增量);断层滑动速度为v0时,接收到的频率带用白色矩形表示,断层滑动速度为vn时,接收到的频率带用黑色矩形表示。因速度是连续变化的,中间有一系列频带没有画出。其重叠部分f0+Δf0至fn是相对高频部分,该频段经多次叠加,振幅会增强。即使断层滑动速度由大变小,只要台站位于断层破裂前方,就会出现高频段振幅增强,图 2中的黑色矩形就是从右向左移动,也就是由高频向相对低频移动。对位于地震断层滑动破裂后方的台站接收到的频率进行同样的分析可以得出,其低频振幅会增强。
|
| 图 2 多普勒效应引起小波谱变化示意图 Fig. 2 Diagram of Wavelet spectrum change caused by Doppler effect |
|
|
地震波小波谱幅值随频率的变化取决两种因素:其一是震中距,由于介质对地震波的吸收衰减作用,使得震中距越大的台站接收到的小波谱幅值越低,并且地震波频率越高,小波谱幅值衰减越快;其二是多普勒效应,在断层滑动破裂垂直方向不产生多普勒效应,在断层滑动破裂前方,多普勒效应使得接收到的小波谱高频幅值因叠加增强,在断层滑动破裂后方,多普勒效应使得接收到的小波谱低频幅值因叠加增强。在断层的垂直方向,小波谱幅值仅仅由介质对地震波的吸收衰减作用决定,其小波谱高频幅值一定会衰减得比低频快,震中距较大台站小波谱低频幅值会大于高频幅值。在断层滑动破裂前方和后方,小波谱幅值由介质对地震波的吸收衰减和多普勒效应共同决定,介质对地震波的吸收衰减作用使小波谱幅值减弱,但高频衰减更快;在断层滑动破裂前方,多普勒效应使得地震波频率向高频移动,并在高频部分叠加而增强,在断层滑动破裂的后方,多普勒效应使得地震波频率向低频移动,并在低频部分叠加而增强。在两种因素的共同作用下,在断层滑动破裂前方,小波谱幅值的高频部分相对于低频会高,在断层滑动破裂后方,小波谱幅值的低频部分相对于高频会高。
在地震断层滑动垂直方向选多个台站,计算其0~5 s的地震记录小波谱,如果小波谱幅值随震中距增大而减小,特别是高频部分衰减得更快,说明该方向没发生多普勒效应。在断层滑动破裂的前方选多个台站,同样计算其0~5 s的地震记录小波谱,如果小波谱低频幅值随震中距增大明显减小,同时小波谱高频幅值明显大于低频部分,说明该方向存在多普勒效应。在断层滑动破裂的后方选多个台站,经同样的处理,如果随震中距的增大小波谱低频幅值明显大于高频部分,同样可以说明该方向存在多普勒效应。
3 汶川地震中的多普勒效应汶川地震震中位于汶川,断层分别向北东和南西向破裂并滑动,以北东向为主[20],我们仅研究沿北东方向的破裂。汶川地震断层是逆冲断层,其水平滑动速度分量不太大,因此该地震的多普勒效应不太明显。
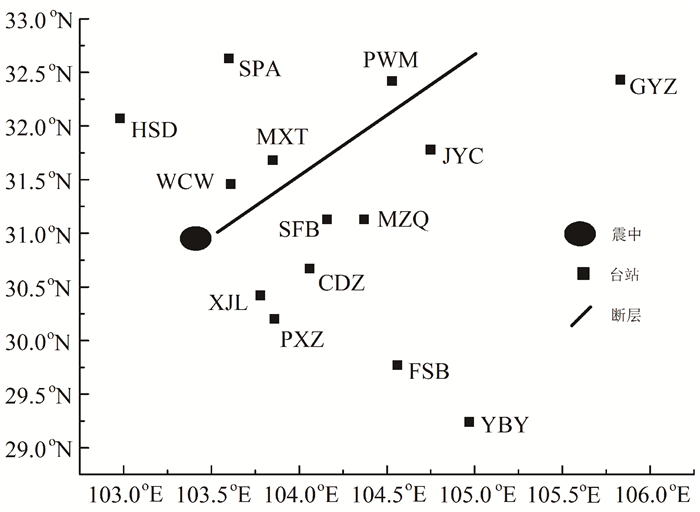
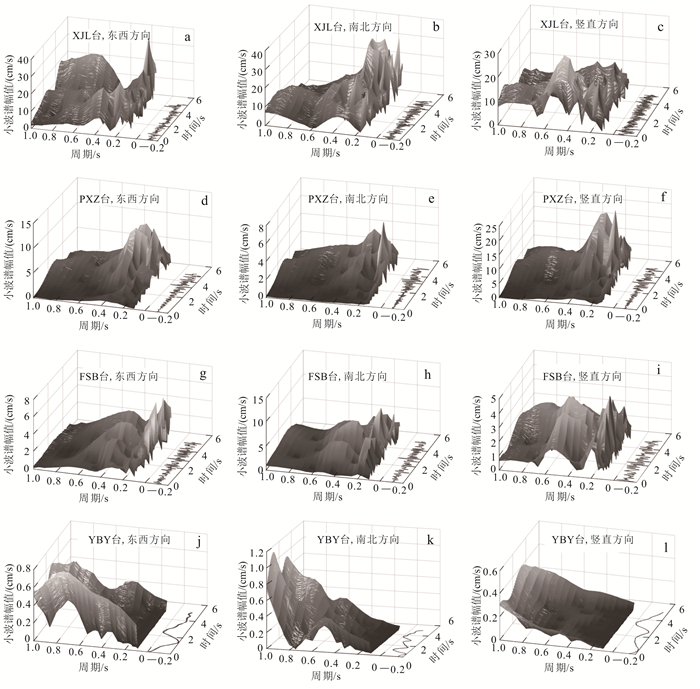
图 3是汶川地震台站和断层示意图。其中XJL和PXZ台站在断层滑动的垂直方向上,FSB和YBY台位于大致与断层滑动的垂直方向,这4个地震接收台站的震中距依次增大。图 4依次是上述四台站东西、南北和竖直方向地震发生0~5 s内的小波谱,小波谱的周期变化范围是0~1 s,对应的频率为1~∞ Hz,实际计算得到的频率范围是1~10 Hz。
|
| 图 3 汶川地震台站分布 Fig. 3 Distributions of stations in Wenchuan earthquake |
|
|
|
| 图 4 与断层滑动方向垂直台站的小波谱 Fig. 4 Wavelet spectrum of stations that are perpendicular to the direction of fault sliding |
|
|
由图 4a、b、c可知,XJL台站东西方向的小波谱在周期为0.1 s(频率为10 Hz,下同)时小波谱幅值达到最大,为34 cm/s,此时南北和竖直方向小波谱幅值分别为30、10 cm/s。由于该台站距离震中最近,相对其他台站周期为0.1~1.0 s,即频率在1~10 Hz的频段内,无论是高频还是低频,其计算得到的小波谱幅值都较高,尤其是高频幅值更高。
由图 4d、e、f可知,PXZ台站东西方向的小波谱在周期为0.1 s时达到最大,为9 cm/s,此时南北和竖直方向小波谱幅值分别为4、15 cm/s。由于该台站震中距大于XJL台站,在周期为0.1~1.0 s时,无论是高频还是低频,其小波谱幅值都较低。
由图 4g、h、i可知,FSB台站东西方向的小波谱在周期0.1 s时达到最大,为2.5 cm/s,此时南北和竖直方向小波谱幅值分别为4.7、2.3 cm/s。由于该台站震中距较大,相对其他台站周期为0.1~1.0 s时,无论是高频还是低频,其小波谱幅值都较低。
由图 4j、k、l可知,YBY台站东西、南北和竖直方向的小波谱在周期为0.1 s时高频处的小波谱都比较低,最大幅值都出现在周期为1.0 s的低频处,高频幅值明显小于低频幅值;表明地震波高频衰减严重,也说明该方向没产生多普勒效应。
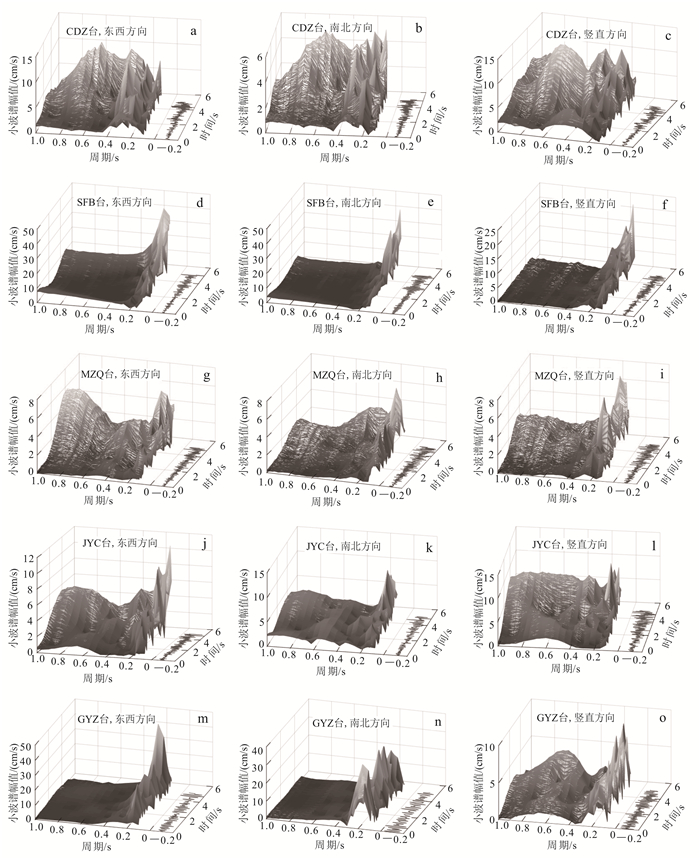
CDZ、SFB、MZQ、JYC和GYZ台站都处于断层走向的东南侧、靠近断层且都处于断层滑动的前方,震中距依次增大。图 5依次是上述五台站东西、南北和竖直方向、地震发生0~5 s内的小波谱,小波谱的周期变化范围是0~1 s,对应的频率为1~∞ Hz,实际计算得到的频率范围是1~10 Hz。
|
| 图 5 断层走向东南侧台站的小波谱 Fig. 5 Wavelet spectrum of the stations along the fault strike in direction of southeast |
|
|
从图 5a、b、c可以看出,CDZ台站三分量小波谱幅值在所在研究时段内相对以后的4个台站比较均匀,高频处也没有明显的高幅值。这是因为该台站震中距较小,各频率的衰减不明显;同时,由于相对于其他台站该台站更接近于与断层滑动方向垂直,所以不会产生明显的多普勒效应。
从图 5d、e、f可以看出,SFB台站三分量小波谱幅值在周期为0.1 s的高频段有明显大于低频部分的幅值。这是因为随着震中距的增加,各频率地震波衰减加剧;同时该台站处于断层滑动前方,会产生多普勒效应,而多普勒效应会使地震波在较高频率处叠加形成高频幅值。
从总体上看,图 5中的MZQ台站、JYC台站、GYZ台站在短周期,也就是高频段附近出现明显大于低频部分的小波谱幅值,都同样可以用多普勒效应得到解释。
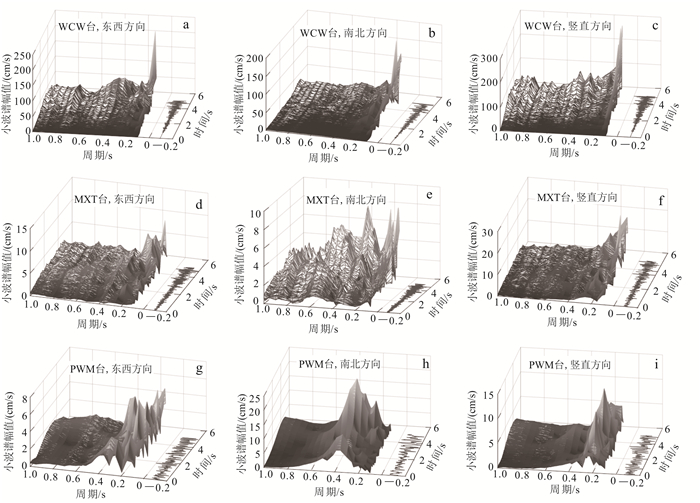
WCW、MXT、PWM台站都处于断层走向的西北侧、靠近断层、且都处于断层滑动的前方,3个地震接收台站的震中距依次增大。图 6依次是上述三台站东西、南北和竖直方向地震发生0~5 s内的小波谱,小波谱的周期变化范围是0~1 s,对应的频率为1~∞ Hz,实际计算得到的频率范围是1~10 Hz。上述台站在短周期,也就是高频段附近出现明显大于低频部分的小波谱幅值,都可以用多普勒效应得到解释。
|
| 图 6 断层走向西北侧台站的小波谱 Fig. 6 Wavelet spectrum of the stations along the fault strike in direction of northwest |
|
|
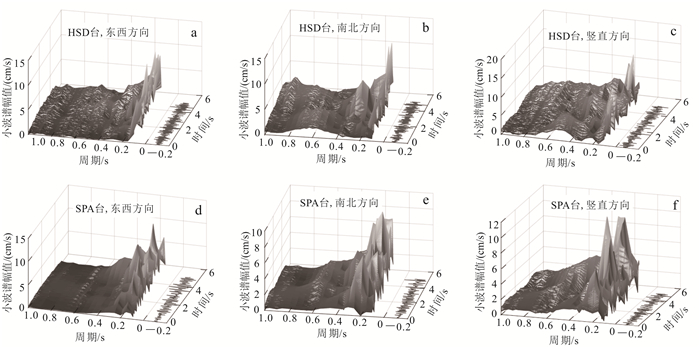
HSD和SPA台站都处于断层走向的西北侧、远离断层、且都处于断层滑动的前方,两个地震接收台站的震中距依次增大。图 7依次是上述二台站东西、南北和竖直方向地震发生0~5 s内的小波谱,小波谱周期实际变化范围是0.1~1.0 s,对应的频率为1~10 Hz。上述台站在周期0.1~0.2 s,也就是5~10 Hz附近出现明显大于低频部分的小波谱幅值,都可以用多普勒效应得到解释。
|
| 图 7 断层走向西北侧、远离断层台站的小波谱 Fig. 7 Wavelet spectrum of stations along the fault in direction northwest, away from the fault |
|
|
目前拾取P波初至确定地震过程中存在多普勒效应的方法理论上是可行的,但对于地震断层滑动速度较小的情况,以及地震记录仪器灵敏度和科技工作者自身能力问题,可能导致无法准确确定多普勒效应的存在。长期以来普遍承认的用地震动的方向性效应、面波震级空间分布、拐角频率空间分布和地震烈度空间分布判定多普勒效应的存在是对多普勒效应的不正确理解,用多普勒效应计算地震断层破裂传播速度在理论上是没依据的。
用小波变换确定地震中的多普勒效应方法强调,在断层滑动破裂的前方,由于滑动速度持续增加使得小波谱高频幅值叠加,并克服地震波传播过程中介质对高频具有的强吸收衰减作用,使得小波谱高频幅值得到增强;在断层滑动破裂后方,断层的滑动使得小波谱低频幅值叠加,并克服地震波传播过程中介质对全部地震波具有的吸收衰减作用,使得小波谱低频幅值得到增强;在断层的垂直方向,仅仅是吸收衰减起作用,该方向上所用小波谱幅值都会降低,并且高频降低得更快。我们完全可以根据断层滑动破裂前方多个台站小波谱高频幅值大于低频,并根据断层滑动破裂后方多个台站小波谱低频幅值大于高频判定多普勒效应的存在。
用小波变换确定地震中的多普勒效应具有明确的物理意义,其中数学运算有理论基础,在使用时要求地震记录台站密集且分布范围广。幸运的是,随着经济的不断发展,我国地震台网的建设已经取得长足的进步,并不断地满足地震工作者研究的需求。对地震过程中多普勒效应的研究是地震工程的一项基础工作,有助于加强对地震工程概念的深入理解,有助于地震工作者在重视地震动幅值的前提下开始重视对地震动频率空间分布的研究。
| [1] |
卓钰如, 李文香, 龚镇雄. 用多普勒效应研究中小地震的破裂面和破裂传播速度[J]. 地震学报, 1982, 4(1): 16-28. Zhuo Yuru, Li Wenxiang, Gong Zhenxiong. A Study of the Rupture Surfaces and Velocity of Propagation of Rupture of Small and Medium Size Earthquakes Based on Their Doppler Effect[J]. Acta Seismological Sinica, 1982, 4(1): 16-28. |
| [2] |
Douglas A, Hudson J A, Marshall P D. Earthquake Seismograms that Show Doppler Effects Due to Crack Propagation[J]. Geophysical Journal International, 1981, 64(1): 163-185. DOI:10.1111/j.1365-246X.1981.tb02664.x |
| [3] |
Ge Jin, Tang Youcai, Zhou Shiyong, et al. Doppler Effect of the Rupture Process of the Great MW7.9 Wenchuan Earthquake[J]. Earthquake Science, 2010, 23(6): 535-539. DOI:10.1007/s11589-010-0752-4 |
| [4] |
刘瑞丰, 邹立晔, 张立文. 汶川地震的面波震级测定及其多普勒效应[J]. 地震学报, 2018, 40(3): 364-373. Liu Ruifeng, Zou Liye, Zhang Liwen. Determination of the Surface-Wave Magnitude of the Wenchuan Earthquake and Its Seismic Doppler Effect[J]. Acta Seismologica Sinica, 2018, 40(3): 364-373. |
| [5] |
Aki K. Seismic Displacement near a Fault[J]. J Geophys Res, 1968, 73: 5359-5376. DOI:10.1029/JB073i016p05359 |
| [6] |
Saburoh M. Rupture History of the 1979 Imperial Valley Earthquake Estimated from EL Centro Strong-Motion Accelerograms[C]//Proceedings of Ninth World Conference on Earthquake Engineering: Vol Ⅱ. Tokyo-Kyoto: Conference Committee, 1988: 277-282.
|
| [7] |
Mavroeidis G P, Papageorgiou A S. Near-Source Strong Ground Motion: Characteristics and Design Issues[C]//Proc of the Seventh U. S. National Conf on Earthquake Engineering (7NCEE). Boston: [s. n. ], 2002: 21-25.
|
| [8] |
Wang G Q, Zhou X Y, Zhang P Z, et al. Characteristics of Amplitude and Duration for near Fault Strong Ground Motion from 1999 Chi-Chi, Taiwan Earthquake[J]. SoilDyn Earthquake Eng, 2002, 22: 73-96. DOI:10.1016/S0267-7261(01)00047-1 |
| [9] |
Somerville P G, Smith N F, Graves R W, et al. Modification of Empirical Strong Ground Motion Attenuation Relations to Include the Amplitude and Duration Effects of Rupture Directivity[J]. Seism Res Lett, 1997, 68: 199-222. DOI:10.1785/gssrl.68.1.199 |
| [10] |
刘启方, 袁一凡, 金星, 等. 近断层地震动的基本特征[J]. 地震工程与工程震动, 2006, 26(1): 1-10. Liu Qifang, Yuan Yifan, Jin Xing, et al. Basic Characteristics of Near-Fault Ground Motion[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(1): 1-10. |
| [11] |
Frez J, Nava F A, Acosta J. Source Rupture Plane Determination from Directivity Doppler Effect for Small Earthquakes Recorded by Local Networks[J]. Bulletin of the Seismological Society of America, 2010, 100(1): 289-297. DOI:10.1785/0120090139 |
| [12] |
He X, Zhan Z, Zhang P, et al. Rupture Directivity of the 18 April 2008 Mt Carmel, Illinois, Earthquake from Modeling of Local Seismic Waveforms[J]. Bulletin of the Seismological Society of America, 2018, 108(6): 3278-3288. DOI:10.1785/0120180156 |
| [13] |
He X, Ni S. Resolving Horizontal Rupture Directivity of Moderate Crustal Earthquake in Sparse Network with Ambient Noise Location[J]. Journal of Geophysical Research: Solid Earth, 2018, 123: 533-552. DOI:10.1002/2017JB014735 |
| [14] |
Xie Junju. Strong-Motion Directionality and Evidence of Rupture Directivity Effects During the Chi-Chi Mw 7.6 Earthquake[J]. Bulletin of the Seismological Society of America, 2019, 109(6): 2367-2383. DOI:10.1785/0120190087 |
| [15] |
Li Qicheng, He Shugeng, Min Ye, et al. The Sliding Speed Calculation of the Wenchuan Earthquake Fault with the Doppler Effect[J]. Applied Geophysics, 2019, 16(3): 1-10. DOI:10.1007/s11770-018-0720-7 |
| [16] |
李启成, 何书耕, 闵也. 龙门山断层破裂的频率方向性效应[J]. 吉林大学学报(地球科学版), 2019, 49(3): 865-871. Li Qicheng, He Shugeng, Min Ye. Frequency Non-Stationary of Longmanshan Fault Rupture[J]. Journal of Jilin University (Earth Edition), 2019, 49(3): 865-871. |
| [17] |
Wan Yongge. Introduction to Seismology[M]. Beijing: Science Press, 2016.
|
| [18] |
Wan Yongge, Shen Zhengkang, Roland B, et al. Fault Geometry and Slip Distribution of the 2008 MW7.9 Wenchuan, China Earthquake Inferred from GPS and InSAR Measurements[J]. Geophysical Journal International, 2016, 208: 748-766. |
| [19] |
张彬, 杨风暴. 小波分析方法及其应用[M]. 北京: 国防工业出版社, 2011. Zhang Bin, Yang Fengbao. Wavelet Analysis Method and Its Application[M]. Beijing: National Defense Industry Press, 2011. |
| [20] |
张勇, 冯万鹏, 许力生, 等. 2008年汶川大地震的时空破裂过程[J]. 中国科学: D辑: 地球科学, 2008, 38(10): 1186-1198. Zhang Yong, Feng Wanpeng, Xu Lisheng, et al. The Time and Space Rupture Process of the Wenchuan Earthquake in 2008[J]. Chinese Science: D Series: Earth Science, 2008, 38(10): 1186-1198. DOI:10.3321/j.issn:1006-9267.2008.10.002 |


