2. 中核集团铀资源勘查与评价技术重点实验室, 北京 100029;
3. 自然资源部东北亚矿产资源评价重点实验室(吉林大学), 长春 130061
2. Key Laboratory of Uranium Resource Exploration and Evaluation Technology, CNNC, Beijing 100029, China;
3. Key Laboratory of Mineral Resources Evaluation in Northeast Asia (Jilin University), Ministry of Natural Resources, Changchun 130061, China
0 引言
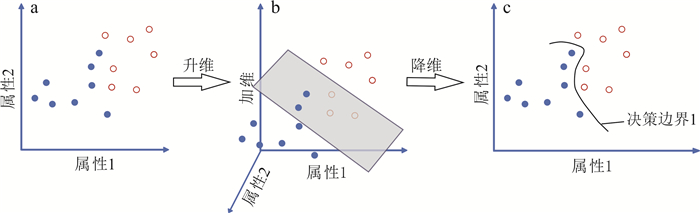
随着以机器学习、深度学习为基础的人工智能技术在社会多个领域展开应用,地质科学领域也逐渐引入机器学习的方法,并开始应用于地球化学数据分类[1-5]、显微镜下矿石矿物的自动识别[6]、异常提取和矿产资源预测[7-11]等领域,已取得了较好的实际效果。采用的机器学习分类算法包括朴素贝叶斯(naive bayesian,NB)、支持向量机(support vector machine,SVM)、随机森林(random forest,RF)、K近邻(K nearest neighbor,KNN)等。不同类型铀矿床的沥青铀矿/晶质铀矿具有不同的稀土元素特征,利用稀土元素配分曲线和w(ΣREE)-(LREE/HREE)N可区分全球主要类型的代表性铀矿床[12-13],并取得了较好的应用效果[13-15]。但是,由于传统地球化学判别图使用维度较少,信息利用不充分,判别图对高维数据的判别准确率难以保障。而机器学习算法可以在高维空间中解决地球化学分类问题,且具有较好的应用效果[16-17]。我们收集了Mercadier等[12]、Frimmel等[13]与Balboni等[18]文章中的216组沥青铀矿/晶质铀矿稀土元素数据,并创建了14维数据集(仅包含稀土元素)与17维数据集(稀土元素、稀土总量、轻重稀土比、铕异常)。两类数据集分别通过PCA(principal component analysis)-SVM算法进行训练并对24组同变质类型胡家峪晶质铀矿进行判别比较,并与稀土元素配分曲线和w(ΣREE)-(LREE/HREE)N图解进行对比分析,以期为进一步深化基于沥青铀矿/晶质铀矿稀土元素数据判别铀矿床类型的研究提供新途径。
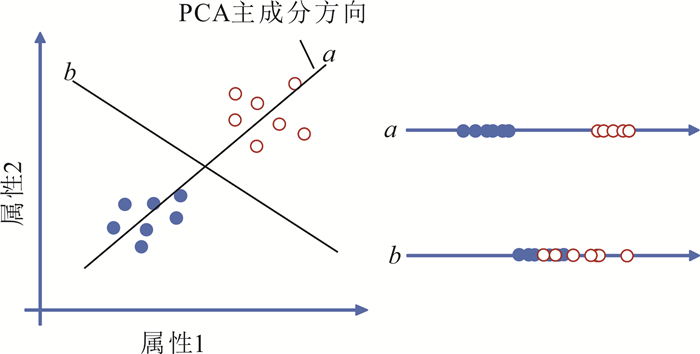
1 PCA/SVM算法原理 1.1 主成分分析主成分分析[19]是一种非监督的机器学习算法。PCA将数据集沿着差异性最大的方向进行投影,且各个投影方向相互垂直。原理如图 1所示,将数据投影在a轴相比投影在b轴有更大的差异性,投影之后丢失的信息更少,a轴代表了数据集差异性最大的方向,即主成分方向,也是数据集信息量最大的方向。PCA处理高维数据集时,会根据每一个主成分信息量占比,从大到小生成与原始数据集相同维数的主成分数据集,应用时在保障信息量足够的前提下,保留前k个主成分就可完成原始数据集的降维。
|
| 实心、空心圈分别代表两组不同的数据。下同。 图 1 主成分分析原理图 Fig. 1 Principle diagram of PCA |
|
|
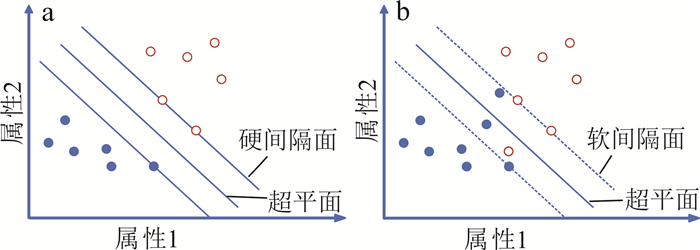
支持向量机[20]是一种二分类模型,目的是寻找一个超平面对样本进行分割,分割原则是间隔最大化。支持向量机主要解决二元分类问题,也可以扩展到多元分类[21]。线性硬间隔SVM分类器是最基本的原型,仅适用于理想的线性可分数据集,其原理如图 2a所示。
|
| a. 硬间隔SVM模型;b. 软间隔SVM模型。 图 2 线性支持向量机模型 Fig. 2 Support vector machine model |
|
|
对于理想的线性可分数据集,硬间隔SVM会寻找一个最优的决策边界(超平面),距离两个类别的最近样本(支撑向量)最远。
软间隔SVM不仅适用于线性可分数据集,还适用于线性近似可分数据集,如图 2b所示。其是对硬间隔SVM条件的改进,允许错误样本跨过软间隔面以及超平面,会得到更合理的分类边界,从而增强模型的泛化能力,模型主要调节的参数是支持向量机的超参数C。
然而稀土元素数据一般线性不可分,对于线性不可分数据集,核函数SVM分类器更适用。如图 3所示,原数据集通过映射函数将原始数据映射到高维空间,从而使样本在高维空间内线性可分,降维之后可得到一条非线性的分类边界。
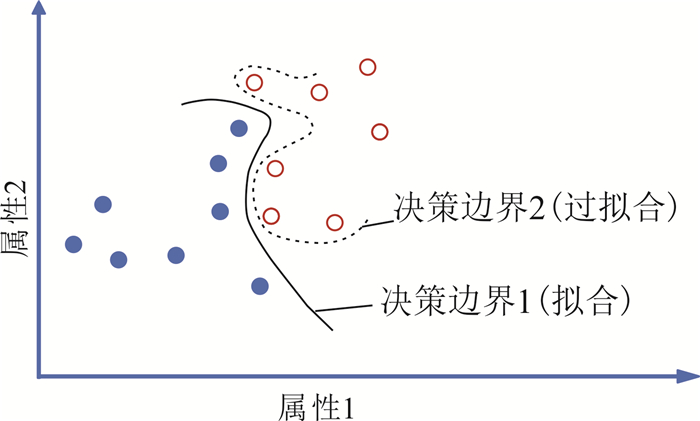
而高斯核函数(radial basis function,RBF)为K(xi, xj)=exp(-γ‖xi-xj‖2),其中,xi, xj为不同的样本,可变参数少且有较宽的收敛域。核函数中的γ值(g)可以控制分类模型的复杂程度,g越小,模型越简单,越接近线性分类;g越大,模型越复杂,越容易过拟合。图 4中,g值过大会形成决策边界2,已明显过拟合。综上,本次实验使用添加高斯核函数的支持向量机进行分析,主要调节的参数有SVM超参数C和核函数参数g,其余参数选择默认值。
|
| 图 4 拟合与过拟合 Fig. 4 Fitting and overfitting |
|
|
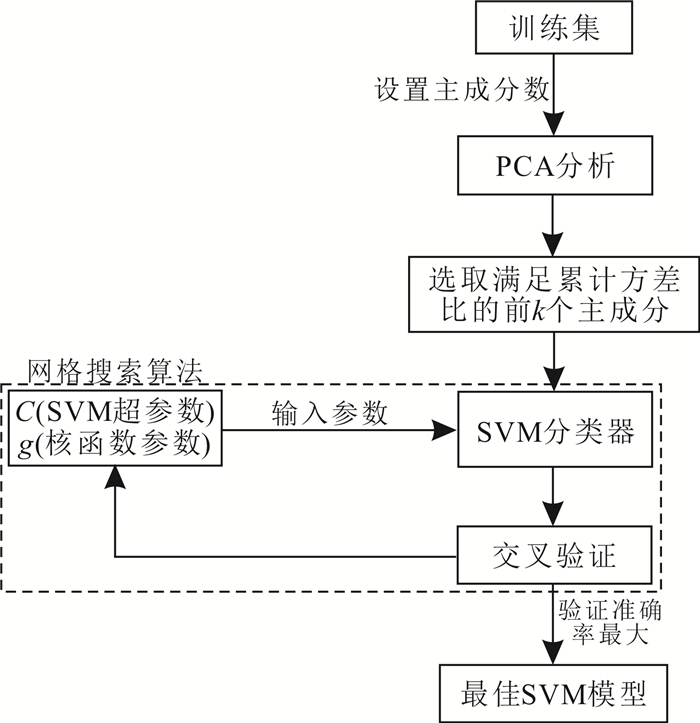
SVM算法可以较好地解决小样本、非线性、高维数的分类问题。对于一个有不同类别的高维数据集而言,噪音数据和冗余数据对分类均有负面影响,全部保留往往使SVM过拟合,降低泛化能力和鲁棒性。因此,数据集在导入SVM训练之前,对原数据集进行PCA特征提取显得尤为重要,其不仅可以剔除噪音和冗余信息,还可加快SVM的收敛。PCA-SVM耦合算法执行过程如图 5所示。首先,将数据集导入PCA进行分析,得到按照信息量从大到小依次排列的主成分数据集,根据累计信息比选取前k个主成分;然后导入带有高斯核函数的SVM,通过网格搜索算法(grid search algorithm,GSA)[23]依次将不同组合的C、g参数配置并生成SVM模型的同时,使用交叉验证[24]获取每个模型验证准确率,根据验证准确率的最大值选出最佳SVM模型。
|
| 图 5 PCA-SVM耦合算法执行流程 Fig. 5 Operational process of the coupled PCA-SVM algorithm |
|
|
PCA主成分的设定是根据主成分累计信息比决定,以此选取主成分数量,降维之后每个主成分方差均保持最大,保留最大信息量的同时剔除噪音与冗余数据。SVM算法是一种通过高维空间超平面来区分不同类别的分类方法,数据集通过PCA降维之后,维数与噪音、冗余数据减少,可大大提高SVM的运算速度与分类准确度。
2 数据收集及处理 2.1 数据收集及清洗收集全球已知典型不同铀矿床类型铀氧化物稀土元素数据,共计223组,其中,伟晶岩型(pegmatite)26组、深熔型(anatexis)21组、矽卡岩/高温变质型(skarn/h-t metamorphic)12组、同变质型(synmetamorphic)15组、热液脉型(hydrothermal vein-type)73组、不整合面型(unconformity-related)69组、火山岩型(volcanic-related)4组和卷状砂岩型(roll-front)3组。本次研究收集的数据集中火山岩型与卷状砂岩型过少,以此构建的分类模型不准确,故仅通过稀土配分曲线来排除胡家峪晶质铀矿类型为火山岩型、卷状砂岩型的可能性,因此,训练集共计216组。对于Gd和Yb元素的空缺值,使用与之同组的元素Sm、Tb、Tm、Lu球粒陨石标准化后,通过公式w(Gd)=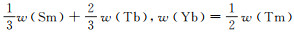
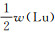
对训练集与测试集进行特征缩放。不同稀土元素之间丰度差距较大,会降低SVM求最优解的收敛速度以及准确度,使用标准差标准化对数据集进行特征缩放,消除了量纲不同及减少异常值影响。标准差标准化公式为
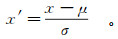
式中:x为原始数据;x′为标准化数据;μ为每一列数据的平均值;σ为标准差。变换后的数据集均值为0,标准差为1。
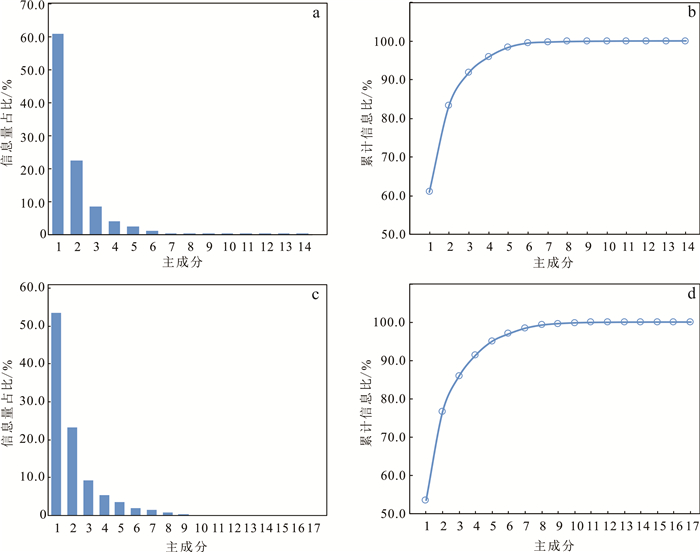
2.3 PCA降维训练数据通过PCA分析得到主成分数据。14维训练集(仅包含稀土元素)和17维训练集(包含稀土元素、稀土总量、轻重稀土比、铕异常)的主成分信息量占比及累计信息比如图 6所示。
|
| a, b. 14维训练集;c, d. 17维训练集。 图 6 主成分信息量图解 Fig. 6 Diagram of principal component information content |
|
|
图 6a、b中,14维训练集的第1主成分包含了数据集61.0%的信息量,随着主成分数增加,信息量急剧减小,且第6主成分之后累计信息比增长十分缓慢,第7与第14主成分信息量几乎为0,因此保留第1至第6主成分。图 6c、d中,17维训练集的第1主成分占总信息量的53.5%,第10至第17主成分信息量几乎为0,累计信息比在第9主成分之后几乎不再增长,因此保留第1至第9主成分。将其余主成分删除,即删除了数据集的冗余信息与噪音数据,两种训练集均保留约99.5%的信息量,保证信息量占比相等。通过PCA降维之后,14维训练集降为6维,17维训练集降为9维。将24组胡家峪晶质铀矿14维数据、17维数据(表 1)导入与之相同维数训练集的PCA模型中,降维之后分别得到6维与9维测试集。
| 编号 | La | Ce | Pr | Nd | Sm | Eu | Gd | Tb | Dy | Ho | Er | Tm | Yb | Lu | ΣREE | (LREE/HREE)N | δEu |
| HJY-01 | 444.1 | 3 581.8 | 863.2 | 5 419.1 | 3 246.2 | 486.5 | 3 311.3 | 649.0 | 3 502.6 | 545.4 | 988.4 | 108.5 | 563.5 | 54.1 | 23 763.7 | 1.5 | 0.4 |
| HJY-02 | 399.9 | 2 978.9 | 719.0 | 4 579.4 | 2 940.3 | 431.3 | 3 016.4 | 603.2 | 3 153.5 | 477.0 | 953.4 | 107.3 | 550.6 | 54.0 | 20 964.1 | 1.3 | 0.4 |
| HJY-03 | 437.6 | 3 263.9 | 822.8 | 5 254.4 | 3 262.9 | 477.7 | 3 524.2 | 689.2 | 3 644.9 | 546.1 | 1 084.3 | 117.3 | 596.8 | 61.6 | 23 783.6 | 1.3 | 0.4 |
| HJY-04 | 428.4 | 3 090.1 | 764.1 | 4 622.1 | 2 730.3 | 444.8 | 2 933.1 | 576.6 | 3 184.4 | 459.9 | 938.4 | 97.9 | 505.2 | 51.6 | 20 826.9 | 1.4 | 0.5 |
| HJY-05 | 423.5 | 3 267.6 | 706.1 | 4 250.4 | 2 604.9 | 408.5 | 2 368.3 | 450.9 | 2 373.6 | 350.0 | 607.1 | 63.3 | 290.6 | 27.5 | 18 192.2 | 2.2 | 0.5 |
| HJY-06 | 542.3 | 4 610.2 | 981.2 | 6 384.6 | 3 455.6 | 586.4 | 2 967.2 | 534.1 | 2 494.1 | 316.8 | 567.3 | 59.2 | 313.7 | 29.2 | 23 842.0 | 3.2 | 0.5 |
| HJY-07 | 494.7 | 3 956.2 | 860.0 | 5 273.2 | 2 879.6 | 481.3 | 2 646.6 | 481.5 | 2 419.1 | 307.2 | 477.6 | 48.6 | 224.6 | 20.6 | 20 570.6 | 3.5 | 0.5 |
| HJY-08 | 229.7 | 1 631.8 | 349.2 | 2 230.1 | 1 321.2 | 208.8 | 1 466.9 | 278.5 | 1 541.9 | 235.8 | 460.9 | 47.0 | 249.8 | 23.8 | 10 275.5 | 1.4 | 0.5 |
| HJY-09 | 335.8 | 2 400.5 | 543.7 | 3 452.9 | 1 931.9 | 319.6 | 1 842.7 | 383.7 | 1 906.0 | 272.8 | 545.2 | 56.5 | 272.9 | 24.4 | 14 288.5 | 1.9 | 0.5 |
| HJY-10 | 513.3 | 4 016.3 | 940.9 | 5 752.3 | 3 285.3 | 520.5 | 2 913.2 | 509.6 | 2 415.2 | 306.8 | 544.5 | 51.7 | 279.0 | 23.4 | 22 071.8 | 3.3 | 0.5 |
| HJY-11 | 413.1 | 3 104.7 | 638.9 | 3 622.6 | 1 657.5 | 387.0 | 1 662.8 | 390.5 | 1 856.7 | 276.5 | 578.1 | 66.4 | 366.9 | 34.2 | 15 055.9 | 1.8 | 0.7 |
| HJY-12 | 454.8 | 3 416.3 | 733.9 | 4 190.2 | 2 134.8 | 454.2 | 2 116.8 | 411.2 | 2 292.4 | 348.9 | 707.2 | 82.4 | 421.7 | 41.7 | 17 806.5 | 1.7 | 0.5 |
| HJY-13 | 159.9 | 1 051.9 | 280.1 | 1 822.5 | 1 164.1 | 171.2 | 1 417.7 | 324.7 | 1 704.4 | 289.4 | 596.4 | 66.8 | 355.0 | 36.5 | 9 440.6 | 0.8 | 0.4 |
| HJY-14 | 170.4 | 1 019.6 | 265.8 | 1 703.1 | 1 163.2 | 152.2 | 1 409.5 | 288.0 | 1 657.8 | 287.1 | 556.0 | 63.6 | 328.6 | 33.0 | 9 098.1 | 0.8 | 0.4 |
| HJY-15 | 406.6 | 2 564.4 | 625.3 | 3 879.4 | 2 423.0 | 344.1 | 2 939.0 | 608.1 | 3 456.5 | 559.8 | 1 202.4 | 134.0 | 707.0 | 71.0 | 19 920.6 | 0.9 | 0.4 |
| HJY-16 | 117.4 | 879.5 | 244.6 | 1 646.0 | 1 138.4 | 156.6 | 1 454.1 | 319.1 | 1 839.7 | 293.8 | 636.1 | 74.4 | 350.7 | 34.0 | 9 184.6 | 0.7 | 0.6 |
| HJY-17 | 192.0 | 1 385.4 | 374.1 | 2 454.9 | 1 589.2 | 202.5 | 2 021.5 | 418.3 | 2 252.3 | 380.4 | 799.8 | 85.2 | 466.7 | 46.8 | 12 669.1 | 0.8 | 0.4 |
| HJY-18 | 344.7 | 3 144.0 | 782.8 | 5 446.1 | 3 350.8 | 506.5 | 3 781.8 | 734.6 | 3 885.5 | 541.9 | 1 038.6 | 113.2 | 601.0 | 60.6 | 24 332.2 | 1.3 | 0.4 |
| HJY-19 | 432.2 | 3 239.5 | 790.1 | 5 280.0 | 3 439.8 | 485.6 | 3 849.0 | 754.7 | 4 062.5 | 606.5 | 1 218.9 | 131.0 | 709.0 | 66.2 | 25 065.0 | 1.1 | 0.4 |
| HJY-20 | 416.5 | 3 444.2 | 804.8 | 5 362.3 | 3 401.4 | 495.2 | 3 584.8 | 702.4 | 3 707.2 | 494.8 | 1 000.7 | 101.7 | 538.2 | 54.6 | 24 108.8 | 1.5 | 0.4 |
| HJY-21 | 344.4 | 2 967.5 | 682.8 | 4 376.2 | 2 667.4 | 415.3 | 2 792.5 | 512.6 | 2 550.9 | 340.9 | 616.7 | 64.2 | 315.9 | 32.0 | 18 679.2 | 2.0 | 0.3 |
| HJY-22 | 379.2 | 3 545.8 | 795.2 | 5 301.3 | 3 234.2 | 512.4 | 3 165.0 | 628.2 | 2 953.4 | 343.7 | 591.9 | 58.0 | 284.3 | 27.8 | 21 820.3 | 2.6 | 0.5 |
| HJY-23 | 341.8 | 3 145.6 | 708.2 | 4 836.4 | 2 928.4 | 443.0 | 2 923.4 | 569.3 | 2 781.0 | 357.9 | 635.6 | 66.7 | 314.7 | 34.3 | 20 086.2 | 2.1 | 0.4 |
| HJY-24 | 359.4 | 3 021.6 | 783.8 | 4 715.6 | 3 028.4 | 431.1 | 3 290.5 | 670.7 | 3 337.1 | 488.2 | 1 012.3 | 112.9 | 561.0 | 57.4 | 21 870.1 | 1.3 | 0.5 |
| 注:稀土元素质量分数单位为10-6。 | |||||||||||||||||
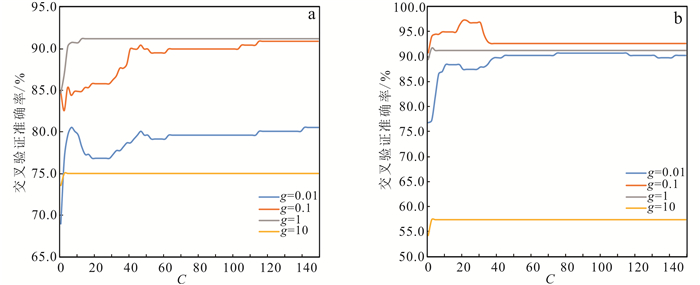
本文采用高斯核函数(RBF)构建非线性SVM分类器,分类器的超参数C和核函数参数g组合不同,其分类准确率和泛化能力亦有优劣[25];网格搜索法是指定参数的一种穷举搜索方法,通过遍历给定的参数组合来优化模型的表现,确定满足条件的分类参数进而得到最佳分类模型。本次SVM实验参数C取值范围为[1, 150],步长为2,g取值范围为[0.01,0.1,1,10],并可视化C、g与验证准确率的关系(图 7)。参数组合模型采用3折交叉验证[26]来评价各个模型,并分别选取14维与17维训练集验证准确率最大模型对胡家峪晶质铀矿类型进行测试。
|
| a. 14维训练集;b. 17维训练集。 图 7 不同C-g值模型交叉验证准确率示意图 Fig. 7 Diagram of cross-validation accuracy for classifiers with different C-g values |
|
|
图 7a中, 14维训练集构建的分类模型的4条g值曲线中,g取1时模型验证准确率大部分在90.0%以上,比其余3条曲线的验证准确率均要高,并在g取1、C取13时达到模型最优,最高验证准确率为91.2%。图 7b中,17维训练集构建的分类模型g值取0.1、1时,模型验证准确率基本在90.0%以上,比0.01与10时的验证准确率高,并在g取0.1、C取21时达到模型最优,最高验证准确率为97.2%,相比14维最优模型高出6.0%,对训练集具有更好的拟合效果。
将24组胡家峪测试集(矿床类型为同变质型)输入两类训练集构建的最优模型进行测试,测试分类结果统计如表 2所示。
| 训练集 | C | g | 最高验证准确率/% | 同变质型 | 伟晶岩型 | 不整合面型 |
| 14维 | 13 | 1 | 91.2 | 1 | 23 | 0 |
| 17维 | 21 | 0.1 | 97.2 | 18 | 3 | 3 |
由表 2可知:使用14维训练集最优模型对胡家峪晶质铀矿测试显示,同变质型占1组,伟晶岩型占23组,测试准确率仅为0.4%;17维训练集最优模型判别同变质型占18组,伟晶岩型与不整合面型各3组,测试准确率为75.0%,较14维训练集大幅提高,提高了74.6%。
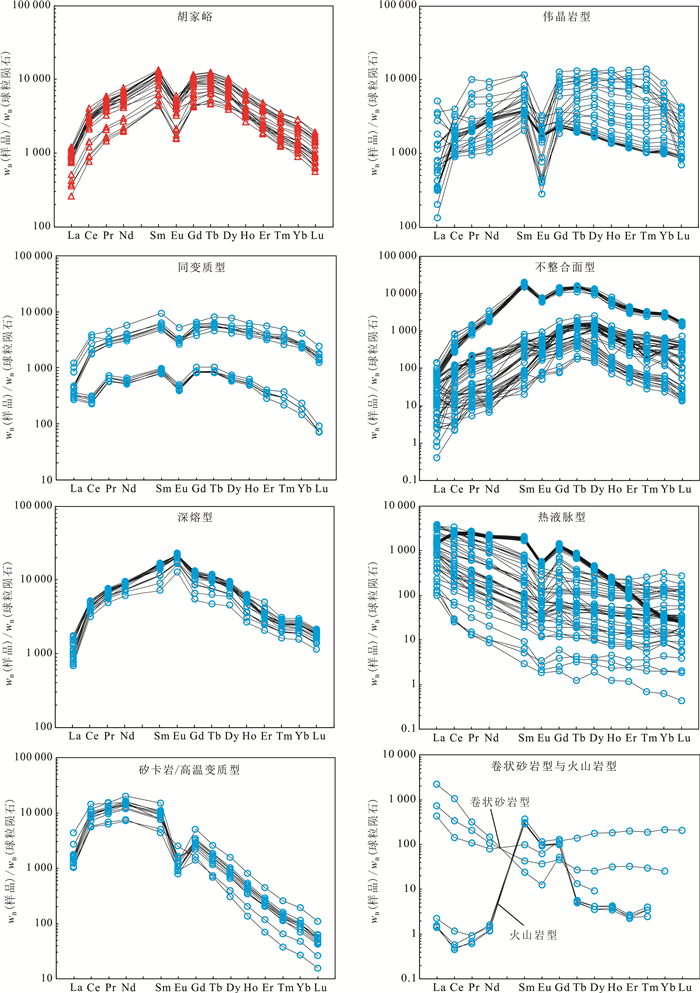
4 讨论晶质铀矿和沥青铀矿是分别生成于高温与低温环境的两种不同的铀氧化物[27]。稀土元素以类质同像的形式存在于沥青铀矿/晶质铀矿中,稀土元素与铀有着相似的活化、迁移及富集过程[28],但在后期流体的影响下,稀土元素相比沥青铀矿有着更好的抗干扰能力[29]。前人[12]的研究也证实了铀氧化物的稀土元素组分具有判别铀成矿时的温度、氧化还原环境和流体成分等物理化学条件的作用。不同类型铀矿床的铀氧化物稀土元素特征由于成因环境的物化特征不同而存在差别,其可作为辨认铀氧化物矿床类型的有力工具[13],恰当应用该特征可为新铀矿床勘探提供类型参考,以优化勘探策略。下面使用收集的8类不同矿床类型沥青铀矿/晶质铀矿稀土配分曲线以及w(ΣREE)-(LREE/HREE)N图解对胡家峪晶质铀矿进行判别。
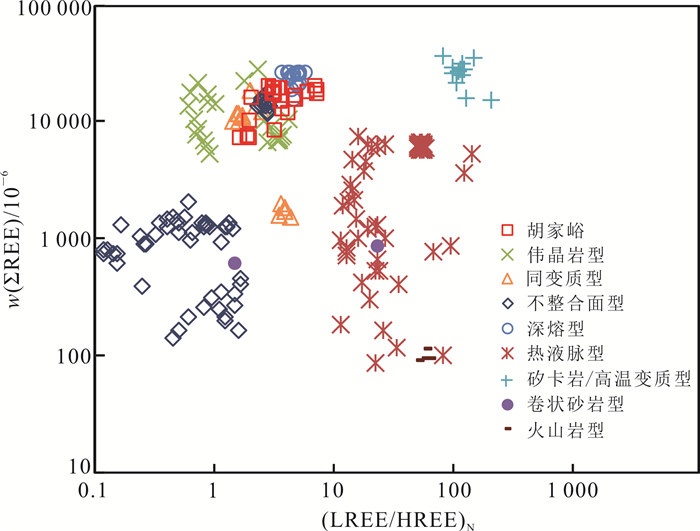
通过图 8对比可知,胡家峪晶质铀矿稀土类型与伟晶岩型、同变质型、不整合面型均有部分重叠。胡家峪晶质铀矿标准稀土配分模式具有富集中稀土和负铕异常(δEu=0.34~0.69)的特征(图 9)。稀土配分曲线对比发现,同变质型、伟晶岩型、不整合面型均与胡家峪铀矿类型近似。因此,传统图解无法分辨胡家峪晶质铀矿类型。而加入传统判别指标的稀土元素训练集经PCA-SVM算法生成的分类模型判定测试集准确率为75.0%,可见同变质型与伟晶岩型、不整合面型在PCA-SVM算法的高维空间内仍有较大差别。
|
| 图 8 胡家峪晶质铀矿以及不同成因类型沥青铀矿/晶质铀矿w(ΣREE)-(LREE/HREE)N图解 Fig. 8 w(ΣREE) vs. (LREE/HREE)N diagram of uraninite from Hujiayu deposit and pitchblende/uraninite of different genetic types from uranium deposits collected |
|
|
14维训练集的预测效果过差的原因是,根据验证准确率选择的14维训练集最优SVM模型是1个过拟合模型,而模型验证准确率最大值仅达到91.2%;而17维训练集最优SVM模型的验证准确率为97.2%,模型却仍然没有过拟合(测试准确率75.0%)。因此,将传统判别指标加入训练集来增加不同类别间的差异,可增强模型拟合效果,并且可有效避免SVM分类器参数寻优的过拟合问题。
PCA-SCM算法整合稀土元素、稀土总量、轻重稀土比和铕异常信息进行分析,经过特征缩放、特征提取、SVM模型建立及交叉验证后,验证准确率最高为97.2%。本次对24组胡家峪测试集测试显示,17维训练集判别出18组数据为同变质型,测试准确率达75.0%,较14维训练集测试准确率提高了74.6%。因此,模型分类准确率的提高,除与训练集特征选择[31]、特征提取[32]、分类算法的选取[1, 33]及模型参数搜索算法的选择[34]等相关之外,将地球化学传统判别指标加入原数据集再训练模型也可提高分类准确率。
5 结论1) 采用PCA-SVM机器学习分类算法,对14维训练集(稀土元素)与17维训练集(稀土元素、稀土总量、轻重稀土比、铕异常)进行挖掘分析得到最优模型,17维训练集模型测试准确率为75.0%,模型泛化能力强,并可有效避免低维训练集模型的过拟合问题,从而提高模型性能。
2) 最优的机器学习模型与单独的稀土元素配分图解、w(ΣREE)-(LREE/HREE)N图解相比,可以更好地解决传统地球化学分类图解法由于分类重合、交叉的问题,得出更加合理的分类结果。
| [1] |
韩帅, 李明超, 任秋兵, 等. 基于大数据方法的玄武岩大地构造环境智能挖掘判别与分析[J]. 岩石学报, 2018, 34(11): 3207-3216. Han Shuai, Li Mingchao, Ren Qiubing, et al. Intelligent Determination and Data Mining for Tectonic Settings of Basalts Based on Big Data Methods[J]. Acta Petrologica Sinica, 2018, 34(11): 3207-3216. |
| [2] |
焦守涛, 周永章, 张琪, 等. 基于GEOROC数据库的全球辉长岩大数据的大地构造环境智能判别研究[J]. 岩石学报, 2018, 34(11): 3189-3194. Jiao Shoutao, Zhou Yongzhang, Zhang Qi, et al. Study on Intelligent Discrimination of Tectonic Settings Based on Global Gabbro Data from GEOROC[J]. Acta Petrologica Sinica, 2018, 34(11): 3189-3194. |
| [3] |
Ueki K, Hino H, Kuwatani T. Geochemical Discrimination and Characteristics of Magmatic Tectonic Settings: A Machine-Learning-Based Approach[J]. Geochemistry, Geophysics, Geosystems, 2017, 19(4): 1327-1347. |
| [4] |
韩启迪, 张小桐, 申维. 基于决策树特征提取的支持向量机在岩性分类中的应用[J]. 吉林大学学报(地球科学版), 2019, 49(2): 611-620. Han Qidi, Zhang Xiaotong, Shen Wei. Application of Support Vector Machine Based on Decision Tree Feature Extraction in Lithology Classification[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(2): 611-620. |
| [5] |
王思琪, 王明常, 王凤艳, 等. 基于SAE-ELM方法的多金属遥感地球化学反演[J]. 世界地质, 2020, 39(4): 195-202. Wang Siqi, Wang Mingchang, Wang Fengyan, et al. Remote Sensing Geochemical Inversion of Multi Metal Materials Based on SAE-ELM[J]. Global Geology, 2020, 39(4): 195-202. |
| [6] |
徐述腾, 周永章. 基于深度学习的镜下矿石矿物的智能识别实验研究[J]. 岩石学报, 2018, 34(11): 3244-3252. Xu Shuteng, Zhou Yongzhang. Artificial Intelligence Identification of Ore Minerals Under Microscope Based on Deep Learning Algorithm[J]. Acta Petrologica Sinica, 2018, 34(11): 3244-3252. |
| [7] |
刘力辉, 陆蓉, 杨文魁. 基于深度学习的地震岩相反演方法[J]. 石油物探, 2019, 58(1): 123-129. Liu Lihui, Lu Rong, Yang Wenkui. Seismic Lithofacies Inversion Based on Deep Learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 123-129. DOI:10.3969/j.issn.1000-1441.2019.01.014 |
| [8] |
闫佰忠, 孙剑, 王昕洲, 等. 基于多变量LSTM神经网络的地下水水位预测[J]. 吉林大学学报(地球科学版), 2020, 50(1): 208-216. Yan Baizhong, Sun Jian, Wang Xinzhou, et al. Multivariable LSTM Neural Network Model for Groundwater Levels Prediction[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(1): 208-216. |
| [9] |
刘艳鹏, 朱立新, 周永章. 卷积神经网络及其在矿床找矿预测中的应用: 以安徽省兆吉口铅锌矿床为例[J]. 岩石学报, 2018, 34(11): 3217-3224. Liu Yanpeng, Zhu Lixin, Zhou Yongzhang. Application of Convolutional Neural Network in Prospecting Prediction of Ore Deposits: Taking the Zhaojikou Pb-Zn Ore Deposit in Anhui Province as a Case[J]. Acta Petrologica Sinica, 2018, 34(11): 3217-3224. |
| [10] |
Zuo R, Xiong Y. Big Data Analytics of Identifying Geochemical Anomalies Supported by Machine Learning Methods[J]. Natural Resources Research, 2018, 27(1): 5-13. DOI:10.1007/s11053-017-9357-0 |
| [11] |
Ghezelbash R, Maghsoudi A, Carranza E J M. Performance Evaluation of RBF- and SVM-Based Machine Learning Algorithms for Predictive Mineral Prospectivity Modeling: Integration of S-A Multifractal Model and Mineralization Controls[J]. Earth Science Informatics, 2019, 12: 277-293. DOI:10.1007/s12145-018-00377-6 |
| [12] |
Mercadier J, Cuney M, Lach P, et al. Origin of Uranium Deposits Revealed by Their Rare Earth Element Signature[J]. Terra Nova, 2011, 23(4): 264-269. DOI:10.1111/j.1365-3121.2011.01008.x |
| [13] |
Frimmel H E, Schedel S, Brätz H. Uraninite Chemistry as Forensic Tool for Provenance Analysis[J]. Applied Geochemistry, 2014, 48: 104-121. DOI:10.1016/j.apgeochem.2014.07.013 |
| [14] |
Eglinger A, André-Mayer A S, Vanderhaeghe O, et al. Geochemical Signatures of Uranium Oxides in the Lufilian Belt: From Unconformity-Related to Syn-Metamorphic Uranium Deposits During the Pan-African Orogenic Cycle[J]. Ore Geology Reviews, 2013, 54: 197-213. DOI:10.1016/j.oregeorev.2013.04.003 |
| [15] |
Gandhi S S, Potter E G, Fayek M. New Constraints on Genesis of the Polymetallic Veins at Port Radium, Great Bear Lake, Northwest Canadian Shield[J]. Ore Geology Reviews, 2018, 96: 28-47. DOI:10.1016/j.oregeorev.2018.04.002 |
| [16] |
Petrelli M, Perugini D. Solving Petrological Problems Through Machine Learning: The Study Case of Tectonic Discrimination Using Geochemical and Isotopic Data[J]. Contributions to Mineralogy and Petrology, 2016, 171(10): 81. DOI:10.1007/s00410-016-1292-2 |
| [17] |
Ren Q B, Li M C, Han S. Tectonic Discrimination of Olivine in Basalt Using Data Mining Techniques Based on Major Elements: A Comparative Study from Multiple Perspectives[J]. Big Earth Data, 2019, 3(1): 8-25. DOI:10.1080/20964471.2019.1572452 |
| [18] |
Balboni E, Jones N, Spano T, et al. Chemical and Sr Isotopic Characterization of North America Uranium Ores: Nuclear Forensic Applications[J]. Applied Geochemistry, 2016, 74: 24-32. DOI:10.1016/j.apgeochem.2016.08.016 |
| [19] |
Abdi H, Williams L J. Principal Component Analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433-459. DOI:10.1002/wics.101 |
| [20] |
Cortes C, Vapnik V. Support-Vector Networks[J]. Machine Learning, 1995, 20(3): 273-297. |
| [21] |
Hsu C W, Lin C J. A Comparison of Methods for Multiclass Support Vector Machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425. DOI:10.1109/72.991427 |
| [22] |
李苍柏, 肖克严, 李楠, 等. 支持向量机、随机森林和人工神经网络机器学习算法在地球化学异常信息提取中的对比研究[J]. 地球学报, 2020, 41(2): 309-319. Li Cangbai, Xiao Keyan, Li Nan, et al. A Comparative Study of Support Vector Machine, Random Forest and Artificial Neural Network Machine Learning Algorithms in Geochemical Anomaly Information Extraction[J]. Acta Geoscientica Sinica, 2020, 41(2): 309-319. |
| [23] |
刘祥楼, 贾东旭, 李辉, 等. 说话人识别中支持向量机核函数参数优化研究[J]. 科学技术与工程, 2010, 10(7): 1669-1673. Liu Xianglou, Jia Dongxu, Li Hui, et al. Research on Kernel Parameter Optimization of Support Vector Machine in Speaker Recognition[J]. Science Technology and Engineering, 2010, 10(7): 1669-1673. DOI:10.3969/j.issn.1671-1815.2010.07.019 |
| [24] |
Arlot S, Celisse A. A Survey of Cross-Validation Procedures for Model Selection[J]. Statistics Surveys, 2010, 4: 40-79. |
| [25] |
宋永东. 支持向量机参数选择的研究[D]. 武汉: 华中师范大学, 2013. Song Yongdong. Research of Parameter Selection for Support Vector Machine[D]. Wuhan: Central China Normal University, 2013. |
| [26] |
Rodriguez J D, Perez A, Lozano J A. Sensitivity Analysis of K-Fold Cross Validation in Prediction Error Estimation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(3): 569-575. DOI:10.1109/TPAMI.2009.187 |
| [27] |
骆金诚. 粤北花岗岩型铀矿床成因机制研究: 矿物学和铀矿物U-Pb年代学及地球化学约束[D]. 北京: 中国科学院大学, 2015. Luo Jincheng. Genesis of Granite-Hosted Uranium Deposits in the Northern Guangdong, China: Constraints from Mineralogy, Uranium Mineral U-Pb Geochronology and Geochemistry[D]. Beijing: University of Chinese Academy of Sciences, 2015. |
| [28] |
McLennan S, Taylor S. Rare Earth Element Mobility Associated with Uranium Mineralization[J]. Nature, 1979, 282: 247-250. DOI:10.1038/282247a0 |
| [29] |
Alexandre P, Kyser T K. Effects of Cationic Substitutions and Alteration in Uraninite, and Implications for the Dating of Uranium Deposits[J]. Canadian Mineralogist, 2005, 43(3): 1005-1017. DOI:10.2113/gscanmin.43.3.1005 |
| [30] |
Anders E, Grevesse N. Abundances of the Elements: Meteoritic and Solar[J]. Geochimica et Cosmochimica Acta, 1989, 53(1): 197-214. DOI:10.1016/0016-7037(89)90286-X |
| [31] |
任秋兵, 李明超, 韩帅. 基于改进遗传算法-神经网络的玄武岩构造环境判别及对比实验[J]. 地学前缘, 2019, 26(4): 117-124. Ren Qiubing, Li Mingchao, Han Shuai. Discrimination and Comparison Experiments of Basalt Tectonic Setting Based on Improved Genetic Algorithm-Optimized Neural Network[J]. Earth Science Frontiers, 2019, 26(4): 117-124. |
| [32] |
刘承照, 韩帅, 李明超, 等. 耦合PCA-SVM算法的金矿矿床规模预测分析研究[J]. 地学前缘, 2019, 26(4): 138-145. Liu Chengzhao, Han Shuai, Li Mingchao, et al. Prediction and Analysis of Gold Deposit Sizes Based on Coupled PCA-SVM Algorithm[J]. Earth Science Frontiers, 2019, 26(4): 138-145. |
| [33] |
张野, 李明超, 韩帅, 等. 基于金矿规格单元数据的机器学习方法在成矿建模分析中的应用[J]. 大地构造与成矿学, 2020, 44(2): 183-191. Zhang Ye, Li Mingchao, Han Shuai, et al. Machine Learning Methods Application in Gold Mineralization Prediction Based on Gold Unit Data[J]. Geotectonica et Metallogenia, 2020, 44(2): 183-191. |
| [34] |
任秋兵, 李明超, 李玉琼, 等. 基于全球橄榄石数据的玄武岩构造环境智能判别方法及其验证[J]. 大地构造与成矿学, 2020, 44(2): 212-221. Ren Qiubing, Li Mingchao, Li Yuqiong, et al. An Intelligent Method for Geochemical Discrimination of Tectonic Settings of Basalt Based on Olivine Composition: GWO-SVM Method and Its Verification[J]. Geotectonica et Metallogenia, 2020, 44(2): 212-221. |