2. 中国地质科学院地球物理地球化学勘查研究所, 河北 廊坊 065000;
3. 吉林省中地岩土工程有限公司, 长春 130000
2. Institute of Geophysical and Geochemical Exploration, Chinese Academy of Geological Sciences, Langfang 065000, Hebei, China;
3. Jilin Zhongdi Geotechnical Engineering Co. LTD, Changchun 130000, China
0 引言
由Verschuur等[1-3]提出的自由表面多次波压制(SRME)迭代算法具有数据驱动,不需要先验速度、结构和层位等地下信息的特点,在工业领域上获得了广泛的应用,是当今地震资料数据处理中的标准多次波压制方法。随后,很多地球物理学家对SRME算法提出了改进,例如:Berkhout和Verschuur[4-5]提出了一种快速收敛的迭代算法;Herrmann[6]提出了一种基于Curvelet变换的多次波压制方法;van Groenestijn等[7]实现了稀疏反演一次波估计(EPSI),该方法避免了SRME方法在多次波预测后自适应相减的步骤;Lopez等[8]提出了一种快速有效的闭合循环SRME(CL-SRME),该方法是一种反演框架下的稳定算法,但反演过程容易陷入局部极小值。在过去的20年中,3D-SRME在多次波去除中具有明显优势,引起了很多学者的关注。van Dedem等[9-11]成功地将SRME方法应用到了三维地震资料的处理;由于理想三维SRME理论需要巨大的数据量,很难用于实际三维地震资料的处理,2005年,van Dedem等[12]又提出了将三维SRME理论和稀疏反演策略相结合的方法预测多次波;2017年,王通等[13]改进了稀疏域中三维自由表面多次波去除方法。2020年,王铁兴等[14]在混采数据中应用一次波估计方法压制多次波。随着计算机和相关技术的发展,3D-SRME逐渐被推广应用。尽管3D-SRME在多次波压制上具有很多优势,但其处理过程算法复杂度高、数据量大,需要消耗大量的计算时间。因此,常规二维条件下的SRME算法仍然是工业中压制多次波的主要方法。
我们可以把自由表面多次波产生过程中,传播路径经过散射体产生的绕射形态多次波称为绕射多次波。海洋陆缘深水区过渡带区域基底复杂,构造线交错,断裂发育,形成潜山、断块山和半地堑式构造,具备了较好的生储油条件。然而,在这个水深变化剧烈、海底地形崎岖、构造复杂多变的区域采集的海洋地震数据中绕射多次波十分发育,地震资料信噪比低[15-16]。Verschuur等[17]、刘琦[18]认为这种复杂绕射多次波是一种3D效应,直接使用常规二维SRME压制这种复杂成因的绕射多次波效果难以达到预期,虽然3D-SRME可以针对这种绕射成因多次波进行压制,但是成本昂贵。
目前,在地球物理领域中,Khaidukov等[19]和Taner等[20]提出地震资料分析处理之前应该将绕射波和反射波进行分离;Verschuur等[17]在进行多次波预测之前对全数据进行反射波场和绕射波场分离,得到4种预测多次波子集,后续的多次波减去过程是逐步在这些子集上进行的;刘琦[18]研究了基于反射和绕射波场分离的多次波消除方法,比较了多种分离方法的分离效果;黎孝璋等[21]提出复杂海底自由表面多次波预测方法,但是这种方法需要预先知道准确的岩石物理模型。
在前人研究的基础上,我们分别对反射、绕射波场分离方法和常规SRME迭代算法过程进行改进,提出基于频率域经验模态分解(frequency-space emperical mod decomposition, f-x EMD)的波场分离算法,其中f表示频率,x表示空间。利用该算法参数设置简单、意义直观等优势对反射波场与绕射波场进行分离。使用分离出来的波场作为多次波预测的输入波场,得到4种波的预测子集。虽然理论上可以获得4种子集,但是实际情况中多种类型的绕射多次波不一定会全部发育,因此只需将常规SRME算法第一步的减去结果作为后续迭代减去过程的输入,使用更加有针对性的绕射多次波预测子集作为预测多次波,从而达到压制绕射多次波的目的。与前人不同的是,我们不再将4个子集逐一减去。
1 算法原理和实现 1.1 基于f-x EMD的反、绕射波场分离在平面波数据域中,反射波场与绕射波场的特征差异主要表现为同相轴倾角大小不同。反射波表现为与地层形态接近的平缓同相轴,而绕射波则表现为高陡倾角近似双曲线的同相轴[22]。频率域经验模态分解算法等价于一个带有对高波数数据自适应切除的f-k(频率-波数)滤波器,对随机噪声和陡倾角连续相关噪声有很好的压制作用[23]。在无噪声的理想条件下,平缓且连续的地震记录同相轴在波数域中表现为低波数特征;而一些陡倾角的相干噪声,例如来自于断层断点处的绕射波,由于横向振幅变化剧烈,在波域数中表现为高波数特征[24]。
f-x EMD算法可以将每一频率下的数据分解为有限数量的本征模函数(IMFs):
 (1)
(1) 式中:n为分解层数;t为时间;ci(t)为各阶IMF;rn(t)为残余项[25]。第一个分量IMF1代表数据中抖动最剧烈的高波束成分,对应于平面波数据中的陡倾角绕射波场成分;其他分量对应于平面波数据中的反射波场成分。利用这个性质,我们可以对平面波数据域中的反射波场和绕射波场进行分离。抽取分量IMF1以达到提取绕射波场的目的,同时将剩余的IMF分量重构成反射波场,进而达到波场分离目的。
当我们使用f-x EMD算法抽取分量IMF1时,将产生一个较高波数范围的有效信号。然而,当形态较陡的有效同相轴信号存在于原始数据半波数范围以外时,直接使用f-x EMD将会导致有效信号损伤。我们需要选择一个合适的数据处理窗口,在每个窗口范围内完成处理。
基于上述理论,总结出基于f-x EMD的反、绕射波场分离算法,具体流程如下。
1) 将炮集记录排列成分裂分布的共炮点记录数据矩阵。
2) 对各共炮点数据记录进行线性拉东变换(τ-p变换,其中τ代表时间,p代表射线参数),抽取数据矩阵中的共p剖面重新排列,形成不同角度入射的平面波震源炮集数据。
3) 选择大小合适的时窗,将共p剖面的地震数据通过快速傅里叶变换(FFT)映射到f-x域。对于每一个频率切片:a. 在空间方向上,将复数数据分离成实部和虚部两部分;b. 对实部数据进行EMD分解,抽取分量IMF1重构作为绕射波场实部,其他分量作为反射波场实部;c. 对虚部数据进行EMD分解,抽取分量IMF1重构作为绕射波场虚部,其余分量作为反射波场虚部;d. 将分离好的实部和虚部数据重构成复数数据;e. 将重构的数据通过快速傅里叶反变换(IFFT)映射到t-x域,生成绕射波场和反射波场两组数据;f. 滑动时窗,对下一个时窗重复以上操作,直到全部数据完成。
4) 将按共p剖面排列的已分离的反射波场和绕射波场重新排列成平面波数据。
5) 做反τ-p变换,将平面波数据变成点源下的反射波场和绕射波场数据。
上面的处理流程实现了基于f-x EMD的波场分解算法,达到反射波场和绕射波场分离的目的。
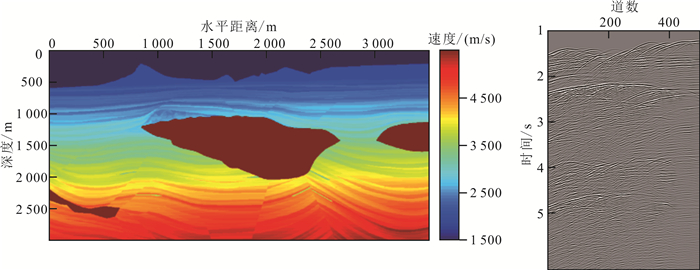
为了证明基于f-x EMD的波场分离算法具有更好的效果,我们设计了对比实验。在Segsbee模型上增加一个起伏的低速界面,用来模拟海底的起伏地表情况;其下第一层用来模拟水层,速度为1 500 m/s;再往下速度逐渐增加至4 500 m/s,中间有个高速盐体,表面起伏,速度约为4 800 m/s(图 1)。模型整体成层性好,可以反映海洋沉积情况;模型中还包含绕射体以及崎岖表面岩体,可以产生强绕射波。我们将模拟的地震数据构建成平面波数据,使用平面波解构滤波器(plane-wave decomposition,PWD)滤波和KL(Karhunen-Loève)变换进行反、绕射波场分离,并与f-x EMD算法的分离结果进行对比,结果如图 2所示。
|
| 图 1 理论模型和数据 Fig. 1 Theoretical model and data |
|
|

|
| 绕射波场:a. f-x EMD算法;b. PWD算法;c. KL变换算法。反射波场:d. f-x EMD算法;e. PWD算法;f. KL变换算法。 图 2 三种算法波场分离结果 Fig. 2 Three kinds of algorithms wavefield decomposition result |
|
|
在复杂模型条件下,限于只针对水平同相轴提取有较好效果的局限性,KL变换算法对绕射波场有很大损伤,图 2c中左上方绕射波同相轴变得十分模糊。PWD算法依赖对同相轴的倾角估计,算法中没有可以直观反映反射波场或者绕射波场信息的控制参数,并且反射波场分离效果依赖原数据中分离出的绕射波场的保幅性,因此很难取得较好的效果,反射与绕射成分混杂(图 2b、e)。f-x EMD算法参数IMF分量直接对应绕射波场组分,重构反射波场过程灵活,反射波场和绕射波场分离结果彻底,可以达到分离目的(图 2a、d)。经过上述3种算法的对比,我们可以得出结论:f-x EMD算法在复杂模型条件下的波场分离中效果最好。下文波场分解均使用f-x EMD算法。
1.2 绕射多次波压制原理首先简单说明常规SRME算法的基本原理。SRME是利用叠前地震数据中的反射波信息构建自由表面多次波数据驱动的多次波压制方法,其最大的特点是不需要详细的地下界面信息,自动得到构建多次波的正确同相轴组合[16]。
设一次波脉冲响应为x0(t),包含自由表面多次波的总体响应为x(t)。表示一次波数据和全波场数据时考虑震源特性s(t),暂不考虑层间多次波问题。一次波数据可以表示为
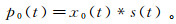 (2)
(2) 式中,*表示卷积。全波场数据可以表示为
 (3)
(3) 同样可以得到隐式关系:
 (4)
(4) 定义表面算子a(t), 使得
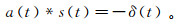 (5)
(5) 式中,δ(t)为震源。考虑到多维情况用矩阵表示,大写字母为对应小写字母的频率域表达式。将式(4)变换到频率域有
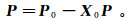 (6)
(6) 将式(5)带入式(2)并且变换到频率域,获得X0的表达式,替换式(6)中的X0可得到
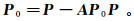 (7)
(7) 式(7)在实际运算过程中是通过给定初始值迭代完成的:
 (8)
(8)  (9)
(9) 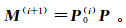 (10)
(10) 式中:P0(i)为频率域第i次迭代后的一次波数据;P为频率域全波场数据;M(i+1)为第i阶自由表面多次波。
然而,崎岖海底绕射波十分发育,导致多次波成分复杂,绕射波与反射波混叠交错。直接进行多次波预测,绕射多次波同相轴无法被准确预测,从而无法达到理想的多次波压制效果。常规SRME算法压制绕射多次波存在的问题:1)反、绕射波场能量差异大,使得绕射多次波被淹没,无法被准确预测;2)绕射波与反射波混叠,绕射多次波如果预测不准确,则同相轴准确匹配比较困难。针对以上问题,我们在前人研究的基础上,改进了波场分离算法,提出了一种新的SRME算法迭代处理流程。首先通过基于f-x EMD的波场分离算法,将全波场数据分成反射部分Pr和绕射部分Ps,则多次波预测式(10)可以进一步展开为
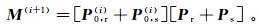 (11)
(11) 将式(11)展开可以获得4种类型预测多次波:反射-反射多次波、反射-绕射多次波,绕射-反射多次波、绕射-绕射多次波[18]:
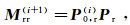 (12)
(12) 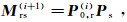 (13)
(13) 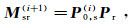 (14)
(14)  (15)
(15) 将式(12)看作常规预测多次波结果,将式(13)—(15)统称为绕射多次波,即绕射预测多次波子集。新的SRME迭代处理流程中将常规SRME算法第一次迭代的结果作为输入,在后续迭代过程中,使用特定的预测多次波子集进行多次波压制。
针对绕射多次波子集的选择,需分析数据中绕射多次波的成因,选择匹配性好的绕射预测多次波子集进行压制,从而达到压制绕射多次波的目的。
2 应用实例 2.1 理论数据试算使用图 1模型模拟海洋拖缆数据,其中会包含大量绕射多次波。图 1起伏界面与海水之间速度差异较大,在这个界面会产生强的反射波,凸起位置相当于散射源,形成强绕射波;下伏层速度变化均匀缓慢,反射波会比较弱;中间位置的高速盐体表面呈波浪状起伏,会形成强绕射波。
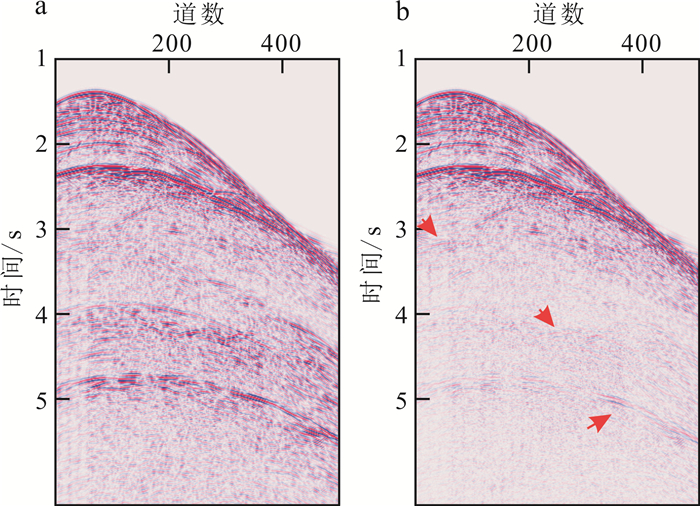
图 3中的拖缆地震数据覆盖范围主要是模型中左端的凸起散射体,模拟数据中理论上应包括绕射-绕射多次波、绕射-反射多次波和反射-绕射多次波。为满足SRME处理数据的要求,使用互易定理对数据进行规则化,如图 4a所示。对于规则化后的数据,首先使用常规SRME算法进行多次波压制。从图 4b中可以看到,常规SRME算法对于这种包含绕射多次波的复杂成因多次波数据具有一定的压制作用,但是残余较多,残余的结果中包含呈明显高陡的绕射多次波。

|
| 图 3 拖缆地震数据 Fig. 3 Streamer seismic data |
|
|
|
| a. 原始数据;b. 常规SRME结果。 图 4 常规SRME算法多次波压制结果 Fig. 4 Conventional SRME result |
|
|
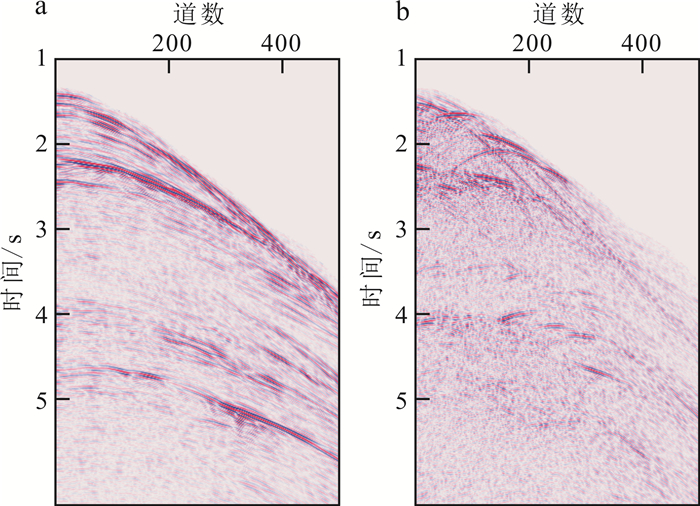
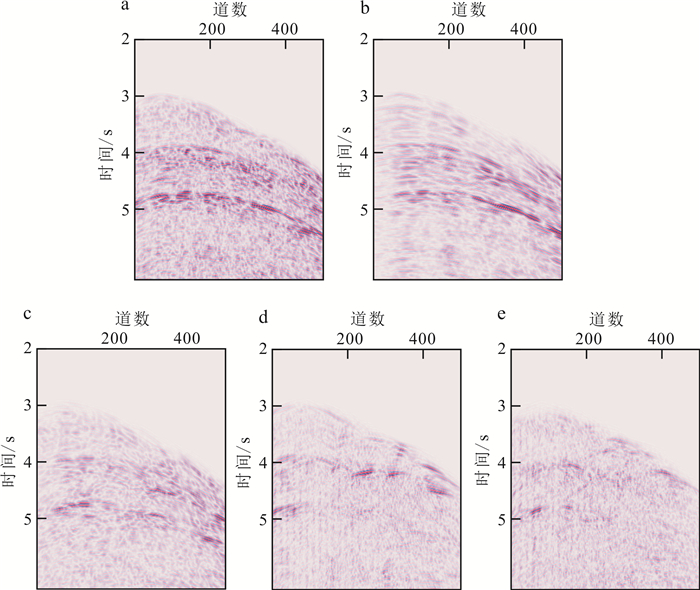
由于绕射波能量相对于反射波较弱,直接进行多次波预测,无法准确预测绕射多次波同相轴,匹配相减过程中能量级相差较大,无法达到理想的多次波压制效果。对此,在多次波预测之前,将全部数据通过f-x EMD算法分离为反射波场数据和绕射波场数据,并补偿加强绕射波场能量到反射波场能量数量级,如图 5所示。使用分离的数据进行多次波预测,得到4种多次波预测子集:反射-反射预测多次波、反射-绕射预测多次波、绕射-反射预测多次波和绕射-绕射预测多次波。反射-反射预测多次波与常规方法预测多次波很相似,波场形态更加平缓(图 6a、b),通过分离突出绕射成分的多次波数据中,陡倾角的绕射波成分多次波更加明显(图 6c、d、e)。
|
| a. 反射波场;b. 绕射波场。 图 5 反、绕射波场分离结果 Fig. 5 Reflected wavefield and diffracted wavefield decomposition |
|
|
|
| a. 常规方法预测多次波;b. 反射-反射预测多次波;c. 反射-绕射预测多次波;d. 绕射-反射预测多次波;e. 绕射-绕射预测多次波。 图 6 基于波场分离的多次波预测结果 Fig. 6 Predicted multiples based on wavefield decomposition |
|
|
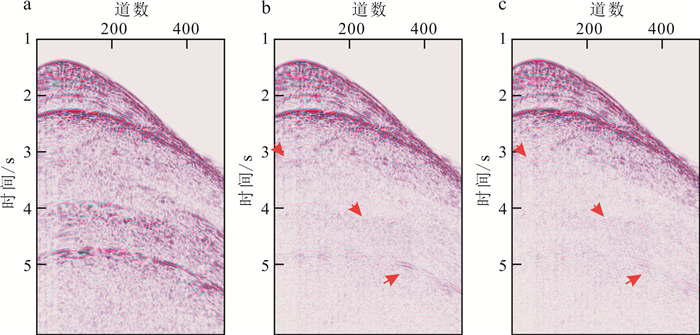
常规SRME处理结果中残余高陡的绕射多次波,与我们预测的绕射-绕射预测多次波形态相似。因此,我们使用绕射-绕射预测多次波进一步压制残余多次波。如图 7所示,新SRME迭代算法相比于常规SRME算法,由于补偿了绕射波能量,预测绕射多次波匹配效果更好:红色箭头指示的中层数据中的大弧形绕射多次波压制效果更好,多次波能量被压制得很弱;深层数据中的高陡倾角多次波压制效果更加明显,几乎看不到明显的多次波同相轴,近偏移距数据中的高陡同相轴压制效果更加彻底。
|
| a. 原始数据;b. 常规SRM结果;c. 本文方法结果。红色箭头指向残余绕射多次波。 图 7 理论数据效果对比 Fig. 7 Theoretical data effect contrast |
|
|
为了进一步验证新SRME迭代算法的有效性和工业使用价值,我们选取某海域的海上实际数据进行试算,并与传统SRME进行对比(图 8)。实际数据中包含大量多次波,中深层位置淹没一次波数据,信噪比很低(图 8a)。使用新SRME迭代算法可以得到更好的多次波压制结果,常规SRME算法相比于新SRME迭代算法结果中残留大量绕射多次波。差剖面中的多次波形态(图 8e)与我们预测的反射-绕射多次波(图 8d)形态十分相似。

|
| a. 原始数据;b. 常规SRME结果;c. 本文方法结果;d. 反射-绕射预测多次波;e. b与c的差剖面。 图 8 实际数据效果对比 Fig. 8 Real data effect contrast |
|
|
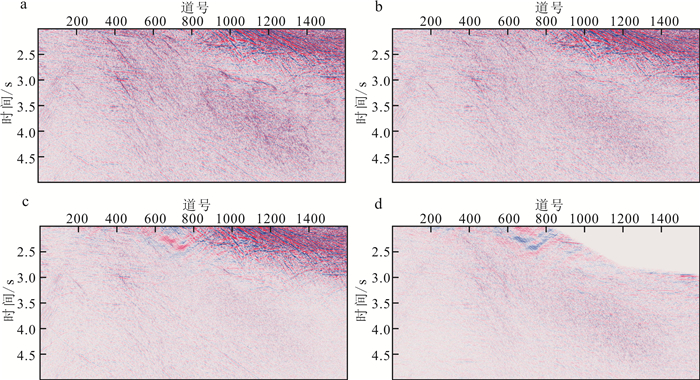
为突出新SRME迭代算法在实际数据中效果更好,我们增加叠加剖面图进行对比(图 9)。常规SRME算法压制结果中深层有大量残余多次波,淹没了一次波信息,无法明显突出连续的一次波同相轴,信噪比低,不利于后续的数据处理(图 9b);新SRME迭代算法的多次波能量被压制得十分彻底,大量的高陡多次波被压制,红色虚线圈中一次波信息明显(图 9c)。图 10为图 9红色虚线圈的局部放大图,可以更加清楚地看到多次波被压制掉。实际数据进一步证明了基于波场分离的多次波预测方法和新SRME迭代算法更加适合在包含复杂绕射多次波的数据中应用。

|
| a. 原始数据;b. 常规SME结果;c.本文方法结果;d. b与c的差剖面。 图 9 实际数据叠加效果对比 Fig. 9 Stack real data effect contrast |
|
|
|
| a. 原始数据;b. 常规SME结果;c.本文方法结果;d. b与c的差剖面。 图 10 局部放大实际数据叠加效果对比 Fig. 10 Partial enlarged stack real data effect contrast |
|
|
1) 基于f-x EMD的波场分离算法是一种十分有效的波场分离方法,利用f-x EMD算法可以压制陡倾角连续相关噪声的特性,在平面波域中实现反射波场与绕射波场分离。
2)f-x EMD算法参数简单、意义直观等优势使得这种分离方法相比于常规波场分离算法具有更好的分离效果。分离过程只需在每一个频率切片上选择合适的数据窗口和IMF分量即可,并且分离算法实现简单。
3) 虽然常规SRME算法理论上可以预测全部多次波,但实际数据错综复杂,常规SRME算法并不能很好地预测和压制绕射多次波。在多次波预测之前,我们使用基于f-x EMD波场分离算法将全数据波场分解为反射部分和绕射部分,从而获得绕射预测多次波子集:反射-绕射多次波、绕射-反射多次波和绕射-绕射多次波。选择更加有针对性的绕射多次波子集进行多次波压制,形成新的SRME迭代处理流程。相比于常规SRME算法,新SRME迭代算法针对复杂绕射多次波在理论数据和实际数据中都具有更好的压制效果,且只是增加波场分离,适合于工业应用。
| [1] |
Verschuur D J. Surface-Related Multiple Elimination: An Inversion Approach[D]. Delft: Delft University of Technology, 1991.
|
| [2] |
Verschuur D J, Berkhout A J, Wapenaar C P A. Adaptive Surface-Related Multiple Elimination[J]. Geophysics, 1992, 57(9): 1166-1177. DOI:10.1190/1.1443330 |
| [3] |
Verschuur D J, Kabir M M N. Comparison of Surface-Related Multiple Elimination with Radon Multiple Elimination[J]. Journal of Seismic Exploration, 1992(1): 363-377. |
| [4] |
Berkhout A J, Verschuur D J. Estimation of Multiple Scattering by Iterative Inversion: Part I: Theoretical Considerations[J]. Geophysics, 1997, 62(5): 1586-1595. DOI:10.1190/1.1444261 |
| [5] |
Verschuur D J. Estimation of Multiple Scattering by Iterative Inversion, Part Ⅱ: Practical Aspects and Examples[J]. Geophysics, 1997, 62(5): 1596-1611. DOI:10.1190/1.1444262 |
| [6] |
Herrmann F J. Curvelet-Domain Multiple Elimination with Sparseness Constraints[J]. Annual International Meeting Seg Expanded Abstracts, 2004, 12(1): 13-33. |
| [7] |
van Groenestijn G J A, Verschuur D J. Estimation of Primaries and Near-Offset Reconstruction by Sparse Inversion: Marine Data Applications[J]. Geophysics, 2009, 74(6): 119-128. |
| [8] |
Lopez G A, Verschuur D J. Closed-Loop Surface-Related Multiple Elimination and Its Application to Simultaneous Data Reconstruction[J]. Geophysics, 2015, 80(6): 189-199. |
| [9] |
van Dedem E J. 3D Surface-Related Multiple Prediction[D]. Deltf: Delft University of Technology, 2002.
|
| [10] |
van Dedem E J, Verschuur D J. Analysis of Surface-Related Multiples in a 3-D Media[C]//Society of Exploration Geophysicists 67th Annual International Meeting. [S. l. ]: Society of Exploration Geophysicists, 1997: 1180-1183.
|
| [11] |
van Dedem E J, Verschuur D J. 3D Surface-Related Multiple Prediction: An Inversion Approach[C]//SEG Technical Program Expanded Abstracts 2000. [S. l. ]: Society of Exploration Geophysicists, 2000: 1965-1968.
|
| [12] |
van Dedem E J, Verschuur D J. 3D Surface-Related Multiple Prediction: A Sparse Inversion Approach[J]. Geophysics, 2005, 70(3): 31-43. DOI:10.1190/1.1925752 |
| [13] |
王通, 王德利, 冯飞, 等. 三维稀疏反演多次波预测及曲波域匹配相减技术[J]. 吉林大学学报(地球科学版), 2017, 47(6): 1865-1874. Wang Tong, Wang Deli, Feng Fei, et al. Multiple Prediction with 3D Sparse Inversion and Curvelet Match[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(6): 1865-1874. |
| [14] |
王铁兴, 王德利, 孙婧, 等. 基于三维稀疏反演的混合震源数据分离与一次波估计[J]. 吉林大学学报(地球科学版), 2020, 50(3): 895-904. Wang Tiexing, Wang Deli, Sun Jing, et al. Separation and Primary Estimation of Blended Data by 3D Sparse Inversion[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(3): 895-904. |
| [15] |
张莉, 王笑雪, 韦振权, 等. 南海北部陆坡区多次波组合压制技术[J]. 物探与化探, 2015(5): 985-993. Zhang Li, Wang Xiaoxue, Wei Zhenquan, et al. Combination of Multiple Attenuation Technique on the Northern Slope of the South China Sea[J]. Geophysical and Geochemical Exploration, 2015(5): 985-993. |
| [16] |
贾连凯, 吴时国, 赵昌垒. 多次波压制技术在南海北部陆缘深水区的应用[J]. 地球物理学进展, 2014, 29(2): 920-930. Jia Liankai, Wu Shiguo, Zhao Changlei. Application of Multiple Elimination Techniques in the Deepwater Continental Margin of Northern South China Sea[J]. Progress in Geophysics, 2014, 29(2): 920-930. |
| [17] |
Verschuur D J, Wang Deli, Herrmann F J. Multi-Term Multiple Prediction Using Separated Reflections and Diffractions Combined with Curvelet-Based Subtractio[C]//Society of Exploration Geophysicists 77th Annual International Meeting. [S. l. ]: Society of Exploration Geophysicists, 2007: 2535-2539.
|
| [18] |
刘琦. 基于反射、散射波场分离的多次波消除方法研究[D]. 长春: 吉林大学, 2009. Liu Qi. Multiple Elimination Study Based on Wavefields Separation Between the Reflecting and Scattering[D]. Changchun: Jilin University, 2009. |
| [19] |
Khaidukov V, Landa E, Moser T J. Diffraction Imaging by Focusing-Defocusing: An Outlook on Seismic Superresolution[J]. Geophysics, 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [20] |
Taner M T, Fomel S, Landa E. Separation and Imaging of Seismic Diffractions Using Plane-Wave Decomposition[J]. SEG Technical Program Expanded Abstracts, 2006, 25(1): 35-41. |
| [21] |
黎孝璋, 邓勇, 赫建伟, 等. 复杂海底自由表面多次波预测方法[J]. 石油地球物理勘探, 2020, 55(1): 64-70. Li Xiaozhang, Deng Yong, Hao Jianwei, et al. Free-Surface-Related Multiple Prediction for Complex Seafloor[J]. Oil Geophysical Prospecting, 2020, 55(1): 64-70. |
| [22] |
Yilmaz O, Taner M T. Discrete Plane-Wave Decomposition by Least-Mean-Square-Error Method[J]. Geophysics, 1994, 59(6): 973-982. DOI:10.1190/1.1443657 |
| [23] |
Maïza Bekara, Baan M V D. Random and Coherent Noise Attenuation by Empirical Mode Decomposition[J]. Geophysics, 2009, 74(5): 89-98. |
| [24] |
Cai Hanpeng, He Zhenhua, Huang Deji. Seismic Data Denoising Based on Mixed Time-Frequency Methods[J]. Applied Geophysics, 2011, 8(4): 319-327. DOI:10.1007/s11770-011-0300-6 |
| [25] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proceedings A, 1998, 454: 903-995. |


