0 引言
我国资源勘探正面临着从浅层向深层,勘探开发难度不断增大的问题[1]。重力勘探已被广泛应用于研究地球深部构造,以及进行油气和矿产普查等工作[2]。与传统的重力勘探不同,重力梯度数据对浅层异常和对微小密度差引起的异常分辨率更高[3]。同时,重力梯度仪受搭载平台在移动测量中的加速度影响较小[4],更加适合于如今发展迅速的可用于多种地形勘探的航空测量。
重力梯度数据的反演问题一般是欠定问题[5]。Li等[6]提出的粗糙度矩阵给出了一种反演的光滑模型;Li[7]进一步将光滑反演方法推广到重力梯度全张量数据的反演中;王浩然等[8]也将重力异常三维反演技术应用于重力梯度张量数据反演,得到了一些有益的结论;Martinez等[4]采用该方法对航空重力梯度张量数据的不同组合进行反演,证明了全张量数据联合反演结果能够更好地反演地质体结构。同时在重力勘探中,为了得到更加准确的反演结果,通常根据一定的先验信息添加反演的约束条件。Silva等[9]讨论了现有物性反演方法中的约束条件,认为应根据实际的地质问题选择约束条件;郭冬[10]研究了如何将地质填图、钻井资料等信息转化成为物性参数进行模型约束。而在重力梯度数据反演中,虽然马国庆等[11]提出了利用重力场的一阶水平导数与异常的比值计算地质体深度,但不可否认重力及其梯度数据对地质体深度信息不敏感,需通过调整深度加权函数的相关参数改善地质体纵向分辨率;郑玉君等[12]引入了基于先验信息的深度加权函数,秦朋波[13]还对比研究了不同深度加权函数的应用效果,这些深度加权函数大多都需要对地质体的埋深有一定的初步估计,故深度信息是重力梯度反演中常用的先验信息。
本文针对目前光滑反演中普遍采用的x, y, z 3方向全局光滑[8, 14-15]得到的反演结果边界模糊且范围扩大、模型分辨率较低的问题,提出了根据地质体埋深、地层倾向等一定先验信息控制光滑范围的局部光滑约束矩阵。需要指出的是,本文所提出的理论还可以添加除深度外的其他先验信息,如地质体倾向[16],将局部光滑约束矩阵加入到重力梯度异常数据三维反演中。同时,本文还提出一种粗糙度矩阵的存储方式,详细介绍了该方式下的反演计算;最后,通过理论模型计算及对黑龙江省勃利双兴铜金矿区实测重力数据转换得到的重力梯度数据的三维反演试算,以证明该算法的准确性及有效性。
1 方法原理 1.1 模型单元剖分及正演计算重力梯度数据的物性反演中通常首先将地下空间剖分为一系列小的模型单元,黄天统等[17]使用了非结构化网格剖分。本文所采用的模型剖分是基于姚长利等[18-19]提出的重力等效存储几何格架技术进行的,将地下范围剖分为大量整齐排列的长方体单元,如图 1所示。

|
| 图 1 地下剖分单元示意图 Fig. 1 Schematicdiagram of underground subdivision unit |
|
|
等效存储几何格架技术是通过观察半空间地下模型单元与地面观测点之间的位置关系,发现同一层各模型单元与观测面之间的相对位置关系存在等价性,使用这个等价性,可以使模型每一层的存储量缩减到一个模型单元的大小,正演计算量大大减少[19]。正演计算采用的是舒晴等[20]推导的无解析奇点的重力梯度全张量正演计算公式。
1.2 光滑反演目标函数对反演的目标函数寻求光滑解是很有意义的,因为光滑产生的模型不但满足数据规定的误差,还通过防止可能导致错误结果的单个参数的无限增长来提高反演的数值稳定性。设地面观测点数为nx×ny,地下模型共有L层,光滑度约束可以按照如下方式引入目标函数[21-22]:
 (1)
(1) 式中:‖·‖表示L2范数;m为模型单元密度矩阵。用有限差分代替微分,转换成矩阵形式:
 (2)
(2) 加入粗糙度矩阵R构造反演目标函数φ(m) 为
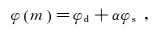 (3)
(3) 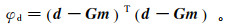 (4)
(4) 式中:φd为拟合函数,用来衡量观测值与反演值的拟合情况;φs为模型的粗糙度约束函数;G为正演核函数矩阵,与观测点和剖分单元的相对位置有关;d为观测数据;α为正则化参数。
为了克服“趋肤效应”,加入积分灵敏度矩阵S,令R0=RxTRx+RyTRy+RzTRz,则
 (5)
(5) 则目标函数可以写成以下增广矩阵的形式[23]:
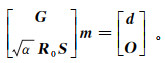 (6)
(6) 式中,O为零向量,行数由R矩阵的大小决定。式(6)明确显示了如何将由指定的约束视为额外数据。这些数据添加到问题中,为模型m提供足够的辅助约束以保证尽可能存在唯一解。
1.3 局部光滑在常见的全局光滑中,每一个剖分单元都存在x, y, z 3方向的光滑约束,粗糙度矩阵Rx,Ry,Rz分别表示如下[15]。
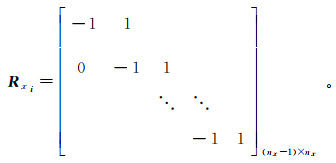 (7)
(7) 式中:nx为x方向上的单元数;i=1,2,…,Lnx,L为模型层数。矩阵Rxi每行仅有-1和1两个非零元素。将Rxi组合得到
 (8)
(8) 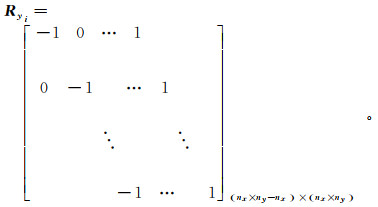 (9)
(9) 式中,ny为y方向上的单元数;i=1,2,…,L。矩阵Ryi每行仅有-1和1两个非零元素,省略号处有nx个零元素。将Ryi组合得到
 (10)
(10) 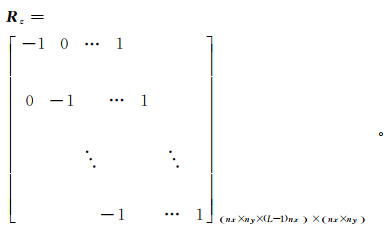 (11)
(11) 矩阵Rz每行仅有-1和1两个非零元素,省略号处有nx×ny个零元素。
最终平滑阵可以写成如下形式:
 (12)
(12) 因为光滑反演约束可以看作是一种“人为划大块”的约束,通过增加剖分单元之间的平滑关系,相当于“减少”剖分单元的块数使反演欠定性得到改善。然而在不满足光滑条件的区域该约束方式是不合理的,如在可能存在地质体的模型空间内,地质体与围岩之间不存在光滑关系。所以在全局光滑的基础上,根据其他地质地球物理信息对式(12)的行数进行删减,删掉不满足光滑反演关系的模型之间的光滑约束。最终形成按照以下示例的形式给出局部光滑粗糙度矩阵:
 (13)
(13) 式中:M为光滑约束的条件数,每一行都代表某两个剖分单元之间具有光滑关系;N为地下模型单元数。需要指出的是,式(13)仅为示例,其含义为在反演过程中仅存在M个x方向的光滑约束,在实际反演计算中,局部粗糙度矩阵的形式由先验信息决定。
1.4 粗糙度矩阵存储前文所述的传统粗糙度矩阵存储的是一个大的稀疏矩阵,当剖分单元较多时,粗糙度矩阵所占空间巨大。针对这种情况,本文提出了一种新的粗糙度矩阵存储方式,即对所有剖分单元按照顺序依次编号,当两单元之间需要进行光滑约束时,仅存储两单元的编号。如1号单元与2号单元之间需要进行光滑约束,则存储为R=[1, 2],3号单元与6号单元之间也需要进行光滑约束,则在[1, 2]下增加一行,粗糙度矩阵为
当反演计算时,计算R与某矩阵A的乘积,仅需计算R中的数字所对应A中元素位置之间的关系即可。因为R第一列代表的数字在传统矩阵中为-1,第二列为1,假如R某行元素为[3, 6],则该行乘以矩阵A中的第i列结果为-A(3, i)+A(6, i),以此类推,分别计算R中每行与A矩阵乘积,得到最终结果。经理论模型计算对比,该存储方式与传统粗糙度矩阵存储得到的结果完全相同。
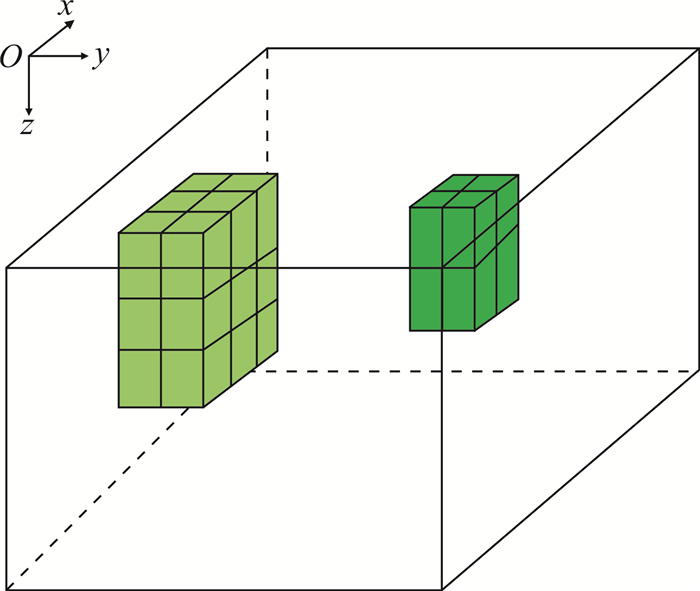
2 模型计算本文模型算例均采用引力位沿z方向的二阶导数,即Vzz分量进行单一分量的重力梯度正反演计算。将地下空间剖分为21×21×10个长方体单位元,其中每个单位元的大小为10 m×10 m×20 m,观测点为最上层每个单位元顶部的中心位置。设计一个地下存在一高一低2个地质体的三维地质模型,如图 2所示。其中;左侧地质体剩余密度为180 kg/m3,大小为30 m×20 m×60 m,顶面埋深为40 m;右侧地质体剩余密度为200 kg/m3,大小为20 m×20 m×40 m,顶面埋深为40 m。三维切片如图 3所示。
|
| 图 2 地质体模型示意图 Fig. 2 Schematic diagram of geological body model |
|
|

|
| 橘色短台阶、黄色长台阶剩余密度分别为180,200 km/m3。 图 3 地质体模型切片图 Fig. 3 Geological body model slice map |
|
|
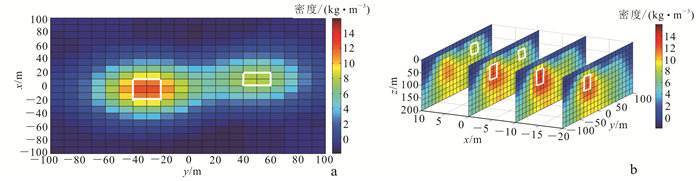
地质体模型全局光滑反演结果如图 4所示。根据前文所述,深度信息是重力梯度反演中很有必要的先验信息。局部光滑时,假设通过其他方式已知地质体埋深作为先验信息,地质体存在的地层空间不应该存在地质体与围岩之间水平方向的光滑关系,故采用左半侧空间上5层仅z方向光滑,右侧空间上4层仅z方向光滑,使该空间范围内单元体之间x, y方向无约束,其余空间位置仍然采用x, y, z 3方向的全局光滑,反演结果如图 5所示。
|
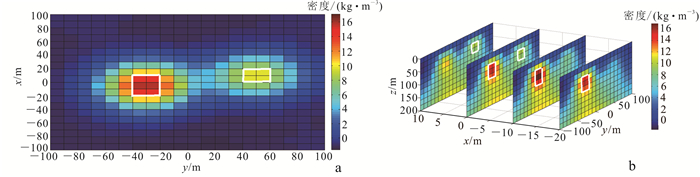
| a. z=60 m切片图;b. x=-20, -10, 0, 10 m切片图。白色线框表示地质体实际位置,后图同。 图 4 全局光滑反演切片图 Fig. 4 Global smooth inversion slice image |
|
|
|
| a. z=60 m切片图;b. x=-20, -10, 0, 10 m切片图。 图 5 局部光滑反演切片图 Fig. 5 Partially smooth inversion slice |
|
|
对比图 4a和图 5a,2种光滑方式均可以确定地质体的水平位置,但局部光滑反演得到的地质体边界位置更加清楚;这是因为在全局光滑中地质体与围岩之间存在光滑约束,使地质体边界模糊。对比图 4b和图 5b,局部光滑相比于全局光滑有明显的优势;在图 4b中右侧异常体纵向位置不明显,而从图 5b中右侧地质体纵向位置可以准确地反演得到;同时对于左侧的异常体,图 5b边界更加清晰且反演得到的剩余密度值更接近于所给定模型的剩余密度值。
对反演结果进行均方根误差计算,全局光滑的反演误差为14.033 1 kg/m3,局部光滑的反演误差为13.922 4 kg/m3,局部光滑反演结果误差更小。
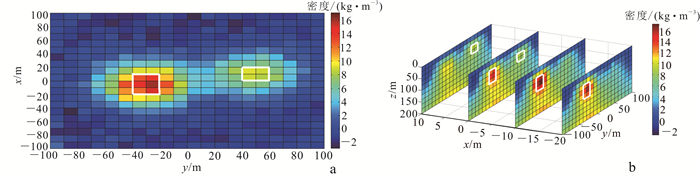
当对图 2所示模型的重力梯度值添加信噪比为15的随机噪声后,仍采用上述局部光滑约束反演,结果如图 6所示。可以看出,在该噪声水平下依然可以得到地质体的水平和纵向位置,证明了该方法计算的稳定性。
|
| a. z=60 m切片图;b. x=-20, -10, 0, 10 m切片图。 图 6 加噪部分光滑反演切片图 Fig. 6 Smooth inversion slice image with noise |
|
|
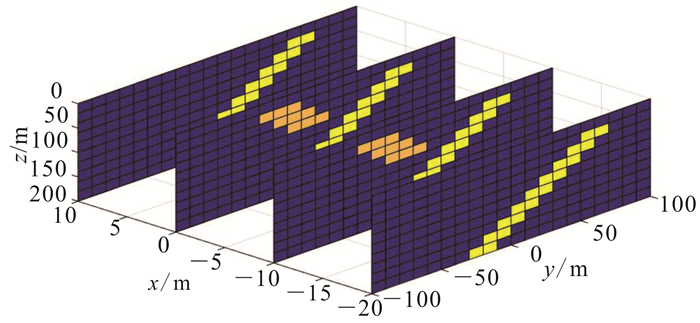
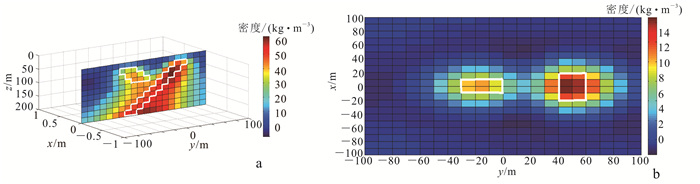
另设计一个Y型岩脉,该模型曾被Li等[6]、陈少华[15]、姚长利等[24]等用于位场的计算分析,切片图如图 7所示。假设该模型中除深度信息外,还已知该地区地层倾向。对该模型采用局部光滑约束为,橘色台阶可能存在的区域添加右倾对角单元之间的光滑关系,黄色台阶可能存在的区域添加左倾对角单元之间的光滑关系;同时为了更好地划分两单元区域,上4层两台阶之间的区域无y方向的光滑约束,反演结果如图 8所示。可以看出,在浅部可以很好地得到地质体的水平位置及纵向位置,在较深部区域水平位置略有偏差,局部光滑反演基本可以得到Y模型的轮廓位置。
|
| 橘色短台阶、黄色长台阶剩余密度分别为180,200 kg/m3。 图 7 Y模型切片图 Fig. 7 Y model slice diagram |
|
|
|
| a. x=0 m切片图;b. z=60 m切片图。 图 8 Y模型部分光滑反演切片图 Fig. 8 Partially smooth inversion slices of Y model |
|
|
为了进一步验证本文方法对实测数据的有效性,本文选取了黑龙江省勃利双兴铜金矿区的重力实测值,测区位置如图 9所示。研究区内的地层以中生界下白垩统东山组为主,其次为东南部的新太古界大马河组和第四系全新统。基于Geosoft软件,将重力值转化为重力沿z方向的导数,即重力梯度值Vzz进行反演试算。测区大小为1 km×1 km,18×34=612个测点,网格化后网格测点数为24×24=576,故将地下模型剖分为24×24×10=5 760个单元,每个单元大小为40 m×40 m×80 m,转换得到的Vzz如图 10所示。利用本文所述算法,得到的反演结果如图 11所示。

|
| 1. 第四系;2. 东山组;3. 大马河组;4. 花岗闪长岩;5. 二长花岗岩;6. 花岗闪长斑岩;7. 铜矿体及编号;8. 实测及推测地质界线;9. 不整合界线;10. 实测性质不明断层;11. 道路;12. 研究区范围。 图 9 勃利双兴铜金矿区地质图 Fig. 9 Geological map of Boli Shuangxing copper-gold mining area |
|
|

|
| 图 10 转换后测区重力梯度图 Fig. 10 Gravity gradient map of the survey area after conversion |
|
|
|
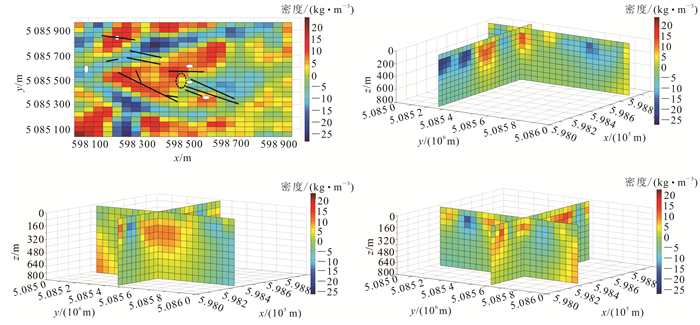
| a. z=200 m,黑色实线为实测断层,黑色虚线为前人划定的矿体区域,白色圆圈为花岗闪长岩;b. x=598 850 m, y=5 085 250 m;c. x=598 600 m, y=5 085 550 m;d. x=598 350 m, y=5 085 600 m。 图 11 反演结果切片图 Fig. 11 Inversion result slice map |
|
|
由反演结果(图 11a)结合该矿区地质图可以看出,负异常带相对于断层带对称分布,推测该地区可能在某一时期受应力作用产生断裂,一块地层沿断裂带一分为二。根据前人[25]划定的铜矿位置,可以看出该地区铜矿呈现正剩余密度且伴随断层位置,而又已知该地区花岗闪长岩为主要赋矿层,判断该地区花岗闪长岩所在位置的正剩余密度异常可能是矿体区域。过满足上述条件的位置做x,y方向的剖面图,结果如图 11b、c、d所示,矿体埋深预计在80~240 m之间,为该地区找矿工作提供了一定的指导意义。
4 结论1) 本文提出的粗糙度矩阵存储方式可以将M×N的稀疏矩阵缩小为M×2,在地下剖分单元较多时可以显著减少计算机计算内存。同时详细介绍了该存储方式下如何进行数据的读取运算,为光滑反演计算提供了便利。
2) 本文提出的基于一定先验信息的局部光滑反演,将局部光滑约束矩阵加入到重力梯度异常数据三维反演中。本文所示算例表明,相比于传统的全局光滑反演,局部光滑具有明显的分辨率优势,且在一定噪声水平下仍然可以得到理想的反演结果。此外,Y模型的算例可以看出,除深度信息外,如果有更多的其他先验信息,所提算法得到的反演结果将更加接近实际模型。
3) 黑龙江省勃利双兴铜金矿区的实测重力转换重力梯度数据反演结果表明,该算法在实际生产中具有一定的有效性和可行性。
| [1] |
李阳, 薛兆杰. 中国石化油藏地球物理技术进展与探讨[J]. 石油物探, 2020, 59(2): 159-168. Li Yang, Xue Zhaojie. Progress and Development Directions of Reservoir Geophysics at SINOPEC[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 159-168. |
| [2] |
刘财, 杨宝俊, 冯暄, 等. 论油气资源的多元勘探[J]. 吉林大学学报(地球科学版), 2016, 46(4): 1208-1220. Liu Cai, Yang Baojun, Feng Xuan, et al. Multivariate Exploration Technology of Hydrocarbon Resources[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1208-1220. |
| [3] |
曾华霖. 重力梯度测量的现状及复兴[J]. 物探与化探, 1999, 23(1): 1-6. Zeng Hualin. Present State and Revival of Gravity Gradiometry[J]. Geophysical and Geochemical Exploration, 1999, 23(1): 1-6. DOI:10.3969/j.issn.1000-8918.1999.01.001 |
| [4] |
Martinez C, Li Y, Krahenbubhl R, et al. Case History 3D Inversion of Airborne Gravity Gradiometry Data in Mineral Exploration: A Case Study in the Quadrilátero Ferrífero, Brazil[J]. Geophysics, 2013, 78(1): B1-B11. DOI:10.1190/geo2012-0106.1 |
| [5] |
王家映. 地球物理反演理论[M]. 北京: 高等教育出版社, 1998. Wang Jiaying. Inverse Theory in Geophysics[M]. Beijing: Higher Education Press, 1998. |
| [6] |
Li Y G, Oldenburg D W. 3-D Inversion of Gravity Data[J]. Geophysics, 1998, 63: 103-119. |
| [7] |
Li Y G. 3-D Inversion of Gravity Gradiometer Data[C]//SEG Technical Program Expanded Abstracts 2001. [S. l. ]: Society of Exploration Geophysicists, 2001: 1470-1474.
|
| [8] |
王浩然, 陈超, 杜劲松. 重力梯度张量数据的三维反演方法与应用[J]. 石油地球物理勘探, 2013, 48(3): 474-481. Wang Haoran, Chen Chao, Du Jinsong. 3-D Inversion of Gravity Gradient Tensor Data and Its Applications[J]. Oil Geophysical Prospecting, 2013, 48(3): 474-481. |
| [9] |
Silva J B C, Medeiros W E, Barbosa V C F. Potential-Field Inversion: Choosing the Appropriate Technique to Solve a Geologic Problem[J]. Geophysics, 2001, 66: 511-520. DOI:10.1190/1.1444941 |
| [10] |
郭冬. 先验地质信息约束下的重磁三维反演研究: 以庐枞矿集区为例[D]. 合肥: 合肥工业大学, 2014. Guo Dong. Geological-Constrained 3D Gravity and Magnetic Inversion Research: A Case Study in Lu-Zong Ore Concentration District[D]. Hefei: Hefei University of Technology, 2014. |
| [11] |
马国庆, 孟庆发, 李丽丽, 等. 利用重/磁场梯度比值函数计算地质体深度[J]. 石油地球物理勘探, 2019, 54(1): 229-234. Ma Guoqing, Meng Qingfa, Li Lili, et al. Gradient Ratio Function of Gravity and Magnetic Data for Geological Body Depth Calculation[J]. Oil Geophysical Prospecting, 2019, 54(1): 229-234. |
| [12] |
郑玉君, 侯振隆, 巩恩普, 等. 基于深度加权的多分量重力梯度数据联合相关成像方法[J]. 吉林大学学报(地球科学版), 2020, 50(4): 1197-1210. Zheng Yujun, Hou Zhenlong, Gong Enpu, et al. Correlation Imaging Method with Joint Multiple Gravity Gradiometry Data Based on Depth Weighting[J]. Journal of Jilin University (Earth Science Edition), 2020, 50(4): 1197-1210. |
| [13] |
秦朋波. 重力和重力梯度数据联合反演方法研究[D]. 长春: 吉林大学, 2016. Qin Pengbo. A Study on Integrated Gravity and Gravity Gradient Data in Inversion[D]. Changchun: Jilin University, 2016. |
| [14] |
陈涛. 三维重力梯度快速正反演研究[D]. 北京: 中国地质大学(北京), 2014. Chen Tao. Fast Forward Mapping and Fast Inversion for Gravity Gradiometer Data[D]. Beijing: China University of Geosciences (Beijing), 2014. |
| [15] |
陈少华. 基于预条件共轭梯度法的重力梯度张量反演研究[D]. 长沙: 中南大学, 2012. Chen Shaohua. Inversion Research of Gravity Gradient Tensor Based on Preconditioned Conjugate Gradient[D]. Changsha: Central South University, 2012. |
| [16] |
高秀鹤, 黄大年, 孙思源, 等. 重力梯度数据协克里金三维反演确定岩脉倾向[J]. 吉林大学学报(地球科学版), 2017, 47(2): 589-596. Gao Xiuhe, Huang Danian, Sun Siyuan, et al. Identify the Dip Angle of the Dipping Dike Model Based on Cokriging Inversion of Gravity Gradient Data[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 589-596. |
| [17] |
黄天统, 彭新发, 朱自强. 基于非结构化网格的重力梯度张量反演[J]. 物探与化探, 2020, 44(1): 132-140. Huang Tiantong, Peng Xinfa, Zhu Ziqiang. Inversion of Gravity Gradient Tensor Based on Unstructured Grids[J]. Geophysical and Geochemical Exploration, 2020, 44(1): 132-140. |
| [18] |
姚长利, 郝天珧, 管志宁, 等. 重磁遗传算法三维反演中高速计算及有效存储方法技术[J]. 地球物理学报, 2003, 46(2): 252-258. Yao Changli, Hao Tianyao, Guan Zhining, et al. High-Speed Computation and Efficient Storage in 3-D Gravity and Magnetic Inversion Based on Genetic Algorithms[J]. Chinese Journal of Geophysics, 2003, 46(2): 252-258. DOI:10.3321/j.issn:0001-5733.2003.02.020 |
| [19] |
姚长利, 郝天珧, 管志宁. 重磁反演约束条件及三维物性反演技术策略[J]. 物探与化探, 2002, 26(4): 253-257. Yao Changli, Hao Tianyao, Guan Zhining. Restrictions in Gravity and Magnetic and Technical Strategy of 3D Properties Inversion[J]. Geophysical and Geochemical Exploration, 2002, 26(4): 253-257. |
| [20] |
舒晴, 朱晓颖, 周坚鑫, 等. 矩形棱柱体重力梯度张量异常正演计算公式[J]. 物探与化探, 2015, 39(6): 1217-1222. Shu Qing, Zhu Xiaoying, Zhou Jianxin, et al. Forward Modeling Expressions for Right Rectangular Prism with Constant Density[J]. Geophysical and Geochemical Exploration, 2015, 39(6): 1217-1222. |
| [21] |
刘天佑. 位场勘探数据处理新方法[M]. 北京: 科学出版社, 2007. Liu Tianyou. A New Method of Data Processing for Potential Field Exploration[M]. Beijing: Science Press, 2007. |
| [22] |
Steven C. Constable, Occam's Inversion: A Practical Algorithm for Generatlng Smooth Models from Electromagnetic Sounding Data[J]. Geophysics, 1987, 52(3): 289-300. |
| [23] |
Portniaguine O, Zhdanov M S. 3-D Magnetic Inversion with Data Compression and Image Focusing[J]. Geophysics, 2002, 67(5): 1532-1541. |
| [24] |
姚长利, 郑元满, 张聿文. 重磁异常三维物性反演随机子域法方法技术[J]. 地球物理学报, 2007, 50(5): 1576-1583. Yao Changli, Zheng Yuanman, Zhang Yuwen. 3-D Gravity and Magnetic Inversion for Physical Properties Using Stochastic Subspaces[J]. Chinese Journal of Geophysics, 2007, 50(5): 1576-1583. |
| [25] |
滕民强. 三维地球物理勘探技术在隐伏矿产勘查中的应用研究报告[R]. 哈尔滨: 黑龙江省地球物理地球化学勘查院, 2019. Teng minqiang. Research Report on the Application of 3D Geophysical Exploration Technology in the Exploration of Hidden Minerals[R]. Harbin: Heilongjiang Institute of Geophysical and Geochemical Exploration, 2019. |



