2. 中南大学资源与安全工程学院, 长沙 410083
2. School of Resources and Safety Engineering, Central South University, Changsha 410083, China
0 引言
冻融对岩石力学性质的劣化作用是诱发寒区地质灾害的主要原因之一[1],目前多位学者在寒区冻融研究方面取得了较为丰富的成果[2-4]。天然岩体中含有大量非连续节理,在温度交替变化作用下,节理内蕴藏的水分经历周期性冻融过程,引起岩石冻胀力的变化,导致岩石内节理裂隙发生扩张,最终导致各节理相互贯通引发岩体失稳。关于冻融对岩石力学性质的影响,国内外学者已做了大量的研究,主要表现在以下几个方面:一方面是循环冻融作用对岩石力学特性的影响,如:Khanlari等[5]、Walbert等[6]、Ishikawa等[7]和Kawabata等[8]讨论了岩石单轴抗压强度、弹性模量、孔隙率等参数在冻融循环作用下的变化;Ghobadi等[9]和Martínez[10]分析了岩性、孔隙率、微裂隙水压力与岩石冻融损伤的关系;Yu等[11]基于多个试样冻融循环下力学性质衰变规律,根据红砂岩冻融循环试验,研究了红砂岩黏聚力、内摩擦角随冻融循环次数的变化规律。另一方面是从微观及理论出发,研究岩石的冻融损伤机理及其表征方法,如:Zhang等[12]、Li等[13]、Liu等[14]和Lu等[15]建立了岩石冻融损伤以及施加荷载共同作用的研究模型,并验证了模型的的适用性;Fang等[16]根据大量冻融试验建立了其损伤统计本构模型,并且给出了冻融条件下参数的确定方法。然而,岩石试样的剪切强度同样受节理形态的影响。如:王乐华等[17]和Chen等[18]研究显示,节理连通率和倾角的差异会影响岩石在三轴围压下的力学特性和剪切力学特性;卢波等[19]的研究得出了节理剪切破坏路径与连通率和不连续面、岩桥的组合路径的关系;胡波等[20]和Kravchenko等[21]的研究表明共面闭合断续节理对岩体直剪强度力学特性有较大影响。
在工程实际中,寒区岩体边坡工程通常都存在因节理及地质构造等因素的共同作用而导致岩体节理连通率存在较大差异的现象。因此,在冻融循环作用下不同连通率节理岩体力学特性难以定量分析,而目前关于此类问题的研究报道相对较少。为此,本文以不同连通率节理的岩石试样为研究对象,通过自动低温循环冻融设备模拟冻融环境,研究循环冻融后的岩石剪切力学性质,并通过对节理破坏形态作深入研究,得出岩石试样的剪切面分形维数、黏聚力损伤因子和内摩擦损伤因子的变化表达式,以期为寒区岩体的工程分析及安全防护提供现实指导依据。
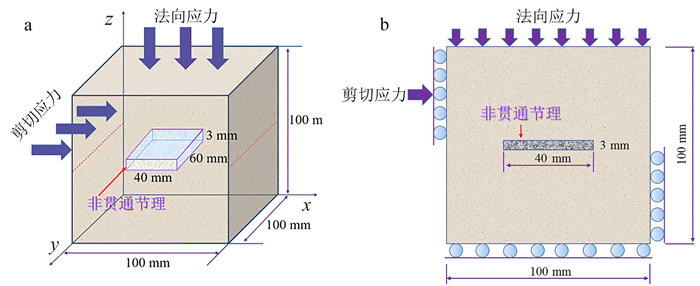
1 试验概述 1.1 试样准备及制作由于在完整岩石上预制节理较为困难,许多学者选用模型试验的方法考察节理对岩体力学强度特性的影响。根据相似理论,本文选用类岩石材料——水泥砂浆进行制样,其中水泥、石英砂、蒸馏水的质量配比为1∶1∶0.4,为保证试样的均质和节理面光滑,选用的石英砂粒径d≤0.5 mm。为制作含节理试样,选取长、宽、高均为100 mm的长方体钢制模具和相对应尺寸的亚克力板,对于不同连通率节理,预制节理尺寸分别为60 mm×20 mm×3 mm、60 mm×30 mm×3 mm、60 mm×40 mm×3 mm的长方体。按上述质量比配制水泥砂浆并搅拌均匀,待浇入模具后立即插入亚克力板并按节理预先尺寸固定,待凝固完好后拔出亚克力板并进行脱模,放置进入恒温养护箱内养护28 d。至此,含不同连通率节理的立方体试样制作完成。取节理试样连通率为L(指预制的节理裂隙宽度与试样宽度之比),则3种节理连通率分别为20%、30%、40%(图 1)。

|
| a. L=20%;b. L=30%;c. L =40%。 图 1 不同连通率节理试样 Fig. 1 Joint specimens with different persistency |
|
|
冻融设备采用TDS-300系列自动低温冻融试验箱(图 2), 剪切设备采用RYL-600型岩石剪切流变仪(图 3), 岩石剪切面形貌扫描采用HL-3DS型拍照式三维扫描仪(图 4),其扫描精度为0.02 mm。选择冻融循环次数N和节理连通率L为试验变量,进行2个因素的全面试验。冻融循环次数分别取0、10、20、30和40次,冻融试验过程可分为以下几步:1)对含节理试样进行饱水,完成以后再将节理中填充满纯净水;2)将3种节理饱和试样按顺序放入循环冻融试验箱中,设置冻结温度为-20 ℃,溶解温度为25℃,总循环次数为40次,每个循环周期为8 h;3)将节理试样总共分为5组,分别冻融0、10、20、30、40次,待40次冻融完成后,试验结束。根据前期的试验观测发现,-20 ℃下冷冻4 h后试块及节理内水已完全冻结,而在25 ℃环境下溶解4 h后节理试样已完全解冻,说明此试验中选取冻结和溶解时间分别为4 h是合理的。

|
| 图 2 TDS-300型全自动低温冻融试验箱 Fig. 2 TDS-300 automatic low temperature freezing-thawing container |
|
|

|
| 图 3 RYL-600岩石剪切流变仪 Fig. 3 RYL-600 rock shear rheometer |
|
|

|
| 图 4 HL-3DS拍照式三维扫描仪 Fig. 4 HL-3DS camera-type 3D scanner |
|
|
在冻融循环作用下,随着水冰相变,节理试样端部产生冻胀应力集中;当冻胀应力达到岩体极限拉应力状态后,最终会对岩石造成损伤导致宏观破坏。观测冻融循环试验过程可知,随着冻融循环作用深入,节理试样呈现局部化损伤现象,如图 5红框标注所示。经历不同冻融循环次数后,以L=40%试样为例,节理试样的劣化损伤典型变化趋势如图 5所示。由图 5可知,冻融循环累积的次数N越增加,冻融循环过程造成的局部化损伤效应越显著。节理岩体在10次冻融循环后即产生沿节理走向的延展裂纹;经过30次冻融后裂纹整体为贯通形态;经过40次冻融循环后,贯通裂纹呈现变宽扩展趋势,冻融损伤劣化加剧。经40次冻融循环后不同连通率节理试样典型损伤形态如图 6所示。由图 6可知:L=20%岩石试样经历冻融循环作用后,节理端部呈现裂纹分叉并先后出现次生裂纹萌生、次生裂纹丛集现象;L=30%、L=40%节理岩石的损伤形态主要为近似沿节理走向产生明显的主裂纹,几乎无裂纹分叉、偏转现象,次生裂纹少。

|
| a. 冻融10次;b. 冻融20次;c. 冻融30次;d. 冻融40次。红框表示局部化损伤现象;a′图为a图的局部放大,其余同。 图 5 L=40%节理试样冻融后裂纹扩展示意图 Fig. 5 Schematic diagram of crack growth of L=40% joint specimens after freezing-thawing |
|
|

|
| a. L=20%;b. L=30%;c. L=40%。 图 6 冻融40次后不同连通率岩体裂纹分布典型形态 Fig. 6 Typical morphology of cracks in rock masses with different persistency after 40 freezing-thawing cycles |
|
|
冻融循环作用易引起节理端部局部化损伤,在试样表面这种损伤程度存在差异,其中表面端部更易出现宏观裂纹,且裂纹较宽;随连通率越大该差异现象越明显。L=20%岩石试样侧面出现宏观裂纹晚于节理表面,随连通率的增加岩石试样侧面出现裂纹的时段逐渐提前。考虑节理中水冻结过程,节理岩体冻胀劣化的一般机制为:在冻融循环的早期阶段,以低温温度应力和冻胀水压力为主,节理开口段形成冰塞效应产生密闭空间是产生冻胀力的必要条件,冻胀水压力的迅速上升会导致节理周围的渗流场和应力场发生改变;当冻胀水压力超过节理扩展阈值时,节理内部逐渐产生部分微小裂纹并不断扩展,节理扩展将导致裂隙容积逐渐增大;当节理内水完全冻结后,冻胀力表现为冻胀冰压力,冻胀冰压力与节理应变场以及周围渗流场逐渐达到平衡后,冻胀力处于稳定阶段,此时节理裂隙冻胀扩展停止。所以, 节理试样内冻胀劣化主要是由于周期性水冰相变产生较大的冻胀力,持续作用于节理内部造成张拉破坏并驱动节理扩展演化的结果。
2.2 节理试样冻融后直剪试验冻融循环试验完成以后,将不同连通率的节理试样放置在剪切试验仪上,分别施加0.5、1.0、1.5、2.0、2.5 MPa的法向应力,以0.5 mm/min的速率施加荷载,直至达到目标位移10 mm为止,记录其剪切应力-位移曲线。利用最小二乘法拟合得到峰值剪切强度与正应力关系,并采用Mohr-Coulomb准则计算节理试样的黏聚力(c)和内摩擦角(φ),结果如表 1所示。节理试样剪切示意图如图 7所示。以L=40%试样为示例,剪切试验过程的剪切应力-位移曲线见图 8。
| L/% | N | 剪切强度参数 | |
| c/MPa | φ/(°) | ||
| 20 | 0 | 3.12 | 55.6 |
| 10 | 2.01 | 50.6 | |
| 20 | 1.93 | 49.1 | |
| 30 | 1.68 | 46.9 | |
| 40 | 1.66 | 46.3 | |
| 30 | 0 | 3.04 | 52.2 |
| 10 | 1.84 | 49.3 | |
| 20 | 1.73 | 46.8 | |
| 30 | 1.61 | 44.2 | |
| 40 | 1.60 | 43.9 | |
| 40 | 0 | 3.01 | 50.2 |
| 10 | 1.56 | 36.5 | |
| 20 | 1.49 | 35.1 | |
| 30 | 1.37 | 34.6 | |
| 40 | 1.29 | 34.2 | |
|
| a. 立体示例;b. 平面示例。 图 7 节理试样剪切示意图 Fig. 7 Schematic diagram of joint specimen shearing |
|
|

|
| a. 冻融0次;b. 冻融10次;c. 冻融20次;d. 冻融30次;e. 冻融40次。 图 8 L=40%节理试样剪切曲线 Fig. 8 Shearing curve of L= 40% joint specimen |
|
|
在L=40%下,对法向应力为1.0 MPa时剪切应力峰值强度的变化(图 8)进行定量分析可知:随着N从0次增至10次,节理试样的峰值强度降低了46.94%,N从10~20、20~30、30~40次增加的3个阶段,峰值强度分别降低了1.76%、2.68%、3.67%。说明在冻融循环10次之前,节理内部受冻融循环影响结构变化较大,冻融作用对峰值剪切强度的劣化显著,但在循环冻融10次后,峰值剪切强度下降幅度较小,冻融作用引起的节理强度劣化相对变缓。残余强度(图 8中曲线平缓阶段)从冻融0~10次降低了2.67%, 10~40次的3个阶段分别降低了4.58%、1.96%、5.86%。说明在冻融循环对节理剪切残余强度的劣化作用相对较小,残余强度均保持在1.0 MPa左右,残余强度的降低幅度与冻融次数间的规律并不明显。
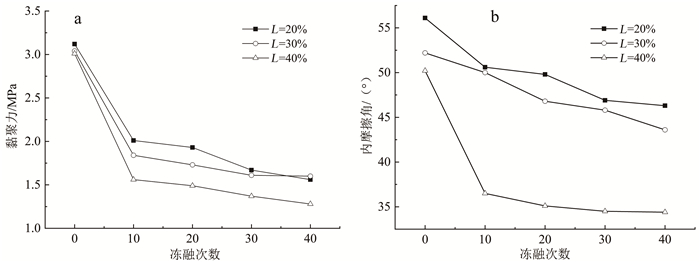
不同连通率节理试样冻融后的黏聚力和内摩擦角随冻融循环次数增加的变化规律曲线如图 9所示。由图 9可知,当N一定时,岩石试样的c、φ值随节理连通率的增大而减小。如: 当冻融循环次数N = 10时,L=30%和L =40%试样相较于L =20%节理试样的c 值分别降低了8.4%和22.3%,而φ值分别降低了1.1%和27.8%,其他冻融循环次数时,c、φ值也有类似的变化规律;而相同连通率的节理试样在经历不同冻融循环次数后的c、φ值,较冻融前节理试样有不同程度的降低,如L =20%时,10次冻融循环作用后试样较冻融前试样的c 值降低了35.5%,而φ值降低了9.8%,且c、φ值的下降幅度随冻融循环次数的增大而加剧,节理试样在其他连通率时,也符合上述变化规律。由此可得,冻融循环作用的累积和节理连通率的增加对岩石试样的抗剪强度特性有显著的劣化作用。
|
| a. 黏聚力变化曲线;b. 内摩擦角变化曲线。 图 9 节理试样剪切强度随冻融循环次数变化曲线 Fig. 9 Curve of shear strength of jointed specimens with freezing-thawing cycles |
|
|
因此,在昼夜温差和季节温差区别明显的寒区,针对岩石试样的剪切特性分析,冻融循环对节理岩体产生的劣化作用以及节理连通率对冻融循环的效果影响,都是需要考虑的主要因素。
2.3 冻融后不同连通率节理试样剪切破坏特征分析冻融循环后的节理岩体易产生裂纹的扩展与贯通,因此,冻融循环作用对节理裂纹演化规律的影响是分析岩石剪切破坏机制的关键[22]。如2.2节所述,冻融循环的劣化作用是节理试样抗剪强度劣化的主要因素之一,此种劣化作用主要是由于节理成为了岩石试样内部的弱面,并且随着冻融循环次数的累积,节理试样的尖端会萌生裂纹并不断扩展。故随冻融循环次数的增加,节理试样内部剪切面的粗糙度有所增大。因此,定量地描述节理内部裂纹的粗糙程度,是分析节理试样抗剪强度的关键因素之一[23-24]。文献[25-28] 同样认为岩体节理粗糙度系数可较为准确地预测其剪切强度。
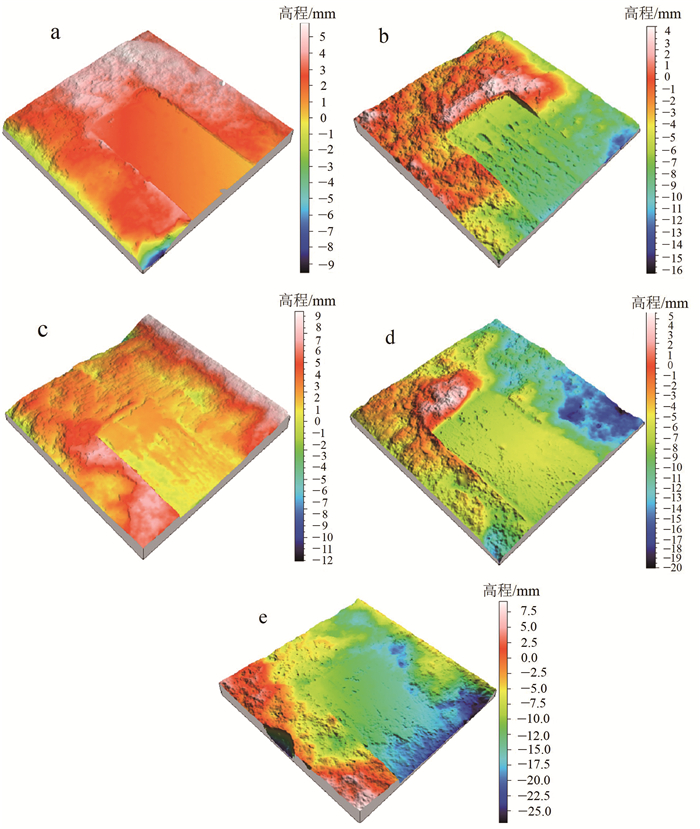
然而,目前获取节理粗糙度系数的各种方法均有缺陷,导致分析结果差异较大。而节理岩石试样的内部组成具有分形特征,因此,不同粗糙度的岩石剪切破坏面同样也具有内部差异的分形特征,不同连通率节理试样在经历不同冻融循环次数后,其剪切破坏面的粗糙程度以及分形特征都发生了较大变化。通过HL-3DS三维扫描仪对试样剪切破坏面进行扫描,并对其破坏面形貌进行重构,根据分形理论对冻融后不同连通率节理试样的剪切破坏面三维粗糙程度差异性进行分析。图 10为L=40%的试样在不同冻融循环次数后,节理试样剪切破坏面效果及三维形貌重构结果,反映了不同冻融次数下剪切面的粗糙程度(其中色度条指代截面上每个点的相对高程数值)。
|
| a. 冻融前剪切面;b. 冻融10次后剪切面;c. 冻融20次后剪切面;d. 冻融30次后剪切面;e. 冻融40次后剪切面。 图 10 L=40% 时试样剪切破坏面形貌三维重构 Fig. 10 Three-dimensional reconstruction of the shear failure surface morphology of the specimen at L= 40% |
|
|
同时由图 10可得,保持节理连通率不变,随着对岩石冻融循环次数的增加,其剪切破坏面的三维粗糙度也随着增大。依据S.M. El-soudani[29]对节理试样剪切破坏面的研究,得出三维粗糙度系数(Rs)的计算公式:
 (1)
(1) 式中:A为节理试样剪切破坏面三维表面积,mm2;A0为剪切破坏面的投影面积,mm2。
其中试样剪切破坏面的三维表面积可根据扫描设备配套处理软件Geomagic studio和talymap对扫描数据进行处理后计算获得。根据分形理论[30],A的表达式为
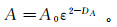 (2)
(2) 式中:ε为测量面基准单元码尺;DA为节理试样剪切破坏面的分形维数。
由于扫描仪的精度为0.02 mm,因此ε取由0.02 mm为边长的等边三角形面积,ε=1.732×10-4 mm2,DA的计算表达式为
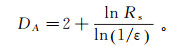 (3)
(3) 由式(3)可得不同连通率节理试样冻融后剪切破坏面的分形维数。
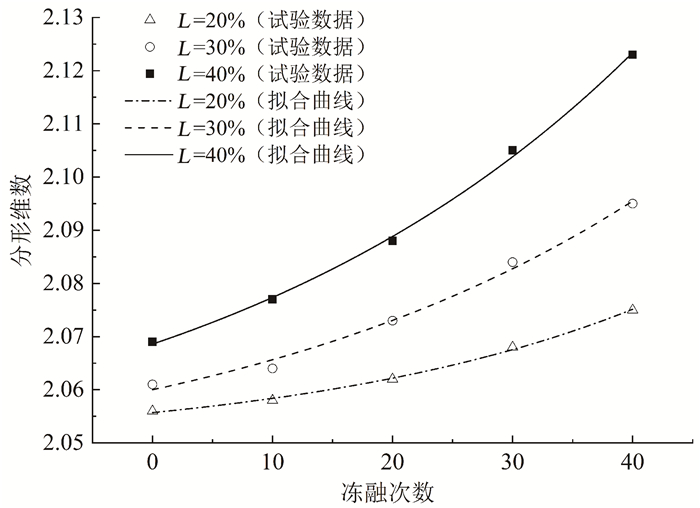
由图 10结合式(3)可知,节理试样的剪切破坏面分形维数增长趋势与冻融循环次数增加趋势基本一致,并且随节理连通率的增加而呈递增趋势。保持节理试样连通率不变时,将试样剪切破坏面分形维数与冻融循环次数的变化趋势进行线性回归分析可得,随冻融循环次数的增加,剪切破坏面的分形维数呈现近指数函数递增的趋势。如图 11中拟合曲线的关系函数为
 (4)
(4)
|
| 图 11 不同连通率试样剪切破坏面分形维数随冻融循环次数的变化规律 Fig. 11 Variation of fractal dimension of shear failure surface of specimens with different persistency under freezing-thawing cycles |
|
|
式中:DA(N~L)为冻融循环N次后节理连通率为L的剪切破坏面分形维数;DA(0~L)为冻融前节理连通率为L的剪切破坏面分形维数;x1、x2为随L变化的函数分项系数。3组拟合函数的相关系数均高于0.99,因此,节理试样的剪切破坏面分形维数随冻融循环次数的变化规律能够以此拟合函数准确表达。
将函数分项系数x1、x2分别与试样的节理连通率L作线性回归分析,可得经历不同冻融循环次数下节理不同连通率试样剪切破坏面分形维数表达式:
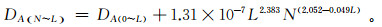 (5)
(5) 由式(5)可知,节理试样剪切破坏面分形维数受冻融循环次数和节理连通率共同作用的影响。
为进一步分析冻融循环对节理试样剪切强度劣化规律与其破坏面分形维数的关系,现引入相同节理连通率黏聚力损伤因子f(c)和内摩擦角损伤因子f(φ),表达式分别为:
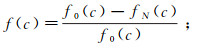 (6)
(6) 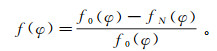 (7)
(7) 式中:f0(c)、f0(φ)分别为冻融前节理试样的黏聚力损伤因子和内摩擦角损伤因子;fN(c)、fN(φ)分别为冻融循环N次后节理试样的黏聚力损伤因子和内摩擦角损伤因子。
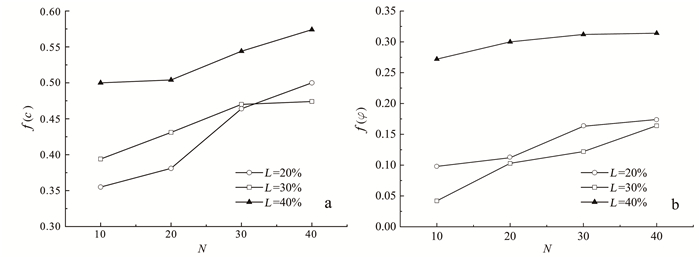
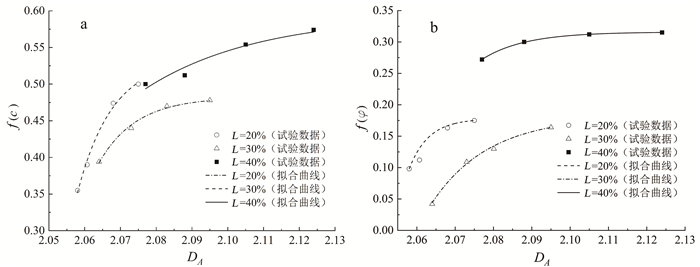
将表 1数据代入式(6)(7)中计算,分别得到各组节理连通率冻融循环后f(c)、f(φ)随冻融循环次数的变化趋势,结果如图 12所示。再结合图 11中分形维数与冻融循环次数的变化规律,可给定f(c)和f(φ)随节理试样剪切破坏面DA的变化规律,对f(c)和f(φ)与DA的变化规律进行线性回归分析,结果如图 13所示。
|
| 图 12 节理试样黏聚力损伤因子(a)和内摩擦角损伤因子(b)随冻融循环次数变化趋势 Fig. 12 Trend of shear strength damage factor of jointed specimens with freezing-thawing cycles |
|
|
|
| 图 13 节理试样黏聚力损伤因子(a)和内摩擦角损伤因子(b)随剪切破坏面分形维数变化规律 Fig. 13 Variation of shear strength damage factor of jointed specimens with fractal dimension of shear failuresurface |
|
|
由图 12可知,f(c)和f(φ)均随着N的增加总体呈现增大趋势,且节理连通率对其也有显著影响:当N≤30次时,f(c)随节理连通率的增长呈增大趋势,当冻融循环次数N>30次时,f(c)随节理连通率的增长呈先减小后增大的趋势;而当冻融次数一定时,内摩擦角损伤因子f(φ)随节理连通率的增长呈先减小后增大趋势。
由图 13可知,f(c)和f(φ)随DA 的变化呈显著的指数函数关系。黏聚力损伤因子f(c)与分形维数DA的拟合函数关系式为
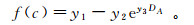 (8)
(8) 式中,y1、y2、y3分别为拟合函数的分项系数,根据节理连通率取值各异,其拟合相关系数高于0.96。
内摩擦角损伤因子f(φ)与分形维数DA的拟合函数关系式为
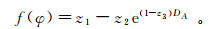 (9)
(9) 式中,z1、z2、z3分别为拟合函数的分项系数,随节理连通率取值各异,其拟合相关系数高于0.95。
由此可见,在冻融循环的作用下,节理岩石试样抗剪强度的损伤因子f(c)和f(φ),可转化为剪切破坏面分形维数的求解,分形维数能够较好地表征不同连通率节理在经历冻融循环后其抗剪强度的劣化程度。
3 结论1) 冻融循环作用对节理试样的剪切应力-位移曲线的变化规律影响显著。具体表现为节理连通率相同时,随着冻融循环次数的增加,剪切应力峰值逐渐降低;冻融次数相同时,随着节理连通率的增大,峰值剪切应力有明显的衰减。
2) 循环冻融作用对节理试样的黏聚力和内摩擦角有显著的劣化效果。节理试样在连通率相同时,黏聚力、内摩擦角随冻融循环作用次数增加有较大幅度降低,其降低程度又随节理试样连通率的增加而加剧。节理试样剪切破坏面的粗糙度随冻融循环次数的累积而呈增大趋势,且随节理连通率上升,粗糙度增大程度更显著。
3) 相同连通率节理试样冻融循环后,其剪切破坏面分形维数随冻融循环次数的增加呈显著的指数函数递增;黏聚力损伤因子和内摩擦角损伤因子随剪切破坏面分形维数的增加呈指数函数递增。
| [1] |
Shen Yanjun, Yang Gengshe, Tang Liyun, et al. Development Trend and Statistics of the Field of Geotechnical Mechanics and Engineering in Cold Regions Funded by NSFC During 2006-2015[J]. Journal of Glaciology & Geocryology, 2015, 37(5): 1294-1303. |
| [2] |
安玉科, 佴磊. 冻融循环作用下节理岩体锚固性能退化机理和模式[J]. 吉林大学学报(地球科学版), 2012, 42(2): 462-467. An Yuke, Nai Lei. Mechanism and Style of Anchorage Degradation in Jointed Rock Mass Under Cycle of Freezing and Thawing[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(2): 462-467. |
| [3] |
战高峰, 朱福, 董伟智, 等. 季冻区低路堤土基强度与影响因素相关性[J]. 吉林大学学报(地球科学版), 2015, 45(3): 869-875. Zhan Gaofeng, Zhu Fu, Dong Weizhi, et al. Influencing Factors of Low Embankment Soil Subgrade Strength in Seasonally Frozen Region[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(3): 869-875. |
| [4] |
张泽, 周泓, 秦琦, 等. 冻融循环作用下黄土的孔隙特征试验[J]. 吉林大学学报(地球科学版), 2017, 47(3): 839-847. Zhang Ze, Zhou Hong, Qin Qi, et al. Experimental Study on Porosity Characteristics of Loess Under Freezing-Thawing Cycle[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(3): 839-847. |
| [5] |
Khanlari G, Sahamieh R Z, Abdilor Y. The Effect of Freeze-Thaw Cycles on Physical and Mechanical Properties of Upper Red Formation Sandstones, Central Part of Iran[J]. Arabian Journal of Geosciences, 2015, 8(8): 5991-6001. DOI:10.1007/s12517-014-1653-y |
| [6] |
Walbert C, Eslami J, Beaucour A L, et al. Evolution of the Mechanical Behaviour of Limestone Subjected to Freeze-Thaw Cycles[J]. Environmental Earth Sciences, 2015, 74(7): 6339-6351. DOI:10.1007/s12665-015-4658-2 |
| [7] |
Ishikawa T, Lin T S, Kawabata S, et al. Effect Evaluation of Freeze-Thaw on Resilient Modulus of Unsaturated Granular Base Course Material in Pavement[J]. Transportation Geotechnics, 2019, 21(1): 833-836. |
| [8] |
Kawabata S, Ishikawa T, Kameyama S. Effects of Freeze-Thaw History on Bearing Capacity of Granular Base Course Materials[J]. Procedia Engineering, 2016, 134(6): 828-835. |
| [9] |
Ghobadi M H, Babazadeh R. Experimental Studies on the Effects of Cyclic Freezing-Thawing, Salt Crystallization, and Thermal Shock on the Physical and Mechanical Characteristics of Selected Sandstones[J]. Rock Mechanics & Rock Engineering, 2015, 48(3): 1001-1016. DOI:10.1007/s00603-014-0609-6 |
| [10] |
Martínez-Martínez J, Benavente D, Gomez-Heras M, et al. Non-Linear Decay of Building Stones During Freeze-Thaw Weathering Processes[J]. Construction & Building Materials, 2013, 38(1): 443-454. |
| [11] |
Jin Yu, Xu Chen, Hong Li, et al. Effect of Freeze-Thaw Cycles on Mechanical Properties and Permeability of Red Sandstone Under Triaxial Compression[J]. Journal of Mountain Science, 2015, 12(1): 218-231. DOI:10.1007/s11629-013-2946-4 |
| [12] |
Zhang Huimei, Yang Gengshe. Research on Damage Model of Rock Under Coupling Action of Freeze-Thaw and Load[J]. Chinese Journal of Rock Mechanics and Engineering, 2010(3): 471-476. |
| [13] |
Li Xinping, Lu Yani, Wang Yangjun. Research on Damage Model of Single Jointed Rock Masses Under Coupling Action of Freeze-Thaw and Loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2307-2315. |
| [14] |
Liu Quansheng, Huang Shibing, Kang Yongshui, et al. Fatigue Damage Model and Evaluation Index for Rock Mass Under Freezing-Thawing Cycles[J]. Chinese Journal of Rock Mechanics & Engineering, 2015, 34(6): 1116-1127. |
| [15] |
Lu Yani, Li Xinping, Chan A. Damage Constitutive Model of Single Flaw Sandstone Under Freeze-Thaw and Load[J]. Cold Regions Science and Technology, 2019, 15(9): 20-28. |
| [16] |
Fang Wen, Jiang Nan, Luo Xuedong. Establishment of Damage Statistical Constitutive Model of Loaded Rock and Method for Determining Its Parameters Under Freeze-Thaw Condition[J]. Cold Regions Science and Technology, 2019, 160: 31-38. DOI:10.1016/j.coldregions.2019.01.004 |
| [17] |
王乐华, 柏俊磊, 孙旭曙, 等. 不同连通率节理岩体三轴加卸荷力学特性试验研究[J]. 岩石力学与工程学报, 2015, 34(12): 2500-2508. Wang Lehua, Bai Junlei, Sun Xushu, et al. Experimental Study on Mechanical Properties of Jointed Rock Masses with Different Connectivity Rates Under Triaxial Loading and Unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(12): 2500-2508. |
| [18] |
Chen Xin, Liao Zhihong, Peng Xi. Deformability Characteristics of Jointed Rock Masses Under Uniaxial Compression[J]. International Journal of Mining Science and Technology, 2012, 22(2): 213-221. DOI:10.1016/j.ijmst.2011.08.012 |
| [19] |
卢波, 陈剑平, 石丙飞, 等. 用遗传算法求解节理岩体三维连通率[J]. 岩石力学与工程学报, 2004, 23(20): 3470-3474. Lu Bo, Chen Jianping, Shi Bingfei, et al. Using Genetic Algorithm to Solve 3D Connectivity of Jointed Rock Masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3470-3474. DOI:10.3321/j.issn:1000-6915.2004.20.014 |
| [20] |
胡波, 王思敬, 刘晓丽. 共面断续节理岩体直剪强度特性模型[J]. 江苏大学学报(自然科学版), 2012, 33(5): 601-605. Hu Bo, Wang Sijing, Liu Xiaoli. Direct Shear Strength Characteristics Model of Coplanar Discontinuous Jointed Rock Mass[J]. Journal of Jiangsu University (Natural Science Edition), 2012, 33(5): 601-605. DOI:10.3969/j.issn.1671-7775.2012.05.021 |
| [21] |
Kravchenko E, Liu Jiankun, Krainiukov A, et al. Dynamic Behavior of Clay Modified with Polypropylene Fiber Under Freeze-Thaw Cycles[J]. Transportation Geotechnics, 2019, 10(2): 82-90. |
| [22] |
Yang Renshu, Chen Jun, Fang Shizheng, et al. Inversion Analysis of M-C Criterion Parameters of Rock Based on Uniaxial Shearing Failure[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(7): 1351-1356. |
| [23] |
Niu Zhiren, Shi Xingjue. Statistical Theory of Rock Fractal Fracture[J]. Chinese Journal of Geophysics, 1992, 35(5): 594-603. |
| [24] |
Fathi A, Moradian Z, Rivard P, et al. Shear Mechanism of Rock Joints Under Pre-Peak Cyclic Loading Condition[J]. International Journal of Rock Mechanics and Mining Sciences, 2016, 83(9): 197-210. |
| [25] |
Zhang Yuyang, Lo S, Cao Chandi. Reassessing the Joint Roughness Coefficient (JRC) Estimation Using Z2[J]. Rock Mechanics & Rock Engineering, 2001, 34(3): 243-251. DOI:10.1007/s006030170012 |
| [26] |
Grasselli S. Shear Strength of Rock Joints Based on Quantified Surface Description[J]. Rock Mechanics & Rock Engineering, 2006, 39(4): 295. DOI:10.1007/s00603-006-0100-0 |
| [27] |
Barton N. Shear Strength Criteria for Rock, Rock Joints, Rockfill and Rock Masses: Problems and Some Solutions[J]. Journal of Rock Mechanics & Geotechnical Engineering, 2013, 5(4): 249-261. |
| [28] |
曹平, 何云, 范祥. 剪切前后节理表面形貌纹理特征变化[J]. 中南大学学报(自然科学版), 2013, 44(11): 4624-4630. Cao Ping, He Yun, Fan Xiang, et al. Changes in Joint Surface Topography and Texture Characteristics Before and After Shearing[J]. Journal of Central South University (Natural Science Edition), 2013, 44(11): 4624-4630. |
| [29] |
El-Soudani S M. Profilometric Analysis of Fractures[J]. Metallography, 1978, 11(3): 247-336. DOI:10.1016/0026-0800(78)90045-9 |
| [30] |
Theiler J. Estimating Fractal Dimension[J]. Journal of the Optical Society of America A, 1990, 7(6): 1055-1073. DOI:10.1364/JOSAA.7.001055 |


