0 引言
我国国土陆地面积的53%位于季节冻土区,为保障工农业正常生产、提高人民生活水平,季节冻土区内也建造了大量输水渠道工程[1]。在季节冻土区,由于冻土的冻胀融沉,渠道冻害问题普遍存在[2-5]。水渠冻胀灾害的形成受到水分迁移、冰水相变、热量传输和能量交换等过程的影响,而渠基土的热参数是影响上述过程的主要因素之一[6-7]。当前,不少学者将计算模型中的热参数视为确定值进行了冻胀灾害的分析研究[8-10]。然而,由于孔隙缺陷、组成成分存在差异等内部因素,以及温度、外载、水分等的随机扰动等外界环境因素影响,寒区渠基土中的热参数存在很强的变异性[11]。因此,在进行水渠灾害问题分析计算时应充分考虑热参数的随机性,以准确分析水渠的冻胀破坏机理。
目前,不少学者对岩土工程中参数的随机性进行了探讨,取得了一些研究进展:罗冲等[12]和杨凯等[13]利用Bayes理论确定了岩土力学参数的概率分布;崔洁等[14]从理论上分析了岩石的抗剪强度服从对数正态分布;李小勇等[15]对太原粉质黏土进行了分析,建立了强度的概率分布模型;李双洋等[11]通过对高温冻结黏土进行大量单轴试验,提出了正态分布及对数正态分布能够反映高温冻土弹性模量的概率分布规律,而威布尔分布能很好地描述冻土的强度分布规律;Łydżba等[16]分析了饱和土体导热系数的随机性;吴晓光[17]通过采用经典分布拟合方法对高温冻土导热系数的概率分布进行了分析;石梁宏等[18]假设热参数服从某几种经典概率分布,并在显著性水平下进行了假设检验,利用通过检验的正态分布函数描述了热参数的随机性。以上研究均以经典概率分布为基础,然而,经典概率分布函数大多为单峰型函数,无法反映随机参数的波动特性,其累计概率分布值也无法达到1.0的精度[19]。
为了克服上述经典概率分布的不足,不少学者采用新的推断方法对岩石力学参数的概率分布规律进行了研究:苏永华等[20]和邓建等[21]采用多项式逼近法对岩石抗压强度进行了统计分析;盛骤等[22]、邓建等[23]和Huang[24]采用最大熵法对岩石抗压强度的概率分布进行了推断;宫凤强等[25]和朱唤珍等[26]研究了正态信息扩散法在推断岩石压缩指数概率分布时的合理性。
当前,多项式逼近法、最大熵法、正态信息扩散法等推断方法主要应用在岩石参数的概率推断分析中;然而,由于寒区渠基黏土中含有冰晶体,存在冰水相变等作用,其物理力学参数区别于一般的岩土体,故存在较强的随机波动特性[27-28]。为此,考虑到寒区渠基黏土参数的特殊性和复杂性,对寒区渠基黏土热参数的概率分布展开研究十分必要。
本文基于4种概率推断理论(多项式逼近法、经典分布拟合法、最大熵法和正态信息扩散法),结合寒区渠基黏土热参数试验样本,利用评价指标和概率拟合曲线,对寒区渠基黏土热参数的离散性和不同概率推断函数的优劣进行了评价,以期为寒冷地区水渠的可靠度研究及今后寒区水利工程的设计和计算提供理论支撑。
1 随机变量概率推断方法 1.1 多项式逼近法多项式逼近法是基于内基空间中的最佳逼近原理[21]。假设X为区间[a,b]上的随机变量,x为随机变量的样本值,其精确的概率密度函数为f(x),随机变量的均值、k阶原点矩和k阶样本中心矩分别为μ、μk和Ak。记内积空间为C,{φi(x)}(i=0, 1, 2,…,n)为内积空间C中的线性无关系,根据最佳平方逼近原理,存在函数P(x):
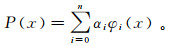 (1)
(1) 利用P(x)逼近函数f(x),选取任意实数αi(i=0,1,2,…,n),使得式(2)[21]成立:
 (2)
(2) 式中, ρ(x)为权函数。为了方便计算,可取ρ(x)=1。
根据多元函数取极值的必要条件,式(2)中的系数αi( i=0,1,2,…,n)满足方程组:
 (3)
(3) 由于{φi(x)}是线性无关的,因此式(3)中系数行列式不为0,方程组有唯一解。
根据内积定义, 可得
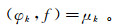 (4)
(4) 依据矩估计理论,样本矩Ak收敛于总体矩μk,即
 (5)
(5) 则由式(5)解出μk,依据式(2)和式(3)可求解得到P(x)的系数αi,代入式(1)中得到概率密度函数f(x)的多项式逼近表达式P(x)。
1.2 经典分布拟合法经典分布拟合法即根据随机变量的分布情况,提出其总体可能服从的经典分布假设[22]。常用的经典概率分布包括了正态分布、对数正态分布、威布尔分布和伽马分布等;参考概率分布假设及样本量,假设检验提出的概率分布函数,由检验的结果确定随机变量的概率分布。根据前人[17-18]研究,冻土的热参数通常采用正态分布进行描述,因此,本文选用正态分布作为经典分布拟合方法,正态分布的概率密度函数f(x)为
 (6)
(6) 式中:μ0为正态分布的期望;σ0为正态分布的标准差(σ>0)。
1.3 最大熵法最大熵法的原理为:在某一给定条件下,随机变量X可能的概率分布中存在一个使得样本信息熵取极大值的分布,此时,得到的概率分布函数是“最小偏见”的[22-24]。由此,可以确定随机变量的概率分布函数。记随机变量的概率密度函数为f(x),则其熵H为
 (7)
(7) 式中:c为常数,c>0;H>0。
将随机变量X的前i阶原点矩μi作为约束条件,则信息熵H取大值的条件为
 (8)
(8) 式中,i 为阶数,i=1,2,…,n。
根据拉格朗日乘子法,建立修正的拉格朗日函数L:
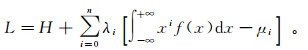 (9)
(9) 式中,λi(i=0, 1, …, n)为f(x)的系数。
根据最小驻值原理可知
 (10)
(10) 得到最大熵概率密度函数为
 (11)
(11) 式中,ai为f(x)的待定系数,i=0, 1, …, n。
1.4 正态信息扩散法正态信息扩散法的原理为:记随机变量X的概率密度函数为f(x),z为(-∞,+∞)上的一个波雷尔可测函数,则总体概率密度f(x)的一个扩散估计函数
 (12)
(12) 式中:z为扩散函数;Δn为窗宽;n为随机变量X的观测值数量。
根据分子扩散理论可推导出随机变量的概率密度函数f(x)的正态信息扩散估计函数fn(x)为
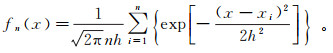 (13)
(13) 式中,h为标准正态信息扩散z的窗宽。
2 随机变量概率推断评价指标 2.1 离散性评价参数离散程度反映了观测个体之间的差异性,本文选用极差和标准差对样本数据的离散性进行评价。
极差R,又称为范围误差,表征统计资料的变异量数和样本的变动范围,极差的计算式为
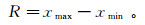 (14)
(14) 式中:xmax为样本的最大值;xmin为样本的最小值。
标准差σ,又称为标准偏差,其反映了组内个体的离散程度,标准差的计算式[27]为
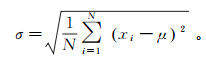 (15)
(15) 式中:N为样本个数。
2.2 拟合度评价参数为了定量地比较不同的概率推断方法与实测值的吻合程度,本文选用两种代表性的评价指标对不同概率推断函数的拟合程度进行评价,以下简要介绍2种评价指标(K-S拟合检验值和χ2拟合检验值)。
K-S拟合检验值的基本思想是求出样本观测值的概率分布F(x)与假设理论分布F′(x)的最大差值,K-S拟合检验值越小,拟合程度越高[27]。其计算式为
 (16)
(16) 式中,D为拟合检验值。
χ2拟合检验值可综合评价实际概率分布与假设概率分布的偏离程度,χ2拟合检验值越小,表示偏离程度越小,拟合程度越高[28]。其计算式为
 (17)
(17) 式中:fi为试验频率;pi为估计频率;m为样本容量。
3 结果分析首先根据试验所得的热参数样本对数据的离散程度进行统计分析,进而利用不同的推断方法计算5种温度条件下热参数的概率密度函数,并从概率密度曲线、拟合检验值、累计概率分布曲线等多个方面比较不同概率推断方法的优劣性,最终确定热参数的最优概率推断函数。
3.1 热参数离散性分析试验取含水量为14%的西北季节冻土区渠基黏土为研究对象,设置5种温度(20、-1、-2、-5、-10 ℃)条件以模拟环境温度的变化,分别测试不同温度条件下土体的导热系数,每种温度条件下各测试50组试验数据。5种温度条件下热参数的离散程度如图 1所示,可以看出不同温度条件下的热参数均存在一定的随机性。

|
| 图 1 导热系数的散点图 Fig. 1 Scatter plot of thermal conductivity |
|
|
由渠基黏土热参数样本的极差和标准差(表 1)计算可知:在20 ℃时,导热系数的极差为0.120 4 W/(m·K),标准差为0.024 8,最大值与最小值之间相差6.78%;在-1 ℃时,导热系数的极差为0.193 0 W/(m·K),标准差为0.035 2,最大值与最小值之间相差高达10.18%;其他3种温度条件下,导热系数的离散程度也较大。因此,导热系数的变异性很强,可将样本数据作为随机变量分析其概率分布规律。
| 温度/℃ | 极差/(W/(m·K)) | 标准差 |
| 20 | 0.120 4 | 0.024 8 |
| -1 | 0.193 0 | 0.035 2 |
| -2 | 0.137 5 | 0.030 5 |
| -5 | 0.137 0 | 0.030 0 |
| -10 | 0.117 7 | 0.022 2 |
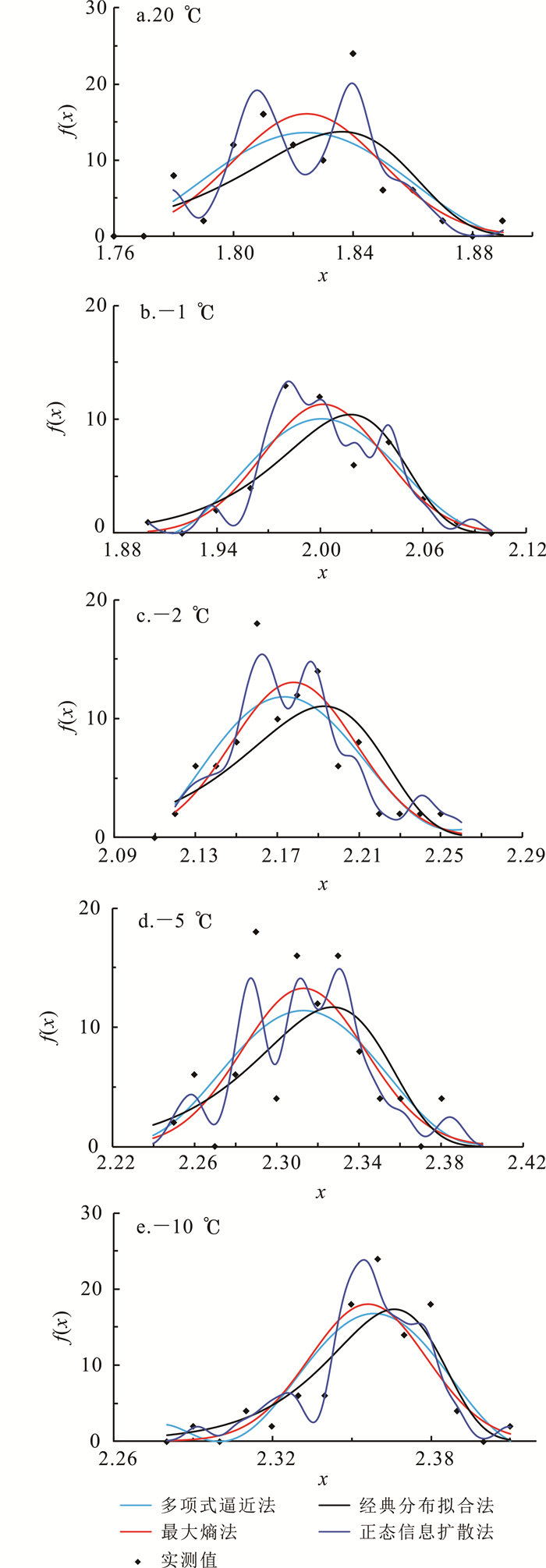
图 2为5种温度条件下不同推断方法的概率密度函数曲线(图中各个概率密度函数根据实测样本区间进行取值并拟合)。从图 2可直观地看出,实测样本数据均存在一定程度的波动。通过比较不同推断方法的概率密度曲线可知: 经典分布拟合法的概率密度函数为单峰值型函数,无法对数据的波动性进行描述;多项式逼近法和最大熵法的拟合曲线虽然具有一定的波动性,但整体上对数据随机性的描述欠佳;而正态信息扩散法能够反映每个区间内数据的波动情况,对样本数据的随机性和实际情况拟合较好。
|
| 图 2 概率密度函数曲线比较 Fig. 2 Comparison of probability density function curves |
|
|
为了准确地对比4种概率推断方法的拟合情况,计算了不同概率推断方法的K-S拟合检验值和χ2拟合检验值,以对不同概率推断方法拟合程度的优劣进行评价。
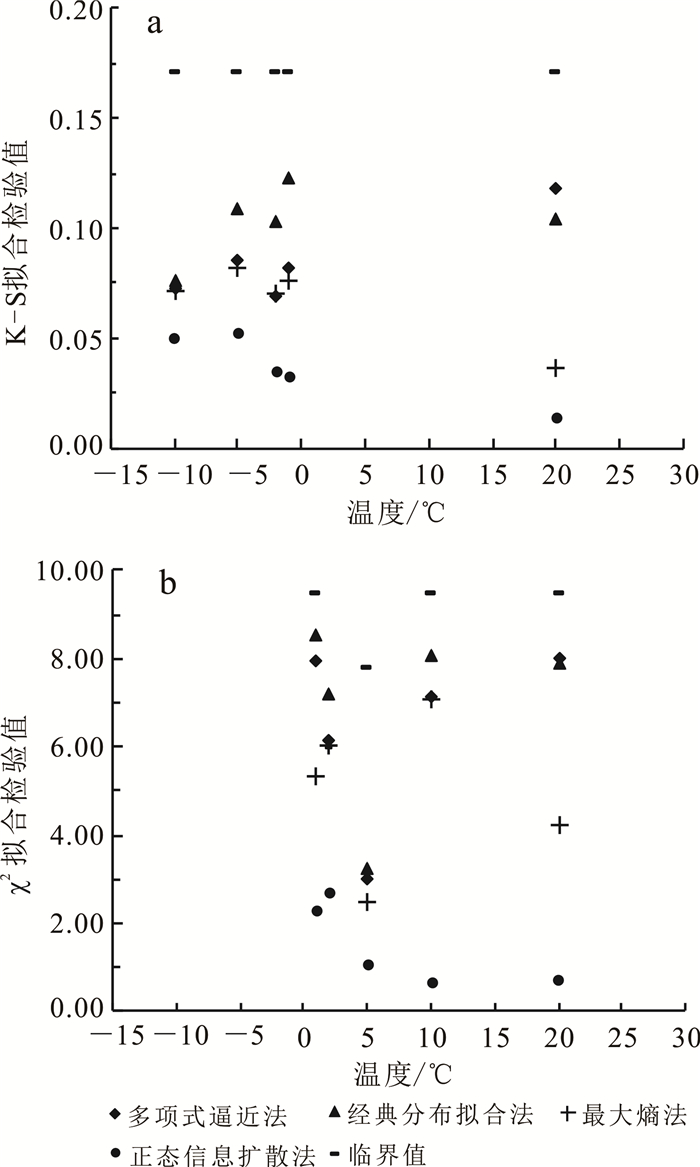
图 3分别列出了不同推断方法的K-S和χ2拟合检验值。从图 3a可以看出,4种概率推断方法的K-S拟合检验值均小于临界值,因此能够通过假设检验,不同方法的K-S拟合检验值大小排序为:在20 ℃时,多项式逼近法>经典分布拟合法>最大熵法>正态信息扩散法;在-1、-5、-10 ℃时,经典分布拟合法>多项式逼近法>最大熵法>正态信息扩散法;在-2 ℃时,经典分布拟合法>最大熵法>多项式逼近法>正态信息扩散法。比较图 3b的χ2拟合检验值发现:在20 ℃时,多项式逼近法>经典分布拟合法>最大熵法>正态信息扩散法;在-1、-2、-5、-10℃时,经典分布拟合法>多项式逼近法>最大熵法>正态信息扩散法。
|
| 图 3 K-S(a)和χ2(b)拟合检验值 Fig. 3 Fitting test values of K-S(a) and χ2(b) |
|
|
在5种温度条件下,综合来看:经典分布拟合法和多项式逼近法的2种拟合检验值均较大,因此对整个样本的拟合精度较低;正态信息扩散法的拟合检验值均为最小,证明了其拟合精度最高;其次是最大熵法,其拟合检验值也较小,拟合精度也较高。
为了进一步比较正态信息扩散法和最大熵法的拟合精度,图 4给出了5种温度条件下最大熵法和正态信息扩散法的累计概率分布曲线。对比发现,在不同的温度条件下,正态信息扩散法的拟合曲线与实测累计概率分布曲线的吻合程度更高。表 2计算了正态信息扩散法和最大熵法的累计概率曲线与实测概率曲线的最大差值,可以发现,在5种温度条件下,正态信息扩散法的最大差值仅为0.044 7,而最大熵法的最大差值为0.096 4。此外,在不同的温度条件下,累计概率分布曲线的最大差值均为最大熵法>正态信息扩散法。因此,正态信息扩散法在拟合实测热参数的概率分布时是最优的。

|
| 图 4 累计概率分布曲线 Fig. 4 Comparison of cumulative probability distribution curve |
|
|
| 温度/℃ | 最大熵法 | 正态信息扩散法 |
| 20 | 0.096 4 | 0.044 7 |
| -1 | 0.045 9 | 0.036 9 |
| -2 | 0.075 9 | 0.031 3 |
| -5 | 0.075 7 | 0.030 4 |
| -10 | 0.089 3 | 0.028 4 |
在实际的统计计算中,由于样本的数量有限,概率分布的区间取值范围可参考样本的最大值和最小值进行确定,但是对于区间的具体上下限范围,目前没有严格的规定。为此,考虑到寒区渠基黏土的复杂性及特殊性,本文参照有关区间确定方法,对寒区渠基黏土中随机参数的概率函数区间取值范围进行讨论分析。
4.1 样本区间确定方法在确定概率区间时,通常要考虑实际分布的偏度c3的影响。
1) 当c3<0时:
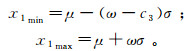 (14)
(14) 式中:x1max为区间上限;x1min为区间下限;ω为常数;c3为偏度,c3=μ/σ3[19]。
2) 当c3>0时:
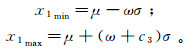 (15)
(15) 考虑寒区渠基黏土的热敏感性,分别取ω=3.0、3.5、4.0和5.0,并对比不同取值区间的概率函数拟合精度。
由于-1 ℃下导热系数的变异性最大,因此以-1 ℃最不利情形为例,对不考虑区间优化和使用不同区间优化的拟合精度进行分析对比。根据式(14)(15),分别取ω为3.0、3.5、4.0和5.0进行区间范围的计算,并利用正态信息扩散法计算不同取值区间对应的χ2拟合检验值和累计概率最大值,进而对比分析拟合精度。图 5为不同取值区间的χ2拟合检验值。从图 5可以看出,随着取值区间的逐渐扩大,χ2拟合检验值逐渐减小,当超过一定界限后,χ2拟合检验值逐渐增大,因此存在最优的取值区间。分析可以发现:以[μ-3σ,μ+3σ]和[μ-3.5σ,μ+3.5σ]为取值区间时的χ2拟合检验值较小,分别为0.596 5和0.625 0,因此最优取值区间为[μ-3σ,μ+3σ]或[μ-3.5σ,μ+3.5σ]。

|
| 图 5 不同取值区间的χ2拟合检验值 Fig. 5 The χ2 test values of differentrange |
|
|
表 3列出了使用不同区间取值的累计概率分布最大值,可以发现,当不调整区间范围,将实际样本的最大值和最小值作为区间上、下限时,正态信息扩散法的累计概率值为0.990 0;当考虑区间调整,以[μ-3σ,μ+3σ]作为取值区间,并考虑偏度影响时,其累计概率值可达到0.997 9;当取i=3.5,即以[μ-3.5σ,μ+3.5σ]作为取值区间,并考虑偏度影响时,可使得累计概率值达到1.000 0的精度。
| 取值区间表达式 | 实际取值区间 | 累计概率值 |
| 按实际样本取值 | [1.895 2,2.088 3] | 0.990 0 |
| [ μ-(3-c3) σ, μ+3 σ] | [1.887 7,2.108 7] | 0.997 9 |
| [ μ-(3.5-c3) σ, μ+3.5 σ] | [1.869 9,2.125 9] | 1.000 0 |
| [ μ-(4-c3) σ, μ+4 σ] | [1.852 1,2.144 1] | 1.000 0 |
| [ μ-(5-c3) σ, μ+5 σ] | [1.816 5,2.179 5] | 1.000 0 |
因此,考虑寒区渠基黏土的复杂性和多变性,在进行寒区水渠等水利工程的热参数概率推断时,使用3.5σ法,将[μ-3.5σ,μ+3.5σ] 作为概率函数推断时的取值区间,同时考虑偏度的影响,可较准确地推断热参数的概率分布函数。
5 结论与建议1) 不同温度条件下,冻结黏土的导热系数均存在较强的变异性,在季节性冻土地区修建水渠等农业水利工程时需充分考虑渠基黏土热学参数的随机性。
2) 多项式逼近法、经典分布拟合法、最大熵法和正态信息扩散法均可描述热参数的随机特征。比较发现,正态信息扩散法基于信息扩散原理,充分利用了样本提供的信息,相较于其他3种方法,可以更好地描述随机变量的波动特性。
3) 4种方法中,正态信息扩散法和最大熵法的拟合检验值较小,对随机热参数的拟合程度较高;进一步对比最大熵法和正态信息扩散法的累计概率分布曲线发现,正态信息扩散函数曲线与实测样本概率曲线的吻合程度更好。可知,正态信息扩散法在4种概率推断方法中具有最优的推断效果。
4) 考虑偏度的影响,提出了一种在寒区工程热参数分析时,样本取值区间调整优化的方法,并指出以3.5σ法为标准,将[μ-3.5σ,μ+3.5σ] 作为概率推断时的取值区间,可使得累计概率分布值达到1.000 0的精度。
5) 由于冻土中涉及复杂的水热力变化过程,关于冻土区渠道的随机冻害机理研究尚在探索阶段,本文虽然对寒冷地区冻结黏土的热参数进行概率分析,并取得了一定的研究进展,但也存在一些局限性,比如,随着温度的变化,冻土中含水率、含盐量及孔隙结构也随之改变,但目前从某单一因素的角度分析研究仍存在困难。但作为初步探索,可为寒区工程的随机场研究及可靠度分析提供一定的理论参考。
| [1] |
刘德仁, 张东, 张世民. 北方寒冷地区封闭渡槽粘贴聚氨酯板提高保温效果[J]. 农业工程学报, 2013, 29(9): 70-75. Liu Deren, Zhang Dong, Zhang Shimin. Increase Insulation Effect of Polyurethane Board Pasting on Closed Aqueduct Surface in Cold Regions[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013, 29(9): 70-75. |
| [2] |
李杨, 王清, 王坛华. 冻土水热耦合模型数值求解及结果检验[J]. 吉林大学学报(地球科学版), 2015, 45(1): 207-213. Li Yang, Wang Qing, Wang Tanhua. Numerical Solution and Test of Results for a Hydrothermal Coupled Model About Frozen Soil[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(1): 207-213. |
| [3] |
王正中, 李甲林, 陈涛, 等. 弧底梯形渠道混凝土衬砌冻胀破坏的力学模型研究[J]. 农业工程学报, 2008, 24(1): 18-23. Wang Zhengzhong, Li Jialin, Chen Tao, et al. Mechanics Models of Frost Heaving Damage of Concrete Lining Trapezoidal Canal with Arc-Bottom[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 24(1): 18-23. |
| [4] |
张泽, 马巍, 齐吉琳. 冻融循环作用下土体结构演化规律及其工程性质改变机理[J]. 吉林大学学报(地球科学版), 2013, 43(6): 1904-1914. Zhang Ze, Ma Wei, Qi Jilin. Structure Evolution and Mechanism of Engineering Properties Change of Soils Under Effect of Freeze-Thaw Cycle[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(6): 1904-1914. |
| [5] |
Li Shuangyang, Zhang Mingyi, Tian Yibin, et al. Experimental and Numerical Investigations on Frost Damage Mechanism of a Canal in Cold Regions[J]. Cold Region Science and Technology, 2015, 116: 1-11. DOI:10.1016/j.coldregions.2015.03.013 |
| [6] |
王正中. 梯形渠道砼衬砌冻胀破坏的力学模型研究[J]. 农业工程学报, 2008, 20(3): 24-29. Wang Zhengzhong. Establishment and Application of Mechanics Model of Frost Heaving Damage of Concrete Lining Trapezoidal Open Canal[J]. Transactions of the Chinese Society of Agricultural Engineering, 2008, 20(3): 24-29. |
| [7] |
齐吉琳, 程国栋, Vermeer P A. 冻融作用对土工程性质影响的研究现状[J]. 地球科学进展, 2005, 20(8): 887-893. Qi Jilin, Cheng Guodong, Vermeer P A. State of the Art of Influence of Freeze-Thaw on Engineering Properties of Soils[J]. Advances in Earth Sciences, 2005, 20(8): 887-893. |
| [8] |
周泓, 张豫川, 张泽, 等. 冻融作用下冻结黄土黏聚力长期强度变化规律[J]. 岩土力学, 2014, 35(8): 2241-2246. Zhou Hong, Zhang Yuchuan, Zhang Ze, et al. Changing Rule of Long-Term Strength of Frozen Loess Cohesion Under Impact of Freeze-Thaw Cycle[J]. Rock and Soil Mechanics, 2014, 35(8): 2241-2246. |
| [9] |
宿晓萍, 王清, 王文华, 等. 季节冻土区盐渍土环境下混凝土抗冻耐久性机理[J]. 吉林大学学报(地球科学版), 2014, 44(4): 1244-1253. Su Xiaoping, Wang Qing, Wang Wenhua, et al. Numerical Solution and Test of Results for a Hydrothermal Coupled Model About Frozen Soil[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(4): 1244-1253. |
| [10] |
高平, 张延军, 方静涛, 等. 浅层岩土室内、室外热物性测试的相关性[J]. 吉林大学学报(地球科学版), 2014, 44(1): 259-267. Gao Ping, Zhang Yanjun, Fang Jingtao, et al. Correlation of Shallow Layer Rock and Soil Thermal Physical Tests in Laboratory and Field[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(1): 259-267. |
| [11] |
李双洋, 赖远明, 张明义, 等. 高温冻土弹性模量及强度分布规律研究[J]. 岩石力学与工程学报, 2017, 26(增刊2): 4299-4305. Li Shuangyang, Lai Yuanming, Zhang Mingyi, et al. Study on Distribution Laws of Eastic Modulus and Strength of Warm Frozen Soil[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 26(Sup.2): 4299-4305. |
| [12] |
罗冲, 殷坤龙, 陈丽霞, 等. 万州区滑坡滑带土抗剪强度参数概率分布拟合及优化[J]. 岩石力学与工程学报, 2005, 24(9): 1588-1592. Luo Chong, Yin Kunlong, Chen Lixia, et al. Probability Distribution Fitting and Optimization of Shear Dtrength Parameters in Sliding Zone Along Horizontal-Stratum Landslides in Wanzhou City[J]. Chinese Journal of Rock Mechanical and Engineering, 2005, 24(9): 1588-1592. |
| [13] |
杨凯, 刘东升, 易前应, 等. 重庆市岩石抗剪强度参数统计分析及应用[J]. 后勤工程学院学报, 2008, 24(2): 18-21. Yang Kai, Liu Dongsheng, Yi Qianying, et al. Parameters Statistics Analysis and Application of Rock Sheering Strength in Chongqing[J]. Journal of Logistical Engineering University, 2008, 24(2): 18-21. |
| [14] |
崔洁, 江权, 冯夏庭, 等. 岩石抗剪强度参数的理论分布形态研究[J]. 岩石力学, 2015, 36(5): 1261-1274. Cui Jie, Jiang Quan, Feng Xiating, et al. Theoretical Probability Distribution of Shear Strength Parameters for Rock[J]. Rock and Soli Mechanics, 2015, 36(5): 1261-1274. |
| [15] |
李小勇, 张瑞婷, 侯晓文, 等. 太原粉质黏土工程性质指标概率特征的分析和研究[J]. 太原理工大学学报, 2000, 31(3): 254-258. Li Xiaoyong, Zhang Ruiting, Hou Xiaowen, et al. The Statistic Characteristics of Engineering Indexes for Taiyuan Silty Clay[J]. Journal of Taiyuan University of Technology, 2000, 31(3): 254-258. |
| [16] |
Łydżba D, Różański A, Rajczakowska M, et al. Random Checkerboard Based Homogenization for Estimating Effective Thermal Conductivity of Fully Saturated Soils[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2017(9): 18-28. |
| [17] |
吴晓光. 概率统计在高温冻土热学及力学性质研究中的应用[D]. 兰州: 兰州大学, 2013: 10-23. Wu Xiaoguang. The Application of Probability and Statistics in the Study on Thermal and Mechanical Properties of Warm Frozen Soil[D]. Lanzhou: Lanzhou University, 2013: 10-23. |
| [18] |
石梁宏, 李双洋, 王冲, 等. 冻土热物理性质的统计特征及分布规律研究[J]. 中南大学学报(自然科学版), 2018, 49(12): 3060-3067. Shi Lianghong, Li Shuangyang, Wang Chong, et al. Study on Statistical Characters and Distribution Laws of Thermophysical Properties of Frozen Soil[J]. Journal of Central South University (Science and Technology), 2018, 49(12): 3060-3067. |
| [19] |
宫凤强, 黄天朗, 李夕兵. 岩土参数最优概率分布推断方法及判别准则研究[J]. 岩土力学与工程学报, 2016, 36(12): 2452-2460. Gong Fengqiang, Huang Tianlang, Li Xibing. Research on Approximation Method and Discriminative Criterion of the Optimal Probability Distribution of Geotechnical Parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 36(12): 2452-2460. |
| [20] |
苏永华, 何满潮, 孙晓明. 大子样岩土参数统计方法[J]. 岩土工程学报, 2001, 23(1): 117-119. Su Yonghua, He Manchao, Sun Xiaoming. Approach on Asymptotic Approximations for Probability Density Function of Geotechnics Random Parameters[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 117-119. |
| [21] |
邓建, 李夕兵, 古德生. 结构可靠度分析的多项式数值逼近法[J]. 计算力学学报, 2002, 19(2): 212-216. Deng Jian, Li Xibing, Gu Desheng. Numerical Approximation Method in Reliability Analysis of Engineering Structure[J]. Chinese Journal of Computational Mechanics, 2002, 19(2): 212-216. |
| [22] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 4版. 北京: 高等教育出版社, 2008. Sheng Zhou, Xie Shiqian, Pan Chengyi. Probability and Mathematical Statistics[M]. 4th ed. Beijing: High Education Press, 2008. |
| [23] |
邓建, 李夕兵, 古德生. 岩石力学参数概率分布的信息熵推断[J]. 岩石力学与工程学报, 2004, 23(13): 2177-2181. Deng Jian, Li Xibing, Gu Desheng. Probability Rock Mechanics by Using Maximum Entropy Method[J]. Chinese Journal of Rock Mechanical and Engineering, 2004, 23(13): 2177-2181. |
| [24] |
Huang F Q. Information Diffusion Techniques and Small-Sample Problem[J]. International Journal of Information Technology and Decision Making, 2002, 1(2): 229-249. |
| [25] |
宫凤强, 李夕兵, 邓建. 小样本岩土参数概率分布的正态信息扩散法推断[J]. 岩石力学与工程学报, 2006, 25(12): 2549-2564. Gong Fengqiang, Li Xibing, Deng Jian. Probability Distribution of Samples of Geotechnical Parameters Using Normal Information Spread Method[J]. Chinese Journal of Rock Mechanical and Engineering, 2006, 25(12): 2549-2564. |
| [26] |
朱唤珍, 李夕兵, 宫凤强. 大样本岩土参数概率分布的正态信息扩散推断[J]. 岩土力学, 2015, 36(11): 3275-3282. Zhu Huanzhen, Li Xibing, Gong Fengqiang. Assessment of Probability Distribution of Large Samples of Geotechnical Parameters by Using Normal Information Spread Estimation Method[J]. Rock and Soil Mechanics, 2015, 36(11): 3275-3282. |
| [27] |
马建全, 李广杰, 徐佩华, 等. 基于拉丁方抽样及K-S检验的边坡可靠性分析[J]. 岩土力学, 2011, 32(7): 2153-2156. Ma Jianquan, Li Guangjie, Xu Peihua, et al. Reliability Analysis of Slope with Latin Hypercube Sampling and K-S Test[J]. Rock and Soil Mechanics, 2011, 32(7): 2153-2156. |
| [28] |
刘红帅, 郑桐, 薄景山, 等. 黏性土剪切波速不确定性的统计分析[J]. 世界地震工程, 2010, 26(增刊1): 99-103. Liu Hongshuai, Zheng Tong, Bo Jingshan, et al. Statistical Analysis of Uncertainty for Shear Wave Velocities of Cohesive Soils[J]. World Earthquake Engineering, 2010, 26(Sup.1): 99-103. |



