2. 长春工业大学应用数学研究所, 长春 130012
2. Institute of Applied Mathematics, Changchun University of Technology, Changchun 130012, China
0 引言
近年来,社会发展和人类活动加剧了水资源的消耗,生活污水、工业废水、农业灌溉等污染行为直接影响了水质状况,世界许多地区的水资源已经受到不同程度的污染。如今,世界各国对于水资源保护的重视程度达到历史新高度,希望通过科学合理的水质评价及预测来支撑水资源的科学管理。
随着大数据时代的到来,传统的水质数据处理方法很难解决如今数据维度高、来源广、容量大等一系列数据处理和数据分析的现实问题,因此如何从海量的水质数据中挖掘出有价值的信息对于水质研究工作具有重要意义。目前,有许多传统的数学方法应用于水质评价问题,如属性识别法、单因子评价法、多元统计分析法等[1-5],但这些传统方法都存在明显不足,无法完全适用于地表水的水质评价问题。深度学习(deep learning,DL)作为人工智能(artificial intelligence,AI)领域中的重要环节,其在理论研究和实际研究方面都取得了重大突破[6-14]。在水质预测研究领域:2015年姚俊杨等[15]建立了基于深度学习方法的模型,成功预测了仿真研究流域的水华爆发;同年,Archana Solanki等[16]使用深度学习方法对研究流域的水质参数进行预测分析,结果表明该方法较经典方法在预测处理方面表现更佳;2016年田亚兰等[17]构建了深度学习模型,预测研究了污水处理数据的结果;2017年王功明等[18]构建了偏最小二乘回归(partial least square regression,PLSR)自适应深度信念网络模型,并实现了对研究流域出水总磷的预测。目前,深度学习在水质预测方向的研究尚处在起步阶段,相关的模型与使用条件还没有形成完整的体系。
本文尝试采用长短时记忆(long short term memory,LSTM)循环神经网络模型对旧金山湾水质即时间序列数据进行分析研究,通过数据平稳性分析、数据清洗和模型建立,对采样站的测量水质数据进行学习、训练,进而对测试集的水质情况进行预测,收集数据分析旧金山湾水质在时间和空间维度的变化,以验证该方法的可行性和有效性。
1 研究区概况旧金山湾(San Francisco Bay),位于美国西部加利福尼亚州旧金山,是世界最佳天然港湾之一,该区域水质的优劣直接影响到当地居民的健康状况。
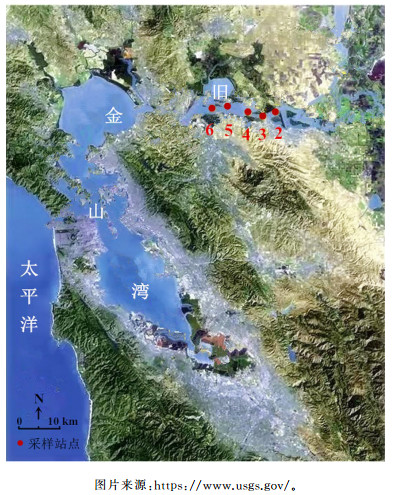
图 1为旧金山湾研究区5个水质采样站点的基本位置情况。
|
| 图 1 采样站点位置分布 Fig. 1 Location of the sampling station |
|
|
表 1所示为旧金山湾水质采样站点的基本信息,包括采样站点、位置名称、地理坐标、平均水深。
| 采样站点 | 位置名称 | 地理坐标 | 平均水深/m |
| 2 | Chain Island | 38°3.8′N, 121° 51.1′W | 11.3 |
| 3 | Pittsburg | 38°3.1′N, 121° 52.8′W | 11.3 |
| 4 | Simmons Point | 38°2.9′N, 121° 56.1′W | 11.6 |
| 5 | Middle Ground | 38°3.6′N, 121° 58.8′W | 9.8 |
| 6 | Roe Island | 38°3.9′N, 122° 2.1′W | 10.1 |
各采样站点之间的距离可利用Haversine公式[19]进行计算:
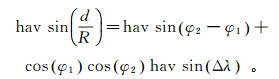 (1)
(1) 其中,
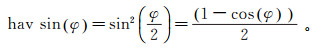 (2)
(2) 式中:d是所求两个采样站点间的距离,km;R为地球半径,km;φ1、φ2表示两个采样站点的纬度值;Δλ表示两个采样站点的经度差值。
使用Haversine公式可得到各采样站点间的距离,2—6号采样站点全长20.50 km,其中:2—3号采样点长3.18 km,3—4号采样点长6.13 km,4—5号采样点长5.06 km,5—6号采样点长6.13 km。
2 LSTM网络模型 2.1 模型简介1997年,Hochreiter等[20]首次提出了LSTM网络,其是基于循环神经网络(recurrent neural network, RNN)架构提出的一种变体网络结构,该网络有效地克服了RNN网络长期依赖和易梯度消失的问题。其特点是网络结构中的记忆细胞具有确定何时遗忘信息的能力,可以达到时间序列问题的最佳时间滞后,同时具有较好的长短期记忆能力。
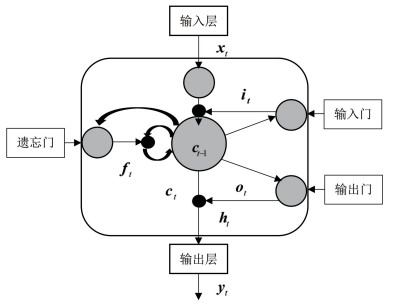
假定t为需要预测的时刻,令it、ft、ot、xt、yt分别表示t时刻的输入门、遗忘门、输出门、输入和输出,ct、ct-1分别表示t时刻和t-1时刻的激活向量,ht为t时刻隐藏层记忆单元的状态;则LSTM网络记忆结构可用图 2表示。
|
| 图 2 LSTM记忆单元结构 Fig. 2 LSTM memory cell structure |
|
|
输入层的水质数据序列x=(x1, x2, …, xt),隐藏层记忆单元的状态h=(h1, h2, …, ht),输出序列y=(y1, y2, …, yt)可由式(3)(4)得出:
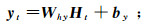 (3)
(3) 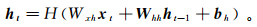 (4)
(4) 式中:Why为隐藏层-输出层的权重矩阵;Ht为t时刻的隐藏层的矢量;by为输出层的偏置向量;H(·)为隐藏层函数;Wxh为输入层-隐藏层的权重矩阵;Whh为隐藏层-隐藏层的权重矩阵;ht-1为t-1时刻隐藏层记忆单元的状态;bh为隐藏层的偏置向量。隐藏层函数可由式(5)—(9)得到:
 (5)
(5) 式中:σ(·)为标准logistic函数;Wxi为输入层-输入门的权重矩阵;Whi为隐藏层-输入门的权重矩阵;Wci为激活-输入门的权重矩阵;ct-1为t-1时刻的激活向量;bi为输入门的偏置向量。
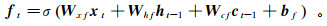 (6)
(6) 式中:Wxf为输入层-遗忘门的权重矩阵;Whf为隐藏层-遗忘门的权重矩阵;Wcf为激活-遗忘门的权重矩阵;bf为遗忘门的偏置向量。
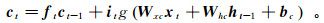 (7)
(7) 式中:g(·)为定义在[-2, 2]上的中心化logistic函数;Wxc为输入层-激活的权重矩阵;Whc为隐藏层-激活的权重矩阵;bc为激活的偏置向量。
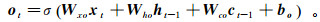 (8)
(8) 式中:Wxo为输入层-输出门的权重矩阵;Who为隐藏层-输出门的权重矩阵;Wco为激活-输出门的权重矩阵;bo为输出门的偏置向量。
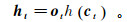 (9)
(9) 式中,h(·)为定义在[-1, 1]上的中心化Logistic函数。
目标函数的表达式为
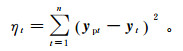 (10)
(10) 式中:ηt为最小化均方误差的总和;ypt则表示在t时刻的水质预测值。
LSTM是一类门控制循环神经网络模型,其导数不会出现消失和爆炸的情况,该模型主要包括输入门、输出门、遗忘门,3种门的相互配合可以有效控制传入模型的信息。此外,LSTM模型的存储模块还可以实现长短时记忆及信息访问,成功降低梯度消失的发生概率。
2.2 评价标准为直观地验证LSTM模型的优劣,需要对预测误差进行具体的量化评价,本文主要采用3个评价标准来衡量LSTM模型的预测精度,分别是平均绝对误差(Ema)、均方误差(Ems)、平均相对误差(Emap)。3个评价标准的值越小,则模型越优。3个评价标准定义如下:
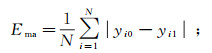 (11)
(11) 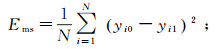 (12)
(12) 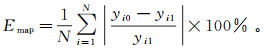 (13)
(13) 式中:N表示测试样本数;yi0表示第i段时间点的预测值;yi1表示第i段时间点的真实值。预测精度即为1与Emap的差。
3 数据分析与处理 3.1 数据准备实验数据来源于美国地质勘探局(United States geological survey,USGS)官方网站https://www.usgs.gov/。根据水质评价参数选取的原则,旧金山湾地表水体主要研究的水质指标包括溶解氧质量浓度、盐度、温度,本文选取2001—2015年旧金山湾地表水质共7 330条数据进行研究,部分数据如表 2所示。
| 日期 | 测量深度/m | ρ(溶解氧)/(mg/L) | 盐度/‰ | 温度/℃ |
| 20010226 | 1 | 10.30 | 0.18 | 10.39 |
| 20010226 | 2 | 10.30 | 0.18 | 10.38 |
| 20010226 | 3 | 10.30 | 0.18 | 10.38 |
| 20010226 | 4 | 10.30 | 0.18 | 10.38 |
| 20010226 | 5 | 10.30 | 0.20 | 10.38 |
| 20010226 | 6 | 10.20 | 0.20 | 10.38 |
| 20010226 | 7 | 10.20 | 0.20 | 10.38 |
| 20010226 | 8 | 10.20 | 0.20 | 10.37 |
| 20010226 | 9 | 10.10 | 0.21 | 10.37 |
| 20010226 | 10 | 10.10 | 0.21 | 10.37 |
| 20010619 | 1 | 7.90 | 3.09 | 22.74 |
| 20010619 | 2 | 7.90 | 3.12 | 22.72 |
| 20010619 | 3 | 7.90 | 3.17 | 22.69 |
| 20010619 | 4 | 7.90 | 3.24 | 22.65 |
| 20010619 | 5 | 7.80 | 3.30 | 22.55 |
| 20010619 | 6 | 7.80 | 3.56 | 22.35 |
| 20010619 | 7 | 7.80 | 3.61 | 22.29 |
| 20010619 | 8 | 7.80 | 3.61 | 22.27 |
| 20010619 | 9 | 7.70 | 3.62 | 22.26 |
| 20010619 | 10 | 7.70 | 3.62 | 22.26 |
由原始数据分析可知:
1) 空间维度:在冬季(当年12月—翌年2月)溶解氧质量浓度较高,随水深的增加有下降的趋势,盐度则处于一个较低的状态(<3.00‰),温度较低,且随水深的增加有降低的趋势;在夏季(当年6月—8月)溶解氧质量浓度较低,随水深的增加同样有下降的趋势,盐度处于较高的状态(>3.00‰),温度较高,且随水深的增加有降低的趋势。
2) 时间维度:以2001年为例(2001—2015年变化情况基本一致),溶解氧质量浓度整体走势先减小后增加,盐度走势先增加后减少,温度变化走势同样是先升高后降低。
3.2 数据平稳性分析统计检验能够对数据做出强有力的假设,表示零假设被拒绝或未被拒绝的程度,同时可以快速检查并确认时间序列是否平稳。本文采用augmented dickey-fuller(ADF)检验方法,该方法使用自回归模型并优化多个不同滞后值的信息标准,可以确定时间序列的趋势强度。
如果检验的零假设可以用单位根表示,表明它是非平稳的(具有一定的时间依赖结构),则替代假设(拒绝零假设)是平稳的。
统计检验中的p值为概率,如果小于等于阈值(0.05),表明拒绝零假设(数据平稳);若高于阈值(0.05),则表明不能拒绝零假设(数据非平稳)。ADF值即ADF检验值,ADF值与临界值比较,一般临界值选1%,小于该临界值即为平稳。
将原始水质数据导入到采用Python源代码所编写的模型中,计算3种水质数据的平均值x和标准方差s,计算结果为x1=2.20,x2=2.16;s1=0.007,s2=0.005。根据变异系数的性质,初步评估该数据集是平稳的。接下来需要对数据做进一步的分析。采用ADF方法对5个采样站点的水质数据进行了统计检验,结果见表 3。
| 采样站点 | ADF | p | 临界值 | ||
| 1% | 5% | 10% | |||
| 2 | -5.24 | 0 | -3.44 | -2.86 | -2.57 |
| 3 | -5.26 | 0 | -3.43 | -2.86 | -2.57 |
| 4 | -4.51 | 0 | -3.44 | -2.86 | -2.57 |
| 5 | -5.48 | 0 | -3.44 | -2.86 | -2.57 |
| 6 | -5.60 | 0 | -3.44 | -2.86 | -2.57 |
由表 3可知,每个采样站点的ADF值均为负值,且这些站点的ADF值小于临界值(1%),表明拒绝零假设,即该时间序列是平稳的。
综上所述,该水质原始数据为平稳数据,下一阶段需要对该数据做数据清洗处理。
3.3 数据清洗数据清洗过程需要删除数据中分散的空值,对于缺失值,根据本文的数据集与研究对象,采用5位移动平均法进行数据补齐,公式如(14)所示。
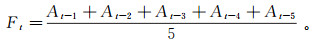 (14)
(14) 式中:Ft为t时刻的缺失值;At-1,At-2,At-3,At-4,At-5分别表示t时刻前面的5个数据值。
简言之,通过删除错误值,填补缺失值完成数据清洗工作。
3.4 数据预处理为更好地进行深度学习分析,对数据集的日期增加了one-hot编码,同时,为使研究该水质数据更有价值,严格选取同一时间点1~10 m的各项指标数据;同时对该数据进行差分预处理,满足时间序列数据平稳的状态,达到时间序列预测模型的基本要求。数据集特征及解释如表 4所示。
| 特征 | 释义 |
| Date | 采样站测量的日期(年月日) |
| Month | 时间特征向量,12维one-hot编码 |
| Year | 时间特征向量,15维one-hot编码 |
| Deep | 采样站测量的水深(m) |
| DO | 采样站测量的溶解氧质量浓度(mg/L) |
| Salinity | 采样站测量的盐度(‰) |
| Temperature | 采样站测量的温度(℃) |
时间序列的数据经过预处理过程,训练效果通常会更好,而且对于时间序列的数据类型,通常我们不希望处理后的数据和真实数据偏差过大;所以本文采用了一种简单有效的方法进行数据的预处理工作。即首先计算整个数据的平均值,然后把每个原始数据都减去这个均值,这样数据整体的变化就在0上下波动。
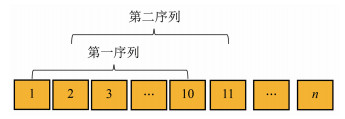
下一步操作是把预处理的数据分为训练集和测试集,本实验选取10%的数据作为测试集,90%的数据进行训练。本文以10个时序长度为例,来创造若干组这样的序列。简言之,用前9个值,去预测第10个值,然后对比预测值与第10个真实值。通过这样的过程不断优化模型。以上的循环取序列的方法如图 3所示,取完10个然后向后退一格,直到不能再取即停止。
|
| 图 3 循环取序列示意图 Fig. 3 Cycle sequence diagram |
|
|
基于前面的分析,为发现旧金山湾水质数据的时序性,使用one-hot编码来加强数据中年份和四季带来的波动。模型依靠的信息源主要有局部特征和全局特征两种。长短时记忆(LSTM)循环神经网络作为RNN网络的改进,可以有效改善RNN网络长期依赖和易梯度消失的问题,使用Python编程可以在深度学习库中搭建用于多变量时间序列预测的LSTM模型,能够有效减小时间序列预测的误差,提高预测精准度。
研究发现,LSTM模型处理时间序列问题具有一定的优势:该模型基于过去值与过去值的预测值来预测未来一段时间的值,这个过程可以使模型更加稳定,而常规方法仅仅使用一些离散不相关特征,模型预测效果不佳。
深度学习时序模型的任务:首先,将未做处理的原始数据集转换成适用于时间序列预测的数据集;然后,处理数据并使其适应用于时间序列预测问题的LSTM模型;最后,模型预测并分析结果。
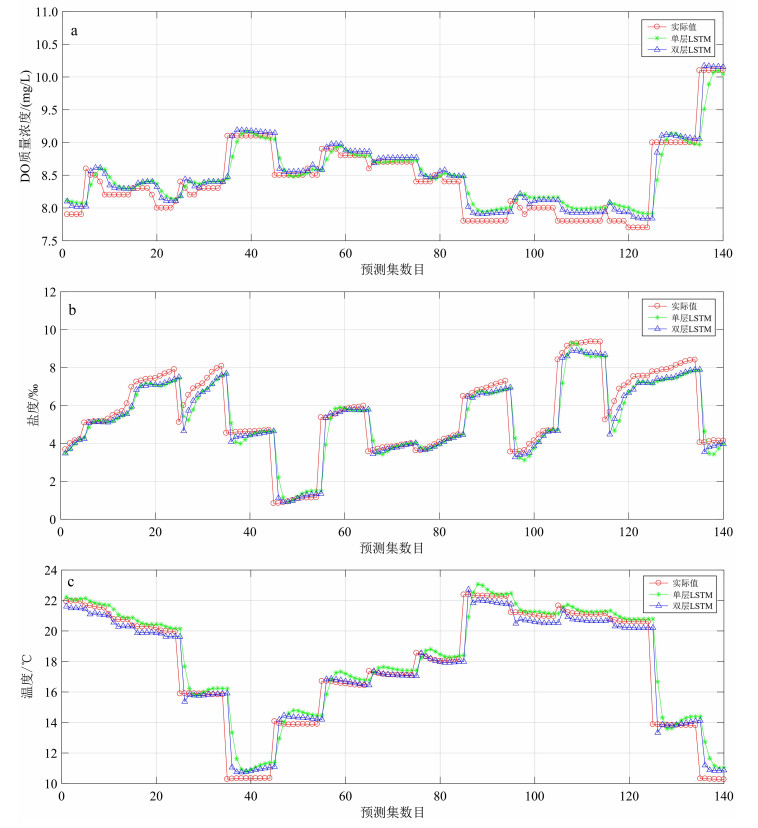
4 模型预测与结果分析实验测试单层LSTM和双层LSTM的预测结果,隐含层的单元数分别为50和100,其取值由前期实验测试经验得到。水质成分溶解氧(DO)、盐度、温度的实际值和预测值对比结果如图 3所示(以2号采样站点为例)。
由图 4a可知,对于两种LSTM方法,水质成分溶解氧预测值的变化与实际值保持相同的趋势,双层LSTM方法较单层LSTM方法的拟合程度更好。
|
| 图 4 2号采样点3种水质成分预测对比结果 Fig. 4 Comparison results of prediction of three water quality components in sampling Site 2 |
|
|
表 5为单层LSTM与双层LSTM模型得出的DO质量浓度评价标准结果,由表 5可知,单层LSTM模型的平均评价标准为Ems=0.09,Ema=0.22,Emap=0.027,双层LSTM模型的平均评价标准为Ems=0.05,Ema=0.13,Emap=0.016,相较预测精度提高了1.1%,3项评价标准结果表明,双层LSTM模型均优于单层LSTM模型。
| 采样站点 | 单层 | 双层 | |||||
| Ems | Ema | Emap | Ems | Ema | Emap | ||
| 2 | 0.08 | 0.21 | 0.025 | 0.05 | 0.14 | 0.017 | |
| 3 | 0.08 | 0.20 | 0.024 | 0.04 | 0.13 | 0.016 | |
| 4 | 0.13 | 0.26 | 0.031 | 0.06 | 0.12 | 0.014 | |
| 5 | 0.08 | 0.21 | 0.025 | 0.04 | 0.11 | 0.013 | |
| 6 | 0.09 | 0.23 | 0.028 | 0.05 | 0.14 | 0.018 | |
| 平均值 | 0.09 | 0.22 | 0.027 | 0.05 | 0.13 | 0.016 | |
由图 4b亦可知,双层LSTM方法的拟合效果优于单层LSTM方法,双层LSTM方法的预测值变化趋势与真实值变化趋势的状态保持平稳。
表 6为单层LSTM与双层LSTM模型得出的盐度评价标准结果,由表 6可知,单层LSTM模型的平均Ems=3.48,Ema=1.60,Emap=0.210,双层LSTM模型的平均Ems=1.58,Ema=0.66,Emap=0.100,相较预测精度提高了11%,3种评价标准的综合表现均为双层LSTM模型表现优于单层LSTM模型。
| 采样站点 | 单层 | 双层 | |||||
| Ems | Ema | Emap | Ems | Ema | Emap | ||
| 2 | 2.23 | 1.29 | 0.272 | 0.92 | 0.52 | 0.127 | |
| 3 | 2.47 | 1.36 | 0.242 | 1.04 | 0.43 | 0.103 | |
| 4 | 2.75 | 1.42 | 0.175 | 1.31 | 0.81 | 0.101 | |
| 5 | 4.23 | 1.78 | 0.187 | 2.10 | 0.68 | 0.082 | |
| 6 | 5.74 | 2.17 | 0.174 | 2.51 | 0.88 | 0.085 | |
| 平均值 | 3.48 | 1.60 | 0.210 | 1.58 | 0.66 | 0.100 | |
从图 4c可以看出,双层LSTM模型的预测值变化趋势与真实值拟合效果良好。
表 7为单层LSTM与双层LSTM模型得出的温度评价标准结果,其中单层LSTM模型的平均Ems=2.74,Ema=1.21,Emap=0.075,双层LSTM模型的平均Ems=1.31,Ema=0.55,Emap=0.036,相较单层LSTM模型预测精度提高了3.9%,3种评价标准的综合表现为双层LSTM模型表现优于单层LSTM模型。
| 采样站点 | 单层 | 双层 | |||||
| Ems | Ema | Emap | Ems | Ema | Emap | ||
| 2 | 1.96 | 0.95 | 0.062 | 1.12 | 0.53 | 0.035 | |
| 3 | 2.94 | 1.43 | 0.083 | 1.09 | 0.46 | 0.030 | |
| 4 | 4.28 | 1.50 | 0.095 | 2.01 | 0.59 | 0.043 | |
| 5 | 2.02 | 0.92 | 0.061 | 1.14 | 0.55 | 0.034 | |
| 6 | 2.51 | 1.26 | 0.076 | 1.19 | 0.64 | 0.038 | |
| 平均值 | 2.74 | 1.21 | 0.075 | 1.31 | 0.55 | 0.036 | |
综上所述,双层长短时记忆循环神经网络模型较单层长短时记忆循环神经网络模型的预测精度平均提高了5.3%,LSTM模型可以对旧金山湾地表水质进行有效的预测评价,并且采用双层LSTM模型的预测结果要优于单层LSTM模型的预测结果。
5 结语1) 针对美国旧金山湾研究区水质数据,运用深度学习时序模型对地表水质进行预测研究,并且使用LSTM模型进行特征提取。对原始数据分别进行了时空维度上的分析和平稳性分析,随后进行数据清洗与数据预处理,将处理后的数据按照1:9的比例分为测试集与训练集。
2) 文中将单层LSTM与双层LSTM均应用到溶解氧、盐度以及温度的建模预测中,通过计算相应的平均绝对误差、均方误差、平均相对误差,结果表明:双层LSTM模型的对这3类数据的建模预测效果均优于单层LSTM,该方法可以作为地表水质预测研究的技术参考。
| [1] |
Kazakis N, Mattas C, Pavlou A, et al. Multivariate Statistical Analysis for the Assessment of Groundwater Quality Under Different Hydrogeological Regimes[J]. Environmental Earth Sciences, 2017, 76: 1-13. DOI:10.1007/s12665-016-6304-z |
| [2] |
张兆吉, 费宇红, 郭春艳, 等. 华北平原区域地下水污染评价[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1456-1461. Zhang Zhaoji, Fei Yuhong, Guo Chunyan, et al. Evaluation of Groundwater Pollution in the North China Plain[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(5): 1456-1461. |
| [3] |
余文忠, 唐德善, 陆廷春. 熵权属性识别法在地下水水质评价中的应用[J]. 水电能源科学, 2013(7): 41-43. Yu Wenzhong, Tang Deshan, Lu Tingchun. Application of Entropy Weight Attribute Recognition Method in Groundwater Quality Evaluation[J]. Hydroelectric Energy Science, 2013(7): 41-43. |
| [4] |
Hosseini-Moghari S M, Ebrahimi K, Azarnivand A. Groundwater Quality Assessment with Respect to Fuzzy Water Quality Index (FWQI):An Application of Expert Systems in Environmental Monitoring[J]. Environmental Earth Sciences, 2015, 74(10): 7229-7238. DOI:10.1007/s12665-015-4703-1 |
| [5] |
Kumar N V, Mathew S, Swaminathan G. Multifactorial Fuzzy Approach for the Assessment of Groundwater Quality[J]. Journal of Water Resource and Protection, 2010, 2(6): 597-608. DOI:10.4236/jwarp.2010.26069 |
| [6] |
虞未江, 贾超, 狄胜同, 等. 基于综合权重和改进物元可拓评价模型的地下水水质评价[J]. 吉林大学学报(地球科学版), 2019, 49(2): 539-547. Yu Weijiang, Jia Chao, Di Shengtong, et al. Groundwater Quality Evaluation Based on Comprehensive Weight and Improved Matter Element Extension Evaluation Model[J]. Journal of Jilin University(Earth Science Edition), 2019, 49(2): 539-547. |
| [7] |
Przydatek G, Kanownik W. Impact of Small Municipal Solid Waste Landfill on Groundwater Quality[J]. Environmental Monitoring and Assessment, 2019, 191(3): 169. DOI:10.1007/s10661-019-7279-5 |
| [8] |
韩彰, 陈健, 李经纬, 等. 改进物元可拓法在水闸工程安全综合评估中的应用[J]. 水力发电, 2015, 41(4): 82-85. Han Zhang, Chen Jian, Li Jingwei, et al. Application of Improved Matter Element Extension Method in Comprehensive Safety Assessment of Sluice Engineering[J]. Hydroelectric Power, 2015, 41(4): 82-85. |
| [9] |
李巧, 周金龙, 高业新, 等. 新疆北部平原区2003-2011年地下水水质变化特征[J]. 地学前缘, 2014, 21(4): 124-134. Li Qiao, Zhou Jinlong, Gao Yexin, et al. Variation Characteristics of Groundwater Quality in the Northern Plain of Xinjiang from 2003 to 2011[J]. Earth Science Frontiers, 2014, 21(4): 124-134. |
| [10] |
何振强, 方诗标, 陈永明, 等. 钱塘江感潮河段污染物迁移扩散数值分析[J]. 环境科学学报, 2017, 37(5): 1668-1673. He Zhenqiang, Fang Shibiao, Chen Yongming, et al. Numerical Analysis of Contaminant Migration and Diffusion in the Tidal River Section of Qiantang River[J]. Journal of Environmental Science, 2017, 37(5): 1668-1673. |
| [11] |
杨佳, 钱会. 时间序列分析在地下水位动态预测中的应用[J]. 水资源与水工程学报, 2015(1): 58-62. Yang Jia, Qian Hui. Application of Time Series Analysis in Dynamic Prediction of Groundwater Level[J]. Journal of Water Resources and Water Engineering, 2015(1): 58-62. |
| [12] |
Najafabadi M M, Villanustre F, Khoshgoftaar T M. Deep Learning Applications and Challenges in Big Data Analytics[J]. Journal of Big Data, 2015, 2(1): 1-21. DOI:10.1186/s40537-014-0007-7 |
| [13] |
Hao X, Zhang G, Ma S. Deep Learning[J]. International Journal of Semantic Computing, 2016, 10(3): 417-439. DOI:10.1142/S1793351X16500045 |
| [14] |
Wu Z Y, El-Maghraby M, Pathak S. Applications of Deep Learning for Smart Water Networks[J]. Procedia Engineering, 2015, 119: 479-485. DOI:10.1016/j.proeng.2015.08.870 |
| [15] |
姚俊杨, 许继平, 王小艺, 等. 基于深度学习的湖库藻类水华预测研究[J]. 计算机与应用化学, 2015, 32(10): 112-115. Yao Junyang, Xu Jiping, Wang Xiaoyi, et al. Prediction of Algal Blooms in Lakes Based on Deep Learning[J]. Journal of Computers and Applied Chemistry, 2015, 32(10): 112-115. |
| [16] |
Solanki A, Agrawal H, Khare K. Predictive Analysis of Water Quality Parameters using Deep Learning[J]. International Journal of Computer Applications, 2015, 125(9): 29-34. DOI:10.5120/ijca2015905874 |
| [17] |
田亚兰.水质预测的粒计算求解与深度学习方法[D].重庆: 重庆邮电大学, 2016. Tian Yalan. Granular Calculation and Deep Learning Method for Water Quality Prediction[D]. Chongqing: Chongqing University of Posts and Telecommunications, 2016. |
| [18] |
王功明, 李文静, 乔俊飞. 基于PLSR自适应深度信念网络的出水总磷预测[J]. 化工学报, 2017, 68(5): 1987-1997. Wang Gongming, Li Wenjing, Qiao Junfei. Prediction of Total Phosphorus in Effluent Based on PLSR Adaptive Depth Belief Network[J]. CIESC Journal, 2017, 68(5): 1987-1997. |
| [19] |
Robusto C C. The Cosine-Haversine Formula[J]. American Mathematical Monthly, 1957, 64(1): 38. DOI:10.2307/2309088 |
| [20] |
Hochreiter S, Schmidhuber J. Long Short-Term Memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |


