2. 河南理工大学物理与电子信息学院, 河南 焦作 454000
2. Institute of Physics and Electronic Information, Henan University of Technology, Jiaozuo 454000, Henan, China
0 引言
通常大地地质构造,包括造山运动、褶皱、断裂等会影响到地下结构的各向异性。所谓的各向异性是指介质的性质或材质随着方向的变化而变化[1-2]。但在以往的研究中,前人主要依据各向同性电阻率介质理论来研究地下介质的大地电磁响应。各向同性介质模型在实践中具有很大的局限性,因为它仅在沿水平方向是各向同性的情况下适用。但是地下的结构并非如此简单,在沉积盆地中,一部分岩层经过压实变质作用,其电阻率在垂向上和倾向上都是变化的;更为一般情况下介质的电阻率沿任意方向都是不均匀的,此时岩层介质表现出各向异性特征,不适合再用各向同性特征去研究。而近些年人们对地下结构的研究逐渐由刚开始的各向同性和无限均匀变为各向异性和不均匀性,各向异性的研究得到更多学者的关注,这是研究大地电磁地表响应的重大突破[3-13]。早在20世纪20年代,Schlum- berger[14]开展了直流点发勘探研究,最先发现地下介质的电导率是各向异性的;到了1934年其又开展了地面电法和地球物理测井工作来研究各向异性的表现形式。20世纪60年代,Keller[15]分别从不同角度讨论分析了岩石中的微各向异性问题;20世纪80年代,陈乐寿[16]从大地电磁各向异性的基础理论出发,研究了层状介质的大地电磁各向异性正反演算法。各向异性研究成果虽然丰富,但直到2000年后其才首次被应用到大地电磁实测资料处理中[17-20]。特别是在2002年,Li等[21]推导出各向异性介质3个主轴上的电导率张量,并分析了参数对各向异性阻抗张量的影响。基于前人的研究成果,笔者从大地电磁各向异性的偏微分方程入手,将面向目标的自适应有限元算法应用于该微分方程中,分别对倾斜、水平和垂直介质模型进行正演模拟,讨论主轴电阻率和偏转角的变化对不同极化模式的影响;进而归纳得到不同参数对大地电磁两种极化模式响应特征的影响,以期为今后研究大地电磁反演和精细化解释提供理论指导。
1 方法原理 1.1 大地电磁各向异性边值问题根据麦克斯韦方程组和各向异性介质的电阻率张量可推导大地电磁各向异性满足的偏微分方程:
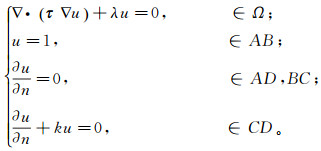 (1)
(1) 式中:∇为拉普拉斯算子;Ω为研究区域;n为研究区域内法线方向;λ=iwμ,其中i为复数单位,w为频率,μ为磁导率;u为场值;k为复波数;AB为研究区域上边界,AD,BC分别为研究区域左右边界,CD为研究区域下边界(图 1);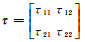

|
| 图 1 研究区域示意图 Fig. 1 Schematic diagram of the study area |
|
|
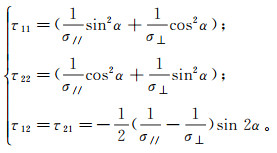 (2)
(2) 式中:σ//为平行层面电导率;σ⊥为垂直层面电导率;α为偏转角。在TE极化模式中, 反对角元素τ12=τ21=0,正对角元素τ11=τ22=σ//; 而在TM极化模式中, 两对角元素则相差较大。
将边界条件代入大地电磁测深各向异性的微分方程式中,利用自适应有限单元法求解该微分方程得到电磁场在各向异性介质中的分布。
1.2 伽辽金法加权余量表达式有限单元法解题的基本思想是将研究区域剖分为许多小单元,在单元内进行插值。本文采用伽辽金加权余量法将微分方程转化为所对应的弱变分形式,设权重因子为ω,式(1)两边同时乘以权重因子并积分可得
 (3)
(3) 式(3)的左边第一项利用矢量运算公式∇·(φA)=∇φ·A+φ∇·A(A为任意向量,φ任意标量)和积分变换公式并带入边界条件可得
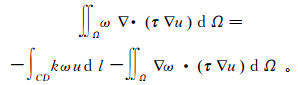 (4)
(4) 将式(4)带入式(3)可得
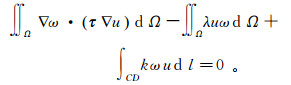 (5)
(5) 取形函数作为权重因子,并令ψ=N, 其中N为形函数,ψ为权重因子,使得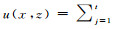
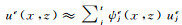
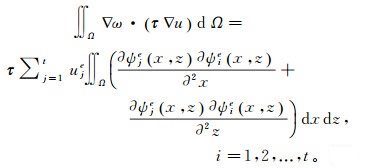 (6)
(6) 其中基函数满足:
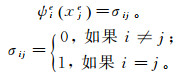 (7)
(7) 由式(6)可得式(5)第一项的积分值,同理可算出式(5)的第二项和第三项的积分值。最后区域网格单元的积分可表示为
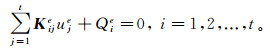 (8)
(8) 式中:Qie为区域网格单元e上的线积分;Kije为刚度矩阵。
利用网格的整体节点编号和局部单元编号合成整个网格节点的大型稀疏矩阵并代入边界条件组成线性方程组,由于总体系数矩阵是对称的,为节省计算机内存,只存储矩阵的下三角或上三角部分。非零元素只存在于三角元顶点编号所对应的行和列的交叉位置上,其他均为零元素。通常只需要存储非零元素。本文采用定带宽存储方式,利用LU分解法求解系数矩阵组成的线性方程组,最终得到全区域上的节点场值uh,至此有限元的求解全部结束。
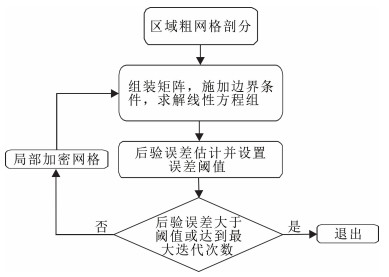
1.3 自适应有限单元法本文采取h-型的自适应有限元(图 2)。首先对给定的模型划分相对较粗糙的网格;然后通过后验误差计算局部误差,并根据误差值指向性地对区域网格进行精细化剖分;再根据细化的区域网格重新生成新的网格,计算局部网格的误差直到误差小于所给定的误差阈值;最终所生成的网格便是我们所需要的网格剖分,在此网格下进行的模拟既能满足精度又能相对提高计算速度。
|
| 图 2 自适应有限元算法流程 Fig. 2 Adaptive finite element algorithm flow |
|
|
在大地电磁偏微分方程的计算中,方程是一个连续性问题,但是在实际的计算机实现中,使用的是离散公式,可写成
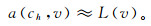 (9)
(9) 式中:a(ch, v)为与ch和v两个任意变量有关的离散性多项式;L(v)为连续性多项式。将上述等式称为离散原始问题,弱残差r(v)可定义为
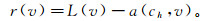 (10)
(10) 通过伽辽金的正交性,可以得出
 (11)
(11) 式(11)如果为0,意味着所有的残差都得到了抵消。利用这个性质可进一步推导误差估计,此时需要预先给定一个容差Tol和一个目标函数M(c)。后验误差η定义为
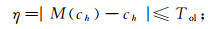 (12)
(12) 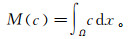 (13)
(13) 通过定义离散的双变分问题推导出后验误差。
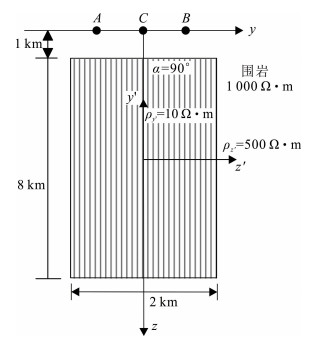
2 算例 2.1 算法有效性验证利用python程序语言结合Fenics函数库编写了大地电磁自适应有限元各向异性正演算法。选用3层地电模型(图 3),通过与MARE2DEM软件的计算结果做对比,以验证算法的有效性。第1层各向同性介质厚度为1 km,电阻率为500 Ω·m;第2层为厚度2 km的各向异性介质,其中在x′、y′、z′3个电性主轴方向[12]上的电阻率ρx′,ρy′,ρz′分别为300,300,20 Ω·m,第2层的平均电阻率约为78 Ω·m;围岩电阻率为1 000 Ω·m。
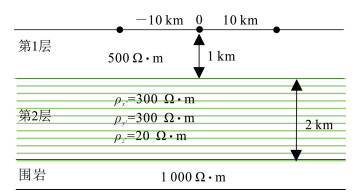
|
| 图 3 层状各向异性地电模型 Fig. 3 Layered anisotropic geoelectric model |
|
|
本模型设置测线长度为20 km,周期范围为10-4~104 s,对比0号测点处的大地电磁各向异性和各向同性响应结果,控制偏转角α=0°。结果见图 4。
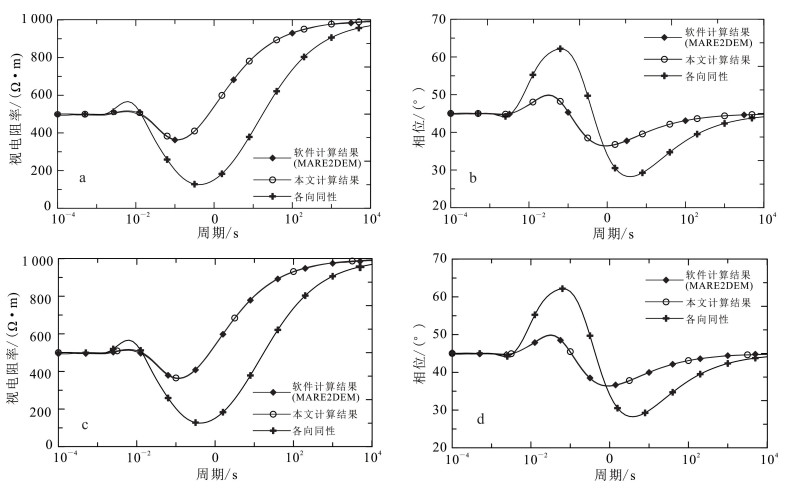
|
| a. TE极化模式的视电阻率响应;b. TE极化模式的阻抗相位响应;c. TM极化模式的视电阻率响应;d. TM极化模式的阻抗相位响应。 图 4 层状各向异性的大地电磁(MT)响应结果 Fig. 4 Layered anisotropy MT response results |
|
|
TE和TM极化模式的响应结果(图 4a,c)表明,两种模式的视电阻率都能很好地反映出3层结构:在高频处(即短周期处),根据趋肤深度可知电磁波还没有穿过第1层,所以视电阻率稳定在500 Ω·m;随着频率的降低,电磁波到达第2层,此时视电阻率趋向第2层的平均电阻率78 Ω·m;当电磁波穿透到最后一层的均匀半空间时,视电阻率会稳定在最后一层的电阻率1 000 Ω·m。各向异性介质和各向同性介质虽然都能反映出3层结构,但两者之间还是存在很大的差异。因此在传统的大地电磁测深方法中,即使平均电阻率是相等的,也要考虑各向异性带来的影响。MARE2DEM和本文算法计算结果表明,视电阻率在高频处有略微差异,其他部分几乎完全重合,造成差异的原因可能是地表网格过稀,由此可以判断本文的计算结果是正确的。TE和TM极化模式阻抗相位的规律与电阻率相似,均为平稳—波动—稳定。
2.2 倾斜各向异性模型倾斜各向异性介质模型见图 5。由于本文的算法是以二维地电结构下的对称各向异性介质为前提, 所以假设水平切面的电阻率始终与y′方向上的相同。
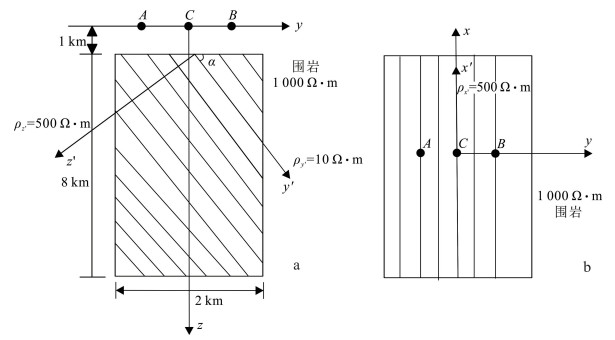
|
| a.倾斜各向异性垂向切面; b.倾斜各向异性水平切面。 图 5 倾斜各向异性模型 Fig. 5 Oblique anisotropy model |
|
|
该模型为地下均匀半空间中存在一个宽为4 km、高为8 km的异常体块。其中围岩的电阻率为1 000 Ω·m,异常体中的电阻率是对称各向异性的。ρx′,ρy′,ρz′依次为500,10,500 Ω·m。x
y平面表示地表,z轴指向地下;则x为地层走向,y′平行于地层面,z′垂直于地层面,因此电导率张量由偏转角α确定,α不同将导致电磁场在地下的分布不同。取不同的α进行正演,分别模拟在周期T=10 s下α为0°,30°,60°,90°时的TE和TM极化模式的电阻率和阻抗相位变化规律。
首先对该模型进行非结构三角粗网格剖分(图 6),初始网格数为70个。其中橘黄色区域为研究区域,区域大小为8 km×20 km;蓝绿色区域为异常体块,大小为4 km×8 km;红色区域为左右和下边界的扩展区域,分别扩展50 km;测点为80个,沿着研究区域与空气层接触面均匀分布;自适应有限元误差阈值设置为1%,迭代10次满足条件得到加密网格(图 7)。
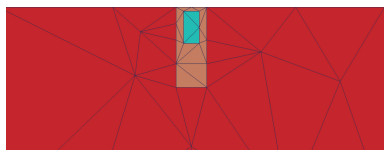
|
| 图 6 倾斜各向异性模型粗网格剖分 Fig. 6 Slanted anisotropic model coarse meshing |
|
|
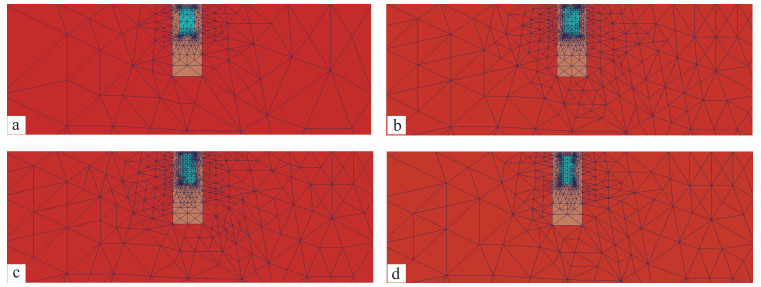
|
| a.偏转角为0°;b.偏转角为30°;c.偏转角为60°;d.偏转角为90°。 图 7 不同角度旋转的自适应局部加密网格 Fig. 7 Adaptive local refined grid rotated at different angles |
|
|
偏转角为0°,30°,60°,90°时的自适应网格加密结果见图 7,最终网格单元数分别为14 080,16 070,15 400,16 800。由图 7可知,在自适应网格的加密过程中,目标体剖分区域得到加密,电性分界面处的网格也进一步细化。由于大地电磁正演计算最终需要的是地表处测点的电场值和磁场值,测点处模型中异常体对电磁场值的影响比较大,因此为了满足误差阈值,在自适应网格加密的过程中,测点处附近的网格也会相应得到加密,并且加密程度会比其他区域更高。在最终网格(图 7)上进行正演计算,得到TE和TM极化模式的视电阻率和相位结果(图 8)。
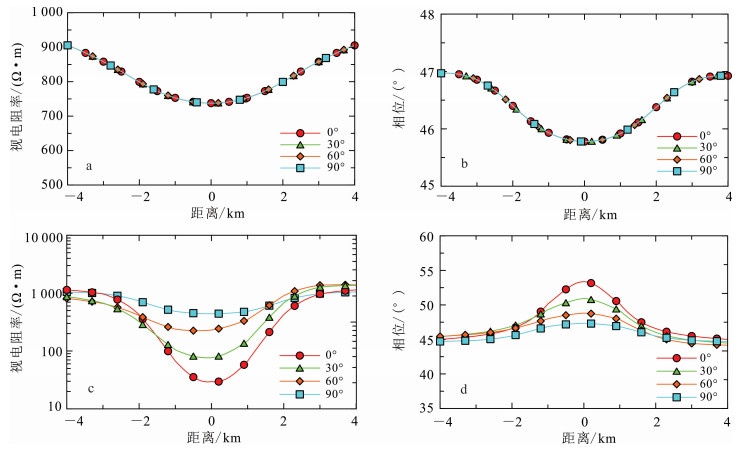
|
| a.TE极化模式的视电阻率响应;b. TE极化模式的阻抗相位响应;c. TM极化模式的视电阻率响应;d. TM极化模式的阻抗相位响应。 图 8 倾斜各向异性的MT响应结果 Fig. 8 Tilt anisotropy MT response results |
|
|
由图 8可知:1)异常体在TE和TM模式下的反应都非常明显,在0°~90°内,随着α增加,其TE极化模式的视电阻率和阻抗相位不变,因此可得TE极化模式中,其结果与偏转角α无关,只与平行于层面的电阻率有关。2)α对TM极化模式的影响比较大,α发生变化时,相应的视电阻率曲线和阻抗相位也会随之发生变化。视电阻率在异常处表现为低值,而阻抗相位在异常体处表现为高值。其中:当α为0°和90°时两种曲线是中心对称的且在中心点比较窄;当α为30°和60°时,两种曲线均中心不对称,顶点向侧面偏移且在中心点处比较宽,越往0°和90°靠近,两种曲线越趋近于中心对称。
2.3 水平各向异性模型水平各向异性(HTI)介质是倾斜各向异性的一种特殊形式(图 9)。当偏转角为0°时,主轴y′方向和观测坐标轴y方向重合,将此介质称之为水平各向异性介质。由于在TE极化模式中视电阻率和阻抗相位只与平行于地层的电阻率ρx′或ρy′有关,不受其他参数影响,与均匀各向同性的计算步骤和算法相同,所以这里不再讨论TE极化模式的响应规律,只考虑TM极化模式的变化规律。在TM极化模式中,水平各向异性受到平行于地层的电阻率ρx′、ρy′和垂直于地层的电阻率ρz′两组参数的影响,因此选择一组参数不变改变另一组参数来研究TM响应的变化规律。在图 9的模型中设置的围岩电阻率为1 000 Ω·m,异常体ρx′、ρy′、ρz′依次为500,500,10 Ω·m。

|
| 图 9 水平各向异性模型 Fig. 9 Horizontal anisotropy model |
|
|
此时我们规定ρz′不变,改变ρx′和ρy′,依次同时设置为100,300,500,800,1 000 Ω·m, 得到视电阻率和阻抗相位如图 10所示。
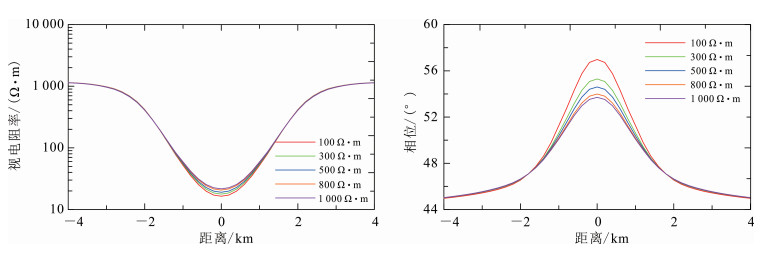
|
| 图 10 改变ρx′和ρy′值时HTI模型的MT响应结果 Fig. 10 MT response result of HTI model when changing the value of ρx′ and ρy′ |
|
|
图 10表明:几种不同电阻率下的响应结果曲线在异常体的上方发生突变;在测线中心点处为异常的极值点,越远离异常体视电阻率越接近于背景电阻率。对比来看,在改变ρx′和ρy′时,几种曲线的视电阻率曲线差异不是很大,而阻抗相位反应要比视电阻率更加灵敏,因此可以得出结论:在平行各向异性介质中,即使平均电阻率不同,视电阻率和阻抗相位的MT响应结果也可能表现为相同的结果,平行层面的电阻率对MT的响应影响不大。
接下来控制ρx′、ρy′不变,改变ρz′,依次取值为100,300,500,800,1 000 Ω·m,来研究MT的响应规律。结果见图 11。
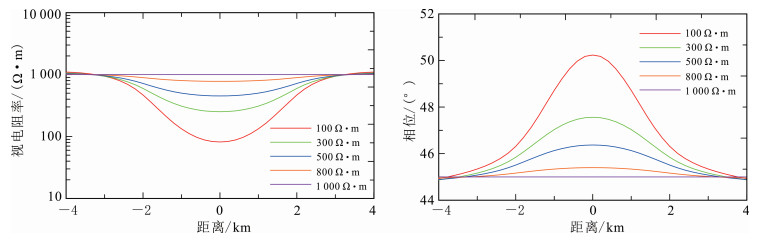
|
| 图 11 改变ρz′值时HTI模型的MT响应结果 Fig. 11 MT response result of HTI model when changing the value of ρz' |
|
|
如图 11所示,当改变z′方向上的电阻率时,MT的响应结果非常灵敏。随着ρz′的增加,视电阻率和阻抗相位的异常极值点也相对发生变化并且相应的异常更难被检测到;当ρz′取值为与围岩电阻率相同的1 000 Ω·m时,视电阻率和阻抗相位曲线均变为一条直线,此时异常体在MT上无响应。可以认为,在平行各向异性介质中,ρz′对MT响应结果的影响很大。
综上所述,在水平各向异性介质中,z′方向上的电阻率占主导作用,比x′和y′方向上的电阻率更易影响MT的响应结果。
2.4 垂直各向异性模型垂直各向异性(VTI)介质是倾斜各向异性的另一种特殊形式(图 12),当偏转角为90°时,主轴与观测轴y垂直。仍旧控制两个主轴方向上的电阻率来研究MT在垂直各向异性介质中的响应规律。
|
| 图 12 垂直各向异性模型 Fig. 12 Vertical anisotropy model |
|
|
首先保持ρz'不变,改变ρx′和ρy′,依次同时取值100,300,500,800,1 000 Ω·m,视电阻率和阻抗相位曲线变化见图 13。
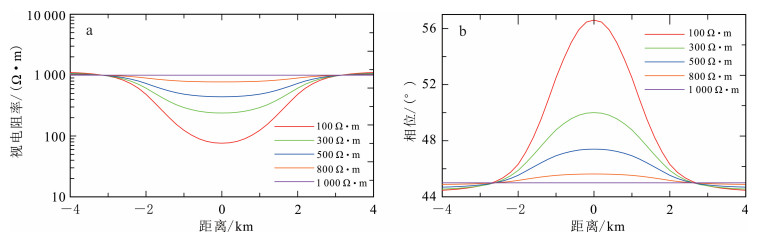
|
| 图 13 改变ρx′和ρy′值时VTI模型的MT响应结果 Fig. 13 MT response result of VTI model when changing the value of ρx′ and ρy′ |
|
|
由图 13可见,随着ρx′和ρy′的增加,异常体的反应变微弱,当电阻率为1 000 Ω·m时,异常体的反应消失。视电阻率和阻抗相位表现出了相同的规律。这与在HTI介质中改变ρz'时表现的规律相同。这应当引起重视,在常规的MT资料反演解释处理中很难发现这一点。经过分析可以得出结论,在VTI介质中,TM的响应结果受到ρx′和ρy′的影响比较大。
接下来控制ρx′和ρy′不变,改变ρz',仍然取值100,300,500,800,1 000 Ω·m,响应结果见图 14。
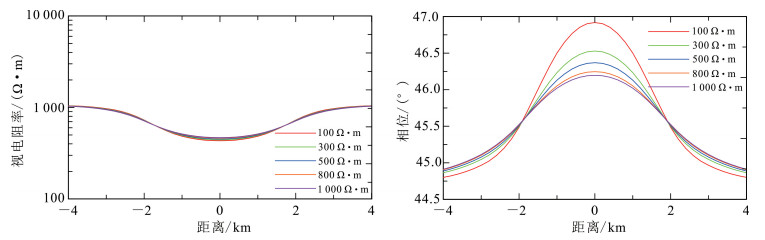
|
| 图 14 改变ρz′值时VTI模型的MT响应结果 Fig. 14 MT response result of VTI model when changing the value of ρz′ |
|
|
从图 14可知,与HTI介质改变ρx′和ρy′时有同样的变化规律,视电阻率和阻抗相位曲线之间有微弱的差别。虽然平均电阻率不同,但是MT的响应结果变化不大。说明在实际应用中,介质为各向同性也可能与各向异性介质表现为同样的结果,这样我们就可以只考虑各向异性中的一个主轴电阻率的影响而忽略另一个主轴的电阻率。经过分析可以得出结论:在VTI介质中,TM的响应结果受ρz′影响比较小。
综上所述,在垂直各向异性介质中,x′,y′方向上的电阻率占主导作用,比z′方向上的电阻率更易影响MT的响应结果。结合前面模型我们可以推测,在本文的坐标系下,二维结构中各向异性介质的TM极化模式响应结果总是由主轴上电阻率在y轴方向上的分量所决定。
3 结论1) TE极化模式的视电阻率和阻抗相位只与平行于地层面方向的电阻率有关,与其他因素无关。
2) TM极化模式的视电阻率和阻抗相位随着偏转角的变化而变化。
3) 在本文的坐标系下,二维结构中各向异性介质的TM极化模式响应结果由主轴上的电阻率在y轴方向上的分量决定。
| [1] |
秦林江.各向异性介质的MT正反演研究[D].杭州: 浙江大学, 2013. Qin Linjiang. Research on MT Forward and Inversion for Anisotropic Media[D]. Hangzhou: Zhejiang University, 2013. |
| [2] |
王堃鹏.基于MPI的海洋可控源电磁法自适应有限元2.5D正演研究[D].成都: 成都理工大学, 2014. Wang Kunpeng. Research on 2.5D Forward Modeling of Adaptive Finite Element Based on MPI for Marine Controllable Source Electromagnetic Method[D]. Chengdu: Chengdu University of Technology, 2014. |
| [3] |
杨淼鑫.二维各向异性大地电磁场的有限元数值模拟[D].成都: 成都理工大学, 2012. Yang Miaoxin. Finite Element Numerical Simulation of 2D Anisotropic Magnetotelluric Field[D]. Chengdu: Chengdu University of Technology, 2012. |
| [4] |
郑彦丰.层状各向异性介质大地电磁正反演研究[D].西安: 长安大学, 2017. Zheng Yanfeng. Study on Forward and Inverse Magnetotelluric Inversion of Layered Anisotropic Media[D]. Xi'an: Chang'an University, 2017. |
| [5] |
李志旋.大地电磁二、三维非结构有限元数值模拟[D].合肥: 中国科学技术大学, 2016. Li Zhixuan. Two-Dimensional and Three-Dimensional Unstructured Finite Element Numerical Simulation of Magnetotelluric Magnetism[D]. Hefei: University of Science and Technology of China, 2016. |
| [6] |
薛帅.大地电磁各向异性介质正演与NLCG反演研究[D].长沙: 中南大学, 2013. Xue Shuai. Research on Forward Modeling of Magnetotelluric Anisotropic Media and NLCG Inversion[D]. Changsha: Central South University, 2013. |
| [7] |
徐震寰.电阻率任意各向异性介质大地电磁场三维正演算法研究[D].青岛: 中国海洋大学, 2015. Xu Zhenhuan. Research on 3D Forward Algorithm of Magnetotelluric Field in Anisotropic Medium with Arbitrary Resistivity[D]. Qingdao: Ocean University of China, 2015. |
| [8] |
杨长福. 大地电磁二维对称各向异性介质的有限元数值模拟[J]. 西北地震学报, 1997, 19(2): 28-34. Yang Changfu. Finite Element Numerical Simulation of Magnetotelluric Two-Dimensional Symmetric Anisotropic Medium[J]. Journal of Northwestern Seismology, 1997, 19(2): 28-34. |
| [9] |
殷长春, 张博, 刘云鹤. 面向目标自适应三维大地电磁正演模拟[J]. 地球物理学报, 2017, 60(1): 327-336. Yin Changchun, Zhang Bo, Liu Yunhe. Target-Oriented Adaptive 3D Magnetotelluric Forward Modeling[J]. Chinese Journal of Geophysics, 2017, 60(1): 327-336. |
| [10] |
Li Y, Key K. 2D Marine Controlled-Source Electromagnetic Modeling:Part 1:An Adaptive Finite-Element Algorithm[J]. Geophysics, 2007, 72(2): 51-62. |
| [11] |
张博.基于非结构有限元的频率/时间域航空电磁系统仿真研究[D].长春: 吉林大学, 2017. Zhang Bo. Simulation Study of Frequency/Time Domain Aeronautical Electromagnetic System Based on Unstructured Finite Element[D]. Changchun: Jilin University, 2017. |
| [12] |
张君涛.大地电磁测深二维各向异性有限元正演模拟[D].成都: 成都理工大学, 2016. Zhang Juntao. Two-Dimensional Anisotropic Finite Element Forward Modeling of Magnetotelluric Sounding[D]. Chengdu: Chengdu University of Technology, 2016. |
| [13] |
张振宇.龙门山构造带中段大地电磁测深研究[D].成都: 成都理工大学, 2010. Zhang Zhenyu. Study on the Magnetotelluric Sounding in the Middle Section of Longmenshan Tectonic Belt[D]. Chengdu: Chengdu University of Technology, 2010. |
| [14] |
Schlumberger. Etude Sur La Prospection Electrique Du Sous-Sol[J]. Phys Earth Planet, 1920, 21: 43-44. |
| [15] |
Keller. Electrical Methods in Geophysical Prospecting[J]. Monographs, 1966, 82(2): 172-174. |
| [16] |
陈乐寿. 有限元法在大地电磁场正演计算中的应用及改进[J]. 石油物探, 1981, 43(3): 243-262. Chen Leshou. Application and Improvement of Finite Element Method in the Forward Calculation of Magnetotelluric Field[J]. Geophysical Prospecting for Petroleum, 1981, 43(3): 243-262. |
| [17] |
Wannamaker P E, Stodt J A, Rijo L. A Stable Finite Element Solution for Two-Dimensional Magnetotelluric Modelling[J]. Geophysical Journal International, 2010, 88(1): 277-296. |
| [18] |
Key K, Weiss C. Adaptive Finite-Element Modeling Using Unstructured Grids:The 2D Magnetotelluric Example[J]. Geophysics, 2006, 71(6): 291-299. |
| [19] |
Liu C, Ren Z, Tang J, et al. Three-Dimensional Magnetotellurics Modeling Using Edgebased Finite-Element Unstructured Meshes[J]. Applied Geophysics, 2008, 5(3): 170-180. |
| [20] |
Liu Y, Xu Z, Li Y. Adaptive Finite Element Modelling of Three-Dimensional Magnetotelluric Fields in General Anisotropic Media[J]. Journal of Applied Geophysics, 2018, 151(2): 113-124. |
| [21] |
Li Yuguo, Pek J. Adaptive Finite Element Modelling of Two-Dimensional Magnetotelluric Fields in General Anisotropic Media[J]. Geophysical Journal International, 2008, 175(3): 942-954. DOI:10.1111/j.1365-246X.2008.03955.x |


