2. 河北省水资源可持续利用与开发重点实验室, 石家庄 050031;
3. 河北省水资源可持续利用与产业结构化协同创新中心, 石家庄 050031
2. Key Laboratory of Sustained Utilization & Development of Water Resources, Hebei Province, Shijiazhuang 050031, China;
3. Collaborative Innovation Center for Sustainable Utilization of Water Resources and Optimization of Industrial Structure, Hebei Province, Shijiazhuang 050031, China
0 前言
水文地质参数是进行地下水资源评价、数值模拟、开发利用与保护及科学管理的重要依据[1]。而抽水试验是水文地质参数求解常用的方法之一。Theis公式[2]自提出以来,由于其具有表达形式简单、可将井函数转化进行配线求解[3]、可简化变为Jacob直线图解法[4]、可与叠加原理结合转化为水位恢复法[5]、可与叠加原理及水位恢复法结合转化为全程曲线拟合法[6]等优势,因而常被用于非稳定流抽水试验水文地质参数的求解。但是,以上这些传统的计算方法在求参过程中未能将全部试验数据加以利用,只应用抽水阶段或水位恢复阶段部分数据进行求参,数据的取舍受人为主观因素影响较大。进行参数率定时,常使用手动试错法[7]进行求解,该法在进行参数调整和选取的过程中,受评定者的主观评判制约,同一个计算将会得到不同的率定参数,结果不够精确;全程曲线拟合法中提出利用最小二乘法作为目标函数,结合试错法调参,对计算水位降深的计算值与实际观测值的拟合程度进行评判,此法优点是能够直观看到两条曲线的拟合程度,缺点是没有统一的评判标准。据此,有学者提出Nach-Sutcliffe效率系数精度评价法[8]结合试错法定量计算水位降深的计算值与实际观测值的拟合程度,进而确定最终参数,这是对最小二乘法评判拟合程度的一次改进;但这些方法的调参过程,往往是人为手动输入参数值变化范围,计算精度不够且过程繁琐。此外,刘国东等[9]利用人工神经网络求解水文地质参数,通过对网络的充分训练得到降深序列与参数导水系数(T)、贮水系数(S)的对应关系,建立非稳定流抽水试验的求参网络,进而根据实际的抽水试验资料进行参数的反解;相比传统配线法,其求解精度更高。郭建青等[10]提出运用随机搜索算法进行参数率定,当达到最大迭代次数或前后两次相邻搜索的目标函数值的误差值小于给定数值时停止运算,得到计算结果;此方法可实现参数的自动求解,但得到的结果只是某种意义上的局部最优解,受给定误差值的影响较大,并非全局最优解。霍小虎等[11-12]利用遗传算法进行水文地质参数的确定,遗传算法能在全局范围内寻找最优值、稳定高效,但遗传算法在识别参数时对初值和参数的设定具有较强的依赖性,可能会出现不收敛的情况,对参数确定产生不利影响。董起广等[13]提出利用改进遗传算法求解水文地质参数,避免了一般的遗传算法收敛速度慢、易早熟等问题。本文应用的遍历搜索算法[14-21]是指在参数空间范围内穷举该问题的部分或所有可能情况,根据问题的约束条件或建立的优化模型,从穷举出的所有情况中筛选出最优解,实现在参数空间范围自动精确求解。由于参数在一个大的空间范围内进行逐步搜索,避免了陷入局部最优解的情况,也不存在利用遗传算法可能出现不收敛的情况,且利用遍历搜索算法求参精度高,稳定高效,受人为主观因素影响小。本文基于Theis公式及叠加原理,以Nach-Sutcliffe效率系数作为评判因子求解水文地质参数,再利用遍历搜索算法,结合Matlab编程对参数进行遍历,构建目标优化模型,拟提高参数的求解精度及自动化程度。
1 基本原理 1.1 抽水试验及目标含水层假定条件Theis公式假定条件为:定流量非稳定流承压水完整井单次完整抽水试验,井径无限小,含水层均质各向同性,等厚,侧向无限延伸,产状水平,天然状态下水力坡度为0,水流服从Darcy定律,水头下降引起的地下水释放是瞬间完成的[3]。
一次完整的抽水试验数据包括抽水阶段和水位恢复阶段全部的降深时间数据。
1.2 计算公式 1.2.1 基于Theis公式的抽水试验求参(抽水阶段)若含水层满足Theis公式假定条件则符合以下公式:
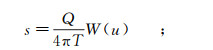 (1)
(1) 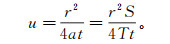 (2)
(2) 式(1)为Theis公式,通常将W(u)展开成以下形式:
 (3)
(3) 式中:s为水位降深值,m;Q为抽水井的流量,m3/d;r为观测井距抽水井的距离(或抽水井半径),m;t为从抽水开始持续的时间,d;S为含水层的贮水系数;a为含水层的导压系数,m2/d;T为含水层的导水系数,m2/d;T=KM,M为含水层厚度,m,K为渗透系数,m/d;W(u)为Theis井函数,u为井函数自变量,当u较小(u≤0.01)时,W(u)可用公式前3项-0.577216-ln u+u近似表示;y为微积分中连续函数;n为级数的离散变量,在此n =2, 3, 4,…, 即n不断增大并趋向无穷。
1.2.2 基于叠加原理的抽水试验求参(水位恢复阶段)对于水位恢复阶段,相当于以流量Q抽水一直延续到t时刻的降深和从停抽时刻起以流量Q注水t-tp时间水位抬升的叠加[3],基于Theis公式和叠加原理,可得水位恢复阶段的降深公式:
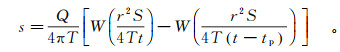 (4)
(4) 式中,tp为停抽时刻的抽水时间,d。
1.2.3 目标函数筛选参数过程中以sic与sio的Nach-Sutcliffe效率系数值达到最大为目标进行优化,计算公式为
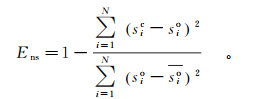 (5)
(5) 式中:Ens为Nach-Sutcliffe效率系数值,用以判定理论计算值与实测值拟合程度好坏的指标,其值范围为-∞~1.000 0,值越接近1.000 0拟合程度越好,一般认为Ens>0.500 0可达到拟合精度[8];sic为第i个记录点的理论计算降深;sio为第i个记录点的实测降深;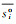
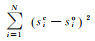
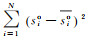
遍历搜索算法是指沿着某条搜索路线,依次对二叉树中每个节点均做一次且仅做一次访问,访问的节点所做的操作依赖于具体的应用问题,进而在空间范围内穷举出问题所有的可能性,根据问题的实际约束条件或目标函数筛选出符合条件的解。其遍历的节点次数取决于空间范围(即遍历的上下限值)及向前遍历一次的步长值,解的精度取决于遍历一次的步长值。
1.3.2 遍历搜索算法确定参数解对于参数的遍历搜索范围,要结合参数对应的经验取值范围。承压含水层贮水系数在10-5~0.05之间[3],而导水系数值取决于含水层的渗透系数及厚度。试验区的含水层厚度可进行测定,而渗透系数取决于含水层的岩性,不同岩性含水层的渗透系数值位于不同的范围内[3]。在此,假定自然界岩层最小渗透系数(0.001 m/d)为下限,自然界岩层最大渗透系数(1 000.000 m/d)为上限。
原则上应在参数的经验范围值内进行遍历搜索。但为了避免有参数经验值的遗漏,将参数T经验值的上限扩大至其100倍作为遍历搜索的上限值,其下限缩小至其0.01倍作为遍历搜索的下限值。由于承压含水层贮水系数的上限不可能超过0.5,故将参数S经验值的上限扩大至其10倍作为遍历搜索的上限值,其下限缩小至其0.01倍作为遍历搜索的下限值,以使得遍历范围能包含参数取值的所有可能值。虽然参数的遍历范围已远超过自然界岩层的经验取值范围,但在函数关系及目标函数的约束下,并不会对参数的最终解造成影响。对于遍历步长值的取值要满足:步长值为参数对应遍历搜索下限值的1/10,以提高解的精确度。根据以上选取原则,对于贮水系数S,取其遍历搜索范围为10-7~0.5,步长值取10-8。对于导水系数T,取其遍历范围为10-5M~ 105M,步长值取10-6M。M的单位均为m。
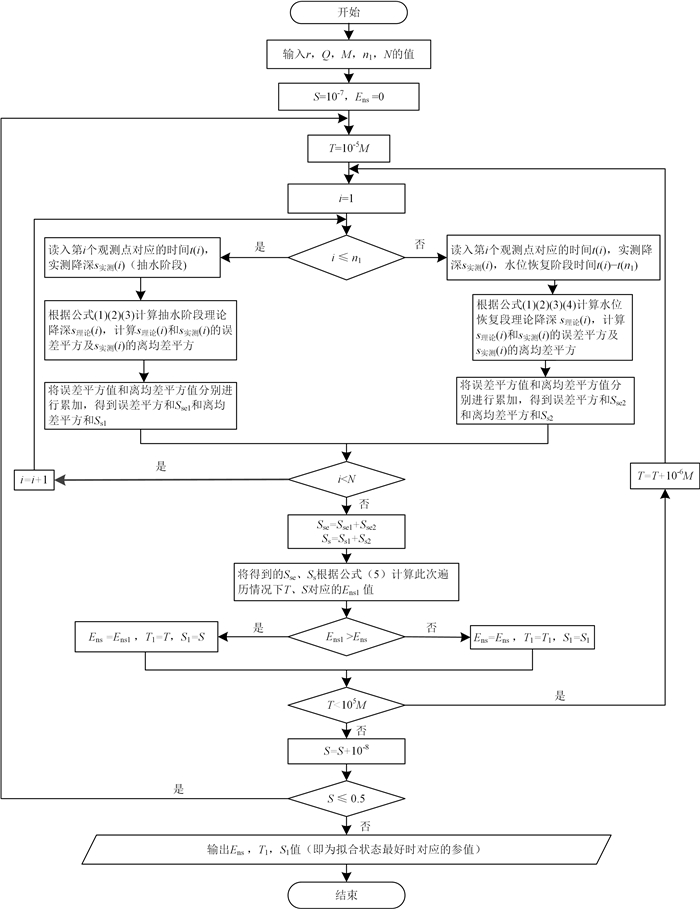
对于抽水试验,需要用到的实测数据有流量Q,抽水开始时间序列t1,t2,t3,…,tN,各时间对应的水位降深序列s1,s2,s3,…,sN, 观测井距主井的距离r,含水层厚度M,抽水阶段的时间记录点个数n1,以及整个抽水试验阶段的记录点个数N。在确定参数的遍历范围后,便可以结合实际的抽水试验数据进行参数的确定,首先从参数初始值(即参数遍历范围的下限)开始进行遍历,并令初始Ens =0。将此时的参数值T、S和对应抽水试验的数据带入抽水阶段的计算公式(1)(2)(3)和水位恢复阶段的计算公式(4)中,可得到一组理论降深值,进而可根据公式(5)求得该数据组理论降深与实际降深的Nach-Sutcliffe效率系数Ens值,并将此时的T、S、Ens值进行记录,完成一次遍历。将参数值T增大一个步长值,S保持不变,进入下一轮的遍历,又可得到另一参数组对应下的Ens值。将前后Ens值进行比较,若后一参数组对应的Ens值比前一组大,说明后一组参数值对应的理论降深与实测降深拟合效果更好,则将后一组Ens值进行替换并记录保留此时的参数值;若否,不保留继续下一轮遍历。当遍历完参数T的全部空间范围,将参数S增大一个步长值,参数T重新从初值开始取值,继续以上步骤,直到遍历完参数T、S的全部空间范围,最终能保留下来的即为最优参数值及其对应的Nach-Sutcliffe效率系数Ens值。遍历搜索算法流程如图 1所示。在Matlab编程环境下,利用遍历搜索算法实现参数自动求解。
|
| 图 1 遍历搜索算法流程图 Fig. 1 Flow chart of the ergodic search algorithm method |
|
|
首先以文献[3]中110页抽水实例为例验证遍历搜索算法的可靠性。试验为承压含水层多孔抽水试验,定流量抽水,流量为60 m3/h,有4个观测孔,选择观15井作为研究对象进行参数的求解[3]。此实例中没有给出水位恢复阶段的数据,即水位恢复阶段记录点数为0。此外,实例中未给出承压含水层的厚度,由文献[3]中求解结果可对参数的遍历范围扩大至100~200倍进行处理。对于参数S,取其遍历搜索范围为10-7~0.5,步长值取10-8。对于参数T,取其遍历范围为1~20 000 m2/d,步长值取10-6 m2/d。取r=110 m,Q=1 440 m3/d,n1=18,N=18。将抽水试验数据带入遍历搜索算法程序中得到的参数值与文献[3]中利用传统方法求参结果见表 1。
由表 1可知,利用遍历搜索算法求得的参数T、S与文献[3]中利用传统方法(配线法、直线图解法)求参的结果十分相近,说明利用遍历搜索算法求解水文地质参的方法是可靠的。利用遍历搜索算法得到的Nach-Sutcliffe效率系数Ens值(0.996 5)相比传统方法更接近1.000 0,说明其拟合效果更好、精度更高;而且其在求参过程受人为主观因素影响小,避免了传统方法的繁琐步骤,且利用了抽水试验的全部数据,可以实现参数的自动精确求解。
2.2 实例2 2.2.1 研究区概况研究区位于黑龙江东南部的密山市,地处穆棱河谷及其支流河谷,第四系较为发育。全新统(Q4)厚度为15~20 m,具有二元结构,上部岩性为粉质黏土、淤泥质粉质黏土,厚度为3~4 m,下部为含砾中粗砂、砂砾石等,厚度为12~16 m,构成潜水含水层;上更新统(Q3)为哈尔滨组冲积-冰水堆积的粉质黏土,厚度为7 m,由于其渗透性较差,构成相对隔水层,为潜水含水层的隔水底板及承压含水层的隔水顶板;中更新统(Q2)荒山组岩性主要为棕色砂(中、粗砂)、砂砾石,厚度为45~46 m,构成承压含水层;下伏新近系始、渐新统虎林组(E2-3 h),岩性为泥岩,完整无裂隙,厚度为5 m,构成承压含水层的底板。研究区抽水试验目的层为第四系中更新统松散碎屑岩类孔隙承压水,含水层岩性为中、粗砂,砂砾石,承压含水层厚度为45.92 m,整个抽水阶段含水层厚度视为不变。研究时共完成水文地质钻孔2个,包括一抽水井和一观测井,抽水井半径为0.265 m,降深1.90 m。观测井距抽水井20 m,降深0.73 m。试验为定流量抽水,抽水量为2 400 m3/d。研究区符合Theis公式的基本假设条件,可以进行参数的求解。
2.2.2 参数求解抽水井附近为三维流,可能存在井损,会对参数求解的精确性造成一定的影响,故本例中选择观测井作为研究对象。由研究区概况及抽水试验数据可知:M=45.92 m,r=20 m,Q=2 400 m3/d,n1=26,N=48。对于S,取其遍历搜索范围为10-7~0.5,步长取10-8。取T遍历范围为4.592×10-4~4.592×106 m2/d,T步长值取4.592×10-5。将抽水试验相关数据代入遍历搜索算法程序中进行求解可得到参数解。此外,本文也利用了直线图解法、水位恢复法、人工试错法3种方法对本例进行求参,4种方法得到的参数T、S结果见表 2。
| 求参方法 | T/(m2/d) | S | Ens |
| 直线图解法 | 2 417.54 | 0.000 470 | 0.964 6 |
| 水位恢复法 | 1 962.47 | 0.003 300 | 0.861 0 |
| 人工试错法 | 2 350.00 | 0.000 680 | 0.962 1 |
| 遍历搜索算法 | 2 405.90 | 0.000 490 | 0.970 8 |
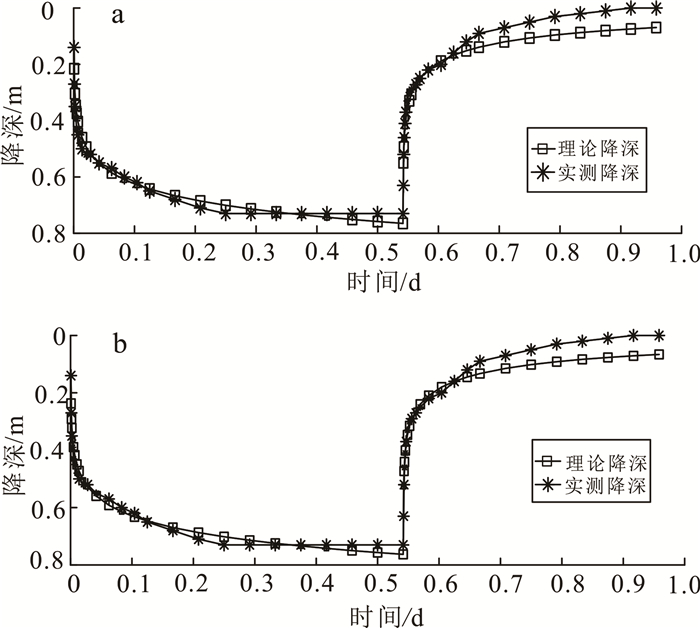
由表 2可知,4种求参方法中, 直线图解法、人工试错法及遍历搜索算法求参结果相近,可认为利用遍历搜索算法求参的方法是有效可信的。而利用遍历搜索算法求得的参数精度更高,Ens值(0.970 8)更接近1.000 0,拟合程度更好,说明利用遍历搜索算法求参结果更精确可靠。而水位恢复法求参结果不够理想,考虑是由水位恢复段数据点较少、代表性不强、水位恢复过程中存在水头惯性滞后等因素造成的。人工试错法与遍历搜索算法求得参数对应的实测降深与计算降深的降深-时间曲线拟合效果图见图 2。
|
| 图 2 人工试错法(a)和遍历搜索算法(b)求得实测降深与理论降深拟合曲线图 Fig. 2 Fitting curve of the observed drawdown data and calculated drawdown calculated by trial error method (a)and ergodic search algorithm method(b) |
|
|
本文中的模型是以承压含水层Theis公式为理论基础建立起来的,故研究区要在符合Theis基本假设条件下使用才能得到较满意的参数解。
Theis公式表明,r为观测点距主井距离,故应用中应以观测井数据值进行计算。对于单井抽水试验,无观测井数据时,可以以主井半径rw代替观测井到主井距离r,以主井观测降深代替观测井降深直接进行调参。经过本文实例计算,主井计算参数数值与观测井计算参数数值有一定偏差,考虑是主井附近存在三维流及井损导致,具体原因分析后续可进一步研究。
在利用遍历搜索算法自动筛选参数时,可能会存在多解性的情况,即多组参数解都能满足优化算法的要求。如在本例中,可能会出现多组参数T、S对应的Nach-Sutcliffe效率系数值相同且接近1.000 0。但是,通过多个实例反复进行验算,发现对于存在多组最优解的情况,各组参数结果与最终的求参结果十分相近,并不会对求参的准确性造成影响,可认为遍历搜索算法存在的多解性情况是可以忽略考虑的,得到的最终参数解值是准确可靠的。
在确定参数的遍历搜索范围时,要结合参数对应的经验取值范围,原则上应在参数的经验值范围内进行遍历搜索,但经验值也只是在某种岩性上对应数量级的大致范围。如砂砾石渗透系数>500.000 m/d,无法给到具体数值。在本文中,假定以自然界岩层的最小渗透系数0.001 m/d作为下限,以自然界岩层的最大渗透系数1 000.000 m/d作为上限,但不能完全保证所有地区岩性的渗透系数都在这个范围内。为了避免有参数经验值的遗漏对求参结果造成影响,使得遍历范围能包含参数取值的所有可能值,需要对参数的经验上下限值进行相对扩大或缩小,使得遍历范围更具有包容性。本文选择对参数缩小至其0.01倍或扩大至其100倍,可能已经脱离了水文地质参数的实际意义,但经过多个实例的不断调试,在函数关系及目标函数的约束下,遍历范围超出经验范围并不会对参数的最终解造成影响。
遍历搜索算法并不只局限于Theis井流模型下的参数求解问题,也可以根据研究区的具体情况对模型进行适当调整,同样可以得出准确度较高的参数解。如抽水井附近存在补给边界或者隔水边界,且边界对地下水流造成明显影响时,则需要利用镜像法原理结合叠加原理求得问题的解。对于不同的水文地质条件的地区,要对地下水的补排情况、含水层的结构和边界条件等有正确的认识,以确定其最合适的数学模型,在此基础上进行参数的反演,才能得出较为准确的结果。
4 结论与建议1) 相比传统的配线法、直线图解法、水位恢复法等,利用遍历搜索算法求参过程中可充分利用抽水试验抽水阶段及水位恢复阶段的全部试验数据,解决了传统求参方法无法利用全部抽水试验数据这一问题。通过2个实例的验证,相比传统的求参方法,利用遍历搜索算法求得的参数结果,其对应理论计算降深与实测降深的Nach-Sutcliffe效率系数值更接近1.000 0,说明拟合程度更好。
2) 遍历搜索算法在求解水文地质参数过程中,需要将实际试验区的含水层厚度(M)、抽水流量(Q)、观测点距抽水井的距离(r)、抽水阶段的记录点数(n1)、整个抽水试验阶段的记录点数(N),这5个数据及抽水试验的降深时间序列数据带入到算法程序中,即可自动筛选出Nach-Sutcliffe效率系数值最大时对应的参数值,受人为主观因素影响相对较小。
3) 基于遍历搜索算法求解水文地质参数,不仅只适用于一次完整抽水试验,也可利用叠加原理进行扩展运用到阶梯状变流量抽水试验、间断性阶梯状抽水试验中等。
| [1] |
赵宝峰, 康卫东, 马莲净, 等. 抽水试验和长观水位联合模拟确定含水层参数[J]. 吉林大学学报(地球科学版), 2009, 39(3): 482-486. Zhao Baofeng, Kang Weidong, Ma Lianjing, et al. Aquifer Parameter Recognition by Combining Simulation of Pumping Test and Water Level of Long-Term Observation Well[J]. Journal of Jilin University (Earth Science Edition), 2009, 39(3): 482-486. |
| [2] |
Theis C V. The Relation Between the Lowering of the Piezometric Surface and the Rate and Duration of Discharge of a Well Using Groundwater Storage[J]. American Geophysical Unions Transactions, 1935, 16: 519-544. DOI:10.1029/TR016i002p00519 |
| [3] |
薛禹群, 吴吉春. 地下水动力学[M]. 3版. 北京: 地质出版社, 2010. Xue Yuqun, Wu Jichun. Dynamics of Groundwater[M]. 3rd ed. Beijing: Geological Publishing House, 2010. |
| [4] |
Hhc J R, Jacob C E. A Generalized Graphical Method for Evaluating Formation Constants and Summarizing Well-Field History[J]. American Geophysical Unions Transactions, 1946, 27: 526-534. DOI:10.1029/TR027i004p00526 |
| [5] |
Bear J. Hydraulics of Groundwater[M]. New York: Mc Graw-Hill, 1979.
|
| [6] |
肖长来, 梁秀娟, 崔建铭. 确定含水层参数的全程曲线拟合法[J]. 吉林大学学报(地球科学版), 2005, 35(6): 751-755. Xiao Changlai, Liang Xiujuan, Cui Jianming. Whole Curve Matching Method for Aquifer Parameters Determination[J]. Journal of Jilin University (Earth Science Edition), 2005, 35(6): 751-755. |
| [7] |
章四龙, 刘九夫. 通用模型参数率定技术研究[J]. 水文, 2005, 25(1): 9-12. Zhang Silong, Liu Jiufu. Research on Calibration Technology of General Model Parameters[J]. Hydrology, 2005, 25(1): 9-12. |
| [8] |
邱淑伟, 梁秀娟, 肖长来, 等. 间断性阶梯状抽水试验求参[J]. 节水灌溉, 2015, 40(5): 60-62. Qiu Shuwei, Liang Xiujuan, Xiao Changlai, et al. Parameters Determination for Intermittent Step-pumping Tests[J]. Water Saving Irrigation, 2015, 40(5): 60-62. |
| [9] |
刘国东, 丁晶, 张翔. 应用人工神经网络求算含水层参数[J]. 工程勘察, 1997, 25(1): 25-28. Liu Guodong, Ding Jing, Zhang Xiang. Determination Aquifer Parameters by Using BP Network[J]. Engineering Investigation, 1997, 25(1): 25-28. |
| [10] |
郭建青, 周宏飞, 李彦, 等. 随机搜索算法在确定含水层参数中的应用[J]. 中国农村水利水电, 2010, 52(12): 48-51. Guo Jianqing, Zhou Hongfei, Li Yan, et al. The Application of Random Search Algorithm to the Analysis of Pumping Test Data for Estimating Aquifer Parameters[J]. China Rural Water and Hydropower, 2010, 52(12): 48-51. |
| [11] |
霍小虎, 黄国如. 遗传算法在水文地质参数确定中的应用[J]. 地下水, 2001, 18(4): 195-197. Huo Xiaohu, Huang Guoru. The Application of Genetic Algorithm for Estimating Aquifer Parameters[J]. Groundwater, 2001, 18(4): 195-197. |
| [12] |
魏连伟, 邵景力, 张建立, 等. 遗传算法在水文地质参数反演中的应用[J]. 工程勘察, 2004, 32(3): 28-31. Wei Lianwei, Shao Jingli, Zhang Jianli, et al. The Application of Genetic Algorithm for Estimating Aquifer Parameters Inversion[J]. Engineering Investigation, 2004, 32(3): 28-31. |
| [13] |
董起广, 周维博, 李云排, 等. 改进遗传算法在泾惠渠灌区水文地质参数求解中的应用[J]. 中国农村水利水电, 2014, 56(5): 27-30. Dong Qiguang, Zhou Weibo, Li Yunpai, et al. The Application of Improved Genetic Algorithm for Hydrogeology Parameters Solution in Jinghui Irrigation Area[J]. China Rural Water and Hydropower, 2014, 56(5): 27-30. |
| [14] |
Jie J I, Tao P J. Circulation Algorithm of MS SQL Server Tree Structure Table's Traversal Search[J]. Computer & Modernization, 2005, 116(4): 7-8. |
| [15] |
Sharma M B, Mandyam N K, Iyangar S S. An Optimal Distributed Depth-First-Search Algorithm[J]. Information Processing Letters, 1989, 32(4): 183-186. DOI:10.1016/0020-0190(89)90041-0 |
| [16] |
Lawrence D. Theory of Optimal Search[M]. Salt Lake City: Academic Press, 1975.
|
| [17] |
Mahdavi M, Fesanghary M, Damangir E. An Improved Harmony Search Algorithm for Solving Optimization Problems[J]. Applied Mathematics and Computation, 2007, 188(2): 1567-1579. DOI:10.1016/j.amc.2006.11.033 |
| [18] |
刘萍, 冯桂莲. 图的深度优先搜索遍历算法分析及其应用[J]. 青海师范大学学报(自然科学版), 2007, 29(3): 41-44. Liu Ping, Feng Guilian. Analysis and Application for Depth-First Search Algorithm of Graph[J]. Journal of Qinghai Normal University (Natural Science Edition), 2007, 29(3): 41-44. |
| [19] |
王一凡, 张乐权, 尹泽文, 等. 基于遍历搜索算法的太阳影子定位技术研究[J]. 科技创新导报, 2017, 14(12): 237-238. Wang Yifan, Zhang Lequan, Yin Zewen, et al. Research on Solar Shadow Location Technology Based on Traversal Search Algorithm[J]. Science and Technology Innovation Herald, 2017, 14(12): 237-238. |
| [20] |
马昌风. 最优化方法及其Matlab程序设计[M]. 北京: 科学出版社, 2010: 87-96. Ma Changfeng. Optimization Method and Matlab Programming[M]. Beijing: Science Press, 2010: 87-96. |
| [21] |
涂鲜萍, 李飞, 雷贤卿, 等. 平面度误差的遍历搜索算法[J]. 河南科技大学学报(自然科学版), 2013, 34(5): 19-22. Tu Xianping, Li Fei, Lei Xianqing, et al. Traversal Searching Algorithm of Flatness Error[J]. Journal of Henan University of Science & Technology(Natural Science Edition), 2013, 34(5): 19-22. |


