0 引言
工程上广泛采用的砂土是典型的离散体材料,其宏观力学性质取决于土体内部细观结构的变化。尽管目前国内外学者对砂土的力学性质进行了较全面深入的研究,但是对于砂土细观力学特性及其影响因素的研究还不充分。
目前对砂土力学特性及其影响因素的研究常采用室内试验与数值模拟相结合的方法[1]。其中,室内剪切试验是研究砂土力学性质常用的试验方法,其能够获得砂土的抗剪强度等宏观力学指标。周杰等[2]利用高压直剪仪研究了砂土抗剪强度在高应力状态下与剪切速率的关系。洪勇等[3]利用DPRI-3型环剪仪研究了不同排水条件下饱和砂的大剪切力学特性,结果表明在不同排水条件下饱和砂的抗剪强度差异明显。孔亮等[4]通过对青岛海砂的研究,得出了级配良好的砂较级配不良的砂具有更高的抗剪强度和较小的剪胀性的结论。
由于常规剪切试验一般无法获取试样内部细观参数的变化,而离散元方法可以从细观层面分析解释土体宏观力学响应,因此离散元方法作为揭示离散体内部力学机理的有效手段在模拟土工试验方面得到了广泛的应用[5]。李爽等[6]通过离散元方法对砂土直剪试验进行了模拟和力学分析,发现剪切带内颗粒应变局部化明显。Alshibli等[7]应用离散元方法研究了直剪试样尺寸对其力学性质的影响,结果表明试样峰值强度大小与试样高度正相关而与宽度负相关。Masson等[8]采用离散元法从宏细观角度对比分析了松密试样的剪切力学特性。Jiang等[9]认为圆形颗粒间的能量消散与滑动转动量有关,并提出了纯转动率(APR)概念。曾远等[10]认为,在颗粒流模拟中,颗粒形状对剪胀效应的影响比颗粒间摩擦系数影响更为显著。
在针对砂土剪切特性的研究中,平均粒径是影响其力学特性的重要因素[4, 14-15],以往的研究中多注重对试样宏观力学性质以及部分细观参数的分析。本文拟在上述相关研究的基础上,结合室内直剪试验,利用二维颗粒流程序的可视化功能,从细观层面详细研究平均粒径对砂土颗粒运动状态及其剪切特性的影响作用。
1 室内直剪试验 1.1 试验仪器和材料本项研究所采用的试验设备为ZJ型应变控制式直剪仪,试验用砂为厦门ISO标准砂。为研究砂土在直剪试验中平均粒径对其力学性质的影响,将标准砂筛分成具有不同平均粒径的均匀砂:细砂(0.08~0.50 mm)、中砂(0.50~1.00 mm)、粗砂(1.00~2.00 mm)。图 1为具体砂土样及其细观形态,各组试样物理指标见表 1。分别对细砂、中砂、粗砂进行固结快剪试验。固结压力分别采用100、200、300、400 kPa,剪切速率为0.8 mm/min。

|
| a, d.细砂;b, e.中砂;c, f.粗砂。 图 1 试验用砂及其细观形态 Fig. 1 Sand for testing and its microstructure |
|
|
| 组别 | 粒径范围/mm | 干密度/(g/cm3) | 最大干密度/(g/cm3) | 最小干密度/(g/cm3) | 相对密实度 |
| 细砂 | 0.08~0.50 | 1.53 | 1.69 | 1.37 | 0.55 |
| 中砂 | 0.50~1.00 | 1.52 | 1.68 | 1.38 | 0.52 |
| 粗砂 | 1.00~2.00 | 1.52 | 1.63 | 1.42 | 0.51 |
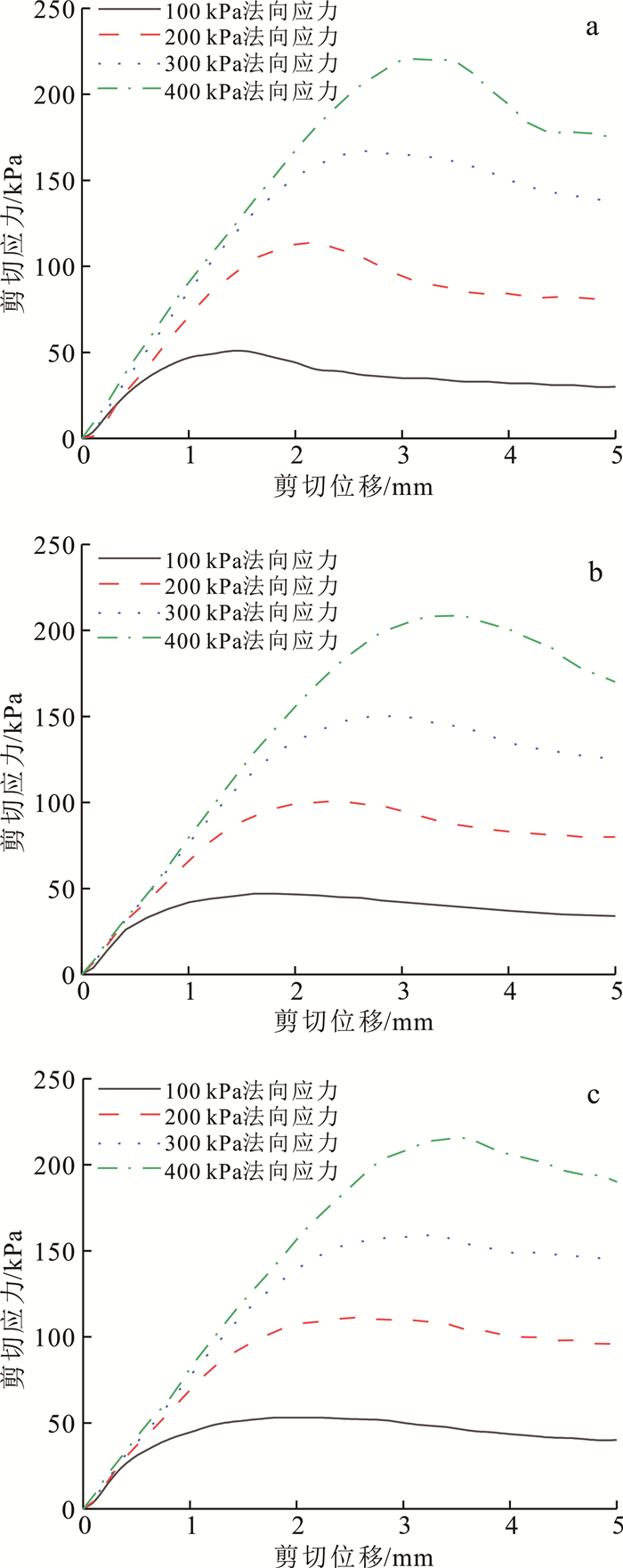
图 2为不同法向应力条件下各组砂土试样剪切应力与剪切位移的关系曲线。
|
| a.细砂;b.中砂;c.粗砂。 图 2 剪切应力与剪切位移关系曲线 Fig. 2 Relation curves between shear stress and shear displacement |
|
|
如图 2所示,在剪切初期,不同试样剪切应力均在较小的剪切位移下迅速增长达到峰值强度,法向应力越大剪切应力增长速率越快,达到峰值强度所需的剪切位移越大。各砂土试样在达到峰值强度后均发生不同程度的应力下降现象,符合密实砂的应变软化特征。
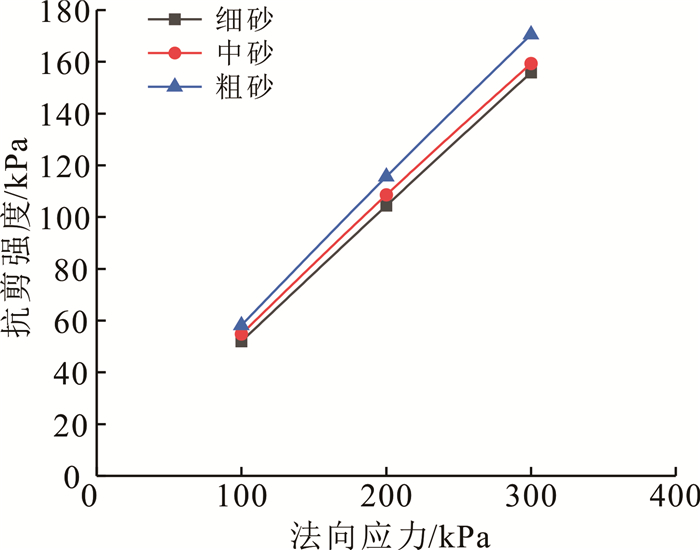
图 3为不同砂土试样在各级法向应力下的抗剪强度曲线。通过对图 3中各曲线进行线性拟合得到各组试样的内摩擦角分别为:细砂26.34°、中砂27.66°、粗砂28.01°。由此可知,砂土内摩擦角随平均粒径的增大而增大。这种现象产生的原因主要是颗粒间的接触面积随颗粒粒径的增大而增大,从而增强了试样的抗剪能力,内摩擦角也因此提高[11]。

|
| 图 3 剪切试验抗剪强度曲线 Fig. 3 Shear strength curves of tests |
|
|
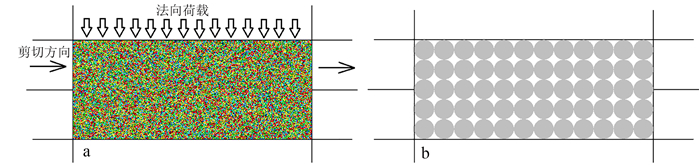
为与实际剪切试验相匹配,砂土离散元模型的尺寸设定为60 mm×25 mm。为符合非黏性土特征,颗粒间接触模型采用线弹性接触模型。试样的主要参数如颗粒间法向和切向接触刚度、墙体刚度、摩擦系数、初始孔隙率等见表 2。根据周健等[12]对砂土双轴试验的颗粒流模拟研究结果可知,细观颗粒摩擦系数是影响砂土数值模拟性质的重要因素。为避免失真,本文摩擦系数取0.5。根据散粒材料弹性理论,颗粒间的接触刚度是决定土体弹性模量的重要参数,当颗粒间接触刚度取值在108~109 Pa之间,颗粒的法向接触刚度与切向接触刚度之比在1~3之间时,模型收敛性良好[13]。本文颗粒间法向接触刚度为1.5×108 Pa,切向接触刚度为1.0× 108 Pa,两刚度之比为1.5,符合模型收敛性良好的条件。根据文献[14-15]对颗粒流模型尺寸效应的研究,当颗粒数大于2 000或者颗粒的最小粒径与试样长度之比小于0.01时,模型具有较好的稳定性。为使各组模型满足要求,将不同粒度砂的粒径缩小至实际粒径的1/2(以增加颗粒数)。模拟试验示意图如图 4a所示,试样生成后,通过伺服程序施加法向荷载进行固结,固结稳定后在维持法向荷载恒定的同时赋予上部墙体一定速度进行剪切,剪切速率与实际试验相同,剪切位移达到5 mm时结束。在剪切过程中为监测试样孔隙率、配位数等细观参数,布设了如图 4b所示的测量圆。
| 组别 | 粒径范围/mm | 颗粒数 | 法向接触刚度/Pa | 切向接触刚度/Pa | 颗粒密度/(kg/m3) | 墙体刚度/Pa | 摩擦系数 | 初始孔隙率/% |
| 细砂 | 0.04~0.25 | 655 082 | 1.5×108 | 1.0×108 | 2 643 | 1.0×109 | 0.5 | 15 |
| 中砂 | 0.25~0.50 | 11 107 | ||||||
| 粗砂 | 0.50~1.00 | 2 769 |
|
| 图 4 模拟试验示意图(a)及测量圆布设图(b) Fig. 4 Schematic diagram of simulation tests(a) and layout of measurement circle(b) |
|
|
通过上述细观参数的设定,分别对细砂、中砂和粗砂3种试样进行法向压力为100、200、300 kPa下的模拟试验。
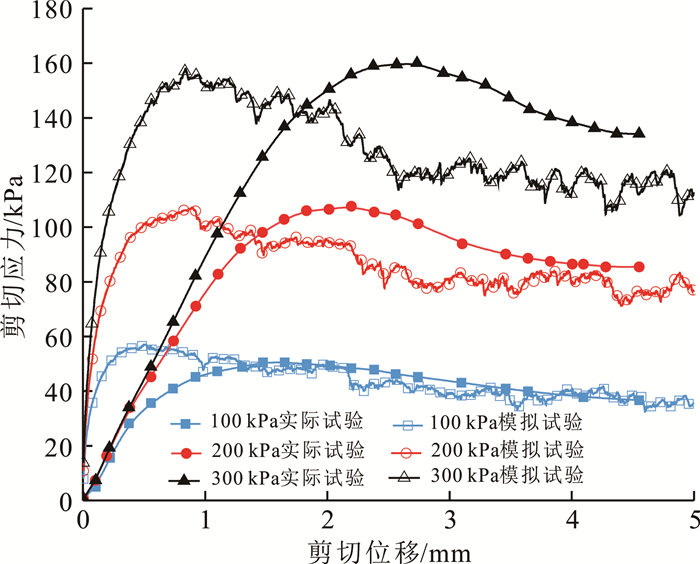
以中砂为例,进行直剪试验与数值模拟对比,结果见图 5。如图 5所示,模拟试验与实际试验剪切应力曲线的变化规律基本一致,峰值强度与残余强度基本匹配。由于模拟试验中的正圆形颗粒已经在固结阶段充分挤密,而实际砂土的挤密过程尚需一定的剪切位移,从而导致数值模拟试验中剪应力的增长速率更大。图 6为根据模拟结果所得到的各组砂土试样抗剪强度曲线。如图 6所示,模拟的砂土平均粒径越大, 其抗剪强度越高(但相差幅度不大),与室内实际剪切试验所得到的结果相符。
|
| 图 5 室内试验与数值模拟结果对比(中砂) Fig. 5 Comparison of numerical simulation and laboratory tests(medium sand) |
|
|
|
| 图 6 模拟试验抗剪强度曲线 Fig. 6 Shear strength curves of simulation tests |
|
|
史旦达等[16]在对砂土直剪力学性状宏细观的机理研究中提出:试样宏观的体积剪胀主要由剪切带内颗粒的运动控制。数值模拟试验可以很好地弥补室内试验无法监测试样体积变化的不足。通过对不同试样进行200 kPa下的模拟试验, 得到不同粒径砂土的体积变化与剪切位移曲线(图 7)。
|
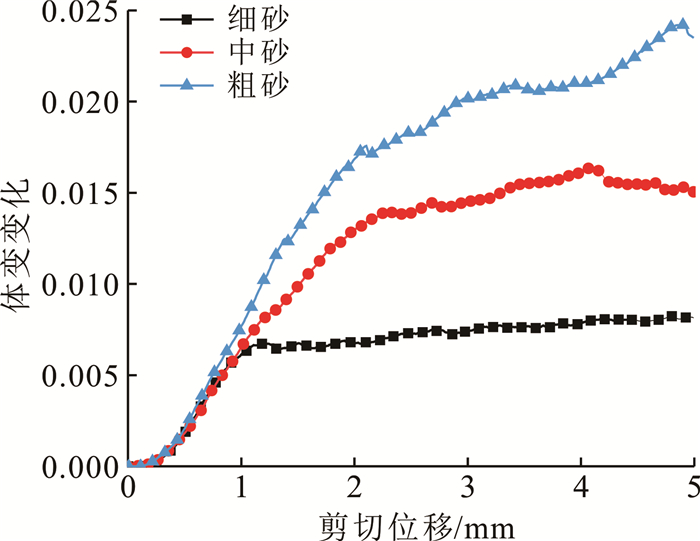
| 图 7 体积变化-剪切位移曲线(200 kPa) Fig. 7 Curves of volume change vs. shear displacement (200 kPa) |
|
|
如图 7所示,不同粒径砂的剪胀效应存在明显差异,其中:细砂体积变化最小,并在剪切位移达1 mm后趋于稳定;中砂在剪切位移达到2 mm时体积变化增速变缓;粗砂体积变化最大,即使在剪切后期体积变化仍呈现逐渐增大的趋势。
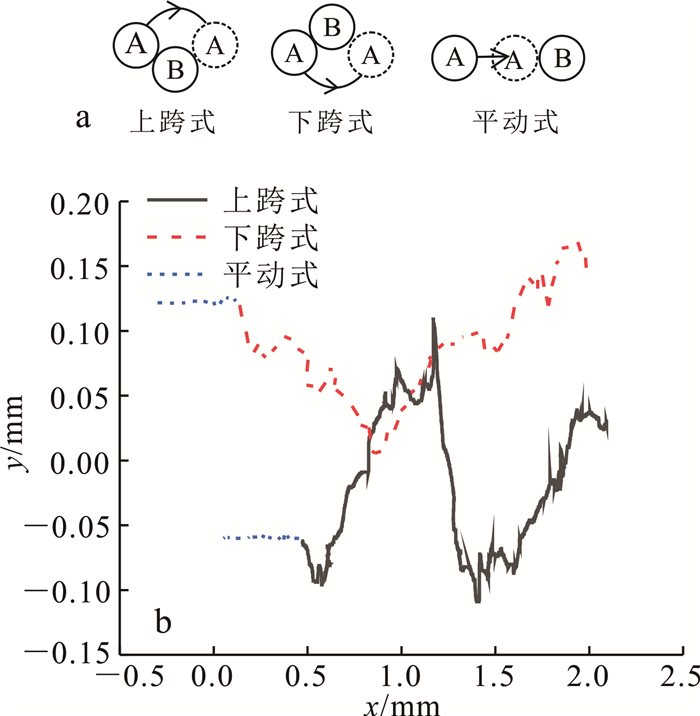
为从细观角度分析试样的剪胀差异,本文监测了各组试样形心范围内颗粒的运动信息,通过对其轨迹形态的分析归纳了颗粒间相互运动的3种基本类型:上跨式、下跨式和平动式,其轨迹特征依次呈“Λ”型、“V”型和“—”型(图 8a)。图 8b为具有上述特征的两枚典型颗粒的运动轨迹,其中,上跨式是所监测颗粒的主要运动形态,其次是下跨式,而平动式多与其他两种运动形态共同存在。
|
| a.颗粒运动的基本类型;b.颗粒运动的轨迹。 图 8 颗粒的运动形态 Fig. 8 Particle motion pattern |
|
|
在剪切过程中,颗粒间发生相互错动,一个颗粒需要跨过另一个颗粒,若颗粒粒径较大,跨越过程中产生的竖向位移也就越大。表 3为上跨式颗粒的坐标变化情况。可以看出,试样平均粒径越大,上跨式颗粒占比越高,平均竖向位移也越大,从细观层面解释了砂土粒径越大其剪胀效应越强的原因。
| 组别 | 样本数 | 上跨式颗粒数 | 最大竖向位移/mm | 最小竖向位移/mm | 平均竖向位移/mm |
| 细砂 | 50 | 24 | 0.19 | 0.13 | 0.14 |
| 中砂 | 30 | 17 | 0.31 | 0.09 | 0.19 |
| 粗砂 | 20 | 15 | 0.47 | 0.12 | 0.25 |
力链网络是颗粒间接触力的宏观表现形式,可以反映颗粒体系在受到外力作用时受力响应机制的敏感性[6]。
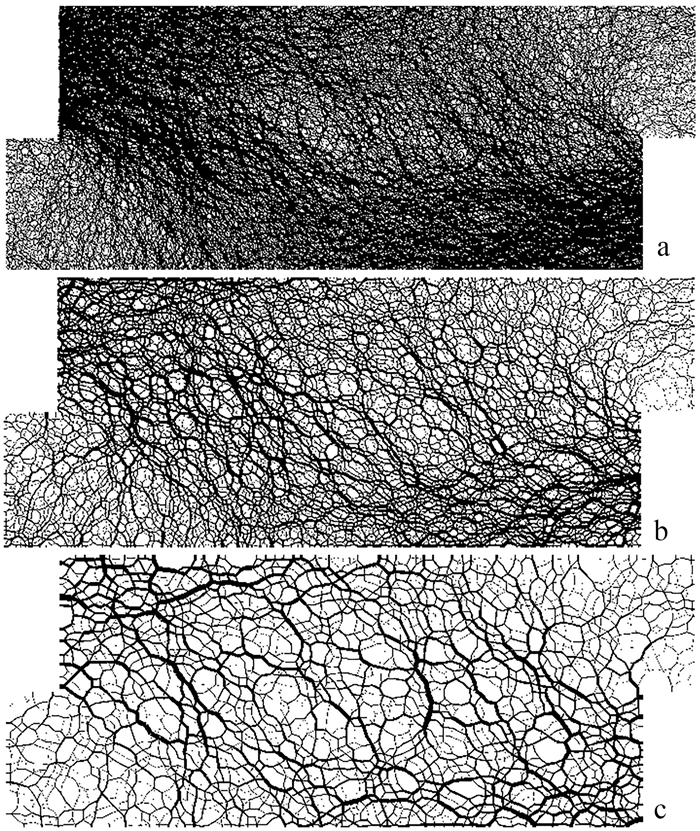
如图 9所示,剪切完成后,砂土样沿对角线方向形成了主力链较为集中的区域。平均粒径越大的试样,其力链网络分布越稀疏、力链骨架越粗;这种现象产生的原因在于试样体积不变的情况下,砂土粒径越大,比表面积越小,粒间接触总数就越少,进而单个颗粒承担的应力也就越大。剪切完成后,剪切盒上部土样的力链均沿剪切方向呈左密右疏分布。这一现象与室内直剪试验过程中剪切盒顶盖出现一端“翘起”的现象相对应,这与密实砂的剪胀特性及直剪试验本身存在的法向应力分布不均等缺陷有关。
|
| a.细砂;b.中砂;c.粗砂。 图 9 不同粒径砂剪切后力链网络 Fig. 9 Force chains of sand with different particle sizes after shear |
|
|
配位数(z)是一定范围内颗粒的平均接触数目,是评价一个颗粒体系接触是否良好、密实的重要指标,其表达式定义为
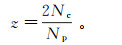 (1)
(1) 式中:Nc为区域内颗粒实际接触的数目;Np为区域内颗粒的总数。配位数能在一定程度上反映试样所处状态的密实程度和应力水平等指标[17]。本文采用条带分析法将剪切试样分为3个不同条带:剪切带上部、剪切带内部和剪切带下部,简称带上、带内和带下区域(图 10)。

|
| 图 10 条带区域划分 Fig. 10 Strip region division |
|
|
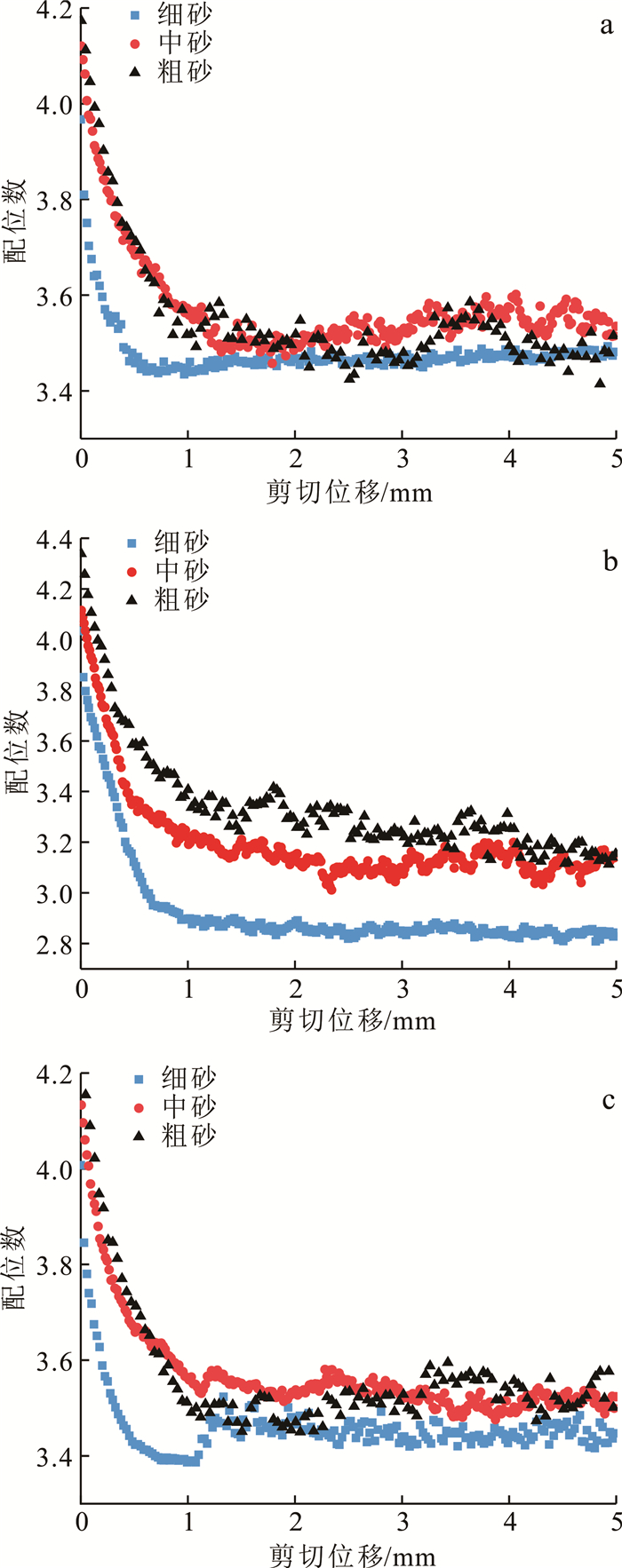
通过模拟得到各组试样在法向应力为200 kPa时剪切过程中不同区域的配位数变化曲线(图 11)。从图 11可以看出,各条带区域颗粒配位数的变化趋势基本相似。各试样配位数均随着剪切位移的增加而急剧降低,细砂降低速率最大,当剪切位移达到1 mm左右后配位数基本保持不变。与剪切带外部配位数变化相比,剪切带内部配位数的变化受砂土粒径的影响最为明显(图 11b),具体表现为:砂土平均粒径越小,带内配位数下降程度越显著,其稳定值越小。这一结果表明,由于细砂剪切带内砂土颗粒间的平均接触数相对较少,因而颗粒间受到的摩阻力更低,这与其抗剪强度略低于粗砂和中砂相对应。
|
| a.剪切带上部;b.剪切带内部;c.剪切带下部。 图 11 各条带配位数变化曲线(200 kPa) Fig. 11 Curves of coordination number of each strip(200 kPa) |
|
|
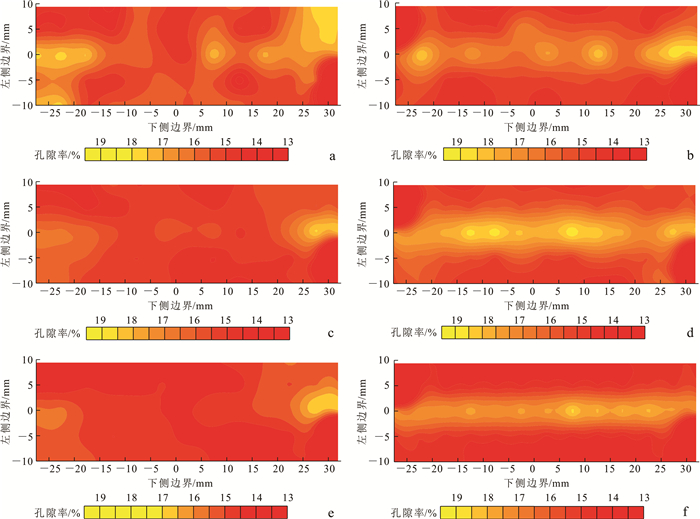
图 12为各组土样通过模拟得到的峰值应力状态及残余应力状态时的孔隙率分布情况。由图 12可见,模拟剪切试验的各组土样孔隙率演变规律基本相同。当砂土样剪切达到其峰值强度时,试样剪切面两端附近区域的孔隙率明显增大,并随着剪切位移的增加逐渐向中部发育直至贯通整个试样;在残余应力状态时砂土体中形成明显的条带区域,这个贯穿试样的区域可以认为是试样剪切面形成的直观反映。Drescher等[18]和Finnon等[19]的研究认为,剪切带是局部区域内发生的集中剪切变形,主要表现为孔隙率的迅速增大。通过上文对剪切带内颗粒的运动形态分析得知,这种剪切变形的具体表现就是颗粒间的相互跨越,这也是造成颗粒间局部孔隙率增大的主要原因。另外,从图 12b、d、f可以明显看出,砂土粒径的大小对剪切带的形态特征有明显的影响。砂土粒径越小,剪切带厚度越小,沿厚度方向的突变越小,即剪切带越平滑。
|
| a.粗砂峰值孔隙率;b.粗砂残余孔隙率;c.中砂峰值孔隙率;d.中砂残余孔隙率;e.细砂峰值孔隙率;f.细砂残余孔隙率。 图 12 不同状态下各组砂孔隙率分布 Fig. 12 Porosity distribution of sand groups under different condition |
|
|
砂土颗粒在剪切过程中转动的原因在于颗粒间的结构体系难以抵抗其粒间的力矩作用。本文基于颗粒流程序可视化功能,对试样颗粒剪切结束时的累计转角进行分析(图 13)。由于模拟时生成的颗粒为正圆型,导致颗粒累计转角过大,因此本文以±200°为界限。图中模拟颗粒转角越大,其颜色也越深。

|
| a.细砂;b.中砂;c.粗砂。 图 13 不同粒径砂的转动情况 Fig. 13 Rotation of sand with different particle sizes |
|
|
如图 13所示,颗粒转动主要集中存在于剪切带处。粗砂颗粒转动带分布具有明显的两端细中间粗的特征;中砂和细砂颗粒转动带分布较为平滑,且带内颗粒转动比粗砂更为充分。颗粒累计转角可以反映砂土颗粒的活跃程度,结合上文对带内颗粒配位数变化情况的分析来看,平均粒径越小,剪切带内颗粒间的平均接触数量越少,因此其带内颗粒间的应力越小,稳定性越差,颗粒旋转就越显著。
3 结论1) 粒径大小对砂土剪切力学特性的影响主要体现在对其抗剪强度和剪胀效应方面,砂土平均粒径越大,其抗剪强度越高,剪胀效应也越明显。
2) 在剪切过程中,通过对颗粒运动形态的分析得知,剪切带内颗粒的运动形态主要有3种类型:上跨式、下跨式和平动式。其中,颗粒间的跨越是决定砂土样剪胀性的重要因素。而平均粒径越大的砂土其上跨式颗粒占比越高,平均竖向位移也越大,从细观层面解释了粗粒砂剪胀效应较强的原因。
3) 不同平均粒径砂土的剪切细观参数存在显著差异,并且其细观参数差异主要集中体现在剪切带处:平均粒径越大的砂土,其剪切带厚度越大,形态差异特征越明显,带内颗粒配位数水平的稳定值也越高;而砂土平均粒径越小,颗粒间的结构体系越脆弱,剪切带内颗粒的转动就越充分。
| [1] |
郑颖人, 孔亮. 岩土塑性力学[M]. 北京: 中国建筑出版社, 2010: 11-14. Zheng Yingren, Kong Liang. Geotechnical Plastic Mechanics[M]. Beijing: China Construction Industry Press, 2010: 11-14. |
| [2] |
周杰, 周国庆, 赵光思, 等. 高应力下剪切速率对砂土抗剪强度影响研究[J]. 岩土力学, 2010, 31(9): 2806-2809. Zhou Jie, Zhou Guoqing, Zhao Guangsi, et al. Effect of Shear Rate on Shear Strength of Sand Under High Stress[J]. Geotechnical Mechanics, 2010, 31(9): 2806-2809. |
| [3] |
洪勇, 周蓉, 郑孝玉. 不同排水条件下饱和砂土快速大剪切力学特性[J]. 吉林大学学报(地球科学版), 2018, 48(5): 1417-1426. Hong Yong, Zhou Rong, Zheng Xiaoyu. Fast Shear Mechanical Properties of Saturated Sand Under Different Drainage Conditions[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(5): 1417-1426. |
| [4] |
孔亮, 季亮亮, 曹杰峰. 应力路径和颗粒级配对砂土变形影响的细观机制[J]. 岩石力学与工程学报, 2013, 32(11): 2334-2341. Kong Liang, Ji Liangliang, Cao Jiefeng. Mechanical Mechanism of Stress Path and Particle Size Matching Sand Deformation[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(11): 2334-2341. |
| [5] |
孙其诚, 王光谦. 颗粒物质力学导论[M]. 北京: 科学出版社, 2009: 1-19. Sun Qicheng, Wang Guangqian. Introduction to Granular Matter Mechanics[M]. Beijing: Science Press, 2009: 1-19. |
| [6] |
李爽, 刘洋, 吴可嘉. 砂土直剪试验离散元数值模拟与细观变形机理研究[J]. 长江科学院院报, 2017, 34(4): 104-110. Li Shuang, Liu Yang, Wu Kejia. Exploring Mesoscopic Deformation Mechanism of Sand in Direct Shear Test by Numverical Simulation Using Discrete Element Method[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(4): 104-110. |
| [7] |
Alshibli K, Stuer S. Shear Band Formation in Plane Strain Experiment of Sand[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2000, 126(6): 456-503. |
| [8] |
Masson S, Martsuoka H. On the Interface Friction in Direct Shear Test[J]. Computers and Geotechnics, 2005, 32(5): 317-325. DOI:10.1016/j.compgeo.2005.05.002 |
| [9] |
Jiang M J, Yu H S, Harris D. Kinematic Variables Bridging Discrete and Continuum Granular Mechanics[J]. Mechanics Research Communications, 2006, 33: 651-666. DOI:10.1016/j.mechrescom.2005.06.013 |
| [10] |
曾远, 周健. 砂土的细观参数对宏观特性的影响研究[J]. 地下空间与工程学报, 2008, 4(3): 499-503. Zeng Yuan, Zhou Jian. Influence of Micro Parameters of Sandy Soil on Its Macro Properties[J]. Chinese Journal of Underground Space and Engineering, 2008, 4(3): 499-503. |
| [11] |
Sitharam T G, Nimbkar M S. Micromechanical Modeling of Granular Materials:Effect of Particle Size and Gradation[J]. Geotechnical and Geological Engineering, 2000, 18(2): 91-117. DOI:10.1023/A:1008982027109 |
| [12] |
周健, 池毓蔚, 池永, 等. 砂土双轴试验的颗粒流模拟[J]. 岩土工程学报, 2000, 22(6): 701-704. Zhou Jian, Chi Yuwei, Chi Yong, et al. Simulation of Particle Flow in Sand-Soil Biaxial Test[J]. Journal of Geotechnical Engineering, 2000, 22(6): 701-704. |
| [13] |
Mishra B K, Meherotra S P. Modeling of Particle Stratification in Jigs by the Discrete Element Method[J]. Minerals Engineering, 1998, 11(6): 511-522. DOI:10.1016/S0892-6875(98)00033-8 |
| [14] |
尹小涛, 郑亚娜, 马双科. 基于颗粒流数值试验的岩土材料内尺度比研究[J]. 岩土力学, 2011, 32(4): 1211-1215. Yin Xiaotao, Zheng Yana, Ma Shuangke. Study of Inner Scale Ratio of Rock and Soil Material Based on Numerical Tests of Particle Flow Code[J]. Rock and Soil Mechanics, 2011, 32(4): 1211-1215. |
| [15] |
刘海涛, 程晓辉. 粗粒土尺寸效应的离散元分析[J]. 岩土力学, 2009, 30(增刊1): 287-292. Liu Haitao, Cheng Xiaohui. Discrete Element Analysis for Size Effects of Coarse-Grained Soils[J]. Rock and Soil Mechanics, 2009, 30(Sup.1): 287-292. |
| [16] |
史旦达, 周健, 刘文白, 等. 砂土直剪力学性状的非圆颗粒模拟与宏细观机理研究[J]. 岩土工程学报, 2010, 32(10): 1557-1565. Shi Danda, Zhou Jian, Liu Wenbai, et al. Exploring Macro- and Micro-Scale Responses of Sand in Direct Shear Tests by Numerical Simulations Using Non-Circular Particles[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(10): 1557-1565. |
| [17] |
石崇, 张强, 王盛年. 颗粒流(PFC5.0)数值模拟技术及应用[J]. 北京:中国建筑工业出版社, 2018, 246-247. Shi Chong, Zhang Qiang, Wang Shengnian. Numerical Simulation Technology and Application with Particle Flow Code(PFC5.0)[J]. Beijing:China Architecture & Building Press, 2018, 246-247. |
| [18] |
Dresche A, Vardoulakis I G, Han C. A Biaxial Apparatus for Testing Soils[J]. Geotechnical Testing Journal, 1990, 13(3): 226-234. DOI:10.1520/GTJ10161J |
| [19] |
Finno R J, Harris W W, Mooney M A, et al. Strain Localization and Undrained Steady State of Sand[J]. Journal of Geotechnical Engineering, 1991, 122(6): 462-473. |


