0 引言
2018年,金沙江上游白格地区两次形成堰塞湖,以及雅鲁藏布江上游米林县形成的堰塞湖,是近年来发生在我国较为著名的大型堰塞湖事件。堰塞湖溃决过程对下游沿岸民众生命财产造成了极大破坏[1-2]。了解和掌握堰塞坝溃坝机理是预测和有效处理堰塞坝溃决的根本途径,该研究长期以来受到众多研究者的广泛关注。从广义上讲,溃坝机理是指溃坝过程各因素之间的因果关系;从狭义上讲,溃坝机理是指溃口三维发展规律以及相互之间的内在联系。
通常堰塞坝沿河流方向堆积较长,因此溃坝研究中重点关注坝体沿水流方向变化和溃口纵向发展过程更有实际意义[3]。堰塞坝溃决研究大致开始于20世纪90年代,研究手段大多采用模型试验[4]。早期研究主要集中于探索黏性坝和非黏性坝差异,得出比较共性的结论是:黏性坝溃坝过程溃口以“陡坎”发展为主要特征,非黏性坝溃坝过程溃口以“层状”发展为主,对于高压实度的非黏性坝也会表现出“陡坎”特征[5]。在国外,早期比较有代表性的研究者主要有Coleman等[6]、Hanson等[7]和Morris[8],后续研究者大都跟随其研究思路,将溃坝过程采用不同的函数关系(如坝体材料、含水率、压实度等)或者将溃坝过程重新划分为不同阶段或者采用不同的观测手段展开研究。例如,Awal等[9]研究了坝体形状、库容、坝体尺寸和材料对溃口流量的影响,但是对溃口演化未做细致讨论;Al-Riffai [10]对非黏性堰塞坝溃坝过程进行了大量试验研究,重点讨论了流量过程,并未涉及溯源过程;Walder等[11]对溃坝过程溃口形状进行了跟踪,并对Coleman等提出的“流量控制面”宽度进行了测量;Zhao[12]对黏性坝溃口演变进行了讨论,但是未分析影响因素与溃口变化之间的关系。国内开展溃坝研究较早且影响较大的单位主要有南京水利水电科学研究院和中国水利水电科学研究院。南京水利水电科学研究院在安徽省滁州大洼水库开展的现场溃坝试验[13]至今保持国内外最大尺度记录(长120 m、宽3 m、高10 m),通过分析该试验结果提出了“双螺旋流淘刷”“单级大陡坎”“剪切坍塌”等溃坝模式。中国水利水电科学研究院的研究则主要针对小尺度模型试验,研究方向侧重于模型相似准则及溃坝水流淹没范围[14]。虽然大部分研究者都会对溃坝过程展开分析和讨论,但是其多停留在定性或半定量水平。例如:柴贺军等[15]对堰塞坝稳定性影响因素进行了研究;王道正等[16]研究了坝体颗粒级配对堰塞坝溃决特征的影响,认为平均粒径越大,坝体整体抗冲刷能力越强,溃口发展速度越慢;付建康等[17]以唐家山滑坡堰塞坝为研究对象,模拟了不同坝后蓄水量、不同水位和不同颗粒物质组成条件下坝体破坏的整个过程;赵高文等[18]采用室内试验水槽对不同压实条件下的滑坡堰塞坝漫顶溢流破坏过程进行了模拟,发现压实度越低,堰塞坝的溃口演化过程持续时间越短;蒋先刚等[19-20]研究了不同底床坡度和不同初始函数率对堰塞坝溃坝过程的影响,将溃口演化过程进行了重新定义和划分;刘杰等[21]讨论了不同初始含水率对非黏性均质堰塞坝溃口演化过程影响,认为存在最不利含水率将导致溃坝过程加快。所有模型试验研究者中,对溃坝机理研究比较系统和经典的当属Coleman等。Coleman等[6]的研究通过模型试验建立了堰塞坝溃口展宽、纵向下切和溯源的数学函数式,讨论了溃口纵向发展和横向展宽的定量关系,并且给出了溃口发展与溃口流量直接的计算公式。然而Coleman等的研究考虑的是坝前水深不变的情况,与大部分堰塞坝情况不相符。到目前为止,鲜有人对不同上下坡面坡度、不同坝体尺寸的堰塞坝溃坝过程溃口纵向下切和溯源过程进行比较分析;且极少有研究者探讨上、下溯源点(其定义在后文给出)在堰塞坝溃坝过程中的运动规律。
基于此,本文通过9组模型试验,定性分析了非黏性堰塞坝溃坝过程溃口纵向下切和溯源过程,从多元溃口参数角度描述和评估堰塞湖溃坝特性;以期进一步提高对堰塞坝溃坝过程的认识,为后续定量研究提供理论基础。
1 试验设置和试验过程本文开展的是基础理论研究,因此并未考虑相似准则问题。所有试验组次采用相同的颗粒级配、统一的筑坝方法和试验过程控制措施。
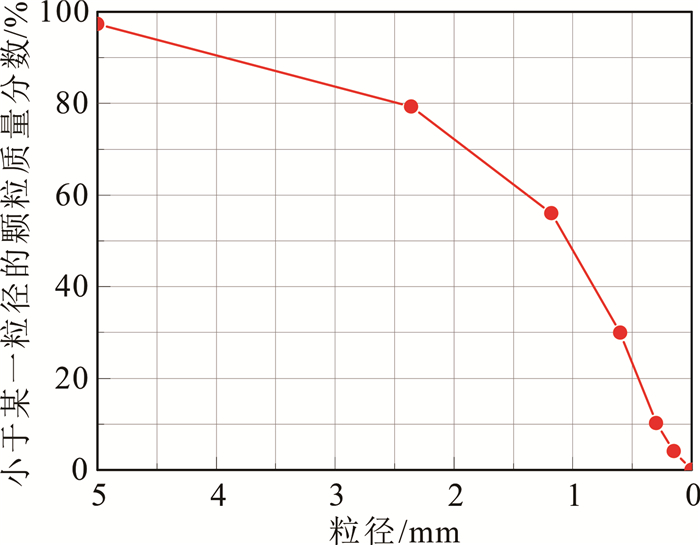
1.1 试验材料及堆坝方式试验采用的坝体填筑材料不同粒径的质量分数如下:< 0.15 mm为4.06%,0.15~0.30 mm为6.08%,0.30~0.60 mm为19.82%,0.60~1.18 mm为26.04%,1.18~2.36 mm为23.32%,2.36~5.00 mm为18.04%,>5.00 mm为2.64%。颗粒级配见图 1。
|
| 图 1 颗粒级配曲线 Fig. 1 Grain-size distribution curve |
|
|
试验模型坝体堆筑采用模具填筑法。首先用木板作为模具固定好坝体上下坡面;然后向模具内分层填筑搅拌均匀的水和沙,每层自然填筑高度大约10 cm;再用木锤夯击大致相等的时间和次数,直到整体坝高超过设计坝高2 cm;最后在坝顶静放一20 kg的重物1 h,取出模具修整坝体轮廓。根据AI-Riffai[10]对坝体压实度(高、中、低)的定义,本文所有试验均对应中压实度。为了保证坝体在试验过程尽量具备同一性,坝体堆筑好后调整各仪器处于待工作状态,通过1台电动水泵向上游库区快速注水到临近坝顶2 cm位置,然后打开各仪器,用自来水管调整固定水流使水位缓慢上涨并漫过坝顶,当水流前锋到达坝趾视为溃坝开始,关闭上游来流。
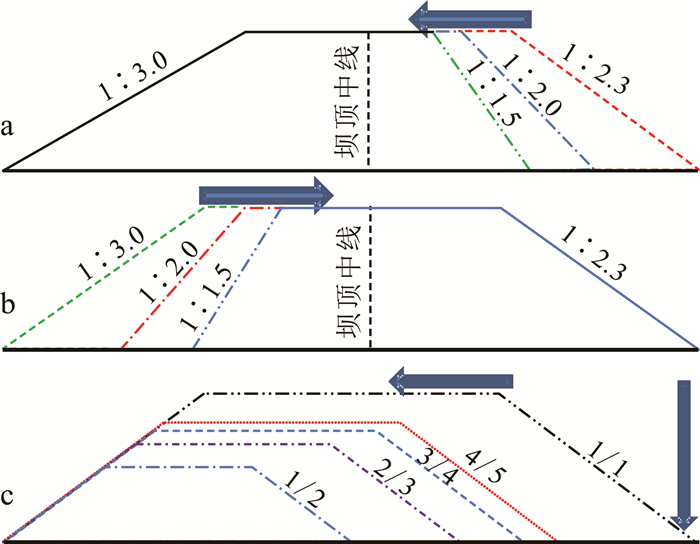
1.2 试验装置及工况试验水槽俯视为L形,全长8.40 m,分为试验段和沉沙池段,试验段长6.60 m,宽0.40 m,高0.75 m,沉沙池段长1.80 m。水槽试验段两侧边壁采用钢化玻璃,并在其中一侧边壁的坝体中部位置粘贴刻度尺,用于测量溃坝过程中溃口底部坝体高程变化。在坝体的正上方、下游和侧面安装了3台高清摄像机,上游库区和下游沉沙池安装了4个高精度浪高仪,沉沙池出口处安装了直角三角堰(使用浪高仪4记录的水头增量计算溃口流量)。试验装置和仪器布置情况如图 2所示。共进行了9组试验,其中:试验1—3为测试坝体上坡面坡度变化对溃坝过程影响;试验1、4、5对比测试下坡面坡度变化对溃坝过程影响;试验1、6、7、8、9为测试坝体尺寸对溃坝过程影响。所有试验工况参数见表 1,不同影响因素实现方式见图 3。图 3中,上、下坡面坡度用坡面竖直高度与水平高度比值表示,坝体相对尺寸是将坝体高宽按照相同比例缩放得到,采用分数表示。

|
| a.水槽侧视图;b.水槽俯视图。 图 2 试验装置示意图 Fig. 2 Schematic diagram of experimental equipment layout |
|
|
| 组次 | 坝高/cm | 顶宽/cm | 底宽/cm | 上坡面坡度 | 下坡面坡度 |
| 试验1 | 30.0 | 30.0 | 190.0 | 1:2.3 | 1:3.0 |
| 试验2 | 30.0 | 25.0 | 175.0 | 1:2.0 | 1:3.0 |
| 试验3 | 30.0 | 22.5 | 158.0 | 1:1.5 | 1:3.0 |
| 试验4 | 30.0 | 22.5 | 145.0 | 1:2.3 | 1:1.5 |
| 试验5 | 30.0 | 25.0 | 160.0 | 1:2.3 | 1:2.0 |
| 试验6 | 15.0 | 15.0 | 95.0 | 1:2.3 | 1:3.0 |
| 试验7 | 20.0 | 20.0 | 127.0 | 1:2.3 | 1:3.0 |
| 试验8 | 22.0 | 22.0 | 139.0 | 1:2.3 | 1:3.0 |
| 试验9 | 24.0 | 24.0 | 151.0 | 1:2.3 | 1:3.0 |
|
| a.上坡面变化;b.下坡面变化;c.坝体相对尺寸变化。 图 3 上、下坡面坡度及坝体相对尺寸变化示意图 Fig. 3 Schematic diagram of upstream and downstream slope and dam relative scale change |
|
|
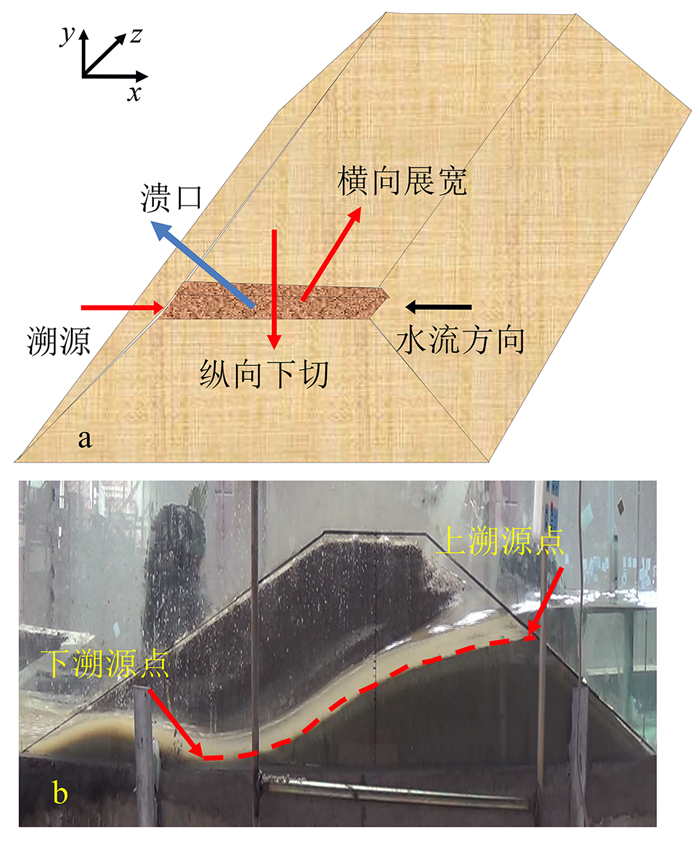
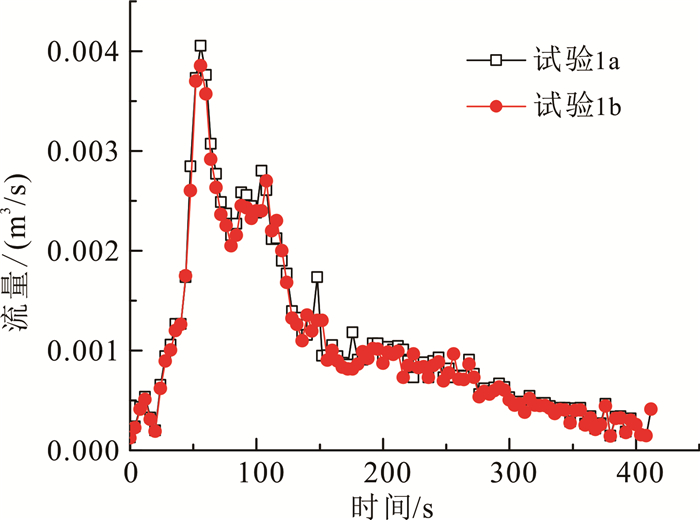
为了便于描述堰塞坝溃坝过程溃口演化,按照笛卡尔直角坐标系,定义溯源冲刷沿x方向(逆流方向)、纵向下切沿y方向(水深方向)、溃口横向发展沿z方向(河宽方向)。定义溃口入口点为上溯源点,溃口水流触底点为下溯源点,如图 4所示。为了便于对溃口变化过程观察,将初始溃口设置在水槽边壁,并将玻璃边壁视为溃口对称面[7],这样在试验过程中溃口宽度将单向发展。由于各组试验采用相同颗粒级配的填筑材料,为了使各组试验结果具备可比性,开展了试验模型可重复性验证,将试验1按相同条件重复2次(分别记为试验1a、1b),对比溃口流量过程线,如图 5所示。从图 5可以看到,两条线重合度很高,说明相同试验条件下的坝体是可重复的,各组试验之间的结果也是可比较的。
|
| a.坐标;b.上、下溯源点。 图 4 溃口侵蚀方式示意图 Fig. 4 Schematic diagram of breach erosion |
|
|
|
| 图 5 可重复性验证 Fig. 5 Repeatability test |
|
|
由于采用的水槽宽度较小,溃口展宽受到边壁限制,因此只讨论溃口纵向下切和溯源发展。
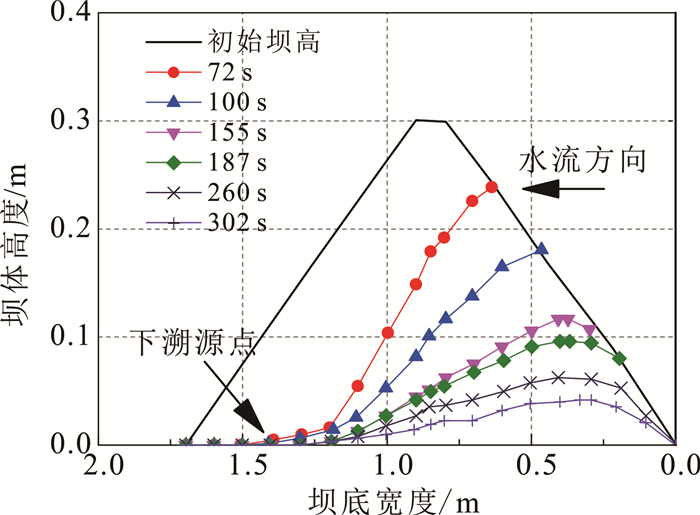
2.1 溃口纵向侵蚀分析受水流冲刷导致溃口底部坝体高程不断下降,从上游坝踵到下游坝趾的溃口各个截面看,溃口底部坝体高程的变化差异较大。图 6展示了试验1的7个典型时刻溃口底部轮廓线变化情况。从图 6可以看到,早期纵向下切发生最快位置发生在坝顶与下坡面交界处,如7 s时刻(图 6a)深度变化最大。根据曼宁公式τ=ρn2v2/h1/3(τ为剪切应力,ρ为水的密度,n为粗糙度系数,v为流速,h为溃口水深)可知,由于坝顶到下坡面交界处地形突然改变,水流速度方向与重力加速度方向夹角减小,导致在该位置的水流加速度最大,从而增强了对底床的剪切力。但是由于前期溃口水流量较少,一部分水流浸润到坝体内部,导致在坝顶与下坡面交界处被起运的泥沙堆积在水流前端;造成一部分水流反射向后淘蚀坝体,后续增多的水流推动堆积沙向前运动的同时翻越堆积沙并重复上述过程。如此反复递进,导致下坡面形成若干大小不等的阶梯状“陡坎”,如25 s时刻(图 6b)。随着溃口增大过流量也相应增大,小阶梯状“陡坎”逐渐变为大阶梯“陡坎”并且数量逐渐减少,如53 s时刻(图 6c)。后续溃口过流量继续增大后,则表现为层状冲刷,如92 s时刻、104 s时刻(图 6d,e)。当出现间歇性边坡坍塌,跌落入溃口的泥沙短暂阻断溃口水流,造成溃口再次形成较大“陡坎”,但是此“陡坎”存在时间仅2~5 s。从溃口残余形状看到,以上坡面与坝顶交界断面位置为界,溃口边坡几乎垂直于坝底,说明本文设置的坝体参数条件下,水流对坝体纵向下切速度快于横向侵蚀速度,如114 s时刻、357 s时刻(图 6f,g)。

|
| a. 7 s;b. 25 s;c. 53 s;d. 92 s;e. 104 s;f. 114 s;g. 357 s。 图 6 溃口纵向发展过程典型时刻展示 Fig. 6 Photo of depth erosion process for different typically moments |
|
|
Coleman等[6]认为堰塞坝溃坝过程溃口断面形状是是抛物线,溃口底部坝体高程Hb是关于时间t的函数,其无量纲表达式为
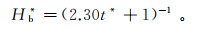 (1)
(1) 式中:Hb*为无量纲溃口底部坝体高程,Hb*=Hb/Hb0,Hb0为坝体初始高程,m;t*为无量纲时间,t*=gt2/Hb0,g为重力加速度,m/s2。
公式(1)针对的是海防工程,即坝前水位恒定(库容无限大)情况。在坝前水位恒定条件下,底部坝体高程可以降低到无限接近坝基(Hb*=0),见图 7。然而,内陆地区的堰塞坝或者人工土石坝库容是有限的,溃坝过程坝前水位不能保持恒定,最终溃口底部坝体高程也很少能降到0,这与坝前水位恒定情况有显著差异(图 8)。图 8展示了试验1—9溃口底部坝体高程随时间变化(坝顶中线位置)过程,可以看到有限库容条件下,不同试验的坝底坝体高程随时间的变化区别较大,主要体现在曲线下降斜率和拐点位置不同。但是,这些试验现象都有一个共同点,即溃坝初期和后期溃口侵蚀较慢,溃坝中期较快。

|
| 图 7 恒定坝前水位条件下溃口底部坝体高程变化 Fig. 7 Bottom elevation change process for constant water reservoir level |
|
|

|
| 图 8 无量纲坝底部坝体高程随时间变化曲线 Fig. 8 Dimensionless bottom elevation of dam breach |
|
|
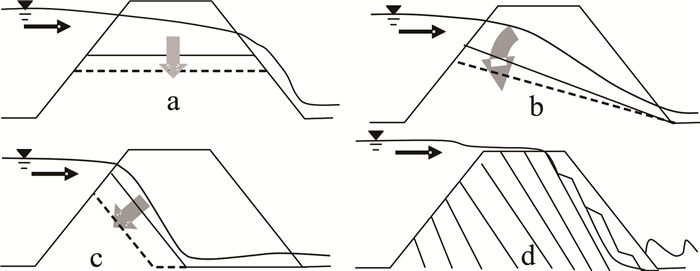
堰塞坝溃坝过程溃口底部地形时刻发生变化,且溃口水流浑浊,无法对溃口底部变化进行直接观测,但是可以根据溃口水流流态进行定性分析。多年来,一些研究者将溃口纵向下切过程定性归类为图 9所示4种情形,其中图 9a—c主要针对非黏性坝,图 9d主要针对黏性坝[22]。通过观察本试验完整视频,发现试验过程溃口底部形态变化表现出了图 9b和9c的部分特征。于是,提出了一种较为细化的非黏性坝溃口纵向下切模式(本文均为非黏性坝),见图 10。非黏性坝溃坝过程依旧主要体现为“层状”冲刷,冲刷面与底床的夹角时刻发生变化(类似于图 9b),某一段时间内冲刷面夹角可能平行于下游坡面(类似于图 9c)。冲刷面上下两点(A,B)按照不同的速率向坝踵处运动。在上游无固定来流情况下,A、B两点最终位置各自有一极限值,即溃坝结束在接近坝踵处将存在一定高度的残余坝体。这与Coleman等[6]提出的恒定库容情况下溯源点是一个固定点有所区别。
|
| 平行于底床;b.旋转支点;c.平行于下坡面;d. “陡坎”冲刷。 图 9 4种溃口纵向下切模式 Fig. 9 Schematic of typical breach depth erosion model |
|
|

|
| A.上溯源点;B.下溯源点。 图 10 非黏性坝溃坝纵向下切新模式 Fig. 10 Schematic of new breach depth erosion model |
|
|
Coleman等[6]研究发现溃坝过程下溯源点最终位置固定(图 11),且与坝体颗粒的中值粒径有关,并给出了下溯源点最终位置相对坝体底部沿水槽方向长度的计算公式:
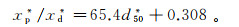 (2)
(2) 式中:xp*=xp/Hb0,xp为下溯源点到下游坝趾距离,m;xd*=xd/Hb0,xd为坝体底部沿水槽方向长度,m;d50*=d50/Hb0,d50为中值粒径,本文为1.2 mm。计算原理见图 12。

|
| xs.上溯源点到坝顶和上坡面交界线所在断面的距离,m;hb.坝顶到上溯源点深度,m;h.上溯源点水深,m。 图 12 下溯源点位置计算示意图 Fig. 12 Schematic diagram of down tracing local estimate |
|
|
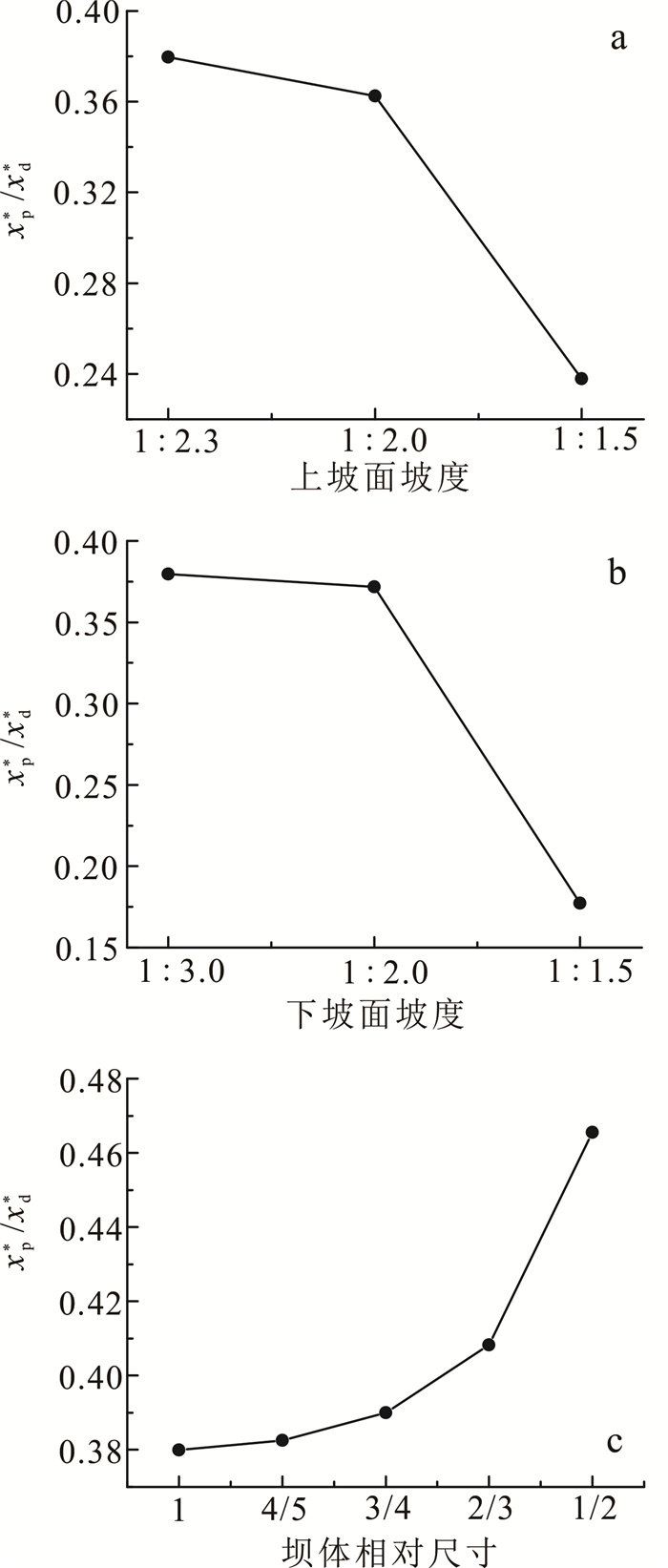
在溃口下切过程中,由于间歇性的边坡坍塌,下溯源点将被反复掩盖。当边坡坍塌的泥沙被溃口水流冲走,下溯源点位置重新发展到或超过边坡坍塌前位置。随着溃口水流量减小,水流速度降低,边坡坍塌的泥沙不能全部冲走,一部分淤积在原下溯源点下游河段,使得下溯源点位置难以继续向上游偏移。然而此时段上溯源点则可继续下移,使得溃口冲刷面坡度减缓。根据视频回放,监测到本文9组试验中下溯源点向上游发展的最大位置(相对最终位置,用xp*/xd*表示)在不同因素影响下变化情况(图 13)。上坡面坡度从1:2.3增大到1:1.5时,xp*/xd*值从0.38降到0.24(图 13a);下坡面坡度从1:3.0增大到1:1.5时,xp*/xd*值从0.37降到0.18(图 13b)。可见上坡面和下坡面坡度对下溯源点最终位置影响规律均表现为,坡度越大则xp*/xd*值越小,即坡度越大溃坝沿水流方向的残存坝体越少。坝体相对尺寸从1减小到1/2时,xp*/xd*值从0.38增大到0.47(图 13c)。对于相同坝形的堰塞坝,坝体尺寸减小后xp*/xd*反而增大,即残余坝体增大。这可能是因为坝体尺寸越小,坝前水位越低,水流下泄的加速度(重力贡献部分)越小,从而对溃口底部的剪切力越小。
|
| a.上坡面坡度;b.下坡面坡度;c.坝体相对尺寸。 图 13 不同影响因素条件下 xp*/xd*值 Fig. 13 Value of xp*/xd* for different impact factors |
|
|
由式(2)可知,本文试验1—5下溯源点最终相对位置为xp*/xd*=0.57,这与本文实际测量值存在较大差异(图 13a, b)。因此,综上所述,堰塞坝溃决过程下溯源点最终位置不仅与中值粒径有关,与坝体上、下坡面坡度和坝体相对尺寸等也密切相关。
2.3 溃口上溯源点移动速度与水深关系Coleman等[6]的研究中提出了“流量控制面”概念,该断面形状为弧形,在溃口入口处,弧形顶点即为本文中的上溯源点。Walder等[11]通过图像分析法并结合堰流理论给出的该断面处流量计算公式是关于水深的函数。由于水深与该断面计算的流量在时间上应该是同步的,因此上溯源点移动情况将通过影响水深进而影响溃口流量该断面计算流量。图 14展示了上溯源点x、y方向移动无量纲速度u*和该点水深h随时间变化关系,其中

|
| 图 14 上溯源点x、y方向移动速度与溃口水深变化之间关系 Fig. 14 Relationship between move velocity of x, y direction and breach water depth for up-tracing point |
|
|
1) 非黏性堰塞坝溃坝过程冲刷面与底床的夹角时刻发生变化,并且上溯源点和下溯源点按照不同的速率向坝踵运动。在上游无固定来流情况下,上、下溯源点最终位置各自有一极限值,即溃坝结束后将存在一定高度的残余坝体。
2) 堰塞坝溃决过程下溯源点最终位置不仅与颗粒中值粒径有关,也与坝体上下坡面坡度和坝体相对尺寸密切相关。坝体上、下游坡度越大,xp*/xd*值越小;对于相同坝形的堰塞坝,坝体相对尺寸越小则xp*/xd*值越大。
3) 上溯源点移动峰值速度与该点峰值水深出现时间不同步,表现为峰值移动速度早于峰值水深出现时间,并且上溯源点x方向移动速度快于y方向移动速度。
本研究主要以定性为主,可为后续实时流量预测和计算提供理论参考;但是本文并未考虑相似理论,这也是后续需要重点突破的方向。
| [1] |
周兴波, 杜效鹄, 姚虞. 金沙江白格堰塞湖溃坝洪水分析[J]. 水力发电, 2019, 45(3): 8-13. Zhou Xingbo, Du Xiaohu, Yao Yu. Research and Analysis on Baige Landslide Dam Break Flood in Jinsha River[J]. Water Power, 2019, 45(3): 8-13. |
| [2] |
陈祖煜, 雷盼, 张强, 等. 白格堰塞体风险后评估:再次堵江洪水分析和应对措施[J]. 水利规划与设计, 2020(1): 1-5, 48. Chen Zuyu, Lei Pan, Zhang Qiang, et al. Post-Evaluation of the Risk of Baige Weir Plug:Analysis and Response Measures of the River Flood[J]. Water Resources Planning and Design, 2020(1): 1-5, 48. |
| [3] |
刘定竺, 崔鹏, 蒋德旺. 堰塞坝溃口展宽过程实验研究[J]. 中国水土保持科学, 2017, 15(6): 19-26. Liu Dingzhu, Cui Peng, Jiang Dewang. Experimental Study on Breach Broadening Process of Landslide Dam[J]. Science of Soil and Water Conservation, 2017, 15(6): 19-26. |
| [4] |
王立辉, 胡四一. 溃坝问题研究综述[J]. 水利水电科技进展, 2007, 27(1): 80-85. Wang Lihui, Hu Siyi. Study on Dam Failure-Related Problems[J]. Advanced in Science and Technology of Water Resources, 2007, 27(1): 80-85. |
| [5] |
ASCE/EWRI Task Committee on Dam/Levee Breach. Earthen Embankment Breaching[J]. Journal of Hydraulic Engineering, 2011, 137: 1549-1564. DOI:10.1061/(ASCE)HY.1943-7900.0000498 |
| [6] |
Coleman S E, Andrews D P, Webby M G. Overtopping Breaching of Noncohesive Homogeneous Embankments[J]. Journal of Hydraulic Engineering, 2002, 128(9): 829-838. DOI:10.1061/(ASCE)0733-9429(2002)128:9(829) |
| [7] |
Hanson G J, Temple D M, Hunt S L, et al. Development and Characterization of Soil Material Parameters for Embankment Breach[J]. Journal of Application Engineering in Agriculture, 2011, 27(4): 587-595. DOI:10.13031/2013.38205 |
| [8] |
Morris M W. IMPACT, Investigation of Extreme Flood Processes and Uncertainty, Final Technical Report[EB/OL]. (20030820) [20191231]. http://www.impact-project.net/AnnexII_Detailed Technical Reports/AnnexII_PartE1_WP6/IMPACT-D6.3attach.pdf.
|
| [9] |
Awal R, Nakagawa H, Fujita M, et al. Experimental Study on Glacial Lake Outburst Floods Due to Waves Overtopping and Erosion of Moraine Dam[J]. Annals of Disaster Prevention Research Institute, 2010, 53: 583-594. |
| [10] |
Al-Riffai. Experimental Study of Breach Mechanics in Overtopped Noncohesive Earthen Embankments[D]. Ottawa: Ottawa University, 2014.
|
| [11] |
Walder J S, Iverson R M, Godt J W, et al. Controls on the Breach Geometry and Flood Hydrograph During Overtopping of Noncohesive Earthen Dams[J]. Water Resources Research, 2015, 51(8): 6701-6724. |
| [12] |
Zhao Gensheng. Breach Growth in Cohesive Embankments Due to Overtopping[D]. Wuhan: Changjiang River Scientific Research Institute, China, 2016.
|
| [13] |
张建云, 李云, 宣国祥, 等. 不同黏性均质土坝漫顶溃坝实体试验研究[J]. 中国科学:E辑:技术科学, 2009, 39(11): 1881-1886. Zhang Jianyun, Li Yun, Xuan Guoxiang, et al. Overtopping Breaching of Cohesive Homogeneous Earth Dam with Different Cohesive Strength[J]. Science of China:Series E:Technical Science, 2009, 39(11): 1881-1886. |
| [14] |
林秉南. 明渠不恒定流研究的现状与发展[M]. 北京: 中国水利水电出版社, 2001: 340-373. Lin Bingnan. Research Status and Development of Unsteady Flow in Open Channel[M]. Beijing: China Water Resources and Hydropower, 2001: 340-373. |
| [15] |
柴贺军, 刘汉超, 张倬元, 等. 天然土石坝稳定性初步研究[J]. 地质科技情报, 2001, 20(1): 77. Chai Hejun, Liu Hanchao, Zhang Daoyuan, et al. Preliminarily Stability Analysis of Natural Rockfield Dam Resulting from Damming Landslide[J]. Geological Science and Technology Information, 2001, 20(1): 77. |
| [16] |
王道正, 陈晓清, 罗志刚, 等. 不同颗粒级配条件下堰塞坝溃决特征试验研究[J]. 防灾减灾工程学报, 2016, 36(5): 827-833. Wang Daozheng, Chen Xiaoqing, Luo Zhigang, et al. Experimental Research on Breaking of Barrier Lake Dam Under Different Grading Conditions[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(5): 827-833. |
| [17] |
付建康, 罗刚, 胡卸文. 滑坡堰塞坝越顶溢流破坏的物理模型实验[J]. 吉林大学学报(地球科学版), 2018, 48(1): 203-212. Fu Jiankang, Luo Gang, Hu Xiewen. Physical Model Experiment on Overtopping Failure of Landslide Dam[J]. Journal of Jilin University(Earth Science Edition), 2018, 48(1): 203-212. |
| [18] |
赵高文, 姜元俊. 不同密实条件的滑坡堰塞坝漫顶溃决实验[J]. 岩石力学与工程学报, 2018, 37(6): 1496-1505. Zhao Gaowen, Jiang Yuanjun. Experimental Investigation on Overtopping Failure of Landslide Dams with Different Conditions of Compactness[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(6): 1496-1505. |
| [19] |
蒋先刚, 吴雷. 不同底床坡度下的堰塞坝溃决过程研究[J]. 岩石力学与工程学报, 2019, 38(1): 3008-3014. Jiang Xiangang, Wu Lei. Influence of Bed Slope on Breaching Process of Natural Dam[J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(1): 3008-3014. |
| [20] |
蒋先刚, 吴雷. 不同初始含水量条件下的堰塞坝溃决机理分析[J]. 吉林大学学报(地球科学版), 2020, 50(1): 185-193. Jiang Xiangang, Wu Lei. Influence of Initial Soil Moisture on Breaching Mechanism of Natural Dam[J]. Journal of Jilin University(Earth Science Edition), 2020, 50(1): 185-193. |
| [21] |
刘杰, 颜婷, 周传兴, 等. 初始含水率及人工干预对堰塞坝溃决影响试验研究[J]. 重庆交通大学学报(自然科学版), 2019, 38(3): 60-67. Liu Jie, Yan Ting, Zhou Chuanxing, et al. Experimental Investigation of Landslide Dam Failure Influenced by Initial Moisture Content and Manual Intervention[J]. Journal of Chongqing Jiaotong University (Natural Science Edition), 2019, 38(3): 60-67. |
| [22] |
Morris M W, Hanson G, Hassan M. Improving the Accuracy of Breach Modeling:Why are We not Progressing Faster?[J]. Journal of Flood Risk Management, 2008, 1(3): 150-161. DOI:10.1111/j.1753-318X.2008.00017.x |