2. 辽宁工程技术大学软件学院, 辽宁 葫芦岛 125105
2. School of Software, Liaoning Technique University, Huludao 125105, Liaoning, China
0 引言
高光谱遥感影像具有超高的光谱分辨率, 可以获取地物上百个连续谱段信息, 从而大幅度提高地物区分能力[1]。高光谱遥感在国防建设和国民经济等方面都发挥着重要作用, 已广泛应用于目标探测[2]、地表分类[3]、环境管理[4]和矿物填图[5]等领域。许多高光谱遥感应用的基础是影像分类, 但高光谱遥感影像的高维特性、波段间高度相关性和样本数量少等使得高光谱遥感影像分类时易产生“维数灾难”现象[6]。因此, 如何通过特征提取方法减少数据维数是高光谱遥感影像分类领域研究的热点问题之一。
特征提取的目的是将高维数据嵌入到较低维的空间, 在降低数据维度的同时尽可能地保持原数据的基本结构信息。近年来, 研究人员已提出一系列有关高光谱遥感影像数据的特征提取方法。主成分分析(PCA)[7]通过计算原始数据的协方差矩阵降低特征维度; 但其作为无监督方法, 不能较好地利用数据类别信息。线性判别分析(LDA)[8]是一种监督特征提取方法, 通过寻找最优投影矩阵, 使得在投影空间中最大化类间散度的同时最小化类内散度; 然而, LDA是一种单模态分析方法, 高光谱影像在很多情况下是多模态的。针对多模态数据分类问题, 可以在降维过程中引入局部信息, 尽可能地保留数据的局部流形结构。局部保持投影(LPP)[9]可以有效保留数据的局部特征, 使原始数据中距离较近的样本在特征空间中仍较为紧凑。Sugiyama[10]结合LDA和LPP方法的特性, 提出一种局部Fisher判别分析(LFDA)特征提取方法, 实验结果表明LFDA方法可以有效嵌入多模态样本数据。Wei等[11]将LFDA分别和支持向量机(SVM)分类器、高斯混合模型(GMM)分类器结合, 提出LFDA-SVM和LFDA-GMM高光谱遥感影像分类方法, 有效提高了分类精度。目前特征提取研究取得了一定的进展, 但是受限于高光谱遥感影像分类时产生的维数灾难现象, 特征提取时仅使用了光谱特征, 忽略了影像的空间特征, 导致分类结果不够理想。
除光谱特征外, 高光谱遥感影像中也包含了十分丰富的空间特征, 空间上距离很近的像元很大概率属于同类地物[12]。因此, 为弥补只利用光谱特征不能够全面有效表达高光谱数据的不足, 研究人员提出了空-谱特征融合的高光谱遥感影像分类方法, 认为空间特征可以作为光谱特征的一种互补。王俊淑等[13]将形态学提取的空间特征和光谱特征融合用于高光谱遥感影像分类, 其分类结果要优于仅使用光谱特征分类方法。Mirzapour等[14]将像元指数特征、灰度共生矩阵纹理特征和光谱特征融合, 提高了分类的精度。叶珍等[15]针对Wei等[11]提出的LFDA-GMM分类方法忽略空间特征的问题, 提出Gabor特征和LFDA特征结合的分类方法, 有效提高了分类精度。黄鸿等[16]提出加权均值滤波(WMF)和流行重构保持嵌入结合的空-谱特征提取方法, 利用WMF消除影像中噪点影响的同时提取出更有效的鉴别特征, 改善了高光谱遥感影像分类效果。综上, 高光谱遥感影像空间特征提取方法主要包含形态学滤波、Gabor特征、灰度共生矩阵和加权均值滤波等。虽然这些方法可以较好地消除噪声和保留地物的空间结构信息, 但其局限性是不能同时实现地物的平滑和边缘细节的描述。
引导滤波(GF)[17]通过建立引导图像和输出图像的局部线性模型, 并求解输入和输出图像间差异函数, 隐式地完成对输入图像的滤波。除实现平滑功能, 引导滤波还具有良好的边缘保持性能, 在图像去燥[18]和图像融合[19]等领域有着广泛地应用。考虑引导滤波的特性, 结合高光谱遥感影像空间一致性和多模态性的特点, 本文提出一种引导滤波与局部Fisher判别嵌入特征相结合的高光谱遥感影像分类方法(GF-LFDA-SVM)。该方法在特征提取过程中充分利用了高光谱遥感影像的空间特征以及像元间的局部信息, 能较好地挖掘出数据的低维嵌入特征。最后在Indian Pines和Pavia University两幅高光谱数据集上验证本文方法的有效性。
1 方法本文方法整体流程如图 1所示。主要步骤包括:1)高光谱影像预处理。将高光谱影像数据进行波段划分和归一化处理。2)引导滤波空间特征提取。利用PCA对归一化后的数据进行特征提取, 得到第一主成分影像作为引导图像, 利用引导滤波分别对各波段影像进行空间特征提取。3)LFDA空间特征低维嵌入。将提取的空间影像特征进行叠加, 利用LFDA进行低维嵌入。4)影像分类。将得到的低维嵌入特征划分为训练样本和测试样本, 分别输入到SVM分类器得到分类结果。

|
| 图 1 GF-LFDA-SVM方法流程图 Fig. 1 Flow chart of GF-LFDA-SVM method |
|
|
引导滤波是一种近年来出现的能够较好保留边缘信息的滤波器。假设输出图像q与引导图像I在以像素k为中心、r为半径的窗口δk中存在局部线性关系:
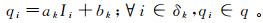 (1)
(1) 式中:qi是输出图像中的第i个像素点; ak和bk是当窗口中心位于k时该线性关系的线性系数; Ii是引导图像中的第i个像素点。对式(1)两边取梯度, 可以得到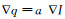
将q表示为输入图像p去除噪声或纹理之后的图像:
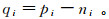 (2)
(2) 式中:pi为输入图像中的第i个像素点; ni表示噪声。
为了求解线性系数ak和bk, 寻求拟合函数的输出值qi与真实值pi之间的最小差距, 转化为最优化问题, 其价值函数为
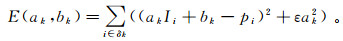 (3)
(3) 式中, ε是防止求得a过大的正则化系数。已有研究表明, ε的取值对滤波结果影响较小[17], 故本文设置ε=0.1。通过最小二乘法求解得到:
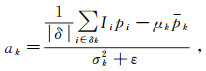 (4)
(4) 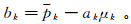 (5)
(5) 式中:μk和σk2分别表示I在窗口δk中的均值和方差; |δ|是窗口δk内的像素数目; 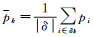
在整幅图像内采取窗口操作时, 某一像素的输出值可以通过该像素的线性函数平均值得到:
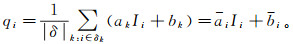 (6)
(6) 式中, ai、bi分别是在所有覆盖了像素i的窗口δk中ak和bk的平均值。
以高光谱遥感影像Indian Pines数据集的第5波段为输入图像, 图 2给出了形态学滤波、加权均值滤波和引导滤波的对比。由图 2可知:窗口半径为1和3的3种滤波影像基本可以较好地提取出各类地物的结构特征; 当窗口半径为5和7时, 形态学滤波影像和加权均值滤波影像中的各类地物结构比较模糊, 而引导滤波影像基本可以保留各类地物的边缘信息和大致轮廓。因此, 相对于形态学滤波和加权均值滤波, 引导滤波可以更好地保留影像中各类地物的结构信息。

|
| a.输入图像; b.引导图像。形态学滤波, 圆形窗口:c. r=1;d. r=3;e. r=5;f. r=7。加权均值滤波, 方形窗口:g. r=1;h. r=3;i. r=5;j. r=7。引导滤波, 方形窗口:k. r=1;l. r=3;m. r=5;n. r=7。 图 2 形态学滤波、加权均值滤波和引导滤波的对比 Fig. 2 Comparison of morphological filtering, weighted mean filtering and guided filtering |
|
|
LFDA是对LDA的一种扩展, 它的基本思想是最大化类间分离的同时保留类内精细复杂的局部结构。为了更好地保留局部特征, LFDA计算数据的局部类内和类间散度矩阵, 通过基于距离的相似度加权矩阵有效保留每个类别的局部多模态性, 使得数据转换时在原始空间中距离较近的样本点在投影空间中仍然保持较为紧凑, 从而达到不同类别的样本在投影空间中具有更好可分离性的目的。
为了获得加权矩阵以有效保留每个类别的局部多模态性, 需要计算样本之间的相似度, Ai, j∈[0, 1], 表示样本xi和xj之间的相似度, 记为
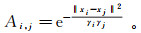 (7)
(7) 式中:γi是xi的局部伸缩, 定义为γi=‖xi-xi(t)‖; xi(t)为xi的近邻; t是邻域数目。LFDA将局部类间散度矩阵Slb和局部类内散度矩阵Slw定义为:
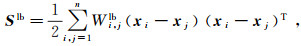 (8)
(8) 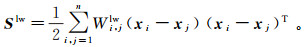 (9)
(9) 其中, 引入两个加权矩阵Wlb和Wlw保留数据局部信息, 它们的第(i, j)个元素Wi, jlb和Wi, jlw分别定义为:
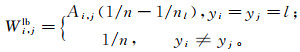 (10)
(10) 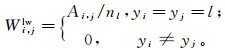 (11)
(11) 式中:n是样本总数; nl是类别l的样本数目; yi和yj分别是样本xi和xj的标记。
转换矩阵WLFDA可以通过计算局部Fisher比率的最优值得到, 即
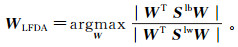 (12)
(12) 式中, W是基向量矩阵。
上述最优化问题可以等价于求解广义特征值分解SlbV=λSlwV, 其中λ是广义特征值, V是对应于Fisher判别方向上的特征向量。假设广义特征值按照降序排列为λ1≥λ2≥…≥λs, 对应的特征向量V1, V2, …, Vs组成最优投影矩阵。
1.3 基于支持向量机的高光谱影像分类假设高光谱遥感影像共有L类地物, 提取影像数据空-谱嵌入特征后, 本文采用支持向量机分类器对影像进行分类。SVM建立在统计学习理论VC(Vapnik-Chervonenkis)维理论和结构风险最小原理基础上, 根据有限样本信息在模型的复杂性和学习能力之间寻求最佳折衷, 以获得最好的泛化能力, 是目前广泛应用于高光谱遥感影像分类的方法之一[20]。本文分类的具体流程如下:
步骤1:数据集划分阶段。将提取的空-谱特征随机分为训练样本和测试样本。
步骤2:训练阶段。将具有N个训练样本的集合{xi∈RD}i=1N(D为波段数目)及其对应标签{yi∈{1, 2, …, L}}i=1N作为最终特征输入, 通过对如下二次规划问题求解得到各个类别的权重ω:
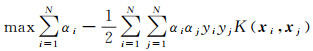 (13)
(13) 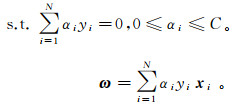 (14)
(14) 式中:K(xi, xj)为满足Mercer定理的正定核函数, 本文方法选择高斯径向基核函数; {αi}i=1N表示拉格朗日乘子; C为惩罚因子。
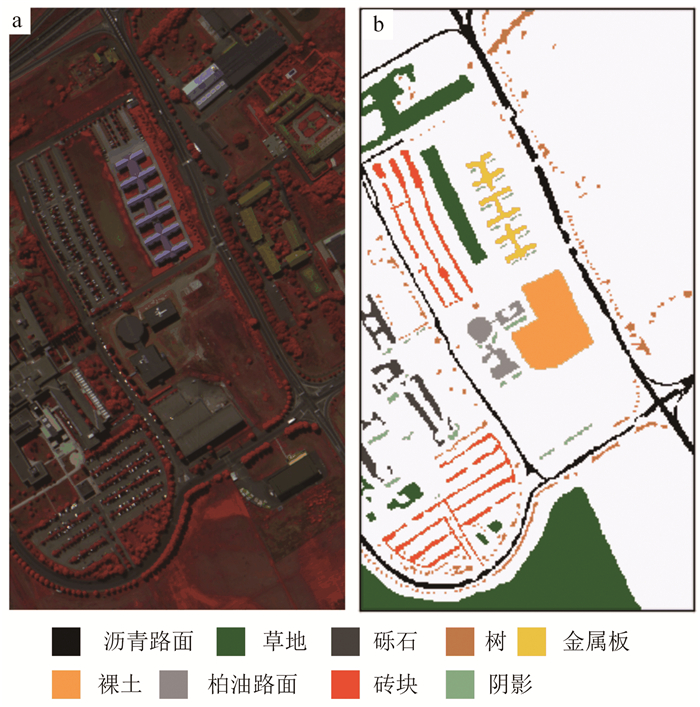
步骤3:测试阶段。将测试样本x′输入到SVM分类器, 利用已学习的各个类别的ω求得该样本对应的类别标签y′:
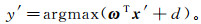 (15)
(15) 式中, d为常数。
2 实验数据为验证方法的有效性, 选取Indian Pines和Pavia University高光谱遥感影像数据集进行分类实验。
1) Indian Pines数据集。该数据集来源于AVIRIS传感器, 反映了美国印第安纳西北部地区的植被种植情况, 影像大小为145像素×145像素, 波长范围为0.4~2.5 μm, 空间分辨率为20 m, 去除噪声波段后, 剩余200个波段用于分类。该数据集共有16类地物, 10 249个样本。该区域的伪彩色图(合成波段:140、80和50)如图 3a所示, 地面参考图如图 3b所示。

|
| a.假彩色影像; b.地面真实数据。 图 3 Indian Pines数据集 Fig. 3 Indian Pines data set |
|
|
2) Pavia University数据集。该数据集来源于ROSIS传感器, 影像大小为610像素×340像素, 波长范围为0.43~8.60 μm, 空间分辨率为1.3 m, 去除噪声波段后, 剩余103个波段用于分类。该数据集共有9类地物, 42 776个样本。该区域的伪彩色图(合成波段:90、60和30)如图 4a所示, 地面参考图如图 4b所示。
|
| a.假彩色影像; b.地面真实数据。 图 4 Pavia University数据集 Fig. 4 Pavia University data set |
|
|
为测试本文方法的性能, 分6组实验对两幅高光谱影像数据分类结果进行对比, 分别是:1)Pal等[20]提出的使用原始光谱特征进行SVM分类(SP-SVM); 2)Wei等[11]提出的LFDA和SVM结合的分类方法(LFDA-SVM); 3)王俊淑等[13]提出的扩展形态学滤波对各波段影像滤波叠加后进行SVM分类(MP-SVM); 4)叶珍等[15]提出的Gabor和LFDA结合的分类方法, 考虑分类器对分类结果的影响, 将文献中GMM分类器用SVM分类器代替(Gabor-LFDA-SVM); 5)利用引导滤波对各波段影像滤波叠加后进行SVM分类(GF-SVM); 6)本文方法(GF-LFDA-SVM)。其中SVM的最佳参数均通过5折交叉验证获取。
3.1 实验结果Indian Pines数据集实验采用平衡训练集(各类训练样本数量和各类样本总量成比例)检验各方法的分类性能, 从各类地物中随机选取10%样本作为训练样本, 剩余样本为测试样本。表 1为实验中各方法对应的各类地物分类精度以及各方法总体精度、平均精度和Kappa系数。由表 1可知, 本文提出的GF-LFDA-SVM方法的分类结果总体精度、平均精度和Kappa系数分别约为98.28%、98.51%和98.05%, 相比SP-SVM、LFDA-SVM、MP-SVM、Gabor-LFDA-SVM和GF-SVM方法的分类结果均有所提高, 总体精度分别提高了18.61%、17.08%、2.70%、5.73%和1.82%, 平均精度分别提高了19.29%、17.85%、6.60%、7.02%和1.03%, Kappa系数分别提高了21.37%、19.50%、3.08%、8.74%、和2.08%。GF-LFDA-SVM方法在13个类别(苜宿、免耕玉米、少耕玉米、草地/牧草、修剪草地、干草料堆、燕麦、免耕大豆、少耕大豆、纯净大豆、小麦、树林和石钢塔)中获得了最佳地物分类精度。图 5给出了随机一次的分类结果。
| 类别 | 训练样本数 | 测试样本数 | 分类精度/% | |||||
| SP-SVM | LFDA-SVM | MP-SVM | Gabor-LFDA-SVM | GF-SVM | GF-LFDA-SVM | |||
| 苜宿 | 5 | 41 | 78.26 | 87.09 | 97.29 | 100.00 | 97.43 | 100.00 |
| 免耕玉米 | 143 | 1 285 | 78.32 | 76.93 | 94.19 | 91.51 | 94.44 | 98.59 |
| 少耕玉米 | 83 | 747 | 78.26 | 77.15 | 90.60 | 88.50 | 89.90 | 95.28 |
| 玉米 | 24 | 213 | 44.20 | 65.35 | 93.12 | 93.43 | 100.00 | 97.25 |
| 草地/牧草 | 48 | 435 | 92.74 | 85.01 | 95.69 | 94.17 | 97.90 | 98.60 |
| 草地/树木 | 73 | 657 | 94.28 | 88.44 | 95.54 | 95.78 | 100.00 | 97.76 |
| 修剪草地 | 3 | 25 | 72.72 | 70.83 | 95.24 | 92.86 | 96.15 | 100.00 |
| 干草料堆 | 48 | 430 | 99.73 | 94.64 | 100.00 | 100.00 | 96.97 | 100.00 |
| 燕麦 | 2 | 18 | 57.14 | 71.43 | 60.87 | 68.75 | 100.00 | 100.00 |
| 免耕大豆 | 97 | 875 | 69.45 | 74.26 | 97.71 | 90.73 | 95.10 | 97.83 |
| 少耕大豆 | 246 | 2 209 | 75.04 | 80.18 | 97.68 | 94.34 | 96.74 | 98.91 |
| 纯净大豆 | 59 | 534 | 69.41 | 71.45 | 90.56 | 83.09 | 96.81 | 97.90 |
| 小麦 | 21 | 184 | 98.90 | 88.94 | 97.35 | 82.47 | 100.00 | 100.00 |
| 树林 | 127 | 1 138 | 98.51 | 95.34 | 99.73 | 95.95 | 98.60 | 99.82 |
| 建筑草地 | 39 | 347 | 60.60 | 64.78 | 90.36 | 94.72 | 99.70 | 94.24 |
| 石钢塔 | 10 | 83 | 100.00 | 98.78 | 74.73 | 62.65 | 100.00 | 100.00 |
| 总体精度/% | 79.67 | 81.20 | 95.58 | 92.55 | 96.46 | 98.28 | ||
| 平均精度/% | 79.22 | 80.66 | 91.91 | 91.49 | 97.48 | 98.51 | ||
| Kappa系数/% | 76.68 | 78.55 | 94.97 | 89.31 | 95.97 | 98.05 | ||
Pavia University数据集实验采用非平衡训练集(各类训练样本数量相同)检验各方法的分类性能, 从各类地物中随机选取100个样本作为训练样本, 剩余样本为测试样本。表 2为实验中各方法对应的各类地物分类精度以及各方法总体精度、平均精度和Kappa系数。由表 2可知, 本文提出的GF-LFDA-SVM方法的分类结果总体精度、平均精度和Kappa系数分别为99.45%、99.35%和99.27%, 相比SP-SVM、LFDA-SVM、MP-SVM、Gabor-LFDA-SVM和GF-SVM方法的分类结果均有所提高, 总体精度分别提高了16.40%、11.82%、2.62%、7.39%和1.50%, 平均精度分别提高了18.79%、17.27%、3.48%、9.87%和1.92%, Kappa系数分别提高了21.15%、15.51%、3.47%、9.71%、和2.00%。GF-LFDA-SVM方法在所有类别都获得了最佳地物分类精度。图 6给出了随机一次的分类结果。
| 类别 | 训练样本数 | 测试样本数 | 分类精度/% | |||||
| SP-SVM | LFDA-SVM | MP-SVM | Gabor-LFDA-SVM | GF-SVM | GF-LFDA-SVM | |||
| 沥青路面 | 100 | 6531 | 97.08 | 89.61 | 97.82 | 91.06 | 97.78 | 98.44 |
| 草地 | 100 | 18 549 | 94.01 | 97.72 | 99.98 | 98.78 | 99.53 | 99.98 |
| 砾石 | 100 | 1 999 | 67.26 | 79.71 | 91.69 | 79.78 | 92.07 | 98.94 |
| 树 | 100 | 2 964 | 57.88 | 52.95 | 96.41 | 85.48 | 95.10 | 99.29 |
| 金属板 | 100 | 1 245 | 98.89 | 90.31 | 99.75 | 99.92 | 100.00 | 100.00 |
| 裸土 | 100 | 4 029 | 74.14 | 85.49 | 87.58 | 81.35 | 96.48 | 100.00 |
| 柏油路面 | 100 | 1 230 | 51.72 | 87.69 | 99.25 | 79.20 | 99.83 | 100.00 |
| 砖块 | 100 | 3 582 | 84.10 | 89.56 | 96.01 | 94.44 | 96.19 | 97.88 |
| 阴影 | 100 | 847 | 100.00 | 65.71 | 94.37 | 95.32 | 99.87 | 100.00 |
| 总体精度/% | 83.05 | 87.63 | 96.83 | 92.06 | 97.95 | 99.45 | ||
| 平均精度/% | 80.56 | 82.08 | 95.87 | 89.48 | 97.43 | 99.35 | ||
| Kappa系数/% | 78.12 | 83.76 | 95.80 | 89.56 | 97.27 | 99.27 | ||
从两组实验结果和分类结果图中可以看出:
1) LFDA-SVM方法的分类结果比SP-SVM方法有所提高(图 5a、b, 图 6a、b), 说明LFDA能够提取有利于分类的特征, 从而提高了分类效果; 但LFDA-SVM方法特征提取时仅利用高光谱遥感影像数据的光谱信息, 提升分类结果有限。
2) Gabor-LFDA-SVM方法特征提取时引入Gabor空间特征, 分类结果有明显提升(图 5d、图 6d), 说明空间特征可以作为光谱特征的一种互补, 提高分类结果。
3) MP-SVM、Gabor-LFDA-SVM和GF-SVM 3种融合空间特征方法的比较中, GF-SVM的分类结果最好(图 5e、图 6e), 说明GF在平滑的同时考虑了地物的边缘信息, 能够更好地提取出影像的空间特征。
4) GF-LFDA-SVM方法(图 5f、图 6f)的分类结果比GF-SVM(图 5e、图 6e)好, 说明GF-LFDA-SVM方法能够针对高光谱数据多模态的特点, 在引入影像空间特征的同时, 考虑了像素的局部信息, 改善了分类结果。
5) 本实验在训练方法模型时, 出现训练样本为2、3和5等小样本现象, 说明GF-LFDA-SVM方法能够较好地处理高光谱遥感影像分类时小样本学习问题。
6) 由图 5和图 6可以看出:SP-SVM和LFDA-SVM方法由于仅利用了光谱特征, 分类结果图中出现严重的“椒盐现象”; MP-SVM和Gabor-LFDA-SVM方法结合了影像的空间特征, 分类结果有明显的提升, 但在地物边缘处有较多的错分结果; GF-SVM和GF-LFDA-SVM方法的分类结果图中地物的边界较清晰, 说明引导滤波可以在实现地物平滑的同时较好保留地物的边缘信息; GF-LFDA-SVM方法在引导滤波提取的空间特征基础上利用像素间局部信息, 得到有利于分类的嵌入特征, 较好地反映出地物的真实分布情况。
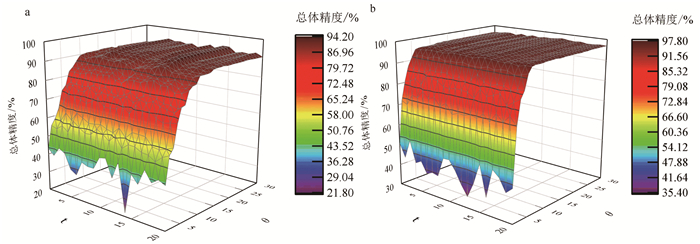
3.3 影像因素分析影响本文方法的参数包括LFDA嵌入的维数θ、邻域数目t和引导滤波器的窗口半径r。本文通过实验分析不同的参数取值对分类结果的影响, 从中选择最佳参数。从两幅数据集的每类地物样本中随机选取100个样本(地物样本总数量不足100时, 选取一半)作为训练样本, 剩余样本作为测试样本。图 7为r=2时不同θ和t对分类精度的影响。
|
| a. Indian Pines数据; b. Pavia University数据。 图 7 GF-LFDA-SVM在不同θ和t下总体分类精度 Fig. 7 Overall classification accuracy of GF-LFDA-SVM under different θ and t |
|
|
对于Indian Pines数据集而言, 当θ和t分别取16和14时, 分类精度最高, 为94.16%;随着θ的增加, 分类精度不断提高, 并逐渐达到最高值, 之后不再提升(图 7a)。这是因为随着嵌入特征维度提高, 其包含的鉴别信息越来越丰富, 分类精度也相应提高, 但当有足够的嵌入信息用于分类时, 特征维度的增加对分类精度的提高作用也是有限的。当t取值不同时, 分类精度出现了起伏变化, 但差异不太明显(图 7a)。对于Pavia University数据集而言, 当θ和t分别取30和13时, 分类精度最高, 为97.74%。
图 8为当θ和t为如图 7所示的最优值时, 不同r对分类精度的影响。由图 8可知:对于Indian Pines数据集而言, 当r=2时分类精度最高, 为94.16%;对于Pavia University数据集而言, 当r=8时分类精度最高, 为99.45%。

|
| 图 8 GF-LFDA-SVM在不同r下的总体分类精度 Fig. 8 Overall classification accuracy of GF-LFDA-SVM under different r |
|
|
1) 针对高光谱遥感影像高分辨率、高维数和数据多模态等特点, 本文提出一种引导滤波联合局部判别嵌入的高光谱影像分类方法(GF-LFDA-SVM), 实验结果表明, GF-LFDA-SVM方法与仅用光谱特征分类方法(SP-SVM和LFDA-SVM)和空谱特征结合分类方法(MP-SVM、Gabor-LFDA-SVM和GF-SVM)相比, 总体精度、平均精度和Kappa系数都有较大幅度的提高。
2) GF-LFDA-SVM方法利用引导滤波提取影像的空间特征, 能够较好地描述地物的结构和边缘信息; 进行空间特征提取的同时顾及了像素间局部关系, 提取出较有效的空-谱特征, 提高了分类精度。
当然, 本文方法仍有待改善之处。例如, 方法参数选择问题, 本文仅在固定区域内选取分类结果最优的参数。如何实现自适应参数, 以提升方法的适用性将作为下一步研究工作的重点。
| [1] |
童庆禧, 张兵, 张立福. 中国高光谱遥感的前沿进展[J]. 遥感学报, 2016, 20(5): 689-707. Tong Qingxi, Zhang Bing, Zhang Lifu. Current Progress of Hyperspectral Remote Sensing in China[J]. Journal of Remote Sensing, 2016, 20(5): 689-707. |
| [2] |
Imani M. Manifold Structure Preservative for Hyperspectral Target Detection[J]. Advances in Space Research, 2018, 61(10): 2510-2520. DOI:10.1016/j.asr.2018.02.027 |
| [3] |
杜培军, 夏俊士, 薛朝辉, 等. 高光谱遥感影像分类研究进展[J]. 遥感学报, 2016, 20(2): 236-256. Du Peijun, Xia Junshi, Xue Zhaohui, et al. Review of Hyperspectral Remote Sensing Image Classification[J]. Journal of Remote Sensing, 2016, 20(2): 236-256. |
| [4] |
Corson M R, Lucke R L, Davis C O, et al. The Hyperspectral Imager for the Coastal Ocean (HICOTM) Environmental Littoral Imaging from the International Space Station[J]. IEEE International Geoscience & Remote Sensing Symposium, 2010, 4(6): 3752-3755. |
| [5] |
蒋夕平, 吴凤凰, 蒋昱, 等. 基于FastICA算法的高光谱矿物丰度反演高光谱矿物填图应用[J]. 吉林大学学报(地球科学版), 2013, 43(5): 1681-1686. Jiang Xiping, Wu Fenghuang, Jiang Yu, et al. Hyper-Spectral Mineral Abundance Inversion Based on FastICA Algorithm[J]. Journal of Jilin University (Earth Science Edition), 2013, 43(5): 1681-1686. |
| [6] |
Xie Weiying, Li Yunsong, Zhou Weiping. Feature Extraction of Hyperspectral Images with a Matting Model[J]. International Journal of Remote Sensing, 2018, 39(5): 1510-1527. DOI:10.1080/01431161.2017.1407049 |
| [7] |
叶涛, 韦阿娟, 黄志, 等. 基于主成分分析法与Bayes判别法组合应用的火山岩岩性定量识别:以渤海海域中生界为例[J]. 吉林大学学报(地球科学版), 2019, 49(3): 873-880. Ye Tao, Wei Ajuan, Huang Zhi, et al. Quantitative Identification of Volcanic Lithology Based on Comprehensive Principal Component Analysis and Bayes Discriminant Method:A Case Study of Mesozoic in Bohai Bay[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(3): 873-880. |
| [8] |
Bandos T V, Bruzzone L, Camps-Valls G. Classification of Hyperspectral Images with Regularized Linear Discriminant Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2009, 47(3): 862-873. DOI:10.1109/TGRS.2008.2005729 |
| [9] |
He Xiaofei, Niyogi P. Locality Preserving Projections[M]. Cambridge: MIT Press, 2003.
|
| [10] |
Sugiyama M. Dimensionality Reduction of Multimodal Labeled Data by Local Fisher Discriminant Analysis[J]. Journal of Machine Learning Research, 2007, 8(1): 1027-1061. |
| [11] |
Wei L, Prasad S, Fowler J E, et al. Locality-Preserving Dimensionality Reduction and Classification for Hyperspectral Image Analysis[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(4): 1185-1198. DOI:10.1109/TGRS.2011.2165957 |
| [12] |
黄鸿, 郑新磊. 高光谱影像空-谱协同嵌入的地物分类算法[J]. 测绘学报, 2016, 45(8): 964-972. Huang Hong, Zheng Xinlei. Hyperspectral Image Land Cover Classification Algorithm Based on Spatial-Spectral Coordination Embedding[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(8): 964-972. |
| [13] |
王俊淑, 江南, 张国明, 等. 融合光谱-空间信息的高光谱遥感影像增量分类算法[J]. 测绘学报, 2015, 44(9): 1003-1013. Wang Junshu, Jiang Nan, Zhang Guoming, et al. Incremental Classification Algorithm of Hyperspectral Remote Sensing Images Based on Spectral-Spatial Information[J]. Acta Geodaetica et Cartographica Sinica, 2015, 44(9): 1003-1013. |
| [14] |
Mirzapour F, Ghassemian H. Improving Hyperspectral Image Classification by Combining Spectral, Texture, and Shape Features[J]. International Journal of Remote Sensing, 2015, 36(4): 1070-1096. |
| [15] |
叶珍, 白璘, 粘永健. 基于Gabor特征与局部保护降维的高光谱图像分类算法[J]. 光学学报, 2016, 36(10): 512-521. Ye Zhen, Bai Lin, Nian Yongjian. Hyperspectral Image Classification Algorithm Based on Gabor Feature and Locality-Preserving Dimensionality Reduction[J]. Acta Optica Sinica, 2016, 36(10): 512-521. |
| [16] |
黄鸿, 郑新磊, 罗甫林. 基于Gabor特征与局部保护降维的高光谱图像分类算法[J]. 光子学报, 2016, 45(10): 152-160. Huang Hong, Zheng Xinlei, Luo Fulin. Hyperspectral Image Classification with Combination of Weighted Mean Filter and Manifold Reconstruction Preserving Embedding[J]. Acta Photonica Sinica, 2016, 45(10): 152-160. |
| [17] |
He K, Sun J, Tang X. Guided Image Filtering[J]. IEEE Transactions on Software Engineering, 2013, 35(6): 1397-1409. |
| [18] |
Kumar P S, Supratim G, Sahu P K. Curvelet-Based Multiscale Denoising Using Non-Local Means & Guided Image Filter[J]. IET Image Processing, 2018, 12(6): 909-918. |
| [19] |
杨艳春, 李娇, 党建武, 等. 基于引导滤波与改进PCNN的多聚焦图像融合算法[J]. 光学学报, 2018, 38(5): 86-95. Yang Yanchun, Li Jiao, Dang Jianwu, et al. Multi-Focus Image Fusion Based on Guided Filtering and Improved PCNN[J]. Acta Optica Sinica, 2018, 38(5): 86-95. |
| [20] |
Pal M, Foody G M. Feature Selection for Classification of Hyperspectral Data by SVM[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(5): 2297-2307. DOI:10.1109/TGRS.2009.2039484 |




