2. 黑龙江省网络化与智能控制重点实验室, 黑龙江 大庆 163318;
3. 东北石油大学计算机与信息技术学院, 黑龙江 大庆 163318
2. Heilongjiang Provincial Key Laboratory of Networking and Intelligent Control, Daqing 163318, Heilongjiang, China;
3. College of Computer and Information Technology, Northeast Petroleum University, Daqing 163318, Heilongjiang, China
0 引言
微地震是地下岩石经受压形变而形成裂缝及其扩展过程的伴生现象,是震级小于三级的地震。相比高震级的天然地震,其能量弱,监测信号信噪比低[1]。微地震震源定位是微地震定位学的核心问题,震源定位技术在地震预报、工程地震、地球结构研究以及地壳应力场分析等诸多方面发挥着很大作用。震源位置的快速测定为地震灾害评估以及应急救援提供了极其关键的信息[2-3]。同时,高精度的震源位置信息对于判别发震断层、研究地震孕育以及触发过程都具有重要的意义[4]。
微地震定位技术在油气藏、矿山和地热行业也得到了长足发展,尤其非常规油气藏的开发是现下的热门趋势。由于这类油气藏具有低渗透率的特点,因此开采过程中往往需要多级压裂形成人工裂缝以促进油气的流动和采集。通过对压裂过程中诱导产生的微地震进行震源定位,能刻画出裂缝属性,评价压裂效果,为后续开采提供指示信息,使其达到经济开发水平[5-6]。因此,提高震源定位精度已成为非常规油气藏增产的主要措施之一。本文通过对国内外各类微地震震源定位方法的简要阐述,归纳总结了微地震震源定位方法的优缺点和基本原理,并对各类微地震震源定位方法的研究现状及发展趋势进行了展望。
1 微地震震源定位方法概述 1.1 基于走时的射线追踪定位方法 1.1.1 几何作图法传统几何作图法是早期应用于震源定位的主要方法,利用台站接收的走时信息和相关几何知识,通过作图形式直观获取震源位置[7],即震源轨迹交切最密集的点为震源点。该方法不需要求解目标函数的偏导或逆矩阵,算法原理简单,且稳健性强,具有观察效果直观和计算效率高等优势,可用于复杂各向异性介质中的微地震定位。
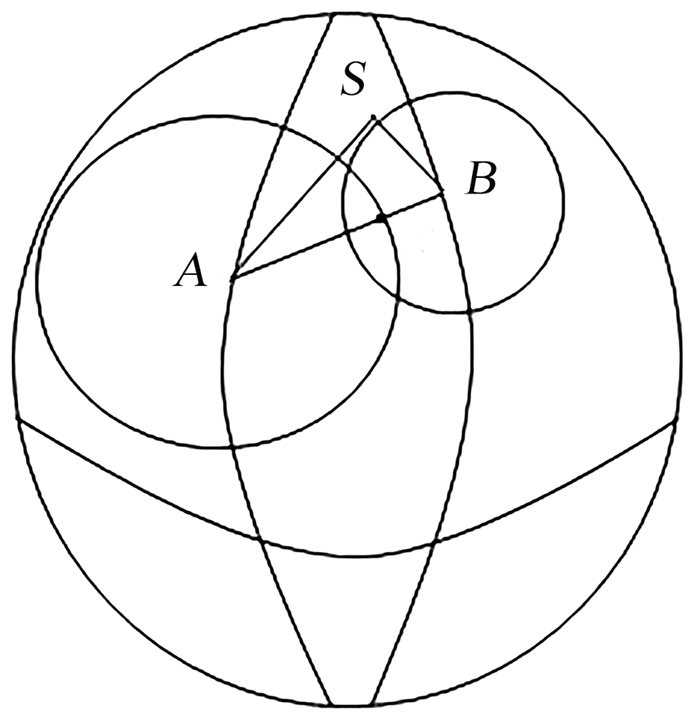
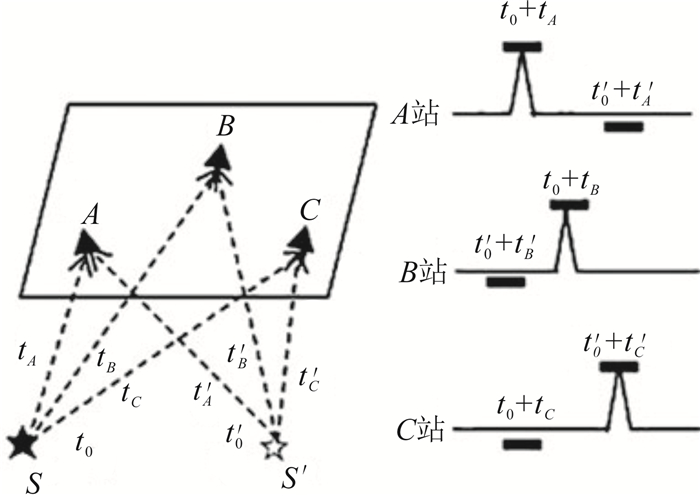
传统几何作图法中比较典型的有廉超等[8]提出的适用于近震及远震定位的球面交切法,通过3个以上台站纵波与横波的到时差计算出震中位置,可在球面上直接进行交切运算,原理如图 1所示。该方法定位结果直观,震源深度以及发震时刻对定位的影响较小; 但仅适应于均匀介质的速度模型,若地质速度模型复杂、震源位置较深,其定位精度和计算效率相对较低。
周建超等[9]提出了适应于三维复杂速度模型的交切定位法,其利用最小走时树射线追踪方法来确定震源轨迹,使用多条震源轨迹进行定位,有助于减少由随机因素导致的定位误差。毛元彤[10]提出了改进最小走时树射线追踪方法,该方法能有效提高计算效率,同时走时计算精度也得到了较大提高。如果将改进最小走时树射线追踪方法用在台网外进行微地震震源定位,则震源位置的约束效果较差; 若还存在扰动观测到时,定位结果会出现不同程度的偏移。
1.1.2 线性定位法线性定位法可分为线性绝对定位法和线性相对定位法。在线性绝对定位法中,大多数是以Geiger[11]提出的经典定位法为基础,将非线性方程线性化,再通过最小二乘法求出震源点。这类方法对初始条件的依赖性较大,若存在台站分布不合理、速度模型精度不理想的情况,则易造成定位发散或得不到定位结果的可能。在早期研究中,研究人员在Geiger法的基础上提出了多事件定位法,致力于解决用简单速度模型代替复杂地壳结构模型的误差问题,定位效率得到提高。LocSAT法[12]采用了阻尼最小二乘法,将观测方程组转化为正规方程组,然后用主元素消去法求解,最终得到震源位置。
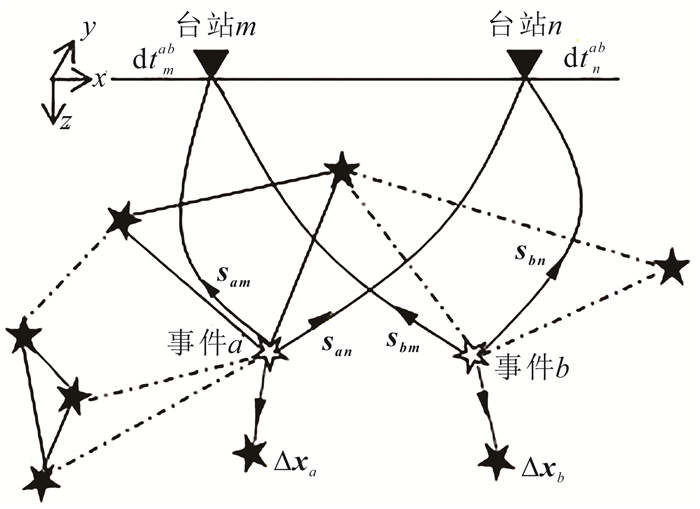
线性相对定位法利用选定的震源位置作为主事件,通过定位目标事件和主事件之间的相对信息进行运算,最终得到震源位置。该方法主要以主事件定位法和双差定位法[13-14]为代表。主事件定位法在空间跨度较大的微地震事件中应用效果较差,同时在近震定位中也不能得到较为准确的震源位置信息。为了克服主事件定位法的缺点,Waldhauser等[15]提出了双差定位法,原理如图 2所示。相比于主事件定位法,该方法具备了对初始迭代值要求低的优势,同时能有效减少由地壳结构复杂性而引起的误差。Tian等[16]在双差定位法的基础上提出了交叉双差定位法,即利用一个事件纵波到时和另一个事件横波到时之间的交叉旅行时差进行反演,能为井下微地震监测的绝对位置和相对位置提供可靠结果。
非线性定位法是一种可以规避易陷入局部极值的有效定位方法。目前使用较为广泛的非线性方法有梯度下降法、牛顿法、全局搜索法、蒙特卡洛法、模拟退火法和遗传算法等。上述定位方法又可分为两类:一类是启发式反演定位法,包括模拟退火法、单纯形搜索法、网格搜索法、匹配定位法、粒子群优化算法、遗传算法、引力搜索法等,它们均是蒙特卡洛类法的延伸;另一类是非启发式反演定位法,包括梯度下降法、牛顿法、Powell法、共轭梯度法、变尺度算法等。
1) 启发式反演定位法
模拟退火法[17]是一种在大空间寻找全局最优解的非线性反演方法,能高效准确地确定微地震的发震位置与发震时刻。为了避免函数陷入局部极值,在迭代过程中一般引入随机干扰,这在一定程度上可达到全局最优解的目的;但存在搜索效率低、计算量大和工作用时长等问题。霍凤斌[18]提出了混沌模拟退火法,其能克服模拟退火法的缺陷,显著减少了计算量,大大缩短优化时间,更为快速可靠地收敛到全局最优解。
A.F. Prugger等[19]将单纯形搜索法(SIMPLEX)应用在微地震震源定位中,这种方法无需考虑计算走时导数,计算过程简单,且能有效降低迭代发散的概率,当迭代次数趋于无穷大时,解唯一趋近真值;但单纯形搜索法在进行波速测定时采用了单向搜索,形式简单,需要对各个方向进行监测,易造成误差而陷入局部最优问题。李健等[20]对单纯形搜索法做了改进,提出了一种无需测速和反演的速度模型,将其应用于单纯形搜索法中,有效解决了局部最优问题,同时定位精度也得到了显著提高。
基于网格搜索法的微地震震源定位方法[21-22]首先将需要检测的区域划分为大小相同的网格,然后通过对每一个网格的分析计算来确定震源位置是否在网格内。该方法可引入较复杂的速度模型,定位精度较高;但网格划分的疏密程度对计算速度有很大的影响,这使得计算精度与计算效率无法平衡。王纪程[23]提出了网格逐次剖分的定位方法,相对于传统网格搜索法,其优势是可大量减少搜索次数,提高全局寻优效率,同时定位精度也得到了很大的提高;但网格逐次剖分算法也存在缺陷,在定位频率较高的微地震事件中会出现无法识别震源事件的情况,即存在高频率的地震波在定位时很容易出现网格中心点无法落入包络区的情况。王云宏[24]提出了基于直接搜索算法的微地震震源快速网格搜索定位法,该方法无需划分网格大小,在计算过程中能根据解的位置,在靠近最优解的地方增大搜索密度,在远离最优解的地方减小搜索密度,使搜索次数大大减少,在一定程度上提高了计算效率,定位精度也得到了较大提高。
Zhang等[25]提出了匹配定位法,该方法通过叠加模板事件的波形和叠加多个台站连续波形中的微弱事件信号实现定位,实现了对微弱信号的拾取,且不依赖所使用速度模型的精度,可在极差条件下实现震源定位。
粒子群优化(PSO)算法最早由Eberhart等[26]在1995年利用群体模型研究鸟群捕食的行为而提出,需初始化设定一组随机解,再通过不断迭代找到最优值。该方法已成功应用于微地震震源定位中,建模简单、实现容易、全局搜索速度快;但也存在迭代过程易发散,迭代后期收敛速度变慢和易陷入局部最优等问题。后经过不断改进,又提出了许多改进算法。1999年Clerc[27]将收缩因子法引入PSO算法,有效解决了震源位置易陷入局部最优的问题。收缩因子法在寻找最优解过程中能够有效搜索不同区域,以保证震源位置的精度和算法的收敛性。
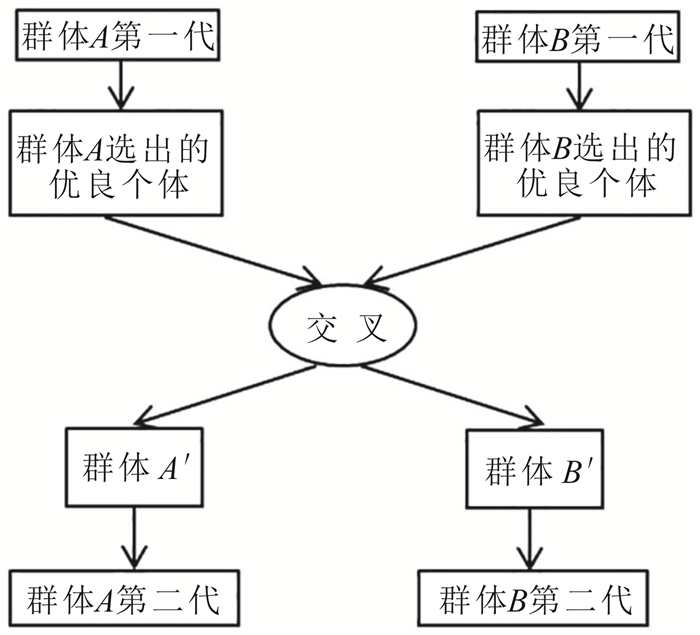
遗传算法[28-29]是借鉴生物自然选择和遗传进化机制开发出的一种面向全局优化的算法。从初始种群中选择、交叉、变异,最终实现所求解的全局优化搜索功能。该方法在迭代前期收敛速度快,到后期收敛速度变慢且易早熟而导致不能得到理想结果。针对遗传算法存在的缺陷,为提高精度及寻优效率,王泉栋等[30]在遗传算法的基础上采用格雷码对震源位置进行编码,在一定程度上提高了遗传算法的局部搜索能力。该方法采用2个群体独立进化,再将各种群中的优秀个体进行交叉运算和变异,产生的新个体能较好地提高搜索能力和定位精度。原理如图 3所示。
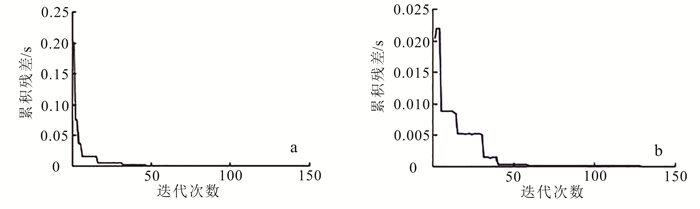
王剑锋等[31]提出了基于引力搜索法(GSA)的微地震震源定位方法,利用引力搜索法搜索微地震残差函数的极小值找到震源位置。相对于PSO算法及单纯形搜索法,该方法定位精度高、收敛速度快,大约10次就可达到稳定效果;但该方法较依赖于初始位置的选取,且在搜索过程中移动具有局限性。GSA算法、PSO算法以及SIMPLEX算法最优残差搜索过程如图 4所示。
综上所述,启发式反演定位法最大的优点是不完全依赖于初始值,编程容易实现且无需求解目标函数的导数,在反演过程中具有直接反演的特点且不易陷入局部极值;但在求取最优解的过程中搜索效率较低,工作量大且耗时。经过改进,寻优效率大大提高,抗噪性较好;但对速度模型比较敏感。总而言之,启发式反演法理论背景简单且方法成熟,能较好地应用于各种情况下的微地震震源定位。
2) 非启发式反演定位法
梯度下降法是目前地球物理反演中比较常用的方法之一,收敛速度快,对于局部而言是最快速的下降方向[32-33];但缺点是搜索过程中收敛速度慢且对初始条件扰动非常敏感,一旦初始值设置不理想,在求解方程时很容易陷入局部极值。
牛顿法[34]在梯度下降法的基础上对搜索方向加以改进,利用搜索方向提供的信息,快速准确地指向最优位置。牛顿法迭代次数少,可很快到达极值点,若初始点选取合理,算法很快就会收敛;但要计算二阶偏导数及其逆矩阵,计算量较大,故收敛性与初始点的选取有很大关系。
Powell法[35]是一种直接搜索目标函数极小值的有效方法,无需对目标函数求导。在计算震源位置时收敛速度快,可靠性好,在地震台网快速自动预报中应用广泛;但它依赖于初始值的选择,在搜索过程中易陷入局部极值,导致无法得到最优解。
共轭梯度法[36]进行震源反演,需要通过数值仿真与实际资料对比,反演效果基本吻合且提高了效率,具有快速、准确、适应复杂构造模型的优点。
崔仁胜等[37]在拟牛顿法的基础上改进算法,将变尺度算法(DFP)应用在小尺度区域微震事件中,其在速度模型精度较高的微地震事件中定位效果突出,同时初至精度对其影响较小;但受速度模型和到时拾取的影响较大。若能减少人为读取的到时误差,并采用较精确的速度模型,可改善定位结果精度、保证定位结果的可靠性。
综上所述,非启发式反演定位法是梯度类算法的延伸,其优势是在求解目标函数的极值时,能快速沿梯度方向最快到达极值点,同时收敛速度较快,能有效提高搜索效率;但该类方法在求解最优解时容易陷入局部极值,同时对速度模型的精度要求较高,对初至也具有较强的依赖性。
1.1.4 混合优化定位法由于单纯采用一种类型的震源定位算法很难满足实际工程应用中对定位精度和效率的要求,经过研究分析,采用两种或多种反演算法的组合方式,可规避单一算法的缺陷,在一定程度上提高反演的精度和效率。
Cary等[38]将蒙特卡洛法与梯度下降法结合起来应用在微地震震源定位中,其先用蒙特卡洛法搜索最合适的初始点,这样可使该初始点比较靠近全局最优值点,然后应用梯度下降法找到全局最优解,极大地提高了计算效率。
王纪程等[39]采用模拟退火法与网格逐次剖分法相联合的方式进行微地震震源定位。网格逐次剖分算法具备不需要对初至信号进行拾取的特点,且可用于复杂速度模型,在低信噪比等极端情况下仍能适用;但在处理高频信号时易出现定位失常的问题。联合算法首先采用模拟退火法在三维目标区域内搜寻能量聚焦较高的圆形区域,然后再利用网格逐次剖分法在区域内寻找能量聚焦的最大值点,有效地提高了微地震震源定位的可靠性与计算效率,从而进一步提高定位精度。
林峰等[40]将线性定位法与Geiger法相结合进行震源定位。线性定位法在计算中速度快且无需反复迭代,如果数据的准确性不高,则定位精度误差较大;而Geiger定位法在求解中出现奇异矩阵,这使得定位误差较大。联合定位算法首先应用线性定位法进行初步定位,再以线性定位的初值作为Geiger定位法的迭代初值进一步求解定位坐标;这样可以利用两者的优势,规避各自的缺点,使定位精度得到较大提高,迭代初值足够接近真实值。
王心强[41]提出将单纯形搜索法与差分进化法相结合的方式进行震源定位。该方法在搜索过程中,以差分进化法的搜索优化结果作为单纯形搜索法的若干单纯形顶点,利用单纯形搜索法的结果指导差分进化法的搜索方向,达到了避免陷于局部最优值的效果,在很大程度上提高了反演效率。
张院生等[42]将模拟退火法和粒子群优化算法相结合寻找震源点。其中:模拟退火法具有概率突跳特性,不易陷入局部最小值,表现结果稳定,搜索效率较高;而粒子群优化算法搜索速度快、效率高;将二者相结合,可达到定位精度高、搜索时间短和计算效率高等效果。
盛冠群等[43]提出了微地震粒子群差分进化定位(DEPSO)算法。粒子群优化算法的全局搜索速度快,将它与差分进化法相结合,针对有扰动初至时间的情况具有更高的精度且震源定位的发散性较传统粒子群定位得到了改善。传统的粒子群优化算法在进行定位时,对速度模型的扰动比较敏感且易发散,使定位结果陷入局部最优;而DEPSO算法在针对初至扰动时仍能有效收敛,使定位精度得到提高(图 5);但该组合优化算法仍有不足之处,采集信号的信噪比对震源定位的精度有较大影响,同时速度模型的精确程度也制约着定位结果。因此,如何进一步改进DEPSO算法,是我们努力的方向。
综上所述,混合优化算法有诸多优势,能够规避单一算法存在的缺陷,一方面具备计算效率高、算法理论成熟、可靠性以及搜索能力强等优势,另一方面可以做到局部优化算法和全局随机性优化算法相结合,不易陷入局部极值,更易于找到反演的全局最优解,极大地减少了目标函数的计算量。混合优化算法虽优势明显,但仍存在局限性,当微地震数据的信噪比低、初至误差拾取大、速度模型精度不高时,其优势就不太明显。
1.2 基于波形的偏移定位方法基于波形的偏移定位方法是现阶段兴起的一类新型震源定位方法。该类方法依据不同的延拓和成像方式分为两类,一类为基于振幅叠加的正演定位法,另一类为基于逆时偏移的定位法。它们都无需进行初至拾取,但对速度模型精度要求较高。
1.2.1 基于振幅叠加的正演定位法Rentsch等[44]提出了使用高斯光束偏移三分量数据的方法。该方法仅通过对检测到的震源所在位置周边的时间差进行初步拾取,而不依赖于初至拾取的精度,并且比标准定位过程中对拾取精度的要求低了很多。研究人员将20%~30%白噪声加入实际微地震数据中[44],该方法仍能有效记录震级小于0级的事件。
Gajeski等[45-46]提出了一种基于逆向建模的定位方法。该方法无需对事件进行任何初至拾取,仅对微地震信号进行偏移叠加,能大幅度减少对地震波初至拾取带来的影响,且能较好地提高震源精度;但该方法对速度模型精度要求较高,这在一定程度上影响着定位精度的准确性。
吴建光等[47]采用基于震幅叠加能量聚焦的微地震震源定位方法,首先全面扫描目标区域,然后依据扫描结果判定震幅叠加后的能量聚焦情况,判断是否有微地震事件发生,最后依次对震源位置与发震时刻进行判定。该方法对微地震信号的质量要求较低,且对噪声具有较强的容忍力。
何勇等[48]在传统震源扫描法的基础上加以改进,将传统方法中只对震源所在位置及发震时刻两者的扫描改进为对震源位置、发震时刻及震源机制三者联合的扫描方式,不但提高了抗噪性和震源定位的精度,而且这种高抗噪性和分辨震源的能力在一定程度上有效避免了人工判断带来的困难与误差。
Kao等[49-50]提出了一种震源扫描法,它能避免对微震走时的识别和拾取,且无需预先知道断层的产状和规模,只需判定振幅和到时等波形数据是否存在震源。其原理如图 6所示。该方法具有一定的稳定性,可用于复杂的实际地震定位;但在利用地面低信噪比微地震资料进行定位时,如增强微震信号,也会相应增加噪声,导致定位误差较大。
综上所述,基于振幅叠加的正演定位法无需对初至进行拾取,算法较为简单,也无需考虑初至拾取的精度,适用于速度模型不准或震相数据不清晰的情况;其相对宽松的定位条件可在很大程度上规避定位效率低的问题,同时在多道振幅叠加后可加强微弱信号,也可在低信噪比条件下得到较好的定位效果。但在扫描过程中存在工作量大、费时的缺点;若速度模型精度较低,则搜索效率更低。
1.2.2 基于逆时偏移的定位法基于逆时偏移的定位法无需拾取震相到时,它通过微地震波场按时间反转和特定震源成像条件,获得震源位置和发震时刻。由于逆时偏移法具备了无需拾取微震走时的特点,所以能更好地适应于低信噪比条件下的微地震数据。
Sava[51]采用稀疏采样数据进行微地震监测,该方法与常规成像条件不同,无需重建波场,利用Wigner函数变换波场。这种成像条件对稀疏数据的采样和随机速度变化引起的噪声起到有效压制作用,同时削弱了稀疏观测以及地下介质速度不准带来的成像假象,提高了成像精度。
许力生等[52]在微地震震源定位方法中采用了互相关技术,该方法用直达波信号构建包络信号,有效提高了观测到时的准确性;同时采用波形聚束方法,有效克服了用最小二乘法求解时出现奇异解的问题,且有高抗噪性。
Li等[53]应用加权弹性波干涉成像法进行定位,利用多波场和多分量微地震数据求解震源,能较好地处理速度扰动、低信噪比条件下的微地震数据,在速度模型存在误差时,仍能保持较高的精度。
Nakata等[54]将互相关成像条件应用在微地震震源定位中,有效地抑制了旁瓣,使其从4D降到3D。互相关成像条件增强了信号且抑制了噪声,使震源成像点的分辨率得到了很大提高。李青峰等[55]提出了分组互相关成像条件,实现自相关与互相关成像条件的联合,可获得空间分辨率很高的震源成像结果。该方法可在低信噪比情况下求得震源位置,具有较高的空间分辨率。
Wu等[56]将反褶积干涉测量法与干涉互相关偏移法相结合应用在微地震震源定位中,具有更高的空间分辨率和较小的定位误差,特别是在有速度模型误差的情况下,提高了震源定位的鲁棒性。
徐克彬等[57]将Levenberg-Mar-Quardt(L-M)法应用在微地震震源定位算法中,以振幅叠加网格搜索法为基础,首先将粗网格进行划分,然后在能量叠加较高的局部区域采用L-M法逐次迭代寻找能量叠加的最大值点(震源点)。这种方法有效提高了计算效率,在定位精度上比单纯的网格搜索法有了很大提高。
综上所述,由于基于逆时偏移的定位法在获取震源位置时使用了所有波场信息(波形、振幅等),同时又不用提取震相到时,所以更加适合地面监测信噪比较低的情况。波场逆时延拓和成像条件是微震逆时成像的关键,在计算过程中为了压制噪声,需要记录更多的地震道数,使得计算量增大,耗时耗力。若存在记录的道数异常,则无法有效定位。
1.3 基于神经网络的微地震震源定位方法卷积神经网络通过搭建数学模型来仿照生物视觉的感受过程。它属于一种深度学习算法,是多层感知器的一个推广变种。其中BP神经网络属于在导师指导下不断学习增长知识的一种网络类型,目前在微地震领域应用较广。
李学政等[58]将BP神经网络应用在震源定位算法中,网络采用梯度下降法进行学习,使权值沿着误差函数方向不断修正,最终得到较为准确的震源位置。然而,在进行网络训练过程中,随着迭代次数的增加,可能会出现不收敛的情况。因此,在学习过程中,选择合适的初始权值及神经元数目非常重要。
Maren Bose等[59]提出了基于神经网络的震源定位方法,基于一个输入层、一个隐藏层和一个输出层组成的两层前馈神经网络进行震源定位。以各台站的到时差作为神经网络的输入,以震源位置坐标作为输出,采用震例样本训练网络,在经过多次迭代、寻优后,最终找到震源。此方法以纵波到达不同传感器的时间差信息来估计震源位置,有效减少了定位误差,定位精度也相对准确。
2 多方法多参数信息融合技术多信息融合技术是现代信息技术与多学科交叉、综合、延拓而产生的一种新型科学研究方法,其将传感器采集到的信息源加以集成,通过给定的要求,按照一定的标准进行综合集成。在集成的综合信息中,寻找出所需要的数据,再对这些集成的数据进行决策和评估,最终完成信息处理[60]。多信息融合技术在国内外各个领域都有很好的发展前景。美国在军用系统大力发展多信息融合技术。国内虽起步较晚,但已成为现下热门研究方向。该技术在军事、环境监测、语音识别、多传感器跟踪与定位、智能机器人等领域得到了长足的发展[61]。
在油气藏方面,通过勘探技术获得地震波(纵波、横波、面波、声波),再利用多方法多参数信息融合技术对各种不同的波形数据进行分析整合从而获得所需要的信息。李绍红等[62]应用多信息融合技术,在不同位置、不同时间及不同空间将由传感器接收到的到时信息加以融合,获取所需要的信息进行综合评估,获得震源解。该方法采用6个独立的检波器进行数据采集,依次实现定位功能。考虑到速度模型的复杂程度,从信息融合角度出发,采用随机模拟方法产出大量波速,再利用粗大误差判别准则进行震源定位。这在一定程度上开拓了多信息融合进行震源定位的先河。虽然多信息融合技术在微地震领域的应用还不广泛,但无可否认该方法所具有的优势以及在微地震领域所发挥出的作用。相信在不久的将来,多信息融合技术一定能够在微地震定位领域大放异彩。
3 结论与展望1) 微地震定位方法是微地震监测技术的关键,国内外学者提出了多种定位方法,理论上较为成熟;然而针对不同的工程背景、地质条件以及人为因素,如何科学合理选择定位方法,较准确地确定震源位置,是我们努力的方向。
2) 传统微地震定位方法的关键之处在于求解目标函数的极小值。根据不同的地质情况,构建目标函数的方法不尽相同。在定位过程中造成误差的原因有很多,如人为因素、仪器自身误差、速度模型精度、台网布置以及震相到时拾取误差等等。而就目前的研究发现,单一的某种定位方法往往不能得到理想的定位结果。采用多种定位方式相结合,可使定位精度得到极大提高,定位结果也更加稳定。在地球物理领域采用的多信息融合技术不但对震源定位意义重大,同时能够较好地还原地震波在介质中的传播路径,实现射线追踪。因此,大力发展多信息融合技术,能够给微震定位技术带来更大的发展空间。
3) 随着非常规油气田开采已成为主流趋势,如何实现工程效益最大化,对微地震定位提出了更高要求。就定位方法中,抗噪性能不够完善、速度模型精度差、计算效率低等问题依然是影响定位精度的主要原因。在今后微地震定位研究中,如何突破这些困境,实现快速、准确的自动微地震定位以及高质量的震相识别技术,仍是我们不懈奋斗的目标。
| [1] |
Cheng Y, Jiang F, Zhang X, et al. C-Shaped Strata Spatial Structure and Stress Field Inlongwall Face Monitored by Microseismic Monitoring[J]. Chinese Journal of Rock Mechanics & Engineering, 2007, 26(1): 102-107. |
| [2] |
Grigoli F, Cesca S, Amoroso O, et al. Automated Seismic Event Location by Waveform Coherence Analysis[J]. Geophysical Journal International, 2014, 196(3): 1742-1753. |
| [3] |
Maxwell S, Deere J. An Introduction to This Special Section:Microseismic[J]. The Leading Edge, 2010, 29(3): 227-235. |
| [4] |
Feng G L, Feng X T, Chen B R, et al. A Microseismic Method for Dynamic Warning of Rockburst Development Processes in Tunnels[J]. Rock Mechanics & Rock Engineering, 2015, 48(5): 2061-2076. |
| [5] |
刘建中, 王春耘, 刘继民, 等. 用微地震法监测油田生产动态[J]. 石油勘探与开发, 2004, 31(2): 71-73. Liu Jianzhong, Wang Chunyun, Liu Jimin, et al. Using Microseismic Method to Monitor Oil Field Production Performance[J]. Petroleum Exploration and Development, 2004, 31(2): 71-73. |
| [6] |
刘高峰, 翁红波, 宋志敏, 等. 煤层气井水力压裂效果评价与消突时间预测研究[J]. 河南理工大学学报(自然科学版), 2015, 34(6): 753-758. Liu Gaofeng, Weng Hongbo, Song Zhimin, et al. Evaluation of Hydraulic Fracturing Effect and Prediction of Outburst Elimination Time for CBM Wells[J]. Journal of Henan University of Technology (Natural Science Edition), 2015, 34(6): 753-758. |
| [7] |
Myers S C, Johannesson G, Hanley W. A Bayesian Hierarchical Method for Multiple-Event Seismic Location[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 171(3): 1049-1063. |
| [8] |
廉超, 李胜乐, 董曼, 等. 球面交切法地震定位[J]. 大地测量与地球动力学, 2006, 26(2): 99-103. Lian Chao, Li Shengle, Dong Man, et al. Seismic Location by Spherical Intersection Method[J]. Geodesy and Geodynamics, 2006, 26(2): 99-103. |
| [9] |
周建超, 赵爱华. 三维复杂速度模型的交切法地震定位[J]. 地球物理学报, 2012, 55(10): 3347-3354. Zhou Jianchao, Zhao Aihua. Intersection Seismic Location of Three-Dimensional Complex Velocity Model[J]. Journal of Geophysics, 2012, 55(10): 3347-3354. |
| [10] |
毛元彤.三维各向异性介质地震波走时计算与地震定位的方法研究[D].北京: 中国地震局物理研究所, 2019. Mao Yuantong. Research on Travel Time Calculation and Seismic Location Methods of Three-Dimensional Anisotropic Media[D]. Beijing: Institute of Physics China Seismological Bureau, 2019. |
| [11] |
Geiger L. Probability Method for the Determination of Earthquake Epicenters from Arrival Time Only[J]. Bull St Louis Univ, 1912, 8(1): 60-71. |
| [12] |
张宇, 康建红, 张晨侠, 等. 采用LOCSAT和HYPOSAT方法对东北深源地震定位分析[J]. 地震地磁观测与研究, 2014, 34(3/4): 96-99. Zhang Yu, Kang Jianhong, Zhang Chenxia, et al. Location and Analysis of Deep-Focus Earthquakes in Northeast China Using LOCSAT and HYPOSAT Methods[J]. Seismic and Geomagnetic Observation and Research, 2014, 34(3/4): 96-99. |
| [13] |
Zhang H, Thurber C. Double-Difference Tomography:The Method and Its Application to the Hayward Fault, California[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 1875-1889. |
| [14] |
Guo H, Zhang H. Development of Double-Pair Double Difference Earthquake Location Algorithm for Improving Earthquake Locations[J]. Geophysical Journal International, 2017, 208(1): 333-348. |
| [15] |
Waldhauser F, Ellsworth W. A Double-Difference Earthquake Location Algorithm:Method and Application to the Northern Hayward Fault[J]. Bulletin of the Seismological Society of America, 2000, 90(6): 1353-1368. |
| [16] |
Tian X, Zhang W, Zhang J. Cross Double-Difference Inversion for Simultaneous Velocity Model Update and Microseismic Event Location[J]. Geophysical Prospecting, 2017, 65(5): 259-273. |
| [17] |
Gauthier O, Virieux J, Tarantola A. Two-Dimensional Nonlinear Inversion of Seismic Waveforms:Numerical Results[J]. Geophysics, 1986, 51(7): 1387-1403. |
| [18] |
霍凤斌.混沌模拟退火算法在储层参数反演中的应用[D].成都: 成都理工大学, 2007. Huo Fengbin. Application of Chaotic Simulated Annealing Algorithms in Inversion of Reservoir Parameters[D]. Chengdu: Chengdu University of Technology, 2007. |
| [19] |
Prugger A F, Gendzwill D. Comment on "Microearthquake Location:A Nonlinear Approach that Makes Use of a Simplex Stepping Procedure"[J]. Bulletin of the Seismological Society of America, 1995(1): 375-377. |
| [20] |
李健, 高永涛, 谢玉玲, 等. 基于无需测速的单纯形法微地震定位改进研究[J]. 岩石力学与工程学报, 2014, 33(7): 1336-1346. Li Jian, Gao Yongtao, Xie Yuling, et al. Improvement of Microseismic Location Based on Simplex Method Without Velocity Measurement[J]. Journal of Rock Mechanics and Engineering, 2014, 33(7): 1336-1346. |
| [21] |
Liao Y C, Kao H, Rosenberger A, et al. Delineating Complex Spatiotemporal Distribution of Earthquake Aftershocks:An Improved Source-Scanning Algorithm[J]. Geophysical Journal International, 2012, 189(3): 1753-1770. |
| [22] |
Lu R, Lazaratos S, Wang K, et al. High-Resolution Elastic FWI for Reservoir Characterization[C]//EAGE Technical Program Expanded Abstracts. London: SEG, 2013: 10-12.
|
| [23] |
王纪程.基于网格剖分的微地震地面监测定位技术研究[D].长春: 吉林大学, 2018. Wang Jicheng. Research on Micro-Seismic Ground Monitoring and Location Technology Based on Grid Division[D]. Changchun: Jilin University, 2018. |
| [24] |
王云宏. 基于DIRECT算法的微震震源快速网格搜索定位方法研究[J]. 地球物理学进展, 2016, 31(4): 1700-1708. Wang Yunhong. Research on Fast Grid Search and Location Method of Microseismic Source Based on DIRECT Algorithm[J]. Progress in Geophysics, 2016, 31(4): 1700-1708. |
| [25] |
Zhang M, Wen L. An Effective Method for Small Event Detection:Match and Locate[J]. Geophysical Journal International, 2015, 200(3): 1523-1537. |
| [26] |
Eberhart R, Kennedy J. Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Piscataway: [s. n.], 1995: 1942-1948.
|
| [27] |
Clerc M. The Swarm and the Queen: Towards a Deterministic and Adaptive Particle Swarm Optimization[C]//Congress on Evolutionary Computation. Piscataway: [s. n.], 2002: 1951-1957.
|
| [28] |
Zurada J M, Marks I R J, Robinson C J, et al. Computational Intelligence Imitating Life[M]. New York: IEEE Press, 1994: 213-222.
|
| [29] |
陈淑珍, 谢秋洪, 刘怀林. 基于遗传算法的弯曲射线成像反演[J]. 工程地球物理学报, 2004, 1(2): 141-144. Chen Shuzhen, Xie Qiuhong, Liu Huailin. Bending Ray Imaging Inversion Based on Genetic Algorithm[J]. Journal of Engineering Geophysics, 2004, 1(2): 141-144. |
| [30] |
王泉栋, 李国和, 吴卫江, 等. 多种群遗传算法在微震震源定位中的应用[J]. 计算机测量与控制, 2015, 23(4): 1285-1288. Wang Quandong, Li Guohe, Wu Weijiang, et al. Application of Multi-Population Genetic Algorithms in Focal Location of Micro-Earthquakes[J]. Computer Measurement and Control, 2015, 23(4): 1285-1288. |
| [31] |
王剑锋, 李天斌, 马春驰, 等. 基于引力搜索法的隧道围岩微震定位研究[J]. 岩土力学, 2019, 40(11): 1-10. Wang Jianfeng, Li Tianbin, Ma Chunchi, et al. Microseismic Location of Tunnel Surrounding Rock Based on Gravity Search Method[J]. Geotechnical Mechanics, 2019, 40(11): 1-10. |
| [32] |
周运波.微震监测反演方法研究[D].荆州: 长江大学, 2012. Zhou Yunbo. Research on Inversion Method of Microseismic Monitoring[D]. Jingzhou: Changjiang University, 2012. |
| [33] |
Li G M, Chen J Y, Han M, et al. Accurate Microseismic Event Location Inversion Using a Gradient-Based Method[C]//The SPE Annual Technical Conference and Exhibition. Texas: [s. n.], 2012: 159187.
|
| [34] |
Thurber C H. Nonlinear Earthquake Location:Theory and Examples[J]. Bulletin of the Seismological Society of America, 1985, 75(3): 779-790. |
| [35] |
Powell M J. An Efficient Method for Finding the Minimum of a Function of Several Variables Without Using Derivatives[J]. The Computer Journal, 1963, 7(7): 155-162. |
| [36] |
宋维琪, 刘军, 陈伟, 等. 改进射线追踪算法的微震源反演[J]. 物探与化探, 2008, 32(3): 274-278. Song Weiqi, Liu Jun, Chen Wei, et al. Microseismic Source Inversion Based on Improved Ray Tracing Algorithm[J]. Geophysical and Geochemical Exploration, 2008, 32(3): 274-278. |
| [37] |
崔仁胜, 陈阳, 王洪体, 等. 基于DFP算法的小尺度微震定位方法研究[J]. 震灾防御技术, 2014, 9(增刊1): 639-647. Cui Rensheng, Chen Yang, Wang Hongti, et al. Small-Scale Microseismic Location Method Based on DFP Algorithm[J]. Earthquake Disaster Prevention Technology, 2014, 9(Sup.1): 639-647. |
| [38] |
Cary P W, Chapman C H. Automatic 1-D Waveform Inversion of Marine Seismic Refraction Data[J]. Geophysical Journal, 1988, 93(3): 527-546. |
| [39] |
王纪程, 陈祖斌, 江海宇, 等. 基于极快速模拟退火与网格逐次剖分的微地震定位算法[J]. 科学技术与工程, 2017, 17(33): 254-258. Wang Jicheng, Chen Zubin, Jiang Haiyu, et al. Microseismic Localization Algorithm Based on Extremely Fast Simulated Annealing and Grid Successive Subdivision[J]. Science and Technology and Engineering, 2017, 17(33): 254-258. |
| [40] |
林峰, 李庶林, 薛云亮, 等. 基于不同初值的微震源定位方法[J]. 岩石力学与工程学报, 2009, 29(5): 996-1002. Lin Feng, Li Shulin, Xue Yunliang, et al. Microseismic Source Location Method Based on Different Initial Values[J]. Journal of Rock Mechanics and Engineering, 2009, 29(5): 996-1002. |
| [41] |
王心强.地面微地震事件的反演定位研究[D].青岛: 中国石油大学(华东), 2012. Wang Xinqiang. Inversion and Location of Surface Microseismic Events[D]. Qingdao: China University of Petroleum (East China), 2012. |
| [42] |
张院生, 高永涛, 王喆, 等. 基于SA-PSO混合算法的微震定位研究[J]. 现代隧道技术, 2016, 53(3): 137-145. Zhang Yuansheng, Gao Yongtao, Wang Zhe, et al. Microseismic Location Research Based on SA-PSO Hybrid Algorithm[J]. Modern Tunnel Technology, 2016, 53(3): 137-145. |
| [43] |
盛冠群, 李振春, 王维波, 等. 水力压裂微地震粒子群差分进化定位算法[J]. 石油学报, 2014, 35(6): 1172-1181. Sheng Guanqun, Li Zhenchun, Wang Weibo, et al. Differential Evolutionary Particle Swarm Optimization Algorithm for Micro-Earthquake in Hydraulic Fracturing[J]. Journal of Petroleum, 2014, 35(6): 1172-1181. |
| [44] |
Rentsch S, Buske S, Lüth S, et al. Fast Location of Seismicity:A Migration-Type Aapproach with Application to Hydraulic-Fracturing Data[J]. Geophysics, 2007, 72(1): S33-S40. |
| [45] |
Gajewski D, Tessmer E. Reverse Modelling for Seismic Event Characterization[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 163(1): 276-284. |
| [46] |
Gajewski D J, Anikiev D V, Kashtan B M, et al. Localization of Seismic Events by Diffraction Stacking[J]. SEG Technical Program Expanded Abstracts, 2007, 26(1): 9355-9362. |
| [47] |
吴建光, 张平, 吕昊, 等. 基于震幅叠加的微地震事件定位在地面监测中的应用[J]. 吉林大学学报(地球科学版), 2017, 47(1): 255-264. Wu Jianguang, Zhang Ping, Lü Hao, et al. Application of Microseismic Event Location Based on Amplitude Superposition in Ground Monitoring[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(1): 255-264. |
| [48] |
何勇, 张建中, 李同宇. 改进的震源扫描定位方法[J]. 中国科技论文, 2016, 11(21): 2450-2455. He Yong, Zhang Jianzhong, Li Tongyu. Improved Focal Scanning Location Method[J]. Chinese Science and Technology Paper, 2016, 11(21): 2450-2455. |
| [49] |
Kao H, Shan S. The Source-Scanning Algorithm:Mapping the Distribution of Seismic Sources in Time and Space[J]. Geophys, 2004, 157: 589-594. |
| [50] |
Kao H, Shan S J, Dragert H, et al. A Wide Depth Distribution of Seismic Tremors Along the Northern Cascadia Margin[J]. Nature, 2005, 436: 841-844. |
| [51] |
Sava P. Micro-Earthquake Monitoring with Sparsely Sampled Data[J]. Journal of Petroleum Exploration & Production Technologies, 2011, 1(1): 43-49. |
| [52] |
许力生, 杜海林, 严川, 等. 一种确定震源中心的方法:逆时成像技术原理与数值实验[J]. 地球物理学报, 2013, 56(4): 1190-1206. Xu Lisheng, Du Hailin, Yan Chuan, et al. A Method for Determining Focal Center:Principle and Numerical Experiment of Reverse-Time Imaging Technology[J]. Journal of Geophysics, 2013, 56(4): 1190-1206. |
| [53] |
Li L, Chen H, Wang X. Weighted-Elastic-Wave Interferometric Imaging of Microseismic Source Location[J]. Applied Geophysics, 2015, 12(2): 221-234. |
| [54] |
Nakata N, Beroza G C. Reverse Time Migration for Microseismic Sources Using the Geometric Mean as an Imaging Condition[J]. Geophysics, 2016, 81(2): KS51-KS60. |
| [55] |
李青峰, 张建中. 基于分组互相关成像条件的微震逆时成像定位方法[J]. 地球物理学进展, 2019, 34(1): 125-135. Li Qingfeng, Zhang Jianzhong. Microseismic Inversion Imaging Positioning Method Based on Grouped Cross-Correlation Imaging Conditions[J]. Progress in Geophysics, 2019, 34(1): 125-135. |
| [56] |
Wu S J, Wang Y B, Zheng Y K, et al. Microseismic Source Locations with Deconvolution Migration[J]. Geophysical Journal International, 2018, 212(3): 2088-2115. |
| [57] |
徐克彬, 陈祖斌, 刘玉海, 等. 基于L-M算法的微地震定位方法[J]. 石油地球物理勘探, 2018, 53(4): 765-769. Xu Kebin, Chen Zubin, Liu Yuhai, et al. Microseismic Location Method Based on L-M Algorithm[J]. Petroleum Geophysical Exploration, 2018, 53(4): 765-769. |
| [58] |
李学政, 雷军. 神经网络方法在爆炸地震震中定位方面的应用[J]. 地震地质, 1999, 21(1): 77-82. Li Xuezheng, Lei Jun. Application of Neural Network Method in Locating the Epicenter of Explosive Earthquakes[J]. Seismology, 1999, 21(1): 77-82. |
| [59] |
Bose M, Wenzel F, Erdik M. PreSEIS:A Neural Network-Based Approach to Earthquake Early Warning for Finite Faults[J]. Bulletin of the Seismological Society of America, 2008, 98(1): 366-382. |
| [60] |
Llinas J, Hall D L. An introduction to Multi-Sensor Data Fusion[J]. Geophysical Journal International, 1998, 85(1): 6-23. |
| [61] |
韩增奇, 于俊杰, 李宁霞, 等. 信息融合技术综述[J]. 情报杂志, 2010, 29(增刊1): 110-114. Han Zengqi, Yu Junjie, Li Ningxia, et al. Overview of Information Fusion Technology[J]. Intelligence Journal, 2010, 29(Sup.1): 110-114. |
| [62] |
李绍红, 朱建东, 白兰英, 等. 联合信息融合和解析方法的微震源定位研究[J]. 煤炭学报, 2018, 43(4): 1065-1071. Li Shaohong, Zhu Jiandong, Bai Lanying, et al. Joint Information Fusion and Analysis for Micro-Focal Location[J]. Journal of Coal Mine, 2018, 43(4): 1065-1071. |