0 引言
微震监测技术在矿山、油田、水坝和地下工程等方面应用十分广泛。尤其在非常规油气开采中发挥着重要作用,它是描述水力压裂引起的裂缝发育形态及压裂效果的重要技术。通过微震监测技术定位震源位置,获得裂缝发展方向和几何形状信息,可为油气开采提供重要参考[1]。
实际的微震记录中,背景噪声的成分和性质十分复杂,几乎完全淹没微震信号,使微地震初至自动拾取极为困难。目前,微震初至拾取方法主要有长短时窗能量比(STA/LTA)[2]法和分形维数法[3]等。STA/LTA法首先确定初至的大概范围,然后在该范围内采用分形维数法拾取事件初至,虽然效率高但并不适用于低信噪比条件。而分形维数法拾取精度高,但是其算法效率偏低,对于低信噪比微震数据很难获得准确的拾取效果。单一化的预处理(如去噪)过程无法消除成分复杂的背景噪声,甚至还会在处理过程中对微震记录的幅频特性造成损失[4-5]。
2018年,Li等[6]提出了时域近似负熵实现初至拾取方法。该方法首先对微震信号进行归一化预处理,然后对归一化数据进行时域分帧,通过近似负熵算法计算每一帧数据,进而得到近似负熵谱曲线;然后设计合适的阈值算法,通过计算找到初至所在的区域;最后根据分帧处理的相关公式,计算得到初至所在的位置。相比于传统的拾取方法,该方法实现了低信噪比信号的初至拾取;但其算法依然进行了信号预处理,通过归一化处理减小噪声对信号处理的影响,没能实现消噪与拾取相结合,增添了算法复杂度,再加上在时域近似负熵特征不够明显,对结果会有影响。
微震信号是一种非平稳信号,时频分析是处理非平稳信号的有效方法之一,它可以完整建立地震波信号在时频域内表示信号能量或强度的联合时频分布,观察信号的演变,提供信号的局部特征[7]。因此,本文提出了一种适用于较低信噪比条件下的微震信号初至拾取新方法。该方法首先利用Stockwell变换(简称S变换)获得含噪微震信号的时频谱图;然后对谱内各个谱点沿频率方向进行分帧操作,并计算每帧频段内的近似负熵值,以最小近似负熵值作为该谱点的负熵值;最后沿时间方向比较各个谱点的负熵值,数值最小处即为初至时刻位置。
1 时频谱熵拾取法原理 1.1 利用S变换将信号从时域转换到时频域S变换是在小波变换和短时傅里叶变换的基础上进行发展的,其不仅能够表现时间和频率的局部特征,而且可以自动调节频率,实现多分辨率分析[8-9];同时,S变换与傅里叶谱保持直接的联系,时频分析能力比窗口傅里叶变换更强。因此S变换更适合非平稳的地震信号[10]。连续S变换过程为
 (1)
(1) 式中:S(τ,f)为时间信号h(t)的S变换;τ反映了高斯窗在时间轴上的位置;f为频率;t为时间;i为虚数单位。式(1)为标准S变换,其高斯窗函数的时窗函数宽度是固定的。
本文在实现S变换过程中使用的合成微震有效信号h(n)为离散信号(其中n表示时域抽样点,n=0, 1, …,N-1,N=1 024),处于0~50 Hz频段内,以1 Hz为频率间隔对单道含噪信号进行S变换。
S变换的具体步骤是,首先对h(n)进行离散傅里叶变换,将时域信号转换到频域:
 (2)
(2) 式中,k为频域序数,k∈[0, 1 023]。
然后将H(k)周期延拓并频移m得到频移谱H(k+m)(频移采样点m=0, 1, 2, ..., 50,由合成微震信号的频率范围决定),计算高斯窗g(t, f)=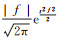
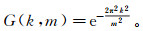 (3)
(3) 最后按m计算H(k+m)G(k, m),将计算结果做傅里叶反变换就可得到m处对应的时域信号幅值hm(n):
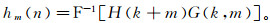 (4)
(4) 式中,F-1[H(k+m)G(k, m)]为H(k+m)G(k, m)的傅里叶反变换。
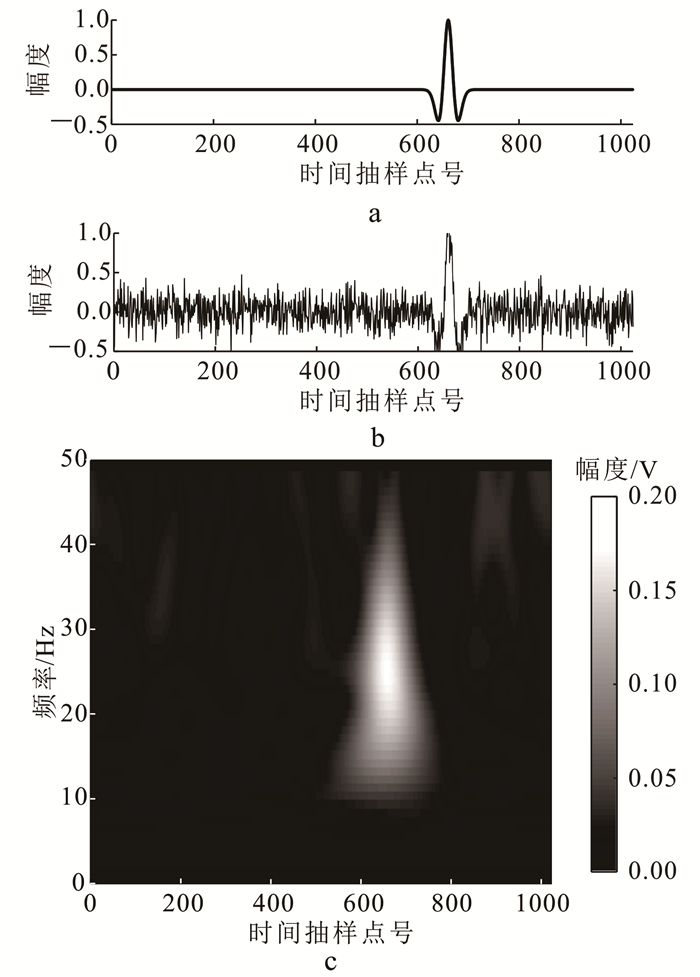
图 1a、b、c分别为一道合成微震信号的有效信号曲线、加高斯白噪声(信噪比为-3 dB)后的信号曲线,以及加噪信号经过S变换得到的频谱图。由图 1c可知,有效信号位置信号幅度较大,频率分布集中在0~50 Hz,相比之下,噪声位置信号幅度小且频率分布非常分散。
|
| a.原始有效信号;b.加噪信号;c.加噪信号时频谱。 图 1 合成微震信号加噪以及S变换结果 Fig. 1 Composite microseismic signal with noise and S transforming results |
|
|
分帧操作大都应用于非平稳信号处理。由于信号不平稳,分析整个信号没有意义,而逐点分析运算量太大,因此将一小段时间范围内的信号视为平稳信号,这一小段时间长度称为窗长,该时间段内信号称为一帧;然后通过在时间域平移窗口并且使两帧之间信号有交集,更合理地实现对信号的分析处理[11-12]。
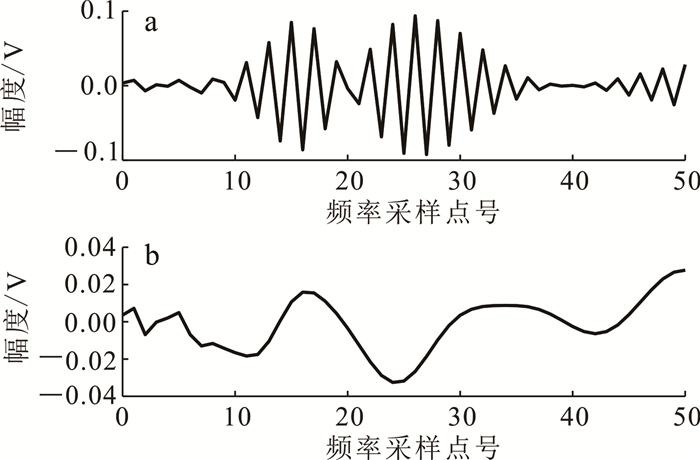
噪声与有效信号所含的频率分量不同,即可认为含噪信号时频谱中各个谱点沿频率方向不平稳。图 2给出了某含噪微震信号S变换时频谱中有效信号与噪声沿频率方向采样点对比图。由图 2可知,噪声与有效信号所含的频率分量有很大差异。因此,我们对S变换时频谱应用分帧技术进行处理。设定一定长度的频段为平稳频段,对每个时间抽样点的频率方向分量进行分帧处理,在每个平稳频段求熵,以达到合理求取该抽样时间点熵值的目的。
|
| a.有效信号;b.噪声。 图 2 频率方向幅度对比图 Fig. 2 Comparison diagram of amplitude in frequency direction |
|
|
设频率取样长度为L,每帧的长度为l,帧移为s,相邻两帧的重叠部分为
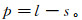 (5)
(5) 则频域数据将被分成的帧数nf为
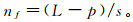 (6)
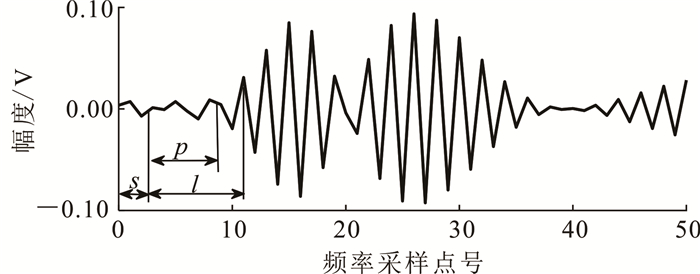
(6) 对时频谱沿频率方向分帧的示意图如图 3所示。
|
| 图 3 时频谱沿频率方向分帧示意图 Fig. 3 Time-frequency spectrum along the frequency direction frame diagram |
|
|
熵是一种衡量信号混乱程度的物理量,变量越随机、有序性越差、混乱程度越高,其信息熵越大;反之,变量越有序、越规律、越平稳,其信息熵越小[13-14]。与熵特性不同,负熵是一种非高斯度量,对高斯变量,其值为零;对非高斯变量,其值总是非负的。负熵不随信号的幅度变化而变化,定义为
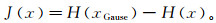 (7)
(7) 式中:x为零均值随机变量;J(x)为x的负熵;xGause是与x具有相同协方差矩阵Σ的高斯变量;H(xGause)、H(x)分别为xGause、x的熵。
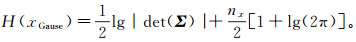 (8)
(8) 式中:nx为x的维数;函数det(·)表示求矩阵的行列式。
然而,负熵的计算通常比较困难,而且依赖于随机变量先验概率密度等多种因素,而微震信号的概率密度未知,因此基于微熵的多项式负熵近似表示为
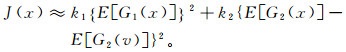 (9)
(9) 根据文献[14],式(9)中:k1、k2为系数,取正数;G1(x)、G2(x)为线性独立函数集;E(·)表示求取均值;v为满足零均值、单位方差的标准正态分布序列。本文经过多次实验后选择合理的G1(x)和G2(x)、k1、k2为:
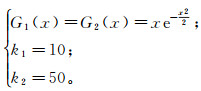 (10)
(10) 则式(9)近似表示为
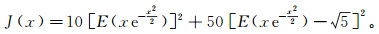 (11)
(11) 本文采取的方法是在频域构造负熵特征,即在时频谱频率方向进行分帧求近似负熵。噪声的随机性大,其近似负熵值较大;而有效信号随机性小,其近似负熵值较小。我们将时频谱每个谱点沿频率方向计算得到的近似负熵最小值作为该谱点的近似负熵值;然后对得到的最小近似负熵值序列沿时间方向再搜索其最小值,在最小值所处位置再频移一个补偿常数值。仿真实验中通过大量实验得出补偿常数值为20,对拾取结果修改后为最终的初至时刻点;实际微震信号拾取实验中取补偿常数值为0,即对拾取结果不进行修正。
基于上述描述,图 4给出了时频谱熵法整体思想示意图。时频谱熵法拾取微震信号的步骤如下。
|
| 图 4 时频谱熵法的信号拾取步骤 Fig. 4 Time-spectral entropy method of signal pickup steps |
|
|
步骤1, 将原始信号进行S变换获得时频谱图,即对应的矩阵。
步骤2, 处理每个时间抽样点的频率方向分量:a.频率方向分帧处理;b.求每一帧的近似负熵;c.取该时间抽样点所有帧近似负熵中的最小值作为该时间抽样点的熵。
步骤3, 将近似负熵值最小的时间抽样点平移一定的补偿常数值作为最终的有效信号拾取位置。
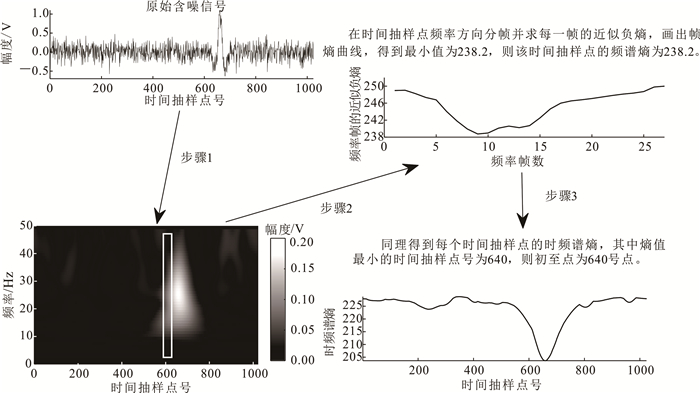
2 模拟微震数据初至拾取本文选用雷克子波模拟微震信号子波,仿真生成一张80道、每道1 024个采样点的合成微震记录,其采样频率为1 000 Hz。对纯净微震记录加入信噪比(SNR)为-5 dB噪声后得到的单道含噪信号如图 5a所示,实际初至时刻为530号时间抽样点。分别利用本文提出的时频谱熵法和STA/LTA法对图 5a信号进行初至拾取;图 5b是近似负熵曲线,使用时频谱熵法,帧长为4 Hz,步长为2 Hz,加汉宁窗,得到24帧,所得的近似负熵最小值(530号时间抽样点)即为初至点;图 5c是STA/LTA曲线,长时窗长设为49个时域取样点,短窗长为25个时域取样点,STA/LTA最大值(520号时间抽样点)处为初至点。时频谱熵法的误差更小,但在实际中误差允许范围内,两种方法均可实现初至拾取。
|
| a.信噪比为-5 dB加噪单道微震信号以及近似负熵曲线与STA/LTA曲线拾取位置;b.近似负熵曲线;c. STA/LTA曲线。 图 5 信噪比为-5 dB加噪单道微震信号初至位置对比图 Fig. 5 Comparison diagram of pick up position of single-channel microseismic signal with SNR -5 dB in two methods |
|
|
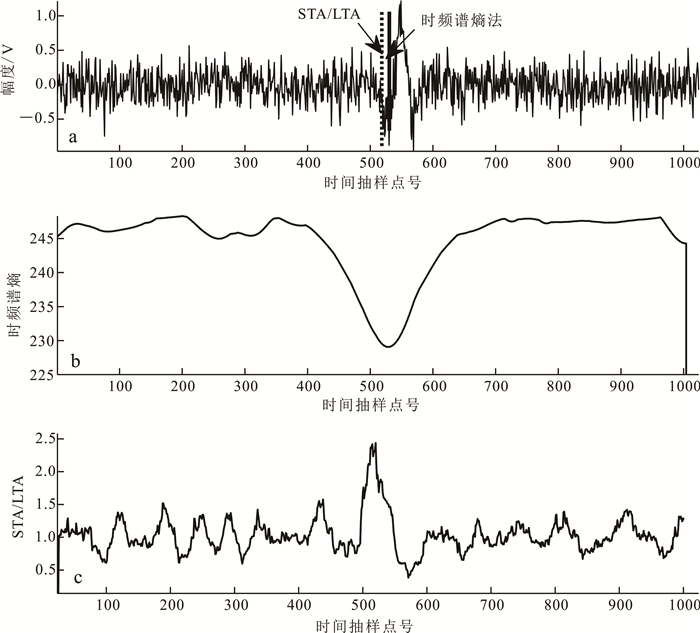
接着,我们对同一道纯净微震记录加入信噪比为-10 dB的噪声后进行处理,得到时频谱熵法的近似负熵曲线和STA/LTA曲线(图 6),使用两种方法时设定的参数与图 5相同。时频谱熵法拾取的初至点为532号时间抽样点;STA/LTA法拾取的初至点511号时间抽样点。在-10 dB信噪比的情况下,时频谱熵法仍然可以稳定拾取初至信号,而STA/LTA法已经产生很大误差。
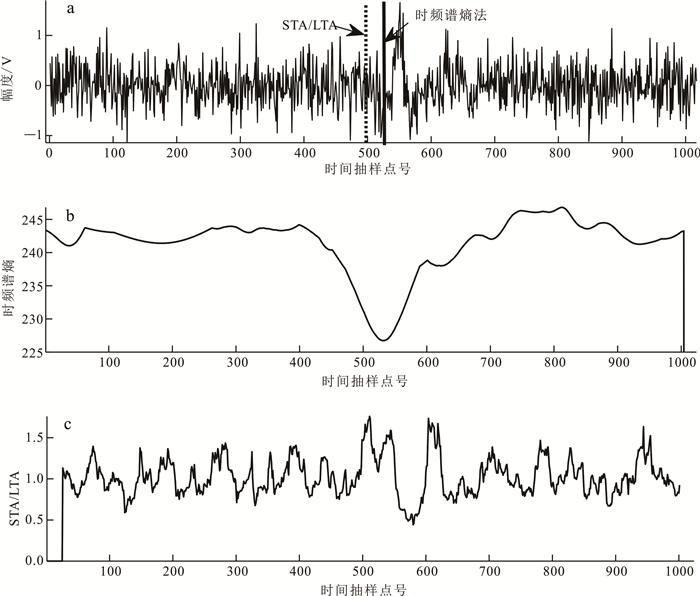
|
| a.信噪比为-10 dB加噪单道微震信号以及近似负熵曲线与STA/LTA曲线拾取位置;b.近似负熵曲线;c. STA/LTA曲线。 图 6 信噪比为-10 dB加噪单道微震信号初至位置对比图 Fig. 6 Comparison diagram of pick up position of single-channel microseismic signal with SNR -10 dB in two methods |
|
|
表 1列出了两种方法对同一道初至点(530号时间抽样点)的微震信号在加入-12~-3 dB之间信噪比噪声后的初至拾取结果。在信噪比大于-6 dB的情况下,时频谱熵法和STA/LTA法都可以较大精度完成信号初至拾取;在信噪比小于等于-6 dB之后,时频谱熵法保持原有的准确程度以及成功率,而STA/LTA法无法准确稳定地拾取,初至拾取成功率很低。
| 信噪比/dB | 初至时间抽样点号 | |
| 时频谱熵法 | STA/LTA法 | |
| -3 | 530 | 528 |
| -4 | 527 | 524 |
| -5 | 530 | 520 |
| -6 | 534 | 952 |
| -7 | 531 | 590 |
| -8 | 532 | 293 |
| -9 | 534 | 604 |
| -10 | 532 | 511 |
| -11 | 528 | 542 |
| -12 | 530 | 557 |
图 7给出了信噪比为-5 dB和-10 dB情况下的多道拾取结果。可以看出:在信噪比为-5 dB时,时频谱熵法和STA/LTA法的拾取效果一样准确;在信噪比为-10 dB时,时频谱熵法的拾取效果依然稳定,而STA/LTA法拾取效果差。可见,时频谱熵法更适合低信噪比情况下的信号初至拾取。
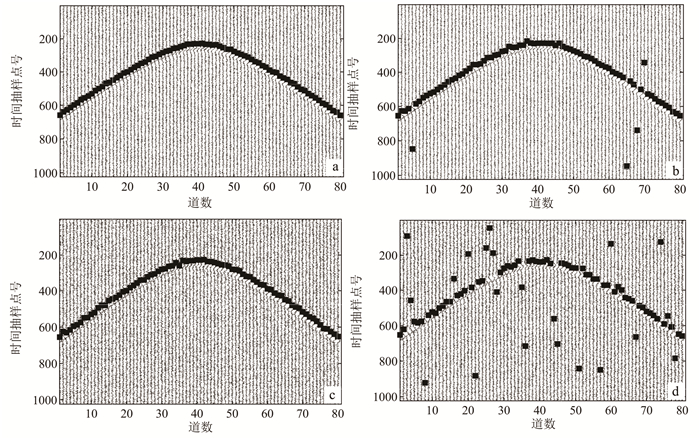
|
| 信噪比为-5 dB:a.时频谱熵法;b. STA/LTA法。信噪比-10 dB:c时频谱熵法;d. STA/LTA法。 图 7 80道信号每道1 024个时间抽样点初至拾取图 Fig. 7 First arrival picking graph of 80 signals with 1 024 time sampling points persigral |
|
|
分别利用时频谱熵法和STA/LTA法对实际微震信号三分量数据共15道信号进行初至拾取,验证新方法的性能。x分量具有较高的信噪比以及多种噪声;y分量主要包含高斯噪声,信噪比较低;z分量噪声成分比较单纯,信噪比较高。图 8为使用时频谱熵法和STA/LTA法对实际地震信号x、y、z分量的信号拾取结果。由图 8可知,x分量时频谱熵法拾取效果较差,y分量STA/LTA法拾取效果较差;z分量两种方法的拾取效果都比较好。究其原因:时频谱熵法使用负熵只对高斯信号敏感,而x分量包含非高斯噪声,因此导致时频谱熵法失去优势效果不佳;y分量信噪比较低,STA/LTA法失去优势,因而差于时频谱熵法;z分量噪声成分单纯且信噪比高,两种方法的拾取效果都很好。可见对于低信噪比信号,时频谱熵法更有优势,但是由于负熵的特点,也有一定局限性。
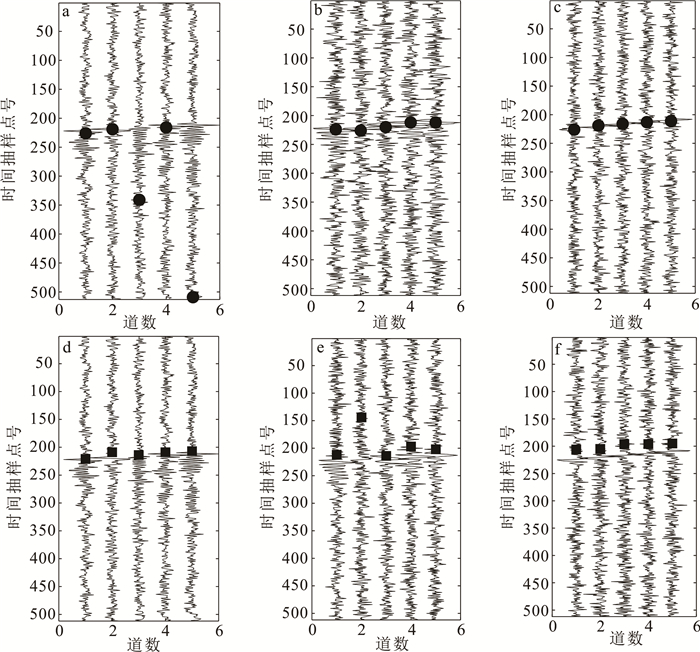
|
| 时频谱熵法:a. x分量;b. y分量;c. z分量。STA/LTA法:d. x分量;e. y分量;f. z分量。 图 8 实际井中微震数据拾取结果 Fig. 8 Pick up results of microseismic data collection in actual wells |
|
|
本文选用雷克子波模拟微震信号子波,仿真生成一张80道、每道1 024个采样点的合成微震记录,其采样频率为1 000 Hz,为仿真的纯净微震信号添加高斯噪声得到以下实验结论:信噪比在-5 dB时,两种方法拾取效果都很好;信噪比在-10 dB时,时频谱熵法拾取效果更好。可见,时频谱熵法在未进行信号预处理的情况下更适合低信噪比微震信号的初至拾取。
而在实际信号的初至拾取实验中,对于信噪比较低的y分量,时频谱熵法的拾取结果优于STA/LTA法的拾取结果,验证了时频谱熵法在低信噪比条件下的优势;同时对于高信噪比的x分量,由于近似负熵无法避免非高斯噪声成分的干扰,导致时频谱熵法的拾取效果不如STA/LTA法的初至拾取效果;而对于噪声成分单纯且信噪比高的z分量,两种方法的拾取效果都很好。
本文研究的时频谱熵法与传统方法相比较的创新点在于完成频域“分帧”处理得到每一个时间抽样点的负熵值,可以在低信噪比以及不进行信号预处理的条件下完成高准确度信号初至拾取,对于实际工作中高效完成低信噪比的微震信号初至拾取有很大用途。
实验过程中,时频谱熵法的仿真实验拾取结果与标准位置差一个常数值,另外实际微震信号初至拾取结果体现出近似负熵在叠加复杂噪声情况下的有限性。在之后的研究中,可以探索该常数值存在的原因,并尝试将更多种信息熵代入时频谱熵法中,比较不同信息熵拾取效果的不同。
| [1] |
焦健, 南雄, 陈德山. 煤矿井下微震监测技术现状与发展[J]. 山东工业技术, 2018(20): 85. Jiao Jian, Nan Xiong, Chen Deshan. Status and Development of Microseismic Monitoring Technology in Coal Mine[J]. Shandong Industrial Technology, 2018(20): 85. |
| [2] |
段建华. 微地震事件不同初至拾取方法的对比分析[J]. 煤田地质与勘探, 2013, 41(3): 82-86. Duan Jianhua. Comparative Analysis of Different Picking Methods of Microseismic Events from the Beginning to the End[J]. Coal Geology & Exploration, 2013, 41(3): 82-86. |
| [3] |
Zhang Z Y, Weller A, Kruschwitz S. Pore Radius Distribution and Fractal Dimension Derived from Spectral Induced Polarization[J]. Near Surface Geophysics, 2017, 15(6): 625-632. DOI:10.3997/1873-0604.2017035 |
| [4] |
程浩, 袁月, 王恩德, 等. 基于小波变换的自适应阈值微震信号去噪研究[J]. 东北大学学报(自然科学版), 2018, 39(9): 1332-1336. Cheng Hao, Yuan Yue, Wang Ende, et al. Study on Adaptive Threshold Microseismic Signal Denoising Based on Wavelet Transform[J]. Journal of Northeastern University (Natural Science Edtion), 2018, 39(9): 1332-1336. |
| [5] |
张雪冰, 刘财, 刘洋, 等. 基于局部均值分解的地震信号时频分解方法[J]. 吉林大学学报(地球科学版), 2017, 47(5): 1562-1571. Zhang Xuebing, Liu Cai, Liu Yang, et al. Time-Frequency Decomposition Method of Seismic Signals Based on Local Mean Value Decomposition[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(5): 1562-1571. |
| [6] |
Li Y, Ni Z, Tian Y. Arrival-Time Picking Method Based on Approximate Negentropy for Microseismic Data[J]. Journal of Applied Geophysics, 2018, 152: 100-109. DOI:10.1016/j.jappgeo.2018.03.012 |
| [7] |
杨千里.广义S变换功率谱在地震监测中的应用研究[C]//国家安全地球物理丛书: 十四: 资源环境与地球物理.北京: 中国地球物理学会, 2018: 301-306. Yang Qianli. Application of Generalized S Transform Power Spectrum in Seismic Monitoring[C]//National Security Geophysics Series: ⅩⅣ: Resources, Environment and Geophysics. Beijing: Chinese Geophysical Society, 2018: 301-306. |
| [8] |
马力, 何健, 李超胜, 等. 基于广义S变换的地震资料处理[J]. 科学技术与工程, 2017, 17(25): 171-175. Ma Li, He Jian, Li Chaosheng, et al. Seismic Data Processing Based on Generalized S Transform[J]. Science, Technology and Engineering, 2017, 17(25): 171-175. DOI:10.3969/j.issn.1671-1815.2017.25.027 |
| [9] |
陈学华, 贺振华, 文晓涛, 等. 基于广义S变换的裂缝分频边缘检测方法[J]. 吉林大学学报(地球科学版), 2011, 41(5): 1605-1609. Chen Xuehua, He Zhenhua, Wen Xiaotao, et al. Frequency Division Edge Detection Method Based on Generalized S Transform[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(5): 1605-1609. |
| [10] |
邓攻, 梁锋, 李晓婷, 等. S变换谱分解技术在深反射地震弱信号提取中的应用[J]. 地球物理学报, 2015, 58(12): 4594-4604. Deng Gong, Liang Feng, Li Xiaoting, et al. Application of S Transform Spectrum Decomposition Technique in Weak Signal Extraction from Deep Reflection Seismic[J]. Chinese Journal of Geophysics, 2015, 58(12): 4594-4604. DOI:10.6038/cjg20151221 |
| [11] |
陈莹莹, 简磊. 基于最大熵谱估计和时频特性的语音端点检测[J]. 计算机应用与软件, 2017, 34(11): 91-96. Chen Yingying, Jian Lei. Speech Endpoint Detection Based on Maximum Entropy Spectrum Estimation and Time-Frequency Characteristics[J]. Computer Applications and Software, 2017, 34(11): 91-96. DOI:10.3969/j.issn.1000-386x.2017.11.017 |
| [12] |
Saulig N, Milanovic Ž, Ioana C. A Local Entropy-Based Algorithm for Information Content Extraction from Time-Frequency Distributions of Noisy Signals[J]. Digital Signal Processing, 2017(70): 155-165. |
| [13] |
倪卓.基于近似负熵算法实现微地震数据初至拾取研究[D].长春: 吉林大学, 2018. Ni Zhuo. Research on Initial Arrival Pickup of Microseismic Data Based on Approximate Negative Entropy Algorithm[D]. Changchun: Jilin University, 2018. |
| [14] |
徐耀华, 郭英, 王刚. 基于负熵的语音端点检测算法[J]. 信号处理, 2009, 25(2): 307-312. Xu Yaohua, Guo Ying, Wang Gang. Speech Endpoint Detection Algorithm Based on Negative Entropy[J]. Signal Processing, 2009, 25(2): 307-312. DOI:10.3969/j.issn.1003-0530.2009.02.028 |



