2. 东北大学深部金属矿山安全开采教育部重点实验室, 沈阳 110819
2. Key Laboratory of Ministry of Education on Safe Mining of Deep Metal Mines, Northeastern University, Shenyang 110819, China
0 引言
全张量重力梯度(full tensor gravity gradiometry, FTG)数据是一种高精度重力勘探数据, 已被广泛应用于矿产勘探等领域, 其对场源边界以及浅部异常体识别具有较高的分辨率。近年来, 基于梯度数据的密度反演[1]、边界检测[2-3]和场源体成像[4]等方法也发展得较为迅速。
相关成像是一种利用相关系数定性解释地质体空间位置和形态的成像方法, 它于1997年首次被提出并应用于自然电场的解释[5]。之后, 国内外学者围绕相关成像开展了大量的研究工作, 先后将其推广到电法[6]、电阻率异常数据[7]以及重力勘探数据[8];Iuliano等[9]综合利用重、磁、自然电位数据对维苏威火山进行了三维相关成像研究, 清晰地描述了火山的岩浆通道系统;王绪本等将相关成像分别应用于自然电场[10]以及大地电磁[11]勘探, 取得了良好的效果;郭良辉等将相关成像分别应用于磁法[12]和重力勘探数据[13], 提出了基于异常分离的三维相关成像;马国庆等[14]利用磁异常的解析信号改进了相关系数的计算方法, 并针对不同模型验证了该算法的可行性;石磊等[15]提出磁总场异常垂直梯度的相关成像, 在模型数据与实际磁测数据中验证了该方法的稳定性;侯振隆等[16]在相关成像理论基础上提出基于泰勒级数的算法, 通过定义新的几何函数提高成像效率。以上研究尽管在改善成像效果方面做出了许多贡献, 但深度方向上的分辨率仍较低, 特别是对目标体底部的识别精度较差。深度加权函数常用于改善物性反演结果的纵向分辨能力, 在过去的研究中, Li等[17]提出了一种经典的深度加权函数形式, 该函数被广泛应用于位场勘探数据反演中;Federico等[18]曾应用构造指数作为加权函数的参数来提高纵向分辨率;Commer[19]提出了一种基于先验深度信息的加权函数, 并将其应用于重力聚焦反演中;Commer等[20]又进一步提出了空间梯度加权函数, 提高了反演效果。为相关成像引入深度加权函数将有利于改善现有方法对目标体的成像能力。
因此, 本文将联合全张量重力梯度数据中的部分分量, 引入深度加权函数以提高纵向成像分辨率, 并通过理论模型和实测数据试验证明该方法的有效性和可行性。
1 方法 1.1 重力梯度数据相关成像在笛卡尔坐标系中, 设O为坐标原点, xOy为水平平面, z轴正方向垂直向下。将地下空间划分为一系列质点, 第j个质点在第i个测点上引起的重力梯度Gαβ, j(xi, yi, zi)为
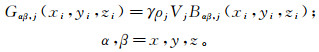 (1)
(1) 式中:γ为万有引力常数;ρj、Vj分别为第j个质点的密度、体积;Bαβ, j(xi, yi, zi)为第j个质点在第i个测点引起的梯度数据的几何函数。
重力位在x、y、z 3个方向上的二阶导数称为重力梯度数据。重力梯度张量由9个重力梯度数据组成:
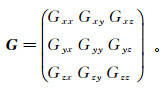 (2)
(2) 由引力场性质可知:Gxy=Gyx, Gxz=Gzx, Gyz=Gzy, Gxx+Gyy+Gzz=0;故在G的9个分量中, Gxy、Gxz、Gyz以及Gxx、Gyy和Gzz中的任意两个量是独立的。重力梯度数据的几何函数[4]如下:
 (3)
(3)  (4)
(4) 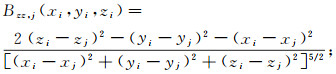 (5)
(5) 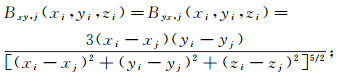 (6)
(6) 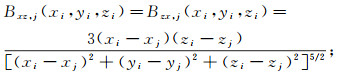 (7)
(7) 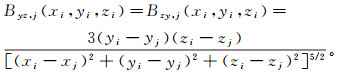 (8)
(8) 第j个质点重力梯度的相关系数可表示为
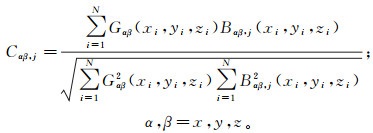 (9)
(9) 式中:Gαβ为重力梯度;N为测区内测点数量。
相关系数的取值范围是[-1, 1], 可用来反映地下质量分布的情况[4]。若相关系数为正, 则表明该点质量盈余, 反之则代表亏损;Gαβ, j越接近1, 表明该点质量剩余的可能性越大, Gαβ, j越接近-1, 表示该点质量亏损的可能性越大[21]。根据式(9), 可推导出多分量重力梯度数据联合相关成像的相关系数为
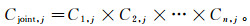 (10)
(10) 式中:Cjoint, j为第j个质点多分量重力梯度数据联合后的相关系数;Cn, j为第j个质点重力梯度的相关系数;n为联合相关系数中使用的重力梯度数据种类数目, n∈[1,6]。
1.2 基于深度加权的相关成像将重力梯度数据应用于相关成像方法, 可以得到较好的横向分辨率;但在深度方向上同其他位场数据一样, 分辨率较低, 结果中甚至存在趋肤效应等问题。因此, 引入深度加权来改善成像结果的纵向分辨能力。在反演中, Li等[17]提出的深度加权函数形式为
 (11)
(11) 式中:z0为一个与异常体深度有关的常数, 取决于地下划分单元的形状和观测点的高度;β为正数, 对于重力异常β=2[22], 对于重力梯度数据β=3[23]。该深度加权函数依赖于z0和β的取值, 对于复杂模型, 不能有效地改善纵向分辨率。
Commer等[20]提出了另一种加权函数——空间梯度加权函数, 它通过引入先验深度信息改善反演结果, 这一加权函数包括x, y, z 3个方向。对于z方向, 其表达式为
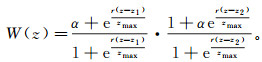 (12)
(12) 式中:zmax为研究区域地下空间范围内的最大深度;α为经验值, 决定近地表处的权值, 为克服趋肤效应, 一般取α=0.001;r为缩放因子, 满足当z→0时, 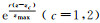
将上述深度加权函数分别应用于相关成像, 则第j个质点的相关系数Clater, j可表示为
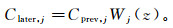 (13)
(13) 式中:Clater, j为深度加权后第j个质点的相关系数;Cprev, j为加权之前第j个质点的相关系数;Wj(z)为第j个质点的深度加权函数。
需要注意的是:当地下空间存在多个目标体时, 式(12)不能对各目标体进行分别加权, 应将地下研究区域先划分, 再将分割后的不同区域分别使用相应的顶面与底面埋深, 在此基础上再应用空间梯度加权函数。
2 模型建立与验证为了验证提出方法的有效性和成像效果, 设计两组长方体组合模型试验讨论梯度数据选取、深度加权效果和抗噪能力等问题。
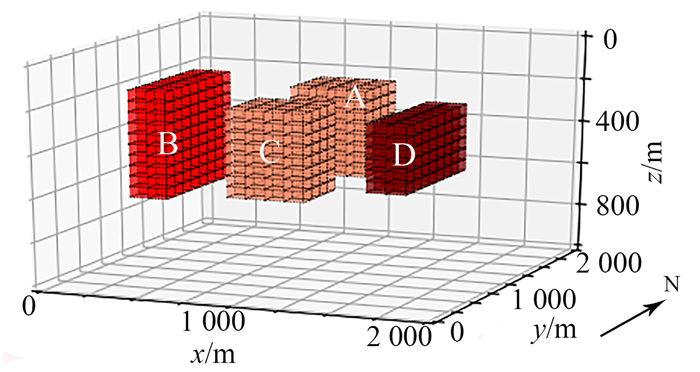
2.1 张量梯度数据组合试验在笛卡尔坐标系下建立模型一。选取x和y方向范围均为0~2 000 m、深度方向范围为0~1 000 m的测区;地下空间被均匀划分为20 × 20 × 20个小立方体, 每个小立方体的大小为100 m × 100 m × 50 m。组合模型由4个长方体A、B、C和D组成(图 1), A、C立方体大小均为400 m × 400 m × 400 m, 剩余密度为1.0 g/cm3;B长方体大小为200 m × 800 m × 500 m, 剩余密度为1.1 g/cm3;D长方体大小为200 m × 800 m × 300 m, 剩余密度为1.3 g/cm3。A、B、C、D的中心坐标依次为(1 000 m, 1 600 m, 400 m)、(200 m, 1 200 m, 450 m)、(1 000 m, 600 m, 400 m)、(1 700 m, 600 m, 350 m), 它们的顶面埋深均为200 m。
|
| 图 1 模型一空间位置示意图 Fig. 1 Spatial location of Model One |
|
|
如何利用好全张量重力梯度数据的6个分量(Gxx、Gxy、Gxz、Gyy、Gyz、Gzz), 是位场数据解译的关键。对比分析各重力梯度分量发现, 在频率域中Gzz、Gxz|Gyz(竖线表示梯度分量之间的组合, 即Gxz|Gyz表示Gxz和Gyz2个单分量的组合, 下同)、Gxx|Gyy|Gxy三组分量组合所包含的信息有一定的相关性, 并且在理想情况下, 这三组分量组合所包含的信息量相当, 反演结果相近[24]。故本文没有使用Gxx和Gyy分量, 而对其余4个分量进行了组合。
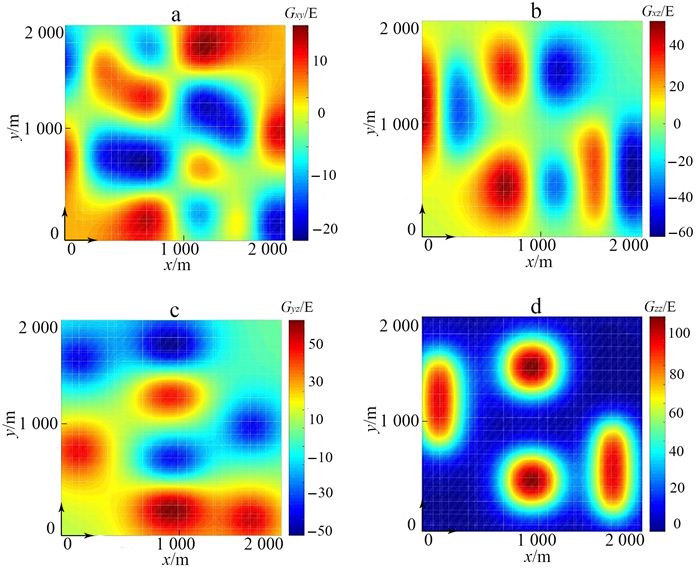
图 2为模型一4个梯度分量图, 可以看出:Gxz的极值可用来识别异常体的南北边界;Gyz的极值可用来识别异常体的东西边界;Gxy包含较多的水平信息;Gzz包含的信息最多, 成像效果最好。
|
| 图 2 模型一重力梯度数据 Fig. 2 Gravity gradiometry data of Model One |
|
|
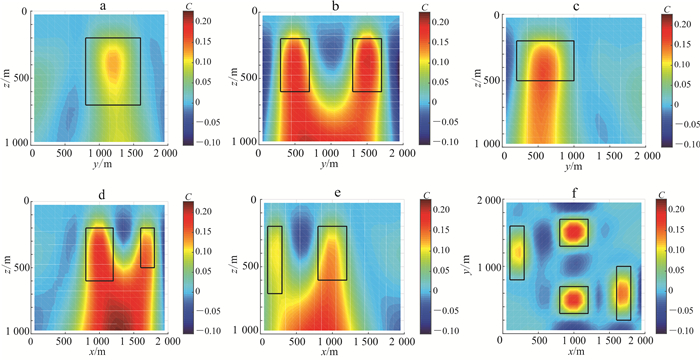
有机地结合各个分量, 能够更准确地解译出地下异常体的空间位置与形态。首先联合2个梯度分量, Gxz|Gyz成像结果见图 3。此分量组合的成像结果在x轴方向上可以清晰地显示出模型的边界, 且能够很好地识别出浅部异常, 成像结果顶部与理论模型较吻合。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d. y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。C.相关系数。 图 3 模型一重力梯度数据Gxz|Gyz成像结果 Fig. 3 Gravity gradiometry data Gxz|Gyz imaging results of Model One |
|
|
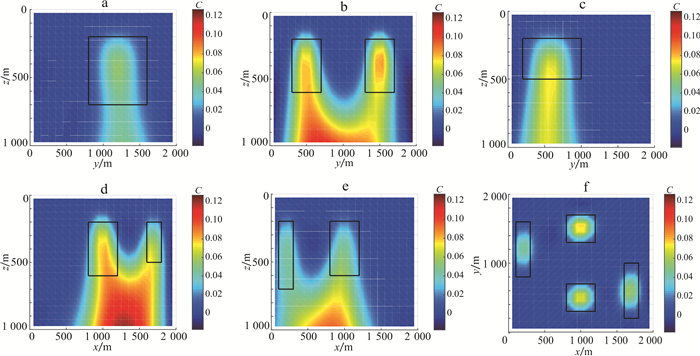
随后将包含最多信息的Gzz分量加入, 成像结果见图 4。与图 3a、b相比, 图 4a、b成像分辨率得到了进一步改善, 尤其是y轴方向异常体的轮廓更加清晰;图 4c、d、e与图 3c、d、e深度方向上的成像结果相近;与图 3f相比, 图 4f水平方向成像结果更加聚焦, 效果更好。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d.y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 4 模型一重力梯度数据Gxz|Gyz|Gzz成像结果 Fig. 4 Gravity gradiometry data Gxz|Gyz|Gzzimaging results of Model One |
|
|
最后加入包含更多水平信息的Gxy分量, 成像结果见图 5。与图 4相比, 图 5成像结果中识别出的模型底部深度仍然下延过深, 且识别出的部分模型范围减小, 分辨率反而有所下降。

|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d. y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 5 模型一重力梯度数据Gxz|Gyz|Gzz|Gxy成像结果 Fig. 5 Gravity gradiometry data Gxz|Gyz|Gzz|Gxy imaging results of Model One |
|
|
综合上面的结果, 说明联合3个重力梯度分量时成像效果最好, 此时的组合是Gxz|Gyz|Gzz。
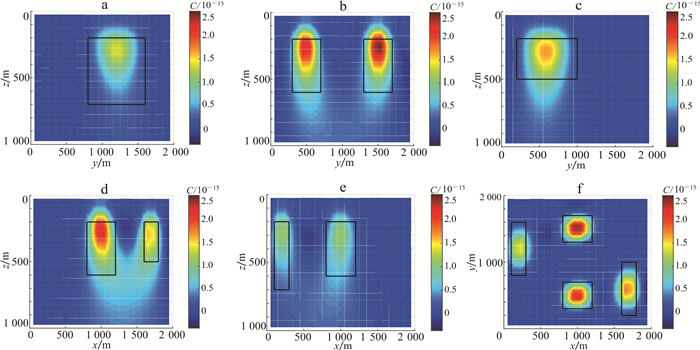
2.2 基于深度加权的成像水平分辨率试验通过2.1节的张量梯度数据组合试验, 得出分量组合Gxz|Gyz|Gzz效果最好, 但在深度方向上的分辨率较低。在此基础上, 本文首先对水平方向存在多个密度体的组合模型进行深度加权, 组合模型为模型一。将深度加权函数(式(11))应用到重力梯度数据Gxz|Gyz|Gzz, 取β=3, z0取模型底部最大深度700 m, 成像结果见图 6。与图 4a、b、c相比, 加入深度加权函数后的成像结果(图 6a、b、c)对模型底部的识别能力有所提升;图 6e浅部存在趋肤效应;图 4f与图 6f水平方向成像结果相近, 说明深度加权函数不会影响成像结果的水平分辨率。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d.y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 6 模型一结合深度加权函数的重力梯度数据Gxz|Gyz|Gzz成像结果 Fig. 6 Combined with depth weighting function gravity gradiometry data Gxz|Gyz|Gzz imaging results of Model One |
|
|
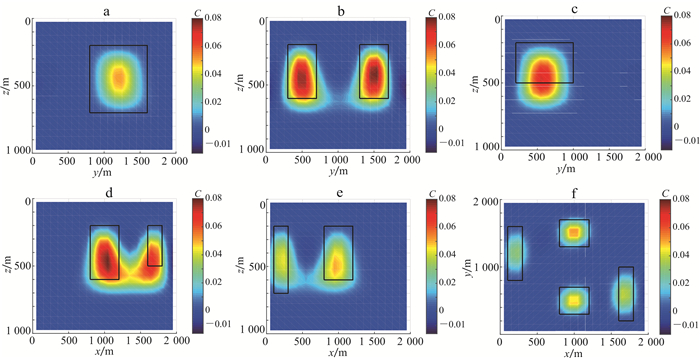
为了避免趋肤效应, 使用空间梯度加权函数(式(12))。令z1=200 m, z2=700 m, α=0.001, zmax=1 000 m, r=20, 成像结果见图 7, 可见成像结果不存在趋肤效应, 且深度方向分辨率得到了较大的提升。由图 7a可以看出, 识别出的长方体B的深度范围接近于理论值, 说明在重力梯度数据联合的基础上使用空间梯度加权函数, 能够进一步提高成像分辨率。但是从图 7b、c、d、e结果来看, 长方体A、C和D的边界仍与准确位置有一定的差异。对比图 4f与图 7f, 可见水平方向成像结果相近, 说明空间梯度加权函数不会影响成像结果的水平分辨率。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d.y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 7 模型一结合空间梯度加权函数的重力梯度数据Gxz|Gyz|Gzz成像结果 Fig. 7 Combined with spatial gradient weighting function gravity gradiometry data Gxz|Gyz|Gzzimaging results of Model One |
|
|
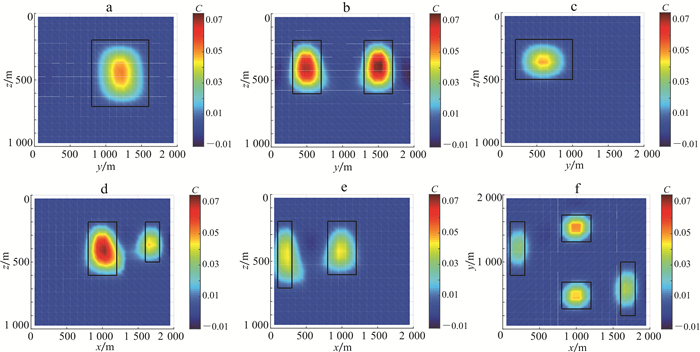
由图 7b、c、d、e可知, 成像结果与理论模型的实际位置有一定的差距, 原因是对空间梯度加权函数中的参数z2取相同值700 m, 但此值与长方体A、C、D的底面深度不符。对地下空间进行划分, 由于模型的顶面深度相同, 故z1取200 m。对分割后的不同区域分别赋予不同的底面深度, 对于长方体A、C, z2=600 m;对于长方体B, z2=700 m;对于长方体D, z2=500 m。在此基础上再应用空间梯度加权函数对分量组合Gxz|Gyz|Gzz进行成像, 成像结果见图 8。与7b、c、d、e相比, 经过分块处理后, 图 8b、c、d、e每个长方体的边界更加精确, 结果的分布范围与理论模型基本一致。对比图 7f与图 8f, 水平方向的成像结果相近, 因此分区加权主要影响模型垂直方向的成像结果。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d. y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 8 模型一结合空间梯度加权函数并分块处理的重力梯度数据Gxz|Gyz|Gzz成像结果 Fig. 8 Combined with spatial gradient weighting function and block processing, gravity gradiometry data Gxz|Gyz|Gzz imaging results of Model One |
|
|
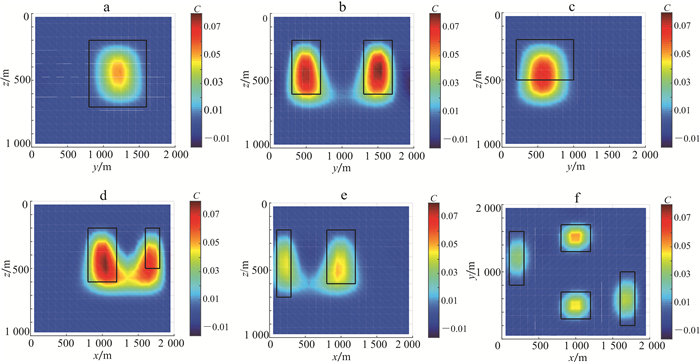
向模型的重力梯度数据加入5%的高斯噪声以验证方法抗噪性。再次将空间梯度加权函数应用到含噪声的Gxz|Gyz|Gzz组合进行联合相关成像。从图 9可以看出, 结果中仍能较清晰地呈现出模型的位置, 说明方法具有良好的抗噪能力, 可以用于实际数据的处理解释工作。
|
| a. x=200 m;b. x=1 000 m;c. x=1 700 m;d.y=500 m;e. y=1 400 m;f. z=300 m。黑色矩形框表示模型位置。 图 9 模型一结合空间梯度加权函数含5%高斯噪声的重力梯度数据Gxz|Gyz|Gzz成像结果 Fig. 9 Combined with spatial gradient weighting function, gravity gradiometry data Gxz|Gyz|Gzz (with 5% Gaussian noise) imaging results of Model One |
|
|
2.2节中的理论模型试验反映了该方法能够很好地圈定水平方向存在多个密度体的情况。为了验证该方法在垂直方向上分布多个密度体的效果, 设计一组垂向上分布多个密度体的组合模型。
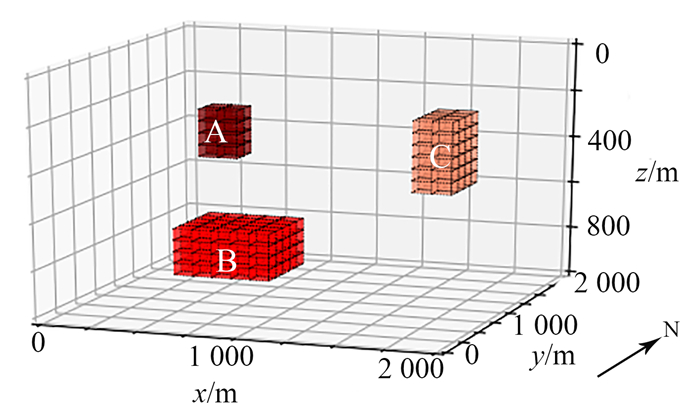
组合模型二由3个长方体A、B、C组成(图 10), A长方体大小为200 m × 200 m × 200 m, 剩余密度为1.6 g/cm3;B长方体大小为500 m × 500 m × 200 m, 剩余密度为1.3 g/cm3;C立方体大小为200 m × 400 m × 300 m, 剩余密度为1.0 g/cm3。A、B、C的中心坐标依次为(600 m, 900 m, 300 m)、(650 m, 950 m, 800 m)、(1 700 m, 1 000 m, 350 m)。测区x和y方向范围均为0~2 000 m, 深度方向范围为0~1 000 m。选取x=600 m和y=900 m两个垂直剖面来进行分析。
|
| 图 10 模型二空间位置示意图 Fig. 10 Spatial location of Model Two |
|
|
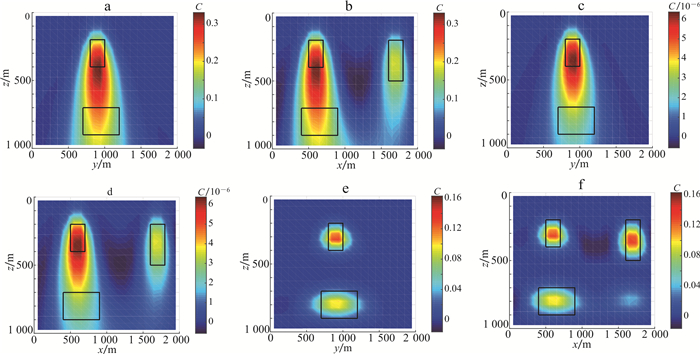
梯度分量组合Gxz|Gyz|Gzz成像结果见图 11。由图 11a、b可见, 没有应用深度加权函数时, 纵向分辨率较低, 异常体的底部不能完全分离。在此基础上应用深度加权函数, z0取模型底部最大深度900 m, 成像结果见图 11c、d。与图 11b对比可见, 图 11d右侧长方体C的底部有一定的提升, 但是仍然不能区分垂直方向分布的长方体A和B。随后将地下空间划分, 对分割后的不同区域分别赋予不同的顶面埋深与底面埋深, 对于长方体A, z1=200 m, z2=400 m;对于长方体B, z1=700 m, z2=900 m;对于长方体C, z1=200 m, z2=500 m;α=0.001, zmax=1 000 m, r=20;再应用空间梯度加权函数对Gxz|Gyz|Gzz分量组合进行成像, 结果见图 11e、f, 模型的轮廓能够被清晰地显示出来, 成像结果与理论模型基本一致。可见, 该方法能够很好地应用于垂直方向分布多个密度体的情形。
|
| a. x=600 m;b. y=900 m;c.结合深度加权函数, x=600 m;d.结合深度加权函数, y=900 m;e.结合空间梯度加权函数并分块处理, x=600 m;f.结合空间梯度加权函数并分块处理, y=900 m。黑色矩形框表示模型位置。 图 11 模型二垂直方向分布多个密度体的Gxz|Gyz|Gzz相关成像 Fig. 11 Corrolation imaging of multiple density bodies distributed vertically with Gxz|Gyz|Gzz of Model Two |
|
|
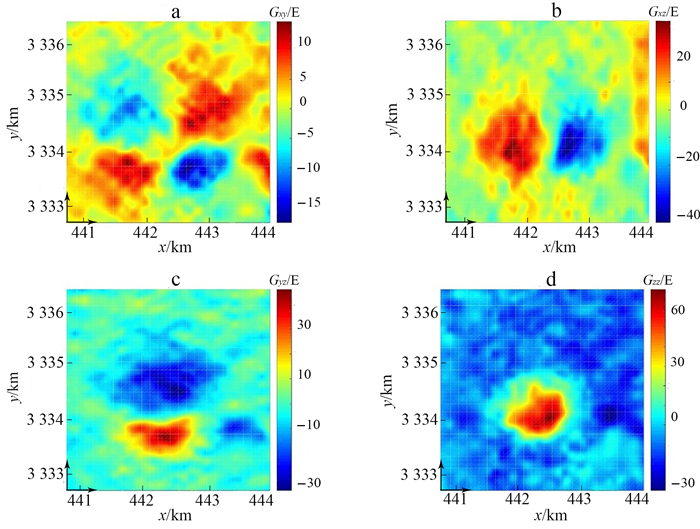
为了验证所提出方法的可行性, 将其应用于美国文顿盐丘地区的航空实测重力梯度数据。文顿盐丘位于德克萨斯州与路易斯安那州的西南部相交地带, 主要由一个大的盐岩和上方的盖岩组成, 盖岩主要是由硬石膏和石灰岩组成的。盖岩的南北向长度为1 280 m, 东西向为1 520 m[25], 根据Ennen等[26-29]的研究, 盖岩的深度范围在160~650 m之间。实测数据位于WGS84坐标系下, x轴对应实测数据的东西方向, 正向为东, y轴对应南北方向, 正向为北;x和y的范围分别为440.5~444.5 km、3 332.78~3 336.78 km, 测区均匀分布100 × 100个测点。设地下最大深度为1 km, 平均分为20层。在成像前对全张量重力梯度数据进行地形校正和高通滤波处理, 图 12给出了所用的梯度分量图。选取剖面x=442.56 km, y=3 334.44 km和z=400 m来进行分析。
|
| 图 12 实测数据重力梯度分量图 Fig. 12 Gravity gradient component map of measured data |
|
|
对实测数据的Gxz|Gyz进行联合相关成像, 结果见图 13。由图 13a、b可以看出, 盖岩的南北向长度约为1 100 m, 东西向约为1 200 m, 且盐丘从西北向东南逐渐变厚, 这一结果与钻井资料[30]吻合。

|
| a. x=442.56 km;b. y=3 334.44 km;c. z=400 m。 图 13 重力梯度数据Gxz|Gyz应用于实测数据 Fig. 13 Gravity gradiometry data Gxz|Gyz applied to measured data |
|
|
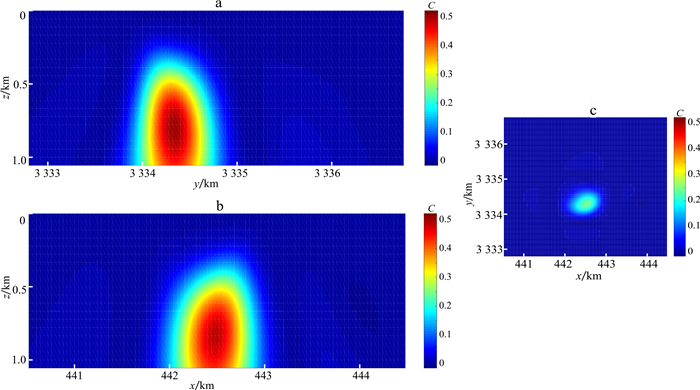
随后对梯度数据Gxz|Gyz|Gzz进行联合相关成像, 结果见图 14, 可以看出, 成像分辨率得到了提升, 盖岩的边界能被清晰地显示出来, 且形态与其他学者研究成果基本相符[27-29]。
|
| a. x=442.56 km;b. y=3 334.44 km;c. z=400 m。 图 14 重力梯度数据Gxz|Gyz|Gzz应用于实测数据 Fig. 14 Gravity gradiometry data Gxz|Gyz|Gzz applied to measured data |
|
|
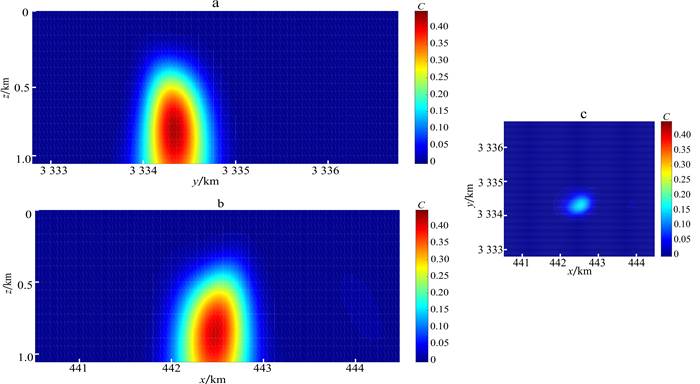
当在此基础上加入分量Gxy后, 对比图 15成像结果改进并不大。且从图 15c可以看出, 由于加入的信息过于集中, 导致水平方向的分辨率反而有所下降。由此可见, 组合Gxz|Gyz|Gzz成像效果最好, 但是纵向上的分辨率较低, 无法判断盖岩的下底深度。
|
| a. x=442.56 km;b. y=3 334.44 km;c. z=400 m。 图 15 重力梯度数据Gxz|Gyz|Gzz|Gxy应用于实测数据 Fig. 15 Gravity gradiometry data Gxz|Gyz|Gzz|Gxy applied to measured data |
|
|
为了确定盖岩的深度分布范围, 对Gxz|Gyz|Gzz梯度数据组合应用深度加权函数, 结合该地的地震[31]与测井[30]资料, z0取500 m, 结果见图 16。与图 14a相比, 图 16a纵向分辨率得到了一定的提升, 但异常体深部仍然存在下延过深的问题。

|
| a. x=442.56 km;b. y=3 334.44 km;c. z=400 m。 图 16 重力梯度数据Gxz|Gyz|Gzz结合深度加权函数应用于实测数据 Fig. 16 Gravity gradiometry data Gxz|Gyz|Gzz combined depth weighting function applied to measured data |
|
|
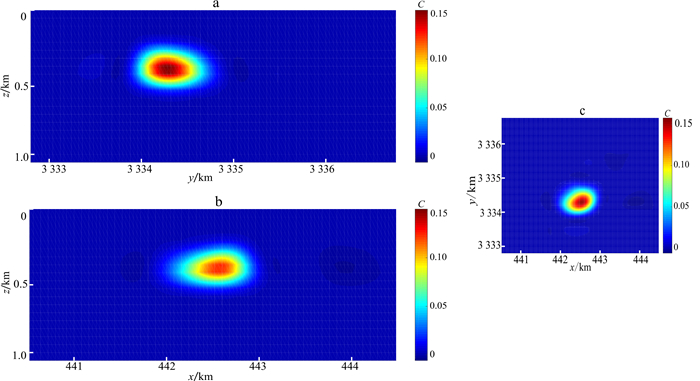
随后对梯度数据组合Gxz|Gyz|Gzz应用空间梯度加权函数, 取α=0.001, zmax=1 000 m, r=20, z1=200 m, z2=500 m, 成像结果见图 17。与图 16a、b相比, 图 17a、b纵向分辨率得到了明显改善, 可以判断出盖岩的深度范围是200~500 m。Ennen等[26]的解译结果为上顶埋深160 m, 下底埋深460 m;Geng等[28-29]给出的反演结果为200~600 m之间;Oliveria等[32]给出的下底深度为460 m;因此, 本文提出的方法具有可靠性和可行性, 能够应用于实测数据解释工作。另一方面, 研究区域内仅存在一个引起异常的主要目标体(盖岩), 不必采取分区加权的方法, 故本文没有对研究区域进行划分。
|
| a. x=442.56 km;b. y=3 334.44 km;c. z=400 m。 图 17 重力梯度数据Gxz|Gyz|Gzz结合空间梯度加权函数应用于实测数据 Fig. 17 Gravity gradiometry data Gxz|Gyz|Gzz combined depth weighting function applied to measured data |
|
|
1) 本文提出了基于深度加权的重力梯度数据联合相关成像方法, 该方法通过组合不同重力梯度数据并引入深度加权函数, 增强了相关成像方法对目标体的识别能力。
2) 理论模型试验证明Gxz|Gyz|Gzz组合效果最好, 成像分辨率得到了显著改善, 特别是能够准确地呈现出目标体的底部位置, 且具有抗噪性。
3) 将该方法应用于文顿盐丘区域的实测数据, 证实了方法的有效性和可行性。
致谢: Bell Geospace公司提供了实测重力梯度数据, 在此表示感谢。
| [1] |
Hou Zhenlong, Wei Xiaohui, Huang Danian. Fast Density Inversion Solution for Full Tensor Gravity Gradiometry Data[J]. Pure and Applied Geophysics, 2016, 173(2): 509-523. |
| [2] |
Oruc B, Sertcelik I, Kafadar O, et al. Structural Interpretation of the Erzurum Basin, Eastern Turkey, Using Curvature Gravity, Gradient Tensor and Gravity Inversion of Basement Relief[J]. Journal of Applied Geophysics, 2013, 88(4): 105-113. |
| [3] |
袁园, 黄大年, 余青露. 利用加强水平方向总水平导数对位场全张量数据进行边界识别[J]. 地球物理学报, 2015, 58(7): 2556-2565. Yuan Yuan, Huang Danian, Yu Qinglu. Using Enhanced Directional Total Horizontal Derivatives to Detect the Edges of Potential-Field Full Tensor Data[J]. Chinese Journal of Geophysics, 2015, 58(7): 2556-2565. |
| [4] |
高秀鹤, 黄大年, 孙思源, 等. 重力梯度数据协克里金三维反演确定岩脉倾向[J]. 吉林大学学报(地球科学版), 2017, 47(2): 589-596. Gao Xiuhe, Huang Danian, Sun Siyuan, et al. Identify the Dip Angle of the Dipping Dike Model Based on Cokriging Inversion of Gravity Gradient Data[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 589-596. |
| [5] |
Patella D. Introduction to Ground Surface Self-Potential Tomography[J]. Geophysical Prospecting, 1997, 45(4): 653-681. DOI:10.1046/j.1365-2478.1997.430277.x |
| [6] |
Mauriello P, Monna D, Patella D. 3D Geoelectric Tomography and Archaeological Applications[J]. Geophysical Prospecting, 1998, 46(5): 543-570. DOI:10.1046/j.1365-2478.1998.00102.x |
| [7] |
Mauriello P, Patella D. Resistivity Anomaly Imaging by Probability Tomography[J]. Geophysical Prospecting, 1999, 47(3): 411-429. DOI:10.1046/j.1365-2478.1999.00137.x |
| [8] |
Mauriello P, Patella D. Localization of Maximum Depth Gravity Anomaly Sources by a Distribution of Equivalent Point Masses[J]. Geophysics, 2001, 66(5): 1431-1437. |
| [9] |
Iuliano T, Mauriello P, Patella D. Looking Inside Mount Vesuvius by Potential Fields Integrated Probability Tomographies[J]. Journal of Volcanology and Geothermal Research, 2002, 113(3): 363-378. |
| [10] |
王绪本, 毛立峰, 高永才. 电磁导数场相关成像方法研究[J]. 成都理工大学学报(自然科学版), 2004, 31(6): 679-684. Wang Xuben, Mao Lifeng, Gao Yongcai. Probability Tomography of Electromagnetic Field-Derivative Method[J]. Journal of Chengdu University of Technology, 2004, 31(6): 679-684. DOI:10.3969/j.issn.1671-9727.2004.06.022 |
| [11] |
毛立峰, 王绪本, 高永才. 大地电磁概率成像的效果评价[J]. 地球物理学报, 2005, 48(2): 429-433. Mao Lifeng, Wang Xuben, Gao Yongcai. Appraisement on the MT Probability Temography[J]. Chinese Journal of Geopysics, 2005, 48(2): 429-433. DOI:10.3321/j.issn:0001-5733.2005.02.028 |
| [12] |
郭良辉, 孟小红, 石磊. 磁异常ΔT三维相关成像[J]. 地球物学报, 2010, 53(2): 435-441. Guo Lianghui, Meng Xiaohong, Shi Lei. 3D Correlation Imaging for Magnetic Anomaly ΔT Data[J]. Chinese Journal of Geophysics, 2010, 53(2): 435-441. |
| [13] |
郭良辉, 孟小红, 石磊, 等. 重力和重力梯度数据三维相关成像[J]. 地球物学报, 2009, 52(4): 1098-1106. Guo Lianghui, Meng Xiaohong, Shi Lei, et al. 3-D Correlation Imaging for Gravity Gradiometry Data[J]. Chinese Journal of Geophysics, 2009, 52(4): 1098-1106. |
| [14] |
马国庆, 杜晓娟, 李丽丽. 改进的位场相关成像方法[J]. 地球科学:中国地质大学学报, 2013, 38(5): 1121-1127. Ma Guoqing, Du Xiaojuan, Li Lili. Improved Potential Field Correlation Imaging Method[J]. Earth Science:Journal of China University of Geosciences, 2013, 38(5): 1121-1127. |
| [15] |
石磊, 郭良辉, 孟小红. 磁总场异常垂直梯度三维相关成像[J]. 地球物理学进展, 2012, 27(4): 1609-1614. Shi Lei, Guo Lianghui, Meng Xiaohong. 3D Correlation Imaging of the Vertical Gradient of Magnetic Total Field Anomaly[J]. Progress in Geophys, 2012, 27(4): 1609-1614. |
| [16] |
侯振隆, 王恩德. 基于泰勒级数的重力异常数据快速相关成像[J]. 东北大学学报(自然科学版), 2019, 40(4): 563-568. Hou Zhenlong, Wang Ende. Fast Probability Tomography of Gravity Anomaly Data Based on Taylor Series[J]. Journal of Northeastern University (Natural Science Edition), 2019, 40(4): 563-568. |
| [17] |
Li Yaoguo, Oldenburg W D. 3-D Inversion of Magnetic Data[J]. Geophysics, 1996, 61(2): 394-408. |
| [18] |
Federico Cella, Maurizio Fedi. Inversion of Potential Field Data Using the Structural Index as Weighting Function Rate Decay[J]. Geophysical Prospecting, 2012, 60(2): 313-336. DOI:10.1111/j.1365-2478.2011.00974.x |
| [19] |
Commer M. Three-Dimensional Gravity Modeling and Focusing Inversion Using Rectangular Meshes[J]. Geophysical Prospecting, 2011, 59(5): 966-979. |
| [20] |
Commer M, Newman G A, Williams K H, et al. 3D Induced-Polarization Data Inversion for Complex Resistivity[J]. Geophysics, 2011, 76(3): 157-171. |
| [21] |
Chen Z, Meng X, Guo L, et al. GICUDA:A Parallel Program for 3D Correlation Imaging of Large Scale Gravity and Gravity Gradiometry Data on Graphics Processing Units with CUDA[J]. Computers & Geosciences, 2012, 46(5): 119-128. |
| [22] |
Li Y, Oldenburg D W. 3-D Inversion of Gravity Data[J]. Geophysics, 1998, 63: 109-119. DOI:10.1190/1.1444302 |
| [23] |
Li Y. 3-D Inversion of Gravity Gradiometer Data[C]//SEG Int'l Exposition and Annual Meeting. San Antonio: [s. n.], 2001: 1470-1473.
|
| [24] |
秦朋波.重力和重力梯度数据联合反演方法研究[D].长春: 吉林大学, 2016. Qin Pengbo. A Study on Integrated Gravity and Gravity Gradient Data in Inversion[D]. Changchun: Jilin University, 2016. |
| [25] |
Ennen C. Mapping Gas-Charged Fault Blocks Around the Vinton Salt Dome, Louisiana Using Gravity Gradiometry Data[D].Houston: University of Houston, 2012.
|
| [26] |
Ennen C, Hall S. Structural Mapping of the Vinton Salt Dome, Louisiana, Using Gravity Gradiometry Data[C]//2011 SEG Annual Meeting.[S. l.]: Society of Exploration Geophysicists, 2011: 15.
|
| [27] |
侯振隆.重力全张量梯度数据的并行反演算法研究及应用[D].长春: 吉林大学, 2016. Hou Zhenlong. Research and Application of the Parallel Inversion Algorithms Based on the Full Tensor Gravity Gradiometry Data[D].Changchun: Jilin University, 2016. |
| [28] |
耿美霞.基于地质统计学的重力梯度全张量数据三维反演方法研究[D].长春: 吉林大学, 2015. Geng Meixia. The Study of 3D Inversion of Full Tensor Gravity Gradiometry Data Based on Geostatistics Method[D]. Changchun: Jilin University, 2015. |
| [29] |
Geng M, Huang D, Yang Q, et al. 3D Inversion of Airborne Gravity Gradiometry Data Using Cokriging[J]. Geophysics, 2014, 79(4): G37-G47. |
| [30] |
Thompson S A, Eichelberger O H. Vinton Salt Dome, Calcasieu Parish, Louisiana[J]. AAPG Bulletin, 1928, 12(4): 385-394. |
| [31] |
Marfurt K J, Zhou H W, Sullivan E C. Development and Calibration of New 3-D Vector VSP Imaging Technology: Vinton Salt Dome, LA[R]. Texas: University of Houston, 2004.
|
| [32] |
Oliveira V C, Barbosa V C F. 3-D Radial Gravity Gradient Inversion[J]. Geophysical Journal International, 2013, 195(2): 883-902. DOI:10.1093/gji/ggt307 |



