2. 河北省地质环境监测院河北省地质资源环境监测与保护重点实验室, 石家庄 050021;
3. 河北建筑工程学院市政与环境工程系, 河北 张家口 075000
2. Hebei Key Laboratory of Geological Resources and Environment Monitoring and Protection, Hebei Geological Environmental Monitoring Institute, Shijiazhuang 050021, China;
3. Department of Municipal and Environmental Engineering, Hebei University of Architecture, Zhangjiakou 075000, Hebei, China
0 引言
抽出-处理技术是有效的地下水修复技术之一,可快速阻断污染物迁移和有效去除地下水中污染物[1-2]。在实施过程中,抽水井的布置及抽水量的大小在很大程度上决定了修复工程的效率及成本,优化抽水方案能够增加抽水井抽出效率,减少修复成本,服务于实际工程[3]。目前,国外主要是通过模拟-优化模型对抽水方案进行优化。Kazemzadeh等[4]将萤火虫算法(FA)与有限元模拟方法(FEM)相结合,提出FA-FEM模型,并利用该方法将运行成本、总抽水量降至最低;Park[5]利用数值模拟软件模拟地下水流动和污染物运移,并用遗传算法对抽水方案进行优化,使修复费用降低20%。国内对于抽出-处理技术的研究起步较晚,抽出-处理技术因操作简单、抽出效果显著而被应用广泛:刘明柱、陈坚等[6-7]对抽出-处理技术影响因素进行分析、并开展了抽水方案优化研究;刘苑、赵勇胜、万鹏、蒲敏等[8-11]分别采用Visual Mdoflow的MGO模块和GMS软件联合MGO程序对抽水方案进行优化,得出最优的抽水方案。目前优化方法多是依据现状污染羽进行优化确定抽水方案,而抽出-处理技术所需修复时间较长,优化的抽水方案仅在一定的时间段内为最优,超过一定时间,优化的抽水方案便会因抽水井位置固定、抽水流量固定等局限而变为一种假性优化方案;同时,优化成本降低幅度也仅限于与优化前相比,未提出一个优化的衡量标准;此外,抽出-处理技术在修复地下水后期存在拖尾与反弹问题,为减少修复成本,可结合其他地下水修复技术联合修复。针对目前优化方法存在的不足以及抽出-处理技术的局限,本研究以抽水井抽出效率大小来定性表征修复成本,提出了一种基于污染羽时空分布及抽水井抽出效率曲线确定优化时间节点及确定抽出终点的方法,以期为地下水修复工程提供参考依据。
1 材料与方法 1.1 场地概况研究区为青海省某铬盐厂,厂区面积为12万m2,主要污染物为六价铬(Cr(Ⅵ))。研究区位于海晏盆地冲积平原,地势较为平坦,东部为山区,西部为哈利涧河,地势东高西低。岩性(厚度)由地表向下依次为杂填土(0.0~18.0 m)、砂卵砾石(20.0~45.0 m)、黏土层(7.5~10.0 m)、砂卵砾石(45.0~60.0 m)。因黏土层厚度较大,下覆承压含水层并未受到污染。本研究以上伏潜水含水层为研究对象。潜水含水层地下水埋深0~18 m,渗透系数为26.58 m/d,地下水流向为自东向西,其补给来源主要为大气降雨补给及区域地下径流,排泄方式主要为人工排泄及径流排泄。
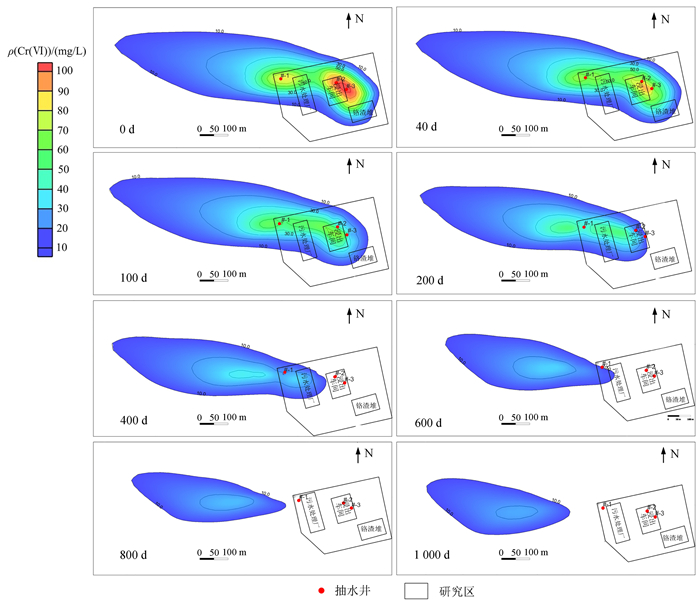
依据调查结果,刻画地下水污染羽的二维分布如图 1。六价铬污染高值区主要处于原厂区内铬渣堆场、浸出车间等处。

|
| 图 1 研究区地下水污染羽分布 Fig. 1 Plume distribution of groundwater pollution in the study area |
|
|
抽水井抽出效率定义为抽水井抽出污染物浓度与抽水井初始污染物浓度比值。假设抽水井布设在浓度最高值区,在抽水流量一定时,抽水井抽出效率越大,单位时间抽出污染物质量越多,含水层中污染物总质量削减越快;反之,抽水井抽出效率越小,单位时间抽出污染物质量越少,含水层中污染物总质量削减越慢。
抽出-处理技术修复地下水工程中成本包括建井费用、污水处理费用、运营费用(管道、电费、人工),大多数地下水抽出-处理修复工程中,污水处理费用及运营费用构成主要修复成本。当含水层中污染物质量、抽水流量一定时,抽水井抽出效率越高,含水层中污染物质量削减速度越快,所需修复抽出地下水量越少、修复时间越短。因此,提高抽水井抽出效率,即是减少修复成本。
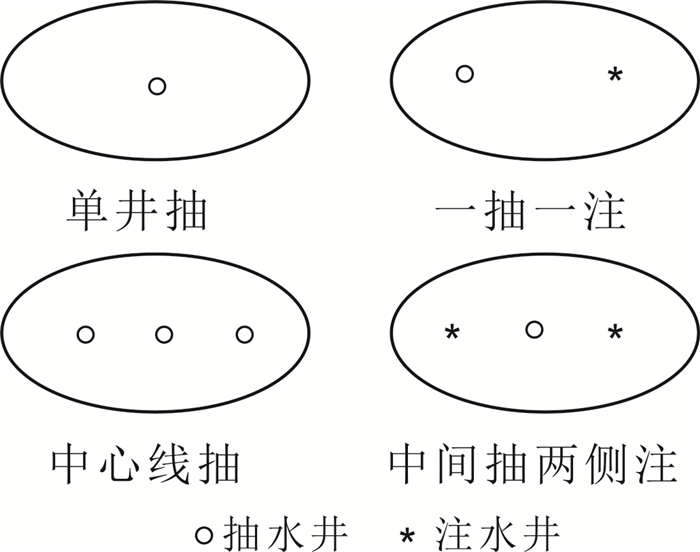
1.3 抽水方案布设方法抽水井/注入井的布设依据主要有两方面[11]:1)参考类似成功修复案列的布井方式;2)采用数值模拟软件,根据场地特征资料,利用不同优化方法模拟不同井布局下的抽水井抽出效率,布设抽水方案。抽/注井布局形式多样[12],主要包括有单井抽、一抽一注、中心线抽、中间抽两侧注等布井方式(图 2),本文采用中心线抽布设方法。目前模拟-优化方法主要有有限元算法、有限差分算法、萤火虫算法、FA-FEM优化方法、遗传算法,本文采用有限元算法模拟等。
|
| 图 2 不同布井方式示意 Fig. 2 Different pattern of well distribution |
|
|
地下水修复技术可分为异位修复技术和原位修复技术。异位修复技术主要为抽出-处理处理技术,将污染地下水先用抽提系统转移到地上,然后再处理。原位修复技术是指在基本不破坏土体和地下水自然环境条件下,在原地进行修复的方法[13]。原位修复技术包括监测自然衰减技术、生物强化修复技术、可渗透反应墙技术、空气曝气技术以及原位化学氧化/还原技术等。抽出-处理技术可与监测自然衰减技术、生物强化技术、原位化学氧化/还原技术联合使用。
1.5 分析方法抽水方案优化的方法主要有解析解方法、数值模拟法、人工判断法。本次研究采取以数值模拟为基础、联合层次分析法和专家打分法、综合抽水井抽出效率和污染羽时空分布动态变化判断抽水方案优化时间节点及抽出终点的方法。
具体步骤为:1)详细刻画污染羽现状,布设初始抽水方案。2)运用数值模拟方法运行初始抽水方案,获取抽水井抽出效率和污染羽时空分布。3)依据抽水井抽出效率和污染羽时空分布,确定抽水方案优化时间节点或抽出终点。4)根据污染羽运移后的时空分布,重新布设抽出效率相对较高的抽水方案或弃用抽出-处理技术,使用其他修复技术,以达到既定修复目标。重新布设抽水方案是指在某一时间节点,关停1个或多个抽水井后继续抽水或关停1个或多个抽水井后重新补充布设抽水井。步骤1)2)4)的实现可参考本文1.3和1.4小节,步骤3)确定抽水方案优化时间节点或抽出终点则通过层次分析法和专家打分法[14-18]来实现。
层次分析法是美国运筹学家T. L. Saaty等于20世纪70年代提出的一种计算各层次指标权重的方法。该方法通过将指标两两进行比较得到判断矩阵,并通过一致性检验,可克服完全靠主观分析判断确定指标权重所造成的片面性,提高分析的客观性和科学性[19]。层次分析法是将决策问题按总目标、各层子目标、评价准则直至具体备选方案的顺序分解为不同的层次结构,然后用求解判断矩阵特征向量的办法求得每一层次的各元素对上一层次某元素的优先权重,最后再用加权和的方法递阶归并各备择方案对总目标的最终权重,此最终权重最大者即为最优方案。近年来,专家-层次分析法在地下水资源评价方面应用广泛,肖云云等[20]运用模糊层次分析法对塔里木河流域农业气候资源进行了综合评价,并对光能资源、热量资源、水分资源在各地区的分布进行了比较。虞未江等、王亚维等[21-22]通过引入层次分析法构建了地下水水质综合评价指标体系;江思义等[23]提出了一种基于专家-层次分析法的地下空间适宜性评价方法,先通过专家打分法选择合适的评价因子,再利用层次分析法确定各评价因子的权数,最后通过MapGIS空间分析功能将各因子的分区图按因子的权重进行叠加,得到适宜性分区图,并作出适宜性评价。利用层次分析法和专家打分法确定抽水方案优化时间节点和抽出终点具有较高的科学性和客观性,其主要步骤包括构建评价指标体系、构建层次结构分析模型、构建判断矩阵,具体如下:
1) 构建评价指标体系
层次分析法的评价指标体系共有3层,依次为目标层(G)、准则层(C)、措施层(P)。目标层即为要解决的问题,准则层是解决目标层需要综合考虑的因素,措施层是根据需要综合考虑的因素来设置的几种措施。本案例中,将确定最佳优化时间节点定为评价一级指标,即目标层。土壤污染风险管控和修复监测技术导则(HJ 25.2—2019)[24]、污染地块地下水修复和风险管控技术导则(HJ25.6—2019)[25]以及新出的地下水污染风险健康风险评估指南中明确指出,不同的场地利用方式影响土壤及地下水的修复目标、修复策略、修复思路;不同地块、不同管理者对于污染地块的修复时间要求也不一样,修复时间的长短严重影响着抽水方案的初始设置、方案优化时间节点以及抽出终点;地区经济发展、污染地块管理者的资本大小以及修复力度的不同均会影响抽水方案后续的优化、抽出终点;抽水时间越长、抽出水量越多,二次污染也越多。本例中,评价二级指标即准则层,经过多次专家论证,将影响最佳优化时间节点的准则设定如下:一是土地利用规划,二是修复成本,三是二次污染情况,四是修复时间,分别用符号C1、C2、C3、C4表示。不同场地可依据实际情况增设准则层的影响因素。本例中,评价三级指标即措施层,抽出效率在0~100%之间,划分抽出效率区间是为了判断优化时间节点和抽出终点,抽出效率划分越详细,抽出时间节点和抽出终点越准确、合理、可行。不同抽出效率下选择联合其他修复技术或重新布设抽水方案会影响场地修复时间、修复成本。不同场地对于抽出效率的划分可依据项目治理、管理、规划要求进行详细/简化划分。本文以青海某铬盐厂为例,结合现场情况,将抽出效率划分了4个档次,分别为A1(80%~100%)、A2 (50%~80%)、A3 (20%~50%)、A4 (0%~20%),故优化方案(措施层)有:抽出效率为A1时重新布设抽水方案、抽出效率为A2时重新布设抽水方案、抽出效率为A3时重新布设抽水方案、抽出效率为A4时重新布设抽水方案、抽出效率为A1时使用其他修复技术、抽出效率为A2时使用其他修复技术、抽出效率为A3时使用其他修复技术、抽出效率为A4时使用其他修复技术等,分别用符号P1、P2、P3、P4、P5、P6、P7、P8表示。
2) 构建层次结构分析模型
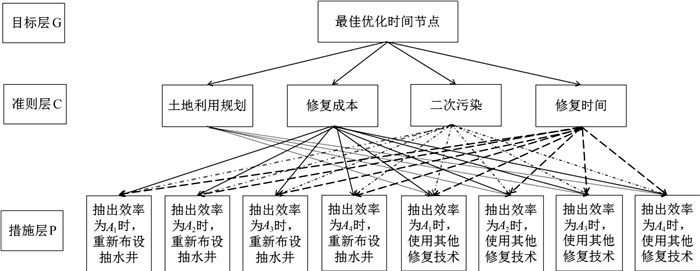
经向专家咨询,构建层次结构分析模型(图 3)。
|
| 图 3 最佳优化时间节点的层次结构分析模型 Fig. 3 Hierarchical structure analysis model of optimal time nodes |
|
|
3) 构建判断矩阵
确定各准则之间的相对重要性采用专家打分方法和九级标度法,项目管理方、政府、专家根据模拟抽水井抽出效率-时间曲线及污染羽时空分布结果对各准则(C1、C2、C3、C4)相对于目标层的重要程度进行评判并给出分值,继而构建判断矩阵G-C、C1-P、C2-P、C3-P、C4-P。其中G-C表示针对目标层(最佳优化时间节点)判断准则层4个影响因素之间的相对重要性,其重要程度利用九级标度法来体现,判断方法则采用专家打分法。Ci与Cj的重要性比较用cij表示,若Ci与Cj的重要程度相同,cij=1;若Ci比Cj的重要程度强,则cij=2, 3, …,9,且随Ci比Cj的重要程度越来越强,cij值依次增大;且规定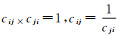
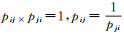
用符号W表示本层要素对上一层要素的重要性即权重向量,W采用求和法计算,其中Wg为准则层C相对于目标层G的重要程度所形成的权重;Wc1、Wc2、Wc3、Wc4分别代表措施层P相对于准则层C的重要程度所形成的权重;WZ为每个措施层P相对于总目标层G的总权重,为Wc1×Wg进行求和。判断矩阵即为上述描述的G-C、C-P等矩阵,衡量判断矩阵一致性的数量指标用符号EI表示,EI= 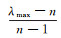
抽出-处理技术主要用于快速抽出高浓度污染物和截获一定浓度的污染羽,以防止地下水中污染物随水流迁移而污染下游地下水。对于以截获为目的的抽水方案,常采用的方法为在污染羽下游以垂直于地下水流方向布设截获井,抽水井的数量主要依据解析解公式对单井捕获半径进行初步计算;对于以抽出更多污染物为目的的布点方案,目前常采用方法为在污染物高浓度区域沿地下水流方向以中心轴线布设抽水井。由于该场地污水日处理能力有限,故布设抽水方案以抽出更多污染物为目的,因此采取在污染羽高值区域沿地下水流方向以中心线布井方式布设抽水井,抽水井抽水流量为300 m3/d,布井示意见图 4。
|
| 图 4 研究区抽出方案初步布设图 Fig. 4 Preliminary layout of the extraction scheme for the study area |
|
|
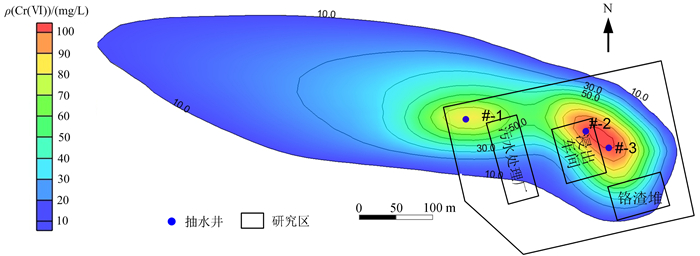
依据模拟数据,绘制抽水方案优化后抽水井的污染羽时空分布图(图 5)和抽出效率时间曲线(图 6)。抽水100 d后:#-2井和#-3井逐渐趋向于污染物低浓度区,#-1井仍位于污染物高浓度区(图 5);#-2井和#-3井抽水井抽出效率分别降为37%和25%,#-1井抽出效率下降较缓慢,降至63%,继续抽水#-2井和#-3井抽水效率将下降至20%以下(图 6)。
|
| 图 5 研究区优化前污染羽时空分布图 Fig. 5 Spatial and temporal distribution of pollution plume before optimization in the study area |
|
|
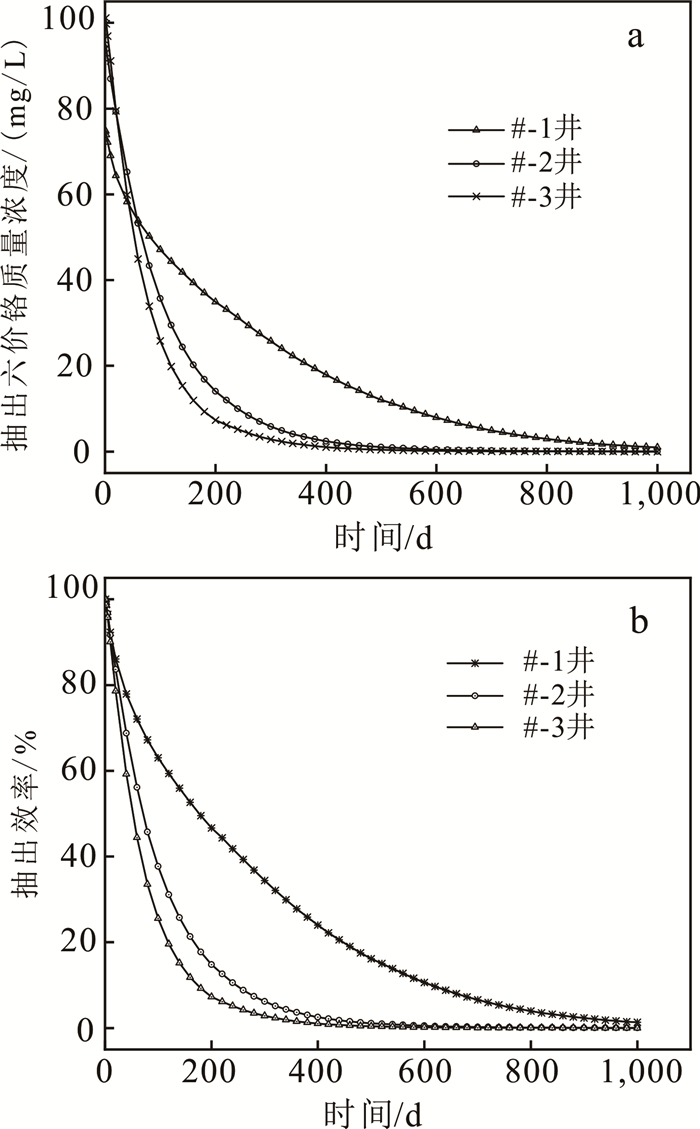
|
| 图 6 抽水井六价铬质量浓度-时间曲线(a)和抽出效率-时间曲线(b) Fig. 6 Concentration-time curve (a)and extraction efficiency-time curve (b)of hexavalent chromium mass concentration in pumping well |
|
|
通过咨询项目管理方、政府、专家,利用专家打分方法结合九级标度法确定各准则之间的相对重要性(表 1—5),构建了适合该场地抽出处理运行的判断矩阵G-C、C1-P、C2-P、C3-P、C4-P。运用Matlab计算判断矩阵G-C、C1-P、C2-P、C3-P、C4-P的最大特征根值,结果显示:判断矩阵G-C中,FI=0.900,EI=0.060,HR=EI/FI=0.067 < 0.1,表示该判断矩阵具有满意的一致性,且Wg=[0.082,0.256,0.278,0.384];判断矩阵C1-P中,FI=1.41,EI =0.060,HR = EI / FI = 0.042 < 0.1,表示该判断矩阵具有满意的一致性,且Wc1=[0.136,0.166,0.159,0.227,0.017,0.040,0.101,0.155];判断矩阵C2-P中,FI =1.41,EI=0.126,HR = EI / FI = 0.089 < 0.1,表示该判断矩阵具有满意的一致性,且Wc2=[0.085,0.056,0.034,0.020,0.295,0.221,0.163,0.124];判断矩阵C3-P中,FI=1.41,EI=0.040,HR = EI/FI = 0.028 < 0.1,表示该判断矩阵具有满意的一致性,且Wc3=[0.136,0.166,0.159,0.227,0.017,0.040,0.101,0.155];判断矩阵C4-P中,FI =1.41,EI =0.086,HR = EI / FI = 0.061 < 0.1,表示该判断矩阵具有满意的一致性,且Wc4=[0.136,0.166,0.159,0.227,0.017,0.040,0.101,0.155]。将根据判断矩阵求得的各准则权重进行层次总排序,结果见表 6。从表 6中可以看出P3所占权重最大,为优化的最佳时间节点和优化方案。最佳优化时间节点为抽水井抽出效率为20%~40%,即抽水100 d后,对抽水方案进行重新布设。
| G | C1 | C2 | C3 | C4 |
| C1 | 1 | 1/3 | 1/5 | 1/4 |
| C2 | 3 | 1 | 1/3 | 1/5 |
| C3 | 4 | 3 | 1 | 1/3 |
| C4 | 5 | 4 | 3 | 1 |
| C1 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| P1 | 1 | 1 | 1 | 1 | 9 | 7 | 6 | 4 |
| P2 | 1 | 1 | 1 | 1 | 8 | 6 | 5 | 3 |
| P3 | 1 | 1 | 1 | 1 | 6 | 5 | 4 | 3 |
| P4 | 1 | 1 | 1 | 1 | 5 | 4 | 3 | 2 |
| P5 | 1/9 | 1/8 | 1/6 | 1/5 | 1 | 1/3 | 1/7 | 1/9 |
| P6 | 1/7 | 1/6 | 1/5 | 1/4 | 3 | 1 | 1/4 | 1/6 |
| P7 | 1/6 | 1/5 | 1/4 | 1/3 | 7 | 4 | 1 | 1/3 |
| P8 | 1/4 | 1/3 | 1/3 | 1/2 | 9 | 6 | 3 | 1 |
| C2 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| P1 | 1 | 1/2 | 1/4 | 1/3 | 5 | 4 | 3 | 2 |
| P2 | 2 | 1 | 1/2 | 1/2 | 6 | 4 | 3 | 2 |
| P3 | 4 | 2 | 1 | 8 | 6 | 5 | 4 | 2 |
| P4 | 3 | 2 | 1/8 | 1 | 5 | 4 | 3 | 2 |
| P5 | 1/5 | 1/6 | 1/6 | 1/5 | 1 | 1/2 | 1/4 | 1/5 |
| P6 | 1/4 | 1/4 | 1/5 | 1/4 | 2 | 1 | 1/3 | 1/4 |
| P7 | 1/3 | 1/3 | 1/4 | 1/3 | 4 | 3 | 1 | 1/3 |
| P8 | 1/2 | 1/2 | 1/2 | 1/2 | 5 | 4 | 3 | 1 |
| C3 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| P1 | 1 | 1/2 | 1/2 | 1/2 | 5 | 4 | 3 | 2 |
| P2 | 2 | 1 | 1/2 | 1/2 | 6 | 5 | 4 | 3 |
| P3 | 2 | 2 | 1 | 1/2 | 7 | 6 | 5 | 4 |
| P4 | 2 | 2 | 2 | 1 | 8 | 7 | 6 | 5 |
| P5 | 1/5 | 1/6 | 1/7 | 1/8 | 1 | 1/2 | 1/3 | 1/4 |
| P6 | 1/4 | 1/5 | 1/6 | 1/7 | 2 | 1 | 1/2 | 1/3 |
| P7 | 1/3 | 1/4 | 1/5 | 1/6 | 3 | 2 | 1 | 1/3 |
| P8 | 1/2 | 1/3 | 1/4 | 1/5 | 4 | 3 | 3 | 1 |
| C4 | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 |
| P1 | 1 | 2 | 3 | 4 | 1/5 | 1/4 | 1/3 | 1/2 |
| P2 | 1/2 | 1 | 2 | 3 | 1/6 | 1/5 | 1/4 | 1/3 |
| P3 | 1/3 | 1/2 | 1 | 2 | 1/7 | 1/6 | 1/5 | 1/4 |
| P4 | 1/4 | 1/3 | 1/2 | 1 | 1/8 | 1/7 | 1/6 | 1/5 |
| P5 | 5 | 6 | 7 | 8 | 1 | 5 | 4 | 3 |
| P6 | 4 | 5 | 6 | 7 | 1/5 | 1 | 4 | 2 |
| P7 | 3 | 4 | 5 | 6 | 1/4 | 1/4 | 1 | 2 |
| P8 | 2 | 3 | 4 | 5 | 1/3 | 1/2 | 1/2 | 1 |
| C1 | C2 | C3 | C4 | 权重 | |
| 0.082 | 0.256 | 0.278 | 0.384 | ||
| P1 | 0.14 | 0.14 | 0.13 | 0.09 | 0.11 |
| P2 | 0.17 | 0.16 | 0.17 | 0.06 | 0.12 |
| P3 | 0.16 | 0.27 | 0.22 | 0.03 | 0.16 |
| P4 | 0.23 | 0.17 | 0.26 | 0.02 | 0.14 |
| P5 | 0.02 | 0.02 | 0.02 | 0.30 | 0.13 |
| P6 | 0.04 | 0.04 | 0.04 | 0.22 | 0.11 |
| P7 | 0.10 | 0.08 | 0.06 | 0.16 | 0.11 |
| P8 | 0.16 | 0.13 | 0.10 | 0.12 | 0.12 |
根据层次分析和专家打分方法确定优化节点为100 d,即抽水100 d后,重新布设抽水方案。从图 5、图 6可知:抽水100 d后,#-2井和#-3井抽出效率分别降至37%和25%,但其位置已偏离地下水中污染羽的高浓度中心,继续使用#-2井和#-3井抽水会导致修复进度缓慢,修复成本增加等问题。从图 5可知,抽水100 d后,含水层中残留污染物质量较多,污染物高浓度分布区相对较大,故采取原方案抽水100 d,随即将#-2和#-3井关闭,在污染物高浓度分布区沿地下水流方向重新布设2眼抽水井分别为#-4井和#-5井,抽水流量保持不变的抽水方案。布井示意如图 7所示。

|
| 图 7 抽出方案优化1次布井分布 Fig. 7 Extraction scheme was optimized for one time well distribution |
|
|
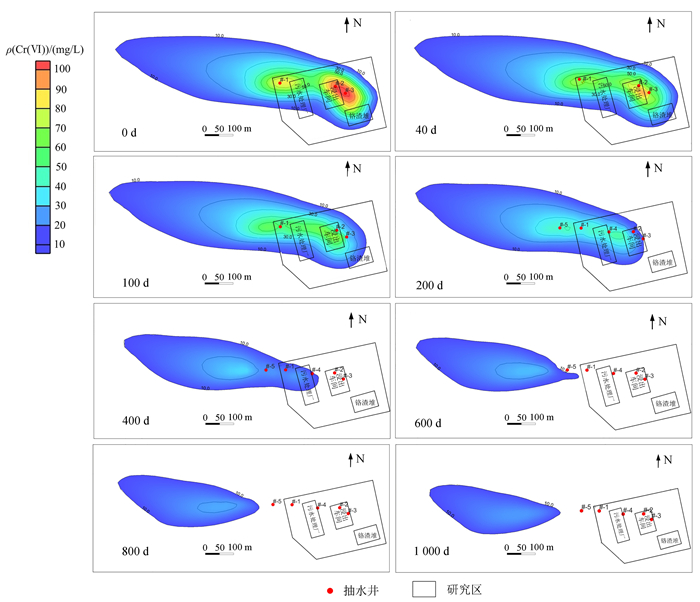
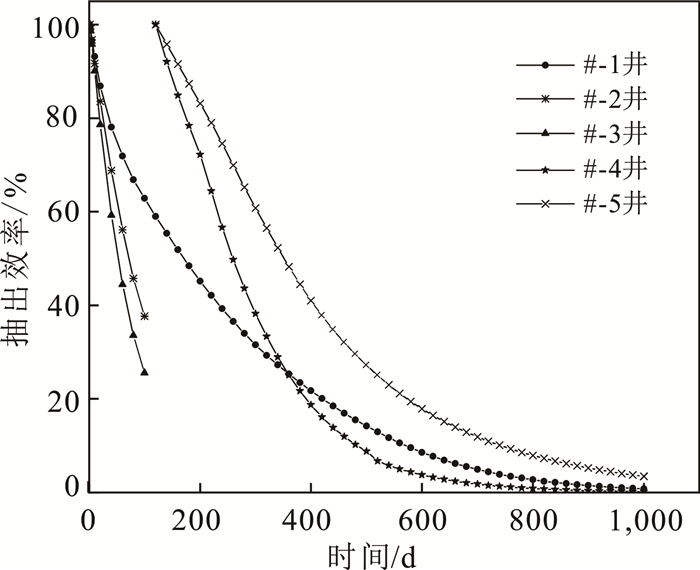
依据模拟数据,绘制抽水方案优化后的污染羽时空分布图和抽水井的抽出效率时间曲线(图 8、图 9),从图 8可知,抽水200 d后,重新布设的#-4井和#-5井依然处于污染物高值区,而#-2井和#-3井早已处于污染物的边缘区;对比图 5和图 8可知,相同抽水时间内,优化后的抽水方案较优化前的抽水方案其污染物分布范围缩减更快,污染物最高浓度更低。从图 9可得:#-2井和#-3井在抽水100 d后,抽水井抽出效率分别降为37%和25%,#-1井抽出效率下降较缓慢,为63%;重新布设的#-4和#-5抽水井在抽水100 d后抽出效率降为72%和83%,下降较缓慢,抽出污染物能力较强。
|
| 图 8 研究区优化后污染羽时空分布 Fig. 8 Spatial and temporal distribution of pollution plume was optimized in the study area |
|
|
|
| 图 9 优化后抽水井六价铬抽出效率-时间曲线 Fig. 9 Extraction efficiency-time curve of hexavalent chromium from the pumping well after optimization |
|
|
基于优化1次后模拟结果,采用层次分析法和专家打分法确定各措施层所占的权重,并进行层次总排序,结果表明P7(即抽出效率在20%~40%之间时联合其他修复技术修复剩余污染地下水)所占权重最大,由抽水井抽出效率时间曲线可知,抽水400 d后,抽水井抽出效率降至20%~40%之间,因此进行第2次优化的时间节点为400 d。
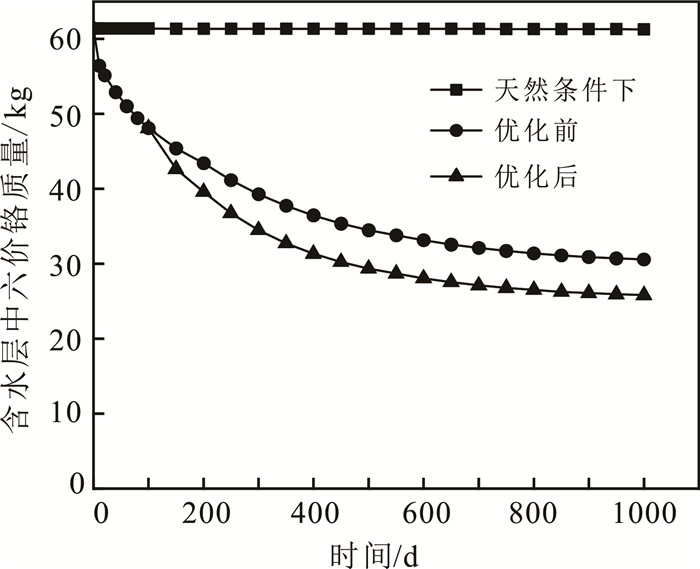
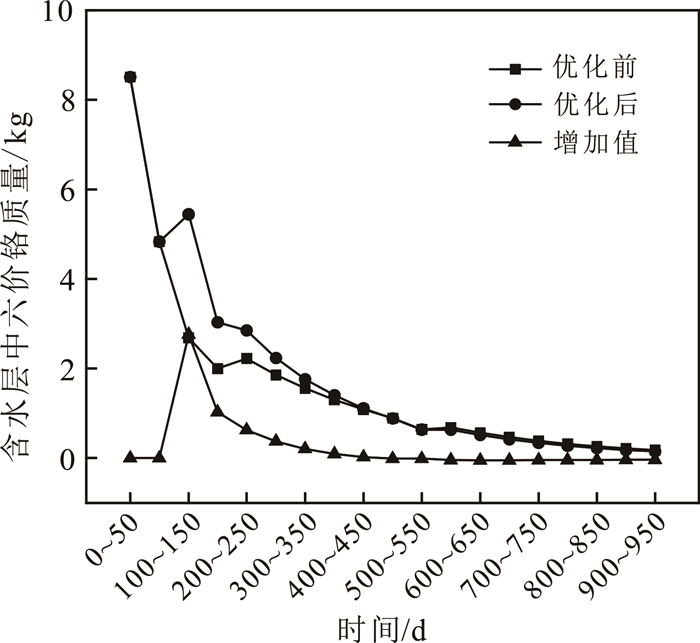
2.5 抽水方案模拟结果对比天然条件、优化前抽水方案抽水、优化后抽水方案抽水3种情况下含水层中六价铬总质量随时间变化曲线(图 10)以及相同时间间隔内2种抽水方案去除含水层中六价铬质量-时间曲线(图 11)可知:抽水400 d后,天然情况下、优化前抽水方案、优化后抽水方案对含水层六价铬总质量去除率分别为0.01%、40.65%、48.96%。从图 8—11可知,用优化后的抽水方案抽水400 d后,含水层中六价铬总质量削减48.96%,此时含水层中污染物最高质量浓度已从109 mg/L下降到21 mg/L左右。
|
| 图 10 含水层中六价铬质量随时间变化曲线 Fig. 10 Mass-time of the hexavalent chromium in the aquifer |
|
|
|
| 图 11 时间间隔为50 d时六价铬质量-时间曲线 Fig. 11 Mass concentration-time when time interval was 50 d of the hexavalent chromium |
|
|
通过2次优化模拟分析,确定最终抽水方案为:原抽水方案抽水100 d后,重新布设抽水方案并继续抽水300 d,共计抽水400 d;400 d后联合其他修复技术修复污染地下水。优化2次后的抽水方案相比于原抽水方案节约抽水时间600 d,在400 d的时间内,优化后抽水方案相比于优化前抽水方案去除含水层中六价铬质量增加了8.31%,降低了污水处理成本以及修复运营成本。
3 结论1) 提出一种融合数值模拟法、层次分析法和专家判断法,基于抽水井抽出效率、污染羽的时空变化和抽水井抽出污染物质量浓度随时间变化情况,优化抽出-处理工作方案,确定抽出终点的方法。通过评估抽水井抽出效率,以分段、多次优化抽水方案提高抽出效率、降低修复成本、减少修复时间为工作思路,建立了抽水方案优化时间节点评价指标体系,运用层次分析法和专家打分法确定各指标权重,定量分析方案优化时间节点选择。
2) 以青海某铬盐厂为例,运用该研究方法,优化抽水方案,原方案抽水100 d后,重新布设抽水井,持续抽水300 d,共计抽水400 d后联合其他修复技术修复污染地下水,经评估优化,减少修复时间600 d,含水层中六价铬去除率增加8.31%,缩减了修复成本及运营成本。
| [1] |
王燕.硝酸盐地下水污染数值模拟与抽出-处理技术抽水井优化研究[D].保定: 河北农业大学, 2014: 10-12. Wang Yan. Numerical Simulation of Nitrate Groundwater Pollution and Optimization of Pumping Well with Extraction and Treatment Technology[D]. Baoding: Agricultural University of Hebei, 2014: 10-12. http://cdmd.cnki.com.cn/Article/CDMD-10086-1015525678.htm |
| [2] |
姜烈, 何江涛, 姜永海, 等. 地下水硝酸盐污染抽出处理优化方法模拟研究[J]. 环境科学, 2014(7): 2572-2578. Jiang Lie, He Jiangtao, Jiang Yonghai, et al. Simulation Study on Optimal Extraction and Treatment Method of Groundwater Nitrate Pollution[J]. Environmental Science, 2014(7): 2572-2578. |
| [3] |
郑春苗. 地下水污染物迁移模拟[M]. 北京: 高等教育出版社, 2009. Zheng Chunmiao. Ground Water Pollutant Migration Simulation[M]. Beijing: Higher Education Press, 2009. |
| [4] |
Kazemzadeh-Parsi M J, Daneshmand F, Ahmadfard M A, et al. Optimal Groundwater Remediation Design of Pump and Treat Systems via a Simulation-Optimization Approach and Firefly Algorithm[J]. Engineering Optimization, 2015(1): 1-17. |
| [5] |
Park Y C. Cost-Effective Optimal Design of a Pump-and-Treat System for Remediating Groundwater Contaminant at an Industrial Complex[J]. Geosciences Journal, 2016, 6: 891-901. |
| [6] |
宫志强, 刘明柱, 刘伟江, 等. 单井捕获地下水污染羽的优化方法[J]. 环境工程学报, 2019, 13(10): 2468-2474. Gong Zhiqiang, Liu Mingzhu, Liu Weijiang, et al. Optimization Method for Single Well Capture of Groundwater Pollution Plume[J]. Journal of Environmental Engineering, 2019, 13(10): 2468-2474. |
| [7] |
宫志强, 陈坚, 杨鑫鑫, 等. 某铬污染场地地下水抽水方案优化[J]. 环境工程, 2019, 37(5): 1-3, 75. Gong Zhiqiang, Chen Jian, Yang Xinxin, et al. Optimization of Groundwater Pumping Scheme for a Chrome-Polluted Site[J]. Environmental Engineering, 2019, 37(5): 1-3, 75. |
| [8] |
刘苑.地下水污染区抽水井优化研究[D].北京: 清华大学, 2008. Liu Yuan. Optimization of Pumping Wells in Groundwater Pollution Areas[D]. Beijing: Tsinghua University, 2008. http://cdmd.cnki.com.cn/Article/CDMD-10003-2009083700.htm |
| [9] |
赵勇胜. 地下水污染场地风险管理与修复技术筛选[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1426-1433. Zhao Yongsheng. Selection of Risk Management and Remediation Techniques for Groundwater Contaminated Sites[J]. Journal of Lilin University (Earth Science Edition), 2012, 42(5): 1426-1433. |
| [10] |
万鹏, 张旭, 李广贺, 等. 基于模拟-优化模型的某场地污染地下水抽水方案设计[J]. 环境科学研究, 2016, 29(11): 1608-1616. Wan Peng, Zhang Xu, Li Guanghe, et al. Design of Groundwater Pumping Scheme for Contaminated Ground Based on Simulation-Optimization Model[J]. Environmental Science Research, 2016, 29(11): 1608-1616. |
| [11] |
蒲敏. 污染场地地下水抽出处理技术研究[J]. 环境工程, 2017(4): 12-14. Pu Min. Study on Groundwater Extraction and Treatment Technology for Contaminated Sites[J]. Environmental Engineering, 2017(4): 12-14. |
| [12] |
Satkin R L, Bedient P B. Effectiveness of Various Aquifer Restoration Schemes Under Variable Hydrogeologic Conditions[J]. Groundwater, 2010, 26(4): 488-498. |
| [13] |
刘姝媛, 王红旗. 地下水污染修复技术研究进展[J]. 科学, 2014, 66(4): 38-40. Liu Shuyuan, Wang Hongqi. Research Progress of Groundwater Pollution Remediation Technology[J]. Science, 2014, 66(4): 38-40. |
| [14] |
潘静静, 杨月锋, 刘家财. 基于层次分析法的教学方法评价:以《现代仓储管理》课程为例[J]. 高教论坛, 2015(6): 87-89. Pan Jingjing, Yang Yuefeng, Liu Jiacai. Teaching Method Evaluation Based on Analytic Hierarchy Process:A Case Study of Modern Warehouse Management[J]. Higher Education Forum, 2015(6): 87-89. |
| [15] |
张耀辉, 郭瑞, 胡蕊, 等. 基于层次分析法的地下水水质综合评价[J]. 兰州交通大学学报, 2015, 34(6): 17-22. Zhang Yaohui, Guo Rui, Hu Rui, et al. Comprehensive Evaluation of Groundwater Quality Based on Analytic Hierarchy Process[J]. Journal of Lanzhou Jiaotong University, 2015, 34(6): 17-22. |
| [16] |
李霄, 王长琪, 崔健. 基于层次分析法提出的辽西地下水污染防治区划[J]. 地质论评, 2017(4): 351-352. Li Xiao, Wang Changqi, Cui Jian. Groundwater Pollution Prevention Regionalization in Western Liaoning Province Based on Analytic Hierarchy Process[J]. Geological Review, 2017(4): 351-352. |
| [17] |
吕敦玉, 余楚, 周爱国, 等. 某油田区地下水综合防污性能评价[J]. 水文地质工程地质, 2012, 39(3): 81-85. Lü Dunyu, Yu Chu, Zhou Aiguo, et al. Evaluation of Comprehensive Anti-Pollution Performance of Groundwater in an Oil Field[J]. Hydrogeology Engineering Geology, 2012, 39(3): 81-85. |
| [18] |
葛世伦. 用1-9标度法确定功能评价系数[J]. 价值工程, 1989(1): 33-34. Ge Shilun. Determination of Functional Evaluation Coefficient by 1-9 Scale Method[J]. Value Engineering, 1989(1): 33-34. |
| [19] |
张凤然, 马全铭. 层次分析法与模糊综合评判法在评价教师课堂教学质量中的应用[J]. 高师理科学刊, 2013, 33(6): 18-20. Zhang Fengran, Ma Quanming. Application of Analytic Hierarchy Process and Fuzzy Comprehensive Evaluation Method in Evaluating Teachers' Classroom Teaching Quality[J]. Journal of Science of Normal University, 2013, 33(6): 18-20. |
| [20] |
肖云云, 欧阳金琼. 塔里木河流域农业气候资源综合评价与区域比较:基于模糊层次分析法[J]. 塔里木大学学报, 2018, 30(3): 87-94. Xiao Yunyun, Ouyang Jinqiong. Comprehensive Evaluation and Regional Comparison of Agricultural Climate Resources in Tarim River Basin:Based on Fuzzy Analytic Hierarchy Process[J]. Journal of Tarim University, 2018, 30(3): 87-94. |
| [21] |
虞未江, 贾超, 狄胜同, 等. 基于综合权重和改进物元可拓评价模型的地下水水质评价[J]. 吉林大学学报(地球科学版), 2019, 49(2): 539-547. Yu Weijiang, Jia Chao, Di Shengtong, et al. Evaluation of Groundwater Quality Based on Comprehensive Weight and Improved Matter-Element Extension Evaluation Model[J]. Journal of Jilin University (Earth Sciences Edition), 2019, 49(2): 539-547. |
| [22] |
王亚维, 王中美, 王益伟, 等. 基于GRA-AHP模型的岩溶地下水水质评价[J]. 水力发电, 2019, 45(8): 1-3, 62. Wang Yawei, Wang Zhongmei, Wang Yiwei, et al. Evaluation of Karst Groundwater Quality Based on GRA-AHP Model[J]. Hydropower, 2019, 45(8): 1-3, 62. |
| [23] |
江思义, 王启耀, 李春玲, 等. 基于专家-层次分析法的地下空间适宜性评价[J]. 地下空间与工程学报, 2019, 15(5): 1290-1299. Jiang Siyi, Wang Qiyao, Li Chunling, et al. Suitability Evaluation of Underground Space Based on Expert-Analytic Hierarchy Process[J]. Journal of Underground Space and Engineering, 2019, 15(5): 1290-1299. |
| [24] |
建设用地土壤污染风险管控和修复监测技术导则: HJ 25.2-2019[S].北京: 中国环境出版社, 2019. Technical Guidelines for Soil Pollution Risk Control and Remediation Monitoring of Construction Land: HJ 25.2-2019[S]. Beijing: China Environmental Press, 2019. |
| [25] |
污染地块地下水修复和风险管控技术导则: HJ 25.6-2019[S].北京: 中国环境出版社, 2019. Technical Guidelines for Groundwater Remediation and Risk Control in Contaminated Land Plots: HJ 25.6-2019[S]. Beijing: China Environmental Press, 2019. |



