0 引言
数字岩心技术是基于扫描电镜图像或CT扫描图像,结合计算机技术对图像进行处理,重新构建三维数字化图像,研究岩心物理性质的一种新兴技术[1]。近年来,随着科学技术的不断发展,X射线CT扫描与电子显微镜等技术在石油领域方面的应用越来越广泛。同时,基于CT扫描图像或扫描电镜图像的数字岩心技术也得到了极大的发展[2-5]。目前,数字岩心的构建主要有物理实验与模拟重构两种方法。物理实验方法主要通过扫描获取的岩心二维图像构建岩心三维图像,如X射线CT扫描法[6]、聚焦离子束扫描电镜等;模拟重构方法是在拥有较少的岩心图像时,利用数学方法对岩心图像进行处理,随机生成新的图像,进而完成岩心三维图像的构建,如高斯模拟法[7]、模拟退火法[8]和过程模拟法[9]等。
由于数字岩心能够完整、真实地展现岩心的结构特征并用于渗流模拟,因此许多学者利用数字岩心技术对岩心结构特征等进行了研究。姚军等[10]利用整合法建立了碳酸盐岩双孔隙网络模型,对碳酸盐岩不同尺度孔隙的渗流规律进行了研究。赵明等[11]基于多孔介质的分形理论,对9块数字岩心孔隙度和渗透率等进行了预测,证明了分形理论在利用数字岩心预测岩心物性方面的准确性。Sun等[12]利用二维扫描电镜图像重构数字岩心,构建了基于数字岩心技术的页岩气藏与致密气藏表观渗透率计算模型,并对表观渗透率的影响因素进行了分析。林承焰等[13]利用CT扫描图像进行数字岩心三维建模,对岩心孔喉特征进行分析计算,并利用模型进行了微观渗流模拟。Golparvar等[14]评价了基于CT扫描图像提取的孔隙网络模型(PNM)在研究多孔介质中流固耦合作用方面的优缺点,并分析了多相流建模面临的挑战。
渗透率作为岩心的一个重要物理参数,其与岩心的微观孔隙结构密切相关,可以直观地表现岩心的渗流能力。合理确定岩心的渗透率对岩心孔隙结构的研究至关重要。本文基于数字岩心技术,结合分形理论,通过求取岩心分形特征参数,构建等效分形介质模型,对岩心渗透率进行预测。
1 数字岩心图像处理及孔隙结构分析CT扫描图像的本质是衰减系数成像。不同物质对X射线的吸收能力不同,锥形X射线从不同方向穿过岩心后得到不同的投影值,利用所得到的投影值求取各个体素的衰减系数,并将其转化为灰度值即可得到岩心CT扫描图像。本次研究选取两块砂岩岩心进行微米CT扫描测试,岩心参数如表 1所示。
| 岩心编号 | 样品长 度/cm |
样品直 径/cm |
孔隙体 积/cm3 |
孔隙 度/% |
渗透率/ mD① |
| B1 | 2.493 | 2.510 | 2.013 | 16.32 | 1.728 |
| B2 | 2.455 | 2.511 | 2.659 | 21.87 | 168.712 |
① mD(毫达西)为非法定计量单位,1 mD=0.987×10-3 μm2,下同。
在岩心CT扫描图像孔隙发育较好的区域截取600像素×600像素×600像素的立方体进行分析。对图像进行中值滤波、阈值分割处理从而得到二值化图像,如图 1所示。二值化图像中黑色部分为孔隙相,其值为1,白色部分为基质相,其值为0。从二值化图像中可以看出,两块岩心孔隙分布具有明显区别:岩心B1的孔隙分布较为分散,孔隙大小较为均匀;岩心B2的孔隙分布较为集中,且存在大孔隙。

|
| a、b、c.岩心B1;d、e、f.岩心B2。 图 1 两块岩心原始图像(a, d)、滤波后图像(b, e)及二值化图像(c, f) Fig. 1 Original image (a, d), filtered image (b, e) and binary image (c, f) of the two sandstones |
|
|
岩心孔隙的连通性是评价岩心的重要指标,为更加直观地观察岩心的孔喉分布及其连通性,利用二维扫描图像构建三维数字岩心,利用最大球法提取岩心的孔隙网络球棍模型[15],如图 2所示。从图 2中可以发现,虽然岩心B1孔隙数目较多,但孔隙、喉道半径小,孔隙连通性差,因此其岩心渗透率较小;而岩心B2存在着较多尺寸较大的孔隙与喉道,连通性较好,因此渗透率较大。

|
| 上图为岩心B1,下图为岩心B2。 图 2 三维数字岩心(左)及孔隙网络球棍模型(右) Fig. 2 Three-dimensional digtial rock (left) and pore network model (right) |
|
|
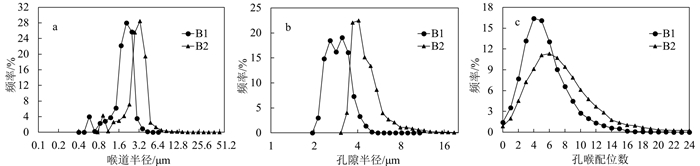
图 3为两块岩心孔隙网络模型的喉道半径分布曲线、孔隙半径分布曲线以及孔喉配位数分布曲线。从图 3中可以看出:岩心B2的孔隙及喉道半径分布偏右,喉道半径分布峰值在3.2 μm左右,且存在较大半径的喉道,喉道半径可高达10 μm,而岩心B1的喉道半径分布峰值在2 μm左右,喉道半径均值小于岩心B2(图 3a);岩心B2的平均孔隙半径大于岩心B1,且两块岩心的孔隙半径分布相差较大,岩心B2的孔隙半径集中分布在4~6 μm处,多数孔隙半径大于岩心B1最大孔隙半径(图 3b);两块岩心的孔喉配位数分布也存在着一定的差异,岩心B1的孔喉配位数主要集中分布在2~6之间,而岩心B2的孔喉配位数分布较岩心B1宽,大于6的孔喉配位数仍占有很大比例(图 3c)。以上分析可以很好地解释岩心B1的渗透率小于岩心B2的渗透率的原因。孔喉半径越大,孔喉配位数越高,孔喉连通性越强,渗流阻力越小,岩心渗透率越大。
|
| 图 3 岩心B1、B2喉道半径(a)、孔隙半径(b)及孔喉配位数(c)分布曲线 Fig. 3 Throat radius distribution (a), pore radius distribution (b) and pore coordination number distribution (c) of core B1 and B2 |
|
|
假设砂岩孔隙由一系列迂曲毛管束组成,根据分形理论可知,毛管束的数目与毛管直径呈幂指数关系[16]:
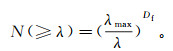 (1)
(1) 式中:λ为孔隙直径;N(≥λ)为孔隙直径大于等于λ的孔隙数目;λmax为最大孔隙直径;Df为分形维数。
假设孔隙分布为连续的,则孔隙直径介于λ与λ+dλ之间的孔隙数目为[17]
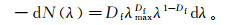 (2)
(2) 假设毛管束的长度也具有分形特征,毛管的迂曲长度Lt与岩心特征长度L0符合下列关系[18]:
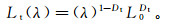 (3)
(3) 式中,Dt为迂曲度分形维数。Dt、L0分别由以下公式求得[18-19]:
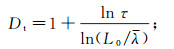 (4)
(4)  (5)
(5) 式中:λ为平均孔隙直径;τ为平均迂曲度;φ为孔隙度。
Wang等[20]结合分形理论与哈根泊肃叶方程,构建了毛管束模型的绝对渗透率计算模型:
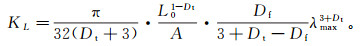 (6)
(6) 式中:KL为岩心绝对渗透率;A为岩心的横截面积,且A=L02。该模型表明岩心的渗透率受分形维数、迂曲度分形维数以及岩心最大孔隙直径的影响。模型中各岩心的分形维数与迂曲度分形维数是二维的,其值介于1~2之间。迂曲度分形维数作为指数,其对渗透率有较大的影响,随着迂曲度分形维数增加,岩心渗透率降低[18]。由于岩心渗透率与最大孔隙直径呈幂指数关系,最大孔隙直径对渗透率影响显著。下面将介绍各模型参数的具体计算方法。
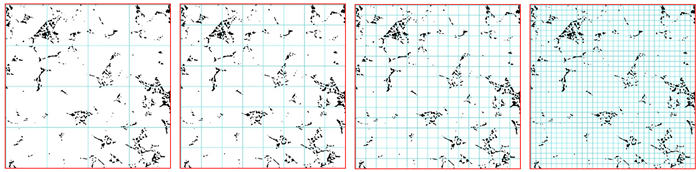
3 分形渗透率模型参数计算方法 3.1 分形维数岩心分形维数可利用不同方法进行求取,本次研究采用盒计数法求取[21-23]。盒计数法是利用不同尺寸的方形盒子对岩心图片进行覆盖(图 4),统计获得不同尺寸盒子下含有孔隙相盒子的数目,在双对数图上所求斜率为分形维数:
|
| 图 4 盒计数法求分形维数示意图 Fig. 4 Schematic diagram of box-counting method for fractal dimension calculation |
|
|
 (7)
(7) 式中,N(δ)为尺寸为δ的盒子含有孔隙相盒子的数目。
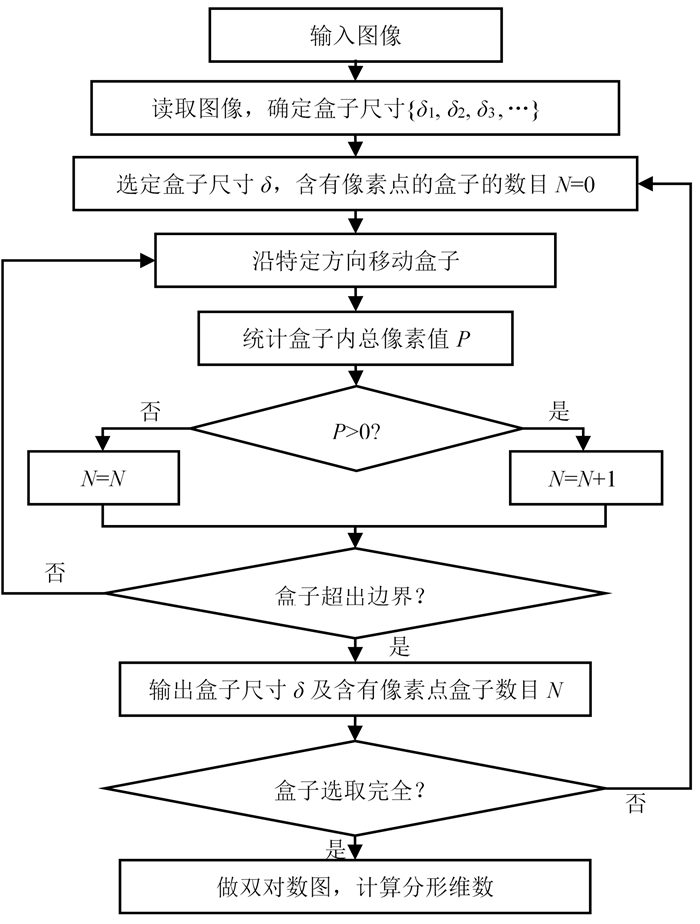
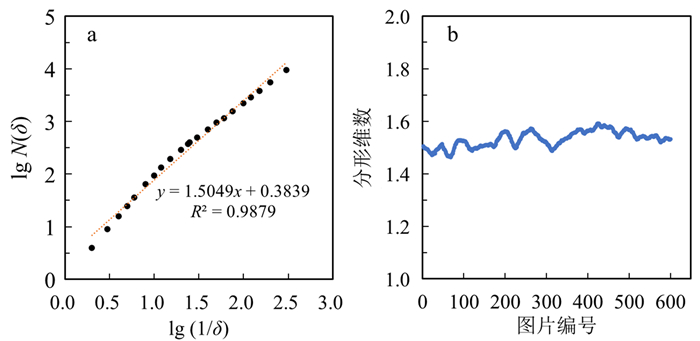
本文利用MATLAB对岩心的分形维数进行求取,流程如图 5所示。图 6为岩心B2单张图片分形维数的求取过程及所有图片分形维数的汇总图。如图 6b所示,每张图片计算得到的分形维数不同,取其平均值作为模型的分形维数。
|
| 图 5 盒计数法计算分形维数流程图 Fig. 5 Flow chart for calculating fractal dimension by box-counting method |
|
|
|
| 图 6 岩心B2单张二维图片分形维数计算(a)与分形维数汇总图(b) Fig. 6 Fractal dimension calculation of single two-dimensional image (a) and summary of fractal dimensions calculated from all the figures (b) of sandstone B2 |
|
|
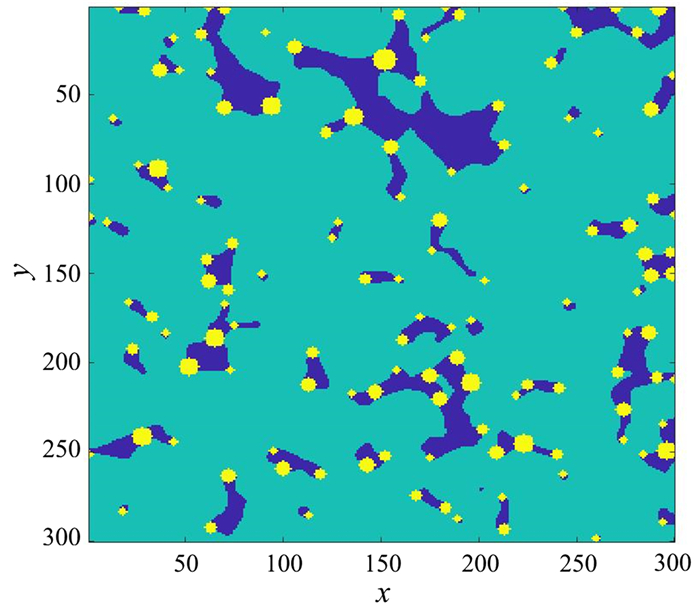
迂曲度对岩心的渗透率具有一定影响,在分形渗透率模型中其以迂曲度分形维数的形式出现。由式(4)可知,为求取迂曲度分形维数,需计算岩心的平均迂曲度。目前求取岩心迂曲度的模型有积分法和孔隙度函数法等,每种方法在计算孔隙迂曲度时具有一定的适应性。而基于流线法取得的迂曲度能更为精确地反映岩心中连通孔径的迂曲程度。Al-Raoush等[24]基于CT扫描图像,利用MATLAB编程,提出了一种迂曲度计算方法。该方法通过对孔隙相周围的像素点进行扫描,标记岩心各个孔隙最小直径(即喉道直径)的位置,如图 7所示。随后选择起始点,搜索连通路径,通过喉道的中点进行连接,将其视为流线,流线长度与岩心长度的比值即为该连通孔径的迂曲度。对岩心中所有连通孔径进行扫描,获取岩心所有连通孔径的迂曲度,求取平均值,将其视为岩心的平均迂曲度。本文中所选取的迂曲度是沿z方向进行搜索所确定的。
|
| 图中蓝色部分为孔隙,黄色点为喉道位置。 图 7 迂曲度连接路径点 Fig. 7 Tortuous connection path |
|
|
获得岩心的平均迂曲度后,将其与岩心的平均孔隙直径、岩心特征长度带入式(4),即可得到迂曲度分形维数。
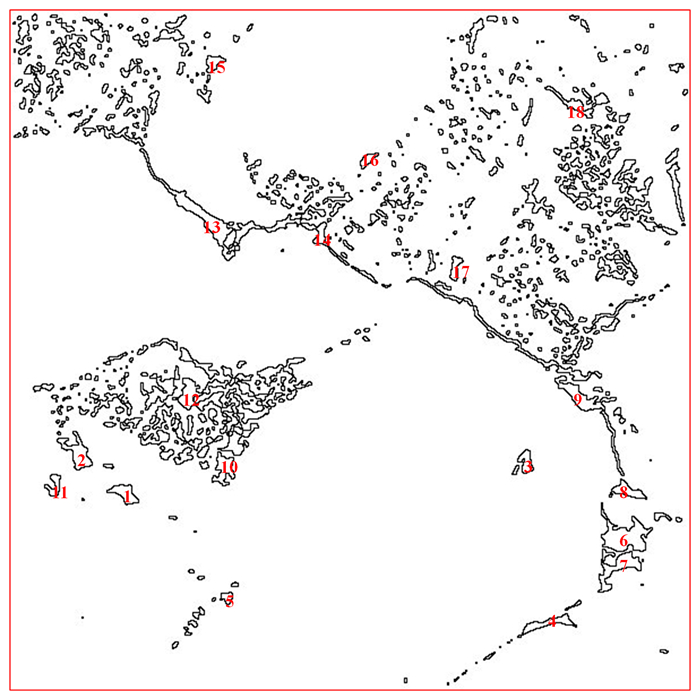
3.3 最大孔隙直径在分形渗透率模型中,最大孔隙直径的指数项放大了岩心中最大孔隙直径对岩心渗透率的影响,因而需要慎重地选择岩心最大孔隙直径。利用Image J软件对岩心CT扫描图像进行处理,可以得到岩心的最大孔隙直径。图 8为确定岩心最大孔隙直径的流程图。首先,确定岩心扫描图片的像素值,根据岩心像素值的不同,划定岩心内孔隙的边界,并对每个孔隙进行编号,部分孔隙标记如图 9所示;然后,根据定义不同,Image J可计算各孔隙面积、周长、最大直径、最小直径等参数,选择需要计算的孔隙参数运行;最后,将计算好的数据导出到Excel表中。利用Image J计算的部分岩心孔隙参数如表 2所示。

|
| 图 8 CT扫描各孔隙参数确定流程图 Fig. 8 Flow chart for determining pore parameters |
|
|
|
| 图中数字为孔隙编号。 图 9 利用Image J软件进行岩心孔隙提取划分 Fig. 9 Extraction and division of pores using software Image J |
|
|
| 孔隙 编号 |
孔隙 面积/μm2 |
孔隙 周长/μm |
最大等效 直径/μm |
最小等效 直径/μm |
| 1 | 12.482 | 12.098 | 5.697 | 3.160 |
| 2 | 7.489 | 8.938 | 4.469 | 3.160 |
| 3 | 187.230 | 58.797 | 19.797 | 17.042 |
| 13 | 112.338 | 52.477 | 23.700 | 8.479 |
| 15 | 134.806 | 60.489 | 20.782 | 12.640 |
由于岩心中孔隙的不规则性,在求取岩心孔隙直径时,可求得几种不同的等效直径。通过比较各种直径的计算结果,选取岩心孔隙的内切圆直径(孔隙等效最小直径)为岩心孔隙的等效直径预测渗透率效果较好。统计每张岩心CT图中各孔隙的直径,获取各扫描图片中的最大孔隙直径。考虑岩心孔隙的连通性质以及岩心孔隙分布的偶然性,求取所有图片的最大孔隙直径,求取其平均值并将其视为岩心的最大孔隙直径。
4 渗透率预测为评估基于数字岩心技术的分形渗透率模型计算方法,对上述两块岩心进行渗透率计算,并将计算得到的结果与岩心渗透率、孔隙网络模型计算得到的渗透率进行对比,如表 3所示。从表 3可以看出,分形渗透率模型计算的岩心渗透率与孔隙网络模型计算的渗透率相差不大,表明通过构建数字岩心的等效分形介质模型继而预测岩心渗透率是可行的。分形渗透率模型计算的渗透率与岩心气测渗透率存在一定的差异,这是由于用于计算的数字岩心只是岩心一个区域,岩心内部存在一定的非均质性,因此数字岩心计算得的渗透率与岩心气测渗透率具有一定的差异。
| 岩心 编号 |
岩心尺寸/ 像素 |
分辨率/ (μm/像素) |
Df | 迂曲度 | Dt | λmax/ μm |
λ/ μm |
计算渗透率/mD | 气测渗透 率/mD |
|
| 分形渗透率 模型 |
孔隙网络 模型 |
|||||||||
| B1 | 600×600 | 1.00 | 1.46 | 11.59 | 1.68 | 52.02 | 8.93 | 0.19 | 0.23 | 1.73 |
| B2 | 600×600 | 1.58 | 1.66 | 1.71 | 1.13 | 308.05 | 13.84 | 225.09 | 485.29 | 168.71 |
为更加准确地验证分形渗透率模型在计算数字岩心渗透率方面的可行性,对帝国理工学院网站公开的9块砂岩数字岩心图像[25]进行处理,求取分形渗透率模型参数并进行渗透率预测。9块数字岩心参数如表 4所示,其中渗透率为孔隙网络模型计算得到的渗透率。基于CT扫描图像计算得到的等效分形介质模型参数如表 5所示。
| 岩心 编号 |
尺寸/ (像素×像素) |
分辨率/ (μm/像素) |
孔隙度/% | 渗透率/mD |
| S1 | 300×300 | 8.68 | 14 | 1 486 |
| S2 | 300×300 | 4.96 | 25 | 3 951 |
| S3 | 300×300 | 9.10 | 17 | 281 |
| S4 | 300×300 | 8.96 | 17 | 169 |
| S5 | 300×300 | 3.98 | 22 | 5 369 |
| S6 | 300×300 | 5.10 | 25 | 11 282 |
| S7 | 300×300 | 4.80 | 27 | 7 926 |
| S8 | 300×300 | 4.89 | 38 | 13 932 |
| S9 | 300×300 | 3.40 | 22 | 3 640 |
| 岩心编号 | Df | 迂曲度 | Dt | λmax/μm | λ/μm | 计算渗透率/mD |
| S1 | 1.51 | 4.31 | 1.65 | 228.90 | 91.83 | 1 730.81 |
| S2 | 1.68 | 2.03 | 1.27 | 156.06 | 38.99 | 2 855.31 |
| S3 | 1.64 | 5.27 | 1.60 | 160.90 | 41.49 | 454.27 |
| S4 | 1.65 | 9.64 | 1.83 | 150.95 | 41.47 | 229.69 |
| S5 | 1.59 | 3.58 | 1.49 | 179.10 | 42.90 | 4 841.49 |
| S6 | 1.63 | 2.40 | 1.32 | 255.18 | 53.51 | 17 098.47 |
| S7 | 1.66 | 1.89 | 1.24 | 196.78 | 43.70 | 8 158.54 |
| S8 | 1.75 | 2.88 | 1.32 | 343.66 | 67.95 | 68 404.27 |
| S9 | 1.60 | 2.60 | 1.36 | 144.13 | 34.55 | 3 506.17 |
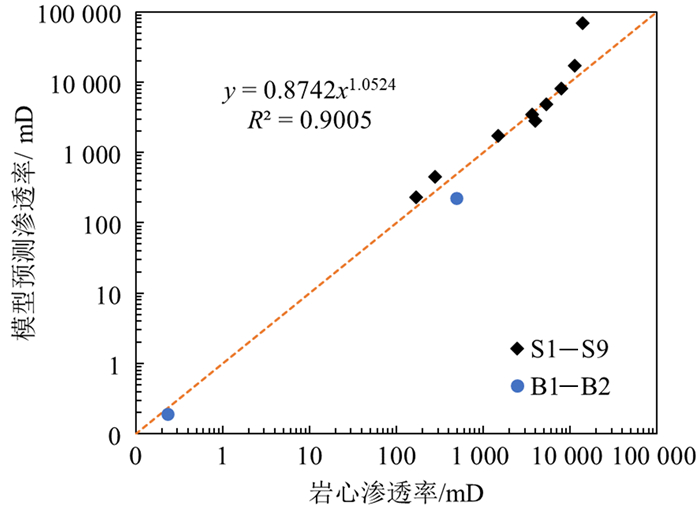
2块微米CT扫描构建的数字岩心与9块帝国理工学院网站公开的数字岩心的等效分形渗透率模型计算结果与孔隙网络计算渗透率对比结果如图 10所示。利用分形渗透率预测模型所计算的渗透率与岩心孔隙网络计算渗透率有着良好的相关性,相关系数高达0.971 5。但结果也表明,随着岩心渗透率的增加,分形渗透率模型计算的渗透率误差增大。表 5中岩心S8的计算渗透率远高于岩心的渗透率,对比其模型参数可以发现,Image J软件计算得到的岩心S8的最大孔隙直径为343.66 μm,最大孔隙直径计算值偏大是造成其预测渗透率值过高的原因。
|
| 图 10 模型预测渗透率与实际渗透率对比 Fig. 10 Comparisons between model predicted permeability and core actual permeability |
|
|
基于微米CT扫描测试得到的数字岩心分析孔隙结构特征,结合分形理论构建数字岩心的等效分形介质模型,并预测岩心渗透率,研究结果表明:
1) 利用CT扫描图像提取的孔隙网络模型能够直观地反映岩心内部的孔喉分布及孔隙的连通性。孔隙与喉道尺寸分布、孔喉配位数分布影响岩心渗透率。孔喉尺寸越大、分布越宽,且孔喉配位数越大、连通性越强,岩心渗透率越高。
2) 通过构建数字岩心的等效分形介质模型预测岩心渗透率是可行的。等效分形介质渗透率计算结果受分形维数、迂曲度分形维数与最大孔隙直径的影响。分形渗透率模型计算得到的渗透率与孔隙网络模型计算得到渗透率具有很好的相关性,可以用于岩心渗透率预测。
3) 最大孔隙直径对分形渗透率模型计算结果影响较大。随着岩心渗透率的增大,利用分形渗透率模型计算的数字岩心渗透率与孔隙网络模型计算的渗透率偏差增大,这可能是由于最大孔隙直径计算值偏大造成的。
| [1] |
姚军, 赵秀才, 衣艳静, 等. 数字岩心技术现状及展望[J]. 油气地质与采收率, 2005, 12(6): 52-54. |
| [2] |
潘汝江, 何翔, 肖维民, 等. CT扫描技术在岩心三维重建中的应用[J]. CT理论与应用研究, 2018, 27(3): 349-356. |
| [3] |
王鑫元, 沈忠山, 张东, 等. 基于全直径岩心CT扫描技术的三元复合驱后微观孔隙结构特征[J]. 大庆石油地质与开发, 2019, 38(2): 81-86. |
| [4] |
Dvorkin J, Walls J, Tutuncu A, et al. Rock Property Determination Using Digital Rock Physics[C]//Geophysics of the 21st Century: The Leap into the Future, SEG Technical Program Expanded Abstracts 2003. Moscow: European Association of Geoscientists & Engineers, 2003: cp-38-00040.
|
| [5] |
李易霖, 张云峰, 丛琳, 等. X-CT扫描成像技术在致密砂岩微观孔隙结构表征中的应用:以大安油田扶余油层为例[J]. 吉林大学学报(地球科学版), 2016, 46(2): 379-387. |
| [6] |
赵玲, 石雪, 夏慧芬. 数字岩心孔隙网络模型的构建方法[J]. 科学技术与工程, 2018, 18(26): 32-38. |
| [7] |
Adler P M, Jacquin C G, Thovert J F. The Formation Factor of Reconstructed Porous Media[J]. Water Resources Research, 1992, 28(6): 1571-1576. |
| [8] |
Hazlett R D. Statistical Characterization and Stochastic Modeling of Pore Networks in Relation to Fluid Flow[J]. Mathematical Geology, 1992, 29(6): 801-822. |
| [9] |
Bryant S, Blunt M. Prediction of Relative Permeability in Simple Porous Media[J]. Physical Review:A:Atomic, Molecular, and Optical Physics, 1992, 46(4): 2004-2011. |
| [10] |
姚军, 王晨晨, 杨永飞, 等. 碳酸盐岩双孔隙网络模型的构建方法和微观渗流模拟研究[J]. 中国科学:物理学力学天文学, 2013, 43(7): 896-902. |
| [11] |
赵明, 郁伯铭. 数字岩心孔隙结构的分形表征及渗透率预测[J]. 重庆大学学报, 2011, 34(4): 88-94. |
| [12] |
Sun H, Yao J, Cao Y, et al. Characterization of Gas Transport Behaviors in Shale Gas and Tight Gas Reservoirs by Digital Rock Analysis[J]. International Journal of Heat and Mass Transfer, 2017, 104: 227-239. |
| [13] |
林承焰, 王杨, 杨山, 等. 基于CT的数字岩心三维建模[J]. 吉林大学学报(地球科学版), 2018, 48(1): 307-317. |
| [14] |
Golparvar A, Zhou Y, Wu K, et al. A Comprehensive Review of Pore Scale Modeling Methodologies for Multiphase Flow in Porous Media[J]. Advances in Geo-Energy Research, 2018, 2(4): 418-440. |
| [15] |
Dong H, Blunt M J. Pore-Network Extraction from Micro-Computerized-Tomography Images[J]. Physical Review E, 2009, 80(3): 036307. |
| [16] |
Mandelbrot B B. The Fractal Geometry of Nature[M]. New York: WH Freeman, 1983.
|
| [17] |
Yu B, Cheng P. A Fractal Permeability Model for Bi-dispersed Porous Media[J]. International Journal of Heat and Mass Transfer, 2002, 45(14): 2983-2993. |
| [18] |
Yu B. Fractal Character for Tortuous Streamtubes in Porous Media[J]. Chinese Physics Letters, 2005, 22(1): 158. |
| [19] |
Wu J, Yu B. A Fractal Resistance Model for Flow Through Porous Media[J]. International Journal of Heat and Mass Transfer, 2007, 50(19/20): 3925-3932. |
| [20] |
Wang F, Jiao L, Lian P, et al. Apparent Gas Permeability, Intrinsic Permeability and Liquid Permeability of Fractal Porous Media:Carbonate Rock Study with Experiments and Mathematical Modelling[J]. Journal of Petroleum Science and Engineering, 2019, 173: 1304-1315. |
| [21] |
尹贤龙. 基于图像分形维数估计的最小盒计数法的研究[J]. 电气应用, 2006, 25(9): 93-96. |
| [22] |
曹俊贤, 宋春林. 分形维数的计算及改进[J]. 信息技术与信息化, 2017(10): 19-23. |
| [23] |
王聪乐.砂岩油藏孔隙结构分形表征与渗透率模型研究[D].北京: 中国石油大学(北京), 2018. Wang Congle. Reasearch on Fractal Characterization of Pore Structure and Permeability Model in Sandstone Reservoirs[D]. Beijing: China University of Petroleum (Beijing), 2018. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=1019926822.nh
|
| [24] |
Al-Raoush R I, Madhoun I T. TORT3D:A MATLAB Code to Compute Geometric Tortuosity from 3D Images of Unconsolidated Porous Media[J]. Powder Technology, 2017, 320: 99-107. |
| [25] |
Imperial Colleage. Micro-CT Images and Networks[DB/OL].[2019-05-23]. http://www.imperial.ac.uk/earth-science/research/research-groups/per-m/research/pore-scale-modelling/micro-ct-images-and-networks/.
|



