0 引言
折射波勘探技术发展较早。由于折射波的震相易于识别等因素,其勘探方法依然在浅层勘探中有较广泛的应用[1-4]。
t0法又称t0差数时距曲线法[5],是解释折射波相遇时距曲线最常用的方法之一。在折射界面曲率半径比其埋深大得多的情况下,t0法目前被认为能够取得良好的效果[6]。本领域技术人员因为该方法是常用的技术方法,故未对其具体内容产生质疑[7-10],多年来,物探教材一直使用这种方法。实际上该方法是存在着问题的:一是计算第二层介质波速近似程度大,计算折射面法线深度理论上需要计算折射面倾角,但实际计算时却忽略了折射面倾角,即其近似的限定条件是统一认为折射面倾角小于等于15°的余弦值都等于1,这样计算的波速误差是明显的;二是该方法引进一个θ(x)函数,用计算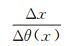
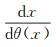
折射波勘探始于20世纪50年代[11],当时计算机和高等数学普及程度不高、各学科融合程度较低,往往习惯用初等数学解决折射波物探问题。折射波物探经常使用的t0法,多年来被科学工作者习惯性使用。一些技术人员在处理数据时,虽然也将先进计算机技术应用到求解的过程中[11],但未考虑利用高等数学理论改进计算过程。本文采用高等数学方法解决目前方法因采用初等数学方法而产生的系统误差问题;采用计算机技术解决目前方法手工操作产生的问题。
1 目前的t0法目前t0法求折射面法线深度原理如图 1所示[1]。S1和S2为两条折射波相遇时距曲线,O1和O2分别为两者的激发点,A、E分别为在O1、O2激发的入射波与折射面的交点,v1和v2分别为第一层波速和第二层波速,且v2 > v1。若在剖面O1O2上任取一点D,则在两条时距曲线S1和S2上可分别得到其相对应的走时t1和t2。th为互换时,i为临界角。当折射面的曲率半径远大于其埋深时,图 1a中的△BCD可近似看作等腰三角形。自D点作BC的垂直平分线DM,DM即为该点的法线深度。

|
| 图 1 目前t0法求折射面原理示意图 Fig. 1 Schematic diagram of the principle of refraction surface by t0 method |
|
|
结合初等数学知识,可得目前t0法计算折射面法线深度h的公式[1]:
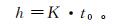 (1)
(1) 其中:
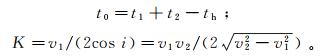
从式(1)可以看出,从时距曲线上读取t1,t2和th,就可以算出各点的t0值,并可在图上绘制出相应的t0(x)曲线,如图 1b所示。v1通常可根据表层的直达波速度来确定,因此计算折射面法线深度的难点是K的计算,也就是v2值的计算。为此,目前方法引进差数时距曲线方程θ(x):
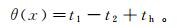 (2)
(2) 对式(2)求导,可得
 (3)
(3) 其中[1]:
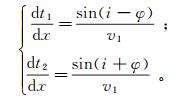 (4)
(4) 式中,φ为折射面倾角。将式(4)代入式(3),经变换后可得
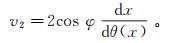 (5)
(5) 当φ≤15°时,式(5)可写成近似式:
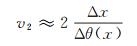 (6)
(6) 因此,目前的t0法只要根据式(2)在相遇时距曲线图上构制θ(x)曲线,并计算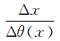
从目前t0法的推导过程可以看出:在计算h的过程中引入θ(x)函数使得计算过程较为繁琐;用式(1)求解h时,重点是求解v2,而从式(5)、式(6)求解v2的过程中作了两次近似,当折射面倾角φ≤15°时,将cos φ近似看成1和用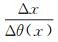
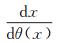
基于目前t0法求解过程存在的上述不足,提出一种改进的确定折射面法线深度的t0法,旨在减少计算强度,简化求解过程;解决原方法求解过程中两次近似计算导致的误差问题,使求解过程的近似问题变成精确计算;改变用手动偏移归位方法确定折射面的现状,减少绘制过程中的人工误差,增加绘制效率。
具体改进方法推导过程如下。
基于式(1),变形可得
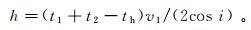 (7)
(7) 从式(7)中可看出,cos i不能直接求出。如果用式(7)计算h,必须计算出i。
式(4)两等式左边两项分别是图 1中S1和S2的曲线斜率,因此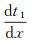
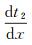
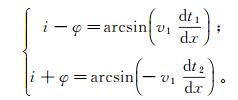 (8)
(8) 对式(8)中两等式进行联立求解,可得:
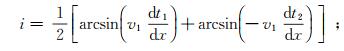 (9)
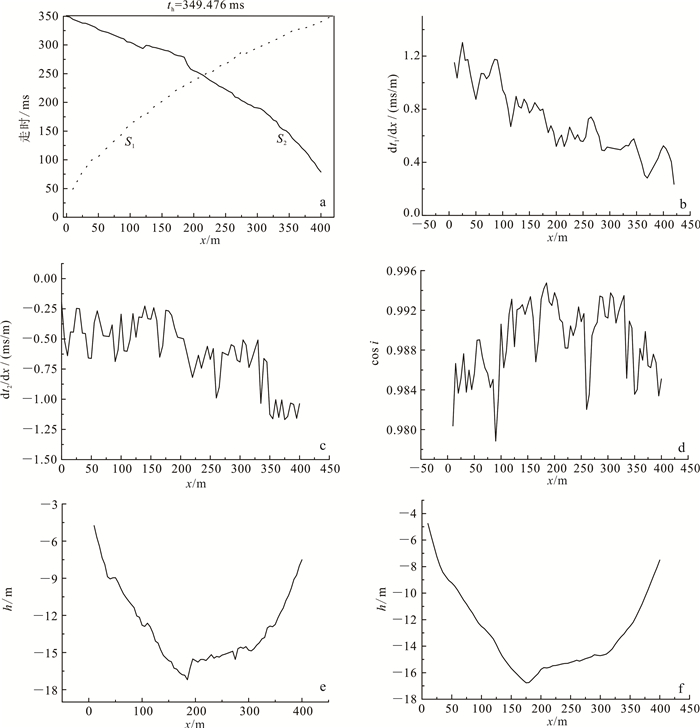
(9) 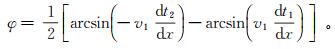 (10)
(10) 用式(9)求出i后,计算cos i,进而可以直接用式(7)计算折射面原始法线深度。
改进的计算法线深度的t0法没有理论上的近似,其结果应更接近实际。我们的推导过程有一个副产品式(10),可以准确计算出折射面倾角。由于在改进的t0法求解折射面法线深度的过程中,折射面倾角不参与计算,所以称其为副产品。
3 改进t0法确定折射面法线深度的步骤步骤1:根据野外相遇时距曲线观测系统记录,做出折射波相遇时距曲线S1、S2。
步骤2:根据式(8)分别对“步骤1”中所绘制的S1和S2曲线进行微分,计算并绘制出两条相遇时距曲线的斜率随位置坐标的变化曲线。
步骤3:根据已知直达波测出v1值,并利用式(9)计算出各测点的临界角,进一步求出其对应的cos i,进而绘制出cos i随位置坐标的变化曲线。
步骤4:根据“步骤3”中求得的cos i,用式(7)计算出所有坐标点的原始法线深度,并绘制得到原始法线深度随坐标变化的曲线。
步骤5:将“步骤4”中原始法线深度随位置坐标变化的数据带入Origin的相邻平均计算程序中进行相邻平均计算,输出相邻平均计算结果,用计算机绘制最终法线深度随位置的变化曲线,即平滑处理后的法线随深度变化曲线。
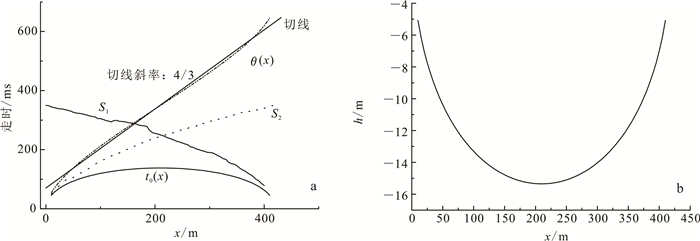
4 应用实例以某地野外折射波勘探为例,将目前方法和改进方法的计算结果进行比较,以对改进方法的有效性进行分析。目前方法及改进方法的计算过程及结果分别如图 2、图 3所示。
|
| a.折射面;b.法线深度。 图 2 目前t0法计算折射面法线深度 Fig. 2 Current t0 method to calculate the normal depth of the refraction surface |
|
|
|
| a.折射波相遇时距曲线;b. S1曲线斜率;c. S2曲线斜率;d.临界角余弦值;e.法线深度;f.平滑后的法线深度。 图 3 改进t0法计算折射面法线深度 Fig. 3 Improved t0 method to calculate the normal depth of the refraction surface |
|
|
对比图 2b和图 3f可看出,目前t0法所求得的法线深度随坐标的变化曲线过于光滑,缺少起伏的细节变化;而改进t0法所求得法线深度随坐标的变化曲线细节变化更为明显,可能更接近真实的折射面形态。
5 讨论对比目前方法和改进方法平滑处理过程可以看出,目前方法使用手动偏移归位的方法,而改进方法使用Origin科学绘图软件中相邻平均法,具体对比如下。
目前方法使用的手动偏移归位方法具体操作如下:求出各测点的法线深度h后,以其中一个观测点D1为圆心,以对应的h为半径画弧,可以得到如图 4a所示的半圆弧,此半圆弧上的任意一点,如A,B,C,...,等都可能是折射面深度的对应点,所以根据一个观测点的数据不能确定整个折射面。进一步根据多个观测点,如以D1,D2,D3,...,等为圆心,以各自对应的h为半径,可以绘制一系列圆弧,如图 4b所示,这些圆弧的包络线,或公切线就是折射面的位置,包络线实质也是对法线深度曲线平滑的结果。
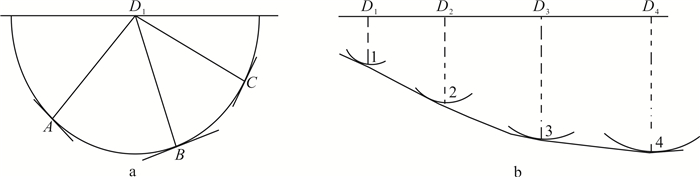
|
| 图 4 目前t0法可能的观测点与反射面(a)、偏移归位示意图(b) Fig. 4 Possible observation point and reflective surface(a)、offset homing schematic(b) of t0 method |
|
|
而相邻平均法的思想是通过一点和邻域内点求平均来去除突变点,也就是滤掉了奇异点,这与目前方法中求一系列圆弧的包络线的思想是一致的,其优点是算法简单,可以用计算机代替手工,计算速度快,也相当于对法线深度曲线做了平滑。
6 结论本文提出了一种改进的确定折射面法线深度t0的方法:
1) 改进t0法不用计算第二层介质的波速,减少了过程量的引入,简化了计算过程。
2) 改进t0法不存在原方法中的过程函数,消除了过程函数相关计算存在的近似,既简洁了计算过程,又减小了误差。
3) 在进行平滑处理时,改进t0法摒弃了手动操作,实现了全过程用计算机处理,提高了工作效率,节省了人力成本。
4) 改进t0法的计算过程不涉及折射界面倾角,消除了折射界面倾角近似导致的误差,并且有一个副产品,可以准确计算出折射面倾角。
| [1] |
陈仲候, 王兴泰, 杜世汉. 工程与环境物探教程[M]. 北京: 地质出版社, 2016: 51-53. Chen Zhonghou, Wang Xingtai, Du Shihan. Engineering and Environmental Geophysical Tutorial[M]. Beijing: Geological Publishing House, 2016: 51-53. |
| [2] |
葛双成, 李小平, 邵长云, 等. 地震折射和电阻率法在水库坝址勘察中的应用[J]. 地球物理学进展, 2008, 23(4): 1299-1303. Ge Shuangcheng, Li Xiaoping, Shao Changyun, et al. Application of Seismic Refraction and Resistivity for Exploration of Reservoir Dam Site[J]. Progress in Geophysics, 2008, 23(4): 1299-1303. |
| [3] |
彭晓, 王鹏. 浅层地震折射波法在候家梁隧道地质勘察中的应用[J]. 工程地球物理学报, 2013, 10(5): 631-636. Peng Xiao, Wang Peng. The Application of Shallow Seismic Refraction to Houjialiang Tunnel Exploration[J]. Chinese Journal of Engineering Geophysics, 2013, 10(5): 631-636. DOI:10.3969/j.issn.1672-7940.2013.05.008 |
| [4] |
包勋, 汤浩, 朱照拔. 综合物探技术在探测隐伏断层中的应用[J]. 人民珠江, 2016, 37(12): 29-32. Bao Xun, Tang Hao, Zhu Zhaoba. Application of Comprehensive Geophysical Prospecting Method to Buried Fault Detection[J]. Pearl River, 2016, 37(12): 29-32. DOI:10.3969/j.issn.1001-9235.2016.12.005 |
| [5] |
Hagedoorn J G. The Plus-Minus Method of Interpreting Seismic Refraction Sections[J]. Geophysical Prospecting, 1959, 7(2): 158-182. DOI:10.1111/j.1365-2478.1959.tb01460.x |
| [6] |
刘四新, 朱怡诺, 王旭东, 等. 工程地震折射波解释方法研究进展[J]. 吉林大学学报(地球科学版), 2018, 48(2): 350-363. Liu Sixin, Zhu Yinuo, Wang Xudong, et al. Progress of Engineering Seismic Refraction Interpretation Method[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(2): 350-363. |
| [7] |
熊章强, 方跟显. 浅层折射波法在隧道工程地质调查中的应用[J]. 水文地质工程地质, 2001, 28(1): 63-66. Xiong Zhangqiang, Fang Genxian. Application of Refractive Method in Tunnel-Engineering Exploration[J]. Hydrogeology and Engineering Geology, 2001, 28(1): 63-66. DOI:10.3969/j.issn.1000-3665.2001.01.018 |
| [8] |
孙茂锐. 折射波法探测断层的实例分析[J]. 工程地球物理学报, 2012, 9(6): 705-707. Sun Maorui. Case Analysis of Refraction Wave to Detect the Fault[J]. Chinese Journal of Engineering Geophysics, 2012, 9(6): 705-707. DOI:10.3969/j.issn.1672-7940.2012.06.011 |
| [9] |
宋国阳, 刘国争. 浅层地震折射波法技术应用[J]. 煤炭技术, 2009, 28(10): 134-136. Song Guoyang, Liu Guozheng. Application of Shallow Seismic Refraction[J]. Coal Technology, 2009, 28(10): 134-136. |
| [10] |
尹志清, 刘福兴. 浅层断层探测技术及工程应用[J]. 科学技术与工程, 2016, 16(7): 103-114. Yin Zhiqing, Liu Fuxing. Shallow Faults Exploration Technology and Its Engineering Application[J]. Science Technology and Engineering, 2016, 16(7): 103-114. DOI:10.3969/j.issn.1671-1815.2016.07.016 |
| [11] |
刘晶. 折射波法地震勘探资料的计算机处理[J]. 勘察科学技术, 1991, 5: 58-59. Liu Jing. Computer Crocessing of Seismic Exploration Data by Refracting Wave Method[J]. Site Investigation Science and Technology, 1991, 5: 58-59. |


