2. 吉林大学仪器科学与电气工程学院, 长春 130026
2. College of Instrumentation and Electrical Engineering, Jilin University, Changchun 130026, China
0 引言
航空重力梯度仪历经二十余年的发展,如今可以达到1~5 E的精度水平[1-4]。超高的精度与灵敏度使航空重力梯度仪在测量中无法忽视一些干扰,比如仪器与载体以及载体内部多种质量体(如飞行员和其他辅助测量仪器)之间相互运动产生的重力梯度效应,即自身梯度效应。自身梯度效应的大小在几厄至几十厄之间,对于相对的加速度计而言不完全属于共模噪声,因此不能以差分与解调的方式完全去除,这会对高精度的重力梯度测量带来严重的干扰。
自身梯度校正已被固化为重力梯度仪原始测量数据处理中的一部分,相关报道可以参见Bell Geospace实验室2004—2013年的一系列生产报告[5-6]。国内关于自身梯度校正的研究起步较晚,原因是国产重力梯度仪刚刚步入工程样机阶段,较低的精度难以精确测量到自身梯度效应量级的重力梯度数据。随着未来国产工程样机的逐步实用化,精度逐渐提高,自身梯度的校正逐渐被一些研发单位提到日程上来。按校正方法可将公开发表的相关文献分为两类:一类为将周围的质量体抽象成简单的模型并逐一求其重力梯度值来完成校正,如Rogers等[7]在研究重力匹配导航中提出的模型体自身梯度校正,袁圆[8]用点源模型推导了飞机姿态变化与油箱质量变化对自身梯度的影响,丁昊等[9]用点源模型推导了基于加速度计位置的自身梯度校正;第二类利用坐标转换方法修正载体姿态变化产生的影响,具体操作是将载体坐标系下的数据转化到地理坐标系下,张量数据的坐标转换参见孙中苗[10]的研究,王泰涵等[11]用坐标系转换的方法进行过自身梯度校正的实验。两类方法都存在难以应用到实际中的缺点,原因是第一类方法无法完全将仪器周围的所有质量体考虑在内,只有在计算油箱这种已知具体目标的影响时才较为合理;第二类方法理论上可以消除载体扰动的影响,但计算的前提是简化载体的质量模型,这一简化过程包含人为误差在内。
尽管在Bell Geospace的诸多生产报告中没有公开校正的数学方法,但是从已经公开的操作步骤中可以推断出该方法的一些特征。公开的操作步骤是,起飞前在地面上进行标定实验并求出一张标定参数表列,在飞行结束后用处理软件将最初地面标定实验产生的参数带入,最后求出自身梯度效应的校正值。整个校正流程中没有用到任何关于飞机质量模型的假设,完全由数据来驱动。笔者关于处理细节的推断如下:在地面上的标定实验生成了载体角度与自身梯度关系的模板,实际飞行中记录载体的角度变化,飞行结束后将实时记录的姿态角变化输入到模板里得到校正值。那么最为贴近上述处理方案的方法就是回归分析。基于上述判断,文章以回归分析作为方法的核心,以单个GGI(gravity gradient instrument)为研究对象,进行自身梯度效应校正仿真实验。
1 基于多元回归分析的自身梯度校正 1.1 回归数据回归分析首先要依据样本的特征建立合适的回归方程,数据样本的完备程度是决定回归方程正确与否的因素之一。为产生较为完备的数据样本,将GGI周围质量体的运动模式设置如下:所有质量体围绕GGI做俯仰角(pitch,记为φ)为±15°、翻滚角(roll,记为θ)为±15°、偏航角(yaw,记为ψ)为360°的周期运动。其中,φ、ψ、θ的采样周期分别为5°、2°、5°。翻滚次序设置为θ φ ψ。在此翻滚次序下,转动后的重力梯度张量T′与转动前的梯度张量T的变换关系为
 (1)
(1) 式中,R为旋转矩阵。令
 (2)
(2) 则
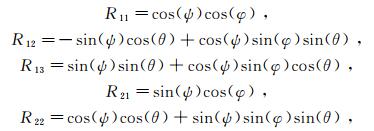
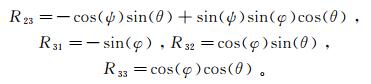
飞机模型选取美国Cessna公司生产的Cessna 208 Caravan航空重力梯度仪测量飞机,飞机参数可以从公司主页获取[12]:机身长11.46 m、高4.53 m、翼展15.87 m;飞机空载2 145 kg,油箱满油重1 009 kg,油的体积为1 257 L,油箱位置通常处于重力梯度仪正下方。根据上述参数,将机身的平均密度设置为0.020 g/cm3,机翼的平均密度设置为0.212 g/cm3,油箱的密度设置为0.802 g/cm3。3种姿态角与简化的模型如图 1所示,坐标原点与重心重合。观测点位于坐标原点。重力梯度张量T的全分量可用长方体重力计算公式求解得出:

|
| 图 1 为产生回归数据所近似的飞机模型 Fig. 1 Aircraft model approximate to the production of regression data |
|
|
 (3)
(3) 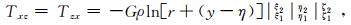 (4)
(4) 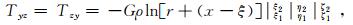 (5)
(5) 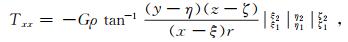 (6)
(6) 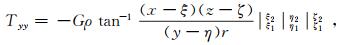 (7)
(7) 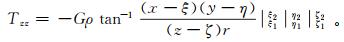 (8)
(8) 式中:G为万有引力常数;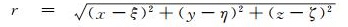
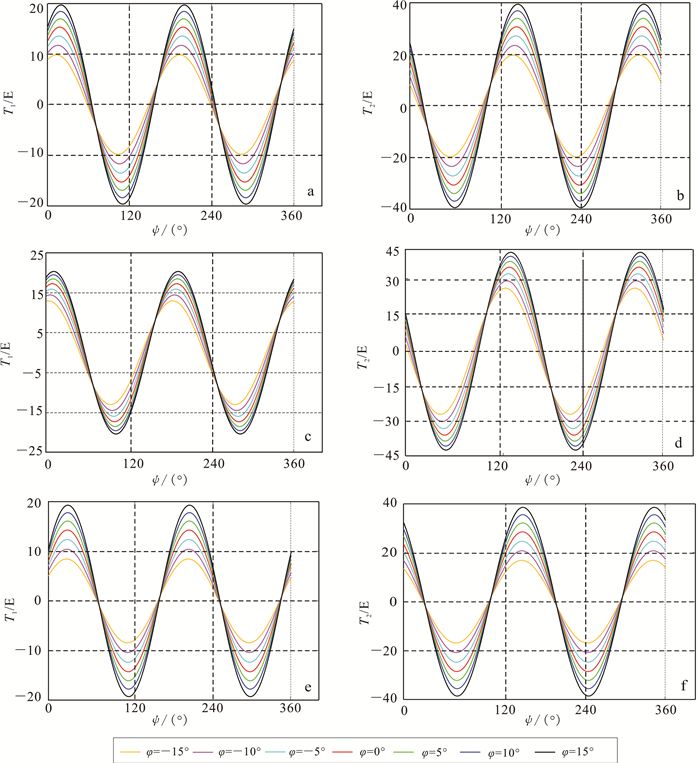
将水平放置的GGI原始输出交线信号(crossline)T1=Txx-Tyy与内联信号(inline)T2=Txy设置为响应变量,将3个姿态角设置为回归变量,寻求响应变量与回归变量之间的关系。当θ分别为-15°、0°、15°时,响应变量的曲线记录如图 2所示。由于计算方法相同,并且所得结果不展示其他物理含义,为节省篇幅,θ为-10°、-5°、5°、10°时的响应变量曲线省略未画出。
1.2 回归分析与回归诊断 1.2.1 回归分析由图 2可知,自身梯度数据T1、T2呈周期性,且与3个姿态角有关。解决周期函数回归拟合的最佳方式为三角函数。设S表示自身梯度效应,拟定的回归公式为
|
| a、b. θ=0°; c、d. θ=-15°; e、f. θ=15°。 图 2 用公式(1)—(8)生成的训练样本 Fig. 2 Training sample got from formula (1) - (8) |
|
|
 (9)
(9) 式中:cn(φ, θ)、dn(φ, θ)为第一层的回归系数;t为第一层展开阶数。
令式(9)中的回归系数组成矩阵A:
A =[c0, c1, ..., ct, d1, d2, ..., dt]。
对A中的元素做回归变量为φ的三角函数回归分析,有
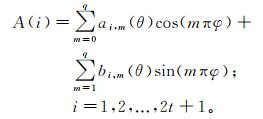 (10)
(10) 式中:ai, m(θ)、bi, m(θ)为第二层的回归系数;q为第二层展开阶数。
同理,令式(10)中的回归系数组成矩阵B,有
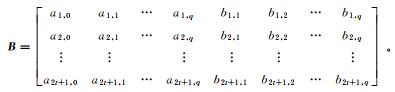
对B中的元素做以回归变量为θ的回归分析,有
 (11)
(11) 式中:αi, j, k与βi, j, k为第三层的回归系数;u为第三层展开阶数。
由于S与αi, j, k、βi, j, k的关系为线性关系,因此这种设定下的回归分析可以被定义为多元线性回归。每一层的展开阶数t、q与u的具体数值可用回归诊断中的显著性诊断来确定。
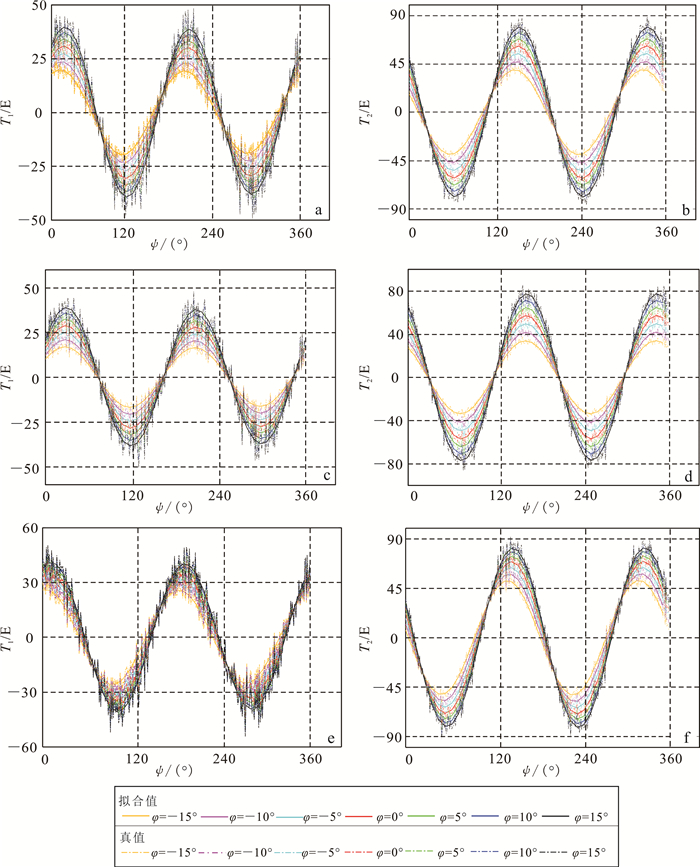
在图 2所示的计算样本中,θ与φ各有7个不同取值(θ其他取值的重力梯度响应在图 2中省略未画出),由于取值数量较小,因此q与u可以全部设置为2。图 2中ψ有180个取值,考虑到计算速度,先将t设置为较小的5。为验证拟合方法的稳定性,在数据中加入10 %的高斯白噪声。用公式(9)—(11)进行回归计算,所得结果见图 3。从图 3可见,用回归分析得到的自身梯度值与真值基本相符,并且对随机噪声有良好的抗性。
|
| a、b. θ=0°; c、d. θ=-15°; e、f. θ=15°。 图 3 含10%高斯噪声的回归分析拟合结果 Fig. 3 Fitting results obtained by regression analysis under 10% gaussian noise |
|
|
公式(9)—(11)做了三层回归分析,现逐层进行回归诊断。回归诊断的目的是:1)检查线性回归关系是否显著,显著性决定了回归变量作用的大小,显著性小的回归变量可以予以剔除;2)检查每一层的拟合残差及其分布,检验拟合精度并检查样本数据中的离群点;3)检验误差正态性以及自变量的线性关系,验证线性回归的前提是否成立;4)进行回归公式预测能力分析,由于加入噪声之后的样本数据更贴合实际情况,因此以加入噪声之后的数据进行分析。
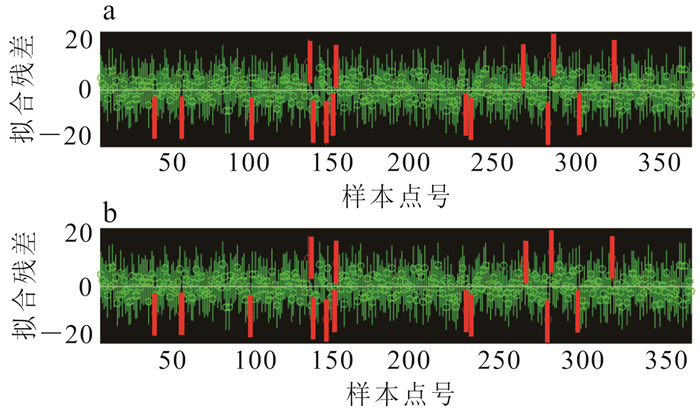
首先对第一层回归分析的cn与dn做回归诊断。以φ=15°、θ=15°为例,t=5,回归系数以及回归系数的95%置信区间见图 4,拟合残差与离群点见图 5,回归系数对应的cos项或者sin项与自身梯度之间的显著性统计指标见表 1。通过图 4得知,cn与dn的置信区间展布范围较小,说明系数的计算结果波动范围小,结果较为稳定。表 1中,显著性水平的最大值出现在c2项与d2项上,分别达到了49.791 320与77.697 870,其余三角函数项的显著性水平较小;出于回归方程简洁性的考虑,可以剔除对自身梯度影响不显著的变量,因此t取2。表 1中的p值描述原假设在极端情况下发生的概率,在本节的回归诊断中,原假设是该回归项与相应变量之间在概率为0.05的水平上不存在关系,当p < 0.05时拒绝该假设。c2项与d2项对应的p值为2.28×10-16与6.03×10-222,极小的p值说明可以拒绝原假设,即这两项与相应变量之间的关系不由抽样误差所引起。图 5中:绿线残差的置信区间包括0点,表明其残差是由于随机波动的影响而产生的;红线为离群点的残差,离群点的存在影响了回归分析的精确性,应当予以剔除。

|
| a.交线测量;b.内联测量。 图 4 θ=15°、φ=15°时第一层回归系数与95%置信区间 Fig. 4 Regression coefficients and their 95% confidence intervals of the first layer when θ=15°, φ=15° |
|
|
|
| a.交线测量;b.内联测量。 图 5 θ=15°、φ=15°、ψ ∈[-180°, 180°]时第一层拟合残差 Fig. 5 Residuals of the fitting in the first layer when θ=15°, φ=15° and ψ ∈[-180°, 180°] |
|
|
| 回归系数 | 回归系数方差 | 显著性水平 | p | |
| c0 | 0.630 700 | 0.413 244 | 0.984 039 | 0.325 780 |
| c1 | 0.404 500 | 0.413 244 | 0.904 460 | 0.366 377 |
| c2 | 20.575 980 | 0.413 244 | 49.791 320 | 2.28×10-16 |
| c3 | -0.217 220 | 0.413 244 | -0.525 650 | 0.599 467 |
| c4 | 0.475 198 | 0.413 244 | 1.149 920 | 0.250 967 |
| c5 | 0.001 143 | 0.413 244 | 0.002 765 | 0.997 795 |
| d1 | -0.188 000 | 0.412 065 | -0.456 240 | 0.648 501 |
| d2 | 32.016 600 | 0.412 065 | 77.697 870 | 6.03×10-222 |
| d3 | 0.324 824 | 0.412 065 | 0.788 282 | 0.431 068 |
| d4 | -0.261 450 | 0.412 065 | -0.634 500 | 0.526 174 |
| d5 | -0.057 770 | 0.412 065 | -0.140 200 | 0.888 580 |
然后检验第一层回归分析的误差正态性以及自变量之间是否存在线性关系。误差正态性检验可以从学生化残差与正态分布函数上α分位点是否呈线性关系来看出,这样的对比图简称为QQ(quantile-quantile)图。模型误差符合正态分布是应用多元线性回归的前提。设公式(9)中的正、余弦项组成的矩阵为X,自变量之间复线性关系的强弱可以用XTX的条件数判断。若条件数较小,则自变量之间的线性关系不显著。
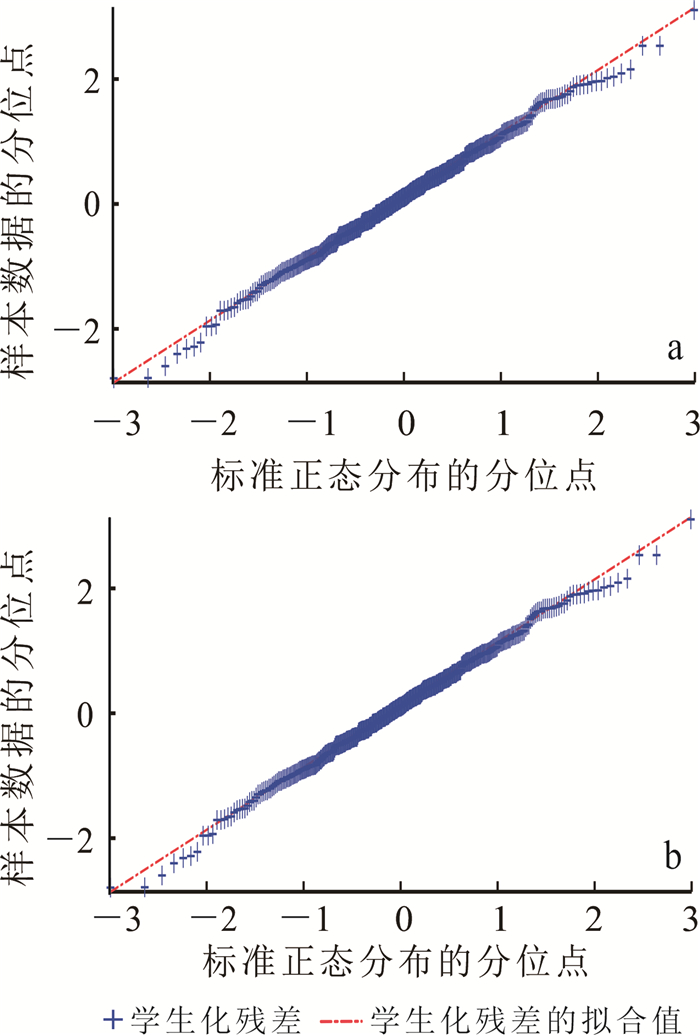
第一层回归分析的QQ图见图 6。从图 6可知,在给定的样本条件下,QQ图呈现明显的线性关系,直线呈45°并且通过原点,说明样本的均值和方差与标准正态分布一致,因此第一层回归分析中用三角函数作为自变量做多元线性回归有充分的合理性。
|
| a.交线测量;b.内联测量。 图 6 第一层回归分析QQ图 Fig. 6 Quantile-quantile figure of the first layer |
|
|
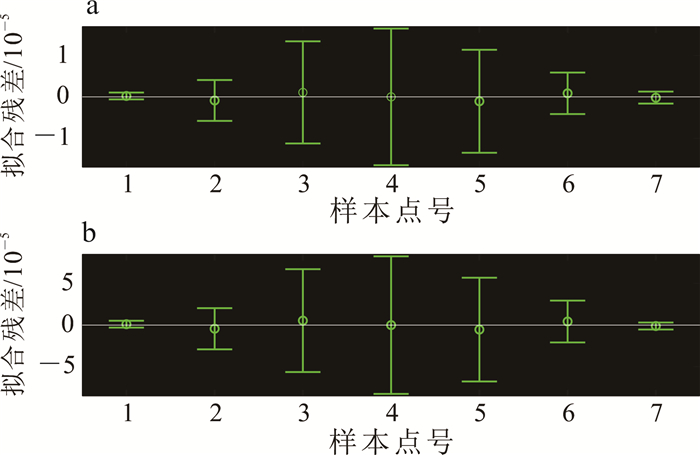
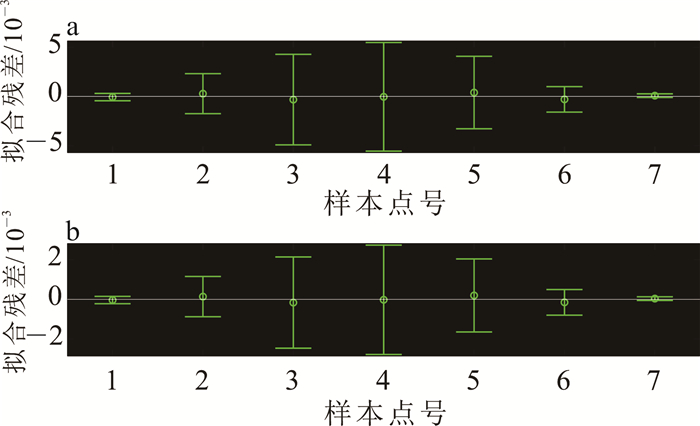
令t=2,对第二层与第三层回归做相同的分析。第二层回归分析的残差见图 7,回归系数及显著性统计见表 2。由表 2可知,在第二层回归分析中,余弦项的显著性水平普遍小于正弦项。第三层完全展开后得到的系数见表 3。根据表 3和公式(9)—(11)可以得到自身梯度值。第三层回归分析的q=2,u=2,因此B有25个元素,每一个元素都可以做出一张残差分布图。由于不同图之间差别不大、统计结论相似,出于篇幅考虑,仅展示B中最后一个元素B[5, 5]的统计结果,如图 8与表 4所示。对比表 4和表 2可知,第三层回归分析无论正弦项还是余弦项的显著性水平都比第二层小,因此B与回归系数的关系更弱一些。所以,第二、三层回归分析用三角函数展开的方式有进一步改进的空间。第二、三层回归分析的拟合残差置信区间全部包括0(图 7、图 8),是因为第一层以及第二层中解算出的系数中不含噪声。
|
| a.交线测量;b.内联测量。 图 7 θ=15°、φ∈[-15°, 15°]时第二层拟合残差 Fig. 7 Residuals of the fitting in the second layer when θ=15°, φ∈[-15°, 15°] |
|
|
| 回归系数 | 回归系数方差 | 显著性水平 | p | |
| a7, 0 | 0.168 600 | 0.357 252 | -0.055 140 | 0.964 935 |
| a7, 1 | 0.122 657 | 0.357 252 | 0.343 335 | 0.789 454 |
| a7, 2 | 0.020 101 | 0.090 219 | 0.222 800 | 0.860 441 |
| b7.1 | 0.095 815 | 0.017 883 | 5.358 006 | 0.117 465 |
| b7, 2 | 0.133 025 | 0.009 059 | 14.684 550 | 0.043 286 |
| i | αi, 1, 0 | αi, 1, 1 | αi, 1, 2 | βi, 1, 1 | βi, 1, 2 | αi, 2, 0 | αi, 2, 1 | αi, 2, 2 | βi, 2, 1 | βi, 2, 2 | αi, 3, 0 | αi, 3, 1 | αi, 3, 2 | βi, 3, 1 | βi, 3, 2 | αi, 4, 0 | αi, 4, 1 | αi, 4, 2 | βi, 4, 1 | βi, 4, 2 | αi, 5, 0 | αi, 5, 1 | αi, 5, 2 | βi, 5, 1 | βi, 5, 2 | ||||
| 1 | 269.355 4 | -184.736 0 | 49.549 960 | -0.700 880 | 2.718 161 | -177.682 000 | 122.912 900 | -32.916 800 | 0.026 714 | -1.410 180 | 43.995 470 | -30.720 600 | 8.323 390 | 0.480 094 | 0.292 883 | 61.884 100 | -40.298 100 | 9.460 301 | -6.493 890 | 3.300 332 | -33.675 800 | 21.898 060 | -5.211 860 | 3.554 596 | -1.694 620 | ||||
| 2 | 172.720 2 | -118.459 0 | 31.773 200 | -0.449 430 | 1.742 981 | -113.936 000 | 78.816 100 | -21.107 400 | 0.017 130 | -0.904 260 | 28.211 460 | -19.699 100 | 5.337 253 | 0.307 853 | 0.187 807 | 39.682 290 | -25.840 600 | 6.066 281 | -4.164 110 | 2.116 290 | -21.594 100 | 14.041 810 | -3.342 030 | 2.279 333 | -1.086 650 | ||||
| 3 | -98.960 06 | 67.871 400 | -18.204 500 | 0.257 504 | -0.998 650 | 65.280 130 | -19.951 800 | 12.093 540 | -0.009 810 | 0.518 096 | -16.163 800 | 11.286 680 | -3.058 000 | 25.029 770 | -0.107 600 | -22.736 100 | -17.544 600 | -3.475 690 | 2.385 841 | -1.212 540 | 12.372 410 | -8.045 300 | 1.914 827 | -3.17 248 | 0.622 600 | ||||
| 4 | -80.284 2 | 55.062 380 | -14.768 900 | 0.208 906 | -0.810 180 | 52.960 100 | -36.635 500 | 9.811 181 | -0.007 960 | 0.420 318 | -13.113 300 | 9.1565 920 | -2.480 870 | -0.143 100 | -0.087 300 | -18.445 200 | 12.011 270 | -2.819 740 | 1.935 572 | -0.983 700 | 10.037 420 | -6.526 940 | 1.553 450 | -1.059 480 | 0.505 099 | ||||
| 5 | -168.163 0 | 138.061 300 | -20.462 000 | 0.523 803 | -2.031 400 | 132.790 100 | -91.858 400 | 24.600 180 | -0.019 960 | 17.228 900 | -30.080 000 | 22.958 890 | -6.687 080 | -0.358 800 | -0.218 880 | -46.248 800 | 30.116 600 | -7.070 110 | 4.853 179 | 10.136 590 | 62.976 670 | -16.365 400 | -2.406 480 | -2.656 510 | 1.266 466 |
|
| a.交线测量;b.内联测量。 图 8 θ∈[-15°, 15°]时第三层拟合残差 Fig. 8 Residuals of the fitting in the third layer when θ∈ [-15°, 15°] |
|
|
| 回归系数 | 回归系数方差 | 显著性水平 | p | |
| α5, 5, 0 | 0.139 980 | 147.090 000 | 0.043 368 | 0.972 408 |
| α5, 5, 1 | 5.044 455 | 147.090 100 | 0.034 295 | 0.978 176 |
| α5, 5, 2 | -1.303 810 | 37.145 650 | -0.035 100 | 0.977 664 |
| β5, 5, 1 | 2.007 294 | 7.362 767 | 0.272 628 | 0.830 558 |
| β5, 5, 2 | -1.028 400 | 3.729 766 | -0.275 730 | 0.828 723 |
第二、三层回归分析的QQ图均为水平直线,但直线不通过原点(图 9),说明误差不符合标准正态分布,但符合正态分布;因此第二层与第三层回归分析可以通过误差正态性的检测。

|
| a.交线测量;b.内联测量。 图 9 第二层与第三层回归分析QQ图 Fig. 9 Quantile-quantile figure of the second and third layer |
|
|
三层展开的阶数t、q、u相等,回归公式的形式一致,因此X T X的条件数也相同。经过计算,三层回归分析X T X的条件数均为2,说明三层回归分析中自变量之间相对独立,不存在明显的线性关系。
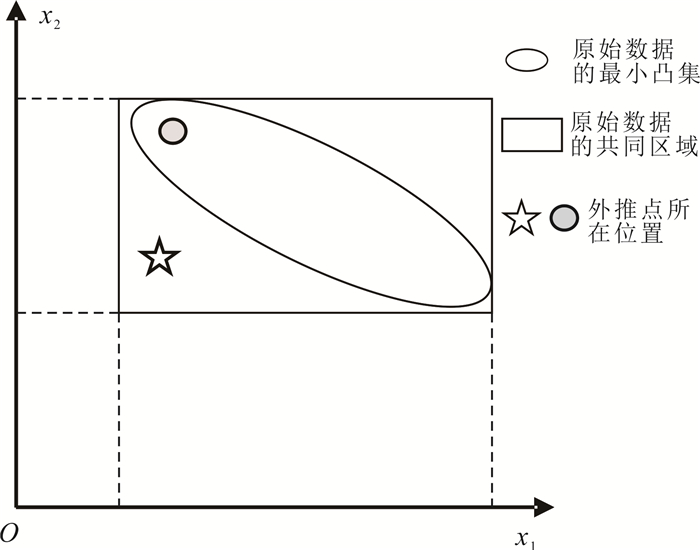
最后一项回归诊断是对回归公式的预测能力进行检验。预测是回归分析的基本用途之一,多元回归中的预测需要注意自变量所处的区间位置。在样本数据分布范围之外的区域进行预测时需要格外小心,一个在原始区域内拟合良好的模型,很可能在原始区域外的拟合失真。如图 10所示,五角星的位置虽然落在原始数据的区间内,但并未落在封闭的最小凸集里;灰色圆圈的位置才落在了最小凸集中。简单比较新数据点对应自变量与原始自变量的范围并不总能探测出隐含的外推可能,因此用一种正规的检测手段是必要的。将包含所有原始数据点的最小凸集定义为回归变量外壳(regressor variable housing, RVH),如果新数据点落在RVH的内部或者边界上,则此时的预测没有外推的风险。
|
| 图 10 多元回归中可能隐含的外推区域示意图 Fig. 10 Schematic diagram of extrapolation region that may be implied in multiple regression |
|
|
定义H=X(X T X)-1X T,H的对角线元素hi, i可用于外推合理性的检验。hi, i的大小与样本中心及样本密度有关,hi, i的最大值点hmax通常分布在样本密度较低区域的边界上。设预测点坐标为x0,若x0满足
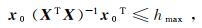 (12)
(12) 则可以说该预测点落在了最小凸集里,此时进行预测分析是安全的。训练样本的数据量越大,最小凸集的范围也越大,预测点则可以说该预测点落在了最小凸集里,此时进行预测分析是安全的。训练样本的数据量越大,最小凸集的范围也越大,预测点x0落在最小凸集之内的概率也会越高。通过式(12)可以计算训练样本数据量的最佳值。
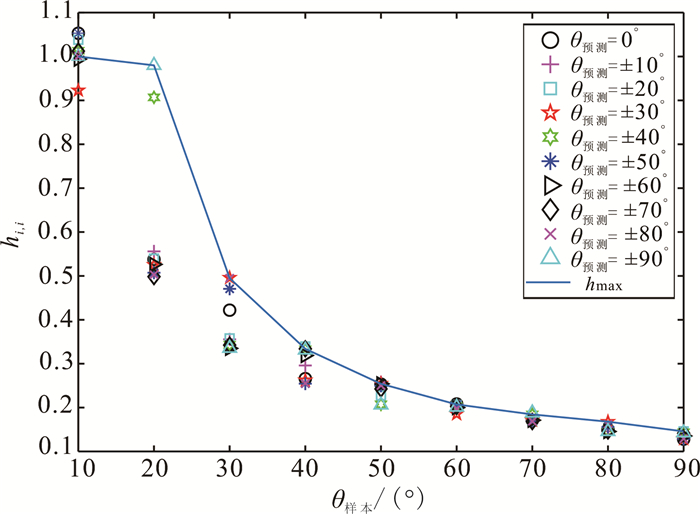
图 11展示了不同训练样本下,用式(12)计算的不同预测角度对应的hi, i值。计算方法是固定φ、φ,设θ为预测角,计算θ在±10°到±90°变化时的hi, i值。如果预测角的hi, i值落在hmax曲线下方,则表示θ处于回归数据的最小凸集之内。从图 11得知,θ在±20°至±90°区间时,大部分预测角的hi, i值都落在hmax曲线下方,说明在3个转角中,仅有1个θ角在样本区间之外时,进行预测的风险不大。
|
| θ预测为预测角;θ样本为训练样本。 图 11 外推预测风险分析 Fig. 11 Risk analysis of extrapolation forecast |
|
|
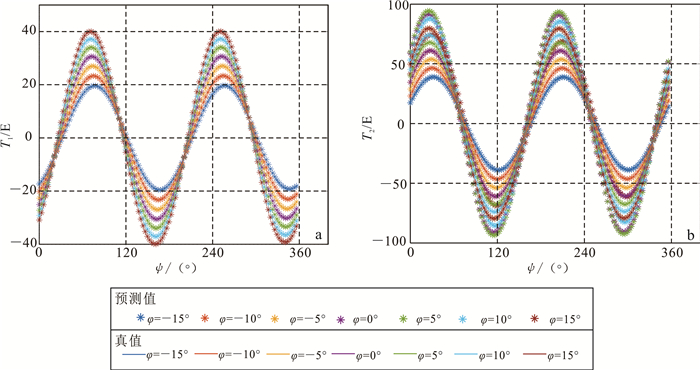
为了验证图 11的正确性,将训练样本中的φ与θ从图 2所示的±15°扩大到±20°,依旧对原始样本数据加入10%的高斯白噪声,并对θ=80°时进行预测,结果如图 12所示。由图 12可知,预测值与样本值完全一致;因此,如果实测数据φ的变化范围在训练样值范围内,则可以对θ取值变化时造成的自身梯度效应进行精准预测。将φ的预测角度扩大到-20°~70°,θ的预测角度仍为80°,得到的结果如图 13所示。从图 13中可以看到,当φ与θ全部超出样本范围时,回归公式的预测能力失效,预测值与真值出现了较大偏差。这提示我们在前置的地面标定时,应当对飞行中的转角变化有一个准确的估计,并在飞行中平稳地控制飞机姿态。
|
| 图 12 预测角φ∈[-15°, 15°]、θ=80°时的交线值(a)与内联值(b)预测 Fig. 12 Prediction of crossline value (a) and inline value (b) with the predition range φ∈[-15°, 15°] and θ=80° |
|
|

|
| 图 13 预测角φ∈[-20°, 70°]、θ=80°时的交线值(a)与内联值(b)预测 Fig. 13 Prediction of (a) crossline value and (b) inline value with the predition range φ∈[-20°, 70°] and θ=80° |
|
|
由于缺少带有3个姿态角的原始数据,为进一步验证回归分析的结果,取加拿大某地上方的实测飞行轨迹,地质模型用长方体模拟,以随机转角来产生自身梯度干扰,并应用回归分析来处理带有干扰的数据。地质模型如图 14所示。模型由两组大小、埋深与密度均不同的棱柱体组成,小而浅的一组棱柱体表示高频信号,大而深的一组表示低频信号, 模型参数如表 5所示。观测面上的飞行轨迹如图 15所示。

|
| 图 14 用长方体模拟地下异常 Fig. 14 Using rectangular to simulate underground anomalies |
|
|
| 编号 | 长/m | 宽/m | 高/m | 中心埋深/m | 剩余密度/(g/cm3) |
| 1 | 1 978 | 629 | 333 | 400 | 1.0 |
| 2 | 1 978 | 629 | 333 | 800 | 3.0 |
| 3 | 1 978 | 629 | 333 | 400 | 1.0 |
| 4 | 1 978 | 629 | 333 | 800 | 3.0 |
| 5 | 7 972 | 3 774 | 400 | 1 200 | 1.5 |
| 6 | 7 972 | 3 774 | 800 | 1 600 | 1.5 |
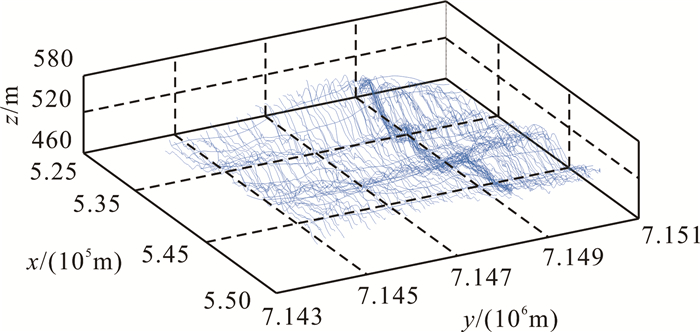
|
| 图 15 取自实际数据的观测面 Fig. 15 Observation surface got from real survey |
|
|
经过正演计算,由观测面上的5个独立分量[Txx, Txy, Txz, Tyy, Tzz]生成的原始交线测量值与内联测量值如图 16a所示;在图 15中加入θ与φ处于[-15°, 15°]中呈均匀分布时飞机产生的自身梯度干扰,交线与内联测量结果如图 16b所示;经过公式(9)—(11)的处理,得到的结果如图 16c所示。

|
| a.原始值;b.添加随机角度产生自身梯度干扰后;c.经公式(9)—(11)改正后。 图 16 模型校正效果验证 Fig. 16 Verification of correction effect under complex model |
|
|
原始的T1和T2值分别在-20.0~19.6 E之间和-38.8~57.2 E之间(图 16a),经公式(9)—(11)改正后的T1和T2值分别在-20.6~20.0 E之间和-38.8~57.5 E之间(图 16c),T1和T2在改正前后基本保持了相同的量级,并且异常的形态保存较为完整。从图 16c上来看,用公式(9)—(11)所计算的结果虽然去除了几十厄的自身梯度效应,但并没有完全消除由随机转角所带来的干扰。
3 结论1) 本文对自身梯度效应的回归分析进行了讨论,用三层逐步回归的方法来寻找飞机的3个转角与重力梯度的关系。
2) 经过计算与回归诊断,验证了这种方法的可行性,证明实际飞机姿态与样本的变化范围相符时可以保证校正的精度。
3) 仿真计算结果表明,拟合误差这种校正方法不需要对飞机的质量分布做出任何假设,以纯数据驱动的方式即可以完成校正,为实际操作带来极大的方便。
| [1] |
Dransfield M, Tiaan L R, Darren B. Airborne Gravimetry and Gravity Gradiometry at Fugro Airborne[C]//Abstracts from the ASEG-PESA Airborne Gravity Workshop. Sydney: [s. n.], 2010: 49-57.
|
| [2] |
Nabighian M N, Ander M E, Grauch V J S. Historical Development of the Gravity Method in Exploration[J]. Geophysics, 2005, 70(6): 63-79. DOI:10.1190/1.2133785 |
| [3] |
Murphy C A. The Air-FTGTM Airborne Gravity Gradiometer System[C]//Airborne Gravity 2004: Abstracts from the ASEG-PESA Airborne Gravity Workshop. Sydney: [s. n.], 2004: 7-13.
|
| [4] |
Difrancesco D. Advances and Challenges in the Development and Deployment of Gravity Gradiometer Systems[C]//EGM 2007 International Workshop.[S. l.]: European Association of Geoscientists & Engineers, 2007: 1-6.
|
| [5] |
Bell Geospace. Air-FTG® Acquisition and Processing Report Geological Survey of Swede Kiruna Survey, Kiruna, Sweden[R/OL].[2013-11-02]. http://www.bellgeo.com
|
| [6] |
Bell Geospace. Processing and Acquisition of Air-FTG® Data and Airborne Magnetics Trill Project and Extension Sudbury Basin, Ontario, Canada for Wallbridge Mining Company Limited[R/OL].[2015-03-01].
|
| [7] |
Marshall M R. An Investigation into the Feasibility of Using a Modern Gravity Gradient Instrument for Passive Aircraft Navigation and Terrain Avoidance[D]. Dayton: Department of the Airforce University, 2009. https://www.researchgate.net/publication/290316241_An_investigation_into_the_feasibility_of_using_a_modern_gravity_gradiometer_instrument_for_passive_aircraft_navigation_and_terrain_avoidance
|
| [8] |
袁圆.全张量重力梯度仪数据的综合分析与处理解释[D].长春: 吉林大学, 2015. Yuan Yuan. Comprehensive Analysis, Processing and Interpretation of the Full Tensor Gravity Gradient Data[D].Changchun: Jilin University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10183-1015587927.htm |
| [9] |
丁昊, 孙晓洁, 李海兵. 旋转式重力梯度仪自身梯度补偿研究[J]. 导航与控制, 2015, 14(2): 29-31. Ding Hao, Sun Xiaojie, Li Haibing. Research on Self-Gradient Compensation of Rotating Accelerometer Gravity Gradiomter[J]. Navigation and Control, 2015, 14(2): 29-31. DOI:10.3969/j.issn.1674-5558.2015.02.005 |
| [10] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 解放军信息工程大学, 2004. Sun Zhongmiao. Throry, Methods and Applications of Airborne Gravimetry[D]. Zhengzhou: Information Engineering University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-90008-2005030005.htm |
| [11] |
王泰涵, 肖锋, 袁园, 等. 航空重力梯度测量飞行姿态影响及误差校正[J]. 世界地质, 2014, 33(3): 680-684. Wang Taihan, Xiao Feng, Yuan Yuan, et al. Impact of Flight Attitude and Error Correction on Airborne Gradiometry[J]. Global Geology, 2014, 33(3): 680-684. |
| [12] |
Specification of Cessna Caravan N208CC[EB/OL].[2019-01-05].http://cessna.txtav.com/en/turboprop/caravan#cvingspan.
|


