2. 上海交通大学高新船舶与深海开发装备协同创新中心海洋工程国家重点实验室, 上海 200240
2. State Key Laboratory of Ocean Engineering, Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai Jiao Tong University, Shanghai 200240, China
0 引言
海底沉积层的声速、密度、孔隙度等声学参数是浅海声场数值预报、海底地貌测绘、沉底和掩埋目标探测等应用中所必须的参数,也是跨海大桥建设、航道运输、港口工程、海底施工和海底油气矿产等资源开发需要获取的重要信息。利用沉积层探针插入或钻孔方式直接测量方法提取海底参数,时间和人工成本较高,且只能得到海底离散有限样本,不能充分反映海底的连续分布状态。假定海底沉积物为均匀液态或固态介质,研究者们通过正、反两方面分析海底声学特性[1-2]。反演的声学参数主要有:海底衰减系数[3-4]、密度、孔隙度、泊松比、体积弹性模量等[5-7]。以贝叶斯统计理论为基础的匹配场反演[8],考虑声场预报和搜索策略两方面问题,估计海底声学参数;基于海底回波到达时间结构及能量信息的脉冲声反演,可提高因距离定位及声速剖面失配所产生的参数反演精度[9];利用海洋波导中简正波的频散关系反演的远距离宽带海底声速和密度等参数,适用于地形和声速剖面变化不大的海区[10];传播损失反演方法利用声速、密度和衰减系数拟合出海底反射损失对掠射角的单参数[11],只需单个水听器, 避免了复杂测量;利用垂直接收阵探测声场匹配反演海底声学特征,将海域视为无限大界面,取得了较好的实验研究成果[12]。根据声场水平纵向相关振荡结构与简正波的本征值和幅度的关系,可反演出海底声速的分层结构[13]。
侧扫声呐海底图像反演通过主动声呐方式连续侧扫或持续走航方式获取大范围覆盖的声学回波,可以得到全面连续的高分辨率图像信息[14]。计算机断层成像(computed tomography,CT)是无损的2D或3D目标断面重建方法[15-16]。衍射CT在水声学问题的求解中,根据测量到的散射声场反演目标的几何形状与声学参数分布重建目标断面图像,这是一个典型的声学反问题。本文在正向散射声场预报的数值计算框架下[17-18],通过声源主动发射线性调频(linear frequency modulation,LFM)脉冲信号照射海底指定区域,根据衍射CT的基本原理反演海水和海底构成的分层介质密度、声速、孔隙度等声学参数,得到二维剖面图像, 以期在不破坏环境的条件下实现连续和大面积的海底环境监控。另外,利用图像的频谱信息进行海底声学参数反演,可充分利用Fourier反变换的快速计算方法,克服基于网格剖分数值计算方法的局限,以提高效率。
1 声场图像模型采用随机生长四参数生成法(quartet structure generation set,QSGS)[19]构造海底微观结构,建立多孔介质水声散射特性分析二维图像模型。
QSGS构造过程如下:
1) 利用图像描述水介质和海底构成的二维声场模型。令海水均匀,海底是密度和声速在一定范围内随机分布的多孔介质,介质参数见表 1。
| 介质 | 密度/(kg/m3) | 声速/(m/s) |
| 水 | 1 000 | 1 500 |
| 海底 | 1 600~1 700 | 1 500~1 600 |
2) 在二维声场计算区域内随机分布固相生长核,固相生长核的分布概率为p(p < 孔隙度n)。
3) 定义二维模型的8个生长方向,如图 1所示。固相生长核向其周围邻域沿8个方向生长,将各方向的生长概率定义为pi,i=1, 2, …, 8。其中:p1—p4表示4个主要方向的生长概率;p5—p8表示4个角方向的生长概率。为获得各向同性结构,主方向与角方向生长比例设为4。逐次将8个方向的邻域点重新生成随机数,当i方向邻域点的随机数小于阈值Di时,该点成为生长相,否则为非生长相,即孔隙。
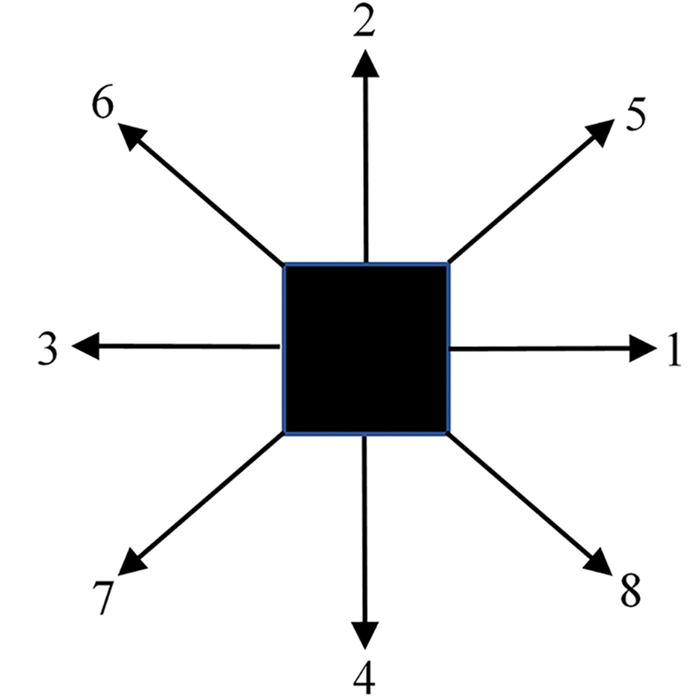
|
| 图 1 二维声场模型的8个生长方向 Fig. 1 Eight growth directions of two-dimensional acoustic model |
|
|
4) 遍历声场区域内全部网格,重复8个方向的随机生长过程,循环操作使得海底区域达到给定的孔隙度。
根据QSGS方法生成两种不同孔隙度n=0.20, 0.47的声场图像模型,如图 2所示。
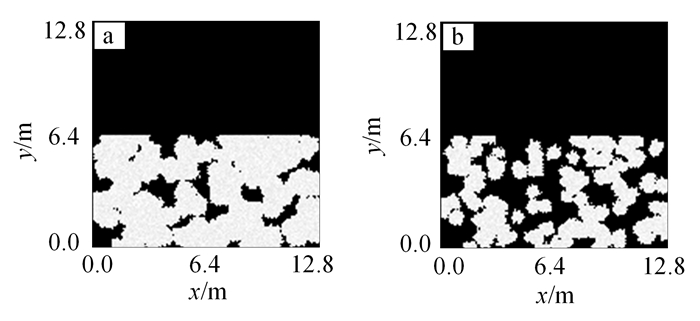
|
| a. n=0.20;b. n=0.47。 图 2 海水与海底沉积层二维声场图像模型 Fig. 2 Two-dimensional sound field image model of water and sediment |
|
|
为保证计算精度,声场计算区域为12.8 m×12.8 m,图像采样间隔为声波波长的1/10。图像的像素值为与不同介质声阻抗特性相关的指数,定义为
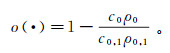 (1)
(1) 式中:ρ0、c0分别为水介质的密度和声速;ρ1、c1分别为海底沉积层的密度和声速。o(·)=0为水域,表示为图像中的黑色像素区域;o(·)= 1-(c0ρ0/c1ρ1)为多孔海底沉积层中的固体介质,表示为声场图像模型中的高亮区域。
2 拓展Fourier衍射定理为将Fourier衍射定理进行拓展,给出单频入射波在所有方向产生的投影关系的数学模型。令入射方向与x轴正方向夹角为φ,波数矢量k=(kx, ky)= (k0cos φ, k0sin φ)(k0为入射波波数),方向矢量r=(x, y),则入射平面波可表示为
 (2)
(2) 在与发射方向垂直的直线y=±l0上,散射波的频域表示为
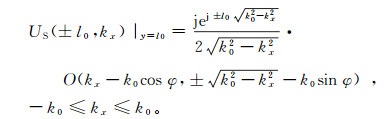 (3)
(3) 式中,O(+)是目标图像的二维Fourier变换。由式(3)可见:受某一方向角为φ的单频平面波照射,前向散射声场的一维频谱与声场图像的二维频谱指定位置的样本值成比例,样本的轨迹位于图 3中虚线表示的过原点半圆弧上。圆弧半径等于k0=2πf0/c0(f0为声波频率),相应的后向散射一维频谱与图 3中实线所示半圆弧上的取值成比例[15]。改变入射方向,圆弧轨迹旋转相同的角度; 改变入射声波频率,相应的圆弧半径发生改变。图 3中分别给出φ=0°、90°、180°、270°时,计算前后散射声压所对应圆弧样本的轨迹。
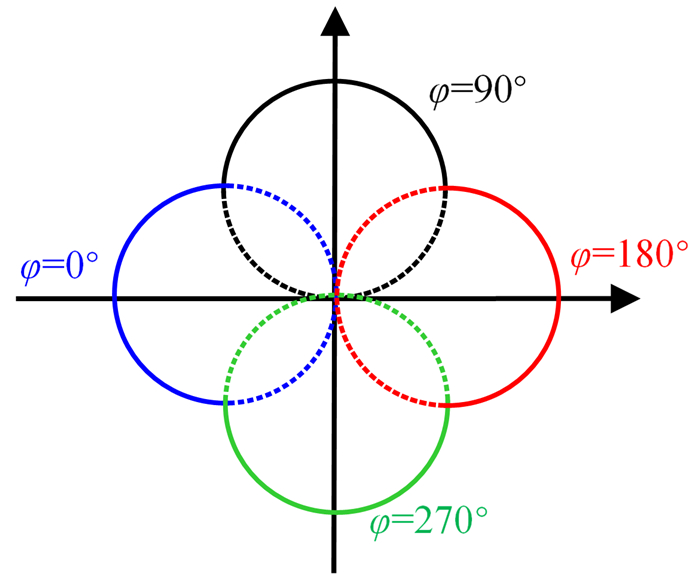
|
| 图 3 前后向散射与二维声场频域样本的关系 Fig. 3 Relationship between forward and backward scattering and two-dimensional spectral samples |
|
|
在此框架下,若目标图像已知,在其频域上提取相应圆弧上的样本,进行一维Fourier反变换后可得到目标的前后向散射声压强度。若前后散射声场的声压已知,求解一维Fourier变换后,将结果插值至二维频域的圆弧上,得到目标频谱的不均匀稀疏样本,再通过二维不均匀Fourier反变换即可重建目标图像。
为了在单一方向入射条件下,利用局部样本反演多孔性海底与水介质构成声场的二维图像剖面,令接收方向与声波入射方向的分置角为θ。为获得收发分置的目标特性,可以固定目标和入射方向不变,改变接收方向;也可以固定目标和接收阵,改变声波入射方向。本文采用前一种方式,并重新推导散射远场与图像频域样本的比例关系:
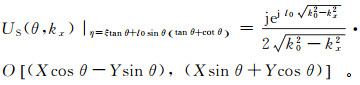 (4)
(4) 其中:
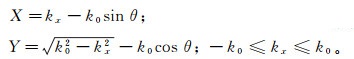 (5)
(5) 式中:kx=kξcos θ+kηsin θ;变量ξ、η为旋转坐标方向。
根据式(4)、(5)得到频域样本轨迹,如图 4所示。由图 4可见:指定入射频率,接收方向数越多,获取样本的圆弧越多;指定入射方向,声波频率间隔越精细,在此方向上不同半径的圆弧越多。因此降低频率间隔或增加方向数,对应的频域样本越密集。
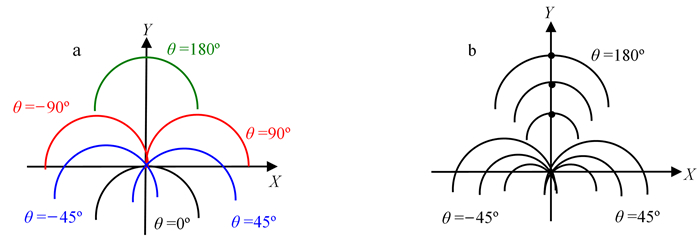
|
| a.单频波入射;b.调频波入射。φ=90°。 图 4 图像频域样本轨迹 Fig. 4 Locus of image spectral samples in frequency domain |
|
|
为了验证本文所建立的散射声场与图像模型关系的正确性,将相同参数的二维声场模型输入COMSOL多物理场平台,运用基于网格剖分的有限元技术计算后向散射声场的频率响应。同时,根据图 4b构建的调频波入射得到的散射声场与图像频域样本关系,在声场图像二维频谱中提取θ=180°时相应黑色圆点位置处的样本即可得到后向散射声场的频率响应,归一化的散射声压对比结果如图 5所示。由图 5可见,本文方法与基于COMSOL多物理场平台的有限元方法结果吻合较好。本文方法存在少量误差是样本提取过程中采用最近邻插值法所造成的。
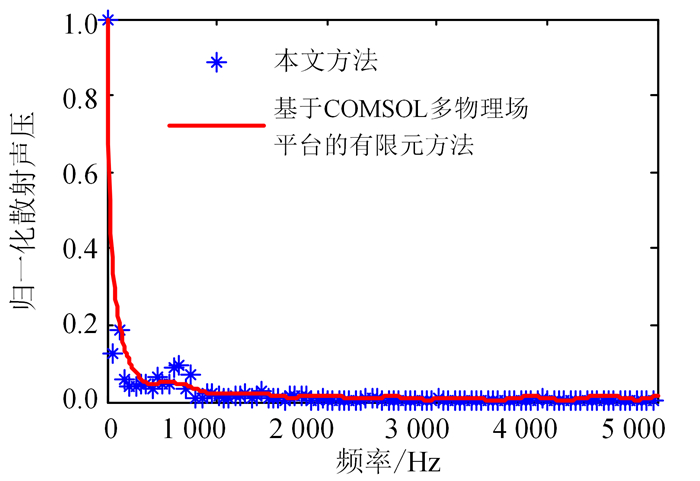
|
| 图 5 归一化散射声压对比 Fig. 5 Comparison of normalized scattering sound pressure |
|
|
图 6给出两种方法计算时间的对比曲线。基于COMSOL多物理场平台的有限元方法计算散射远场随带宽增加和频率间隔减小,所需时间呈现指数增长。而本文方法的计算量主要来自于从二维图像到频谱的变化、频域插值及二维谱的反变换,由于Fourier正反变换都存在快速算法,因此计算时间随计算频率间隔减小和m增加的变化不明显。在满足计算精度的前提下,与基于COMSOL多物理场平台的有限元方法相比,本文方法计算效率提高约两个数量级。
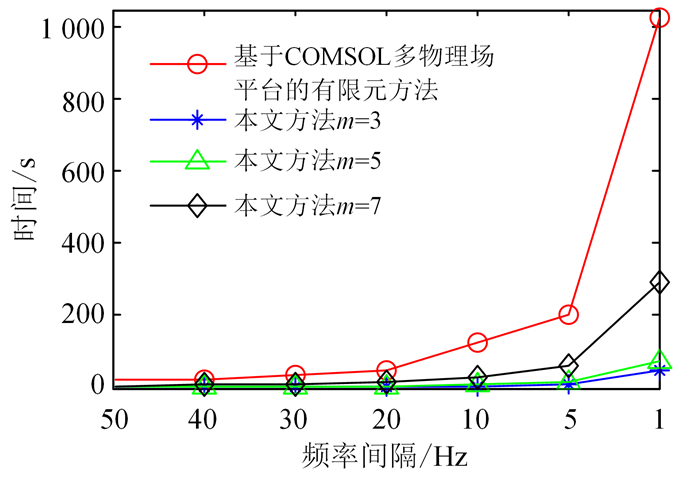
|
| m.方向数。 图 6 计算时间比较 Fig. 6 Comparison of calculation time |
|
|
假定声源为调频声波(10~5 000 Hz),垂直水平面照射海底,声场模型见图 2b。求解其二维快速Fourier变换得到频谱,根据式(4)、(5)提取一组不同半径的圆弧轨迹处样本,利用二维不均匀反变换的快速算法重建图像。海水为均匀介质,海底为孔隙度为0.47的多孔介质,忽略海底弹性。
图 7和图 8分别给出测试方向数与频率间隔(Δf)变化时重建的图像视觉效果。由图 7可见,利用宽带调频信号作为声源照射目标,获取少量方向的样本值,即可完成高精度的重建结果。由图 8可见,投影样本方向数固定不变,频率间隔越小,重建图像视觉效果越好。
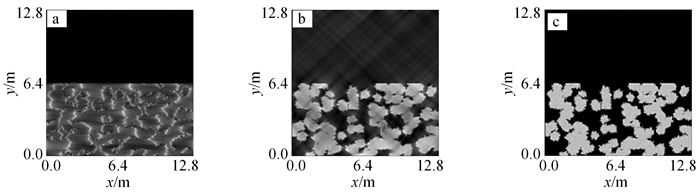
|
|
a. m=3(θ=-45°、0°、45°);b. m=5(θ=-60°、-30°、0°、30°、60°);c. m=7(θ=-120°、-80°、-40°、0°、40°、80°、120°)。 Δf=50 Hz。 图 7 重建二维声场图像与方向数 Fig. 7 Relationship between reconstructed image of two-dimensional sound field and direction number |
|
|

|
| a. Δf=500 Hz;b. Δf=300 Hz;c. Δf=10 Hz。m=5;θ=-60°、-30°、0°、30°、60°。 图 8 重建二维声场图像与频率采样间隔 Fig. 8 Relationship between reconstructed image of two-dimensional sound field and frequency interval |
|
|
为了给出重建精度与发射声波频率间隔的关系,图 9给出孔隙度与海底固体区域平均阻抗指数I(I为海底区域o(·)的平均值)随频率间隔和方向数变化的反演结果。
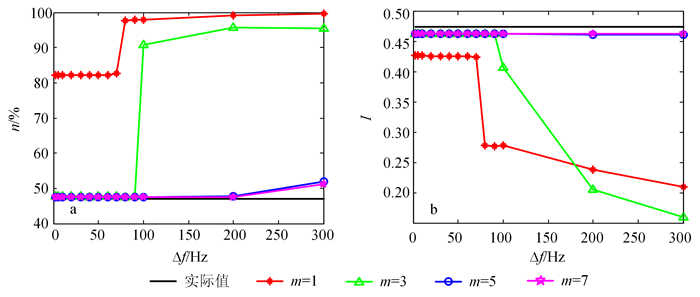
|
| 图 9 声学参数重建 Fig. 9 Acoustic parameter reconstruction |
|
|
图 9可见:Δf越小、m越大,通过数值方法反演的多孔介质声学参数越近于实际设定值;m < 3、Δf >80 Hz时不能正确反演参数;m固定不变,当Δf < 80 Hz时,继续减小Δf对提高参数反演精度的帮助不明显;当m达到5时,即使采用较大的Δf,仍然可得到较高的反演精度。但是,从图 9b中也明显看出,实际平均阻抗指数为0.470左右,而反演结果为0.465;这个差异是由于频域圆弧样本在非图像网格上时采用线性插值方法提取像素值所造成的。
4 结论本文从水中目标散射特性分析出发,结合医学Fourier衍射CT定理进行目标重建和声场快速预报,根据水中目标散射回波强度与计算区域二维剖面图像频谱样本之间的关系反演海底声学参数,方法有效。结果表明:
1) 计算时间取决于Fourier正反变换及提取样本的插值过程,与基于网格剖分的有限元方法相比,在保证精度的前提下,计算效率提高约两个数量级。
2) 反演精度取决于发射声波的频率间隔和方向数,方向数达到5个以上、频率间隔在80 Hz以下可以满足反演精度。
3) 平均阻抗指数的反演值略低于实际值,需要进一步研究合适的样本提取方法,提高精度。另外,还需将算法拓展至三维,以满足实际声场环境需求。
| [1] |
陈勃, 赵梅, 胡长青, 等. 射线理论下浅海声环境噪声声场空间相干性分析及海底声学参数反演[J]. 声学学报, 2018, 43(3): 298-306. Chen Bo, Zhao Mei, Hu Changqing, et al. Analysis on Spatial Coherence of Ambient Noise and Geoacoustic Inversion in Shallow Water[J]. Acta Acustica, 2018, 43(3): 298-306. |
| [2] |
傅磊, 刘四新, 吴俊军, 等. 频率域海底电磁法三维正演研究[J]. 吉林大学学报(地球科学版), 2010, 40(增刊1): 67-69. Fu Lei, Liu Sixin, Wu Junjun, et al. Three Dimensional Forward Study of Electromagnetic Method in Frequency Domain[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(Sup.1): 67-69. |
| [3] |
李佳蔚, 鹿力成, 郭圣明, 等. Warping变换提取单模态反演海底衰减系数[J]. 物理学报, 2017, 66(20): 204301. Li Jiawei, Lu Licheng, Guo Shengming, et al. Inversion of Seabed Attenuation by Using Single Mode Extracted by Warping Transform[J]. Acta Physica Sinica, 2017, 66(20): 204301. DOI:10.7498/aps.66.204301 |
| [4] |
李梦竹, 李整林, 李倩倩. 南海北部负跃层环境下海底参数声学反演[J]. 声学学报, 2019, 44(3): 321-328. Li Mengzhu, Li Zhenglin, Li Qianqian. Geoacoustic Inversion for Bottom Parameters in a Thermocline Environment in the Northern Area of the South China Sea[J]. Acta Acustica, 2019, 44(3): 321-328. |
| [5] |
倪然, 李红星, 谢青, 等. 基于Gassmann理论与遗传算法的海底沉积物物理参数声速反演方法[J]. 科学技术与工程, 2018, 18(6): 223-228. Ni Ran, Li Hongxing, Xie Qing, et al. Acoustic Inversion Method for Parameters of Seafloor Sediment Based on Gassmann Theory and Genetic Algorithm[J]. Science Technology and Engineering, 2018, 18(6): 223-228. DOI:10.3969/j.issn.1671-1815.2018.06.034 |
| [6] |
于盛齐, 黄益旺, 吴琼. 基于等效密度流体近似反射模型反演海底参数[J]. 声学学报, 2014, 39(4): 417-427. Yu Shengqi, Huang Yiwang, Wu Qiong. Bottom Parameters Inversion Based on Reflection Model of Effective Density Fluid Approximation[J]. Acta Acustica, 2014, 39(4): 417-427. |
| [7] |
Li Hongxing, Tao Chunhui, Liu Cai, et al. Acoustic Inversion Method for Parameters of Sediments Based on Adaptive Predatory Genetic Algorithm[J]. The Journal of the Acoustical Society of America, 2018, 143(1): 141. DOI:10.1121/1.5020272 |
| [8] |
肖灵, 张仁和, 李风华, 等. 测量海底声学参数的匹配场反演方法[J]. 热带海洋学报, 2001, 20(4): 20-27. Xiao Ling, Zhang Renhe, Li Fenghua, et al. A Matched-Field Inversion for Measuring Acoustic Sea-Bottom Properties[J]. Journal of Tropical Oceanography, 2001, 20(4): 20-27. |
| [9] |
徐东, 李风华, 郭永刚. 利用脉冲声反演深海海底声学参数[J]. 声学技术, 2016, 35(6): 178-181. Xu Dong, Li Fenghua, Guo Yonggang. Geoacoustic Inversion in Deep Water by Using Pulse Signal[J]. Technical Acoustics, 2016, 35(6): 178-181. |
| [10] |
郭晓乐, 杨坤德, 马远良. 一种基于简正波模态频散的远距离宽带海底参数反演方法[J]. 物理学报, 2015, 64(17): 174302. Guo Xiaole, Yang Kunde, Ma Yuanliang. A Far Distance Wideband Geoacoustic Parameter Inversion Method Based on a Modal Dispersion Curve[J]. Acta Physica Sinica, 2015, 64(17): 174302. DOI:10.7498/aps.64.174302 |
| [11] |
屈科, 胡长青, 赵梅. 利用传播损失反演海底单参数[J]. 声学学报, 2013, 38(4): 472-476. Qu Ke, Hu Changqing, Zhao Mei. Single Parameter Inversion Using Transmission Loss in Shallow Water[J]. Acta Acoustic, 2013, 38(4): 472-476. |
| [12] |
鹿力成, 马力. 浅海海底反演实验研究[J]. 声学技术, 2008, 27(5): 56-57. Lu Licheng, Ma Li. Geoacoustic Inversionsfrom Experiment Data in Shallow Water[J]. Technical Acoustics, 2008, 27(5): 56-57. |
| [13] |
苏晓星, 李风华, 简水生. 浅海低频声场的水平纵向相关性[J]. 声学技术, 2007, 26(4): 579-583. Su Xiaoxing, Li Fenghua, Jian Shuisheng. Horizontal-Longnitudinal Correlations of Low-Frequency Acoustic Field in Shallow Water[J]. Technical Acoustics, 2007, 26(4): 579-583. DOI:10.3969/j.issn.1000-3630.2007.04.007 |
| [14] |
赵建虎, 尚晓东, 张红梅. 侧扫声呐图像反演海底地形的一种线性算法[J]. 哈尔滨工业大学学报, 2017, 45(9): 80-86. Zhao Jianhu, Shang Xiaodong, Zhang Hongmei. Obtaining High-Resolution Seafloor Topography from Side Scan Sonar Image Using a Linear Algorithm[J]. Journal of Harbin Institute of Technology, 2017, 45(9): 80-86. |
| [15] |
Kak A C, Slaney M. Principles of Computerized Tomographic Imaging[M]. New York: Society of Industrial and Applied Mathematics, Ed, Philadelphia, 2001.
|
| [16] |
Chu Dezhang, Tang Dajun, Austin T C, et al. Fine-Scale Acoustic Tomographic Imaging of Shallow Water Sediments[J]. IEEE Journal of Oceanic Engineering, 2001, 26(1): 70-83. DOI:10.1109/48.917930 |
| [17] |
Zhang Peizhen, Wang Shuozhong, Wang Runtian. Reducing Frequency-Domain Artifacts of Binary Image Due to Coarse Sampling by Repeated Interpolation and Smoothing of Radon Projections[J]. Journal of Visual Communication and Image Representation, 2012, 23(5): 697-704. DOI:10.1016/j.jvcir.2012.04.001 |
| [18] |
Zhang Peizhen, Wang Shuozhong. Fast Prediction of Scattered Sound Field Based on Fourier Diffraction Theory Under Second-Order Born Approximation[J]. Acoustical Physics, 2014, 60(4): 379-386. DOI:10.1134/S1063771014040198 |
| [19] |
李仁民, 刘松玉, 方磊, 等. 采用随机生长四参数生成法构造黏土微观结构[J]. 浙江大学学报(工学版), 2010, 44(1): 1897-1901. Li Renmin, Liu Songyu, Fang Lei, et al. Micro-Structure of Clay Generated by Quartet Structure Generation Set[J]. Journal of Zhejiang University (Engineering Science), 2010, 44(1): 1897-1901. |


