2. 青岛理工大学理学院, 山东 青岛 266520
2. School of Science, Qingdao University of Technology, Qingdao 266520, Shandong, China
0 引言
高温岩体广义上指深埋于地下的低孔隙度、低渗透性、高温的岩体,狭义上专指埋深较浅(3~10 km)、温度较高(150~650 ℃)、岩体致密且内部不存在流体或仅有少量流体的具有经济开发价值的岩体,具有产热量稳定、储量大、能源清洁等优点[1-4]。据中国地质调查局2015年调查评价结果,我国大陆埋深在3 000~10 000 m的干热岩资源量折合856万亿t标准煤[5]。我国已将地热能开发利用纳入“十三五”能源发展规划[6]。开采高温岩体地热资源的主要手段是通过水力压裂建造高温岩体储留层。要实现高温岩体储留层中地热资源的高效利用,必须弄清储留层中注入水与岩体之间的热交换规律。同时,高温岩体储留层建造成本较高,缝网间距对地热开发效率和储留层温度影响较大,高温岩体储留层的原位实验和室内实验复杂、成本高,因此对储留层的模拟研究十分必要[7-9]。
针对高温岩体理论的研究,赵阳升等[10]提出了高温岩体开发的块裂介质热流固耦合模型,研究了岩体温度分布、岩体基质岩块裂隙内应力以及裂缝宽度随地热能开采的变化规律。段云星[11]采用正交设计方法,研究井间距、注入流体温度流量和储留层渗透率对增强型地热系统开采的影响,同时分析了水平井和竖直井对增强型地热系统开采的影响。康健等[12]研究了热膨胀系数在正态和韦伯两种分布下温度场及应力场的分布及变化规律。Vik等[13]通过将裂缝视作三维模型中的不连续表面,模拟研究了竖直井多个缝网之间的相互作用。Sun等[14]研究了水平井开发地热的模型,提出了利用水平井开采地热能的优化策略。上述学者对高温岩体储留层热流固耦合规律的研究,考虑的多是单缝网或固定缝网间距下的高温岩体储留层中注入水与岩体之间的热交换规律。在实际工程中,合理的缝网间距对储留层中地热能的开采有着重要意义。因此,本文利用数值模拟方法分析高温岩体储留层中缝网间距对储留层热交换的影响规律,以指导高温岩体地热开发的工程实践。
1 高温岩体储留层数学模型高温岩体储留层热交换和考虑高温岩体储留层中渗流场、应力场和温度场的耦合作用是复杂过程,为了简化模型,作如下假设[15-17]:
1) 将高温岩体储留层看作各向同性的饱和多孔介质,只考虑固体骨架的弹性变形。
2) 由于高压的作用,认为水不会发生汽化,岩体被单相水所饱和,渗流符合达西定律。
3) 岩体的变形为小变形。
4) 岩体中的热量可以通过传导、对流、辐射的方式进行传递,仅考虑热传导和热对流形式的热量交换。
5) 材料的热力学参数是各向同性且不随温度和压力而变化的。
对于完全饱和的多孔介质,考虑温度效应的影响,其有效应力为
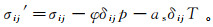 (1)
(1) 式中:σij′为有效应力;i, j=x, y;σij为总应力;φ为多孔介质的孔隙度;δij为Kronecker符号;p为孔隙水压力;as为多孔介质的热力耦合系数,且as=(2G+3λ)βs,G和λ为Lame常数,βs为固体骨架的热膨胀系数;T为温度。等式右边第一项为多孔介质的总应力项;第二项为孔隙水压力作用产生的应力项;第三项为温度变化引起的应力项。
岩体骨架的平衡方程为
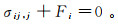 (2)
(2) 式中:σij, j为σij在j方向的偏导数;Fi为体力。岩体骨架的几何方程为
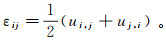 (3)
(3) 式中:εij为应变;ui, j为岩体位移ui在j方向的偏导数。弹性本构方程为
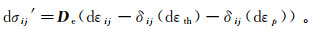 (4)
(4) 式中:σij′为有效应力增量;De为弹性矩阵;dε ij为总应变增量;dε th为热应变增量;dε p为孔隙内流体压力产生的应变增量。
饱和多孔介质热流固耦合的渗流场控制方程可由连续方程和单相饱和孔隙介质达西渗流方程得到。其中,孔隙流体和岩体骨架的连续方程分别为:
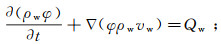 (5)
(5) 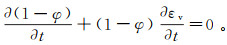 (6)
(6) 式中:ρw为水的密度;t为时间;vw为水的绝对速度,vw=vr+vs,vr为孔隙流体相对于岩体骨架的速度, vs为岩体骨架运动速度;Qw为流体的源汇项;εv为固体骨架的体积应变。单相饱和孔隙介质的达西渗流方程为
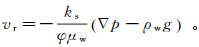 (7)
(7) 式中:ks为固体骨架的绝对渗透率;g为重力加速度;μw为水黏度。
将式(5)、(6)联立,考虑非等温过程下岩体和流体密度随温度和孔隙水压力的变化,将式(7)代入联立后的方程,整理得
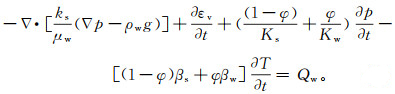 (8)
(8) 式中:Ks为固体骨架的体积模量;Kw为水的体积模量;βw为水的热膨胀系数。等式左边第一项为孔隙流体渗流项;第二项为多孔介质固体骨架变形对孔隙流体渗流的影响项;第三项为孔隙水压力对孔隙流体渗流的影响项;第四项为温度对孔隙流体渗流的影响项。
温度场方程可由热平衡方程得到。在单位时间单位体积内,岩体骨架由于热传导和岩体质点运动产生的热流量差分别为ΔQ1和ΔQ2:
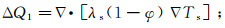 (9)
(9)  (10)
(10) 式中:λs为岩体骨架的导热系数;Ts为岩体骨架温度;ρs为岩体骨架密度;cs为岩体骨架比热。岩体骨架和孔隙内流体的热交换差值ΔQ3为
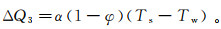 (11)
(11) 式中:α为有效换热系数;Tw为水的温度。岩体骨架的温度变化ΔQs为
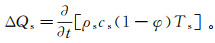 (12)
(12) 由热平衡方程,将式(9)—(12)联立后整理可得岩体骨架温度场方程为
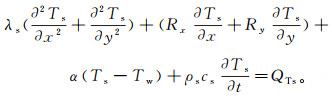 (13)
(13) 式中: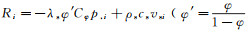

对于孔隙流体,考虑孔隙流体内部的热对流效应,同理可得孔隙流体温度场方程为
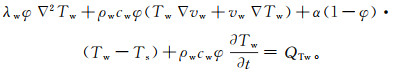 (14)
(14) 式中:λw为水的导热系数;cw为水的比热;QTw为流体方程的热量源汇项。等式左侧第一项为流体的热传导项;第二项为孔隙中流体运动产生的热对流项;第三项是孔隙流体和岩体之间的热交换项;第四项是孔隙流体的吸热项。
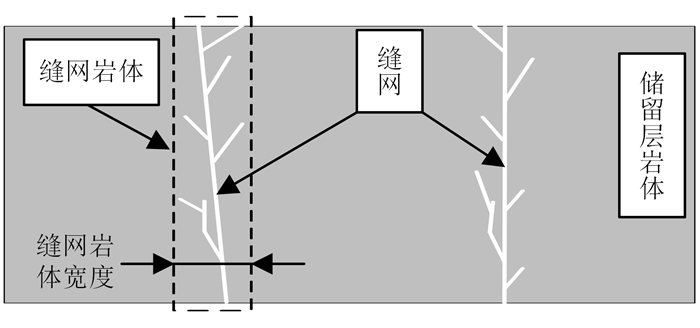
2 注水过程中储留层温度变化规律 2.1 高温岩体储留层模型缝网是由水力压裂所形成裂隙构成的网络。为了简化模型,将缝网及其附近的岩体看作一个等效的多孔介质,称作缝网岩体,将储留层中其他岩体称作储留层岩体(图 1)。在模型中,缝网岩体被赋予与储留层岩体不同的物理力学性质,以实现对储留层中缝网的模拟。表 1分别列出了缝网岩体和储留层岩体的物理力学参数。
|
| 图 1 缝网在储留层中示意图 Fig. 1 Principle of fracture-networks in HDR geothermal reservoirs |
|
|
| 岩体 | 密度/ (kg/m3) | 杨氏模量/ GPa | 泊松比 | 渗透系数/ (m/s) | 孔隙比 | 热传导系数/ (W/(kg·K)) | 比热/ (J/(kg·K)) |
| 缝网岩体 | 1 070 | 2.84 | 0.25 | 0.111 | 0.010 | 2.58 | 4 050 |
| 储留层岩体 | 2 850 | 4.84 | 0.15 | 1.150×10-9 | 0.001 | 0.15 | 1 080 |
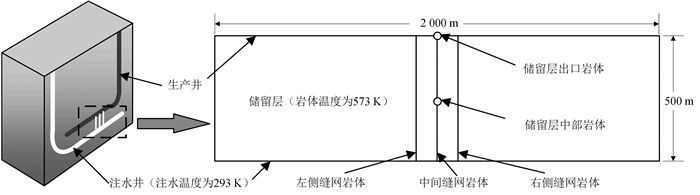
如图 2所示,本文选用水平井模型建立了考虑热对流作用的含3簇缝网的高温岩体储留层热流固耦合二维多簇缝网模型(记为多簇缝网模型)。模型的地层深度为4 km,尺寸为2 000 m×500 m。模型下边界为注水井,上边界为生产井,注水井和生产井之间由缝网连通,单个缝网岩体的宽度为5 m,各簇缝网之间的水平间距相等。
|
| 图 2 高温岩体储留层二维模型建立示意图 Fig. 2 Principle of two-dimensional formation model of HDR geothermal reservoirs |
|
|
本文利用Python编程语言,对ABAQUS软件进行了二次开发,通过提取每个载荷步的计算结果进行交叉迭代的方法,将ABAQUS中流固耦合分析与热传导分析进行了耦合,实现了对含缝网高温岩体储留层注水过程热流固耦合的模拟。
文中以多簇缝网模型储留层在中间缝网中部和出口处的岩体(分别记为储留层中部岩体和储留层出口岩体)为对象来研究注水作用下不同缝网间距对应的岩体温度变化规律。
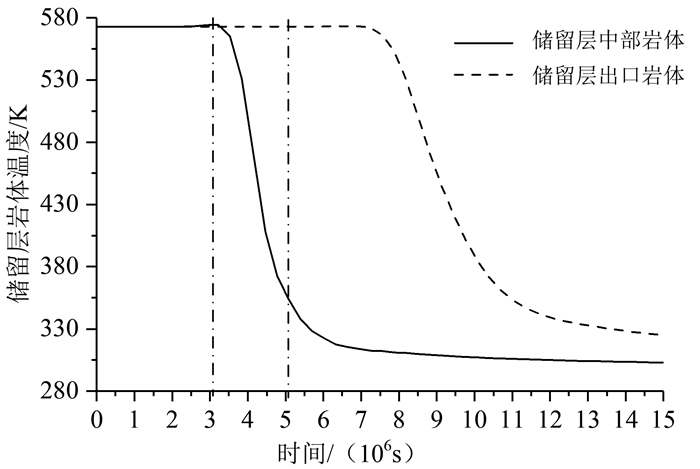
2.2 储留层岩体温度变化规律图 3是缝网间距为100 m、注水温度为293 K、注水压力为8 MPa条件下,多簇缝网模型的岩体温度随时间变化曲线。从图 3可以看出:储留层中部岩体和出口岩体温度随时间下降,储留层岩体温度曲线在下降阶段呈现负指数规律(T=ae-bt+ce-dt);储留层出口岩体的温度下降较储留层中部岩体滞后约4.50×106 s,且储留层出口岩体的最终温度比储留层中部岩体高,但两条曲线具有相同的下降规律。以储留层中部岩体温度下降曲线为基础,将其温度下降分为3个阶段。
|
| 图 3 多簇缝网模型储留层岩体温度随时间变化曲线 Fig. 3 Temperature change of HDR geothermal reservoirs with time of water injection in the model of multiple-fracture-network |
|
|
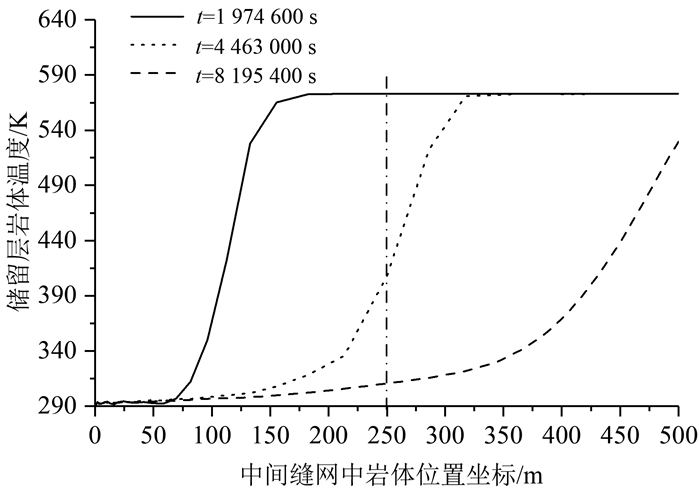
1) 第一阶段是3.00×106 s以前,不论是储留层中部岩体还是储留层出口岩体均维持岩体原有温度不变。此时储留层沿中间缝网的岩体温度分布如图 4中的t=1 974 600 s曲线所示(图中横坐标原点为注水点,250 m处为储留层中部,500 m处为储留层出口)。由曲线可知,尽管此时注水点附近(横坐标≤150 m)的岩体温度已经开始下降,但尚未到达储留层中部和储留层出口的岩体处,因此没能造成这两点处岩体温度的下降。
|
| 图 4 不同时刻储留层岩体温度沿中间缝网分布 Fig. 4 Distribution of HDR geothermal reservoirs temperature along the middle fracture-network at different times |
|
|
2) 第二阶段是3.00×106~5.00×106 s时间段内,储留层中部岩体的温度快速下降,储留层出口岩体的温仍维持岩体原有温度不变。图 4中的t=4 463 000 s曲线给出了此时高温岩体储留层温度沿中间缝网的分布情况,可知储留层中岩体温度开始快速下降是由于此时储留层中部岩体已经处于注入水形成的低温影响区中,所以其岩体温度在注入水的作用下持续降低。
3) 第三阶段是5.00×106 s以后,储留层中部岩体温度的下降曲线变缓,并最终趋于注入水温度。结合图 4中的t=8 195 400 s时的高温岩体储留层温度沿中间缝网分布曲线,可知此时储留层出口岩体也处在了注入水形成的低温影响区中,岩体温度开始了下降。
3 缝网间距对岩体温度的影响选取注水压力为8 MPa、注水温度为室温(293 K)的条件,模拟得到了缝网间距10~400 m范围内多簇缝网模型在储留层中部岩体和储留层出口岩体处的温度随时间变化曲线。作为对比,也进行了相同条件下单缝网模型(在多簇缝网模型的基础上去掉了左侧和右侧缝网岩体,其数值结果被视为缝网间距无穷大的情况)的数值模拟。
模拟结果表明,储留层出口岩体的温度与缝网间距之间的规律和储留层中部岩体的规律相同。为直观反映储留层岩体的温度变化规律与缝网间距之间的关系,以储留层中部岩体为对象,按其温度下降的3个阶段分别阐述缝网间距对其岩体温度的影响。
1) 第一阶段(t≤3.00×106 s)
在该阶段,岩体温度尚未开始下降,缝网间距的不同对储留层中部岩体温度无影响,多簇缝网模型和单缝网模型的岩体均保持在初始温度。
2) 第二阶段(3.00×106 s < t≤5.00×106 s)
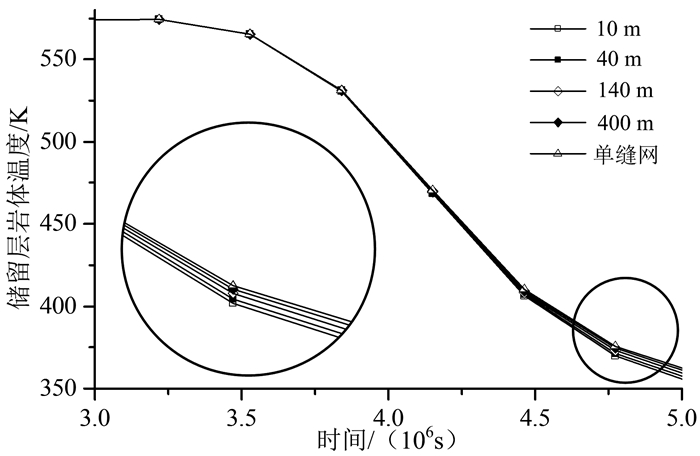
图 5给出了t=3.00×106~5.00×106 s内单缝网模型和不同缝网间距下多簇缝网模型所对应的储留层中部岩体温度随时间变化曲线(选取10~400 m缝网间距内具有代表性的曲线)。在岩体温度下降前段(4.00×106 s以前),不同缝网间距所对应的岩体温度下降曲线基本重合,此时缝网间距改变对岩体温度下降曲线的影响很小;在后段(4.00×106 s以后),不同缝网间距所对应的岩体温度变化曲线不再重合,缝网间距越大,其对应的温度下降曲线下降得越缓慢。这是因为当缝网间距变大后,缝网之间的高温岩体体积也相应变大,在开采阶段,缝网间距大的模型相对缝网间距小的模型能从高温岩体储留层中获取到更多的热量,因此该阶段缝网间距越大,其岩体温度下降得越慢。
|
| 图 5 第二阶段不同缝网间距下储留层中部岩体温度下降曲线 Fig. 5 Temperature drop curves of the middle part of HDR geothermal reservoirs with different fracture-network spacings in the second stage |
|
|
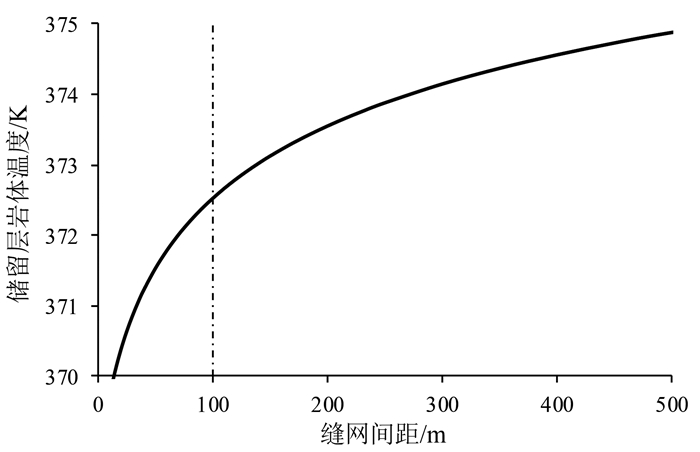
为具体说明4.00×106 s以后缝网间距与岩体温度之间的关系,取t=4 773 990 s时缝网间距与岩体温度间对应的数据绘图(图 6)。此刻,岩体温度与缝网间距之间为正相关关系,缝网间距越小,同一时刻所对应曲线的岩体温度越低,即相同时间内岩体温度下降地越多;缝网间距越大,同一时刻所对应曲线的岩体温度越高,且趋向单缝网模型的岩体温度。当缝网间距小于100 m时,缝网间距的缩小对岩体温度的影响较缝网间距大于100 m时显著。
|
| 图 6 t=4 773 990 s时缝网间距对储留层中部岩体温度影响曲线 Fig. 6 Influence curves of fracture-network spacing to the middle part of HDR geothermal reservoirs temperature at t=4 773 990 s |
|
|
3) 第三阶段(t>5.00×106 s)
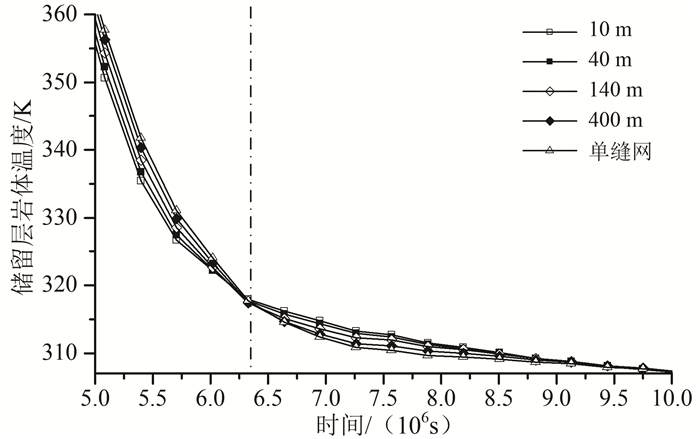
图 7给出了t>5.00×106 s时单缝网模型和不同缝网间距下多簇缝网模型所对应的储留层中部岩体温度变化曲线。曲线的变化可以以6.35×106 s和9.50×106 s为界分为3个时段,各时段缝网间距与岩体温度之间的关系不相同。
|
| 图 7 第三阶段不同缝网间距下储留层中部岩体温度下降曲线 Fig. 7 Temperature drop curves of the middle part of HDR geothermal reservoirs with different fracture-network spacings in the third stage |
|
|
当5.00×106 s < t≤6.35×106 s时,缝网间距越大,同一时刻所对应曲线的岩体温度越高。这一阶段缝网间距与岩体温度之间的关系曲线与图 6相同,不再赘述。
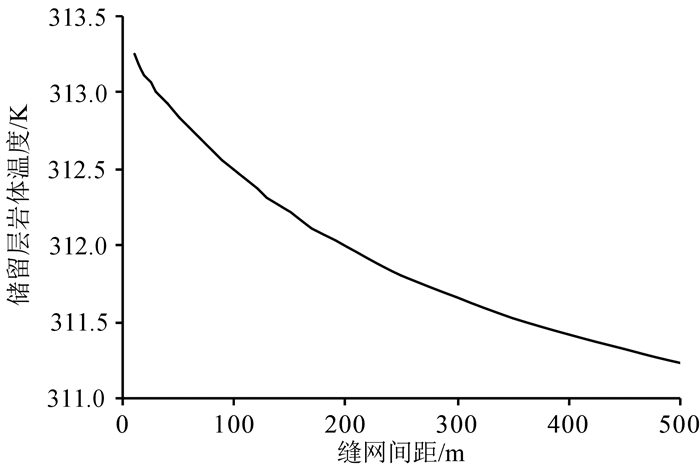
当6.35×106 s < t≤9.50×106 s时,为直观说明该阶段岩体温度与缝网间距之间的关系,取t=7 262 310 s时缝网间距与岩体温度间对应的数据绘图(图 8),此时缝网间距越大,储留层中部岩体的温度反而越低,这与5.00×106 s < t≤6.35×106 s时的规律是不同的。
|
| 图 8 t=7 262 310 s时缝网间距对储留层中部岩体温度影响曲线 Fig. 8 Influence curves of fracture-network spacing to the middle part of HDR geothermal reservoirs temperature at t=7 262 310 s |
|
|
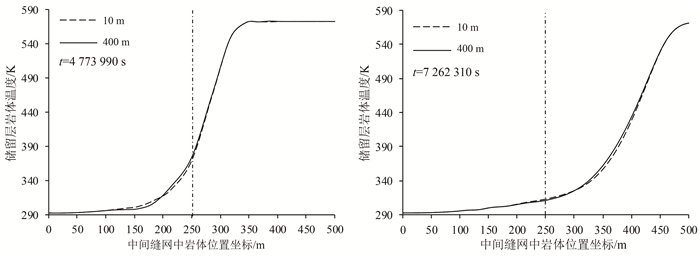
为解释这一现象,图 9给出了岩体温度沿中间缝网在空间上的分布曲线,以中间缝网在注水井端的岩体为坐标原点,中间缝网在生产井端的岩体坐标为500 m。从图 9可以看出:在岩体温度较高的部分(>320 K),缝网间距越小,温度变化梯度越大;在岩体温度较低的部分(≤320 K),缝网间距越小,温度变化梯度越小。而且,随着时间的增加,岩体温度分布曲线以该规律由注水井端向生产井端推进。
|
| 图 9 不同缝网间距下储留层岩体温度沿中间缝网分布图 Fig. 9 Distribution of HDR geothermal reservoirs temperature along the middle fracture-network with different fracture-network spacings |
|
|
正是由于岩体温度空间分布曲线呈现由注水井向生产井推进且规律不变的情况,导致了在不同时间阶段内,缝网间距对岩体温度变化影响规律发生变化的现象,表现为岩体温度较高时(>320 K), 缝网间距越大,岩体温度越高,而岩体温度较低时(≤320 K),缝网间距越大,同一时刻的岩体温度越低。
当t>9.50×106 s时,各缝网间距所对应的岩体温度变化曲线基本和单缝网模型的岩体温度变化曲线重合,此时缝网间距对岩体温度的影响很小,且不同缝网间距对应的岩体温度都趋近于注入水温度,该高温岩体储留层已不能继续开采。
4 结论1) 将高温岩体储留层缝网及其周围岩体简化为等效的多孔介质,利用ABAQUS二次开发建立了考虑流固耦合与热对流耦合的高温岩体储留层热流固耦合模型。
2) 注水过程中,储留层的岩体温度变化经历3个阶段:保持初始岩体温度阶段、岩体温度快速下降阶段和缓慢下降平稳阶段,储留层岩体温度曲线在下降阶段呈现负指数规律。
3) 时间上,在储留层岩体温度变化的第一阶段和第二阶段前期,缝网间距对岩体温度无影响;在第二阶段后期和第三阶段前期,缝网间距与储留层岩体温度之间呈正相关关系,缝网间距越大,储留层岩体温度下降得越慢,岩体温度越高;在第三阶段后期,缝网间距与储留层岩体温度之间的关系呈负相关,缝网间距越大,储留层岩体温度下降得越快,岩体温度越低。地热开发过程中缝网间距的确定要综合考虑地热储层条件、地热井服务寿命、不同阶段开采效益等多种因素。
4) 空间上,缝网间距改变所引起的岩体温度变化的差异主要出现在岩体温度发生下降的区域。在岩体温度较低的区域(≤320 K),缝网间距越大,岩体温度变化梯度就越大;在岩体温度较高的区域(>320 K),缝网间距越大,岩体温度变化梯度反而越小。
| [1] |
许天福, 袁益龙, 姜振蛟, 等. 干热岩资源和增强型地热工程:国际经验和我国展望[J]. 吉林大学学报(地球科学版), 2016, 46(4): 1139-1152. Xu Tianfu, Yuan Yilong, Jiang Zhenjiao, et al. Hot Dry Rock and Enhanced Geothermal Engineering:International Experience and China Prospect[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1139-1152. |
| [2] |
黄顺平.地热能开采过程多场耦合数值模拟与分析[D].北京: 北京交通大学, 2018. Huang Shunping. Numerical Simulation of Multi-Field Coupling Process and Analysis in Geothermal Energy Mining[D]. Beijing: Beijing Jiaotong University, 2018. |
| [3] |
赵延林, 王卫军, 赵阳升, 等. 双重介质热-水-力三维耦合模型及应用[J]. 中国矿业大学学报, 2010, 39(5): 709-715. Zhao Yanlin, Wang Weijun, Zhao Yangsheng, et al. 3D Dual Medium Model of Thermal-Hydro-Mechanical Coupling and Its Application[J]. Journal of China University of Mining & Technology, 2010, 39(5): 709-715. |
| [4] |
陈必光.地热对井裂隙岩体中渗流传热过程数值模拟方法研究[D].北京: 清华大学, 2014. Chen Biguang. Study on Numerical Methods for Coupled Fluid Flow and Heat Transfer in Fractured Rocks of Doublet System[D]. Beijing: Tsinghua University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10003-1015811852.htm |
| [5] |
蔺文静, 刘志明, 马峰, 等. 我国陆区干热岩资源潜力估算[J]. 地球学报, 2012, 33(5): 807-811. Lin Wenjing, Liu Zhiming, Ma Feng, et al. An Estimation of HDR Resources in China's Mainland[J]. Acta Geoscientica Sinica, 2012, 33(5): 807-811. |
| [6] |
国家发展和改革委员会, 国家能源局. 能源发展"十三五"规划[J]. 中国电力企业管理, 2017(1): 7. National Development and Reform Commission, National Energy Administration of the People's Republic of China. The 13th Five-Year Plan for Energy Development[J]. China Power Enterprise Management, 2017(1): 7. |
| [7] |
国务院办公厅. 能源发展战略行动计划(2014-2020年)(摘录)[J]. 上海节能, 2014(12): 1-2. General Office of the State Council of the People's Republic of China. Energy Development Strategic Action Plan (2014-2020) (Excerpt)[J]. Shanghai Energy Conservation, 2014(12): 1-2. |
| [8] |
陆川, 王贵玲. 干热岩研究现状与展望[J]. 科技导报, 2015, 33(19): 13-21. Lu Chuan, Wang Guiling. Current Status and Prospect of Hot Dry Rock Research[J]. Science & Technology Review, 2015, 33(19): 13-21. DOI:10.3981/j.issn.1000-7857.2015.19.001 |
| [9] |
廖志杰, 万天丰, 张振国. 增强型地热系统:潜力大、开发难[J]. 地学前缘, 2015, 22(1): 335-344. Liao Zhijie, Wan Tianfeng, Zhang Zhenguo. The Enhanced Geothermal System(EGS):Huge Capacity and Difficult Exploitation[J]. Earth Science Frontiers, 2015, 22(1): 335-344. |
| [10] |
赵阳升, 王瑞凤, 胡耀青, 等. 高温岩体地热开发的块裂介质固流热耦合三维数值模拟[J]. 岩石力学与工程学报, 2002, 21(12): 1751-1755. Zhao Yangsheng, Wang Ruifeng, Hu Yaoqing, et al. 3D Numerical Simulation for Coupled THM of Rock Matrix-Fractured Media in Heat Extraction in HDR[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(12): 1751-1755. DOI:10.3321/j.issn:1000-6915.2002.12.001 |
| [11] |
段云星.干热岩地热资源开采井网优化数值模拟研究[D].北京: 中国地质大学(北京), 2017. Duan Yunxing. Numerical Simulation of Well Pattern Optimization for Hot Dry Rock Geothermal Resources Exploitation[D] Beijing: China University of Geosciences(Beijing), 2017. http://cdmd.cnki.com.cn/Article/CDMD-11415-1017129867.htm |
| [12] |
康健, 赵明鹏, 赵阳升, 等. 随机介质固热耦合模型与高温岩体地热开发人工储留层二次破裂数值模拟[J]. 岩石力学与工程学报, 2005, 24(6): 969-974. Kang Jian, Zhao Mingpeng, Zhao Yangsheng, et al. Random Non-Homogeneous Solid-Heat Coupled Model and Numerical Simulations of Second Fracturing for Man-Made-Reserve Stratum in HDR[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(6): 969-974. DOI:10.3321/j.issn:1000-6915.2005.06.012 |
| [13] |
Vik H S, Salimzadeh S, Nick N M. Heat Recovery from Multiple-Fracture Enhanced Geothermal Systems:The Effect of Thermoelastic Fracture Interactions[J]. Elsevier Ltd, 2018, 121: 606-622. |
| [14] |
Sun Z X, Xin Y, Yao J, et al. Numerical Investigation on the Heat Extraction Capacity of Dual Horizontal Wells in Enhanced Geothermal Systems Based on the 3-D THM Model[J]. MDPI, 2018, 11(2): 280. |
| [15] |
王曌龙.裂隙岩体热流固耦合模型研究及应用[D].徐州: 中国矿业大学, 2015. Wang Zhaolong. Study on the Coupled Thermal-Hydrologic-Mechanical Model in Fractured Rock Mass and Its Application[D]. Xuzhou: China University of Mining and Technology, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10290-1015971160.htm |
| [16] |
王瑞凤.高温岩体地热开发的固流热多场耦合与数值仿真[D].太原: 太原理工大学, 2002. Wang Ruifeng. 3D Solid-Fluid-Heat Coupled Numerical Simulation in Exploitation of HDR[D]. Taiyuan: Taiyuan University of Technology, 2002. http://d.wanfangdata.com.cn/Thesis/W028423 |
| [17] |
白冰. 饱和多孔介质热-水-力控制方程耦合项的意义及耦合影响分析[J]. 岩土力学, 2006, 27(4): 519-524, 536. Bai Bing. Effects of Coupling Schemes of Thermo Hydro-Mechanical Governing Equations for saturated Porous Medium[J]. Rock and Soil Mechanics, 2006, 27(4): 519-524, 536. DOI:10.3969/j.issn.1000-7598.2006.04.003 |


