2. 中国铁路青藏集团有限公司, 西宁 810007;
3. 中国铁路总公司拉林铁路建设总指挥部, 拉萨 850000;
4. 中国中铁二院工程集团有限责任公司, 成都 610031
2. China Railway Qinghai-Tibet Group Co., Ltd., Xining 810007, China;
3. Lhasa-Nyingchi Railway Headquarter, China Railway Corporation, Lhasa 850000, China;
4. China Railway Eryuan Engineering Group Co., Ltd., Chengdu 610031, China
0 引言
地应力是引起隧道工程破坏和变形的根本原因之一,是隧道设计和施工必须要考虑的因素。从1912年瑞士地质学家海姆(A.Heim)提出了地应力概念和静水压力假设,1926年前苏联学者金尼克(A.H.ДИННИК)对静水压力假设进行了修正以来[1];到现在,人们逐渐认识到地应力与地心引力、板块构造、地热和地球自转速度等诸多因素有关。目前,工程界一般从构造应力场和重力场两方面去考虑地应力[2]。比较有名的地应力研究是E.T.Brown等[3]统计了世界范围内的地应力测量结果,发现平均水平应力与垂直应力之比随深度的变化在两个双曲线之间分布(霍克-布朗曲线)。而赵德安等[4]、景锋等[5]、王艳华等[6]则对中国大陆原地应力测量数据进行统计分析,也得到了类似的结论。上述研究成果不仅证明了构造应力场的存在,也表明了地应力存在极强的地域性问题。
青藏高原地区在欧亚陆块和印度陆块强烈的碰撞、挤压地质构造运动中,形成了大小、长短不一的板块缝合带。目前对于板块缝合带的研究大多与板块构造或缝合带本身的地质特性相关,如:吴珍汉等[7]在分析青藏高原中段古近纪早期构造演化的基础上,着重研究了区域各活动性断裂构造特征;劳雄[8]和刘小汉等[9]先后对雅鲁藏布江断裂带的形成及区域构造进行了研究;鲍杰[10]以“拉萨—林芝地块”的地壳岩体和板块构造为研究对象,通过现场调研、计算及总结前人研究成果,分析了该地区的地球动力学环境、岩石建造特征、断裂构造及应力-形变作用机制;肖序常等[11-12]研究了青藏高原地区的板块构造分布及特征,描述了高原内部的4条板块界线、缝合带特征及其证据,并推演了高原区板块构造的演化过程,分析了板块构造与青藏高原隆升的因果关系。
可以发现, 上述研究成果中关于板块缝合带区域隧道地应力特征的研究较少,但现有设计规划中几乎所有的进藏铁路、公路都必须穿越这些缝合带以及缝合带之间的次级地块。其中川藏线拉林铁路就是西藏地区东南部的一条重要交通干线,拉林铁路全线几乎沿雅鲁藏布江缝合带展布,且隧线比超过50%,高地应力问题十分严重。因此,研究板块缝合带区域隧道的地应力特征对进藏交通隧道的安全施工具有十分重要的意义,尤其对控制因高地应力造成的隧道岩爆和大变形将起到重要作用。
1 工程概况拉林铁路是连接拉萨市拉萨站—林芝市巴宜区林芝站的铁路,是国铁Ⅰ级单线电气化快速铁路。起于拉萨火车站(货车起于拉萨南站),沿拉萨河而下,经贡嘎转向东,经山南、朗县、米林,跨越雅鲁藏布江到林芝站。拉林铁路全长433 km,与拉日铁路共线近33 km,新建里程400 km,设计时速160 km/h,沿线隧道共46座,计206.984 km,占线路长度51.66%。
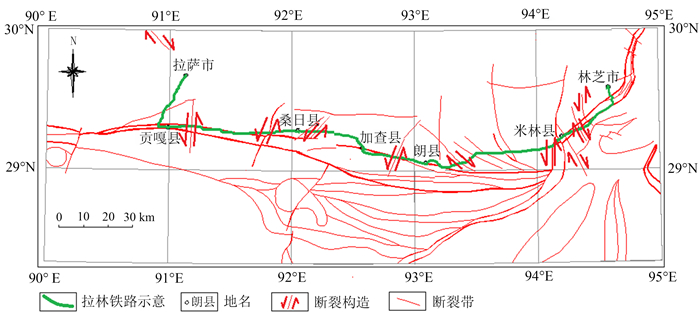
拉林铁路所在的拉萨—林芝地块位于青藏高原东南部,处于印度板块与欧亚板块的接合部,属于喜马拉雅构造带东构造结,从南到北分别涉及喜马拉雅造山带(Ⅳ)、雅鲁藏布江缝合带(Ⅲ)、冈底斯-念青唐古拉地块(Ⅱ)等3个地质构造单元,拉林铁路穿越板块构造如图 1所示,研究区断裂构造及应力场分布如图 2所示[10]。雅鲁藏布江缝合带是南、北两大陆块挤压-碰撞的缝合线,总体上是一条由不同时代、不同建造类型的构造块体拼合而成的蛇绿构造混杂岩系[10]。拉林铁路沿线隧道大多沿雅鲁藏布江缝合带修建,隧址区山高谷深,岩石建造和地质构造复杂,构造变形强烈,高地应力问题十分突出,隧道施工中常出现岩爆和大变形等围岩失稳现象,极大地影响了隧道施工的安全性。

|
| Ⅰ.班公湖怒江缝合带;Ⅱ.冈底斯念青唐古拉地块(Ⅱ1.那曲洛隆弧前盆地;Ⅱ2.昂龙岗日班戈腾冲岩浆弧;Ⅱ3.狮泉河嘉黎帕隆藏布结合带;Ⅱ4.措勤申扎岛弧;Ⅱ5.隆格尔工布江达复合岛弧带;Ⅱ6.冈底斯下察隅岩浆弧;Ⅱ7.日喀则弧前盆地带);Ⅲ.雅鲁藏布江缝合带;Ⅳ.喜马拉雅造山带(Ⅳ1.北喜马拉雅构造带;Ⅳ2.高喜马拉雅构造带;Ⅳ3.低喜马拉雅构造带);Ⅴ.印度陆块;Ⅵ.羌塘地块。 图 1 拉林铁路板块构造划分示意图 Fig. 1 Diagram of plate tectonic division of Lhasa-Nyingchi Railway |
|
|
|
| 图 2 拉林铁路区域构造示意 Fig. 2 Regional tectonic condition of Lhasa-Nyingchi Railway |
|
|
运用地质力学的方法分析区域的地质构造,只能定性地分析该区域构造应力的方向,而不能得到准确的量值。要确定一个地区地应力的量值,最好的方式就是进行现场原位测量。拉林铁路沿线隧道的原位地应力测试采用空心包体法进行。空心包体法测量地应力本质上是应力解除法测量地应力的一种,是将一段岩石通过取心(套心技术)从周围岩体施加给它的应力场内隔离开来,改变岩体的应力状态,使岩体产生应变响应的简捷方法[13]。
现场地应力测试的测点数目共计33个,分布在拉林铁路15个隧道的不同里程处,测点埋深分布于52~1 446 m范围内。限于篇幅限制,仅选取9个不同埋深和里程的代表性测点,将其测试结果列于表 1。
| 序号 | 里程 | 测点埋深/m | 最大主应力 | 中间主应力 | 最小主应力 | ||||||||
| σH /MPa | 方位/(°) | 倾角/(°) | σv/MPa | 方位/(°) | 倾角/(°) | σh/MPa | 方位/(°) | 倾角/(°) | |||||
| 1 | DK63+615 | 80 | 3.0 | 192.0 | -17.6 | 1.5 | -88.0 | 55.4 | 0.7 | 129.5 | 28.6 | ||
| 2 | D1K182+455 | 923 | 45.4 | 184.7 | -3.0 | 25.4 | -77.8 | -67.4 | 20.8 | 93.4 | -22.3 | ||
| 3 | DK194+200 | 1 446 | 49.7 | 197.7 | 2.3 | 37.0 | 86.7 | 83.5 | 36.1 | 108.0 | -6.1 | ||
| 4 | DK284+965 | 755 | 29.6 | 101.3 | 4.6 | 15.2 | 12.5 | -75.5 | 15.0 | 173.1 | -13.7 | ||
| 5 | DK300+335.1 | 574 | 25.4 | 142.3 | 5.0 | 13.3 | -63.5 | 84.4 | 12.0 | 232.0 | -2.4 | ||
| 6 | DK317+800 | 1 000 | 43.3 | 157.3 | -3.6 | 20.4 | 49.4 | -78.2 | 17.8 | 248.0 | -11.1 | ||
| 7 | D1K327+984 | 1 000 | 36.9 | 207.4 | 10.7 | 30.1 | -77.2 | -53.1 | 19.6 | 125.0 | -34.7 | ||
| 8 | DK331+900 | 1 322 | 46.3 | 191.7 | -2.3 | 21.2 | -76.3 | -50.9 | 15.5 | 98.8 | -38.9 | ||
| 9 | D2K379+691 | 780 | 26.7 | 105.3 | 3.2 | 16.5 | -4.2 | 80.5 | 11.5 | 195.8 | 8.9 | ||
剔除异常数据后,对表 1中主应力大小、方向、倾角及主应力侧压系数等方面进行统计和分析。可以得到:最大主应力倾角平均值为7.0°,最大值为21.4°;最小主应力倾角平均值为20.1°,最大值为38.9°;中间主应力倾角平均值为67.5°,最大值为84.4°;最大和最小主应力方位角之差的平均值为84.4°。由此看出,最大与最小主应力倾角很小,呈近水平分布,可分别称为最大水平主应力(σH)和最小水平主应力(σh);而中间主应力倾角较大,可近似认为是垂直方向的主应力,可称之为垂直主应力(σv),且σH和σh是相互垂直的主应力[14]。
2.1 主应力与埋深的关系对最大、中间和最小主应力的原位地应力测量数据与埋深(h)的关系做统计分析,结果如图 3所示。

|
| R2为决定系数。 图 3 主应力与埋深的关系 Fig. 3 Relationship between the principal stress and the buried depth of tunnel |
|
|
由图 3可知,各主应力与埋深之间都表现出了较好的线性相关性,σH、σv和σh与埋深的拟合曲线的决定系数分别为0.899 7,0.832 9和0.782 5,拟合程度高,相关性良好。且认为σH=0.0337h+5.0743可作为拉林铁路沿线隧道最大主应力的估算公式,即最大主应力与埋深的梯度为0.033 7 MPa/m。因上述测点埋深在300 m以下和1 500 m以上的数据点偏少,因此该公式对埋深在400~1 000 m时的最大主应力有较好的估算效果。
另从主应力与埋深的趋势线分布可以看出,整体上,拉林铁路沿线隧道的最大水平主应力>垂直主应力>最小水平水应力。
2.2 主应力量值统计对所有原位地应力测量的地应力量值进行统计,如图 4所示。

|
| 图 4 主应力量值统计 Fig. 4 Statistic result of principal stress |
|
|
由图 4可知,各测点σH量值分布在20~50 MPa范围内的占86%,σv分布在0~30 MPa范围内的占93%,σh分布在0~20 MPa范围内的占89%。据此得出,拉林铁路沿线隧道的主应力量值大多小于50 MPa,且最小主应力的与中间主应力量值的分布范围较为接近。
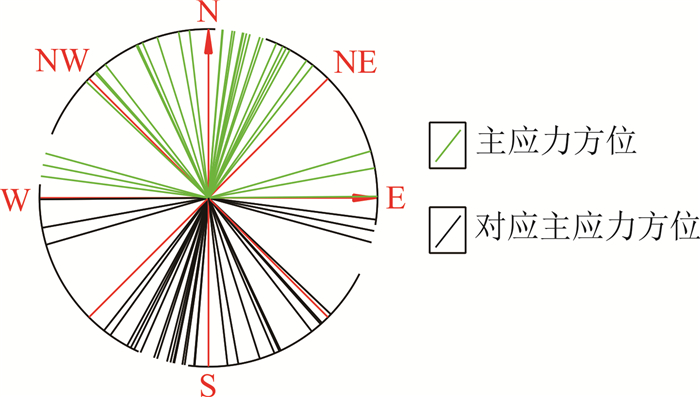
2.3 最大主应力方向对各测点最大主应力的方位角进行统计:方位角有4个在90°~135°之间,有9个在135°~180°间的,有15个在180°~225°间,3个在225°~270°间。考虑最大主应力是成对出现的,故绘出最大主应力方位角平面图,如图 5所示。可以清晰看到,拉林铁路沿线隧道的最大主应力方向为北北西—北北东向范围,这是由于印度板块与欧亚板块的碰撞推挤作用,导致青藏高原缝合带区域构造应力场以近南北向的压应力为主,东西向张应力为辅,这与文献[10]的研究结论相同。最大主应力方向与拉林铁路线整体走向近似垂直,对隧道修建是不利的。
|
| 图 5 最大主应力方位角分布 Fig. 5 Azimuthal distributions of the maximum principal stress |
|
|
对上述测点原位地应力的第一侧压系数(σH/σv)和第二侧压系数(σh/σv)与埋深h的关系进行统计分析,绘出侧压系数分布图,见图 6。

|
| 图 6 侧压系数与埋深的关系 Fig. 6 Relationship between the lateral pressure coefficient and the buried depth of tunnel |
|
|
由图 6a可知,第一侧压系数均大于1.0,即σH>σv,表明该地区应力场以构造应力场为主。第一侧压系数总体分布在1.2~2.2之间,平均值为1.76,部分数据异常点可能跟地形因素和构造应力场的影响有关,表现出应力集中或应力释放。因400 m以下和1 000 m以上埋深的测点数据较少,第一侧压系数与埋深之间并未发现明确的函数对应关系;但总体上看,埋深越大,第一侧压系数越有减小的趋势。
由图 6b可知,第二侧压系数均小于1.0,即σv>σh,在1 500 m埋深范围内,第二侧压系数表现得较为稳定,总体分布在0.5~1.0之间,平均值为0.76。表明同一板块区域内,第二侧压系数可认定为常量。
2.5 地应力对隧道岩爆的影响拉林铁路板块缝合带地区水平构造应力突出,且整体线路走向与最大水平主应力方向近似垂直,在地应力较大、围岩硬度高,且岩体完整性好的地区,隧道施工过程中的岩爆灾害将十分突出。笔者对部分隧道的围岩进行了室内声发射实验,结果显示桑珠岭隧道和巴玉隧道的岩心试样最大单轴抗压强度可达100 MPa,而其最大水平主应力分别为45.4 MPa和49.7 MPa,根据“谷-陶”岩爆判据[15],σ1>0.4Rc(σ1为初始最大主应力,Rc为岩石单轴抗压强度),发生岩爆的等级可能为高岩爆活动。随着桑珠岭和巴玉隧道的开挖,事实证明这两座隧道均发生了上千次的岩爆灾害(图 7)。

|
| a.拱顶岩爆;b.边墙岩爆。 图 7 巴玉隧道岩爆实例 Fig. 7 Example of rockburst in Bayu Tunnel |
|
|
以第一和第二平均侧压系数为基准,即令初始地应力为σxx=1.8σzz,σyy=0.8σzz(σxx为垂直于隧道走向的水平应力,σyy为平行于隧道走向的水平应力,σzz为竖向应力),建立埋深为400 m的有限元模型,对隧道进行模拟开挖,可得隧道下部结构为底板和仰拱两种不同断面形式下,隧道开挖后的最大主应力结果如图 8所示。

|
| a.底板式断面隧道最大主应力;b.仰拱式断面隧道最大主应力。 图 8 隧道不同断面形式下的最大主应力 Fig. 8 Maximum principal stress of tunnels with different types of cross sections |
|
|
由图 8可知,在板块缝合带区域的特殊初始地应力环境下,两种不同断面形式的隧道开挖后,最大主应力量值无太大差异,且在拱顶附近均有较大的主应力集中,两侧拱脚处主应力降低,但底板式断面的隧道会在左、右两墙脚位置产生较大的应力集中,而仰拱式断面的隧道则在仰拱下方一定深度处才有应力集中现象。根据岩爆的强度应力法判据,底板式断面隧道结构的受力状况更差,墙脚处岩爆发生的可能性更大。
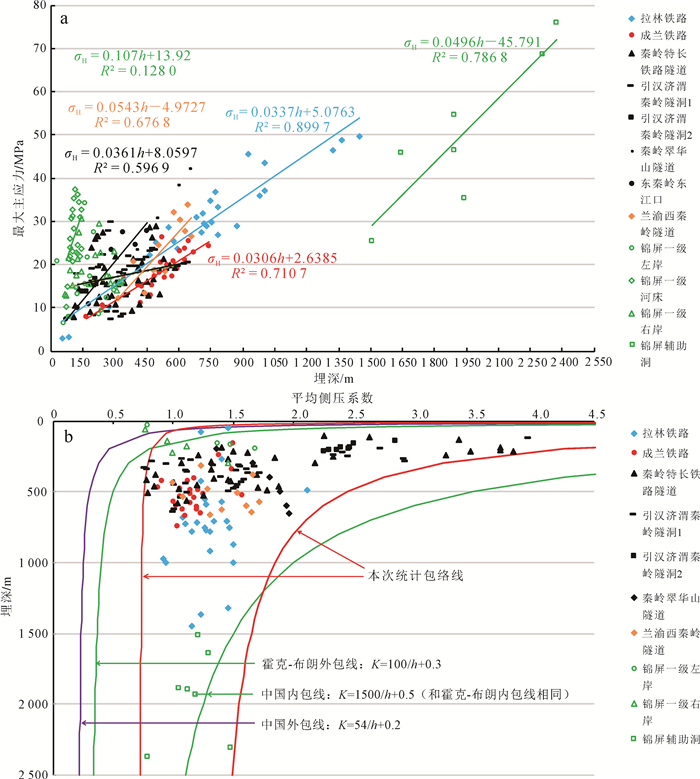
3 板块缝合带地应力特征为更详细地研究拉林铁路板块缝合带区域隧道的地应力特征,采用文献调研的方式对成兰铁路工程[16-17]、兰渝铁路西秦岭隧道[18]、秦岭地区[19-23]和锦屏水电站工程[24-25]等几个典型区域的隧洞地应力测试数据进行对比分析,得出地应力数据统计结果,如图 9所示。
|
| K为平均侧压系数。 图 9 典型工程最大主应力(a)和平均侧压系数(b) Fig. 9 Aaximum principal stress (a) and average lateral pressure coefficient (b) of the typical projects |
|
|
由图 9a可知:成兰铁路工区的地应力量值总体处于较低的水平;兰渝西秦岭隧道在450 m埋深内主应力量值较低,但与埋深变化的梯度为0.054 3 MPa/m,高于拉林铁路地区(0.033 7 MPa/m);秦岭地区(含秦岭特长铁路隧道、引汉济渭秦岭隧洞等工程)因测点分布范围太广,故其主应力量值的变化范围也很广,其中东秦岭东江口地区的主应力量值比拉林地区的主应力量值高;锦屏水电站工区(含锦屏一级左岸、一级右岸、一级河床、辅助洞等区域)测点在浅埋深时主应力量值极高,其随埋深增加的增速也很快,但在大埋深的锦屏辅助洞区域,主应力量值的增速则大大减小,根据趋势线预测,锦屏水电站辅助洞在一定埋深范围内的主应力量值比拉林铁路地区小。
从图 9b可知:拉林、成兰和锦屏等几个典型工区的平均侧压系数(K=(σH+σh)/2σv)仍表现出在两条双曲线(红色线)间分布的特点,且随着埋深的增大,平均侧压系数逐渐减小,这与文献[3-6]的结论一致;但上述几个典型工区的平均侧压系数比霍克布朗曲线和文献[4]中的中国外包线更靠右,即上述地区的平均侧压系数更大,说明所选典型工区的构造应力较中国其他地区更为突出。其中,从平均侧压系数的大小和分布范围看:秦岭地区平均侧压系数分布范围最广,整体量值最高;兰渝铁路西秦岭隧道次之;锦屏水电站工区和拉林铁路再次;成兰铁路的平均侧压系数和分布范围最小。拉林铁路的平均侧压系数分布在1.0~1.5之间。
综上所述,拉林铁路板块缝合带区域隧道的特点可以概括为:埋深大;主应力量值较大;构造应力作用突出。拉林线线路走向和最大主应力方向近似垂直,围岩强度高,或许是拉林铁路隧道易发生岩爆的重要原因。
4 结论通过采用空心包体法对拉林铁路沿线隧道进行原位地应力测试,并与锦屏、成兰等区域的地应力特征进行对比分析,得出以下结论:
1) 拉林铁路板块缝合带区域隧道的构造应力作用强烈,最大水平主应力与埋深的梯度为0.033 7 MPa/m,总体表现为最大水平主应力>垂直主应力>最小水平主应力;最大主应力方向分布范围为北北西—北北东,优势方向为近南北向。
2) 拉林铁路板块缝合带区域的隧道埋深大,最大主应力量值高,平均侧压系数分布较为集中(约1.0~1.5),且处于较高水平。
3) 特殊的初始地应力环境会造成拉林铁路隧道开挖后拱顶主应力集中,拱脚主应力降低,且隧道采用仰拱结构比底板结构的受力情况更好,墙脚发生岩爆的可能性更低。
| [1] |
丁健民, 高莉青. 地壳水平应力与垂直应力随深度的变化[J]. 地震, 1981(2): 46-48. Ding Jianmin, Gao Liqing. Horizontal Geostress and Vertical Geostress Varying with Depth Crustal[J]. Earthquake, 1981(2): 46-48. |
| [2] |
周洪福, 聂德新. 水电工程坝址区构造应力场三维数值反演[J]. 吉林大学学报(地球科学版), 2012, 42(3): 785-791. Zhou Hongfu, Nie Dexin. 3D-Numerical Back Analysis of Tectonic Stress Field in Dam Site of Hydropower Project[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(3): 785-791. |
| [3] |
Brown E T, Hoek E. Trends in Relationships Between Measured In-Situ Stresses and Depth[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts, 1978, 15(4): 211-215. |
| [4] |
赵德安, 陈志敏, 蔡小林, 等. 中国地应力场分布规律统计分析[J]. 岩石力学与工程学报, 2007, 26(6): 1265-1271. Zhao Dean, Chen Zhimin, Cai Xiaolin, et al. Analysis of Distribution Rule of Geostress in China[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1265-1271. DOI:10.3321/j.issn:1000-6915.2007.06.024 |
| [5] |
景锋, 盛谦, 张勇慧, 等. 中国大陆浅层地壳实测地应力分布规律研究[J]. 岩石力学与工程学报, 2007, 26(10): 2056-2062. Jing Feng, Sheng Qian, Zhang Yonghui, et al. Research on Distribution Rule of Shallow Crustal Geostress in China Mainland[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(10): 2056-2062. DOI:10.3321/j.issn:1000-6915.2007.10.014 |
| [6] |
王艳华, 崔效锋, 胡幸平, 等. 基于原地应力测量数据的中国大陆地壳上部应力状态研究[J]. 地球物理学报, 2012, 55(9): 3016-3027. Wang Yanhua, Cui Xiaofeng, Hu Xingping, et al. Study on the Stress State in Upper Crust of China Mainland Based on In-Situ Stress Measurements[J]. Chinese Journal of Geophysics, 2012, 55(9): 3016-3027. |
| [7] |
吴珍汉, 胡道功, 叶培盛, 等. 青藏高原中段古近纪早期古构造演化[J]. 地球学报, 2009, 30(6): 749-760. Wu Zhenhan, Hu Daogong, Ye Peisheng, et al. Paleocene-Eocene Tectonic Evolution in Central Tibetan Plateau[J]. Acta Geoscientica Sinica, 2009, 30(6): 749-760. DOI:10.3321/j.issn:1006-3021.2009.06.007 |
| [8] |
劳雄. 雅鲁藏布江断裂带的形成[J]. 地质力学学报, 1995(1): 53-59. Lao Xiong. On the Formation of Yarlung Zangbo River Fault Zone[J]. Journal of Geomechanics, 1995(1): 53-59. |
| [9] |
刘小汉, 李广伟, 刘小兵, 等. 雅鲁藏布江缝合带区域性构造-沉积特征[J]. 地质科学, 2009, 44(4): 1312-1326. Liu Xiaohan, Li Guangwei, Liu Xiaobing, et al. Regional Tectono-Sedimentary Feature of the Yarlung Zangbo Suture Zone[J]. Chinese Journal of Geology, 2009, 44(4): 1312-1326. DOI:10.3321/j.issn:0563-5020.2009.04.018 |
| [10] |
鲍杰. "拉萨-林芝地块"地壳岩体的现今应力-形变作用机制数值模拟研究[D].成都: 成都理工大学, 2012. Bao Jie. Numerical Simulation Study on the Present Stess-Deformation Mechanisms of the Crustal Rock Mass of "Lhasa-Linzhi Block"[D]. Chengdu: Chengdu University of Technology, 2012 http://cdmd.cnki.com.cn/Article/CDMD-10616-1012499743.htm |
| [11] |
肖序常, 汤耀庆, 高延林. 再论青藏高原的板块构造[J]. 地球学报, 1986(3): 18-30. Xiao Xuchang, Tang Yaoqing, Gao Yanlin. Reexposition on Plate Tectonics of the Qinghai-Tibet Plateau[J]. Acta Geoscientica Sinica, 1986(3): 18-30. |
| [12] |
肖序常, 李廷栋, 李光岑, 等. 青藏高原的构造演化[J]. 中国地质科学院院报, 1990(1): 123-125. Xiao Xuchang, Li Tingdong, Li Guangcen, et al. Tectonic Evolution of the Qinghai-Xizang(Tibet) Plateau[J]. Bulletin of the Chinese Academy of Geological Sciences, 1990(1): 123-125. |
| [13] |
高峰. 空心包体原岩应力测量方法及其工程应用[J]. 山西建筑, 2010, 36(12): 353-354. Gao Feng. On Measurement Methods of Hollow Enclave Original Rocks Stress and Project Application[J]. Shanxi Architecture, 2010, 36(12): 353-354. DOI:10.3969/j.issn.1009-6825.2010.12.222 |
| [14] |
姚瑞, 杨树新, 陆远忠, 等. 在地应力测量中准确求解最大、最小水平应力问题的探讨[J]. 岩土工程学报, 2012, 34(2): 317-325. Yao Rui, Yang Shuxin, Lu Yuanzhong, et al. Computing Maximum and Minimum Horizontal Stresses in In-Situ Stress Measurements[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(2): 317-325. |
| [15] |
张镜剑, 傅冰骏. 岩爆及其判据和防治[J]. 岩石力学与工程学报, 2008, 27(10): 2034-2042. Zhang Jingjian, Fu Bingjun. Rockbrust and It's Criteria and Control[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(10): 2034-2042. DOI:10.3321/j.issn:1000-6915.2008.10.010 |
| [16] |
包林海, 杜义, 郭啟良, 等. 成兰铁路地应力测量与构造应力场分布规律研究[J]. 地质力学学报, 2017, 23(5): 734-742. Bao Linhai, Du Yi, Guo Qiliang, et al. In-Situ Stress Measurement and Research on Tectonic Stress Field Distribution Law of Chengdu-Lanzhou Railway[J]. Journal of Geomechanics, 2017, 23(5): 734-742. DOI:10.3969/j.issn.1006-6616.2017.05.010 |
| [17] |
袁传保, 宋章. 成兰铁路地应力分布特征及工程评价[J]. 建筑技术开发, 2014, 41(7): 16-22. Yuan Chuanbao, Song Zhang. Distribution Characteristics and Project Appraisal of Crustal Stress for Chengdu-Lanzhou Railway[J]. Building Technique Development, 2014, 41(7): 16-22. DOI:10.3969/j.issn.1001-523X.2014.07.005 |
| [18] |
周泉. 兰渝线西秦岭特长隧道地应力特征及危害[J]. 西南交通大学学报, 2012, 47(增刊): 217-221. Zhou Quan. Analysis of the Complexity of the Stress on Lanzhou-Chongqing Railway West Qinling Special Long Tunnel[J]. Journal of Southwest Jiaotong University, 2012, 47(Sup.): 217-221. |
| [19] |
宋丙林. 秦岭隧道钻孔实测应力分析与探讨[J]. 铁道工程学报, 1996, 13(4): 54-59. Song Binglin. Practical Stress Measuring Results in Boreholes at Qinling Tunnel and Discussions[J]. Journal of Railway Engineering Society, 1996, 13(4): 54-59. |
| [20] |
王朋.引汉济渭秦岭深埋特长隧洞高地应力与岩爆关系研究[D].成都: 西南交通大学, 2014. Wang Peng. Study on the Relationship Between Ground Stress and Rock Burst on the Deep-Buried of Water Diverstion Project from the Han River to the Wei River[D].Chengdu: Southwest Jiaotong University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10613-1014252079.htm |
| [21] |
杜卫长.引汉济渭工程秦岭隧洞地应力测试研究[D].郑州: 郑州大学, 2017. Du Weichang. Research on In-Situ Stress Measurement of Qinling Mountain Tunnel of the Han to the Wei River Project[D]. Zhengzhou: Zhengzhou University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10459-1017139449.htm |
| [22] |
杜世回. 秦岭翠华山特长隧道高地应力问题研究[J]. 铁道工程学报, 2012, 29(2): 55-58. Du Shihui. Study on High Stress of Cuihuashan Super Long Tunnel in Qinling Mountain Area[J]. Journal of Railway Engineering Society, 2012, 29(2): 55-58. DOI:10.3969/j.issn.1006-2106.2012.02.012 |
| [23] |
韩金良, 吴树仁, 谭成轩, 等. 东秦岭东江口花岗岩体水压致裂法与AE法地应力测量对比研究[J]. 岩石力学与工程学报, 2007, 26(1): 81-86. Han Jinliang, Wu Shuren, Tan Chengxuan, et al. Studies on Geostress by Comparing Result of AE Method with that of Hydraulic Fracturing Technique in Dongjiangkou Granite in East Qinling[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(1): 81-86. DOI:10.3321/j.issn:1000-6915.2007.01.011 |
| [24] |
谭成轩, 张鹏, 郑汉淮, 等. 雅砻江锦屏一级水电站坝址区实测地应力与重大工程地质问题分析[J]. 工程地质学报, 2008, 16(2): 162-168. Tan Chengxuan, Zhang Peng, Zheng Hanhuai, et al. An Analysis on In-situ Crustal Stress Measurements and Major Engineering Geology Issues at the Dam Site Area of Jinping First Stage Hydropowers Station[J]. Journal of Engineering Geology, 2008, 16(2): 162-168. DOI:10.3969/j.issn.1004-9665.2008.02.003 |
| [25] |
赵国平, 黄鑫. 断层对锦屏地区地应力特征的影响[J]. 中国水运, 2017, 17(8): 315-316. Zhao Guoping, Huang Xin. The Influence of Geological Fault on the Characteristics of Crustal Stress in Jinping Area[J]. China Water Transport, 2017, 17(8): 315-316. |


