0 引言
泥石流是山区特有的一种突发性自然地质灾害现象,是一种包含大量泥沙、石块和巨砾的固液两相流体,呈黏性层流或稀性紊流等运动状态,是山地环境恶化的产物。泥石流具有爆发突然、运动快速、历时短暂等特点[1];因此,泥石流一旦爆发,势必会对其堆积扇处的公共设施与居民区造成严重破坏。故对泥石流堆积范围的预测具有重要意义。水山高久等[2]基于泥沙运动模拟实验,运用圣维南方程建立了泥石流危险范围预测模型,但由于该模型参数多、计算繁琐,实际应用时较为困难;刘希林等[3]在蒋家沟现场进行了泥石流危险范围的模型实验,根据泥石流冲出量与堆积区坡度等数据,建立了泥石流危险范围的数学模型并给出了一次泥石流危险范围平面形态的判定准则,该预测模型在云南和甘肃得到了实践应用;O’Brien等[4]基于二维洪水模型和流体流变方程开发了模拟泥石流危险范围的软件Flo-2D,在应用于区域泥石流危险范围模拟方面取得了较好的成果,但该模型没有考虑沟道下切作用以及水流侵蚀作用;Patra等[5]基于Iverson模型[6-7]和GIS开发了TITAN2D,该模型在模拟坡面型泥石流时得到了比较精确的结果,但对于黏性泥石流和沟谷型泥石流模拟效果较差[8];Han等[9]基于计算机数值模拟方法对于溃坝引起的泥石流泛滥过程进行了研究,该数学模型体现了泥石流流速快、历时短暂的特点,但其对于复杂的机理研究尚不完善,在应用时对一些参数的选定也十分困难。此外,Iverson等[10]基于GIS平台结合9座火山的27条火山泥石流创建了半经验的数学模型,以此模型建立了LAHARZ软件来模拟火山泥石流的堆积范围;因泥石流在原理上与火山泥石流相近,Griswold等[11]又将LAHARZ软件应用于泥石流。
本文根据北京密云县喇嘛栅子南沟小流域的数字高程模型(DEM)图,运用LAHARZ软件对该泥石流的堆积范围进行预测,计算中引入北京地区泥石流数据对原模型进行修正,以使泥石流堆积预测范围更为可靠,力求为泥石流的防治提供科学依据。
1 LAHARZ模拟堆积范围的原理LAHARZ泥石流模拟程序是基于GIS平台开发的软件。在LAHARZ中,核心数学模型为火山泥流体积与沟谷横截面积和平面堆积面积的关系,如图 1 [10]所示。

|
| L为火山口至火山末端的水平距离;H为火山口至火山末端的垂直距离。 图 1 LAHARZ原理图 Fig. 1 Schematic diagram of LAHARZ |
|
|
Iverson等[10]在开发LAHARZ时,假设爆发泥石流的体积为V,且在流经沟谷过程中泥石流的质量与体积密度均不发生变化,则
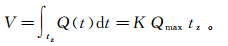 (1)
(1) 式中:V为泥石流总体积(m3);K为流量形状系数,对于泥石流,K=0.5;Q(t)为随时间变化的流量(m3/s);t为时间(s);Qmax为洪峰流量(m3/s);tz为泥石流流经截面的总时间(s)。
假设泥石流在洪峰流量时生成最大横截面积Amax,结合明渠稳定流体与非稳定流体相关原理[12],定义洪峰流量无量纲参数Qmax*为
 (2)
(2) 式中:g为重力加速度;R为水力半径。定义泥石流经过截面的时间无量纲参数tz* [10]为
 (3)
(3) 将式(2)、式(3)代入式(1),可得泥石流体积无量纲参数V*:
 (4)
(4) 令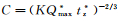
 (5)
(5) 为探究泥石流爆发后的平面堆积范围,假设整个过程中物源总量不发生改变,即泥石流体积为恒量,则
 (6)
(6) 式中:h为堆积厚度(m);h为平均厚度(m);B为平面堆积面积(m2)。若泥石流流经路径彼此几何相似,则h
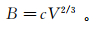 (7)
(7) 式中,
综上,式(5)和式(7)即为LAHARZ模拟泥石流堆积范围的数学模型。
在Iverson的假设中,泥石流的体积和体积密度在泥石流过程中全程不发生变化,但这在实际中是不可能的。因为泥石流在向下游流经的过程中,水和固体物质含量的不断变化,泥石流体积和体积密度也在不断变化。通常情况下,在泥石流发生过程中,泥石流的体积不断增加[13],并且在流经途中不会遗留大量沉积物[14],因此根据此假设所得的泥石流堆积范围结果会偏小。对于泥石流流经路径几何相似的假设,在实际中也是不存在的,但是如果

Iverson等[10]于1998年通过收集墨西哥境内9座火山中27条火山泥流的数据,用统计分析方法确定了式(5)和式(7)的系数,即C=0.05,c=200,并基于此模拟了火山泥石流堆积范围。2008年Griswold等[11]又将此模拟应用到泥石流,在导入泥石流相关数据后得到了泥石流堆积范围的模型:Amax=0.1V2/3,B=20V2/3。为了更好地模拟我国泥石流堆积范围,本文引入我国部分地区的泥石流相关资料对LAHARZ原模型进行修改,以求得系数c。
由式(7)可知,泥石流体积与堆积面积B之间存在指数关系,即
 (8)
(8) 式中,ω为参数。为了便于分析,将式(7)两边取对数,得到
 (9)
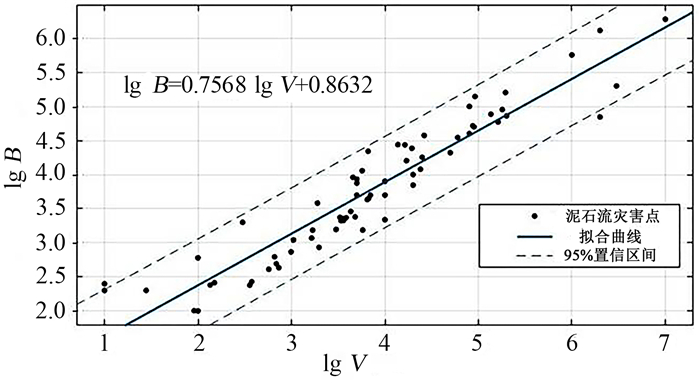
(9) 通过查阅相关资料与文献[15-16],收集到了中国部分地区泥石流总体积与平面堆积面积的数据,结合原模型数据[10],将泥石流堆积平面面积与泥石流体积数据取对数后制成拟合曲线,如图 2所示。
拟合曲线方程如下:
 (10)
(10) 将式(10)代入(9)中,再化为指数形式:
 (11)
(11) Amax与V的关系采用Griswold等[11]的模型得到:
 (12)
(12) 式(11)和式(12)即为本文确定的泥石流堆积范围的数学模型,将其导入LAHARZ软件中即可得到泥石流模拟堆积范围。
2.2 模型可靠度的验证得到堆积范围数学模型后,需要对其进行验证,对于一元回归模型,本文采用拟合优度检验[17]。拟合优度检验是对样本回归直线与样本观测值之间拟合程度的检验,度量拟合优度的指标有可决系数(R2)、误差平方(SSE)和与标准差(RMSE)。其中:可决系数表示解释变量引起的变动占总变动的百分比,R2越接近1,表明实际观测点离样本线越近,拟合优度越高,一般要求R2≥0.7;SSE与RMSE数值越小,表示拟合效果越好。对泥石流堆积范围模型进行拟合优度检验,得到各项参数见表 1。
| 模型参数 | lg c | ω | SSE | RMSE | R2 |
| 修改后模型参数 | 0.863 2 | 0.756 8 | 7.31 0 | 0.322 8 | 0.890 5 |
| 原模型参数 | 1.301 0 | 0.666 7 | 8.73 1 | 0.358 3 | 0.869 2 |
从表 1中看出,修改后模型参数SSE、RMSE相比原模型参数小,R2相比原模型参数更接近1.000 0;故修改后模型拟合效果较好。
3 基于LAHARZ的泥石流堆积范围数值模拟 3.1 研究区概况研究区位于北京市密云县南部。密云县总地势呈三面环山、西南开口、中部较低缓的簸箕形,地貌间呈阶梯分布,相对高差较大,地表切割深、土层薄,坡地多,平坦地势少,水土流失较为严重。密云地区地质构造十分复杂,主要由新华夏构造断裂、几组NE向及EW向主要构造带构成基本构造格式。密云县地层太古界,元古界,古生界寒武系,中生界侏罗系、白垩系都有出露,新生界第四系亦有出露。密云县的水文地质条件相对复杂,山地地区的地下水主要埋藏在基岩裂隙中,第四系地层中亦有埋藏。密云县的气候为暖温带季风型大陆性半湿润半干旱型,四季较为分明,干湿冷暖变化明显。密云县属于旱、水、雹、虫、地震等自然灾害多发地区,其中水造成的灾害主要是山洪灾害与泥石流灾害。密云县平均降水量为661.3 mm,年平均降水日数为75 d;季节对比来看,夏季降水最多,占全年降水量的76.4%,夏季降水又集中在7月下旬至8月上旬的20 d内,平均降水量为194.1 mm,占夏季降水量的38.7%和全年降水量的29.4%。查阅相关资料,喇嘛栅子南沟历史上未曾发生过泥石流[18]。
喇嘛栅子南沟沟口位置位于116°48′14.75″E,40°42′46.32″N,总体流向呈正北方向,靠近形成区区域流向大致为32°NE,流通区至下游沟口流向大致为正北方向,流域轮廓北侧较窄、南侧较宽,流域周边的山峰岩性主要为片麻岩。流域内主沟上游沟道较窄,宽度介于13~15 m之间;流通区至沟口沟道宽度逐渐变宽,沟口宽217 m。泥石流主沟西侧发育3条支沟,东侧发育2条支沟。喇嘛栅子南沟主沟长约2 322 m,流域最大相对高差315 m,流域面积2.507 km2。喇嘛栅子南沟物源大部分集中于主沟与支沟1交汇的下游处,主沟上游和支沟2沟内存在少量物源,主沟下游区域有多处居民住宅,若发生泥石流,将会对居民区造成威胁。沟谷平面形态如图 3所示。

|
| 图 3 喇嘛栅子南沟泥石流平面图 Fig. 3 Plan of the Southern Lamazhazi debris flow |
|
|
喇嘛栅子南沟沟源最高点高程960 m,沟口高程645 m,总体坡降约为13.6%。主沟沟道整体上可分为两段:形成区段和流通区段,其纵剖面图见图 4。主沟形成区段长度大约为650 m,主沟在形成区段的纵坡降大约为23.5%,沟床坡度达11°,沟床宽度为20~100 m,下切深度为2.0~3.0 m;流通区段长度约为1 672 m,主沟在流通区段内的纵坡坡降明显变缓,流通区内总体坡降为12.7%,沟床坡度约为6°,沟床宽度50~140 m,其中上游宽度较窄,向下游逐渐变宽,主沟流通区下切深度大约为2.5~9.7 m。自上游向下游切割深度逐渐变小,在流通区上游段的尽头可见此现象。

|
| 图 4 喇嘛栅子南沟主沟纵剖面 Fig. 4 Longitudinal plan of the main channel in the Southern Lamazhazi debris flow |
|
|
在使用LAHARZ时,需要准备研究区域的数字高程模型,即DEM图。DEM图以栅格形式储存着实际地形的地理位置和高程信息,因其在制作过程中本身会出现一些错误,即生成一些比实际高程低的洼地,导致泥石流的流动方向发生改变,故需要对其做填充处理。研究区域生成的DEM图中最低高程为610 m,故将填充阈值设置为610 m。
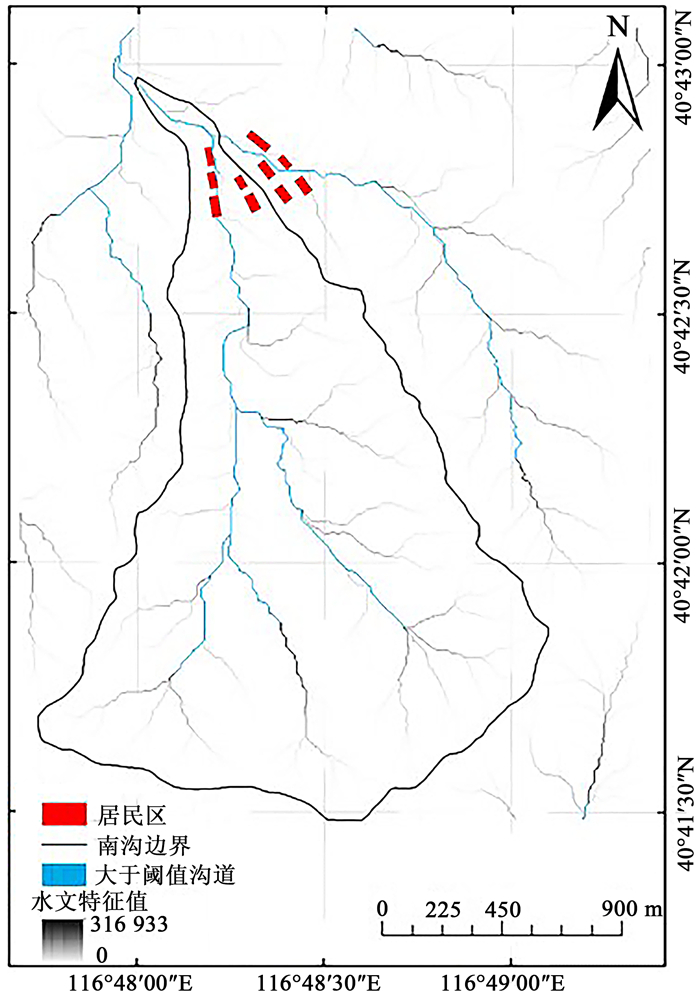
3.3 沟道网格计算LAHARZ软件计算泥石流地表流动时采用了D8单流向法[19]。即某一栅格有8个可流动的方向,通过计算该栅格与周围8个栅格的高程差后,高程差最大的栅格将作为此栅格的下一个流动方向,以此类推,即可得出整体流动方向。水文特征值储存在每个栅格中,代表着汇入其中的周围栅格的数目。水文特征值越大,表示其汇流能力越好,实际地形可能为地势较低的区域;反之,水文特征值越小,表示其汇流能力越差;若水文特征值为0,其可能代表着分水岭。基于此可确定该区域的流域边界。栅格中的水文特征值会进行累积叠加,在LAHARZ中设定了沟道阈值,水文特征值大于该阈值的栅格才会显现,以此构成了网格。根据研究区实际地形,当沟道阈值设计值为15 000时,得到与实际沟谷相接近的沟道,如图 5所示。
|
| 图 5 水文特征值分布及大于阈值的沟道 Fig. 5 Distribution of hydrological characteristic values and greater than the threshold of channel |
|
|
喇嘛栅子南沟泥石流体积值根据不同暴雨设计频率下的泥石流流量得出,设计频率为10年、20年、50年、100年一遇的暴雨条件。首先估算各设计频率下喇嘛栅子南沟的洪峰流量,估算方法参考《北京市水文手册》[20],联立式(13)、式(14)可得:
 (13)
(13)  (14)
(14) 式中:QP为暴雨频率为P(a)的清水流量(m3/s);Al为流域面积(km2);ht为净雨量(m);th为汇流时间(h);θ为流域特征参数,θ=S/J1/3(其中S为沟长(km),J为平均坡降(%));m为汇流系数,通过查阅水文手册得到。
得到各暴雨频率下的清水流量后可计算泥石流洪峰流量:
 (15)
(15) 式中:QC为暴雨频率为P时的泥石流洪峰流量(m3/s);φ为泥石流泥沙修正系数,取1.443;DC为泥石流堵塞系数,取1.10。
QP、QC计算结果见表 2。
| P/a | QP/(m3/s) | QC/(m3/s) |
| 10 | 45.0 | 71.4 |
| 20 | 58.0 | 92.1 |
| 50 | 75.0 | 119.0 |
| 100 | 90.0 | 142.9 |
参考蒋家沟泥石流全过程的平均值给出北京地区喇嘛栅子南沟流域各泥石流沟平均历时建议值,如表 3所示,之后可根据式(16)计算各暴雨频率下的一次最大冲出量,结果见表 4。
 (16)
(16) | 县区 | 流域名 | 面积/km2 | 沟长/km | 坡降/% | 历时/h |
| 东川 | 蒋家沟 | 47.100 | 12.100 | 18.0 | 4.6 |
| 密云县 | 喇嘛栅子南沟 | 2.507 | 2.322 | 13.6 | 0.8 |
| 沟名 | P/a | |||
| 10 | 20 | 50 | 100 | |
| 喇嘛栅子南沟 | 56 500 | 72 900 | 94 200 | 113 100 |
式中:Q为暴雨频率为P时的一次泥石流总量(m3);KA1为修正系数,当流域面积Al<5 km2时,KA1=0.202。
根据式(16)计算可得到泥石流一次最大冲出量(表 4),即为喇嘛栅子南沟泥石流体积值。将表 4中的4个体积值导入LAHARZ中,对喇嘛栅子南沟泥石流堆积范围进行模拟,如图 6所示。

|
| 图 6 泥石流堆积范围 Fig. 6 Accumulation area of debris flow |
|
|
从图 6可以看出,随着泥石流体积的增加,堆积面积逐渐增加。计算得知:当泥石流体积值为56 500 m3时,堆积面积最小,为28 819 m2,堆积最远距离约为356 m,泥石流对村庄无威胁;当泥石流体积值为72 900 m3时,堆积面积为34 949 m2,堆积最远距离约为400 m,泥石流对村庄无威胁;当泥石流体积值为942 00 m3时,堆积面积为42 431 m2,堆积最远距离约为430 m,泥石流对村庄亦无威胁;当泥石流体积值为113 100 m3时,堆积面积最大,为48 729 m2,堆积最远距离约为490 m,泥石流末端离村庄较近,对村庄构成了威胁。
由图 6可知,在百年一遇暴雨条件下,泥石流堆积展布范围已临近村庄。为探究泥石流堆积范围抵达村庄边界的体积阈值,设定120 000,130 000,140 000,150 000 m3 4个体积值,带入LAHARZ中,得到结果如图 7所示。结果表明,当泥石流体积为140 000 m3时,泥石流堆积至村庄,因此泥石流体积阈值可设定为140 000 m3。

|
| 图 7 泥石流体积阈值的确定 Fig. 7 Determination of debris flow volume threshold |
|
|
1) 在LAHARZ软件的基础上增加了我国部分泥石流平面堆积面积与泥石流体积相关数据,获得了修正的预测数学模型。
2) 对密云县喇嘛栅子南沟在10年、20年、50年和100年一遇降雨条件下泥石流的堆积范围进行模拟计算,根据100年一遇暴雨条件下的堆积范围求得了泥石流抵达村庄的体积阈值。模拟结果表明,100年一遇暴雨条件下已对下游村庄构成了威胁,应给予防范。
3) 受地形因素的影响,泥石流在流动过程中,在转弯处有一定的能量损失,模拟模型没有考虑这样的能量损失。另外由于基础数据分辨率的原因,堆积末端产生了不规则锯齿边界,不符合实际,后续有待改进。
| [1] |
唐邦兴. 中国泥石流[M]. 北京: 商务印书馆, 2000. Tang Bangxing. Debris Flow in China[M]. Beijing: Commercial Press, 2000. |
| [2] |
水山高久, 北原一平. 土石流泛滥夕三口卜夕日夕毛于沙上为土石流对策的效果评价[J]. 新砂防, 1989, 40(5): 14-21. Takahisa Mizuyama, Ippei Kitahara. Effectiveness Evaluation of Countermeasures for Debris Flow on Sandy Soil[J]. New Sand Protection, 1989, 40(5): 14-21. |
| [3] |
刘希林, 唐川, 陈明, 等. 泥石流危险范围的模型实验预测法[J]. 自然灾害学报, 1993(3): 67-73. Liu Xilin, Tang Chuan, Chen Ming, et al. Model Experimental Prediction Method for Debris Flow Hazard Range[J]. Journal of Natural Disasters, 1993(3): 67-73. |
| [4] |
O'Brien J S, Julian P Y, Fullerton W T. Two-Dimensional Water Flood and Mudflow Simulation[J]. Journal of Hydraulic Engineering, 1993, 119(2): 244-261. DOI:10.1061/(ASCE)0733-9429(1993)119:2(244) |
| [5] |
Patra A K, Bauer A C, Nichita C C, et al. Parallel Adaptive Numerical Simulation of Dry Avalanches over Natural Terrain[J]. Journal of Volcanology and Geothermal Research, 2005, 139: 1-21. DOI:10.1016/j.jvolgeores.2004.06.014 |
| [6] |
Iverson R M, Denlinger R P. Flow of Variably Fluidized Granular Masses Across Three-Dimensional Terrain:1:Coulomb Mixture Theory[J]. Journal of Geophysical Research, 2001, 106(B1): 537-552. DOI:10.1029/2000JB900329 |
| [7] |
Denlinger R P, Iverson R M. Flow of Variably Fluidized Granular Masses Across Three-Dimensional Terrain:2:Numerical Predictions and Experimental Tests[J]. Journal of Geophysical Research, 2001, 106(B1): 553-566. DOI:10.1029/2000JB900330 |
| [8] |
余斌. 美国纽约州立大学布法罗分校火山碎屑流和泥石流数学模型研究近况[J]. 山地学报, 2005, 23(1): 126-128. Yu Bin. Research on the Numerical Model of Pyroclastic Flow and Debris Flow in the State University of New York at Buffalo[J]. Mountain Research, 2005, 23(1): 126-128. DOI:10.3969/j.issn.1008-2786.2005.01.017 |
| [9] |
Han G, Wang D. Numerical Modeling of Anhui Debris Flow[J]. Journal of Hydraulic Engineering, 1996, 122(5): 262-265. DOI:10.1061/(ASCE)0733-9429(1996)122:5(262) |
| [10] |
Iverson R M, Schilling S P, Vallance J W. Objective Delineation of Lahar-Inundation Hazard Zones[J]. Geological Society of America Bulletin, 1998, 110(8): 972-984. DOI:10.1130/0016-7606(1998)110<0972:ODOLIH>2.3.CO;2 |
| [11] |
Griswold J P, Iverson R M. Mobility Statistics and Automated Hazard Mapping for Debris Flows and Rock Avalanches[M].[S.l.]: US Department of the Interior, US Geological Survey, 2008.
|
| [12] |
Savage S B, Hutter K. The Motion of A Finite Mass of Granular Material Down a Rough Incline[J]. Journal of Fluid Mechanics, 1989, 199: 177-215. DOI:10.1017/S0022112089000340 |
| [13] |
Pierson, Thomas C, Thoure J C, et al. Perturbation and Melting of Snow and Ice by the 13 November 1985 Eruption of Nevado del Ruiz, Colombia, and Consequent Mobilization, Flow and Deposition of Lahars[J]. Journal of Volcanology and Geothermal Research, 1990, 41(1/2/3/4): 17-66. |
| [14] |
Scott K M, Vallance J W. Debris Flow, Debris Avalanche and Flood Hazards at and Downstream from Mount Rainier, Washington[J]. Hydrologic Atlas. |
| [15] |
燕继宇.内蒙克旗泥石流堆积区平面形态和危险范围预测模型[D].长春: 吉林大学, 2015. Yan Jiyu. The Study of Flat Shape of Alluvial Fans and the Model for Predicting Deposition of Debris Flow in Inner Mongolia[D]. Changchun: Jilin University, 2015. |
| [16] |
Li Yaoming, Ma Chao, Wang Yujie. Landslides and Debris Flows Caused by an Extreme Rainstorm on 21 July 2012 in Mountains near Beijing, China[J]. Bulletin of Engineering Geology and the Environment, 2019, 78: 1265-1280. DOI:10.1007/s10064-017-1187-0 |
| [17] |
王松桂. 线性模型引论[M]. 北京: 科学出版社, 2004. Wang Songgui. Introduction to Linear Model[M]. Beijing: Science Press, 2004. |
| [18] |
陈剑平, 王常明, 张文, 等.北京泥石流灾害预测预警[R].长春: 吉林大学, 2016. Chen Jianping, Wang Changming, Zhang Wen, et al. Debris Flow Disaster Prediction and Early Warning System in Beijing[R]. Changchun: Jilin University, 2016. |
| [19] |
O'Callaghan J F, Mark D M. The Extraction of Drainage Networks from Digital Elevation Data[J]. Computer Vision, Graphics, and Image Processing, 1984, 28(3): 323-344. DOI:10.1016/S0734-189X(84)80011-0 |
| [20] |
赵志新, 高振宇, 杜文成, 等. 北京市水文手册[M]. 北京: 北京市水务局, 2005. Zhao Zhixin, Gao Zhenyu, Du Wencheng, et al. Beijing Hydrological Manual[M]. Beijing: Beijing Water Bureau, 2005. |