0 前言
随着陆地油气勘探工作的深入与完善,我国大量的地震勘探工作已在海洋区域展开。与陆地勘探工作不同,海洋地震勘探面临一些独有的地质条件,如崎岖海底、大陡坡、海底火山等。认识地震波在这些特殊地质条件下的传播规律,对于海洋地震勘探具有重要的意义。射线追踪算法是一种高效且能直观刻画地震波运动学特征的方法,在地震勘探的很多方面发挥着重要作用[1-2]。因此,对海洋特殊地质条件下的射线追踪算法进行研究,并分析地震波运动学特征,具有重要的理论意义和实用价值。
在过去30余年的时间里,由于各种地震数据处理技术的广泛需要,以计算地震波走时与射线路径为目的的射线追踪类方法得到了全面而深入的发展,相继发展出两点射线追踪法[3]、最短路径射线追踪法[4]、有限差分法[5-8]、插值法[9-11]、波前构建法[12]等算法。这些算法各有特点,其中:两点射线追踪法在早期天然地震数据处理中起到了非常重要的作用;最短路径射线追踪法能获得精度很高的走时信息[13-14];由于各种波前扩展方式和差分格式的引入,有限差分法具有较高的计算效率、不错的计算精度和稳定性[15-20];插值法可在任意网格中被推广,且具有近似于二阶差分格式的计算精度[21-24];波前构建法可同时获取走时和射线信息,若加入动力学射线追踪系统还可以获取振幅信息。除了以上阐述的几种主流算法外,射线追踪类方法近些年还发展出辛几何算法[25]、基于几何作图的走时算法[26]、神经网络法[27]、模拟退火法[28]和计算复走时的扰动法[29]等。
与常规条件下的方法不同,上述方法在面对如崎岖海底、海底大陡坡、海底火山等特殊复杂海底地质条件时存在一些局限性和缺陷。首先,虽然有限差分方法具有很好的计算效率,但其不易适应本文为了准确刻画崎岖海底、大陡坡等复杂海底地质条件而采用的混合网格;其次,虽然插值法有着相对不错的计算精度和能适应任意复杂网格形态的能力,但其波前扩展方式的计算效率较低。鉴于此,考虑复杂海底地质条件下算法的计算精度、计算效率、数值稳定性、灵活性等因素后,本文综合迎风有限差分法计算效率较高且无条件稳定的优势和线性插值法计算精度较高且灵活(适应任意网格形态)的优势,实现一种快速推进迎风插值法;并以该方法为正演模拟工具,分析复杂海底地震波运动学特征,以期提出针对复杂海底地震数据采集和处理的思考与建议。
1 复杂海底地质模型建立复杂海底地质模型的关键是对崎岖海底及海底以下复杂界面和地质构造形状的准确刻画,其涉及的核心问题是采用怎样的网格进行剖分。从数值计算的角度考虑,该网格剖分技术应该尽可能降低计算的复杂程度并减少计算量,同时还能很好地保证数值算法的稳定性和计算精度。因此,网格剖分技术是保证数值算法计算效率、计算精度及稳定性的基础。
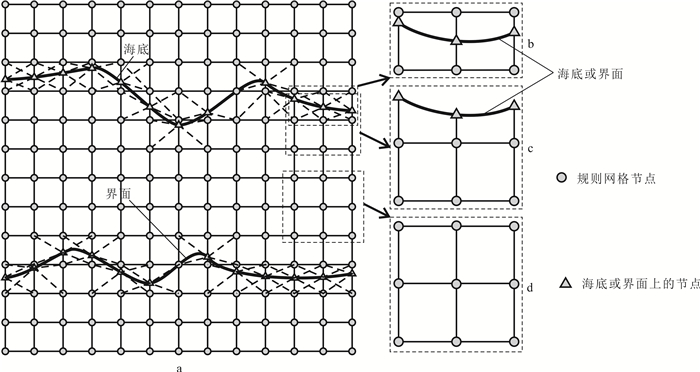
为了更好地刻画崎岖海底及海底以下复杂界面的形态,并同时保证算法的大部分计算工作在规则均匀的正方形网格中进行,采用混合网格法建立复杂海底地质模型(图 1)。具体实现步骤为:
|
| 图 1 混合网格法剖分复杂海底模型 Fig. 1 The method based on the hybrid grid for building the complex seabed model |
|
|
① 获取海水及海底以下介质中地震波传播的速度参数分布、海底水深、复杂界面位置等信息,并确定相关计算参数(计算区域尺度、正方形网格间距)。
② 综合利用海平面位置、崎岖海底水深、复杂界面位置、计算区域尺度等信息构建模型的整体框架。
③ 根据计算要求选取网格间距,采用均匀的正方形网格剖分整个模型框架,采用三角网格剖分崎岖海底及复杂界面附近区域。
④ 根据各网格节点的位置和其邻近网格单元地震波速度参数的分布情况,采用面积加权平均法计算各网格节点的地震波速度参数,并按照一定存储格式输出模型参数以备后续数值计算使用。
2 射线追踪算法针对复杂海底地质条件的特点,并为了很好地适应上述混合网格模型和复杂介质,通过综合利用快速推进法和线性插值法各自的优势,实现一种基于迎风差分思想的快速推进线性插值法来进行射线追踪。
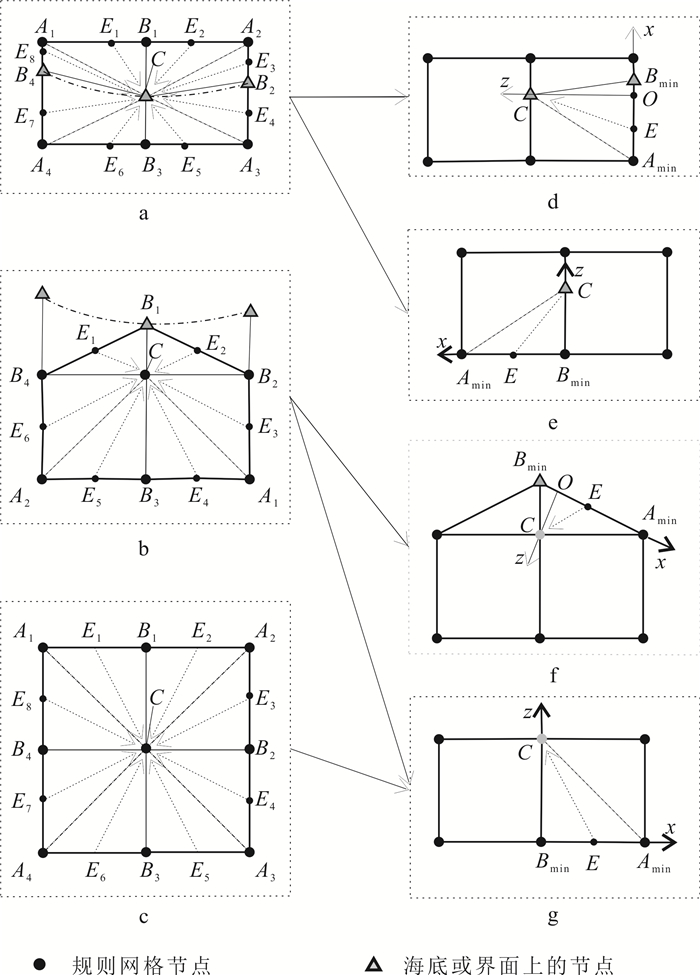
2.1 基于迎风差分思想的线性插值公式为了解决混合网格模型(针对复杂地表问题)中地震波走时的计算问题,笔者曾经将线性插值法引入到快速推进法中,提出过一种基于线性插值和窄带技术的走时算法[15, 23]。该算法能够很大程度上提高快速推进法的计算精度,但需引入一种局部实现策略来保证线性插值公式很好地与窄带技术兼容(保持算法的无条件稳定性)。如图 2a-c所示,这种局部实现策略通过繁琐的判断对比来保证算法的稳定性:在对应的正方形和三角形网格中,在包围被算点的8或6条线段上分别采用线性插值公式进行计算,然后根据费马原理选取其中的最小走时作为最终的计算结果。实际上,原快速推进法中的迎风差分格式本身就具有无条件稳定性[15, 17]。因此,下面将基于迎风差分格式的基本思想来推导局部走时计算公式,以保证无条件稳定性在算法的实现过程中得以自动满足,进而降低局部算法的复杂程度。
|
| a.海底或界面上;b.海底或界面附近;c.正常规则正方形网格处;d.情况a中的一般三角形网格;e.情况a中的直角三角形网格;f.情况b中的直角三角形网格;g.情况b和c中的正方形网格。 图 2 基于迎风差分思想的线性插值公式推导示意图 Fig. 2 Sketch of the upwind linear travel-time interpolation solvers in different types of grid |
|
|
如图 2a、b所示,在海底或界面上及附近,需要在一般三角形网格或直角三角形中求解点C的走时tC。首先,根据迎风思想选取与C直接相邻的4个网格节点(B1、B2、B3、B4)走时中的最小者tBmin;然后,选取与点Bmin直接相邻的2个点中走时较小者tAmin;最后,直接以tAmin、tBmin为已知条件,采用线性插值法即可获得一般三角形网格(图 2d)计算tC的迎风线性插值公式:
 (1)
(1) 式中:Δt=tBmin-tAmin;d1、d2、d3分别表示线段AminBmin、AminO、OC的长;s表示当前计算所在局部网格的平均慢度;E点为线段AminBmin上到达被算点C的射线的入射点。
 (2)
(2) 式中:d为线段CBmin的长;h为正方形网格的网格间距。
如图 2c所示,在正方形网格中,同样采用上述方法,首先确定如图 2g所示走时为已知的线段AminBmin,然后采用线性插值法即可获得正方形网格中计算tC的迎风线性插值公式:
 (3)
(3) 综上所述,公式(1)-(3)分别为海底或界面上及附近、直角三角形及规则正方形网格中的局部走时计算公式,这3个公式对应着明确的物理意义:它们建立的实质控制原理是迎风基本思想的融入,即选择被算点已知条件的所在方向,应该是当前被算点的前时刻地震波传来的方向(迎着地震波传来的方向),在这个方向上被算点附近的走时分布是包围被算点的一条闭合曲线上已知走时分布中的最小走时(即图 2d-g中的线段AminBmin均为被算点C周围的最小走时线段),这种迎风数值实现策略实际上是对地震波射线局部传播Fermat原理的自然满足,所以其能保证算法的无条件稳定性。
至此,混合网格中的走时计算公式就建立完成了。此外,基于Asakawa等[9]在1993年提出的线性插值法思想,计算射线路径的公式已经在走时计算公式推导过程中产生。实际上,射线路径的计算公式即为图 2中各种情况下E点的坐标公式。与式(1)、(2)、(3)对应的E点的坐标公式分别为:
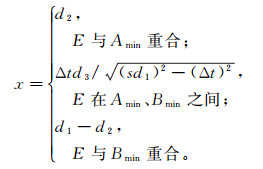 (4)
(4) 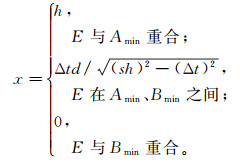 (5)
(5) 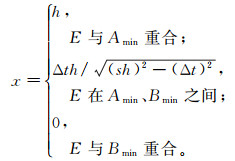 (6)
(6) 公式(4)-(6)即为各种网格情况下射线路径的计算公式。
2.2 基于多级次快速推进法的走时计算由于满足地震波传播过程中的“熵守恒”理论、计算效率高、具有对复杂介质模型的适应性,在此选择快速推进法作为走时计算整体实现策略的基础算法。
如图 3所示,常规快速推进法在实现时首先将计算区域内的全部网格分类为完成点、窄带点、远离点。其中:完成点表示走时计算已经完成的网格节点;窄带点表示窄带内,即当前波前上的网格节点;远离点表示走时计算还没有进行的网格节点。常规快速推进法的实现包括初始化和循环计算两个步骤。初始化时:设震源点为唯一的完成点,其走时值为零;设与震源点直接相邻的几个网格节点为窄带点,其走时值通过解析公式进行计算,它们构成了初始窄带,即初始波前;设其余的全部网格节点为远离点,它们的走时值设为无穷大。循环计算包括如下步骤。

|
| a.从震源到海底的入射波;b.绕射波网格节点的重新初始化;c.拾取海底节点的入射波走时值;d.绕射点到海平面的绕射波追踪;e.海底到界面的透射波追踪;f.海底到海平面的反射波追踪;g.拾取界面上的透射波走时值;h.界面到海平面的反射波追踪。 图 3 走时计算的整体实现策略 Fig. 3 Integral implementation strategy for travel-time computation |
|
|
① 通过比较选出窄带内走时最小的节点作为波前上的子震源点。
② 将步骤①选出来的子震源点的属性由窄带点改为完成点。
③ 以子震源点为扩展点,先判断与其直接相邻的每个网格节点的走时:若该网格节点为完成点,则保持其原有属性不变;若该网格节点为窄带点,则采用相应的公式计算其走时,并将计算结果与其原来的走时进行比较,若计算结果为较小者则用其替换原来的走时,否则保持原来的走时不变;若该网格节点为远离点,则采用相应公式计算其走时,并将其网格属性由远离点变为窄带点。
④ 对窄带进行判断,若窄带内网格节点数为零则计算结束,若其不为零则跳回①继续进行循环计算。
与常规快速推进法的实现策略略有不同,此处快速推进法在实现时会遇到不规则的三角形网格;不过快速推进法的实现不受网格形状的限制,只需要在扩展时对子震源点周围网格节点的属性进行判断,并根据判断结果进行相应的处理。在处理时略有不同的是,采用的计算公式需要根据网格形态的不同对应地选择上一节建立起来的计算公式。
此外,常规快速推进法在实现时只能计算初至波的走时。如图 3所示,为了计算海洋特殊地质条件下各种地震波的走时,在此有针对性地采用如下不同波型的多级次快速推进法实现步骤。
① 计算点绕射波走时,采用如图 3所示的a→b→d的步骤:首先,计算震源点到达绕射点的入射波走时;其次,把绕射点当作新的震源点,并重新初始化模型;最后,计算绕射点到达海平面上各接收点的绕射波走时。采用上述步骤的基本依据:绕射波的计算步骤实际上与绕射波的产生机制是相吻合的,绕射点实际上可以视为二次震源点,而到达每个接收点的绕射波走时等于震源点到达绕射点走时与绕射点到达接收点走时的和。
② 计算海底反射波走时,采用如图 3所示的a→c→f的步骤:首先,计算震源点到达海底的入射波走时;其次,提取海底的入射波走时为初始条件并重新初始化整个模型;最后,计算海底到达海平面上各接收点的海底反射波走时。采用上述步骤的基本依据:要计算反射波的走时首先需要计算到达目标界面的入射波的走时,而把界面上的入射波的走时作为反射波走时计算时的初始窄带,则是依据入射波到达反射界面的时刻作为反射波产生的时刻,即反射波开始向上传播的时刻。
③ 计算到达界面入射波(透射波)走时,采用如图 3所示的a→c→e→g的步骤:首先,计算震源点到达海底的入射波走时;其次,提取海底上的入射波走时为初始条件并重新初始化整个模型;最后,计算海底到达界面的入射波(透射波)走时。采用上述步骤的原因:一层一层向下计算透射波的走时,与初至波走时计算不同,不是采用一种一步式完整的波前扩展过程,而是采用逐层扩展的方式,这样能避免到达界面的部分走时不是直达波而是折射波的问题;因为当下伏地层速度高时,界面处的初至波中必然包括着下伏高速层上传的首波信息,而该信息并不是透射波的走时。关于该问题,在后续计算实例分析部分还将详细分析。
④ 计算界面反射波走时,采用如图 3所示的a→c→e→g→h的步骤:首先,计算震源点到达界面的入射波走时;其次,提取界面的入射波走时为初始条件并重新初始化整个模型;最后,计算界面到达海平面上各接收点的海底反射波走时。该方案的依据与上述②中阐述的实现步骤的基本依据一致。
⑤ 计算海底和海平面间自由表面多次波走时,采用类似于上述情况②的步骤,不断地在海底和海平面之间重复模型重新初始化和反射波走时计算的步骤即可。与反射波走时计算的实现策略的依据类似,此处多次反射波的走时计算实际上是不断重复计算海底和海平面间的反射波的走时,同样一个海底或海平面的反射波产生时刻即为入射波的到达时刻。
⑥ 计算海底和界面层间多次波走时,采用类似于上述情况③的步骤,不断地在海底和界面之间重复模型重新初始化和反射波走时计算的步骤即可。同样,与步骤⑤的多次反射波走时计算步骤类似,此处的不同在于计算的是层间(海底和界面间)的多次反射波走时。
综上所述,分别采用上述①-⑥各自的计算步骤,并在每个步骤中均采用模型重新初始化结合快速推进法,即可完成各种波型的走时计算,并在此基础上开展射线路径的计算。
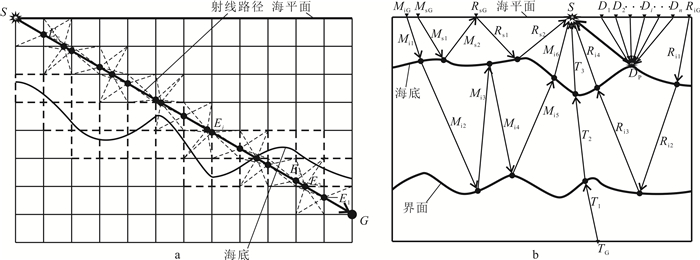
2.3 基于逆向追踪的各种波型射线路径计算基于常规线性插值法的基本思想,射线路径的计算是在走时计算完成后开始的,具体实现策略(图 4a)为:首先,确定射线路径的终点G位置,即从震源出发的射线最终要到达的位置;其次,根据公式(4)-(6),以及当前被算点周围的走时分布情况,计算当前被算点的上一级子震源点E1;然后,再把新算出来的上一级子震源点作为新的被算点,继续追踪其上一级子震源点E2;最后,如上不断追踪下去获得一系列子震源点Ei,并直到追踪到震源点S为止。
|
| a.常规线性插值法射线追踪步骤;b.本文多波型射线追踪步骤。S.震源;MiG.层间多次反射波接收点;RsG.海底反射波接收点;Di.绕射波接收点;G.接收点;MsG.海底多次反射波接收点;RiG.界面反射波接收点;Dp.绕射波绕射点;TG.透射波接收点。 图 4 各种类型的地震波的射线路径计算 Fig. 4 Computation of ray-path for different types of seismic waves |
|
|
上述步骤为常规线性插值法的射线路径计算的步骤,只能计算初至波的射线路径。以该步骤为基础,结合上述2.2节中各种波型走时计算的逆过程,即可获得各种波型射线路径的计算步骤(图 4b):①当计算点绕射波的射线路径时,采用(D1, D2, …, Di, …, Dn)→DP→S的实现步骤;②当计算海底反射波的射线路径时,采用RsG→Rs1→Rs2→S的实现步骤;③当计算到达界面的入射波(透射波)的射线路径时,采用TG→T1→T2→T3→S的实现步骤;④当计算界面反射波的射线路径时,采用RiG→Ri1→Ri2→Ri3→Ri4→S的实现步骤;⑤当计算海底和海平面间的自由表面多次波的射线路径时,采用MsG→Ms1→Ms2→RsG→Rs1→Rs2→S的实现步骤;⑥当计算海底和界面间的层间多次波的射线路径时,采用MiG→Mi1→Mi2 →Mi3→Mi4→Mi5→Mi6→S的实现步骤。上述各种波型的射线路径计算有一个共同点:始于接收点、终于震源点,这实际上是一步一步逆向追踪射线路径的策略,并且在每一步追踪进行之前,需要根据射线路径传播到的位置和方向来选择利用不同的走时信息作为已知条件。
综上所述,综合利用基于迎风差分思想的线性插值公式、基于多级次快速推进法的各种波型的走时计算和基于逆向追踪的各种波型的射线路径计算,即可获得各种波型的走时和射线路径。下面先对该方法进行精度分析,确认方法的有效性后,即可基于它们的计算结果,分析海洋复杂海底条件下的地震波的运动学特征。
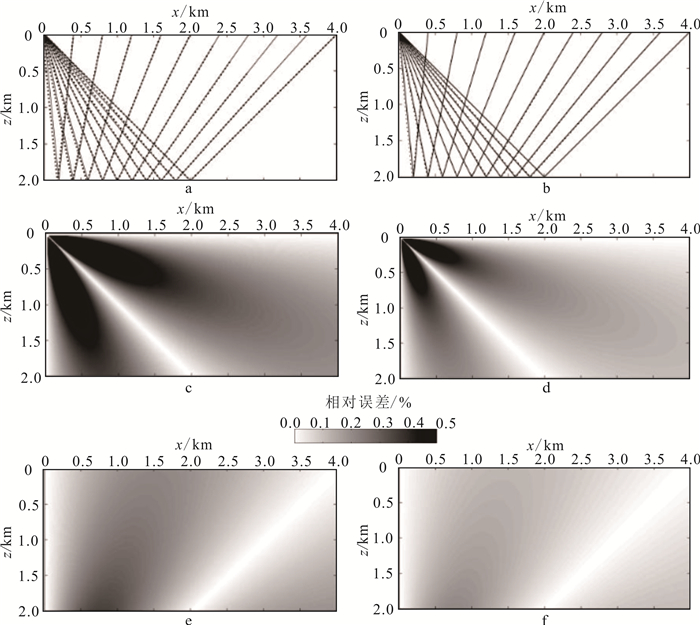
3 算法精度为了分析上述方法的计算精度,采用如图 5所示的均匀介质模型。模型大小为4.0 km×2.0 km,震源置于(0.0 km,0.0 km)处,网格间距分别采用20.0 m(图 5a、c、e)和10.0 m(图 5b、d、f)。对比图 5a、b可以发现:总体上本文方法的射线路径与精确射线路径有着很好的吻合程度;网格间距越小,数值计算出的射线路径与精确射线路径吻合得越好。对比图 5c、d可以发现:本文走时计算方法在震源附近计算误差较大,随着与震源距离的增加,走时计算误差逐渐减小;另外,网格间距越小,走时计算误差越小。对比图 5e、f也可以发现:网格间距越小,反射波走时计算误差越小。此外,对比图 5c、e或者对比图 5d、f可以发现,整体上反射波走时计算的精度远远高于入射波走时计算;这个现象与上述提及的离震源点越远的区域走时计算误差越小是统一的。
|
| a、b.精确射线路径(虚线)与本文方法射线路径(实线);c、d.入射波走时计算误差;e、f.反射波走时计算误差。a、c、e、h=20.0 m; b、d、f、h=10.0 m。 图 5 走时与射线路径计算的精度分析 Fig. 5 Accuracy analysis for the travel-time and ray-path |
|
|
通过以上精度分析可知:本文算法具有很好的计算精度,其计算结果能与解析值很好地吻合;同时,多级次算法随着级次的升高计算精度不断增高,说明本文算法的计算精度是随级次收敛的。
4 复杂海底各种地震波的运动学特征为了验证本文算法在面对复杂海底条件时的有效性,并分析各种类型地震波在复杂海底条件下的运动学特征,下面给出两个具体的计算实例。
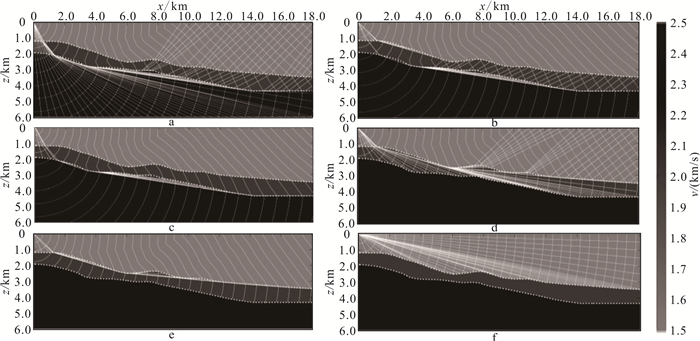
4.1 崎岖海底与海底大陡坡模型图 6给出的是一个崎岖海底与海底大陡坡模型,模型大小为18.0 km×6.0 km,整个介质由三层组成,第一层海水的速度为1 500.0 m/s,第二、三层介质速度分别为2 000.0 m/s、2 500.0 m/s。计算时网格间距为10.0 m,震源置于(0.0 km, 0.0 km)处。
|
| a.整个模型的初至波;b.到达海底的初至波(大部分由海底以下的所有高速层折射产生);c.到达界面上的初至波;d.到达整个界面上的入射波(透射波);e.到达海底的初至波(大部分由海底与界面间的高速层折射产生);f.到达整个海底的入射波(直达波)。v.地震波传播速度。 图 6 崎岖海底与海底大陡坡模型中初至波和入射波(透射波)的走时与射线路径分布 Fig. 6 Contours of travel-time and ray-paths of the first-arrival, refracted and incident (transmitted) waves superimposed on a model with rugged seabed and steep seabed slope |
|
|
分析图 6a可以发现:当地震波传到海底时,由于海底地层地震波速度比海水速度大,因此会在海底以下地层产生明显的折射波,图 6a中海平面上炮检距大于9.0 km的范围初至波基本都由该折射波构成。分析该图 6b、c可以发现,到达海底和界面上的初至波大部分由海底或界面以下高速层产生的折射波构成。图 6d给出了仅在界面以上进行走时和射线路径计算的结果,分析该结果可以得出到达整个界面的完整的入射波(透射波),而海底上到达的明显是来自海底和界面间的高速层的折射波(图 6e)。图 6f给出了仅在海水中进行走时和射线路径计算的结果,分析该结果可以得出到达海底的完整的入射波(直达波)。通过上述的分析可以得出如下结论:如果采用常规算法不加控制,在整个模型中进行走时和射线路径计算(图 6a),那么到达海底或地下界面处的波型大部分由来自更深层的折射波构成(图 6b、c、e);但是,如果对计算空间加入指向性的特殊控制(图 6d、f),就可以得到到达指定界面的入射波(透射波或直达波)。上述这一结论,对于计算反射波或者多次反射波的走时值时尤为重要,因为我们首先必须计算出反射界面上精确的入射波,并要尽可能地屏蔽掉到达反射界面的来自下伏高速地层的折射波。
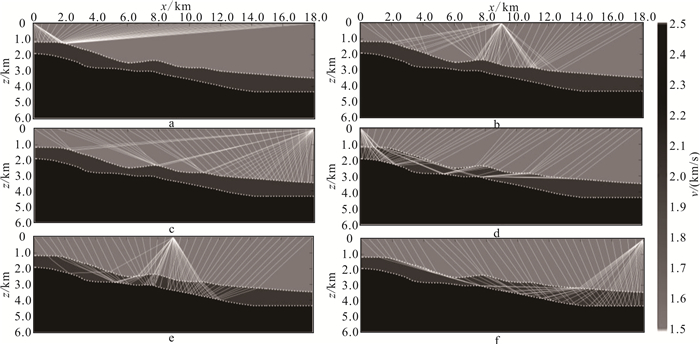
图 7给出了与图 6相同的模型中震源置于不同位置时海底和海底以下一个界面反射波的射线路径分布。在此,首先需要说明:此处在计算反射波之前的海底和界面上的入射波分布采用的是图 6f、d的计算结果,而并非直接在图 6a的计算结果中直接提取到达海底和界面的初至波。这点与地震波传播的基本物理事实是吻合的,即产生反射波的时刻是反射界面上入射波(透射波或直达波)到达的时刻,而非初至波(折射波)到达的时候。分析图 7可以发现:①对于大陡坡模型,当震源置于不同位置时,反射波对海底和界面的覆盖程度不同(图 7a-f);震源置于陡坡的倾斜下降方向时反射波对地下反射界面的覆盖范围大(图 7c、f),而在陡坡的倾斜上升方向的覆盖范围小(图 7a、d);②对于大陡坡模型,当海底和海底以下地层的坡度很大时,同时震源也置于陡坡的倾斜上升方向时,反射波将会传播到距离震源点很远的位置,即地下某一反射点的反射波需要在距离反射点的很大炮检距范围外才能被接收到(图 7a、d)。实际上,上述发现对于大陡坡复杂海底条件下地震数据采集观测系统的设计和地震数据处理中偏移成像孔径的选择具有重要意义,其可以提供定量化的参考数据。
|
| a—c.震源分别置于(0.0 km, 0.0 km)、(9.0 km, 0.0 km)、(18.0 km, 0.0 km)时海底产生的反射波;d—f.震源分别置于(0.0 km, 0.0 km)、(9.0 km, 0.0 km)、(18.0 km, 0.0 km)时界面产生的反射波。 图 7 崎岖海底与海底大陡坡模型中反射波的射线路径分布 Fig. 7 Ray-paths of the reflected waves superimposed on the model with rugged seabed and steep seabed slope |
|
|
图 8给出了与图 6相同的模型中震源置于不同位置时海水中和海底以下某地层中的多次反射波的射线路径分布。分析图 8可以发现:①当崎岖海底存在时,海底的多次波的传播路径非常复杂,一些从震源点传出的经过多次反射后的波会传播到距离源点很远距离的位置,而有些则经过多次反射后被传回到源点附近区域;②在海平面附近的一条测线上,不同区域接收到的多次波的发育程度明显不同。实际上,这些多次波存在的现象会让多次波消除问题变得非常复杂和困难,但是却可以为多次波利用(多次波成像)提供一些参考信息。

|
| a—c.震源分别置于(0.0 km, 0.0 km)、(9.0 km, 0.0 km)、(18.0 km, 0.0 km)时海底和海平面间产生的自由表面多次反射波;d—f.震源分别置于(0.0 km, 0.0 km)、(9.0 km, 0.0 km)、(18.0 km, 0.0 km)时海底和界面间产生的层间多次反射波。 图 8 崎岖海底与海底大陡坡模型中多次反射波的射线路径分布 Fig. 8 Ray-paths of the multiple superimposed on the model with rugged seabed and steep seabed slope |
|
|
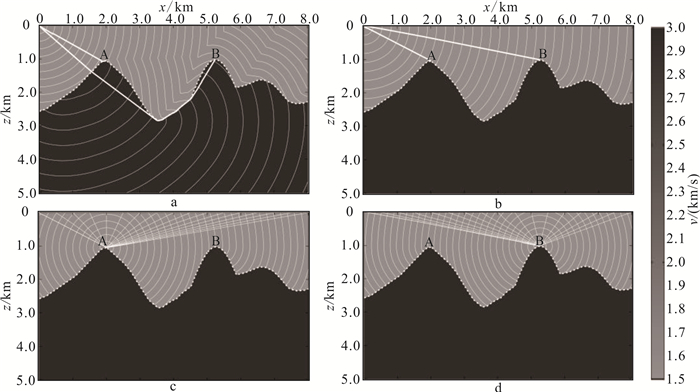
图 9给出的是一个海底火山模型,模型的大小为8.0 km×5.0 km,模型由速度分别为1 500.0 m/s的海水和3 000.0 m/s的海底以下地层组成,模型中有两座海底火山,山顶坐标分别为(2.0 km,1.0 km)和(5.26 km,1.00 km),在此分别设置它们为绕射点A和绕射点B。计算网格间距为10.0 m,源点置于(0.0 km,0.0 km)处。
|
| a.整个模型中的初至波;b.海水中传播的直达波;c、d.海水中传播的绕射波。 图 9 海底火山模型中初至波、直达波和绕射波的走时和射线路径分布 Fig. 9 Travel-time contours and ray-paths of the first arrivals, direct and diffracted waves superimposed on a model with submarine volcano |
|
|
对比图 9a、b可以发现:①初至波的传播路径非常复杂,介质的复杂性造成了初至波信息中包含丰富的折射波信息,而直达波传播路径相对简单一些;②到达点绕射点A的初至波路径与直达波是一致的,但是到达点绕射点B的却完全不一样,到达绕射点B的初至波是从震源点出发后穿越海底以下的高速层后才到达绕射点B(图 9a),而直达波则直接从震源点出发到达绕射点B(图 9b)。实际上,这种现象对绕射波的走时和射线路径的计算影响非常大。图 9c、d分别给出绕射点A和B的绕射波的走时和射线路径分布,这里首先需要特别说明:根据上面初至波和直达波的对比分析,当计算绕射波的入射波时绕射点A可以直接采用初至波,而绕射点B则不行,其需要采用直达波。这警示我们:当采用绕射波通过绕射叠加对特殊地质体(如海底火山口)进行成像时,在对成像质量有重要影响的射线追踪环节要非常小心(因为一般成像算法中,采用的是初至波,而非直达波),否则计算结果将不正确,同时正演计算内容部分也不符合地震波传播的物理规律。
5 讨论与结论围绕复杂海底条件下各种地震波的射线追踪及运动学特征分析问题,本文主要展开了如下两个方面的研究工作:①基于融入迎风差分思想的线性插值公式和多级次的快速推进法,实现了针对复杂海底条件下的各种类型的地震波的走时与射线路径计算;②以第①方面的方法为基础,计算了两个有代表性的复杂海底模型中的初至波、折射波、入射波(透射波)、反射波、多次反射波、直达波、绕射波的走时和射线路径,并基于这些计算结果分析了复杂海底条件下各种地震波的传播规律。
通过对上述两方面工作的研究,可以得出如下结论:
1) 快速推进迎风插值法兼顾了快速推进迎风差分法无条件稳定性的优势,以及线性插值法计算简洁、灵活、精度高、适应于任意复杂网格的优势,算法可以获得精度较高的计算结果。
2) 算法的计算误差分布与距震源点的距离、网格间距、入射与反射等因素密切相关,随着距震源距离的增加误差逐渐降低,网格间距越小误差越小,反射波计算的误差远小于入射波的误差。
3) 基于走时和射线路径计算的复杂海底条件下地震波运动学特征分析结果表明,复杂海底条件下初至波的传播规律非常复杂,海底及海底以下高速界面处存在明显的折射波,它们的存在会对入射波(直达波或透射波)、反射波、绕射波等走时和射线路径的计算造成重要影响,更会对采用初至波走时进行偏移成像的实现策略产生重要影响,因此很有必要进行屏蔽折射波初至走时的偏移成像算法研究。
4) 在海洋水深剧变的大陡坡地质条件下,海底或海底以下界面的反射波会传播到与反射点(或震源点)水平相距很远的位置,因此在对大陡坡模型进行偏移成像时应尽可能多考虑远道数据或加大偏移孔径,这样可能会得到很好的效果,并且在这些区域进行数据采集时可以考虑增大数据采集的长度(大偏移距)和范围。
5) 当存在明显较浅水深处如海底火山的绕射地质构造时,考虑绕射波的影响是很有必要的,同时再进行绕射波的走时和射线路径计算时,需要特别小心初至波并不能完全直接作为入射波,否则计算结果会不符合地震波传播的基本物理规律。
6) 上述3)-5)的结论是在两个有代表性的具体模型实例中、对地震波在复杂海底条件下的传播特征进行分析总结而得出的一些特定现象,其并非被理论证明了的固定不变且完全通用的物理定律,虽然这些现象的存在对于研发有针对性的复杂海底条件下地震数据采集观测系统的设计和地震数据处理的偏移成像技术意义重大,但是这些现象的存在与否和程度大小与介质参数的分布特征密切相关,所以其不能被作为一种普适的规律而被千篇一律的应用。
| [1] |
Valente L S S, Santos H B, Costa J C, et al. Time-to-Depth Conversion and Velocity Estimation by Image-Wavefront Propagation[J]. Geophysics, 2017, 82(6): U75-U85. DOI:10.1190/geo2016-0570.1 |
| [2] |
Huang Xingguo, Sun Hui, Sun Jianguo. Born Modeling for Heterogeneous Media Using the Gaussian Beam Summation Based Green's Function[J]. Journal of Applied Geophysics, 2016, 131: 191-201. DOI:10.1016/j.jappgeo.2016.06.004 |
| [3] |
Julian B R, Gubbins D. Three-Dimensional Seismic Ray Tracing[J]. Geophysics, 1977, 43: 95-113. |
| [4] |
Moser T J. Shortest Path Calculation of Seismic Rays[J]. Geophysics, 1991, 56(1): 59-67. DOI:10.1190/1.1442958 |
| [5] |
Vidale J. Finite-Difference Calculation of Travel Times[J]. Bull Seism Soc Am, 1988, 78(6): 2062-2076. |
| [6] |
Hao Q, Alkhalifah T. An Acoustic Eikonal Equation for Attenuating Transversely Isotropic Media with a Vertical Symmetry Axis Acoustic Attenuating VTI Media[J]. Geophysics, 2017, 82(1): C9-C20. |
| [7] |
Waheed U B, Alkhalifah T. A Fast Sweeping Algorithm for Accurate Solution of the Tilted Transversely Isotropic Eikonal Equation Using Factorization[J]. Geophysics, 2017, 82(6): WB1-WB8. DOI:10.1190/geo2016-0712.1 |
| [8] |
Hu J, Cao J, Wang H, et al. 3D Travel-Time Computation for Quasi-P-Wave in Orthorhombic Media Using Dynamic Programming[J]. Geophysics, 2017, 83(1): C27-C35. |
| [9] |
Asakawa E, Kawanaka T. Seismic Ray Tracing Using Linear Traveltime Interpolation[J]. Geophysical Prospecting, 1993, 41(1): 99-111. DOI:10.1111/gpr.1993.41.issue-1 |
| [10] |
Schneider W A J, Ranzinger K A, Balch A H, et al. A Dynamic Programming Approach to First Arrival Traveltime Computation in Media with Arbitrarily Distributed Velocities[J]. Geophysics, 1992, 57(1): 39-50. |
| [11] |
Han S, Zhang W, Zhang J. Calculating QP-Wave Traveltimes in 2-D TTI Media by High-Order Fast Sweeping Methods with a Numerical Quartic Equation Solver[J]. Geophysical Journal International, 2017, 210(3): 1560-1569. DOI:10.1093/gji/ggx236 |
| [12] |
Vinje V, Iversen E, Gjoystdal H. Traveltime and Amplitude Estimation Using Wavefront Construction[J]. Geophysics, 1993, 58(8): 1157-1166. DOI:10.1190/1.1443499 |
| [13] |
Leidenfrost A, Ettrich N, Gajewski D, et al. Comparison of Six Different Methods for Calculating Traveltimes[J]. Geophysical Prospecting, 1999, 47: 269-297. DOI:10.1046/j.1365-2478.1999.00124.x |
| [14] |
徐涛, 徐果明, 高尔根, 等. 三维复杂介质的块状建模和试射射线追踪[J]. 地球物理学报, 2004, 47(6): 1118-1126. Xu Tao, Xu Guoming, Gao Ergen, et al. Block Modeling and Shooting Ray Tracing in Complex 3-D Media[J]. Chinese Journal of Geophysics, 2004, 47(6): 1118-1126. DOI:10.3321/j.issn:0001-5733.2004.06.027 |
| [15] |
Sun Jianguo, Sun Zhangqing, Han Fuxing. A Finite Difference Scheme for Solving the Eikonal Equation Including Surface Topography[J]. Geophysics, 2011, 76(4): T53-T63. DOI:10.1190/1.3580634 |
| [16] |
Zhou B, Greenhalgh S. Shortest Path' Ray Tracing for Most General 2D/3D Anisotropic Media[J]. Geophysics, 2005, 2: 54-63. |
| [17] |
Sethian J A, Popovici A M. 3-D Traveltime Computation Using the Fast Marching Method[J]. Geophysics, 1999, 64: 516-523. DOI:10.1190/1.1444558 |
| [18] |
熊金良, 李国发, 王濮, 等. 地震波走时计算的逆风差分算法[J]. 物探化探计算技术, 2004, 26(4): 295-298. Xiong Jinliang, Li Guofa, Wang Pu, et al. Upwind Finite-Difference Solution of Eikonal Equation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2004, 26(4): 295-298. DOI:10.3969/j.issn.1001-1749.2004.04.002 |
| [19] |
Rawlinson N, Sambridge M. Multiple Reflection and Transmission Phases in Complex Layered Media Using a Multistage Fast Marching Method[J]. Geophysics, 2004, 69(5): 1338-1350. DOI:10.1190/1.1801950 |
| [20] |
Li Zhenchun, Liu Yulian, Zhang Jianlei, et al. Finite-Difference Calculation of Traveltimes Based on Rectangular Grid[J]. Acta Seismologica Sinica, 2004, 26(6): 644-650. |
| [21] |
Liu Zhenwu, Sun Yonghe, Sun Jianguo, et al. A Method for Computing the 2D Seismic Traveltime Including the Surface Topography by Combining the Linear Interpolation and the Narrow Band Technique[C]//International Geophysical Conference & Exposition. Beijing: CPS/SEG, 2009: 130.
|
| [22] |
Wang Huazhong, Kuang Bin, Ma Zaitian, et al. 3-D Traveltime Calculation in Arbitrary Velocity Distribution with Dynamic Programming Approach[J]. Chinese Journal of Geophysics, 2001, 44. |
| [23] |
孙章庆, 孙建国, 韩复兴. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算[J]. 地球物理学报, 2009, 52(11): 2846-2853. Sun Zhangqing, Sun Jianguo, Han Fuxing. Traveltimes Computation Using Linear Interpolation and Narrow Band Technique Under Complex Topographical Conditions[J]. Chinese Journal of Geophysics, 2009, 52(11): 2846-2853. |
| [24] |
孙章庆.起伏地表条件下的地震波走时与射线路径计算[D].长春: 吉林大学, 2011. Sun Zhangqing. The Seismic Traveltimes and Raypath Computation Under Undulating Earth's Surface Condition[D]. Changchun: Jilin University, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10183-1011105855.htm |
| [25] |
高亮, 李幼铭, 陈旭荣, 等. 地震射线辛几何算法初探[J]. 地球物理学报, 2000, 43(3): 402-410. Gao Liang, Li Youming, Chen Xurong, et al. An Attempt to Seismic Ray Tracing with Symplectic Algorithm[J]. Chinese Journal of Geophysics, 2000, 43(3): 402-410. DOI:10.3321/j.issn:0001-5733.2000.03.014 |
| [26] |
Bancroft J C, Du Xiang. The Computation of Traveltimes When Assuming Locally Circular or Spherica Wavefronts[C]//76th Annual International Meeting. New Orleans: SEG, 2006: 2231-2235.
|
| [27] |
Kononov A, Gisolf D, Verschuur E. Application of Neural Networks to Travel-Times Computation[C]//77th Annual International Meeting. San Antonio: SEG, 2007: 1785-1789.
|
| [28] |
Bóna A, Slawinski M A, Smith P. Ray Tracing by Simulated Annealing:Bending Method[J]. Geophysics, 2009, 74(2): T25-T32. DOI:10.1190/1.3068006 |
| [29] |
Huang X, Greenhalgh S. Linearized Formulations and Approximate Solutions for the Complex Eikonal Equation in Orthorhombic Media and Applications of Complex Seismic Traveltime[J]. Geophysics, 2018, 83(3): C115-C136. DOI:10.1190/geo2017-0620.1 |



