0 引言
各向异性走时计算是全波形反演和层析成像等各向异性地震模拟和成像技术的基础。走时计算方法的选择需要综合考虑算法的精度、效率及稳定性等因素。层析成像是一种层状介质速度和各向异性参数建模方法,其结果往往用于为全波形反演提供初始模型,但与波形反演中的旅行时信息不同,其核心之一就是模型初至波走时计算。层析成像是一种迭代反演算法,需要通过正演结果与实际数据的残差不断调整初始模型。走时计算的精度、效率与稳定性和层析成像计算的精度、效率与稳定性息息相关。因此,高效高精度且稳定的走时计算方法是各向异性介质偏移和层析成像等建模技术实现的关键。
传统的走时计算方法是射线追踪方法,包括试射法(shooting trace)和弯曲法(bending trace)[1-3]。这两种方法的理论基础是费马原理。试射法是初值问题,即将固定的震源点和检波点作为问题的初值,通过扰动入射角直至射线经过检波点;而弯曲法是极值问题,即先初始化炮检点之间的射线路径,通过不断扰动射线路径求取最小走时。这两种方法在传统的地震勘探中普遍应用,但由于其求取的走时只对应单炮单道问题,应用于多炮多道数据计算时效率偏低。
射线追踪技术结合图形理论和复杂网格技术,在局部进行射线追踪。主要衍生出的方法有插值法和最短路径射线追踪算法等。插值法[4-8]运用网格模型来计算网格边界插值点的走时和确定射线路径。该方法精确稳定,对复杂介质有较好的效果;但在模型速度变化较大的区域,其合理性有待商榷。最短路径射线追踪方法[9-10]很好地结合了图形理论和地震波射线理论,计算精度较高,相对于传统射线追踪方法可以更好地解决复杂介质模型问题;但网络计算量较为庞大,限制了其实际应用。
走时计算的另一种方法是波前面追踪,其包括两种方法。一种方法是基于运动学射线追踪系统的波前构建法;另一种方法是通过求解波动方程WKB(Wentzel,Kramers和Brillouin)展开的零阶近似[11],即程函方程,求取速度场,而后从检波点延时间场梯度方向获得射线路径。最早出现的解程函方程的方法是Vidale法[12],该方法基于矩形网格离散模型,从震源点出发,以矩形形式逐层向外求取各点走时。为了保证因果关系,每次从最小走时网格点向外计算。该方法的主要优点是计算速度非常快,并且与传统射线追踪方法相比,阴影区问题得到了很好的解决;局限性是当局部速度变化过大时计算可能出现不稳定现象,而且其网格推进方式不符合物理规律,因此只能应用于初至波走时计算,不适用于反射波。
后来衍生出的方法根据波前扩展方法的不同可分为迎风差分法[13]、波前扩展法、快速推进法(fast matching method, FMM)、波前整体推进法、辛几何法[14-15]等。FMM[16-19]是至今为止效率和精度最高的方法。
FMM是由Sethian[20]于1996年提出的,该方法的核心是构建有限差分格式求解程函方程,运用窄带思想完成波前推进。由于方法中的差分格式为迎风差分格式,满足“熵”条件,因此该方法在复杂模型下具有较高的稳定性。FMM的基本方法和实现策略在很多领域(医学成像、光刻技术、沉积学相关问题等[20-21])得到了广泛的应用。1999年,Sethian[21]将FMM应用到地球物理领域后,该方法得到了很好的发展[22-26]。目前,该方法在各向异性走时层析成像中的射线追踪计算、Kirchhoff深度偏移走时计算等建模计算中广泛应用。
国内对于各向异性走时计算的方法研究起步较晚,其中以何樵登[27-29]为代表,在各向异性射线理论正演模拟方面做了较多的研究。张文生等[27]在1997年对横向各向同性介质进行了研究。董良国等[28]在1999年对横向各向同性介质中的P波、SV波及SH波做了研究,并得到了3种波的速度变化规律。孟庆生等[29]在2002年对比研究了P波和SV波在横向各向同性介质中的传播规律。张建中[30]在2005年研究了三维介质的射线追踪和走时计算。郝奇[31]在2010年实现了具有垂直对称轴的横向各向同性(VTI)层状模型块状建模法,推导了VTI介质倾斜界面情况下的Snell定律,模拟了反射波射线追踪的方法。白海军等[32]在2011年将波前构建与射线追踪结合,实现了具有倾斜对称轴的横向各向同性(TTI)介质波前构建法的射线追踪。李晓玲等[13]在2013年研究了起伏层状横向各向同性(TI)介质中多次波的射线追踪。现阶段国内对波前面追踪方面的研究较少,本文针对各向异性介质层析成像中的走时计算问题,实现了非均匀网格化VTI介质地震波走时的计算。
在各向异性介质中,走时计算不只依赖速度场,随着各向异性参数的增多,构建迎风差分格式求取走时也越来越困难。本文主要利用扰动理论及泰勒公式将VTI介质程函方程展开,完成了对VTI介质程函方程的降维处理。对降维后的VTI介质程函方程构建迎风差分格式并分别进行求解,完成单点走时计算。结合窄带推进理论,构成了各向异性的波前面追踪走时计算方法。首先对均匀弱VTI各向异性介质进行计算并与解析值相减评估其误差;然后为验证其稳定性和有效性,又计算了VTI各向异性层状介质模型的走时;最后以盐丘模型作为测试模型,进行了走时正演试算。
1 算法原理和实现 1.1 VTI介质程函方程展开在VTI介质中,声波近似的程函方程为以下格式[33]:
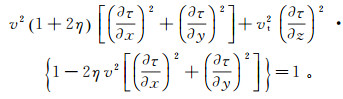 (1)
(1) 式中:τ(x, y, z)是震源到坐标点(x, y, z)的走时;vt和v分别为介质速度和NMO(normal moveout,NMO)速度;η为各向异性参数。二维情况下,方程(1)可以写为
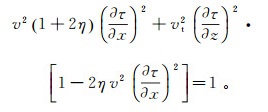 (2)
(2) 此四次方程的非线性程度强于各向同性和椭圆各向异性的程函方程,因此VTI介质程函方程需要更为复杂的有限差分近似。为解此方程,我们可以利用扰动理论[34],运用一系列线性方程逼近公式(2)。假设η是常量且较小,我们可以将τ写为一系列关于η的泰勒公式[35]:
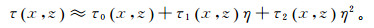 (3)
(3) 式中,τ0、τ1、τ2是式(2)中各向异性参数η不同阶数项的系数。考虑到实用性,只在此进行三项展开。将假设解式(3)代入式(2)中,我们得到一个较长的公式。设η=0,得到0次项公式:
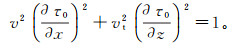 (4)
(4) 方程(4)是椭圆各向异性介质的程函方程,独立参数η相同阶数项的系数相等。首先计算一次η项的系数,将一次η项系数相等的公式通过式(4)简化后得到
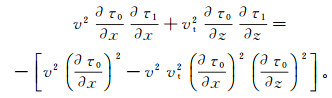 (5)
(5) 同理,可得到η平方项的系数公式:
 (6)
(6) 为求取VTI介质走时的解析解,首先从均匀介质背景速度模型出发。为求取式(4)的解析解,设η=0,此时背景模型是椭圆各向异性介质。在这种情况下,震源位于x=0、z=0处的走时解析解如下:
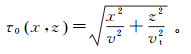 (7)
(7) 该结果满足方程(4)。通过式(7)可求出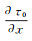
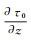
 (8)
(8) 同理,计算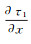
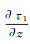
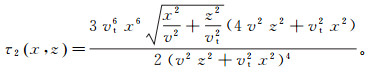 (9)
(9) 将式(7)、(8)、(9)代入式(3)中,即可求取该点走时的解析值。
1.3 非均匀介质FMM单点走时计算在均匀介质中,上述公式的推导是基于VTI介质声波近似程函方程(1)进行的,因此得到的近似结果描述的是介质的群速度。而在非均匀介质正方形网格条件下,由于无法确定指定网格中的震源位置,因此上述公式不能简单地应用于非均匀介质走时计算中。
对于此种情况,我们引入FMM。FMM的基本原理是将程函方程的时间梯度项近似为满足波前传播“熵守恒”理论的数值离散形式,通过数值计算来求取黏滞解。这种离散形式为
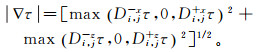 (10)
(10) 式中:Di, j-xτ、Di, j+xτ、Di, j-zτ、Di, j+zτ分别为在坐标(i, j)网格处x和z方向走时函数τ向前、后方向的差分算子,x、z表示差分方向,“+”为前方,“-”为后方,具体为
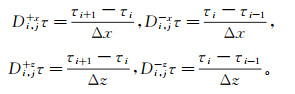 (11)
(11) 该方法对于波前传播过程中尖角拐角和拓扑结构变化等问题的有效性在文献[5]中有较为详细的论述。在VTI介质情况下,由于程函方程变为四次方程,按照常规思路, 直接对式(2)进行离散不仅解方程的难度较大,在选择黏滞解时也会造成较大干扰。为解决此问题,首先,对公式(4)(5)(6)中的走时梯度项分别进行离散化,即:
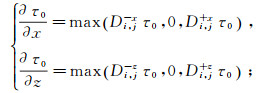 (12)
(12) 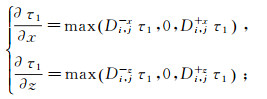 (13)
(13)  (14)
(14) 然后,将式(12)代入式(4)中,通过计算可以求出点(i, j)处的τ0(i, j)、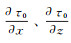
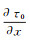
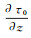
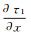

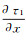

FMM的实现策略主要为“熵守恒”理论,该理论可以这样理解:传播的初至波波前可以看做在纸上燃烧的火焰。如果纸上的某个位置被火焰燃烧了,那么这一位置将一直保持着被烧过的状态,后续不会再被燃烧。类比于初至波在空间中的传播,即初至波波前不会两次经过同一个点,每个点的走时是关于位置的单值函数。同时由于波是单向传播的,总是由走时较小点传播至走时较大点,因此,1.3节中所述单点走时计算的循环起点应位于走时最小值点。
文中采用了窄带技术作为波前模拟技术,通过排序选择窄带内走时最小的点作为延拓点,再通过对网格节点属性的设定来“储存”已经完成计算的网格节点,最后通过窄带内网格节点的走时更新来模拟波前的演化。整体步骤可分为初始化和循环两部分。
1) 初始化
根据上文所述,将整个网格空间分为接受点、窄带点和远离点3种属性。接受点为网格点中已经完成走时计算的点;窄带点为近似波前上的点;远离点是指除了接受点和窄带点之外的所有点。接受点初始化为震源点,其走时值初始化为τ(is, js)=0。窄带点初始化为震源节点周围的4个节点,其走时为
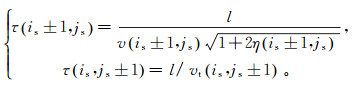 (15)
(15) 式中:l为网格节点的间隔长度;v(is±1, js)、vt(is, js±1)和η(is±1, js)分别为对应网格点处的NMO速度、速度,以及各向异性参数η的值。远离点的走时值初始化为绝对大的值,远大于所有可能算出的走时值。
2) 循环
循环过程分为以下4个步骤。
① 从窄带内选取最小走时点τ(imin, jmin)。
② 将点(imin, jmin)的属性改为接受点。
③ 对点(imin, jmin))的4个临近点的属性进行判断:如果为接受点则走时值保持不变;如果为窄带点,则运用1.3节中所述的单点走时计算方法更新其走时;如果为远离点,则将其属性修改为窄带点,并运用1.3节中所述的单点走时计算方法计算其走时。
④ 判断窄带是否为空,如果窄带为空则终止循环,否则跳回①继续计算。
2 算法精度及稳定性分析 2.1 算法精度由于复杂界面非均匀模型的走时解析值较难求取,为了便于分析本文方法的正确性及精度,我们首先用一个水平界面均匀弱VTI各向异性模型计算走时,并用走时的解析值与之对比(由于后文复杂模型通过速度及各向异性参数δ和ε定义,因此本文中所有模型均用vt、ε和δ 3个参数进行定义,并通过公式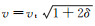
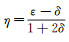
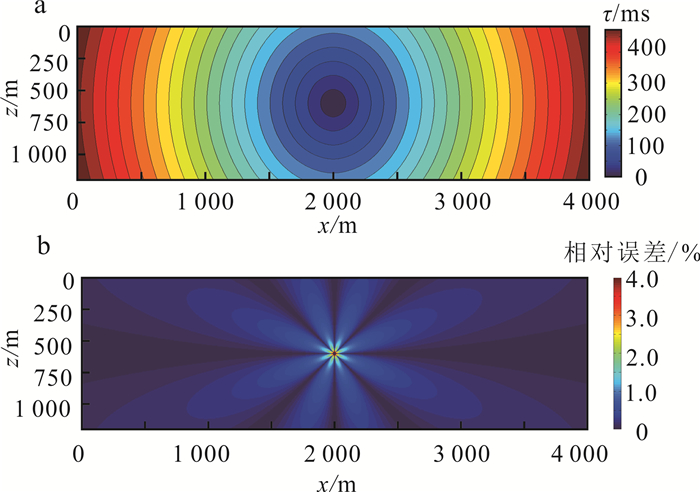
水平界面均匀介质模型的大小为4 000 m×1 200 m,介质速度为4 000 m/s,各向异性参数δ=0.1,ε=0.1,网格间距为5 m,震源位置为(2 000 m, 600 m)。使用本文方法的走时计算结果见图 1a。走时解析值通过1.2节中叙述的方法求取,将走时计算值(图 1a)与解析值相减后得到误差,误差占解析值的比例(相对误差)见图 1b。
|
| 图 1 水平界面均匀弱VTI各向异性模型走时计算结果(a)及相对误差(b) Fig. 1 Travel time calculation results (a) and relative error (b) of horizontal interface weak VTI anisotropic model |
|
|
由图 1b可知:在震源附近走时计算结果的相对误差较为明显,主要分布在1.5%~4.0%之间,其原因是差分网格长度太大,对震源处的差分网格进行进一步细分,该现象会有所改善;在远偏处误差趋于稳定,相对误差稳定在0.5%以下。
2.2 算法稳定性为了验证本算法对复杂介质模型的稳定性和有效性,分别选取双层、多层和盐丘介质模型进行试算。
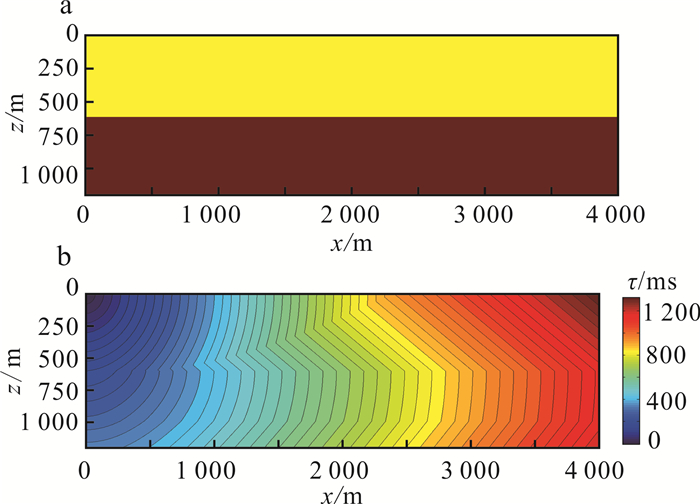
2.2.1 双层介质模型对双层VTI各向异性介质模型进行数据试算。该模型的大小为4 000 m×1 200 m,震源点位于坐标(0, 0)处。模型参数见表 1,模型结构见图 2a,使用本文方法试算的走时结果见图 2b。
| h/m | v/(m/s) | δ | ε | |
| 第一层 | 600 | 2 500 | -0.03 | 0.11 |
| 第二层 | 1 200 | 4 000 | 0.73 | 0.33 |
| 注:h.深度。 | ||||
|
| 图 2 双层VTI各向异性介质模型(a)及走时试算结果(b) Fig. 2 Two-layer VTI anisotropic media model (a) and travel time trial results (b) |
|
|
地震观测点最先接收到的波称为初至波。在层状介质中,随着偏移距及入射角的增大,下层介质的折射波渐渐取代直达波被率先接收,在某节点产生“毛刺现象”。通过观察图 2b可以发现,第一层近偏处与均匀介质传播规律一致,随着偏移距增加,在坐标(500,600)处产生了“毛刺现象”,折射波取代了直达波率先被接收。
2.2.2 多层介质模型对多层VTI各向异性介质模型进行数据试算。该模型的大小为4 000 m×1 200 m,震源点位于坐标(0, 0)处。模型参数见表 2,模型结构见图 3a,使用本文方法试算的走时结果见如图 3b。
| h/m | v/(m/s) | δ | ε | |
| 第一层 | 500 | 3 370 | -0.035 | 0.110 |
| 第二层 | 800 | 3 930 | 0.730 | 0.334 |
| 第三层 | 1 000 | 4 350 | 0.148 | 0.091 |
| 第四层 | 1 200 | 4 970 | -0.003 | 0.056 |

|
| 图 3 多层VTI各向异性介质模型(a)及走时试算结果(b) Fig. 3 Multi-layer VTI anisotropic media model (a) and travel time trial results (b) |
|
|
由于多层模型的速度变化与双层模型相比较慢,因此其等时线变化较为平缓,近偏处对速度突变层的表现不明显。但在偏移距1 000~2 500 m处,我们可以较清晰地分辨出3个层的折射波对于初至走时的影响,偏移距2 500 m之后,第二、三层的折射波渐渐被第四层的折射波所取代,并体现于等时线上。
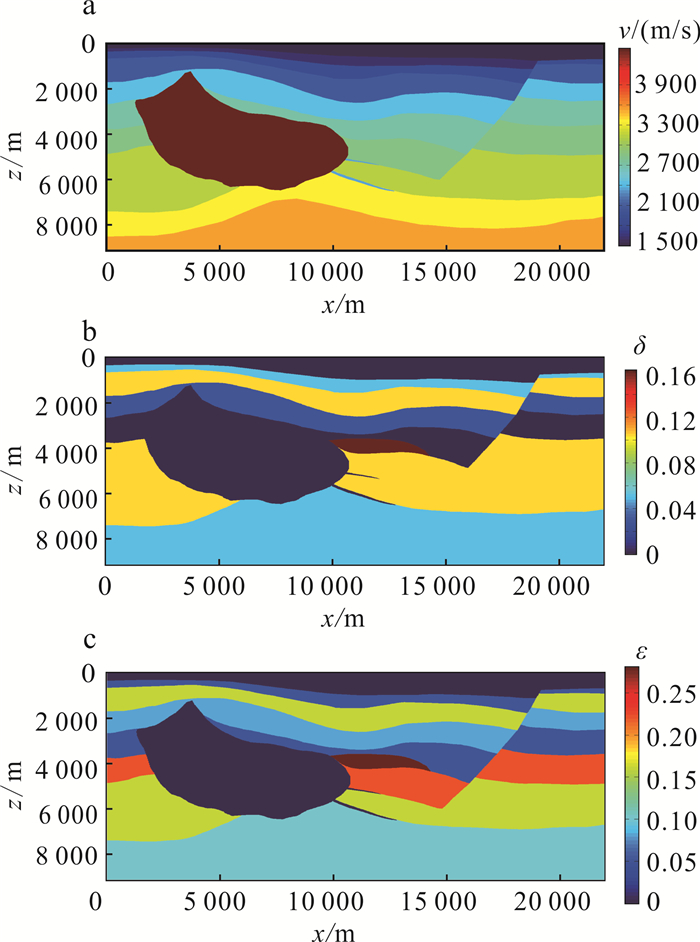
2.2.3 盐丘介质模型对盐丘介质模型进行数据试算。该模型大小为21 940 m×9 144m,模型速度及各向异性参数结构如图 4所示。
|
| 图 4 盐丘介质模型速度及各向异性参数δ、ε模型 Fig. 4 Velocity model and anisotropic parameter δ、ε model of salt mound medium model |
|
|
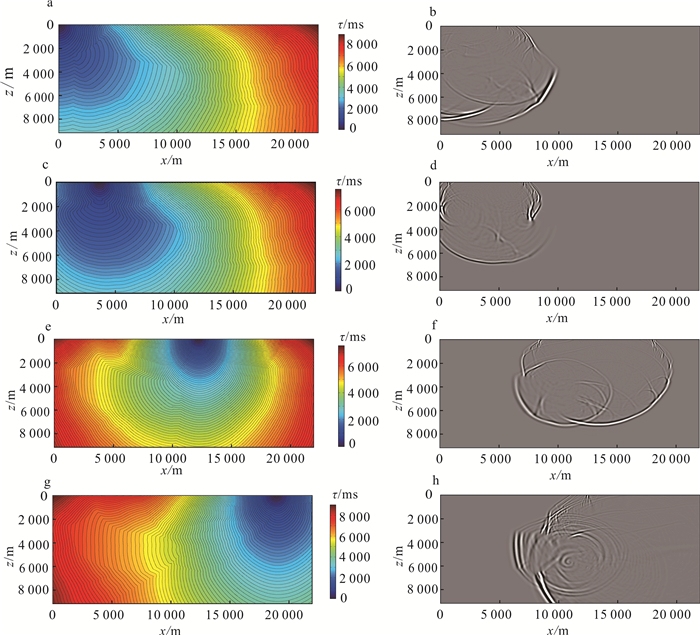
该模型x轴2 000~10 000 m处为一较明显的高速体,15 000~19 000 m处为一断层,两个比较突出的结构体之间是由起伏层状介质连接(图 4a)。在层状地质体中,x轴10 000~14 000 m、深度约4 000 m处有一强各向异性体(图 4b、c)。我们在模型x轴方向0、3 650、12 200、19 000 m处分别设置炮点,观察其在特殊地形下的试算效果,并与有限差分正演的波场快照进行对比,结果如图 5所示。
|
| a. 0 m炮点处走时;b. 0 m炮点处3 000 ms波场快照;c. 3 650 m炮点处走时;d. 3 650 m炮点处2 000 ms波场快照;e. 12 200 m炮点处走时;f. 12 200 m炮点处4 000 ms波场快照;g. 19 000 m炮点处走时;h. 19 000 m炮点处5 500 ms波场快照。 图 5 盐丘介质模型走时试算结果及波场快照 Fig. 5 Travel time trail results and wavefield snapshot of salt mound medium |
|
|
从图 5a可以看出,高速体对走时场的影响十分明显。通过与波场快照(图 5b)对比可以发现,排除波场快照中界面之间反射波的影响,3 000 ms等值线与波场快照中的波前面完全吻合。
由于图 5c中炮点位置位于高速体深度最小的地面投影处,因此选择2 000 ms的波场快照(图 5d)进行对比。可以看出:波场快照0~3 000 m深度处与等时线吻合;5 000 m以下受到高速体的影响,波场快照中波前发生分裂,但是最高能量的波前面与等时线依然吻合。
排除反射波的影响,从图 5e、f可以清晰地看到,不论是在深度0~3 000 m的层状介质处,还是在深度3 000~5 000 m的高速体和断层处,波场快照都与波前面清晰地吻合。
由于图 5g中震源点的位置是在断层正上方,为观察到高速体的影响,因此将波场快照的时间设置为5 500 ms(图 5h)。可以清晰地看到深度0~3 000 m的波前面与等时线吻合;而对于高速体,由于偏移距过大的原因,有限差分正演受到反射波、绕射波等因素的影响,波场快照中最高能量波前面较难分辨。
综上所述,经过多个模型的测试,本文提出的方法在不同地下构造及不同偏移距下的稳定性和准确性得到了较好的验证,其计算结果合乎地震波传播规律,能够准确地反映出地下介质的结构。
3 结论1) 本文将基于波前面追踪的走时计算方法引入各向异性介质走时计算当中,实现了网格化非均匀VTI介质走时计算。首先对程函方程中的走时参数τ进行展开,成功将四次方程分解为一个二次方程和两个一次方程;然后将各向同性快速匹配走时计算方法引入VTI介质中,对展开的VTI介质程函方程组进行离散化并求解,得到介质的走时。
2) 大量模型试算检验证明,本文提出的VTI介质声波走时计算方法是有效的,该方法的模型试算结果能够较好地反映出地下复杂介质中地震波的传播规律。虽然本文中用于试算的模型不能涵盖地下介质的所有情况,但本文中的计算方法可以适用于绝大部分随机不均匀分布的各向异性介质模型中。
3) 该方法大大提高了VTI各向异性介质走时计算的效率。对各向异性层析成像等处理具有重大意义,同时也可以为全波形反演提供更加高效的初始模型,在实际生产中具有重要的意义。
| [1] |
Um J, Thurber C. A Fast Algorithm for Two-Point Seismic Ray Tracing[J]. Bulletin of the Seismological Society of America, 1987, 77(3): 972-986. |
| [2] |
Moser T J, Nolet G, Snieder A R. Ray Bending Revisited[J]. Bulletin of the Seismological Society of America, 1992, 82(1): 259-288. |
| [3] |
Langan R T. Tracing of Rays Through Heterogeneous Media:An Accurate and Efficient Procedure[J]. Geophysics, 1985, 50(9): 1456-1465. DOI:10.1190/1.1442013 |
| [4] |
Dijkstra E W. A Note on Two Problems in Connection with Graphs[J]. Numerische Mathematics, 1959, 1(1): 269-271. |
| [5] |
孙章庆, 孙建国, 韩复兴. 复杂地表条件下基于线性插值和窄带技术的地震波走时计算[J]. 地球物理学报, 2009, 52(11): 2846-2853. Sun Zhangqing, Sun Jianguo, Han Fuxing. Traveltimes Computation Using Linear Interpolation and Narrow Band Technique Under Complex Topographical Conditions[J]. Chinese Journal of Geophysics, 2009, 52(11): 2846-2853. |
| [6] |
孙章庆, 孙建国, 岳玉波, 等. 基于快速推进迎风双线性插值法的三维地震波走时计算[J]. 地球物理学报, 2015, 58(6): 2011-2023. Sun Zhangqing, Sun Jianguo, Yue Yubo, et al. 3D Traveltime Computation Using Fast Marching Upwind Bilinear Interpolation Method[J]. Chinese Journal of Geophysics, 2015, 58(6): 2011-2023. |
| [7] |
李培明, 梅胜全, 马青坡. 一种改进的双线性插值射线追踪方法[J]. 石油地球物理勘探, 2013, 48(4): 553-558. Li Peiming, Mei Shengquan, Ma Qingpo. An Improved Bilinear Interpolation Traveltime Ray Tracing Method[J]. Oil Geophysical Prospecting, 2013, 48(4): 553-558. |
| [8] |
梅胜全, 邓飞, 钟本善, 等. 基于改进的双线性走时插值的三维射线追踪[J]. 物探化探计算技术, 2010, 32(2): 152-157. Mei Shengquan, Deng Fei, Zhong Benshan, et al. The 3D Ray Tracing Method Base on the Improved Bilinear Traveltime Interpolation[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(2): 152-157. DOI:10.3969/j.issn.1001-1749.2010.02.008 |
| [9] |
Alkhalifah T. Traveltime Computation with the Linearized Eikonal Equation for Anisotropic Media[J]. Geophysical Prospecting, 2000, 50(4): 373-382. |
| [10] |
Vidale J. Finite-Difference Calculation of Travel Times[J]. Bulletin of the Seismological Society of America, 1988, 78(6): 2062-2076. |
| [11] |
孙章庆, 孙建国, 韩复兴. 三维起伏地表条件下地震波走时计算的不等距迎风差分法[J]. 地球物理学报, 2012, 55(7): 2441-2449. Sun Zhangqing, Sun Jianguo, Han Fuxing. Traveltime Computation Using the Upwind Finite Difference Method with Nonuniform Grid Spacing in a 3D Undulating Surface Condition[J]. Chinese Journal of Geophysics, 2012, 55(7): 2441-2449. |
| [12] |
李兴旺, 白超英, 李晓玲. 四面体单元剖分下三维各向异性TI介质中多次波射线追踪[J]. 石油地球物理勘探, 2017, 52(1): 48-55. Li Xingwang, Bai Chaoying, Li Xiaoling. Multiples Raytracing in 3D Anisotropic TI Media with a Tetrahedron Cell Model[J]. Oil Geophysical Prospecting, 2017, 52(1): 48-55. |
| [13] |
李晓玲, 白超英, 胡光义. 起伏层状TI介质中多次波射线追踪[J]. 石油地球物理勘探, 2013, 48(6): 924-931. Li Xiaoling, Bai Chaoying, Hu Guangyi. Multiple Ray Tracing in an Undulated Layered TI Media[J]. Oil Geophysical Prospecting, 2013, 48(6): 924-931. |
| [14] |
高亮, 李幼铭, 陈旭荣, 等. 地震射线辛几何算法初探[J]. 地球物理学报, 2000, 43(3): 402-410. Gao Liang, Li Youming, Chen Xurong, et al. An Attempt to Seismic Ray Tracing with Symplectic Algorithm[J]. Chinese Journal of Geophysics, 2000, 43(3): 402-410. DOI:10.3321/j.issn:0001-5733.2000.03.014 |
| [15] |
秦孟兆, 陈景波. Maslov渐近理论与辛几何算法[J]. 地球物理学报, 2000, 43(4): 522-533. Qin Mengzhao, Chen Jingbo. Maslov Asymptotic Theory and Symplectic Algorithm[J]. Chinese Journal of Geophysics, 2000, 43(4): 522-533. DOI:10.3321/j.issn:0001-5733.2000.04.013 |
| [16] |
Cameron M, Fomel S, Sethian J. Time-to-Depth Conversion and Seismic Velocity Estimation Using Time-Migration Velocity[J]. Geophysics, 2008, 73(5): 205-210. DOI:10.1190/1.2967501 |
| [17] |
Rawlinson N, Sambridge M. Multiple Reflection and Transmission Phases in Complex Layered Media Using a Multistage Fast Marching Method[J]. Geophysics, 2004, 69(5): 1338-1350. DOI:10.1190/1.1801950 |
| [18] |
Rawlinson N, Sambridge M, Saygin E. A Dynamic Objective Function Technique for Generating Multiple Solution Models in Seismic Tomography[J]. Geophysical Journal International, 2008, 174(1): 295-308. DOI:10.1111/gji.2008.174.issue-1 |
| [19] |
Hao Q, Alkhalifah T. An Acoustic Eikonal Equation for Attenuating Transversely Isotropic Media with a Vertical Symmetry Axis[J]. Geophysics, 2017, 82(1): C9-C20. DOI:10.1190/geo2016-0160.1 |
| [20] |
Sethian J A. AFast-Marching Level Set Method for Monotonically Advancing Fronts[J]. Proceedings of the National Academy of Sciences of the United States of America, 1996, 93(4): 1591-1595. DOI:10.1073/pnas.93.4.1591 |
| [21] |
Sethian J A. Level Set Methods and Fast Marching Method[M]//Sethian J A. Level Set Methods and Fast Marching Methods. London: Cambridge University Press, 1999: 400.
|
| [22] |
Alkhalifah T, Fomel S. Implementing the Fast Marching Eikonal Solver:Spherical Versus Cartesian Coordinates[J]. Geophysical Prospecting, 2010, 49(2): 165-178. |
| [23] |
Popovici A M, Sethian J A. 3-D Imaging Using Higher Order Fast Marching Traveltimes[J]. Geophysics, 2002, 67(10): 604-609. |
| [24] |
Rawlinson N, Sambridge M. Wave Front Evolution in Strongly Heterogeneous Layered Media Using the Fast Marching Method[J]. Geophysical Journal of the Royal Astronomical Society, 2004, 156(3): 631-647. DOI:10.1111/gji.2004.156.issue-3 |
| [25] |
Rawlinson N, Sambridge M, Rawlinson N, et al. The Fast Marching Method:An Effective Tool for Tomographic Imaging and Tracking Multiple Phases in Complex Layered Media[J]. Exploration Geophysics, 2005, 36(4): 341-350. DOI:10.1071/EG05341 |
| [26] |
De Kool M, Rawlinson N, Sambridge M. A Practical Grid-Based Method for Tracking Multiple Refraction and Reflection Phases in Three-Dimensional Heterogeneous Media[J]. Geophysical Journal of the Royal Astronomical Society, 2006, 167(1): 253-270. DOI:10.1111/gji.2006.167.issue-1 |
| [27] |
张文生, 何樵登, 朱建伟, 等. 横向各向同性介质中群速度的计算[J]. 物探化探计算技术, 1997, 19(2): 97-102. Zhang Wensheng, He Qiaodeng, Zhu Jianwei, et al. Calculation of Group Velocity in Transversely Isotropic Media[J]. Geophysical and Geochemical Exploration Technology, 1997, 19(2): 97-102. |
| [28] |
董良国, 魏建新. 横向各向同性介质中弹性波的物理模拟[J]. 石油物探, 1999, 38(1): 76-84. Dong Liangguo, Wei Jianxin. Physical Simulation of Elastic Waves in Transversely Isotropic Media[J]. Petroleum Geophysical Exploration, 1999, 38(1): 76-84. |
| [29] |
孟庆生, 何樵登, 王德利. 均匀横向各向同性介质中P波及SV波的射线规律[J]. 吉林大学学报(地球科学版), 2002, 32(4): 378-381. Meng Qingsheng, He Qiaodeng, Wang Deli. Ray Law of P Wave and SV Wave in Uniform Transversely Isotropic Medium[J]. Journal of Jilin University (Earth Science Edition), 2002, 32(4): 378-381. |
| [30] |
张建中.三维TI介质中P波NMO速度及VSP走时联合反演[D].北京: 中国地震局地质研究所, 2005. Zhang Jianzhong. P-Wave NMO Velocity and VSP Travel Time Joint Inversion in 3D TI Media[D]. Beijing: Institute of Geology, China Earthquake Administration, 2005. http://cdmd.cnki.com.cn/article/cdmd-85402-2006048173.htm |
| [31] |
郝奇. VTI介质速度和各向异性参数建模研究[D].长春: 吉林大学, 2010. Hao Qi. Modeling of Velocity and Anisotropy Parameters of VTI Media[D]. Changchun: Jilin University, 2010. http://cdmd.cnki.com.cn/article/cdmd-10183-2010106889.htm |
| [32] |
白海军, 孙赞东, 王学军. 基于波前构建法的TTI介质射线追踪[J]. 石油地球物理勘探, 2011, 46(a01): 1-6. Bai Haijun, Sun Zandong, Wang Xuejun. TTI Media Ray Tracing Based on Wavefront Construction[J]. Oil Geophysical Prospecting, 2011, 46(a01): 1-6. |
| [33] |
Alkhalifah T. Acoustic Approximations for Seismic Processing in Transversely Isotropic Media[J]. Geophysics, 1998, 63(2): 623-631. DOI:10.1190/1.1444361 |
| [34] |
Bender C M, Orszag S A. Advanced Mathematical Methods for Scientists and Engineers[M]. London: McGraw-Hill, 1999.
|
| [35] |
Alkhalifah T. Scanning Anisotropy Parameters in Complex Media[J]. Geophysics, 2011, 76(2): U13-U22. DOI:10.1190/1.3553015 |


