2. 绍兴文理学院土木工程学院, 浙江 绍兴 312000;
3. 浙江省岩石力学与地质灾害重点实验室, 浙江 绍兴 312000
2. Faculty of Civil Engineering, Shaoxing University, Shaoxing 312000, Zhejiang, China;
3. Key Laboratory of Rock Mechanics and Geohazards of Zhejiang Province, Shaoxing 312000, Zhejiang, China
0 引言
边坡稳定性是露天矿安全生产的关键问题,是岩石力学等相关学科的研究热点,其严重影响着矿山的采掘安排[1]。露天矿在形成高陡边坡后,由于采掘、降雨、地质活动以及边坡角度增加等原因,边坡稳定性降低,滑坡、坍塌等安全问题大量显现[2-3],因此,如何确保露天矿的边坡稳定性至关重要。
在边坡稳定性方面,目前已进行过大量研究工作[4-7]:郑颖人等[8]通过分析有限元强度折减法的计算精度和影响因素,给出了提高计算精度的具体措施;张振华等[9]研究了边坡在采掘中的动态变形监测预警指标;黄盛铨等[10]通过自行编制程序实现自动强度折减,分析了滑块在边坡上的稳定性;杨天鸿等[11]通过流变试验研究,提出了基于岩体流变特性预测边坡长期稳定性的失效标准;王述红等[12]、胡高建等[13]应用块体理论,研究了结构面切割块体对边坡稳定性的影响;王培涛等[14]建立了分层岩体的各项异性计算模型,研究了表征分层岩石的力学行为和方法;常晓军等[15]从内部和外部两个因素分析了福建东门旗山的滑坡诱发机理;谭福林等[16]从滑带参数弱化的角度阐述了不同类型滑坡的渐进演化过程。这些研究从理论、预警、块体滑动等方面进行了边坡问题的细致研究,但是对露天矿高陡边坡工程,大滑坡体的滑移破坏机理以及滑坡与地表渗水、岩体优势结构面产状和控制弱层等具体关系的研究还不够深入。
在边坡稳定性评价上,有限元强度折减法应用广泛[17-18]。赵尚毅等[19]推导了各种常用屈服准则的代换关系,并将其应用于强度折减中;年廷凯等[20]通过对ABAQUS有限元软件的二次开发,研究了非饱和-非稳定渗流下的土坡稳定性;陈国庆等[21]基于动态和整体强度折减法,研究了边坡的稳定性。RFPA (rock failure process analysis)强度折减法是在强度折减法的基础上,引入RFPA的细观本构模型,从细观角度分析边坡的破坏模式[22]。RFPA强度折减法在研究岩土介质边坡破裂过程方面优势明显,能自动搜索滑动面并求出安全系数。唐春安等[23]通过工程实例,论述了RFPA强度折减法在边坡稳定性分析中的应用;李连崇等[24]应用RFPA强度折减法原理,对节理边坡的破裂过程进行了研究,获得了边坡滑移破坏面。
笔者应用红外监测技术,岩体分级、卫星监测技术和微震监测技术等技术手段,确定了边坡的滑移轮廓;基于RFPA强度折减法原理,研究了开采到最终境界时的边坡滑坡机理,提出了两阶段内排压脚的防治措施,研究了内排压脚对滑坡的抑制效果,以期实现对边坡破坏过程的认识,用于指导矿山安全生产。
1 RFPA强度折减法原理在岩土工程中,强度折减法的基本原理是对岩体强度参数c(黏聚力)和φ(摩擦角)同时折减,得到折减后的c′和φ′值,然后将c′和φ′值作为新的输入参数进行计算。当计算不收敛时,可认为岩体平衡达到极限状态,求出的折减系数即为岩体稳定性安全系数。
RFPA强度折减法假设岩石的细观力学性质具有统计性,使用Weibull统计分布函数描对岩石进行离散来获得细观基元,再考虑岩石非均匀性特征进行赋值。Weibull统计分布函数公式为
 (1)
(1) 式中:α为基元力学性质参数;α0为基元力学性质均值;m为分布函数形状参数;φ(α)为基元体力学性质α的统计分布密度。
以步长作为折减条件逐步折减,每折减一次,软件自动迭代计算一次,直至岩体最终破坏。RFPA强度折减法以摩尔库伦准则和最大拉应力准则作为判断基元破坏的准则,当最大拉应力达到拉伸阈值时,即认为发生拉伸破坏;当没有拉伸破坏发生时,应用摩尔库伦准则考虑剪切破坏。基元损伤的本构关系如图 1所示。

|
| fc0.细观基元的单轴抗压强度;fcr.基元残余抗压强度;ft0.基元的单轴抗拉强度;ftr.基元初始拉伸破坏时的残余强度;εc0.基元最大压缩主应变;εt0.弹性极限时的拉伸应变;εtu.基元极限拉伸应变。 图 1 基元在单轴应力下弹性损伤本构关系 Fig. 1 Elastic damage constitutive law of element subjected to uniaxial stress |
|
|
RFPA强度折减法的边坡失稳根据滑动面连通状态和基元破坏数来判定,安全系数Fs定义为:当岩体强度参数c和φ分别用临界强度参数ci和φi替代后,边坡处于临界平衡状态,公式如下:
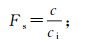 (2)
(2) 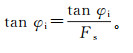 (3)
(3) 抚顺西露天矿位于抚顺市工业密集区,地质条件复杂,在此之前,边坡治理主要集中在北帮。但近年来,南帮千台山山顶形成两条长3 090 m的大裂缝,宽度为20~30 cm,裂缝走向NE70°~80°,矿区长度处于西500勘探线至东2300勘探线(W500—E2300)之间,在矿区东部与F5断层斜交。裂缝的出现导致千台山出现山体错位和地表变形,局部区域错位深度达1~2 m,造成地表建筑物出现严重破坏,制约到矿山的安全生产。南帮西200勘探线至东400勘探线(W200—E400)区域边坡变形最为严重,变形造成3号公路路面断裂,坑底-309 m泵站处产生隆起,且该区域存在着大量反倾断层。随着裂缝的持续开裂和坑底的不断变形,整个南帮有明显的滑坡趋势,一旦滑坡真实发生,大量土石方倾泻而下,将在整个矿区产生无法估量的损失。因此,南帮边坡的治理迫在眉睫,进行南帮边坡的滑移轮廓确定和破坏机理分析以及内排压脚措施研究尤为重要。南帮边坡地质条件见图 2。

|
| 图 2 南帮边坡地质条件汇总 Fig. 2 Geological conditions of the South slope |
|
|
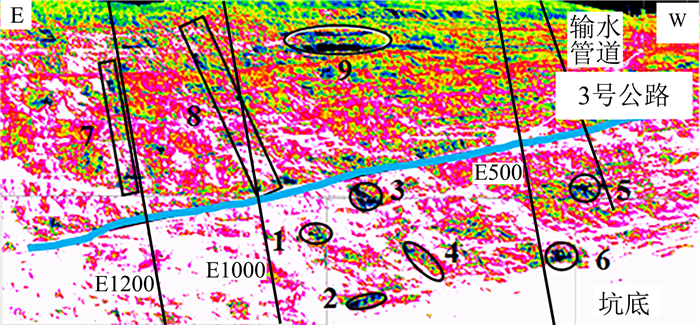
渗水区域红外监测主要是利用红外热像仪[25]监测研究区域的温度场信息,圈定出温度异常区域并确定出边坡渗水点及渗水区域,依据渗水区域推断出断层和破碎带,作为边坡稳定性研究的依据。监测区域为整个南帮,边坡热成像监测结果见图 3。
|
| 图 3 南帮边坡热成像监测结果 Fig. 3 Thermal imaging monitoring results of the South slope |
|
|
由图 3可知:在3号公路的下部边坡、输水管道以东、E1000线以西区域存在6个明显温度较低的区域,即图中圈定的1、2、3、4、5、6号区域,这些区域的温度比正常岩石的温度低4~5 ℃,经勘查研究确定为反倾断层引起的低温渗水点;在3号公路以上的边坡的E1000—E1200勘探线之间存在2个垂直方向的低温条带,即图中7号、8号区域,探测显示这2个区域出水范围较广、出水量集中,勘查确定为大面积的渗水条带;此外,在30 m水平靠近地表的位置存在大片显著低温区域,即图中9号区域,该区域的温度比正常岩石的温度低6~8 ℃,经确定也为渗水区域,且该处现场岩壁上可见到明显水流。渗水点及渗水条带的存在,造成了局部岩体的稳定性降低。
2.3 岩体危险区域确定岩体危险区域的确定主要是先通过现场结构面数字摄影测量技术[26]获得岩体参数信息,再通过广义修正Hoek-Brown强度准则计算岩体强度参数,并进行边坡岩体质量分级,确定出软弱岩体区域。
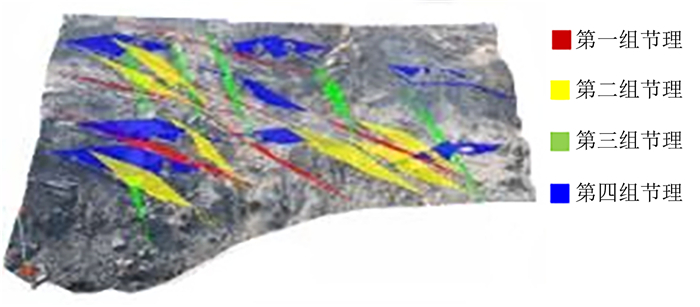
结构面测量选用先进的ShapeMetriX 3D软件系统,该系统主要包括现场相机拍照,软件合成以及后处理模块。工作原理如下:首先选定研究区域,校准相机,在岩体不同方位进行摄影成像测量,选择效果好的照片导入ShapeMetriX 3D的软件系统中,根据标定的参考点进行三维图片合成; 然后根据测量距离等要素对合成图片进行尺寸、角度的标定,最终获得真实的三维岩体合成图片。对图像合成后,通过对节理后处理,描绘显示出表面节理倾角、走向等参数,并进行分析研究,如图 4所示。
|
| 图 4 南帮边坡节理分组识别结果 Fig. 4 Consequence of joint grouping identify of the South slope |
|
|
在南帮边坡7处不同平台位置选取17组测量地点,测量统计出2 200多条结构面,按结构面倾向倾角等因素归纳分析,获得优势产状为339°∠34°,次要产状为285°∠52°和106°∠54°。根据国标《工程岩体分级标准》GB50218—94[27]提出的分级方法和标准进行岩体质量分级,将E400—E1600区域岩体分为Ⅲ级和Ⅳ级岩体。其中Ⅳ级岩体处于E1000—E1300区域,标高-200~20 m,东西区间宽度为400 m,垂直高度220 m,为强风化玄武岩,凝聚力450 kPa,摩擦角30°,节理发育。
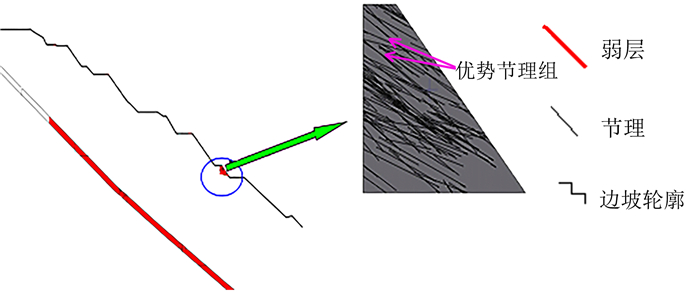
结构面的产状会影响边坡的稳定性,通过分析主要优势结构面产状来研究结构面对边坡的切割作用。将主要优势结构面产状(339°∠34°)标记在E1200剖面图上,如图 5所示。
|
| 图 5 -20 m(E1200)边坡平台结构面分布 Fig. 5 Structural plane distribution in -20 m level (E1200) |
|
|
对于单个台阶,结构面以34°倾角切割台阶,台阶会以34°倾角产生破坏;对于整个边坡,当以339°∠34°的优势结构面产状作用边坡时,边坡会产生34°倾角的顺倾滑坡。因坑底-309 m泵站位置已经出现底鼓现象,说明边坡优势结构面的切割作用已经形成,整体边坡有以34°倾角滑坡的趋势。
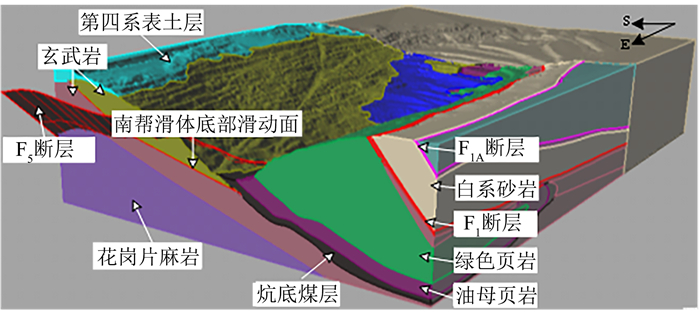
2.4 边坡滑移轮廓确定西露天矿地质构造如图 6所示,该地质构造图包括断层、软弱结构面、煤层和岩层等信息[28]。已知的边坡滑移边界包括:东部边界为F5断层;顶部边界为千台山裂缝;底部边界为坑底的底鼓鼓起;未知的边界为西部边界。当西部边界确定后,即可获得边坡整体滑移轮廓。
|
| 图 6 西露天矿地质构造图 Fig. 6 Geological structure map of West open-pit mine |
|
|
南帮滑体西部边界形态主要应用INSAR卫星监测技术和微震监测技术共同确定,具体的西部边界形态的确定过程参见文献[27]。通过INSAR卫星监测技术和微震监测技术结合,确定出滑体的西部边界位于南帮边坡W500与W750之间,滑移边界线的平均倾角为47°。再结合已知的边坡东侧的F5大断层和千台山山顶的平行大裂缝,最终确定出南帮边坡的滑移轮廓为:东侧边界为F5断层,顶部边界为千台山大裂缝,西部边界位于南帮W500与W750之间;滑移边界线的平均倾角为47°,底部滑体切出位置为-309 m水平底板,切出角度为34°。
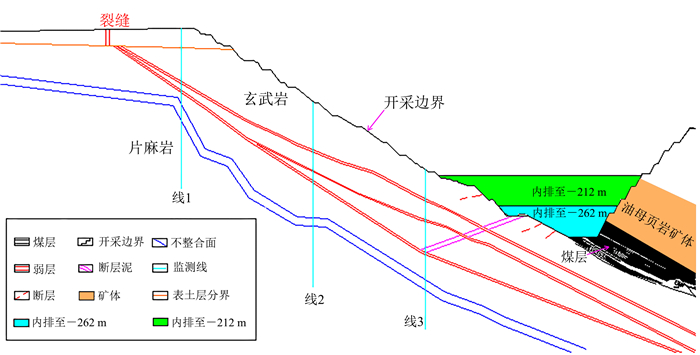
3 边坡破坏机理分析在进行边坡破坏机理分析前,首先需要确定用于力学计算的典型剖面,其根据以下3个方面确定:1)红外监测表明E1000—E1200区域出水量较大;2)岩体质量分级确定出E1000—E1300区域为Ⅳ级岩体,稳定性低;3)坑底-309 m泵站出现底鼓,该底鼓处于E1200勘探线位置。所以选取E1200勘探线处剖面作为典型剖面,E1200地质剖面图见图 7。
|
| 图 7 E1200剖面地质层位图 Fig. 7 Geological layer of E1200 profile |
|
|
E1200处剖面岩体层位主要由浅部的玄武岩和深部的花岗质片麻岩组成,玄武岩和片麻岩呈角度不整合接触,不整合接触面局部产状为344°∠45°,花岗岩组按风化程度由上而下主要分为玄武岩、玄武岩夹煤层及玄武岩夹凝灰岩层3层,产状335°~25°∠23°~48°,厚度3.52~136.37 m,平均89.67 m。在玄武岩层位内,赋存有破碎带、凝灰岩以及薄煤线等3条弱层层位,按埋深分别定为浅部弱层、中间弱层和深部弱层。在边坡的上部、中部和下部3个不同位置,定义3条监测线,见图 7中线1、线2和线3,以研究滑坡发生时监测线上的位移变化。
计算采用RFPA软件进行,应用强度折减法原理,计算模型尺寸1 650 m×820 m,岩体强度参数见表 1。由于RFPA在求解计算过程中,是按一定步长逐渐折减,每折减一次,应力分析程序将进行迭代计算,直至边坡宏观失稳破坏,在此过程中程序自动保存每一步求解图片;因此要保存大量高清图片,占用大量内存,耗费大量时间。根据文献[22-23]中的RFPA软件原理及计算过程中基元破裂原理,重点考虑岩石破裂过程中基元的破坏过程,在数值模拟过程中开启步中步功能,步中步的步数设置为10,折减系数选定为0.01。这样,在岩体开始发生破裂的瞬间,软件自动启用步中步功能,详细记录下破裂过程中基元的破坏过程。研究的工况为开采到最终境界时的边坡破坏机理。
| c/kPa | φ/(°) | E/MPa | ρ(g/cm3) | |
| 玄武岩岩体 | 900 | 42 | 7 000 | 2.8 |
| 破碎带 | 450 | 30 | 2 000 | 1.2 |
| 不整合面 | 500 | 33 | 2 500 | 2 |
| 注:E为弹性模量;ρ为密度。 | ||||
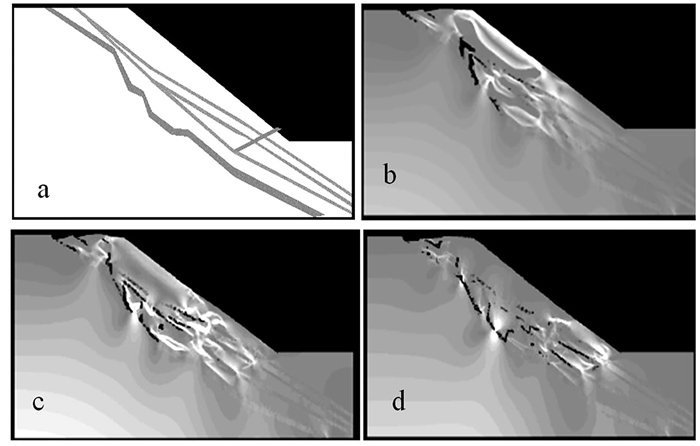
数值模拟结果见图 8,其中a为计算模型图,b、c、d为应力场图。当折减开始后,边坡破坏最先在坡体上部产生,沿软弱层交汇处向下延伸,并扩展至不整合面,边坡上部地表形成应力集中并形成张拉破坏(图 8b);随着强度折减持续,坡体破坏沿着弱层和不整合面向下移动,此时应力主要集中在中间和浅部弱层上(图 8c);当破坏扩展到边坡下部后,由于下部不整合面埋深较大,滑动被抑制,破坏开始沿中间弱层向下发展,最终在坡脚处剪坏坡底,形成贯通坡底的大破坏(图 8d)。因此,当滑坡发生时,底部中间弱层为应力集中区,属于控制滑坡的主要层位,控制着边坡滑移剪出位置,滑坡发生时边坡安全系数为0.988。
|
| a.计算模型图;b.第8步;c.第9步;d.第10步。 图 8 最终境界的边坡应力场图 Fig. 8 Slope stress field distribution of the final boundary |
|
|
3条监测线上的位移见图 9。线1处(图 9a):距地面3~5 m深度边坡有顺倾方向破坏;10~200 m埋深范围内,由于边坡剪切陷落使得岩体逆边坡水平左移;在210 m埋深以下,即不整合面以下埋深位移很小,岩体基本稳定,不会产生滑移。线2处(图 9b):埋深在0~180 m时,位移始终为负值;埋深在180~230 m时,位移由负值逐渐转变为正值,且在230 m时,位移为0,表明破坏由逆边坡滑移转化为顺边坡滑移;到埋深270 m时,对应的层位为不整合面,深部弱层对岩体位移的影响已经很小,主要的影响层位为浅部和中深部弱层。线3处(图 9c):在埋深0~72 m时,边坡位移范围为-2.0~-1.5 m,为逆边坡左移,位移主要受到浅部弱层的影响;在埋深72~131 m时,位移由-1.5 m逐渐减为0 m;在埋深131 m以下,位移量都变为正值,表明岩体开始顺边坡左移,此时的主要影响层位为深部弱层。

|
| a.线1处;b.线2处;c.线3处。 图 9 最终境界时水平位移曲线 Fig. 9 Drift displacement curve of the final boundary |
|
|
整个边坡变形程度大,变形范围广,很难有可行的加固措施。为控制大滑坡体的产生,提出了内排土压脚的防治措施,考虑到内排所需空间及时间关系,内排压脚方案分两个阶段实施:第一阶段内排土工程由西向东实施,排弃到界标高为-262 m,第二阶段内排土工程排弃到界标高为-212 m。
4.1 内排标高至-262 m后边坡破坏模式当内排土至-262 m时,回填高度为50 m,边坡折减后的滑坡应力场见图 10,其中a为计算模型图,b、c、d为应力场图。从模拟效果看,内排压脚对边坡底部的滑移有较好的抑制作用,但边坡中上部的破坏和应力集中依然存在(图 10b);受内排土影响,底部弱层和不整合面上的破坏受到部分抑制,应力集中自坡脚处向上转移(图 10c);浅部弱层的底部因内排土的原因,原贯通破坏的位置被填埋,应力集中点向上转移,在边坡上部相对软弱的地方寻找新的破裂点,造成新的贯通滑移破裂(图 10d)。内排标高至-262 m后的安全系数为1.067。

|
| a.计算模型图;b.第11步;c.第12步;d.第13步。 图 10 内排至-262 m时边坡应力场图 Fig. 10 Slope stress field distribution of dumping to -262 m |
|
|
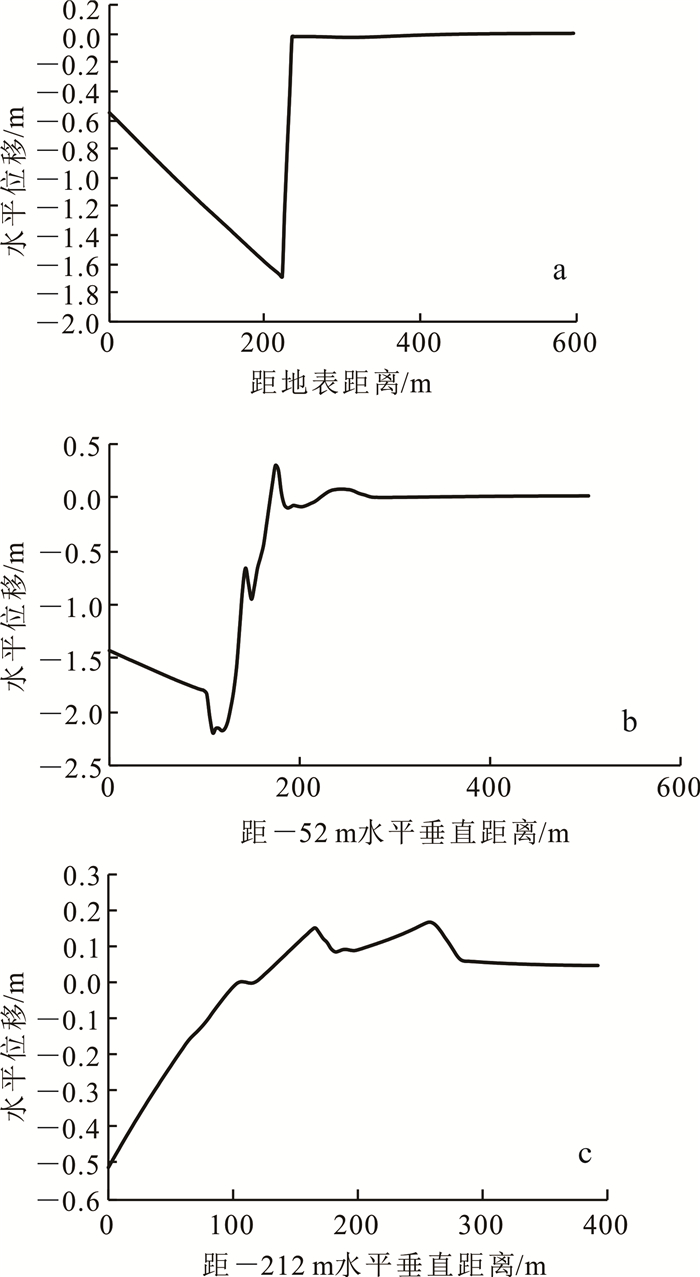
内排到-262 m后监测线上的位移见图 11。线1处(图 11a),边坡上部岩体的位移变化趋势与未内排压脚时相比没有明显的变化,只是在位移量上有细微差别,说明内排土对边坡上部的岩体位移没有明显的影响,该处位移的主要影响因素仍为标高-78 m水平的不整合面和弱层所致;线2处(图 11b),对比未内排土时的曲线数据发现,内排土对弱层滑移产生了影响,在200 m埋深时,位移波动很小,大于250 m埋深时,位移几乎为0,说明内排土对浅部和中部弱层的滑移具有很好的控制效果;线3处(图 11c),最大位移只有0.5 m,表明内排土对坑底处的弱层有非常好的抑制作用,底鼓现象消失。
|
| a.线1处;b.线2处;c.线3处。 图 11 内排至-262 m时水平位移曲线 Fig. 11 Drift displacement curve of dumping to -262 m |
|
|
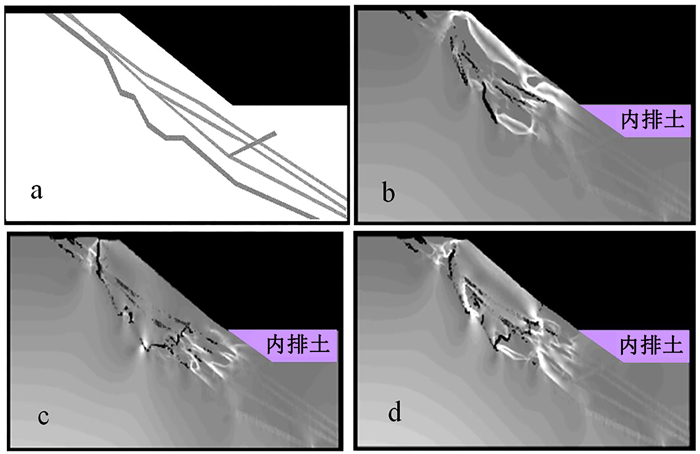
当内排标高至-212 m时,边坡折减后应力场见图 12,此时回填高度为100 m,相比内排至-262 m时,内排高度增加了50 m。从模拟效果看,压脚效果更加明显,实施边坡内排压脚的区域,弱层的滑动被有效抑制,底部高应力集中现象消除(图 12b);边坡底脚处滑坡受到抑制后,应力集中会沿着坡体内较软弱的层位向上迁移,并在薄弱部位造成相互贯通(图 12c);当边坡强度折减到一定程度,弱层间的贯通会持续扩展,应力集中持续迁移,向着边坡最软弱的部位发展,最终在边坡表面寻找一个新的破坏点来释放应力,造成坡体新的滑移破坏(图 12d)。内排标高至-212 m后的安全系数为1.324。
|
| a.计算模型图;b.第14步;c.第15步;d.第16步。 图 12 内排至-212 m时边坡应力场图 Fig. 12 Slope stress field distribution of dumping to -212 m |
|
|
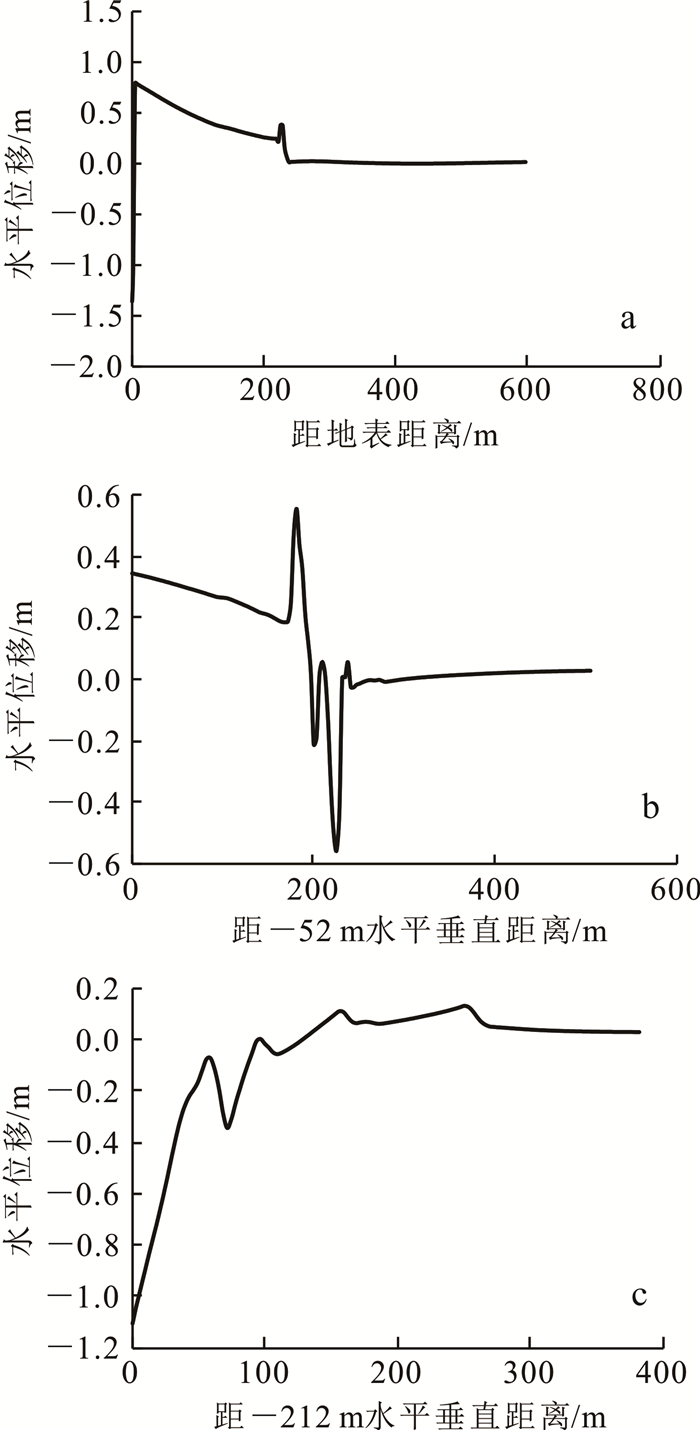
内排到-212 m后监测线上的位移见图 13,对比内排-262 m时的位移可以发现:线1处(图 13a),0~200 m处位移由负值变为正值,表明因内排高度增加,上部软弱层位也受到一定影响,不再产生塌陷破坏,而是顺倾滑移;线2处(图 13b)位移量明显减小到0.4 m以下,250 m以下位移量几乎为0,表明底部弱层和不整合面的滑动被抑制,内排土对边坡中部岩体滑坡产生了显著抑制效果。
|
| a.线1处;b.线2处;c.线3处。 图 13 内排至-212 m时水平位移曲线 Fig. 13 Drift displacement curve of dumping to -212 m |
|
|
根据DZ/T0218-2006《滑坡防治工程勘查规范》[29]规定,滑坡稳定状态与稳定安全系数关系按表 2确定。
| 安全系数Fs | 滑坡稳定状态 |
| < 1.00 | 不稳定 |
| 1.00~1.05 | 欠稳定 |
| 1.05~1.15 | 基本稳定 |
| ≥1.15 | 稳定 |
当矿体开采到最终境界时,安全系数为0.988,小于1.00,边坡处于不稳定状态,必须进行必要的治理;当内排土回填至-262 m时,安全系数为1.067,处于区间1.05~1.15中,边坡处于基本稳定状态,表明回填土起到了一定的控制效果;当内排土回填至-212 m时,安全系数为1.324,大于1.15,边坡处于稳定状态,表明该阶段内排土回填起到了很好的滑坡控制效果。
5 结论1) 红外热像监测显示,E1000—E1200勘探线之间存在两条低温渗水条带和一片大面积渗水区域,坑底反倾断层位置存在6个渗水点,这些渗水条带和渗水点降低了局部岩体的稳定性。
2) 边坡的滑移轮廓为:东侧边界为F5断层,顶部边界为千台山大裂缝,西部边界位于南帮W500与W750之间,滑移边界线的平均倾角为47°,底部滑体切出位置为-309 m水平底板,切出角度为34°。
3) 边坡破坏机理为:破坏最先发生在边坡上部,在边坡中部沿着弱层和破碎带运动,到边坡下部不整合面处受到抑制,最后在边坡底部沿中间弱层切出坑底,形成滑坡轮廓,影响滑坡的关键层位为中间弱层。
4) 两阶段内排压脚方案能明显抑制弱层的错动,当内排到-262 m水平时,可部分抑制底部弱层处滑移,底鼓现象消失;当内排到-212 m水平时,可完全抑制住底部弱层的滑动,此时边坡安全系数为1.324,满足安全要求。
| [1] |
杨天鸿, 张锋春, 于庆磊, 等. 露天矿高陡边坡稳定性研究现状及发展趋势[J]. 岩土力学, 2011, 32(5): 1437-1452. Yang Tianhong, Zhang Fengchun, Yu Qinglei, et al. Research Situation of Open-Pit Mining High and Steep Slope Stability and Its Developing Trend[J]. Rock and Soil Mechanics, 2011, 32(5): 1437-1452. DOI:10.3969/j.issn.1000-7598.2011.05.025 |
| [2] |
卢世宗. 我国矿山边坡研究的基本情况和展望[J]. 金属矿山, 1999(9): 6-10. Lu Shizong. Basic Conditon and Prospect of China's Mine Slope Research[J]. Metal Mine, 1999(9): 6-10. |
| [3] |
杨天鸿, 解连库, 唐春安, 等. 抚顺西露天矿北帮边坡治理工程效果初步评价[J]. 岩石力学与工程学报, 2005, 24(11): 1841-184. Yang Tianhong, Xie Lianku, Tang Chun'an, et al. Effect Evaluation of Distortion for North Project of Side Slope in Fushunwest Open Cast[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(11): 1841-1846. DOI:10.3321/j.issn:1000-6915.2005.11.004 |
| [4] |
Geeralt V D H, Joachim R, Thomas M, et al. Finite Element Simulation of a Slow Moving Natural Slope in the Upper-Austrian Alps Using a Visco-Hypoplastic Constitutive Model[J]. Geomorphology, 2009, 103(1): 136-142. DOI:10.1016/j.geomorph.2007.10.019 |
| [5] |
Li A J, Merifield R S, Lyamin A V. Stability Charts for Rock Slopes Based on the Hoek-Brown Failure Criterion[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 689-700. DOI:10.1016/j.ijrmms.2007.08.010 |
| [6] |
Lysandros P. Rock Slope Stability Assessment Through Rock Mass Classification Systems[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 46(2): 315-325. DOI:10.1016/j.ijrmms.2008.06.003 |
| [7] |
Masoud Z N, Rafael J, Reza K K, et al. A New Open-Pit Mine Slope Instability Index Defined Using the Improved Rock Engineering Systems Approach[J]. International Journal of Rock Mechanics & Mining Sciences, 2013, 61(5): 1-14. |
| [8] |
郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381-3388. Zheng Yingren, Zhao Shangyi. Application of Strength Reduction FEM in Soil and Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. DOI:10.3321/j.issn:1000-6915.2004.19.029 |
| [9] |
张振华, 冯夏庭, 周辉, 等. 基于设计安全系数及破坏模式的边坡开挖过程动态变形监测预警方法研究[J]. 岩土力学, 2009, 30(3): 603-612. Zhang Zhenhua, Feng Xiating, Zhou Hui, et al. Research on Dynamic Early Warning Method of Slope Deformation Monitoring During Excavation Based on Designed Safety Factor and Failure Mode[J]. Rock and Soil Mechanics, 2009, 30(3): 603-612. DOI:10.3969/j.issn.1000-7598.2009.03.005 |
| [10] |
黄盛铨, 刘君, 孔宪京. 强度折减DDA法及其在边坡稳定分析中的应用[J]. 岩石力学与工程学报, 2008, 27(增刊1): 1799-1806. Huang Shengquan, Liu Jun, Kong Xianjing. DDA with Strength Reduction Technique and Its Application to Stability Analysis of Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(Sup.1): 1799-1806. |
| [11] |
Tianhong Yang, Tao Xu, Hongyuan Liu, et al. Rheological Characteristics of Weak Rock Mass and Effects on the Long-Term Stability of Slopes[J]. Rock Mechanics and Rock Engineering, 2014, 47(6): 2253-2263. DOI:10.1007/s00603-013-0527-z |
| [12] |
Wang S H, Ni P. Application of Block Theory Modeling on Spatial Block Topological Identification to Rock Slope Stability Analysis[J]. International Journal of Computational Methods, 2014, 11(1): 390-400. |
| [13] |
胡高建, 杨天鸿, 师文豪, 等. 安家岭煤矿岩体结构数字识别及关键块体确定[J]. 煤炭学报, 2014, 39(12): 2412-2417. Hu Gaojian, Yang Tianhong, Shi Wenhao, et al. Digital Recognition and Key Block Identification of Rock Mass Structure in Anjialing Coal Mine[J]. Journal of China Coal Society, 2014, 39(12): 2412-2417. |
| [14] |
Wang P, Cai M, Ren F, et al. Theoretical Investigation of Deformation Characteristics of Stratified Rocks Considering Geometric and Mechanical Variability[J]. Geosciences Journal, 2017, 21(3): 213-222. |
| [15] |
常晓军, 葛伟亚, 于洋, 等. 福建省永泰县东门旗山滑坡诱发机理与防治措施[J]. 吉林大学学报(地球科学版), 2019, 49(4): 1063-1072. Chang Xiaojun, Ge Weiya, Yu Yang, et al. Mechanism and Mitigation Measures of Qishan Landslide, Yongtai, Fujian Province[J]. Journal of Jilin University (Earth Science Edition), 2019, 49(4): 1063-1072. DOI:10.13278/j.cnki.jjuese.20180082 |
| [16] |
谭福林, 胡新丽, 张玉明, 等. 考虑渐进破坏过程的滑坡推力计算方法[J]. 吉林大学学报(地球科学版), 2018, 48(1): 193-202. Tan Fulin, Hu Xinlin, Zhang Yuming, et al. Calculation Method of Landside Thrust Considering Progressive Failure Process[J]. Journal of Jilin University(Earth Science Edition), 2018, 48(1): 193-202. |
| [17] |
郑颖人. 岩土数值极限分析方法的发展与应用[J]. 岩石力学与工程学报, 2012, 31(7): 1297-1316. Zheng Yingren. Development and Application of Numerical Limit Analysis for Geological Materials[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(7): 1297-1316. DOI:10.3969/j.issn.1000-6915.2012.07.001 |
| [18] |
郑颖人, 赵尚毅. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报, 2004, 23(19): 3381-3388. Zheng Yingren, Zhao Shangyi. Application of Strength Reduction FEM to Soil and Rock Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(19): 3381-3388. DOI:10.3321/j.issn:1000-6915.2004.19.029 |
| [19] |
赵尚毅, 郑颖人, 时卫民, 等. 用有限元强度折减法求边坡稳定安全系数[J]. 岩土工程学报, 2002, 24(3): 343-346. Zhao Shangyi, Zheng Yingren, Shi Weimin, et al. Analysis of Safety Factor of Slope Stability by Strength Reduction FEM[J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 343-346. DOI:10.3321/j.issn:1000-4548.2002.03.017 |
| [20] |
年廷凯, 万少石, 蒋景彩, 等. 库水位下降过程中土坡稳定强度折减有限元分析[J]. 岩土力学, 2010, 31(7): 2264-2270. Nian Tingkai, Wan Shaoshi, Jiang Jingcai, et al. Finite Element Analysis of Slope Stability Under Drawdown Conditions by Strength Reduction Technique[J]. Rock and Soil Mechanics, 2010, 31(7): 2264-2270. DOI:10.3969/j.issn.1000-7598.2010.07.041 |
| [21] |
陈国庆, 黄润秋, 周辉, 等. 边坡渐进破坏的动态强度折减法研究[J]. 岩土力学, 2013, 34(4): 1140-1146. Chen Guoqing, Huang Runqiu, Zhou Hui, et al. Research on Progressive Failure for Slope Using Dynamic Strength Reduction Method[J]. Rock and Soil Mechanics, 2013, 34(4): 1140-1146. |
| [22] |
朱万成, 唐春安, 杨天鸿, 等. 岩石破裂过程分析(RFPA2D)系统的细观单元本构关系及验证[J]. 岩石力学与工程学报, 2003, 22(1): 24-29. Zhu Wancheng, Tang Chun'an, Yang Tianhong, et al. Constitutive Relationship of Mesoscopic Elements Used in RFPA2D and Its Validations[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(1): 24-29. DOI:10.3321/j.issn:1000-6915.2003.01.004 |
| [23] |
唐春安, 李连崇, 李常文, 等. 岩土工程稳定性分析RFPA强度折减法[J]. 岩石力学与工程学报, 2006, 25(8): 1522-1530. Tang Chun'an, Li Lianchong, Li Changwen, et al. RFPA Strength Reduction Method for Stability Analysis of Geotechnical Engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(8): 1522-1530. DOI:10.3321/j.issn:1000-6915.2006.08.002 |
| [24] |
李连崇, 唐春安, 邢军, 等. 节理岩质边坡变形破坏的RFPA模拟分析[J]. 东北大学学报, 2006, 27(5): 559-562. Li Lianchong, Tang Chun'an, Xing Jun, et al. Numerical Simulation and Analysis of Deformation and Failure of Jointed Rock Slopes by RFPA-Slope[J]. Journal of Northeastern University, 2006, 27(5): 559-562. DOI:10.3321/j.issn:1005-3026.2006.05.023 |
| [25] |
刘善军, 王植, 毛亚纯, 等. 矿山安全与环境的多源遥感监测技术[J]. 测绘与空间地理信息, 2015, 38(10): 98-100. Liu Shanjun, Wang Zhi, Mao Yachun, et al. Multi-Source Remote Sensing Technology for Monitoring Safety and Environment in Mine[J]. Geomatics & Spatial Information Technology, 2015, 38(10): 98-100. DOI:10.3969/j.issn.1672-5867.2015.10.031 |
| [26] |
杨天鸿, 于庆磊, 陈仕阔, 等. 范各庄煤矿砂岩岩体结构数字识别及参数表征[J]. 岩石力学与工程学报, 2009, 28(12): 2482-2489. Yang Tianhong, Yu Qinglei, Chen Shikuo, et al. Rock Mass Structure Digital Recognition and Hytromechanical Parameters Characterization of Sandstone in Fangezhuang Coal Mine[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(12): 2482-2489. DOI:10.3321/j.issn:1000-6915.2009.12.014 |
| [27] |
工程岩体分级标准: GB 50218-2014[S].北京: 中国计划出版社, 2014. Engineering Rock Mass Classification Standard: GB 50218-2014[S]. Beijing: China Planning Press, 2014. |
| [28] |
张飞, 杨天鸿, 王植, 等. 某露天矿南帮滑体西部边界形态测定[J]. 东北大学学报(自然科学版), 2017, 38(9): 1335-1340. Zhang Fei, Yang Tianhong, Wang Zhi, et al. Determination of West Boundary for Landslide Body of the South Slope in an Open-Pit Mine[J]. Journal of Northeastern University (Natural Science), 2017, 38(9): 1335-1340. |
| [29] |
滑坡防治工程勘查规范: DZ/T 0218-2006[S].北京: 中国标准出版社, 2006: 18-20. Specification of Geological Investigation for Landslide Stabilization: DZ/T 0218-2006[S]. Beijing: Standards Press of China, 2006: 18-20. |


