2. 同济大学现代工程测量国家测绘地理信息局重点实验室, 上海 200092
2. Key Laboratory of Modern Engineering Surveying, National Administration of Surveying, Mapping, and Geo-Information, Shanghai 200092, China
0 引言
道路平曲线计算中常采用线元法。计算前通常要分门别类并针对各个门类提出计算方法,这使计算工作变得很复杂。有鉴于此,一些学者提出了针对各线元构造统一数学模型的简化方法,本文将在此基础上研究高斯积分如何用于计算局部坐标系下的待定点。
在国内,李青岳等[1]介绍过道路曲线几何形位知识与测设要点,总结了最基本的计算公式。王科[2]总结了不同类型的复曲线拼接与计算,发表了相应的综述。冯晓等[3]、高淑照等[4]、孔晨辉等[5]在平曲线计算与测设方面的研究成果被广泛引用,他们提出:一些数值计算方法在曲线积分中具有使用价值,利用几何关系函数进行曲线反算效率很高。李全信[6-7]在道路曲线计算方面很有心得,他曾对道路平曲线正反算进行过详细介绍,提出通用Gauss-Legendre公式适用于计算线路中边桩,性能稳定可靠。孙建国等[8]在研究地震波射线路径计算时, 提到Chebyshev多项式适用于解决最小零偏差逼近及最佳平方逼近问题,用来估计原函数可以取得良好效果。李孟山等[9]提出数值计算方法可以应用于曲线积分。李文科等[10]、李自康[11]、黄金满等[12]则在线元模型构建方面取得了成果。
至于国外,Wladyslaw Koc等[13]总结了不同类型缓和曲线的解析方法,如一般回旋线、四次抛物线、Bloss曲线、余弦线等。Andrzej Kobryń等[14]提出了基于线元模型和边界条件推导出的回旋线型缓和曲线计算的通用方法(多项式形式),这种方法适用于设计道路曲线。相比于Gauss-Legendre公式,Gauss-Chebyshev公式的表达式更为简单直观。基于该式编写的计算程序有一个突出的优点:在结构不变的情况下可以任意增加节点。M. R. Eslahchi等[15]结合边界条件对Gauss-Chebyshev公式进行了拓展与改进,提出了多项式形式的改进计算公式,具有更高的代数精度。本文对Eslahchi改进的公式、Gauss-Chebyshev公式和5点Gauss-Legendre公式进行了比较,旨在探讨Gauss-Chebyshev积分用于平曲线计算的效果。
1 平曲线预处理预处理开始前要检查确认断链被完全排除,桩号连续。确认无误后可以将原始数据整理成理想形式,线元表中每一条记录对应一个独立的局部坐标系(x′, y′)。局部坐标系与线元对应关系如表 1所示。
| 线元类型 | 局部坐标系定义 |
| 直线 | 以曲线段起点为原点,x′轴与本曲线段重合,里程变大的一侧为正方向 |
| 圆曲线 | 以曲线段起点为原点,x′轴与原点处的切线重合,里程变大的一侧为正方向 |
| 缓和曲线 | 原点在缓和曲线曲率零点处,确定其位置可能需要绘出该缓和曲线线元的延长线:从小曲率圆曲线一侧出发,补完伪缓和曲线,伪直缓点即为坐标原点。x′轴与原点处的切线重合,里程变大的一侧为正方向 |
通用的线元模型至少要有7个参数[11-12, 16],如表 2所示。利用这些参数可以完成线元局部坐标系的搭建。对于直线和圆曲线,其局部坐标系原点即线元起点,无需处理。
| 线元参数 | 标识符号 |
| 原点里程 | lO′ |
| 原点横坐标 | x0 |
| 原点纵坐标 | y0 |
| x′轴方位角 | α′ |
| 起点曲率 | ks |
| 终点曲率 | ke |
| 曲线长度 | L |
| 注:该线元表是对传统线元表进行处理产生的结果,用局部坐标系原点里程和线元曲线长度替代线元起点里程和终点里程,用局部坐标系原点坐标替代线元起点坐标,用x′轴方位角替代线元起点方位角。 | |
获得缓和曲线线元的部分参数并建立局部坐标系相对要复杂一些,这里简要介绍。
记α0为线元起点切线在工程坐标系(x, y)下的方位角,l′=L/(ke-ks)ks为线元起点到局部坐标系原点(即完整缓和曲线的(伪)直缓点)的曲线长度。若线元起点里程为Ls,则坐标原点里程LO′=Ls-l′。根据l′可以求出在局部坐标系下线元起点的切线方位角β(l′),易知局部坐标系x′轴在工程坐标系下的方位角为αx′=α0-β(l′)。再根据缓和曲线计算公式计算局部坐标系下线元起点坐标:
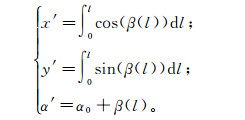 (1)
(1) 式中:l=-LO′+L待求, L待求为待求点里程; β(l)是局部坐标系下待求点的切线方位角。
再结合线元起点在工程坐标系下的坐标与αx′,经坐标转换得x0、y0。
2 坐标正算坐标正算指根据里程L待求与偏距d,可以求得待求点实地坐标(x, y)。
2.1 坐标正算步骤根据线元表中的lO′、ks、ke、L可以还原出一个线元起点与终点的里程,得到里程区间,并计算局部坐标系中起终点的伪里程(用来计算其在局部坐标系下的坐标)。
1) 查询L待求落在哪个线元的里程区间(LO′+l′, LO′+l′+L)内;
2) 根据式(1)先计算待定点在局部坐标系下的坐标;
3) 根据α′以及x0、y0可以对待定点进行坐标转换。
计算待定点局部坐标实质就是计算定积分。与直线和圆曲线相比,缓和曲线定积分计算要困难一些,下面简要讨论。
2.2 基于Gauss-Chebyshev积分的计算方法使用传统方法对定积分做近似计算时一般会将被积函数展开成简单的多项式并对其进行积分。梯形法、Simpson公式及其衍生方法在计算缓和曲线定积分时都比较常用[9-10]。在此基础上,也可以采用插值方法(例如牛顿插值)估算部分定积分。
Gauss型积分公式也是一种常见的定积分计算工具。Gauss型积分公式应用广泛,目前也能达到令人满意的效果[7, 16]。其中Gauss-Chebyshev积分公式表达形式简单,适用于编程以实现求解坐标的最后一步——定积分计算。
一般情况下,高斯型积分的表达形式是[17]
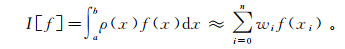 (2)
(2) 式中,ρ(x)≥0,是已知权函数,在该权函数框架下:n为采用的高斯点数目;wi为高斯系数;xi为高斯点。式(2)在n→∞时收敛。当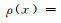
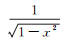
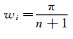
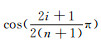
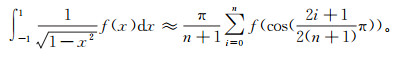 (3)
(3) 为求解x′、y′,对式(1)中x′和y′的积分进行整理:将积分上限改写为lu,做变量代换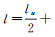
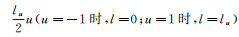
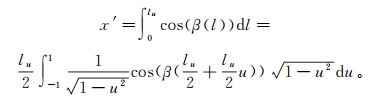 (4)
(4) 对照式(3)得到
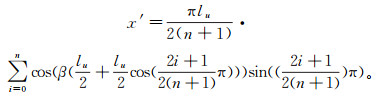 (5)
(5) 同样地,对于y′,有
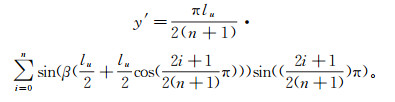 (6)
(6) 在式(3)的基础上,M. R. Eslahchi等[15]提出了改进公式,代价是调整了积分区间(取用(-1, 1)的子区间)与被积函数,需要另行计算高斯点与高斯系数。基于式(2),以不大于给定阶数的单项式取代原函数,有
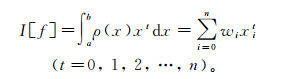 (7)
(7) 记I[f]为yt,指定a与b后即可罗列方程。构造方程组
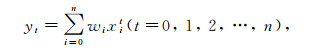
解方程组即可求得高斯点与高斯系数。
改进式(7)代数精度更高,也适用于该类定积分计算;但高斯点与高斯系数计算方式复杂,当单项式最高阶数大于2时求解非常困难[18]。
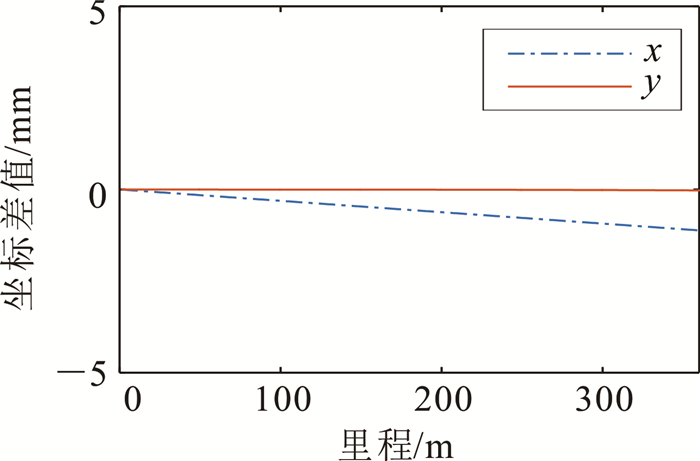
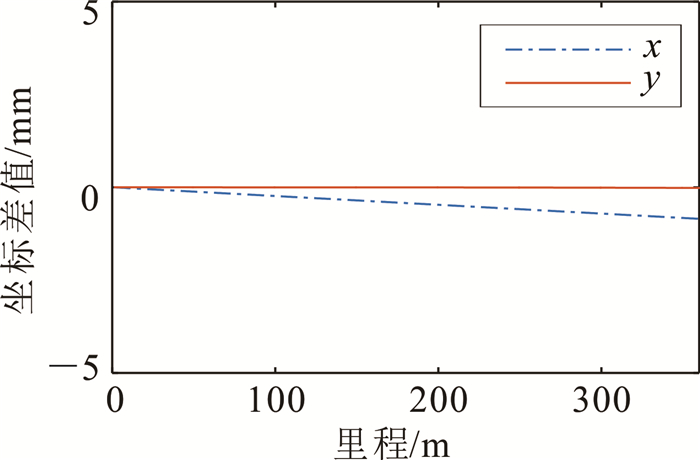
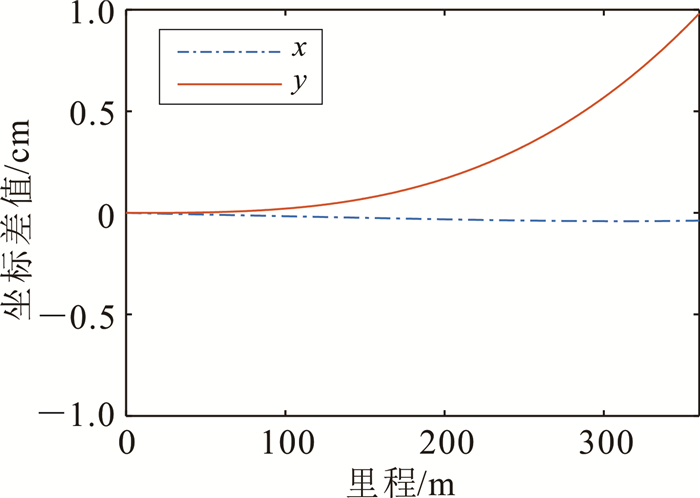
图 1—图 3显示了部分数值实验结果(L=360 m,R=4 500 m,R为与缓和曲线邻接的圆曲线的半径),可以得出两个结论:在道路的缓和曲线(回旋线型)参数
|
| 图 1 360点Gauss-Chebyshev积分与5点Gauss-Legendre积分计算结果差值 Fig. 1 Differences between numerical results based on 360-point Gauss-Chebyshev quadrature rule and those based on 5-point Gauss-Legendre quadrature rule |
|
|
|
| 图 2 360点与720点Gauss-Chebyshev积分计算结果差值 Fig. 2 Differences between numerical results based on 360-point Gauss-Chebyshev quadrature rule and those based on 720-point Gauss-Chebyshev quadrature rule |
|
|
|
| 图 3 5点改进型Gauss-Chebyshev积分与5点Gauss-Legendre积分计算结果差值 Fig. 3 Differences between numerical results based on Improved 5-point Gaussian quadrature rule and those based on 5-point Gauss-Legendre quadrature rule |
|
|
坐标反算指根据待求点实地坐标(x, y),求里程L待求与偏距d。
3.1 判定待求点所属线元此处将线元称为区间。在判定待定点归属前需要构造一个表用于存放待求点、备选区间以及候选偏距。判定流程如下:
1) 根据设计曲线上的n个端点获得n-1个区间与n个切线向量,取第一个待定点为当前待定点。
2) 从第一个区间开始,验证当前区间是否为当前待求点的备选区间。构造区间起点切线向量vs、区间终点切线向量ve,再分别以区间两端作为向量起点、以待求点为向量终点获得两个向量v1和v2,分别与vs和ve相乘得到数量积t1和t2。若t1t2 < 0,则采纳该区间为待求点的备选区间。
3) 对其他的区间重复流程2),直到当前待求点的所有备选区间被确认,将备选区间全部纳入备选区间记录表(表 3)中。
| 待求点 | 坐标 | 备选区间 | 偏距计算结果 |
| P1 | (x1, y1) | (l11s, l11e) | d11 |
| P1 | (x1, y1) | (l12s, l12e) | d12 |
| P1 | (x1, y1) | (l13s, l13e) | d13 |
| P2 | (x2, y2) | (l21s, l21e) | d21 |
| P2 | (x2, y2) | (l22s, l22e) | d22 |
| 注:待求点解数目等于备选区间数目;若其大于1,则需要排除不合理的解。 | |||
4) 转向下一个待定点,对其执行流程2)、3)。
记dij为第i个待定点的第j个备选偏距解,给定一个距离判别阈值dmax,用来排除不合理的解:若|dij| >dmax,则放弃dij。排除掉不合理的解以后,在剩余可用解中取偏距绝对值最小的一组作为可行解。
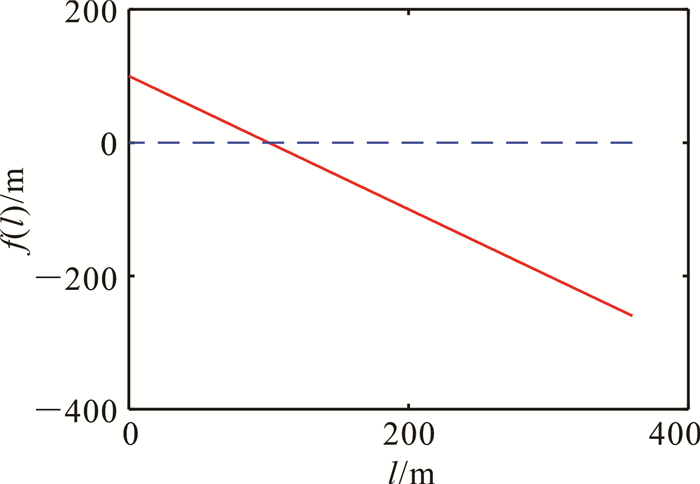
3.2 里程与偏距反算步骤对任一待定点,计算其里程(及偏距)都是一个迭代过程。在众多求解方法中,割线法简单有效,这里采用之。割线法数量积函数图像如图 4所示,函数零点即为所求里程。
|
| 图 4 割线法数量积函数 Fig. 4 Dot-product function induced by the secant method |
|
|
先给定迭代里程差阈值δl=5×10-5m以及迭代次数上限nit,求解步骤如下。
1) 指定(xi, yi)为第i个待定点;
2) 对待定点的第j个备选区间取初值l0=lO′+l′、l1=l0+L。
3) 构造函数
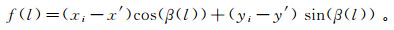 (8)
(8) x′、y′为经过坐标正算得到的平曲线上里程为l处点的坐标。显然,函数(8)的零点就是该线元上待定点的里程。
4) 对此函数求解零点,割线法迭代表达式为
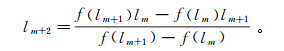
当m < nit时,若|lm+2-lm+1| < δl,迭代终止,取(xi, yi)的里程li=lm+2,求出对应的dij,分别作为备选里程与偏距。若迭代次数达到nit后仍不满足条件,则放弃。
5) 对下一备选区间重复步骤2)—4),直到获得该待定点全部的备选解,从中筛选可行解。
4 计算案例计算所用某铁路平曲线数据如表 4所示(积木法计算格式):先根据16个待定点的里程与偏距计算对应的坐标,再根据这些坐标对上述待定点进行反算,得到反算结果(计算坐标时,使用360点Gauss-Chebyshev积分计算相应的定积分)。将一开始输入的里程和偏距与反算计算得到的输出里程和输出偏距进行比较,结果见表 5。对比输入与输出的数据可以确认:里程和偏距的计算足够精确;在原始偏距绝对值较大的情况下,反算偏距与原始偏距的偏差也不超过1 mm。
| 序号 | 起点里程/m | 止点里程/m | 起点坐标 | 起点方位角 | 起点半径/m | 止点半径/m | 转向 | |
| x/m | y/m | |||||||
| 1 | 7 152.556 0 | 7 586.706 4 | 3 378 672.978 | 453 219.837 7 | 98°56′55.62″ | 0 | 0 | 0 |
| 2 | 7 586.706 4 | 7 946.706 4 | 3 378 605.445 | 453 648.703 5 | 98°56′55.62″ | 0 | 4 500 | 1 |
| 3 | 7 946.706 4 | 11 766.030 0 | 3 378 544.714 | 454 003.518 1 | 101°14′26.20″ | 4 500 | 4 500 | 1 |
| 4 | 11 766.030 0 | 12 126.030 0 | 3 376 389.890 | 457 018.324 2 | 149°52′11.10″ | 4 500 | 0 | 1 |
| 5 | 12 126.030 0 | 13 346.960 0 | 3 376 073.845 | 457 190.654 0 | 152°09′41.70″ | 0 | 0 | 0 |
| 输入里程/m | 输入偏距/m | 坐标 | 输出里程/m | 输出偏距/m | |
| x/m | y/m | ||||
| 7 360.000 | -3.000 | 3 378 643.673 | 453 425.223 | 7 360.000 | -3.000 |
| 7 440.000 | -3.000 | 3 378 631.229 | 453 504.250 | 7 440.000 | -3.000 |
| 7 520.000 | -3.000 | 3 378 618.785 | 453 583.276 | 7 520.000 | -3.000 |
| 7 600.000 | -3.000 | 3 378 606.340 | 453 662.302 | 7 600.000 | -3.000 |
| 8 200.000 | 6.000 | 3 378 482.566 | 454 248.934 | 8 200.000 | 6.000 |
| 8 300.000 | 6.000 | 3 378 456.547 | 454 345.349 | 8 300.000 | 6.000 |
| 8 400.000 | 6.000 | 3 378 428.392 | 454 441.163 | 8 400.000 | 6.000 |
| 8 500.000 | 6.000 | 3 378 398.115 | 454 536.327 | 8 500.000 | 6.000 |
| 11 760.000 | -12.000 | 3 376 401.141 | 457 025.664 | 11 760.000 | -12.000 |
| 11 820.000 | -12.001 | 3 376 348.967 | 457 055.594 | 11 820.000 | -12.001 |
| 11 880.000 | -12.000 | 3 376 296.480 | 457 084.917 | 11 880.000 | -12.000 |
| 11 940.000 | -12.001 | 3 376 243.752 | 457 113.748 | 11 940.000 | -12.001 |
| 12 000.000 | -12.000 | 3 376 190.849 | 457 142.202 | 12 000.000 | -12.000 |
| 12 060.000 | -12.000 | 3 376 137.838 | 457 170.397 | 12 060.000 | -12.000 |
| 12 120.000 | -12.000 | 3 376 084.782 | 457 198.449 | 12 120.000 | -12.000 |
| 12 180.000 | -12.000 | 3 376 031.725 | 457 226.468 | 12 180.000 | -12.000 |
| 注:就这16条记录而言,反算里程与原始里程的偏差均在0.1 mm以下。 | |||||
本文讨论了平曲线正反算方法,并着重研究了缓和曲线计算,在这些工作基础上得到了下列结论:
1) 构造线元表是一种优秀的预处理方法,有利于理清平曲线坐标计算思路,也适用于编程。
2) 在道路缓和曲线(回旋线型)参数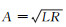
3) 某铁路平曲线数据16个临近点的反算结果与起始给定数据基本吻合,各点偏距偏差均在1 mm以下。
| [1] |
李青岳, 陈永奇. 工程测量学[M]. 3版. 北京: 测绘出版社, 2008: 182-186. Li Qingyue, Chen Yongqi. Engineering Surveying[M]. 3rd Ed. Beijing: Surveying and Mapping Press, 2008: 182-186. |
| [2] |
Wang Ke. Research on Calculation Method of Complex Curve of Railway Lines[J]. Lanzhou:Lanzhou Jiaotong University, 2018. |
| [3] |
冯晓, 李敏, 杨佳, 等. 不同类型缓和曲线的正算与反算的通用算法[J]. 测绘通报, 2008(6): 10-13. Feng Xiao, Li Min, Yang Jia, et al. A General Method of Direct and Inverse Coordinate Computation for Different Types of Transition Curve[J]. Bulletin of Surveying and Mapping, 2008(6): 10-13. |
| [4] |
高淑照, 史东宴. 缓和曲线非线性方程的快速解算[J]. 测绘通报, 2006(3): 28-30. Gao Shuzhao, Shi Dongyan. A Quick Solution to a Nonlinear Equation of Spiral Curve[J]. Bulletin of Surveying and Mapping, 2006(3): 28-30. DOI:10.3969/j.issn.0494-0911.2006.03.010 |
| [5] |
孔晨辉, 翁呷. 线路曲线的测设[J]. 测绘地理信息, 2017, 42(6): 69-72. Kong Chenhui, Weng Ga. Surveying of the Line Curve[J]. Journal of Geomatics, 2017, 42(6): 69-72. |
| [6] |
李全信. 线路测量中的正反算问题及应用[J]. 测绘通报, 2006(2): 36-38. Li Quanxin. The Direct and Inverse Solution in Route Survey and Its Application[J]. Bulletin of Surveying and Mapping, 2006(2): 36-38. DOI:10.3969/j.issn.0494-0911.2006.02.012 |
| [7] |
李全信. 线路中边桩坐标计算的通用Gauss-Legendre公式[J]. 工程勘察, 2002(3): 61-64. Li Quanxin. A Universal Gauss-Legendre Quadrature Formula for Computing Coordinates of Center and Side Stakes in Route Survey[J]. Geotechnical Investigation and Surveying, 2002(3): 61-64. |
| [8] |
孙建国, 苗贺. 基于Chebyshev走时逼近的三维多次反射射线计算[J]. 吉林大学学报(地球科学版), 2018, 48(3): 890-899. Sun Jianguo, Miao He. Computation of Three Dimensional Multi-Reflection Rays Based on Traveltimes Numerical Approximation[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(3): 890-899. |
| [9] |
李孟山, 李少元. 数值积分法计算线路中线坐标[J]. 石家庄铁道学院学报, 1999(3): 51-53. Li Mengshan, Li Shaoyuan. The Coordinate Computation of Central Line Using Numerical Integral[J]. Journal of Shijiazhuang Railway University, 1999(3): 51-53. |
| [10] |
李文科, 敖亭芝. 曲线坐标模型在道路计算中的应用[J]. 北京测绘, 2013(4): 59-62. Li Wenke, Ao Tingzhi. Application of Curvilinear Integral Model in Coordinate Calculation of Center Line[J]. Beijing Surveying and Mapping, 2013(4): 59-62. DOI:10.3969/j.issn.1007-3000.2013.04.017 |
| [11] |
李自康. 公路曲线线元坐标计算通用模型[J]. 勘察科学技术, 2017(5): 20-23. Li Zikang. General Model for Coordinate Calculation of Highway Curve Elements[J]. Site Investigation Science and Technology, 2017(5): 20-23. DOI:10.3969/j.issn.1001-3946.2017.05.005 |
| [12] |
黄金满, 林从谋, 李军心. 高速公(铁)路平竖曲线正反算的统一解法[J]. 测绘科学, 2008, 40(10): 3-10. Huang Jinman, Lin Congmou, Li Junxin. A General Method of Direct and Inverse Coordinate Computation for Korizontal and Vertical Curves of Expressway and Highspeed Railway[J]. Science of Surveying and Mapping, 2008, 40(10): 3-10. |
| [13] |
Koc W. Identification of Transition Curves in Vehicular Roads and Railways[J]. Logistics Infrastructure, 2015, 28(4): 31-40. |
| [14] |
Kobryń A. Universal Solutions of Transition Curves[J]. Journal of Surveying Engineering, 2016, 142(4): 04016010. DOI:10.1061/(ASCE)SU.1943-5428.0000179 |
| [15] |
Eslahchi M R, Dehghan M, Masjed-Jamei M. On Numerical Improvement of the First Kind Gauss-Chebyshev Quadrature Rules[J]. Applied Mathematics and Computation, 2005, 165: 5-21. DOI:10.1016/j.amc.2004.06.102 |
| [16] |
李德光.铁路线路中线空间坐标与里程换算模型的研究[D].成都: 西南交通大学, 2012. Li Deguang. The Research (on) Conversion Model Between Spatial Coordinate and Mileage in Railway Centerline[D]. Chengdu: Southwest Jiaotong University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10613-1012391987.htm |
| [17] |
同济大学计算数学教研室. 现代数值计算[M]. 北京: 人民邮电出版社, 2009: 123-132. Teaching and Research Section in School of Mathematical Science, Tongji University. Advanced Numerical Computing[M]. Beijing: Posts and Telecom Press, 2009: 123-132. |
| [18] |
李炯城, 林惜斌, 肖恒辉, 等. 高阶高斯型积分计算机求解算法[J]. 计算机工程与设计, 2012, 33(5): 1871-1875. Li Jiongcheng, Lin Xibin, Xiao Henghui, et al. Computer Algorithm for High-Degree Gauss-Type Quadrature[J]. Computer Engineering and Design, 2012, 33(5): 1871-1875. DOI:10.3969/j.issn.1000-7024.2012.05.039 |


