0 引言
近年来,随着无人机的应用发展,无人机航空磁力探测在航空物探领域发挥着重要的作用[1-2]。在航磁测量中,飞机上磁性元件产生的磁场叠加在地磁场之上会对磁力仪产生很大干扰,此叠加干扰磁场随着飞机飞行方向和姿态变化。干扰补偿模型是1950年Tolles首先根据磁干扰产生的原因及性质将磁干扰分解为恒定磁场、感应磁场和涡流磁场,并建立了磁干扰场的数学模型Tolles-Lawson方程(T-L方程)。1961年,Leliak[3]基于T-L方程设计了一套北—东—南—西航向的参考机动,干扰场是关于飞机机动的函数,从而建立了16项系数方程,根据系数求出干扰,最后将干扰从航磁数据中剔除;但该方法通过姿态角解算方向余弦的过程复杂。Leach[4]给出了利用三轴磁通门数据获取与飞机机动有关的方向余弦。Zhang等[5]认为不能直接获得目标磁场的方向余弦值,只能间接使用总场的强度来表示它。Zhou等[6]将磁通门传感器的进行数据滤波后用于表示方向余弦。王婕等[7]在固定翼无人机上安装磁通门开展补偿试验,但模型中忽略了涡流场对应的干扰项,模型中方向余弦的准确性对系数的稳定性有很大影响。吴佩林等[8]在无人直升机上以三轴磁通门求解方向余弦,并通过前馈网络实现了数据补偿。
本文以Leach磁通门数据求解方向余弦的方法进行航磁补偿,建立三轴磁通门数据理论模型,并以此验证补偿方法效果。最后,将此方法应用云南某无磁异常地区试飞磁通门数据进行干扰补偿。
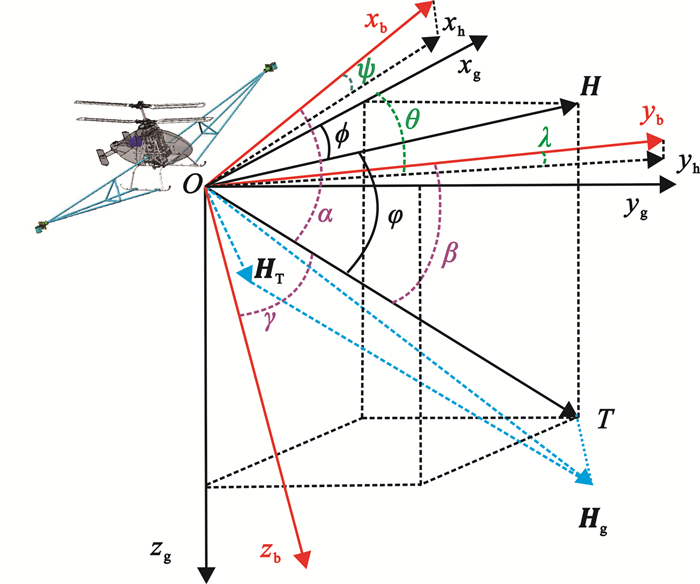
1 飞机磁场模型建立及求解 1.1 坐标系与飞机姿态飞机坐标系[9-10](图 1)坐标原点选在磁力仪探头的中心O;xb轴与飞机横轴平行,左机翼方向为正;yb轴与飞机纵轴平行,机首方向为正;zb轴与xb、yb轴所在平面正交,垂直机身,向下为正。在飞行试验平台上,磁力仪的三轴分别平行于飞机坐标系的xb、yb、zb轴。当地水平坐标系[9-10]原点与飞机坐标系原点重合,xg轴指向当地北子午线,yg轴垂直于xg轴指向东,zg轴与xg、yg所在平面正交垂直向下。
|
| 图 1 坐标系及飞机姿态 Fig. 1 Coordinate system and aircraft attitude |
|
|
飞机飞行姿态[3]可以分解为侧滚角(ψ)、俯仰角(λ)和侧滑角(θ)。其中:ψ为xb轴与xgOyg所在平面之间的夹角(xh为xb轴在xgOyg平面上的投影),自左翼向下为正;λ为yb轴与xgOyg所在平面之间的夹角,自机头向下为正;θ为yb轴在xgOyg平面上投影yh与xg轴的夹角,由北逆时针为正。
1.2 磁补偿模型建立飞机磁干扰场主要由恒定场、感应场和涡流场组成[11]。恒定场(Hp)为由飞机内铁磁性物体的剩余磁化产生的磁场,感应场(Hi)为由飞机内铁磁性物体受地磁场磁化产生的磁场,涡流场(Hec)为由飞机机身、机翼等软磁性金属材料切割地磁场产生的磁场,分别表示为:
 (1)
(1) 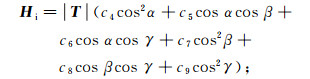 (2)
(2) 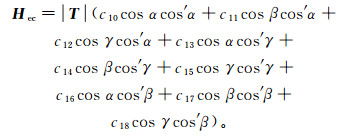 (3)
(3) 式中:T表示地磁场;c1,c2,…,c18为变量系数;α、β、γ分别表示飞机xb、yb、zb轴与T之间的夹角;cos′α、cos′β、cos′γ表示方向余弦cosα、cosβ、cosγ关于时间t的微分。则飞机干扰总磁场Ht表示为
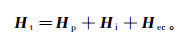 (4)
(4) 根据余弦函数关系式
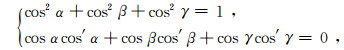 (5)
(5) 并结合式(1)—(4)整理得到
 (6)
(6) 式中, d1,d2,…,d16为16项补偿系数。
1.3 方向余弦获取三轴磁力仪测地磁场方向余弦存在测量误差[5](图 1),可能会对方向余弦产生一定影响。图 1中Hg表示Ht与T的矢量和。在磁通门求解方向余弦模型中,光泵磁力仪为原点O,飞机产生的干扰磁场强度大多在100~1 000 nT之间,并且传感器与飞机之间的距离越远,检测到的干扰越小。在本次试验飞行平台上,可将正北方向平飞时的三轴磁通门数据与地磁场在地面坐标系下的三分量值进行对比。经分析,干扰对地磁场矢量和磁通门矢量夹角余弦值产生的误差最大为1%;因光泵磁力仪固有特点,数据可用于16项补偿系数方程中干扰值Ht的求解。
假设Tbx,Tby,Tbz分别为地磁总场Tt在飞机坐标系下xb、yb、zb轴方向的投影大小,在忽略飞机干扰产生误差的条件下,可认为

则关于时间连续的方向余弦可表示为
 (7)
(7) 最小二乘法是求解多元线性回归的常用方法。此外,还有Praga-Alejo等[12]提出的岭回归估计改进算法等。假设光泵磁力仪和三轴磁通门有效采样点数为N,则根据式(6)可以列出含有n个方程的超定方程[13],线性方程可表示为
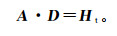 (8)
(8) 其中:
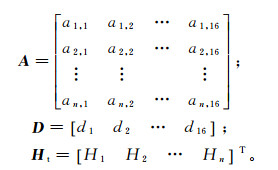
式中:
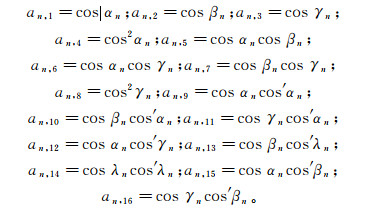
结合Leliak给出的参考机动,采用加拿大国立研究院航空处(National Aeronautical Establish-ment, NAE)提出的“1/2 FOM机动飞行”[14]方法,即在北—东—南—西上做±10°侧滚、±5°俯仰、±5°侧滑的机动(图 2),每种姿态时长5s,并间隔设置5s的水平飞行。
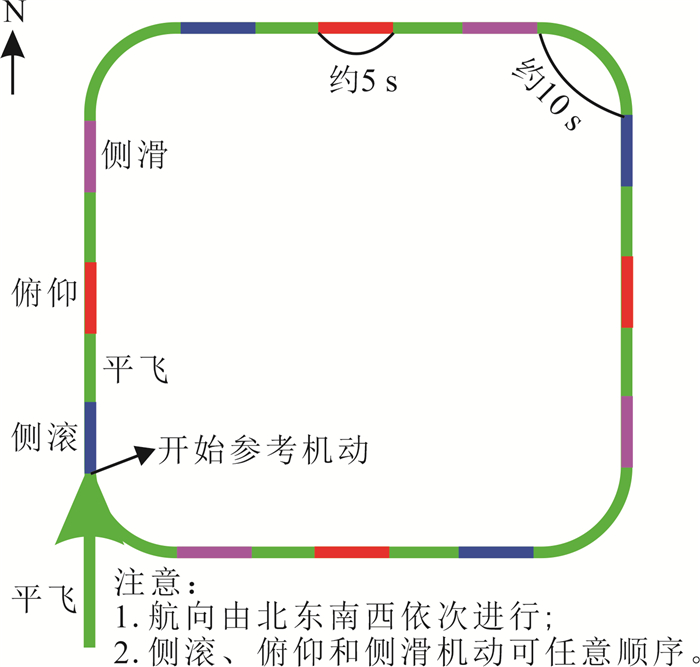
|
| 图 2 参考机动示意图 Fig. 2 Schematic of reference maneuver |
|
|
T-L方程中假设补偿飞行的场地地磁场强度恒定,因此当地水平坐标系下的地磁场三分量与飞机坐标系下的磁场三分量之间存在着坐标系旋转的关系[9-10],即地磁场三分量Tgx、Tgy、Tgz依次转动θ、ψ、λ,可获得飞机坐标系下的磁场三分量Tbx、Tby、Tbz:
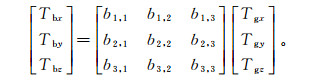 (9)
(9) 式中:
b1, 1=cosθcosψ;b1, 2=sinθcosψ;b1, 3=-sinψ;b2, 1=cosθsinλsinψ-sinθcosλ;b2, 2=sinθsinλ· sinψ+cosθcosλ;b2, 3=sinλcosψ;b3, 1=cosθ· cosλsinψ+sinθsinλ;b3, 2=sinθcosλsinψ- cosθ·sinλ;b3, 3=cosλcosψ; Q取值在北航向为±5°, 在东航向为90°±5°,在南航向为180°±5°,在西航向为270°±5°。
以云南某地试验场磁场为例,由WMM2015[15]模型计算得到T=46 861.6 nT, μ=-1.297 6°, φ=36.662 7°, (μ为磁偏角,φ为磁倾角),则可得到Tgx、Tgy、Tgz,进而得到三轴与飞机坐标系平行的磁通门Tbx、Tby、Tbz数据模型。此模型要求飞机严格按照参考机动飞行(北—东—南—西依次进行),否则难以验证模型误差。同时在光泵数据中设置20 nT的异常信号,用于验证补偿效果。
依照图 2所示参考机动设计姿态角理论模型,通过式(9)计算得到磁通门、光泵磁力仪理论模型分别如图 3、图 4所示。
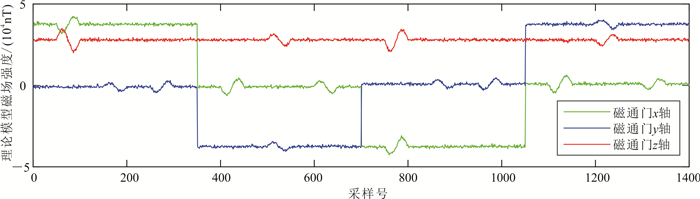
|
| 图 3 三轴磁通门理论模型 Fig. 3 Three-axis fluxgate theory model |
|
|
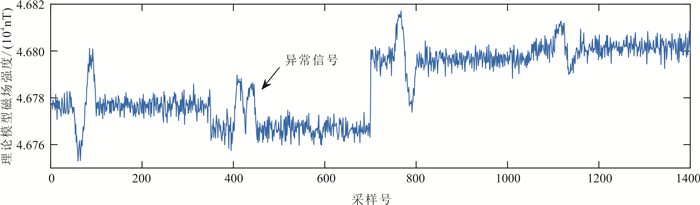
|
| 图 4 光泵磁力仪理论模型 Fig. 4 Optical pumping magnetometer theory model |
|
|
本次研究基于Matlab软件编写了补偿程序。只需输入三轴磁通门磁力仪三分量数据、光泵磁力仪总场数据以及飞行姿态所在时间段数据,即可完成补偿。
通过理论模型验证补偿程序,图 5表示自行设计的补偿程序能检测出磁异常信号。
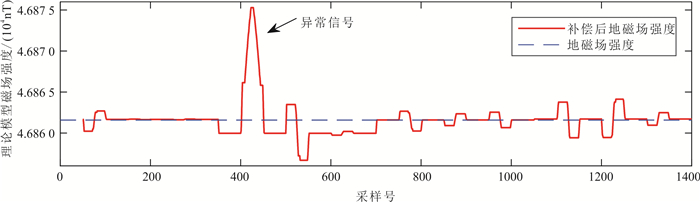
|
| 图 5 理论模型补偿结果 Fig. 5 Theoretical model compensation result |
|
|
试验飞行平台采用吉林大学自研重载荷智能化物探专用无人直升机[16](图 6),采用自研发靶向溅射技术喷射低磁防静电材料作为机身涂层,导电性能大幅提高,易于放电,由机动产生的干扰较小。平台搭载TFM100-G2型三轴磁通门磁力仪和加拿大GEM公司的GSMP-35A型高精度钾光泵磁力仪,配套航磁收录系统,该系统磁场范围为20 000~ 100 000 nT,采样率10 Hz。

|
| 图 6 重载荷智能化物探专用无人直升机 Fig. 6 Heavy-duty intelligent exploration special unmanned helicopter |
|
|
依托前期在云南某试验场地开展的航磁系统性能测试,该试验场地地磁场变化小,地形较为平坦。并在此进行了补偿飞行试验,飞行路线如图 7所示,飞行高度平均155 m(基于大地水准面)。
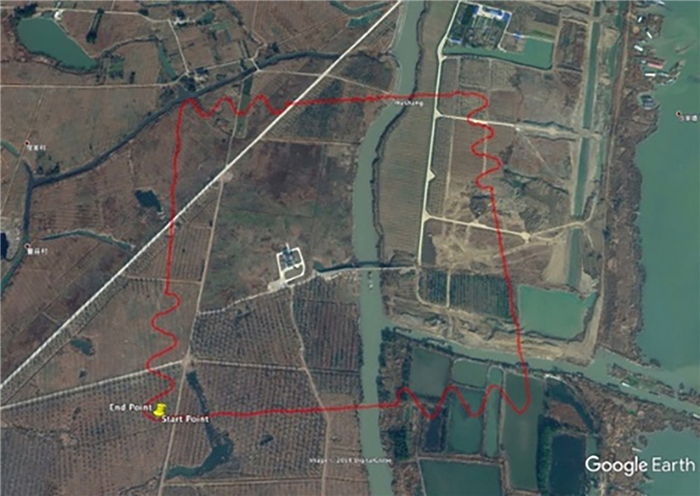
|
| 图 7 飞行轨迹 Fig. 7 Flight trajectory |
|
|
测量数据包含许多不同类型的噪音,为得到只受飞机磁干扰的总场数据,在补偿过程中须对数据进行滤波[17-18]。为了叙述方便,本文采用巴特沃斯滤波器以三轴磁通门数据为列进行滤波处理(图 8),滤波后可更精确地估算16项补偿系数。
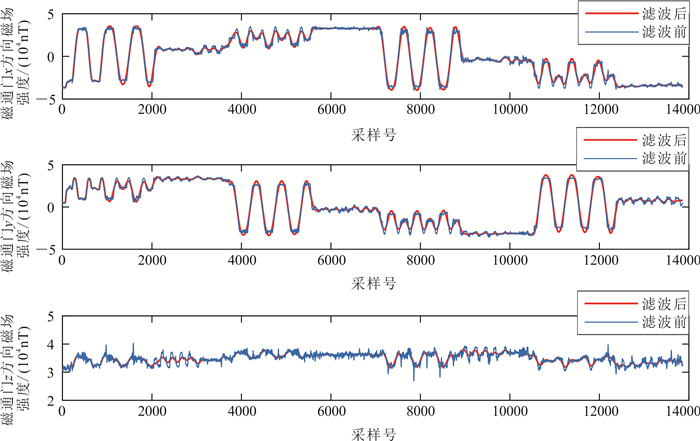
|
| 图 8 实测三轴磁通门数据巴特沃斯滤波 Fig. 8 Measured three-axis fluxgate data with Butterworth filter |
|
|
将滤波后的数据以最小二乘法解出16项补偿系数,再从总场值中剔除干扰场,从而得到补偿后的地磁场(图 9)。从图 9中补偿曲线可以看出补偿效果明显,自行设计的程序可以完成航磁补偿任务。
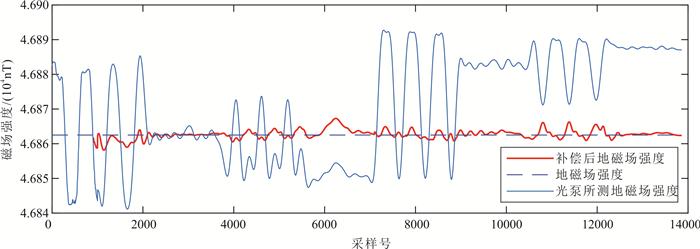
|
| 图 9 实测数据补偿后磁场强度对比 Fig. 9 Compensated magnetic field amplitude comparison of measured data |
|
|
目前实际探测工作中主要使用的量化指标为NAE提出的补偿后残留磁干扰标准差σ[19],并以“改善比”(Ri)辅助评估补偿效果。σ是根据参考机动补偿后剩余磁干扰的标准差,小于标准值0.08视为合格;Ri为补偿前后标准差的比值,其值越高,说明补偿效果越好。经计算,σ=0.144,Ri=10.611;在高精度航磁测量中,磁日变将在航磁数据中引入较大的误差,因此,进行磁日变矫正是十分必要的。去除日变后,σ=0.069,Ri=19.364,对比去除日变前效果有明显提升,达到补偿标准值的要求。
5 结论1) 机载磁测系统需要高精度磁干扰补偿算法,基于T-L方程建立了飞机磁干扰补偿模型,并计算了16项补偿系数。以坐标旋转关系构建的磁通门理论模型,可在飞行试验前用于验证补偿模型的可信度。三轴磁通门理论模型数据经补偿后,补偿系统能消除干扰场,并保留异常信号。
2) 利用磁通门三轴数据解算方向余弦可免去方向余弦繁琐的计算过程。将本文设计的补偿算法用于云南某试验区的实测航磁数据,采用标准差能准确地评价磁补偿效果,实际补偿效果较好;基于磁通门估计的航磁补偿方法是有效的。
| [1] |
耿美霞, 黄大年, 杨庆节. 改进的TRUST方法在航磁数据线性特征增强中的应用[J]. 吉林大学学报(地球科学版), 2014, 44(4): 1333-1339. Geng Meixia, Huang Danian, Yang Qingjie. Application of Improved TRUST Method in Enhancing Linear Trends of Aeromagnetic Data[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(4): 1333-1339. |
| [2] |
黄大年, 于平, 底青云, 等. 地球深部探测关键技术装备研发现状及趋势[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1485-1496. Huang Danian, Yu Ping, Di Qingyun, et al. Development of Key Instruments and Technologies of Deep Exploration Today and Tomorrow[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5): 1485-1496. |
| [3] |
Leliak Paul. Identification and Evaluation of Magnetic Field Sources of Magnetic Airborne Detector Equipped Aircraft[J]. IRE Trans Aerospace Navigational Elect, 1961, 8(3): 95-105. |
| [4] |
Leach B W. Aeromagnetic Compensation as a Linear Regression Problem[J]. Information Linkage Between Applied Mathematics and Industry, 1980, 2(2): 139-161. |
| [5] |
Zhang Ning, Lin Chunsheng. Study on Model Compensation of Aircraft Magnetic Interference[J]. Intelligent Computing and Intelligent Systems, 2010, 10(2): 782-785. |
| [6] |
Zhou Jianjun, Lin Chunsheng, Chen Hao. A Method for Aircraft Magnetic Interference Compensation Based on Small Signal Model and LMS Algorithm[J]. Chinese Journal of Aeronautics, 2014, 27(6): 1578-1585. DOI:10.1016/j.cja.2014.10.025 |
| [7] |
王婕, 郭子祺, 乔彦超. 固定翼无人机航磁测量系统的磁补偿问题初探[J]. 地球物理学进展, 2015, 30(6): 2931-2937. Wang Jie, Guo Ziqi, Qiao Yanchao. Magnetic Compensation of the Fixed-Wing UAV Aeromagnetic Detection System[J]. Progress in Geophysics, 2015, 30(6): 2931-2937. |
| [8] |
吴佩霖, 张群英, 李光, 等. 航磁全轴总场梯度系统补偿算法研究[J]. 电子与信息学报, 2017, 39(12): 3030-3038. Wu Peilin, Zhang Qunying, Li Guang, et al. Research on Compensation Algorithm for Three Axial Gradient Aeromagnetic Prospection System[J]. Journal of Electronics & Information Technology, 2017, 39(12): 3030-3038. |
| [9] |
李康, 黄胜, 赵辉. GPS坐标系的转换及其在姿态求解中的应用[J]. 指挥控制与仿真, 2008, 30(5): 113-118. Li Kang, Huang Sheng, Zhao Hui. Transformation of GPS Coordinate Systems and Its Application in Attitude Determination[J]. Command Control and Simulation, 2008, 30(5): 113-118. DOI:10.3969/j.issn.1673-3819.2008.05.032 |
| [10] |
陈哲. 全姿态飞机捷联式系统姿态角的计算[J]. 航空学报, 1982, 18(3): 76-85. Chen Zhe. Calculation for Attitude Angles of an All Attitude Strapdown System[J]. Journal of Aeronautics, 1982, 18(3): 76-85. |
| [11] |
Bickel S H. Small Signal Compensation of Magnetic Fields Resulting from Aircraft Maneuvers[J]. IEEE Trans on AES, 1979, 15(4): 518-525. |
| [12] |
Praga-Alejo R J, Torres-Trevio L M, Pia-Monarrez M R. Optimal Determination of K Constant of Ridge Regression Using a Simple Genetic Algorithm[J]. Electronics, Robotics and Automotive Mechanics Conference, 2008, 62(2): 39-44. |
| [13] |
刘首善, 唐林牧, 许庆丰, 等. 航磁补偿技术及补偿质量的评价方法[J]. 海军航空工程学院学报, 2016, 31(6): 641-647. Liu Shoushan, Tang Linmu, Xu Qingfeng, et al. Investigation of Seromagnetic Compensation Technology and Performance Assessment Method[J]. Journal of Naval Aeronautical and Astronautical University, 2016, 31(6): 641-647. |
| [14] |
Noriega G. Performance Measures in Aeromagnetic Compensation[J]. Leading Edge, 2011, 30(10): 1122-1127. DOI:10.1190/1.3657070 |
| [15] |
徐如刚, 黎哲君, 张玮晶, 等. EMM2010模型在中国大陆的精度评估及其适用性[J]. 吉林大学学报(地球科学版), 2014, 44(3): 1018-1030. Xu Rugang, Li Zhejun, Zhang Weijing, et al. Accuracy and Application of EMM2010 in Chinese Mainland[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(3): 1018-1030. |
| [16] |
于显利.重载荷无人直升机多任务航空物探系统[C]//2014年中国地球科学联合学术年会: 专题65: 深部探测技术与实验: 探测仪器与装备论文集.北京: 中国地球物理学会, 2014: 4. Yu Xianli. Heavy-Duty Unmanned Helicopter Multi-Task Aeronautical Geophysical System[C]//2014 China Earth Science Joint Academic Annual Meeting: Special 65: Deep Exploration Technology and Experiments: Proceedings and Equipment Proceedings. Beijing: China Geophysical Society, 2014: 4. |
| [17] |
蔡剑华, 肖晓. 基于组合滤波的矿集区大地电磁信号去噪[J]. 吉林大学学报(地球科学版), 2017, 47(3): 874-883. Cai Jianhua, Xiao Xiao. De-Noising of Magnetotelluric Signal in the Ore Concentration Area Based on Combination Filter[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(3): 874-883. |
| [18] |
朱凯光, 李玥, 孟洋, 等. 最小噪声分离在航空电磁数据噪声压制中的应用[J]. 吉林大学学报(地球科学版), 2016, 46(3): 876-883. Zhu Kaiguang, Li Yue, Meng Yang, et al. Application of Minimum Noise Fraction on Noise Removal for Airborne Electromagnetic Data[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(3): 876-883. |
| [19] |
王林飞, 薛典军, 段树岭, 等. 航磁软补偿动作规范性评价[J]. 物探与化探, 2016, 40(2): 365-369. Wang Linfei, Xue Dianjun, Duan Shuling, et al. The Method of Quality Assessment for Digital Magnetic Compensation and Software Realization[J]. Geophysical and Geochemical Exploration, 2016, 40(2): 365-369. |



