2. 中国核电工程有限公司郑州分公司, 郑州 450012
2. Zhengzhou Branch, China Nuclear Power Engineering Co., Ltd., Zhengzhou 450012, China
0 引言
确定地质体边缘位置是重磁解释的一项重要内容。为了更好地刻画位场源的边界,国内外学者提出了很多高效的边缘增强算法。垂向导数法利用位场数据垂向导数零值位置来圈定地质体边界[1-2]。Cordell[3]于1979年提出利用总水平导数极大值来刻画不同密度体的边缘位置。1972年,Nabighian用二维解析信号振幅法对磁力异常的边界进行了识别[4],随后其又提出了三维解析信号的理论,并获得广泛应用和进一步发展[5-6]。Miller等[7]在1994年采用倾斜角法均衡了强弱异常的幅值,对埋深较深地质体的边缘起到了增强作用。Verduzco等[8]在2004年利用倾斜角总水平导数对源边界信息进行加强。θ图方法由Wijns等[9]于2005年提出,通过计算总水平导数与总梯度模量之比的最大值来圈定异常地质体的边界位置,取得了很好的识别效果。Fitzgerald等[10]在2006年利用反双曲斜导数进行边界信息加强。杨高印等[11]提出具有低通滤波性质的小子域滤波方法,提高了对目标地质体边界的辨别能力。Cooper等[12]在2008年通过归一化标准差法对地质体的边界进行识别。Ma等[13]在2012年利用归一化总水平导数方法对地质体边界进行识别,并取得了较好的效果。王彦国等[14]提出归一化差分法,在边界增强方面取得了较好的效果。Zhou等[15]将图像处理领域的三维构造张量引入到位场数据边界增强中,并定义了基于构造张量的边界识别滤波器。除此之外,还有许多学者提出了其他形式的滤波器。以上这些滤波器多数是基于位场数据的导数构建而成的,常存在的问题包括抗噪能力较差、导数计算时带入误差、增强结果出现虚假边界等[16-18]。
数学形态学是基于积分几何、随机集合论等数学理论发展来的一种非线性图像(信号)处理和分析理论,由法国地质学家Matheron和Serra于1964年共同创立。Serra[19]在1982年出版了专著《ImageAnalysis and Mathematical Morphology》之后,数学形态学进入到一个新的发展阶段,理论变得更加成熟,应用领域亦更加广泛。经过几十年的发展,数学形态学已在图像处理、图形分析、计算机视觉、电能扰动和边缘检测等方面得到了成功的应用[20-23]。刘循等[24]通过多尺度形态滤波对图像边缘进行检测,得到噪声存在条件下较为理想的图像边缘。王慧锋等[25]利用复合形态学滤波器对图像进行处理,得到较好的图像边缘信息。李杰等[26]在2012年采用数学形态学细化算法对图像边缘进行细化处理,并取得了较好的结果。数学形态学在地球物理信号处理领域也有一定应用,但主要集中在地震信号和电磁信号的处理方面。王润秋等[27]于2005年通过数学形态学滤波器压制地震记录中的野值脉冲噪声。Faucon等[28]将数学形态学应用到地震裂缝的检测,并取得了较好的结果。陈辉等[29]在2009年将数学形态学与地震信号处理相结合,探讨了数学形态学在地震信号处理中的应用。2012年,汤井田等[30]采用数学形态学滤波器,有效地剔除了大尺度干扰及基线漂移,较好地还原了大地电磁信号的原始特征。Huang等[31-32]将数学形态学滤波应用于地震数据的噪声处理中,并取得了较好的效果。李振苓等[33]于2017年通过实际数据测试,验证了数学形态学滤波方法用于电成像测井资料缝洞孔隙度谱计算的有效性。在位场数据边缘增强方面,Li等[34]采用总水平导数的数学形态学腐蚀结果和总水平导数的数学形态学膨胀结果的比值(EMM)来圈定位场源的边缘,但该方法对噪声比较敏感,且针对同时含有正负异常的地质情况,输出结果中有额外边缘的产生。
为了实现更好的位场数据边缘增强效果,本文将数学形态学的腐蚀、膨胀、开、闭等4个基本运算进行组合叠加,构造了一个新的位场数据边缘增强滤波器。并利用合成和实测数据测试该滤波器的应用效果,以期更清晰地对地质体边缘进行刻画。
1 方法原理 1.1 数学形态学基本运算数学形态学的基本思想是通过集合来定量描述目标信号的几何结构,即利用预先定义好的结构元素与信号的几何特征进行局部匹配或修正,同时保留目标信号的主要形状特征,以达到抑制噪声提取有用信息的目的。其中,结构元素是数学形态学的基本要素,具有任意形状和尺寸。
数学形态学的基本运算包括腐蚀、膨胀、开运算和闭运算。以离散化的重力数据为例,设f(x, y, E)为(x, y)点的重力异常值,E(i, j)为结构元素,则数学形态学膨胀和腐蚀运算分别定义为:
 (1)
(1)  (2)
(2) 式中:符号⊕和Θ分别表示膨胀和腐蚀运算;P、Q分别为异常值和结构元素的定义域。
数学形态学膨胀、腐蚀实质上是在结构元素定义域内的极大、极小运算。膨胀运算可以填平边界不平滑的凹陷部分,腐蚀运算可以剔除边界不平滑的凸起部分。形态学开、闭运算是在膨胀和腐蚀运算基础上组合而来的,分别定义如下:
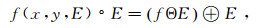 (3)
(3)  (4)
(4) 式中,符号°和·分别表示形态开和形态闭运算。开运算用来消除目标信号中不必要的细节,使目标信号的轮廓光滑,可以抑制正脉冲噪声;闭运算用来填平目标信号中的小空洞,可以抑制负脉冲噪声。因此,为了更好地提取目标信号的几何结构,往往通过多个数学形态学基本运算的变形叠加来构建效果较好的复合数学形态学滤波器。
1.2 结构元素选取结构元素在数学形态学运算中的作用类似于一般信号处理时的滤波窗口或参考模板,其形状和尺寸都对形态学的运算结果产生影响。常见的结构元素有直线形、正方形、菱形、六边形、圆盘形等。直线形结构元素较为简单,其按照一定方向处理图像。从本质上说,其他任何形状的结构元素都可以看成是直线形结构元素矩阵的叠加。在实际应用中,结构元素的形状设计通常取决于待处理目标信号的几何性质,但有时并不是越贴近实际复杂程度越好,还需要兼顾运算效率。从结构元素的尺寸上来说,当采用小尺度的结构元素提取目标信号边缘特征时, 可以获得较为准确的边缘位置,且保留较多的边缘细节,得到更为连贯的边缘曲线;当采用大尺度的结构元素时,所获得的边缘较粗,只能描述待处理信号的大致边缘轮廓[35]。因而,需要获得较为丰富的目标信号几何形状时,一般选取较小尺度的结构元素。
1.3 数学形态学滤波器构造基于数学形态学的基本运算,可以构造出抗噪膨胀型形态边缘检测算子Md(x, y, E)和抗噪腐蚀型形态边缘检测算子Me(x, y, E),分别如下[36]:
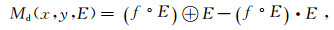 (5)
(5)  (6)
(6) 这两个算子在噪声污染的图像边缘检测中可以有效滤除噪声,取得较好的边缘图像。但由于以膨胀运算为基础的边缘检测往往使输出图像边缘变得模糊,而以腐蚀运算为基础的边缘检测会使输出结果丢失一些细节[36]。为了减小输出结果的模糊性,同时保留较多的边缘细节,可以将Md和Me算子进行改进。通过结合不同算子的特点,构造出新的边缘增强滤波器MEA:
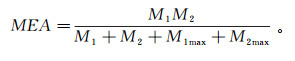 (7)
(7) 其中:
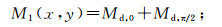 (8)
(8) 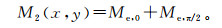 (9)
(9) 式中:Md,0和Me,0分别为算子Md和Me在结构元素为E0时的结果;Md,π/2和Me,π/2分别为算子Md和Me在结构元素为Eπ/2的结果;M1max和M2max分别为M1和M2的最大值。在兼顾滤波效果的前提下,尽可能简化结构元素设计,故本文选取线形结构元素。水平方向的结构元素对竖直方向的边缘比较敏感,竖直方向的结构元素对水平方向的边缘比较敏感,因此本文选择0°和90°两个方向的线形结构元素来对位场数据进行边缘刻画。为了使输出结果保留较多的边缘细节,两个方向结构元素的尺度大小均为3×3,E0和Eπ/2分别为水平方向和竖直方向的线形结构元素。M1max和M2max可以避免分母中零值情况的出现。通过滤波器MEA输出结果的极大值位置可以对位场数据的边缘进行圈定。
2 合成数据试验 2.1 板状体模型试验板状体是简单且典型的地质体模型,可以代表实际情况下沿走向方向延伸较长的一些岩脉、矿脉、岩墙等[37]。通过板状体产生的位场数据来测试滤波器MEA对位场数据边缘增强的有效性(图 1)。
首先建立单一的有限延伸板状体模型(图 1e),板状体宽20 m,高30 m,水平中心位置为0 m,中心埋深为17 m,剩余密度为2×103 kg/m3。图 1a显示了图 1e模型的重力异常。图 1c是图 1a重力异常的MEA滤波结果,可以看出曲线极大值位置与水平方向上-10 m与10 m处准确对应。
然后构造一个由两个板状体组成的地质模型(图 1f),这两个板状体的宽均为20 m,高均为30 m,水平中心位置分别为-20 m和20 m,中心埋深均为17 m,剩余密度分别为2×103 kg/m3和-2×103 kg/ m3。该模型的重力异常如图 1b所示。图 1d为滤波器MEA对图 1b异常的处理结果,可以看出两板状体的边界位置与曲线极大值位置准确吻合。
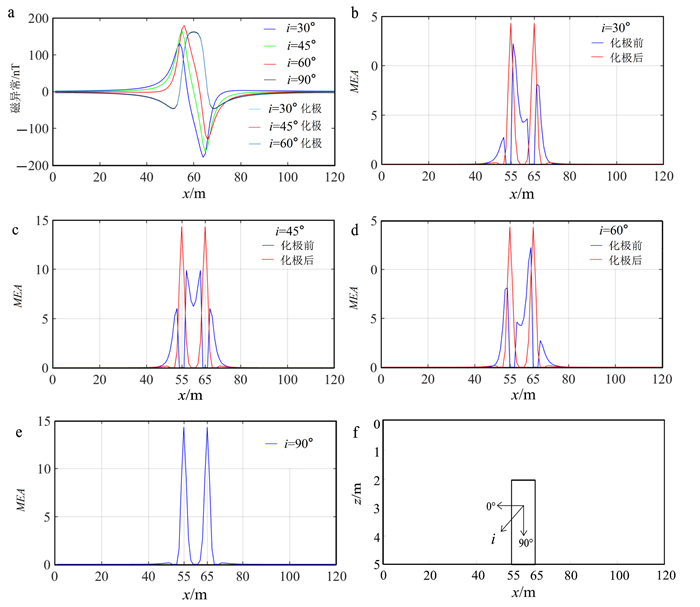
为进一步展示所提出方法的有效性,利用滤波器MEA对板状体产生的磁异常数据进行处理,结果如图 2所示。图 2a显示了一个宽10 m的板状体在有效磁化倾角分别为30°、45°、60°和90°时的磁异常结果,板状体模型位置如图 2f所示。利用滤波器MEA分别对这些原始磁异常进行了处理,可以看出:当有效磁化倾角为30°和60°时(图 2b、d蓝色曲线),曲线中两个较高的波峰位置与模型的实际边缘有一定对应,但不准确;当有效磁化倾角为45°时(图 2c蓝色曲线),MEA对板状体磁异常处理所获得的边缘与实际边缘偏差较大,曲线极大值位置与板状体边缘均没有较好地对应;当有效磁化倾角为90°时(图 2e),曲线极大值位置与模型边缘准确对应。
|
| a.板状体模型磁异常及其化极结果;b、c、d、e.有效磁化倾角(i)为30°、45°、60°、90°时的MEA处理结果;f.模型位置示意图。 图 2 板状体模型磁异常及MEA方法边缘增强结果 Fig. 2 Magnetic anomalies of plate models and edge enhancement results by MEA method |
|
|
为了更好地对磁异常数据的边缘进行增强,尝试通过对磁异常作化极处理,消除倾斜磁化的影响后再进行MEA计算。有效磁化倾角分别为30°、45°、60°的板状体磁异常化极后的结果如图 2a所示,可以看出,它们化极后的曲线与有效磁化倾角为90°时磁异常的曲线重合。对化极后的结果分别进行MEA处理,结果如图 2b、c、d中红色曲线所示,可以看出,所识别的边缘位置与板状体的实际边缘位置准确吻合。因此使用MEA方法刻画磁异常边缘之前,应先对磁异常数据进行化极处理。
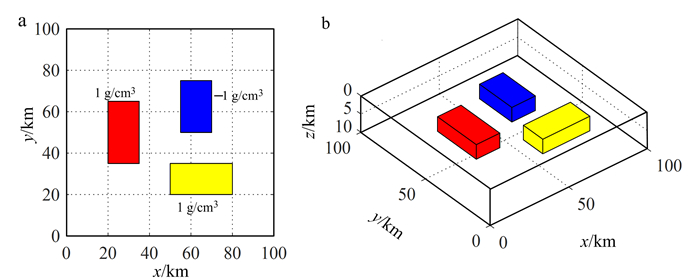
2.2 三维模型试验及与传统方法对比直角棱柱体是一个很有实际意义的地质体模型,当底面很深时可代表侵入岩,当厚度较小时可表示岩床等。因而本文通过建立一个由3个棱柱体组成的地质模型来测试MEA方法的应用效果,并将其与以往典型方法的处理效果进行对比。首先假设3个棱柱体的剩余密度分别为1、1、-1 g/cm3,中心埋深分别为4、3和4 km,3个棱柱体的位置平面图和三维图如图 3所示。图 4a为该地质体模型的原始重力异常。采用倾斜角法、倾斜角总水平导数法、θ图法、EMM、M1、M2和MEA方法分别对图 4a中的重力异常进行边缘增强,结果如图 4b—h所示。
|
| a.平面图;b.三维图。 图 3 三维模型位置图 Fig. 3 The location of the 3D model |
|
|

|
| a.原始重力异常;b.倾斜角法;c.倾斜角总水平导数法;d. θ图法;e. EMM法;f. M1法;g. M2法;h. MEA法。 图 4 三维模型数据边缘增强结果 Fig. 4 Edge enhancement results of 3D-model data |
|
|
由图 4b可见,倾斜角能很好地对模型中的正异常边缘信息进行增强,但在负异常周围存在明显的虚假异常,增加了异常数据的解释难度。由图 4c可以看出,倾斜角总水平导数法对于实际地质体的边缘位置描述不准确,不仅出现了虚假边界,而且输出边缘比较发散。θ图法能同时增强正负重力异常的边缘位置,但结果比较发散,而且由于额外边界的存在,使增强的边界信息有连接在一起的趋势(图 4d)。由图 4e可以看出,EMM方法获得的结果边缘比较收敛,线条较细,但不足的是,在模型异常体的周围存在虚假边缘信息,增加异常数据的解释难度。M1、M2、MEA这3种方法对含有负异常的地质体模型边缘有很好的增强效果,输出结果的局部极大值位置对应地质体的边缘位置(图 4f、g、h)。相比前几种方法,将抗噪腐蚀性和抗噪膨胀性算子结合起来的MEA方法所增强的边缘比较收敛,且不存在虚假边界,能更加清晰地刻画出地质异常体的边缘位置(图 4h)。
为了进一步展示MEA方法的应用效果,对添加噪声的三维模型进行了测试,并与其他几种方法的处理效果进行了对比。图 5a为图 4a的重力异常添加了均值为0、方差为2的高斯白噪声的结果,利用以上几种边缘增强方法分别对该结果进行处理。图 5b是倾斜角法的处理结果,可以看出该方法对高斯噪声非常敏感,尽管在正异常局部对异常体的边缘有一定的显示,但在负异常周边,根据倾斜角的零值点位置,几乎不能识别出负异常体的边缘。倾斜角总水平导数法不能有效滤除高斯噪声的干扰,导致异常体边缘的增强效果较差(图 5c),基本失去对异常体边缘的刻画能力。θ图法对图 5a模型的处理结果如图 5d所示,在异常体实际位置附近,结果中局部极大值表现出一定的连续性,与异常体的边缘有一定对应;但由于该方法与前两种处理方法一样,表现出较差的抗噪能力,并不能真正描述出实际异常体的边缘位置。这3种方法抗噪能力差,边缘增强能力不佳,主要因为这3种方法的滤波算子都是基于位场数据导数构建的结果。EMM方法基于数学形态学的膨胀和腐蚀运算构建,能大致圈定出异常体的边缘位置,但由于算子比较简单,导致结果出现斑点状高值,给边缘的识别带来了一定的干扰(图 5e)。图 5f是MEA方法的处理结果,该方法对噪声不敏感,可以很好地消除高斯噪声的干扰,能有效增强异常体的边缘位置,且相比前几种边缘增强方法,MEA方法抗噪能力更强,所获得的结果更清晰。

|
| a.原始重力异常;b.倾斜角法;c.倾斜角总水平导数法;d. θ图法;e. EMM法;f. MEA法。 图 5 含噪声的三维模型数据边缘增强结果 Fig. 5 Edge enhancement results of 3D-model data with noise |
|
|
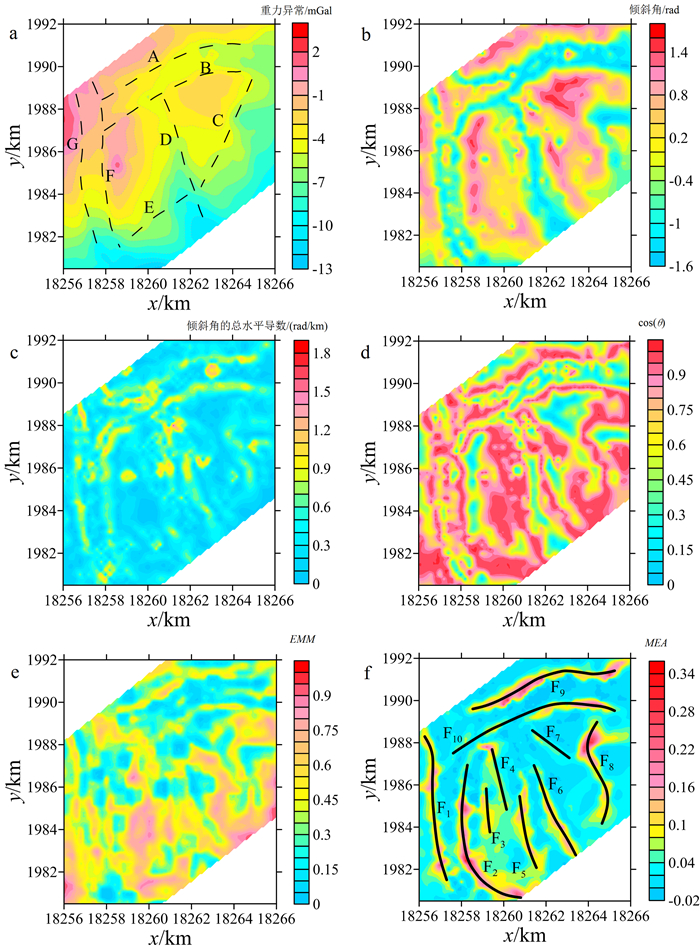
为了验证所提出方法的实际应用效果,本文对老挝万象盆地钾盐矿区的布格重力数据进行处理。重力测量比例尺为1:50 000,异常精度约为0.036 6 mGal。图 6a是研究区布格重力异常图,可以看出研究区布格重力异常值较小,除西北部显示出一定的正异常外,其余区域多表现为重力负异常。前人[38]认为,万象盆地区域低重力异常主要由低密度的岩盐和钾盐矿所引起,代表盐类矿物埋藏浅、厚度大,高重力异常则代表盐类矿物埋藏深、厚度小;而且该区域有利的钾盐成矿区均处于低异常区的边缘位置。研究区内存在两个明显的低异常圈闭,因此对该重力异常数据进行边缘增强具有重要意义。图 6a中的虚线是根据遥感数据推断的构造线位置[39],但并不足够详细。为了更好地确定研究区内重力异常数据的边缘位置,利用倾斜角法、倾斜角总水平导数法、θ图法、EMM方法及MEA方法分别对该重力数据进行处理,从而对研究区的构造进行更好地划分。处理结果显示,以几种方法可以大致刻画出一些主要的构造线,且这些构造线形态与遥感数据推断的构造线A、B、D、F、G基本吻合,但也存在一些不足:倾斜角法处理结果中具有孤立的较小零值点圈闭存在,给重力异常数据的解释带来困难(图 6b);倾斜角总水平导数法所显示的边缘增强结果比较杂乱,推断是由于该方法对噪声比较敏感造成的(图 6c);θ图法和EMM方法结果的最大值所对应的边缘位置连续性差,而且所识别出的边缘不光滑(图 6d、e)。相比前几种方法,根据MEA方法所获得的地质体边缘比较清晰连续,且与遥感数据所推断的结果吻合较好;同时相比遥感结果,利用该方法呈现出的构造信息更加丰富(图 6f)。
根据图 6f的结果,该区的构造线主要可分为北东东向和北北西向两组:北东东向构造线包括F9、F10,北北西向构造线主要包括F1、F3、F4、F5、F6等。从构造规模上来讲,F1、F2、F9和F10规模较长,推测其控制盆地的形成;作为次一级构造,F3、F4、F5和F6规模较小,且在走向上与F1大致平行,推测它们与F1在同一应力的作用下形成于同一时期。从切割关系来讲,北东东向的断裂切割北北西向的断裂,因此,相比F1、F3、F4等,F9和F10形成时间较晚。构造交汇处往往是矿床富集的最佳部位,同时,该区低异常区的边缘部位是钾盐矿的有利赋存位置;因而推断F9和F10的形成可能为钾盐矿床提供了更加有利的成矿环境,而且成矿的有利位置可能处于F9和F10与北北西向构造线的交汇部位。
4 结论1) 本文基于数学形态学膨胀、腐蚀、开、闭等算子的性质特点,提出了一种新的边缘增强方法(MEA)。该方法容易实现,且不需要计算位场数据的导数。
2) 板状体模型试验表明,新提出的MEA方法可以有效地对异常体的边缘进行增强;另外,在对磁异常进行MEA处理时,应当先对磁异常数据进行化极。
3) 三维模型试验及与前人几种方法对比的结果表明:MEA方法具有更强的适用性,能够更加清晰地圈定地质体的边缘位置;在地质模型中正负密度体同时存在时,MEA方法不产生虚假的额外边界;MEA方法具有更强的抗噪能力,能较好地消除高斯噪声干扰。
4) 将MEA方法应用到老挝万象盆地钾盐矿区的布格重力异常数据处理与解释中,亦取得了较好的效果,即获得的构造线更加连续清晰,并且结合以往地质资料,对研究区的有利成矿位置作了进一步推断。
| [1] |
Evjen H M. The Place of the Vertical Gradient in Gravitational Interpretations[J]. Geophysics, 1936, 1(1): 127-136. DOI:10.1190/1.1437067 |
| [2] |
Hood P J, Teskey D J. Aeromagnetic Gradiometer Program of the Geological Survey of Canada[J]. Geophysics, 1989, 54(8): 1012-1022. DOI:10.1190/1.1442726 |
| [3] |
Cordell L. Gravimetric Expression of Graben Faulting in Santa Fe Country and the Espanola Basin[C]//Ingersoll R V, Woodward L A, James H. New Mexico Geological Society 30th Annual Fall Field Conference Guidebook.[S. l.]: New Mexico Geological Society, 1979: 59-64.
|
| [4] |
Nabighian M N. The Analytic Signal of Two-Dimensional Magnetic Bodies with Polygonal Cross-Section:Its Properties and Use for Automated Anomaly Interpretation[J]. Geophysics, 1972, 37(3): 507-517. DOI:10.1190/1.1440276 |
| [5] |
Roest W R, Verhoef J, Polkington M. Magnetic Interpretation Using the 3-D Analytic Signal[J]. Geophysics, 1992, 57(1): 116-125. DOI:10.1190/1.1443174 |
| [6] |
Hsu S, Sibuet J C, Shyu C. High-Resolution Detection of Geologic Boundaries from Potential Field Anomalies:An Enhanced Analytic Signal Technique[J]. Geophysics, 1996, 61(2): 373-386. DOI:10.1190/1.1443966 |
| [7] |
Miller H G, Singh V. Potential Field Tilt:A New Concept for Location of Potential Field Sources[J]. Journal of Applied Geophysics, 1994, 32: 213-217. DOI:10.1016/0926-9851(94)90022-1 |
| [8] |
Verduzco B, Fairhead J D, Green C M. New Insights into Magnetic Derivatives for Structural Mapping[J]. The Leading Edge, 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [9] |
Wijns C, Perez C, Kowalczy K P. Theta Map:Edge Detection in Magnetic Data[J]. Geophysics, 2005, 70(4): 39-43. DOI:10.1190/1.1988184 |
| [10] |
Fitz Gerald D J, Holstein H. Innovative Data Processing Methods for Gradient Airborne Geophysical Data Sets[J]. The Leading Edge, 2006, 25(1): 87-94. DOI:10.1190/1.2164762 |
| [11] |
杨高印. 位场数据处理的一项新技术:小子域滤波法[J]. 石油地球物理勘探, 1995, 30(2): 240-244. Yang Gaoyin. A New Technique for Potential-Field Data Processing:Small Subdomain Filtering[J]. Oil Geophysical Prospecting, 1995, 30(2): 240-244. |
| [12] |
Cooper G R J, Cowan D R. Edge Enhancement of Potential-Field Data Using Normalized Statistics[J]. Geophysics, 2008, 73: H1-H4. DOI:10.1190/1.2837309 |
| [13] |
Ma G, Li L. EdgeDetection in Potential Fields with the Normalized Total Horizontal Derivative[J]. Computers & Geosciences, 2012, 41: 83-87. |
| [14] |
王彦国, 张凤旭, 王祝文, 等. 位场归一化差分法的边界检测技术[J]. 吉林大学学报(地球科学版), 2013, 4(2): 592-602. Wang Yanguo, Zhang Fengxu, Wang Zhuwen, et al. Edge Detection of Potential Field Using Normalized Differential[J]. Journal of Jilin University (Earth Science Edition), 2013, 4(2): 592-602. |
| [15] |
Zhou S, Huang D N, Jiao J. Total Horizontal Derivatives of Potential Field Three Dimensional Structure Tensor and Their Application to Detect Source Edges[J]. Acta Geophysica et Geophysica, 2016, 52(3): 1-13. |
| [16] |
周文纳, 杜晓娟, 李吉炎. 改进的角度边界识别方法及其在延吉盆地的应用[J]. 地球科学:中国地质大学学报, 2013, 38(6): 1339-1346. Zhou Wenna, Du Xiaojuan, Li Jiyan. Improved Angle Edge Detection Method and Its Application in Yanji Basin[J]. Earth Science:Journal of China University of Geosciences, 2013, 38(6): 1339-1346. |
| [17] |
Yuan Y, Huang D N, Yu Q, et al. Edge Detection of Potential Field Data with Improved Structure Tensor Methods[J]. Journal of Applied Geophysics, 2014, 108: 35-42. DOI:10.1016/j.jappgeo.2014.06.013 |
| [18] |
Blakely R J, Simpson R W. Approximating Edges of Source Bodies from Magnetic or Gravity Anomalies[J]. Geophysics, 1986, 51(7): 1494-1498. DOI:10.1190/1.1442197 |
| [19] |
Serra J. Image Analysis and Mathematical Morphology[M]. New York: Academic Press, 1982.
|
| [20] |
张建成, 吴新杰. 形态滤波在实时信号处理中应用的研究[J]. 传感技术学报, 2007, 20(4): 828-831. Zhang Jiancheng, Wu Xinjie. Research on Applications of Morphological Filtering in Real-Time Signal Processing[J]. Chinese Journal of Sensors and Actuators, 2007, 20(4): 828-831. DOI:10.3969/j.issn.1004-1699.2007.04.027 |
| [21] |
蒋立辉, 耿蒙, 赵春晖. 基于广义形态滤波和模糊逻辑的散斑噪声抑制[J]. 红外与激光工程, 2005, 34(1): 80-83. Jiang Lihui, Geng Meng, Zhao Chunhui. Speckle Suppressing Based on Generalized Morphological Filter and Fuzzy Logic[J]. Infrared and Laser Engineering, 2005, 34(1): 80-83. DOI:10.3969/j.issn.1007-2276.2005.01.020 |
| [22] |
Margos P, San F K. Measuring the Fractal Dimensions of Signals:Morphological Coversand Iiterative Optimization[J]. IEEE Trans on Signal Processing, 1993, 41(1): 108-121. |
| [23] |
李兵, 张培林, 任国全, 等. 基于数学形态学的分形维数计算及在轴承故障诊断中的应用[J]. 振动与冲击, 2010, 29(5): 191-194. Li Bing, Zhang Peilin, Ren Guoquan, et al. Mathematic Morphology Based Fractal Dimension Calculation and Its Application in Fault Diagnosis of Roller Bearings[J]. Journal of Vibration and Shock, 2010, 29(5): 191-194. DOI:10.3969/j.issn.1000-3835.2010.05.042 |
| [24] |
刘循, 游志胜. 多尺度形态学图像边缘检测方法[J]. 光电工程, 2003, 30(3): 56-58. Liu Xun, You Zhisheng. An Image Edge Detection Method Based on Multi-Scale Morphology[J]. Opto-Electronic Engineering, 2003, 30(3): 56-58. DOI:10.3969/j.issn.1003-501X.2003.03.017 |
| [25] |
王慧锋, 站桂礼, 罗晓明. 基于数学形态学的边缘检测算法研究及应用[J]. 计算机工程与应用, 2009, 45(9): 223-226. Wang Huifeng, Zhan Guili, Luo Xiaoming. Research and Application of Edge Detection Operator Based on Mathematical Morphology[J]. Computer Engineering and Application, 2009, 45(9): 223-226. DOI:10.3778/j.issn.1002-8331.2009.09.065 |
| [26] |
李杰, 彭月英, 元昌安, 等. 基于数学形态学细化算法的图像边缘细化[J]. 计算机应用, 2012, 32(2): 514-516, 520. Li Jie, Peng Yueying, Yuan Chang'an, et al. Edge Thinning Based on Mathematical Morphology Thinning Algorithm[J]. Journal of Computer Applications, 2012, 32(2): 514-516, 520. DOI:10.3969/j.issn.1001-3695.2012.02.030 |
| [27] |
王润秋, 郑桂娟, 付洪洲, 等. 地震资料处理中的形态滤波去噪方法[J]. 石油地球物理学报, 2005, 40(3): 277-282. Wang Runqiu, Zheng Guijuan, Fu Hongzhou, et al. Noise-Eliminated Method by Morphologic Filtering in Seismic Data Processing[J]. Oil Geophysical Prospecting, 2005, 40(3): 277-282. |
| [28] |
Faucon T, Decenciere E, Magneron C. Morphological Segmentation Applied to 3D Seismic Data[C]//Ronse C, Najman L, Decencière E. Mathematical Morphology: 40 Years on, [s.l.]: Springer, 2005: 475-484.
|
| [29] |
陈辉, 郭科, 胡英. 数学形态学在地震信号处理中的应用研究[J]. 地球物理学进展, 2009, 24(6): 1995-2002. Chen Hui, Guo Ke, Hu Ying. A Study on Application of Mathematical Morphology to Seismic Signal Processing[J]. Progress in Geophysics, 2009, 24(6): 1995-2002. DOI:10.3969/j.issn.1004-2903.2009.06.009 |
| [30] |
汤井田, 李晋, 肖晓, 等. 数学形态学滤波与大地电磁噪声压制[J]. 地球物理学报, 2012, 55(5): 1784-1793. Tang Jingtian, Li Jin, Xiao Xiao, et al. Mathematical Morphology Filtering and Noise Suppression of Magnetotelluric Sounding Data[J]. Chinese Journal of Geophysics, 2012, 55(5): 1784-1793. |
| [31] |
Huang W L, Wang R Q, Zhang D, et al. Mathematical Morphological Filtering for Linear Noise Attenuation of Seismic Data[J]. Geophysics, 2017, 82(6). |
| [32] |
Huang W L, Wang R Q, Zu S H, et al. Low-Frequency Noise Attenuation in Seismic and Microseismic Data Using Mathematical Morphological Filtering[J]. Geophysical Journal International, 2017, 211(3): 1296-1318. DOI:10.1093/gji/ggx371 |
| [33] |
李振苓, 沈金松, 李曦宁, 等. 用形态学滤波从电导率图像中提取缝洞孔隙度谱[J]. 吉林大学学报(地球科学版), 2017, 47(4): 1295-1307. Li Zhenling, Shen Jinsong, Li Xining, et al. Estimating Porosity Spectrum of Fracture and Karst Cave from Conductivity Image by Morphological Filtering[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(4): 1295-1307. |
| [34] |
Li L L, Ma G Q, Du X J. Edge Detection in Potential-Field Data by Enhanced Mathematical Morphology Filter[J]. Pure and Applied Geophysics, 2013, 170(4): 645-653. DOI:10.1007/s00024-012-0545-x |
| [35] |
邓彩霞, 王贵彬, 杨鑫蕊. 改进的抗噪形态学边缘检测算法[J]. 数据采集与处理, 2013, 28(6): 739-745. Deng Caixia, Wang Guibin, Yang Xinrui. Improved Algorithm of Morphology in Edge Detection for Noise Resistance[J]. Journal of Data Acquisition and Processing, 2013, 28(6): 739-745. DOI:10.3969/j.issn.1004-9037.2013.06.007 |
| [36] |
同小玲.基于数学形态学的图像边缘检测算法研究[D].西安: 长安大学, 2013. Tong Xiaoling. The Research of Image Edge Detection Algorithm Based on Mathematical Morphology[D]. Xi'an: Chang'an University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014023878.htm |
| [37] |
焦新华, 吴燕冈. 重力与磁法勘探[M]. 北京: 地质出版社, 2009: 1-328. Jiao Xinhua, Wu Yangang. Gravity and Magnetic Prospecting[M]. Beijing: Geological Publishing House, 2009: 1-328. |
| [38] |
赵国兴.老挝万象地区钾盐矿重力数据处理与解释[D].长春: 吉林大学, 2017. Zhao Guoxing. The Processing and Interpretation of Gravity Data on the Potash Mine of Vientiane in Laos[D]. Changchun: Jilin University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10183-1017147954.htm |
| [39] |
Xu M L, Yang C B, Wu Y G, et al. Edge Detection in the Potential Field Using the Correlation Coefficients of Multidirectional Standard Deviations[J]. Applied Geophysics, 2015, 12(1): 23-34. DOI:10.1007/s11770-014-0473-5 |