2. 国土资源部应用地球物理重点实验室, 长春 130026;
3. 中石化东北油气分公司科技信息部, 长春 130062
2. Key Laboratory of Applied Geophysics, Changchun 130026, China;
3. Information and Technology Department, Northeast Oil and Gas Branch Sinopec, Changchun 130062, China
0 引言
重力归一化总梯度法是在20世纪60—70年代,由苏联科学家B.M.别列兹金提出的[1-3]。它计算简便,不需要任何附加条件,是利用高精度重力异常来确定异常源分布的一种方法。传统计算重力归一化总梯度是采用正弦滤波因子压制下延过程中的振荡效应,利用正弦级数展开的方法进行导数计算。为了提高归一化总梯度结果的计算精度,曾华霖等[4]提出了改进的三维重力归一化总梯度算法,获得了更加稳定的结果;张凤旭等[5]和肖鹏飞等[6]针对计算过程中的延拓方法和圆滑因子开展研究;Aghajani等[7]将归一化总梯度用于油气区域的圈定。
Hartley变换是一种实数域内的变换,是酉变换的一种,比傅里叶变换至少减少一半的空间和时间,其变换前后的信号熵和能量不变。Al-Garni Mansour等[8]将Hartley变换应用于重磁位场数据处理和转换中;武立华等[9]将Hartley变换应用到磁异常延拓积分迭代法中来提高运算效率。重力归一化结果的稳定计算是其研究热点,因此采用Hartley变换计算导数不仅速度快而且精度高。
本文采用Hartley变换实现重力归一化总梯度的计算,并采用新的余弦滤波因子来压制下延的不稳定性。为了达到提高归一化总梯度稳定性和计算精度的目的,令滤波因子的幂次为深度的函数,使其具有随深度变化自动改变滤波性质的功能。
1 方法原理重力归一化总梯度法的根本在于重力位及其导数都是解析函数。虽然函数在场源处失去解析性,但是从已知区域(例如地表实测值)解析延拓到场源以外的区域仍保持其解析性。使函数失去解析性质的点叫做奇点。根据这一原理,可以将确定重力场源的问题归结为通过解析延拓和求导来寻找解析函数的奇点问题[10-13]。
重力归一化总梯度表达式为
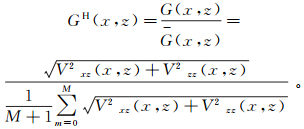 (1)
(1) 式中:x=mdx,dx为采样间隔;M为x方向采样点数;G(x, z)为观测点所在xoz铅垂面上重力总梯度的模;G(x, z)为深度z上M+1个点的总梯度模的平均值;Vxz、Vzz分别为重力g对x、z的偏导数。
Hartley[14]在傅里叶变换基础上进行改进提出了Hartley变换(HT)。Hartley变换正、逆变化的一维形式分别为:
 (2)
(2) 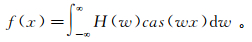 (3)
(3) 其中,
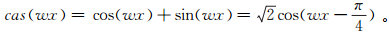
式中:f(x)为一实波形;w为频率。
Hartley变换与傅里叶变换具有相似的性质[15],因此可以用Hartley级数表示区间(0,L)上的重力异常[10]:
 (4)
(4) 其中,

式中,N为谐波数。
实测重力数据为离散序列,相应的重力异常一阶导数计算公式为:
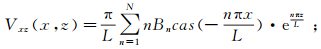 (5)
(5) 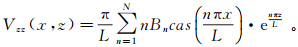 (6)
(6) Bn可表示为
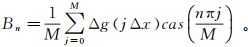 (7)
(7) 式中:Δx为点距;M=L/Δx。
为了压制向下延拓的高频震荡,需乘上一个圆滑滤波因子来增强下延的稳定性[16-18]。一般为正弦滤波因子qm,可表示为
 (8)
(8) 式中:n=1, 2, …, N; m=1, 2, 3, …。在解决地球物理问题时,m=2比较合适。
比较正弦与余弦滤波器在相同条件下的滤波性质(图 1):从图 1后半段(N=25~35)可以看出,余弦滤波因子对高频干扰的压制作用要好一些,能很好地增强下延过程的稳定性;但是在前半段(N=1~24),余弦滤波因子对低、中频有用信息的压制相对于正弦滤波因子则要大一些,这是其不足之处。

|
| 图 1 不同圆滑滤波因子性质比较 Fig. 1 Comparison of properties of different slick filter factors |
|
|
在实际处理中,随着下延深度的增加,误差会越来越大,因此不同层位采用不同的圆滑滤波因子会更有效[19-20]。针对正弦滤波因子的缺陷,本文提出一种新的圆滑滤波因子——余弦滤波因子:
 (9)
(9) 式中,n=1, 2, 3, …, N;$φ$(z)为深度z的函数,具有随深度增加而变大的特征。由于重力梯度和下延均会引起数据的高频震荡,因此较深层数据的导数所受到的高频震荡更加严重,采用随深度增大压制效果更佳的随深度变化的函数可获得更加稳定的结果。
综上,改进的水平一阶导数Vzx(x, z)与垂直一阶导数Vzz(x, z)表示为:
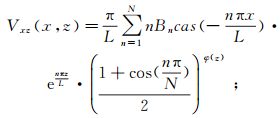 (10)
(10)  (11)
(11) 将式(10)、(11)带入式(1)就可以得到改进的重力归一化计算公式。
2 模型试验 2.1 单异常体模型为了对比改进后的重力归一化总梯度和传统重力归一化总梯度的精度,建立了如下模型:在长为600 m的剖面上,水平位置300 m处存在一个埋深为50 m的无限长水平圆柱体,圆柱体半径为20 m,与围岩的密度差为2 g/cm3(图 2)。

|
| 图 2 单异常体模型示意图 Fig. 2 Schematic of single anomalous body model |
|
|
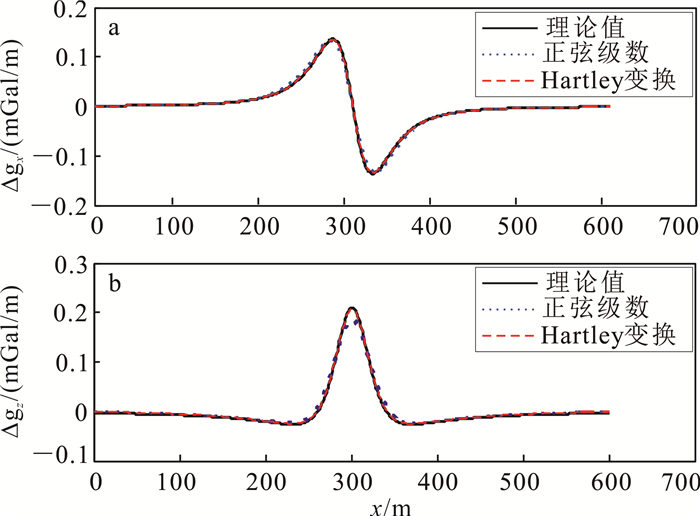
为了更加直观地对比新、旧方法的计算精度,将从不同的角度进行对比。首先对Hartley变换和正弦级数法计算得到z=0深度上的水平与垂直一阶导数(图 3)进行对比。为了对比导数的计算精度,圆滑滤波因子的幂次取为0。从图 3中可以看出:两种方法计算得到水平导数均与理论值相差很小;而对于垂直一阶导数,Hartley变换的计算精度明显高于正弦级数的计算精度。
|
| a.水平一阶导数;b.垂直一阶导数。 图 3 单异常体模型z=0深度上不同方法计算得到的导数 Fig. 3 Derivatives of single anomalous body model calculated by different methods at the depth of z=0 |
|
|
然后比较余弦滤波因子与正弦滤波因子的滤波性质。采用Hartley变换对含有随机噪声的重力异常(噪声幅值为1)进行求导,分别采用不同的圆滑滤波因子进行滤波(图 4),圆滑滤波因子的幂次均取1。从图 4中可以看出,虽然余弦滤波因子相对于正弦滤波因子对有用异常的削弱程度要大一些,但其压制噪声的能力较强,相对于其在压制有用异常方面的弊端,该滤波因子在去除干扰方面的优越性更加明显。而对于实际情况,噪声是进行反演的重要阻碍,因此在进行重力归一化总梯度进行计算时,选用余弦滤波因子更适宜。

|
| a.水平一阶导数;b.垂直一阶导数。 图 4 单异常体模型含噪异常z=0深度上不同滤波因子计算得到的导数 Fig. 4 Derivatives of single anomalous body model with noise anomaly calculated by different filter factors at the depth of z=0 |
|
|
最后分别利用传统导数计算公式(5)、(6)和改进后导数计算公式(10)、(11)计算原始异常在z=10 m深度上的水平和垂直一阶导数。从图 5中可以看出,传统计算方法所得到的结果精度较差,而改进后方法的计算结果与理论结果差距较小。综上所述,Hartley变换与余弦滤波因子组合能更好地完成各个高度上导数的计算。

|
| a.水平一阶导数;b.垂直一阶导数。 图 5 单异常体模型z=10 m深度上不同方法计算得到的导数 Fig. 5 Derivatives of single anomalous body model calculated by different methods at z=10 m depth |
|
|
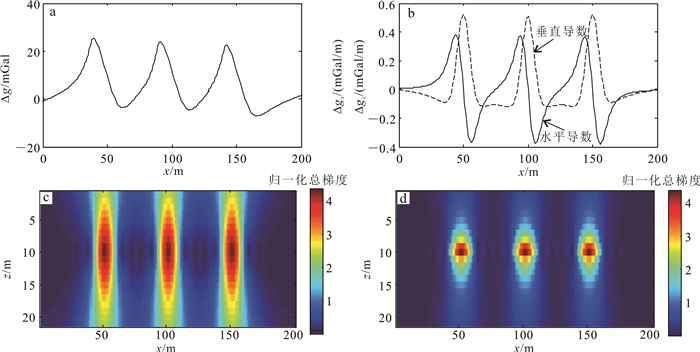
建立如下模型进行方法试验(图 6):在长为200 m的剖面上,水平位置50、100、150 m处存在3个埋深为10 m的水平圆柱体,圆柱体半径为10 m,与围岩的密度差为2 g/cm3。图 6a、b分别为圆柱体模型的重力异常和导数。图 6c为传统正弦展开计算得到的重力归一化总梯度,可以看到结果能有效地标识地质体的分布,但结果较发散。图 6d为改进方法计算得到的归一化总梯度结果,可以看到成像结果更加收敛,这主要是由于本文方法对于数据的压制效果更佳,从而避免了数据的发散;因此本文方法更加易于完成结果的解释。
|
| a.原始重力异常;b.水平与垂直导数;c.传统方法计算结果;d.改进方法计算结果。 图 6 多异常体模型重力归一化总梯度图 Fig. 6 Gravity normalized total gradient map of multiple anomalous body model |
|
|
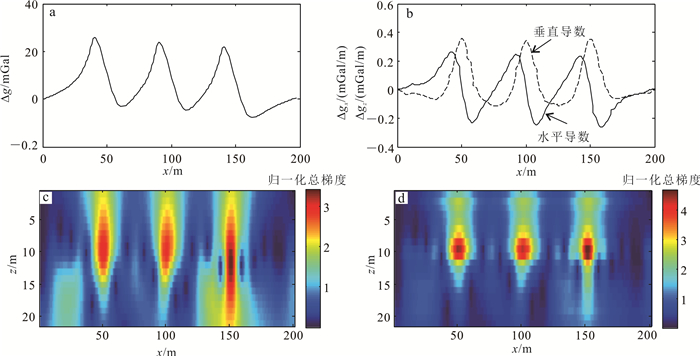
实测测量中噪声是不可避免的。在图 6a的模型异常中加入均方差为1的随机噪声,图 7a和图 7b分别为含噪重力异常及其导数,可以看出,导数的计算会增大噪声的干扰。图 7c和图 7d分别为传统方法和改进方法计算得到的归一化总梯度计算结果,可以看出改进方法结果更加稳定,能有效地压制噪声的干扰。
|
| a.含噪重力异常;b.水平与垂直导数;c.传统方法计算结果;d.改进方法计算结果。 图 7 多异常体模型含噪异常归一化总梯度图 Fig. 7 Normalized total gradient map of multiple anomalous body model with noise anomalies |
|
|
本次试验目的是玲珑金矿区采空区探测。早期的胡乱开采,使很多采空区的位置、深度无法确定,因此引发了很多安全事故,造成了严重的损失。矿区内游散电流大、接地电阻高、爆破震源多、地质条件复杂,地质雷达、高密度电法、地震等方法无法得到应用。矿区岩体多为花岗岩,密度为2.6~2.8 g/cm3,采空区密度为1.0~1.6 g/cm3,两者之间存在密度差,可以选用重力方法进行测量。但由于采空区体积较小,所以采空区引起的异常仅为(0.3~1.3)×10-6 m/s2,因此采用高精度的测量和数据处理手段是必要的。本次测量所采用的仪器精度为0.01×10-6 m/s2的加拿大CG-5型重力仪,检查点精度为0.069×10-6 m/s2,该精度保证了实测弱异常的可信度。应用改进的重力归一化总梯度法对采空区实测高精度重力异常进行反演。在此之前,首先确定$φ$(z)与z的关系。通过对该地区资料的研究,确定该地区$φ$(z)和深度z的大致关系为
 (12)
(12) 式中:a=-0.006 5;b=0.004 2;c=0.5。
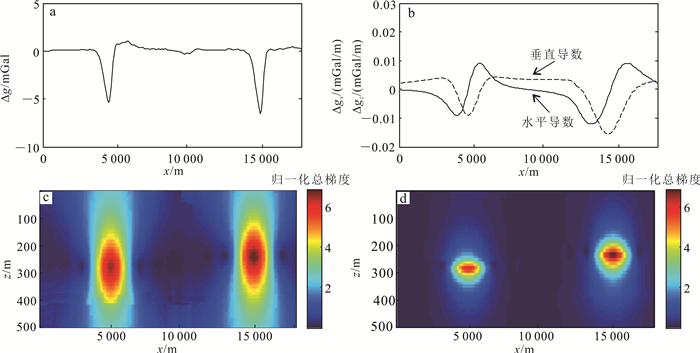
利用改进的重力归一化总梯度对该地区的数据进行处理(图 8)。从图 8中可以看出,测线范围内存在两个采空区,位置分别为(5 000, 270)和(14 900,220)。
|
| a.实测重力异常;b.水平与垂直导数;c.传统方法计算结果;d.改进方法计算结果。 图 8 玲珑金矿区实测重力异常的归一化总梯度图 Fig. 8 Normalized total gradient map of measured gravity anomalies in Linglong Goldfield |
|
|
从以上结果中看出,改进后的重力归一化总梯度能很好地完成采空区弱异常的反演,具有很好的实际应用价值。
4 结论1) 本文提出采用Hartley变换实现重力归一化总梯度的计算,并采用随深度变化的余弦滤波因子来获得更加稳定的归一化总梯度结果。
2) 模型试验表明Hartley变换计算所得到的导数更加稳定,且边部损失较少;随深度变化的余弦滤波因子能更好地压制噪声的干扰;本文基于Hartley变换的重力归一化总梯度法能获得更加收敛的成像结果,且对于噪声的压制效果更好,能更好地实现数据的解释工作。
3) 通过实际数据的应用,圈定了玲珑金矿区的两个采空区。
| [1] |
Березкин B M. Применение гравиразведки для поисков место рождений не фти и газа[M]. Москва: Недра, 1973.
|
| [2] |
B·M·别列兹金.物探数据的总梯度解释法[M].陆克, 刘文锦, 焦恩富译.北京: 地质出版社, 1994. Березкин Березкин B M. Interpretation Method of Normalized Full Gradient to Geophysical Data[M]. Translated by Lu Ke, Liu Wenjin, Jiao Enfu. Beijing: Geological Publishing House, 1994. |
| [3] |
孟平, 秦瞳, 吴云海. 关于归一化总梯度异常多解性问题的研究[J]. 石油物探, 2003, 42(2): 252-255. Meng Ping, Qin Tong, Wu Yunhai. Study of Nonuniqueness of the Solution to Normalized Total Gradient Method[J]. Geophysical Prospecting for Petroleum, 2003, 42(2): 252-255. DOI:10.3969/j.issn.1000-1441.2003.02.022 |
| [4] |
曾华霖, 李小孟, 姚长利, 等. 改进的重力归一化总梯度法及其在胜利油区油气藏探测中的应用效果[J]. 石油地球物理勘探, 1999, 26(6): 1-6. Zeng Hualin, Li Xiaomeng, Yao Changli, et al. The Modified Normalized Full Gradient of Gravity Anomalies and Its Application to Shengli Oil-Field, East China[J]. Petroleum Exploration and Development, 1999, 26(6): 1-6. |
| [5] |
张凤旭, 孟令顺, 张凤琴, 等. 波数域重力归一化总梯度法中的圆滑滤波因子[J]. 物探与化探, 2005, 29(3): 248-252. Zhang Fengxu, Meng Lingshun, Zhang Fengqin, et al. A Study of Smoothing Filter Operator for Narmalized Full Gradient of Gravity Anomaly in Wave Number Domain[J]. Geophysical and Geochemical Exploration, 2005, 29(3): 248-252. DOI:10.3969/j.issn.1000-8918.2005.03.016 |
| [6] |
肖鹏飞, 李明, 徐世浙, 等. 重力归一化总梯度的稳定解法[J]. 石油地球物理勘探, 2006, 41(5): 596-598. Xiao Pengfei, Li Ming, Xu Shizhe, et al. Stable Solution of Normalized Total Gravity Gradient[J]. Oil Geophysical Prospecting, 2006, 41(5): 596-598. DOI:10.3321/j.issn:1000-7210.2006.05.021 |
| [7] |
Aghajani H, Moradzadth A, Aydin A, et al. Using Normalized Full Gradient Method to Interpret Gravity Anomalies on Synthetic and Field Data[J]. Conference Proceeding, 2009, 14(1): 725-734. |
| [8] |
Al-Garni Mansour A, Sundararajan N. Hartley Spectral Analysis of Self-Potential Anomalies Caused by a 2-D Horizontal Circular Cylinder[J]. Arabian Journal of Geosciences, 2012, 5(6): 1341-1346. DOI:10.1007/s12517-011-0285-8 |
| [9] |
武立华, 刘志海, 孟霆, 等. 基于Hartley变换的地磁场延拓技术[J]. 物理实验, 2018, 38(7): 23-25. Wu Lihua, Liu Zhihai, Meng Ting, et al. Geomagnetic Field Extension Technology Based on Hartley Transform[J]. Physical Experiment, 2018, 38(7): 23-25. |
| [10] |
罗孝宽, 郭绍雍. 应用地球物理教程:重力、磁法[M]. 北京: 地质出版社, 1991: 139-154. Luo Xiaokuan, Guo Shaoyong. Applied Geophysics Course:Gravity and Magnetism[M]. Beijing: Geological Publising House, 1991: 139-154. |
| [11] |
孟令顺, 杜晓娟. 勘探重力学与地磁学[M]. 北京: 地质出版社, 2008: 216-220. Meng Lingshun, Du Xiaojuan. Explorational Gravitation and Magnetism[M]. Beijing: Geological Publising House, 2008: 216-220. |
| [12] |
马国庆.汶川大地震区构造特征与均衡效应研究[D].长春: 吉林大学, 2010. Ma Guoqing. Research of Wenchuan Earthquake Zones Structural Feature and Equilibrium Effect[D]. Changchun: Jilin University, 2010. |
| [13] |
肖一鸣. 重力归一化总梯度法[J]. 石油地球物理勘探, 1981, 16(3): 47-56. Xiao Yiming. Normalized Ttotal Gradient Method of Gravity[J]. Oil Geophysical Prospecting, 1981, 16(3): 47-56. |
| [14] |
Hartley R V L. A More Symmetrical Fourier Analysis Applied to Transmission Problems[J]. Proceedings of the IRE, 1942, 30: 144-150. DOI:10.1109/JRPROC.1942.234333 |
| [15] |
肖一鸣, 张林详. 重力归一化总梯度法在寻找油气中的应用[J]. 石油地球物理勘探, 1984, 19(3): 247-254. Xiao Yiming, Zhang Linxiang. The Application of Total Gradient of Gravity in Funding Oil-Gas[J]. Oil Geophysical Prospetcting, 1984, 19(3): 247-254. |
| [16] |
甘利灯. Hartley变换及其性质[J]. 石油地球物理勘探, 1992, 27(5): 605-616. Gan Lideng. Hartley Transform and Its Properties[J]. Oil Geophysical Prospecting, 1992, 27(5): 605-616. |
| [17] |
王宝仁, 王芳. 归一化总梯度方法的计算新技术[J]. 物探化探计算技术, 1991, 13(2): 141. Wang Baoren, Wang Fang. A New Computing Technique of Normalized Total Gradient[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1991, 13(2): 141. |
| [18] |
毛小平, 吴蓉元, 曲赞. 频率域位场下延拓的振荡机制及消除方法[J]. 石油地球物理勘探, 1998, 33(3): 230-237. Mao Xiaoping, Wu Rongyuan, Qu Zan. Oscillation Mechanism of Potential Field Downward Continuation in Frequency Domain and Its Elimination[J]. Oil Geophysical Prospecting, 1998, 33(3): 230-237. |
| [19] |
王家林, 王一新, 万民浩, 等. 用重力归一化总梯度法确定密度界面[J]. 石油地球物理勘探, 1987, 22(6): 684-692. Wang Jialin, Wang Yixin, Wan Minhao, et al. The Determination of Density Interface Using the Normalized Total Gravity Gradient Method[J]. Oil Geophysical Prospecting, 1987, 22(6): 684-692. |
| [20] |
马国庆, 孟庆发, 黄大年. 基于重力异常的松辽盆地构造特征识别[J]. 吉林大学学报(地球科学版), 2018, 48(2): 507-516. Ma Guoqing, Meng Qingfa, Huang Danian. Structure Identification by Grabity Anomaly in Songliao Basin[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(2): 507-516. |



