2. 中国石油集团测井有限公司长庆分公司, 西安 710201
2. Logging Changqing Branch, CNPC, Xi'an 710201, China
0 引言
由于常规化石能源有限且不可再生,全球节能减排呼声不断高涨,地热能作为一种经济、可再生、环保的新型能源,已受到世界各国的高度重视[1-4]。增强型地热系统(enhanced geothermal systems, EGS)作为干热岩开采技术之一,美国能源部的定义是采用人工形成地热储层的方法,从低渗透性岩体中经济地采出深层热能的人工地热系统,因此一般需要人工压裂的方式形成“人造”储层,故EGS中的核心问题是人工热储层中复杂裂缝网络系统的准确刻画和高效模拟。
目前,研究EGS裂缝流体的运移模拟主要包括连续介质模型[5-6]及离散裂缝网络模型[7-9]等。其中:连续介质模型假设水通过均匀多孔介质在注水井和生产井之间流动,无法准确描述裂缝性质,特别是大裂隙,因此存在一定的局限性;离散裂缝网络模型假定储层由大量裂缝网络相互构成,更加符合实际情况,但前提是必须明确裂缝的分布。目前地热多场耦合模型主要包括基于连续介质的数值模拟软件如TOUGH[10-11],以及基于离散网络模型的模拟软件如COMSOL[9-12]、open-source software OpenGeoSys (OGS)[13-14]等。离散裂缝网络模型[15-17]主要针对流动问题,而针对地热储层多物理场耦合的解析方法研究较少。本文基于离散裂缝网络模型,将流体的不稳定渗流和热流进行耦合建立了相应的数学模型,采用Laplace变换得到模型的解析解,并对工程问题的注采参数包括井网模型、井距、注水速率和注水温度进行了分析,以期为增强型地热系统的高效开发方案设计提供指导。
1 增强型地热系统离散裂缝网络模型 1.1 物理模型干热岩储层地热资源的开采一般采用增强型地热系统,利用水力压裂技术在热储层形成复杂裂缝网络,使冷水通过注水井进入热储层,实现水在注水井、热储层和生产井之间的循环,由此提取热量的过程。为了准确模拟地热储层的热、流等复杂机理,本文基于离散裂缝网络模型构建了增强型地热系统五点井网模型(图 1),其中:采用一维的线单元代表二维的矩形裂缝,假定流体水只沿裂缝网络进行流动,忽略基岩中水的流动;离散裂缝内为不稳定渗流,以热对流进行热交换,基岩中热量通过热传导对水进行导热;离散裂缝网络模型主要由注水井、生产井、裂缝网络构成,只有相互沟通的裂缝参与流体流动,而只有一个相连节点的裂缝无流体流动。
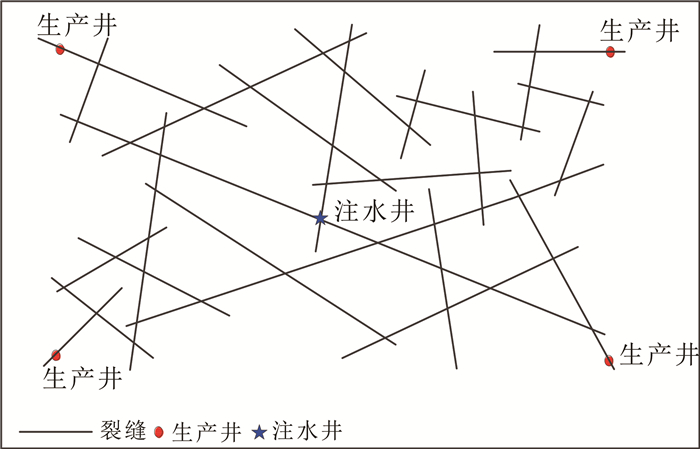
|
| 图 1 增强型地热系统五点井网模型 Fig. 1 Five point well pattern of enhanced geothermal system |
|
|
假定裂缝中的流动为不稳定渗流过程,首先以两个节点(j, j+1)间的单条裂缝i(图 2)为研究对象,沿裂缝中流体流动方向z建立裂缝中的流动方程:
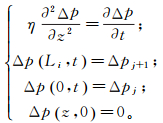 (1)
(1)

|
| 图 2 单条裂缝示意图 Fig. 2 Single fracture diagram |
|
|
式中:Δp为裂缝中的压差,Δp=p0-p(p0为地层原始压力,MPa;p为裂缝内压力,MPa),MPa;t为流动时间,s;η为裂缝的导压系数,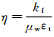
对方程组(1)采用Laplace变换,因此Laplace空间的裂缝压差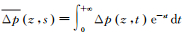
 (2)
(2) 其中:
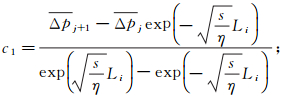 (3)
(3) 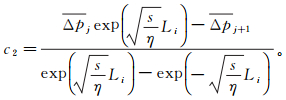 (4)
(4) 式中: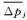

基于质量守恒方程,以任意一个节点n作为研究对象,假定该点处流入与流出的质量相等:当该节点为注水井时,定注水量生产,因此水的质量变化minj已知;当节点为生产井时,定生产压力pw,则该节点的压力p已知。因此对于节点n可建立质量守恒方程:
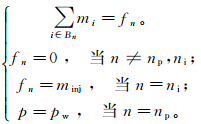 (5)
(5) 式中:Bn为与节点n相连的所有边;fn为第n个节点的流入流出质量差,kg/s;np表示为生产井井点;ni表示注水井井点;pw为生产井压力,MPa;mi为与节点n相连的第i条裂缝流过节点n的质量流量,mi=ρwviAi(ρw为水的密度,kg/m3;vi为节点处的流速,m/s;Ai为裂缝面的截面积,m2,Ai=wiH,wi为该裂缝的平均开度,m;H为裂缝的厚度,m),kg/s。
裂缝中的流动服从Poiseuille流动规律,因此
 (6)
(6) 式中: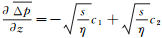
为了求解离散裂缝网络模型的流动,取任意一条裂缝i作为研究对象,由于假设流体只在裂缝中流动,沿着裂缝建立相应的坐标,如图 3所示。

|
| 图 3 单条裂缝坐标示意图 Fig. 3 Schematic diagram of a single fracture coordinates |
|
|
建立基岩中一维热传导数学模型:
 (7)
(7) 式中:无因次温度Ψ=(Ti-Tw)/(Tr-Tw)(Ti为地热储层初始温度,℃;Tr为初始储层温度,℃;Tw为注水温度,℃);ar为基岩的热扩散系数,ar=Kr/ρrCr(Kr为岩石导热系数,W/(m·℃);ρr为岩石的密度,kg/m3;Cr为岩石的比热,J/(kg·℃)), m2/s。故无因次温度的范围为[0, 1]。
裂缝中对流的流体在边界处,通过热传导的方式获取基岩中热量,忽略岩石与水界面阻力,假定水的温度与裂缝表面温度相等,即
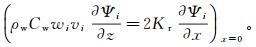 (8)
(8) 将一维热传导方程(7)(8)变换到Laplace空间,则方程转化为
 (9)
(9) 常微分方程的通解为
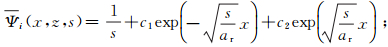 (10)
(10) 代入初始和边界条件方程(8)可得单条裂缝的温度分布为
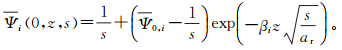 (11)
(11) 式中,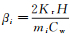
当裂缝为离散裂缝网络时,第i条裂缝的初始温度由上一级裂缝j的温度决定,故
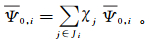 (12)
(12) 式中:
将方程(12)代入到方程(11)得:
 (13)
(13) 其中: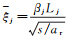
 (14)
(14) 其中:sk为到达裂缝i的所有路径;ni为到达裂缝i的所有路径总数目。
最后,将Laplace空间温度分布进行Laplace反演,得到实空间下裂缝网络中,任意一条裂缝的温度分布为
 (15)
(15) 其中:
本文基于离散裂缝网络模型,建立了热流耦合解析模型。由于储层开采主要以五点井网为主,且五点井网为对称型井网,因此在此只分析1/4井网结构,即一注一采的情况。采用直井或水平井进行开采,可把开采模型分为4类(图 4):直井注直井采(模型Ⅰ)、水平井注直井采(模型Ⅱ)、直井注水平井采(模型Ⅲ)、水平井注水平井采(模型Ⅳ)。在此对不同类型的模型的求解过程进行说明。
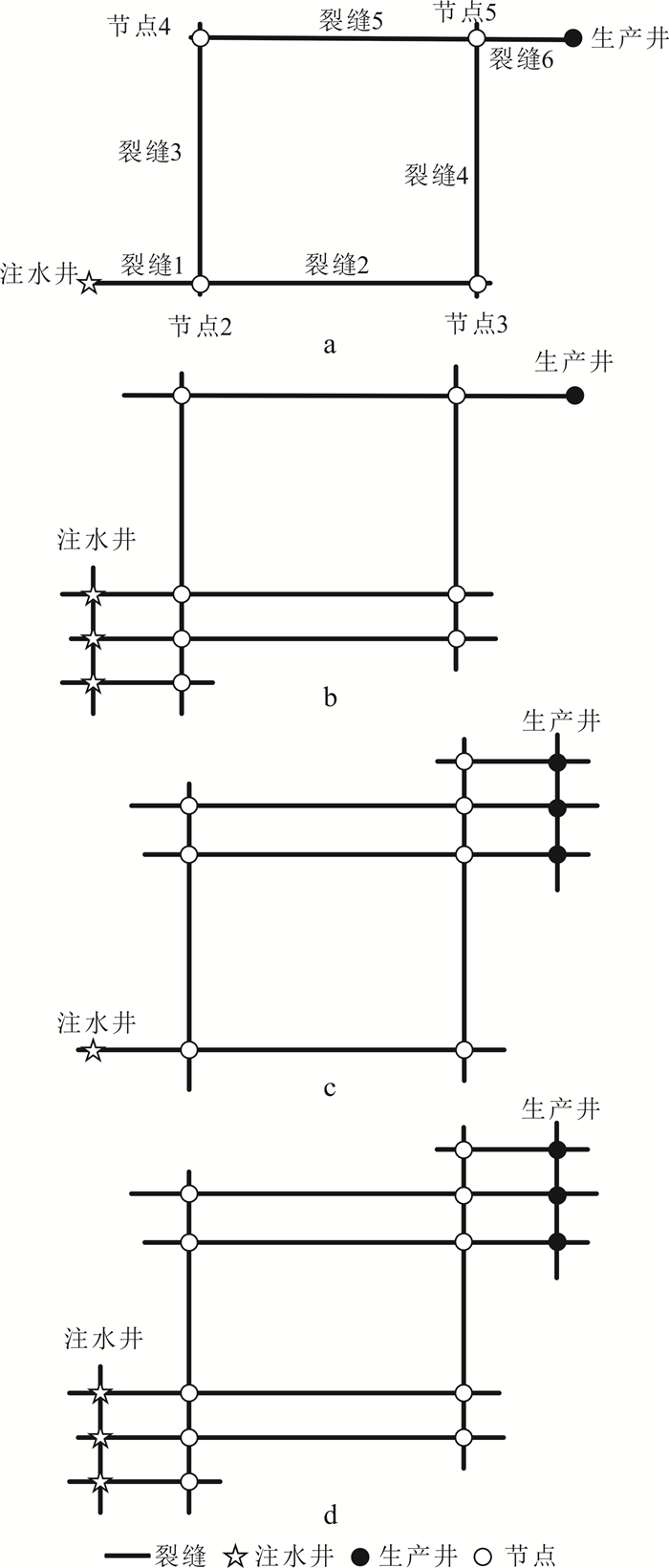
|
| a.直井注直井采(模型Ⅰ);b.水平井注直井采(模型Ⅱ);c.直井注水平井采(模型Ⅲ);d.水平井注水平井采(模型Ⅳ)。 图 4 4种不同类型井网模型示意图 Fig. 4 Schematic diagram of four different well patterns |
|
|
如图 4所示,地热储层模型中包含一口注水井和一口生产井,假定注水井定注水量,生产井定生产压力,可将离散裂缝网络模型耦合求解过程分为3步。
1) 求解各节点的压力及相连处裂缝的质量分布:如图 4a所示,包括注水井和生产井共有6个节点,首先通过方程(5)建立Laplace空间方程Dp=F, (其中D为6×6的系数矩阵,p为各节点的Laplace空间压力值,F为边界条件得到的列向量),通过Stehfest数值反演[18]到实空间;然后通过方程(6)计算与节点相连的各裂缝流速,再利用mi=ρwviAi计算质量流量。
2) 求解各裂缝的温度分布:首先, 如果某条裂缝只与单个节点相连,则认为该裂缝中流体不流动;其次, 如果裂缝与两个节点相连,则分析流入裂缝的网络路径,如图 4a从注水井到生产井可能流动的路径为s1={1, 3, 5}和s2={1, 2, 4};最后将两条路径s1,s2代入方程(15),则裂缝6的温度分布可表示为
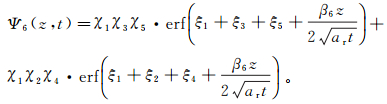 (16)
(16) 3) 在井网模型为水平井情况下,主要改变离散裂缝网络模型的边界条件,以注水井定注水量,生产井定生产压力为例,计算井网的压力及温度分布。如图 4d所示,注水井和生产井分别与3条裂缝相连:首先注水井定注水量,则相交3个节点的流量之和为定值,各裂缝流量的大小与裂缝的分布相关;其次生产井定生产压力,即假定与生产井相连的3个节点压力为定值,建立质量守恒方程(5),计算得到各节点的压力分布;最后由步骤2)计算得出各裂缝及生产井的温度分布,再由各裂缝质量加权平均计算得到水平井出口端的温度。
3 模型正确性验证及参数敏感性分析为了验证模型的正确性及五点井网情况下不同井网模型对增强型地热系统开采的影响,采用表 1中的基本参数,分别对不同井网模型、不同井距、不同注水速率和不同注水温度对出口端温度进行对比分析。
| 参数名称 | 数值 | 单位 | |
| 流体参数 | 水密度 | 1 000 | kg/m3 |
| 水比热 | 4 300 | J/(kg·℃) | |
| 水黏度 | 1 | mPa·s | |
| 岩石参数 | 岩石比热 | 1 050 | J/(kg·℃) |
| 岩石密度 | 2 700 | kg/m3 | |
| 岩石导热系数 | 2.7 | W/(m·℃) | |
| 裂缝参数 | 裂缝初始开度 | 0.003 | m |
| 裂缝渗透率 | 10 | μm2 | |
| 裂缝宽度 | 1 | m | |
| 出口端裂缝长度 | 100 | m | |
| 压裂裂缝间距 | 50 | m | |
| 其他裂缝长度 | 500 | m | |
| 边界条件 | 地层初始压力 | 25 | MPa |
| 注水量 | 0.1 | kg/s | |
| 生产井定压力 | 10 | MPa | |
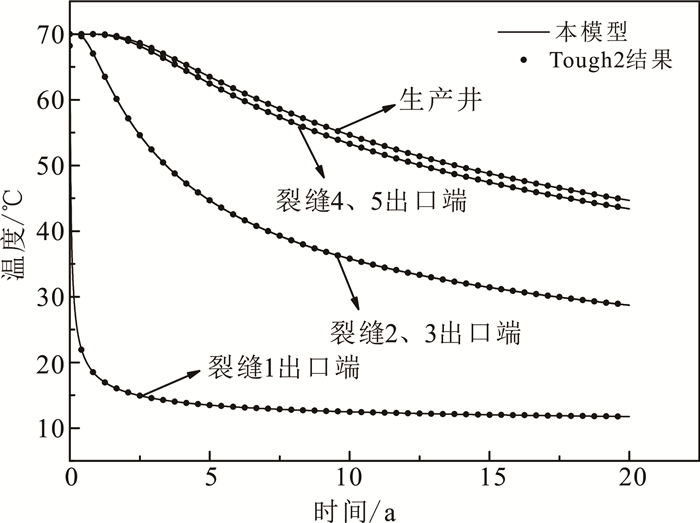
基于离散裂缝网络模型热流耦合模型,针对图 4a直井注直井采模型,将裂缝网络中各裂缝的温度分布与Tough2数值计算结果进行对比,结果如图 5所示。由图 5可见本模型解析解结果与数值解Tough2计算结果吻合,只是在生产井出口端早期稍有误差,但随着时间增加结果几乎一致,说明本解析模型的可行性及正确性。
|
| 图 5 解析模型与Tough2结果对比 Fig. 5 Comparison between analytic model and Tough2 results |
|
|
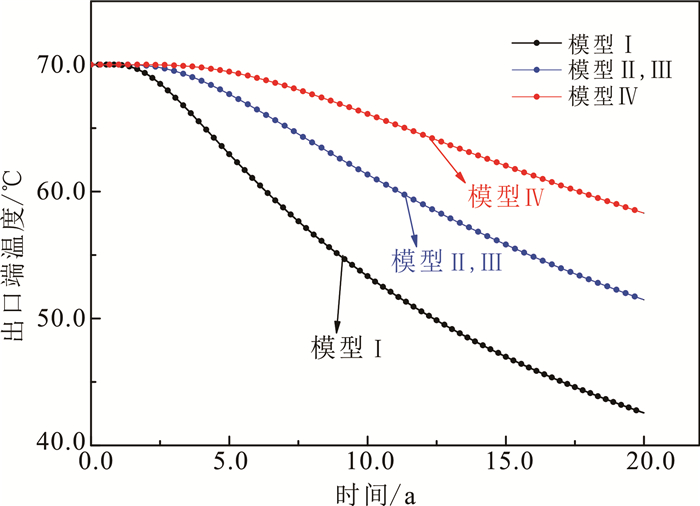
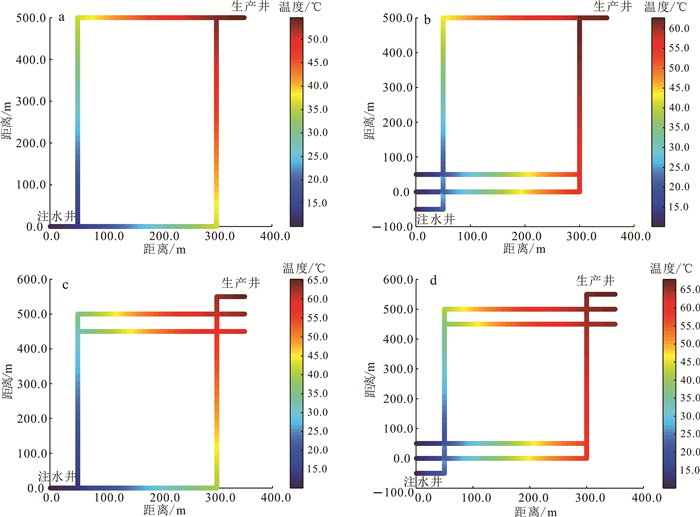
为了分析不同类型井网对热开采的影响,针对图 4中4种不同模型进行求解。4种组合情况下的裂缝出口端温度随时间变化情况见图 6,开采10.0 a后的温度分布见图 7。
|
| 图 6 出口端温度随时间变化 Fig. 6 Outlet temperature changes with time |
|
|
|
| a.模型Ⅰ;b.模型Ⅱ;c.模型Ⅲ;d.模型Ⅳ。 图 7 4种井网模型生产10.0 a后温度分布图 Fig. 7 Temperature profile of ten years for different models |
|
|
由图 6可见:随着10 ℃冷水的恒定注水,出口端初始地层温度为70 ℃,并在一定时间热突破,出口端温度迅速降低,但降低速度随着时间的增加逐渐变缓;不同注采井网模型下热突破的时间不同,模型Ⅰ的热突破时间最早,大概为2.4 a,模型Ⅱ、Ⅲ由于路径对称出口端温度相同,热突破时间也相同,大概为3.5 a,模型Ⅳ流动路径最长,热突破时间最晚,约为5.2 a。由图 7可见,在生产10.0 a后各模型已经热突破,出口端温度均小于70.0 ℃,出口端温度最低者为模型Ⅰ,而模型Ⅳ出口端温度明显高于其他井网模型。故本研究最优模型为模型Ⅳ。可见热突破的时间与井网模型类型和离散裂缝的路径有关,因此得到和刻画准确的离散裂缝网络模型对热开采的模拟准确性至关重要。
3.2.2 井距为了分析不同井距大小对热开采的影响,分别计算不同井距时(d=50,100,200 m)裂缝出口端温度随时间变化(图 8)。由图 8可见,不同井距大小对热开采有明显的影响,在相同裂缝网络下,井距越大,热突破时间越晚,且温度下降越慢。以红色曲线模型Ⅳ为例:当井距为50 m时,热突破时间大约为2.0 a;井距为100 m时,热突破时间为5.2 a;而井距为200 m时,热突破时间为15.0 a以后,且出口端温度下降明显变缓。故本研究最优井距为模型Ⅳ下200 m。不同井网模型之间的规律与前面类似,出口端温度模型Ⅳ变化最缓,其次为模型Ⅱ、Ⅲ,变化最快为模型Ⅰ。综合可见,为了对干热岩储层进行开采,需要对井网模型、井距等参数进行优化,以达到在设定合理目标的情况下,使能量开采最大化。

|
| 图 8 不同井距出口端温度对比 Fig. 8 Comparison of the outlet temperature at different well spacing |
|
|
为了分析不同注水速率(q)对热开采的影响,分别计算4类井网模型不同注水速率下裂缝出口端温度随时间变化(图 9)。由图 9可见,不同注水速率对出口端温度变化有明显的影响,在同一井网模型开采下,注水速率越大,热突破时间越早,出口端温度下降越快。以蓝色曲线模型Ⅲ为例,生产20.0 a以后:注水速率0.1 kg/s时,温度降为53.0 ℃;注水速率0.2 kg/s时,温度降为34.5 ℃;注水速率0.3 kg/s时,温度降为26.8 ℃。说明随着注水速率的增加,下降幅度变缓,由此可见为了对干热岩储层进行最有效合理的开采,还需要考虑注水速率的影响,设置合理注水速率。本研究最优注水速率为0.1 kg/s。

|
| 图 9 不同注水速率温度对比 Fig. 9 Comparison of the outlet temperature at different injection rates |
|
|
为了分析不同注水温度大小对热开采的影响,分别计算4类井网模型不同注水温度下裂缝出口端温度随时间变化(图 10)。由图 10可见,不同注水温度对出口端温度有较大影响。以黑色曲线模型Ⅰ为例:在不同注水温度(5,10,15 ℃)下,热突破时间几乎不变,为2.4 a左右,故不同注水温度对热突破时间影响较小;注水温度越高,出口端温度下降越慢,出口端温度越高,不同的流动模型不同注水温度的影响规律相同。本研究最优注水温度为模型Ⅳ下15 ℃。

|
| 图 10 不同注水温度下生产井出口端温度对比 Fig. 10 Comparison of the outlet temperature at different injection water temperatures |
|
|
为了对比分析不同参数之间对干热岩开采的影响大小,在此通过正交实验方法对注采参数进行研究,为地热的生产设计提供理论指导。选定影响因素4个,井网模型(由于模型Ⅱ、Ⅲ计算结果相同,在此选取模型Ⅱ)、井距、注水速率以及注水温度。每个因素选取3个水平,选取正交实验表L9(34),以生产20.0 a出口端的累计热量为评价指标:

式中:Wtotal为累计热量,kJ;qpro为生产端流动速率,kg/s;hpro, hinj分别为生产端和注水端焓值,kJ/g, 焓值求解公式见参考文献[19-20]。计算各个实验方案下对应的累计热量,得到的计算结果见表 2。
| 参数标号 | 井网模型 | 井距/m | 注水速率/(kg/s) | 注水温度/℃ | 累计能量/(109kJ) |
| 1 | 模型Ⅰ | 50 | 0.1 | 5 | 8.34 |
| 2 | 模型Ⅰ | 100 | 0.2 | 10 | 15.40 |
| 3 | 模型Ⅰ | 200 | 0.3 | 15 | 25.90 |
| 4 | 模型Ⅱ | 50 | 0.2 | 15 | 10.30 |
| 5 | 模型Ⅱ | 100 | 0.3 | 5 | 22.90 |
| 6 | 模型Ⅱ | 200 | 0.1 | 10 | 15.40 |
| 7 | 模型Ⅳ | 50 | 0.3 | 10 | 14.50 |
| 8 | 模型Ⅳ | 100 | 0.1 | 15 | 13.20 |
| 9 | 模型Ⅳ | 200 | 0.2 | 5 | 31.30 |
| K1 | 49.64 | 33.14 | 36.94 | 62.54 | |
| K2 | 48.60 | 51.50 | 57.00 | 45.30 | |
| K3 | 59.00 | 72.60 | 63.30 | 49.40 | |
| k1 | 16.55 | 11.05 | 12.31 | 20.85 | |
| k2 | 16.20 | 17.17 | 19.00 | 15.10 | |
| k3 | 19.67 | 24.20 | 21.10 | 16.47 | |
| R | 3.47 | 13.15 | 8.79 | 5.75 | |
| 注:K1、K2、K3分别表示对应列(因素)在水平1、2、3的数据和;k1、k2、k3分别表示各水平的综合平均(如k1=K1/3);R为各因子的极差,极差R表示某因子的ki中最大值与最小值之差,反映了指标变化幅度。 | |||||
由表 2可知:本正交实验采用4因素3水平,计算结果表明4个因素的极差排序为:R2>R3>R4>R1(图 11)。因此根据极差大小,影响因素由主到次的顺序为:井距、注水速率、注水温度、井网模型。
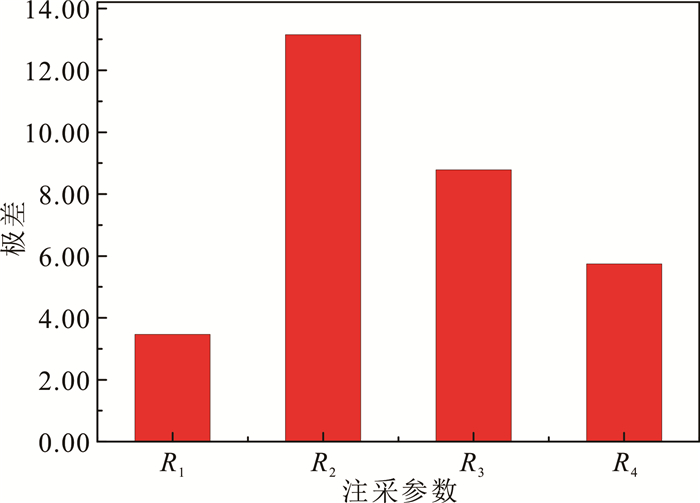
|
| R1、R2、R3、R4分别为井网类型、井距、注水速率和注水温度。 图 11 注采参数极差图 Fig. 11 Range analysis diagram of injection and production parameters |
|
|
在此水平下,选取累计能量最大值,则各因子的最优组合为:网络模型Ⅳ,井距200 m,注水速率0.2 kg/s和注水温度5 ℃。因此,干热岩开采过程中设计合理的井距和注水速率,对干热岩开采效果有重要影响,注水温度和井网模型的影响次之。
4 结论与建议1) 五点井网采用不同井网模型进行开采出口端温度模拟,可见不同裂缝网络和井网模型下温度下降幅度和热突破的时间不同,其中模型Ⅳ出口端温度较高,模型Ⅰ出口端温度较低;不同井距大小对热开采有明显的影响,在相同裂缝网络下,裂缝间距越大,热突破时间越晚,且温度下降越慢。因此,准确的离散裂缝网络模型构建是热开采的模拟的基础,对井网模型、井距等参数进行合理优化,使能量开采最大化。
2) 在同一井网模型开采下,注水速率越大,热突破时间越早,出口端温度下降越快,随着注水速率的增加,下降幅度变缓;在不同注水温度下,热突破时间几乎不受影响,注水温度越高,出口端温度下降越慢,出口端温度越高,不同注水温度下不同的流动模型的影响规律相同。
3) 以生产20.0 a后出口端累计热量为指标,通过正交实验分析方法,得到注采参数的影响大小由主到次的顺序为:井距大小、注水速率、注水温度、井网模型。因此,干热岩开采过程中设计合理的井距和注水速率,对干热岩开采效果有重要影响。
4) 解析模型还存在许多不足之处有待改善,包括没有考虑基岩的渗透性、裂缝开度随地层压力的变化而变化、实际裂缝的复杂性等情况的完善。
| [1] |
Tester J, Anderson B, Batchelor A, et al. The Future of Geothermal Energy: Impact Geothermal System (EGS) on the United States in the 21st Century[R]. Cambridge: Massachusetts Institute of Technology, 2006.
|
| [2] |
许天福, 袁益龙, 姜振蛟, 等. 干热岩资源和增强型地热工程:国际经验和我国展望[J]. 吉林大学学报(地球科学版), 2016, 46(4): 1139-1152. Xu Tianfu, Yuan Yilong, Jiang Zhenjiao, et al. Hot Dry Rock and Enhanced Geothermal Engineering:International Experience and China Prospect[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(4): 1139-1152. |
| [3] |
汪集旸, 胡圣标, 庞忠和, 等. 中国大陆干热岩地热资源潜力评估[J]. 科技导报, 2012, 30(32): 25-31. Wang Jiyang, Hu Shengbiao, Pang Zhonghe, et al. Estimate of Geothermal Resources Potential for Hot Dry Rock in the Continental Area of China[J]. Science & Technology Review, 2012, 30(32): 25-31. DOI:10.3981/j.issn.1000-7857.2012.32.002 |
| [4] |
Hori Y, Kitano K, Kaieda H, et al. Present Status of the Ogachi HDR Project, Japan, and Future Plans[J]. Geothermics, 1999, 28(4): 637-645. |
| [5] |
Zeng Yuchao, Zhan Jiemin, Wu Nengyou, et al. Numerical Simulation of Electricity Generation Potential from Fractured Granite Reservoir Through Vertical Well at Yangbajing Geothermal Field[J]. Energy, 130: 290-304.
|
| [6] |
Gelet R, Loret B, Khalili N. A Thermos-Hydro-Mechanical Coupled Model in Local Thermal Non-Equilibrium for Fractured HDR Reservoir with Double Porosity[J]. Journal of Geophysical Research, 2012, 117: 1-23. |
| [7] |
Gan Q, Elsworth D. Production Optimization in Fractured Geothermal Reservoirs Coupled Discrete Fracture Network Modeling[J]. Geothermics, 2016, 62: 131-142. DOI:10.1016/j.geothermics.2016.04.009 |
| [8] |
Maffucci R, Bigi S, Corrado S, et al. Quality Assessment of Reservoirs by Means of Outcrop Data and "Discrete Fracture Network" Models:The Case History of Rosario De La Frontera (NW Argentina) Geothermal System[J]. Tectonophysics, 2015, 647: 112-131. |
| [9] |
孙致学, 徐轶, 吕抒桓, 等. 增强型地热系统热流固耦合模型及数值模拟[J]. 中国石油大学学报(自然科学版), 2016, 40(6): 109-117. Sun Zhixue, Xu Yi, Lü Shuhuan, et al. A Thermo-Hydro-Mechanical Coupling Model for Numerical Simulation of Enhanced Geothermal Systems[J]. Journal of China University of Petroleum (Natural Science), 2016, 40(6): 109-117. DOI:10.3969/j.issn.1673-5005.2016.06.014 |
| [10] |
Cao Wenjiong, Huang Wenbo, Jiang Fangming. A Novel Thermal-Hydraulic-Mechanical Model for the Enhanced Geothermal System Heat Extraction[J]. International Journal of Heat and Mass Transfer, 2016, 100: 661-671. DOI:10.1016/j.ijheatmasstransfer.2016.04.078 |
| [11] |
雷宏武, 金光荣, 李佳琦, 等. 松辽盆地增强型地热系统(EGS)地热能开发热-水动力耦合过程[J]. 吉林大学学报(地球科学版), 2014, 44(5): 1633-1646. Lei Hongwu, Jin Guangrong, Li Jiaqi, et al. Coupled Thermal-Hydrodynamic Processes for Geothermal Energy Exploitation in Enhanced Geothermal System at Songliao Basin, China[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(5): 1633-1646. |
| [12] |
Sun Zhixue, Zhang Xu, Xu Yi, et al. Numerical Simulation of the Heat Extraction in EGS with Thermal-Hydraulic-Mechanical Coupling Method Based on Discrete Fractures Model[J]. Energy, 2017, 120: 20-33. DOI:10.1016/j.energy.2016.10.046 |
| [13] |
Norbert B, Norihiro W, Gorke U, et al. Geoenergy Modeling I:Geothermal Processs in Fractured Porous Media[M]. Cham: Springer International Publishing, 2016.
|
| [14] |
Norihiro W, Guido B, Mauro C, et al. Geoenergy Modeling Ⅲ:Enhanced Geothermal Systems[M]. Cham: Springer International Publishing, 2016.
|
| [15] |
Brian B. Characterizing Flow and Transport in Fractured Geological Media:A Review[J]. Advances in Water Resources, 2002, 25: 861-884. DOI:10.1016/S0309-1708(02)00042-8 |
| [16] |
Fu Pengcheng, Scott M J, Carrigan R C. An Explicitly Coupled Hydro-Geomechanical Model for Simulating Hydraulic Fracturing in Arbitrary Discrete Fracture Networks[J]. Int J Numer Anal Meth Geomech, 2013, 37: 2278-2300. DOI:10.1002/nag.v37.14 |
| [17] |
朱家玲, 张国伟, 李君, 等. 裂隙通道内流固换热系数解析解及敏感性分析[J]. 太阳能学报, 2016, 37(8): 2019-2025. Zhu Jialing, Zhang Guowei, Li Jun, et al. Analytical Solution and Sensitivity Analysis of Fluid-Solid Heat Transfer Coefficient in Fracture Channel[J]. Acta Energiae Solaris Sinica, 2016, 37(8): 2019-2025. DOI:10.3969/j.issn.0254-0096.2016.08.018 |
| [18] |
同登科, 陈钦雷. 关于Laplace数值反演Stehfest方法的一点注记[J]. 石油学报, 2001, 22(6): 91-92. Tong Dengke, Chen Qinlei. A Note on the Laplace Numerical Inversion Stehfest Method[J]. Acta Petrolei Sinica, 2001, 22(6): 91-92. DOI:10.3321/j.issn:0253-2697.2001.06.020 |
| [19] |
Wagner W, Cooper J R, Dittmann A, et al. The IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam[J]. Journal of Engineering for Gas Turbines and Power, 2000, 122(1): 150-182. DOI:10.1115/1.483186 |
| [20] |
Zeng Yuchao, Wu Nengyou, Su Zheng, et al. Numerical Simulation of Heat Production Potential from Hot Dry Rock by Water Circulating Through a Novel Single Vertical Fracture at Desert Peak Geothermal Field[J]. Energy, 2013, 63: 268-282. DOI:10.1016/j.energy.2013.10.036 |



