2. 水利部山洪地质灾害防治工程技术研究中心, 武汉 430010;
3. 长江水利委员会长江水资源保护科学研究所, 武汉 430051
2. Research Center on Mountain Torrents and Geological Disaster Prevention, Ministry of Water Resources, Wuhan 430010, China;
3. Changjiang Water Resources Protection Institute, Changjiang Water Resources Commission, Wuhan 430051, China
0 引言
地下水运动时刻伴随着能量的传递,受含水层水文地质条件和边界温度的影响,地质体温度存在一定时空差异,这些差异能够用来表征地下水活动[1]。作为一种低成本、易操作、能够连续监测的天然示踪方法,地质体温度在示踪地下水流速方面具有一定优势[2]。随着温度场与渗流场耦合机理研究的深入,以及水热物理方程求解方法的快速发展,温度示踪方法在推算区域地下水流速[3-4]、剖析地表水-地下水交互作用[5-8]、率定含水层水文地质参数[9-10]和探测工程地下水渗漏[11-13]等方面得到了广泛的应用。
在地下水活跃运动含水层,地表温度变化主要通过水体流动引起的热对流作用向地壳岩层深处传递,对温度随深度的变化曲线(温深曲线)产生干扰,温度信号偏离程度可用于推算地下水流速[2-4]。Bredehoeft等[14]推导了边界温度恒定一维稳定流水热运移方程解析解,并求出不同流速的标准温深曲线,比对率定含水层流速。受全球气候变暖和城市化进程影响,地表温度增加趋势明显,相关研究分别使用线性[3-4, 15]、阶跃[16-17]和指数[18]函数来描述地表温度变化情况,并提出相应的垂向一维水热运移方程解析解用以计算地表暖化影响下地下水渗透速度。但是,地表温度与气温变化具有一定相似性,单一函数无法准确描述其细节变化,对温度示踪流速准确性产生一定影响,采用数值方法[19-20]可有效模拟地表温度变化在含水层中的热传递过程,提高示踪地下水流速精确性。
当前国内关于温度示踪地下水活动研究侧重于河岸带潜流层[6-8]和复杂地质条件[11-13, 20]地下水流动过程的精细刻画,对区域尺度地下水流动特征的研究尚不多。本文基于垂向一维非稳定流水热运移方程数值解,采用最小二乘法推算雷州半岛东北部地下水渗流速度,并分析城市热岛效应对地表、地下温度的影响及其对渗流速度计算结果的影响,以期构建温度示踪方法测算地下水流速技术体系,并应用于区域地下水资源评价。
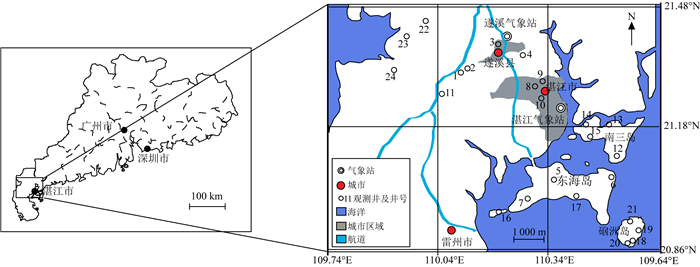
1 研究区域与方法 1.1 研究区域与数据来源研究区域位于广东省南端雷州半岛东北部(图 1),面积约800 km2,包括遂溪县东北部、湛江市中部、南三岛、东海岛和硇洲岛,土地利用类型主要为农业、森林和城市用地。湛江市1951—2016年均降水量为1 633.72 mm,年均气温为23.25 ℃。研究区域以半岛陆域为主,总体地势北高南低,北部以遂溪断层为界,基岩由片岩、石英岩、砾岩、砂岩、泥岩和玄武质火山岩组成,上层为松散冲积土和湖相沉积物覆盖。区域地下水类型有松散岩类孔隙水、火山岩孔洞裂隙水和基岩裂隙水。区域地下水系统由3个含水层和2个弱透水层组成,主要包括:埋深30 m左右的浅层水、50~200 m的中层承压水和250~500 m的深层承压水[21]。区域地下水补给主要来源于降水和河道、水库渗漏;地下水以向海排泄或人工抽水形式消耗。
|
| 图 1 研究区域示意图 Fig. 1 Sketched map of the study area |
|
|
为探究研究区域地下水流动特征,在2016年12月对研究区域24口观测钻孔温度进行测量。观测钻孔温度通过温度探头(日本川铁高等科技公司)进行测量,精度为0.001 ℃。探头由350 m长测绳沿钻孔进行拖曳,每隔1~2 m,待显示数据稳定后进行一次读数,温度测量3次求均值作为测量结果,用以消除测量误差。测量钻孔的直径约为20 cm,水体上方空气温度对地温影响可以忽略。观测井大多于2010年成井,当前地质体温度已经趋于稳定,观测钻孔内地下水温度可以代表周边地质体温度。研究区域地下水埋深为地下4~41 m,地下水位为-20.68~77.55 m,观测钻孔深41~289 m。
24口观测钻孔由广东省环境监测站管理,用于地下水水位监测,其中20口观测钻孔位于郊区,地表被耕地或林地覆盖,剩余4口观测钻孔位于城区,地表为城市住宅地。城市热岛效应可能会造成城区地表温度增加,从而影响研究区域地下温度;因此,研究搜集了湛江和遂溪气象站的气温和地表温度数据,分别用以表征城区和郊区地表暖化过程。
1.2 研究方法利用温度计算地下水流速理论基础是Stallman[22]提出的各向同性、均质、饱和、多孔介质三维非稳定水-热流运移控制方程。考虑研究区域以垂向地下水流动为主,使用垂向一维非稳定流水-热运移方程对垂向分层地下水平均流速进行计算,方程为
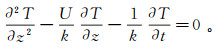 (1)
(1) 式中:T为地下温度(℃);z为由地表向下深度(m);k为地质体热扩散率(m2/a);t为时间(a);U为地下水垂向达西流速常数倍流速(m/a)。
U按照下式进行定义和计算:
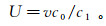 (2)
(2) 其中:v是地下水垂向达西流速(m/a);c0和c1分别是水体和地质体的质量热容(J/(kg·℃))。
本文使用交替方向隐格式差分法(ADI)对方程(1)进行差分,可将偏微分方程转化为线性方程:
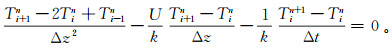 (3)
(3) 其中:i和n分别是空间和时间网格数; Δz和Δt分别是空间和时间步长。
代入初始和边界条件,可以将不同节点上线性方程(3)组成的方程组化为三对角矩阵,使用追赶法实现对矩阵的求解。方程的上边界条件通常使用地表温度测量数据代入,缺乏地表温度数据时,相关研究[3-4, 15]表明可使用近地表气温数据进行代替。方程的下边界条件一般近似恒定,可设定为常数。方程的初始条件一般设定为背景地温梯度,可由测量的地温数据确定。
上述数值方法提供了一种基于测量地温数据计算地下水流速的方法。传统的地下水流速率定方法是标准曲线法[14]:将不同流速计算得到的标准温深曲线绘制在图表上,同时将野外实测得到的温深曲线绘制在同一图表上,比对选择与实测温深曲线最接近的标准曲线,其对应的流速作为计算结果。上述方法某种程度上受人为影响,鉴于此,研究采用最小二乘法对地下水流速进行推算,构建如下目标函数:
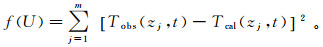 (4)
(4) 其中:m为测量温度数据数目;Tobs和Tcal分别为测量温度和计算温度(℃);zj为测量温度的埋深(m)。使目标函数(4)值最小时对应的U值为推算的地下水流速的倍数。
本文引入Levenberg-Marquardt算法[23]对上述非线性方程进行求解。Levenberg-Marquardt算法通过赋初值和数值迭代算法使目标函数达到最小值,在每次迭代过程中,使用新参数γ+δ代替原始参数变量γ。其中新参数增量δ通过求解以下线性方程组得到:
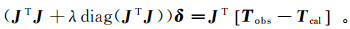 (5)
(5) 其中:J是雅各比矩阵;JT是J的转置矩阵;λ是每一个迭代过程中的衰减因子;diag表示对角矩阵。
雅各比矩阵J的第i行向量Ji按照下式进行计算:
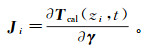 (6)
(6) 地表温度和近地表气温均可以作为模型计算的上边界条件。地表温度和气温在较长时间尺度(年代、世纪)上互相耦合,具有较强的一致性;在短时间尺度(年、月、日、小时)则存在较大的差异性[24]。为了提高地温的模拟精度,对1954—2016年湛江站和1961—2016年遂溪站地表温度和气温数据(图 2)进行分析, 结果显示:气温与地表温度具有较强的相关性(R2>0.700,R为相关系数); 研究区域地表温度总体上比近地表气温高,可能是由地面长波辐射能量造成的[24]。

|
| 图 2 遂溪站(a)和湛江站(b)观测气温和地表温度对比图 Fig. 2 Comparison of SAT and GST in Suixi (a) and Zhanjiang (b) station |
|
|
为了揭示研究区域近地表气温和地表温度的时间变化特征,将两个站点的气温和地表温度数据列于图 3。气温和地表温度时间序列在过去50年均显示了明显的增加趋势,但增幅不同。遂溪气象站气温和地表温度增长率基本一致,湛江气象站地表温度增长率几乎为气温增长率的2倍。湛江气象站地表温度较高增长率可能是由城市热岛效应造成的:湛江气象站位于市区,周边地表为水泥硬化地面,在城市化过程中,新建水泥路面材料的高导热率和对太阳能量高吸收率导致地表温度增加率较高[25]。遂溪和湛江气象站年均地表温度高于气温约2 ℃,年均气温的波动特征与地表温度保持高度的一致性,表明两者相关性较强。图 3显示地表温度的显著增加主要集中在2011—2016年间。研究使用遂溪和湛江气象站地表温度数据序列作为模型计算的上边界条件,分别表示郊区和城区情景。

|
| 图 3 遂溪站(a)和湛江站(b)观测气温和地表温度时间序列图 Fig. 3 Observed SAT and GST data and fitted lines in the Suixi (a) and Zhanjiang (b) station |
|
|
模型计算中涉及的主要参数包括地质体热扩散率、地温梯度和地下水流速常数倍流速。研究区域基岩与覆盖物的成分[21]与日本熊本平原基本一致,因此采用其参数值20.5 m2/a[15]作为研究区域地质体热扩散率值。相关研究[2-3]表明:在地下水活动活跃地层,温深曲线在入渗和排泄条件下向上分别呈现“凹”和“凸”不同形态,入渗和排泄速度越大,曲线弯曲程度越大;同时,地表暖化造成浅层地温增加,在近地表区域出现地温负梯度。因此,选择曲线弯曲程度较小、埋深大于50 m的地温测量数据来估算研究区域背景地温梯度。钻孔3、5、6、7、8、9和20地温数据线性拟合结果如表 1所示,各钻孔估算地温梯度处于0.013~0.046 ℃/m,均值为0.033 ℃/m。温度数据与深度具有较高的相关系数(R2>0.880),且假设检验p值均小于0.001,因此,拟合得到的均值可作为模型中的地温梯度参数。
| 钻孔 | 率定地温梯度/(℃/m) | R2 | p |
| 3 | 0.039 | 0.983 | <0.001 |
| 5 | 0.041 | 0.977 | <0.001 |
| 6 | 0.039 | 0.983 | <0.001 |
| 7 | 0.040 | 0.885 | <0.001 |
| 8 | 0.013 | 0.941 | <0.001 |
| 9 | 0.024 | 0.917 | <0.001 |
| 20 | 0.046 | 0.988 | <0.001 |
本文使用交替方向隐格式差分法对垂向一维非稳定流水-热运移方程进行求解,采用遂溪和湛江气象站地表温度数据作为模型的上边界条件,下边界条件设定为恒定温度。模型的初始条件为无地下水流影响、稳定状态下的温度分布。模型设定条件和相关参数如表 2所示。
| 属性 | 赋值 |
| 水体热容量/(J/m3·℃) | 4.18×106 |
| 地质体热容量/(J/m3·℃) | 2.50×106 |
| 地质体热扩散率/(m2/a) | 20.5 |
| 模型垂向深度/ m | 3 000 |
| 下边界温度/℃ | 104 |
| 地温梯度/(℃/m) | 0.033 |
| 时间步长/a | 1 |
| 空间步长/m | 1 |
| 郊区地温模拟时长 | 1961—2016 |
| 城区地温模拟时长 | 1954—2016 |
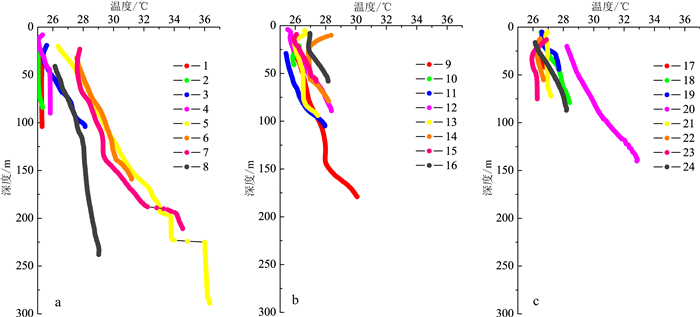
图 4展示了研究区域24口观测钻孔地温数据,可见大多数钻孔随着深度的增加温度显示增加趋势,可能是地温梯度对钻孔温度产生的影响。24口钻孔温深曲线呈现非线性形态,显示了地下水活动对地温的扰动。钻孔温度在浅层呈现负梯度,则可能是地表暖化过程[3, 26]对地温的影响造成的。观测钻孔3、8、9和10位于城区,其测量地温值高于周边郊区钻孔温度,表明城市热岛效应对地下温度产生显著影响;钻孔5的温深曲线在222 m深处发生了显著变化,可能是由于此深度为不同含水层作用界面,水文地质条件的变化导致地温梯度发生改变[27]。
|
| 图 4 钻孔1—8(a),钻孔9—16(b)和钻孔17—24(c)测量地温数据 Fig. 4 Observed borehole temperatures in Well 1-8 (a), Well 9-16 (b) and Well 17-24 (c) |
|
|
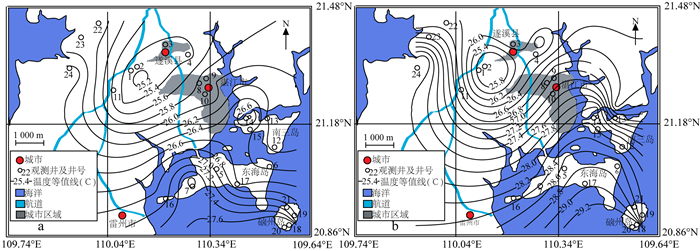
根据观测钻孔实测温度数据,绘制了埋深30和75 m处的温度等值线图(图 5),分别用以表征研究区域第一和第二含水层温度空间分布特征。图 5显示研究区域含水层温度自西北向东南递增,这可能与区域地下水运动情况相关。西北部低地温区域(遂溪县附近)地下水以补给为主,低温地表水渗漏进入含水层,导致地下水温度降低;东南部高地温区域(东海岛、南三岛、硵州岛)地下水以排泄为主,高温地下水向上流动,抑制地表温度对地下温度的影响,造成地下水温度升高。湛江市和遂溪县城区域地下水温度较同纬度区域地温高,表明城市热岛效应对地温影响明显。因此,地温可以作为一种示踪剂,有效揭示地下水流动状况和反演地表温度变化。
|
| 图 5 研究区域30 m(a)和75 m(b)埋深处温度等值线图 Fig. 5 Isothermal lines of groundwater at the depth of 30 m (a) and 75 m (b) |
|
|
采用交替方向隐格式差分法对垂向一维非稳定流水-热运移方程进行数值求解,基于最小二乘法对不同观测钻孔的地下水流速进行估算。地下水流速计算结果、地下水水位,以及实测与模拟地温间的R2和均方根误差(RMSE)如表 3所示。计算得到研究区域地下水补给速度处于0.066~2.580 m/a之间,均值为0.796 m/a;地下水排泄速度为0.050~0.770 m/a,均值为0.269 m/a。计算结果与Zhou等[21]使用数值模拟对研究区域地下水流速计算结果基本一致。地下水流速为正值的11口观测钻孔多位于研究区域西北部,表明地下水入渗以此区域降水和河道渗漏为主;地下水流速为负值的13口观测钻孔多位于研究区域东南海岛,其中地下水排泄入海主要发生在东海岛、南三岛和硵州岛。温度示踪解析区域地下水流动情况与地下水位分布情况相一致。除了钻孔1、2、10、14和23,其余钻孔观测和计算地温数据具有较强相关性(R2>0.50);各钻孔观测和计算地温数据的均方根误差处于0.119~2.905之间,均值为0.748。上述统计结果表明,研究提出的模型可以较好地模拟地表暖化影响下地下水流动对温深曲线的扰动量,率定得到的地下水流速具有较强的可信性。
| 钻孔 | 地下水流速/(m/a) | 地下水水位/m | R2 | RMSE |
| 1 | 1.382 | 71.05 | 0.025 | 0.138 |
| 2 | 1.248 | 77.55 | 0.375 | 0.239 |
| 3 | 0.444 | -3.70 | 0.976 | 0.717 |
| 4 | 2.580 | 7.92 | 0.922 | 0.273 |
| 5 | -0.489 | -11.68 | 0.982 | 2.905 |
| 6 | -0.288 | -20.68 | 0.988 | 1.139 |
| 7 | -0.234 | -9.38 | 0.864 | 1.935 |
| 8 | 0.792 | 12.77 | 0.859 | 1.266 |
| 9 | 0.495 | 14.16 | 0.945 | 1.168 |
| 10 | 0.581 | 16.97 | 0.104 | 0.143 |
| 11 | 0.475 | 10.95 | 0.980 | 0.621 |
| 12 | -0.079 | 0.35 | 0.983 | 0.870 |
| 13 | 0.315 | -0.95 | 0.620 | 0.475 |
| 14 | -0.169 | -3.50 | 0.114 | 0.605 |
| 15 | -0.050 | -2.79 | 0.975 | 0.465 |
| 16 | -0.441 | -4.94 | 0.812 | 0.576 |
| 17 | -0.066 | 2.04 | 0.970 | 0.119 |
| 18 | -0.315 | 5.51 | 0.983 | 0.730 |
| 19 | -0.408 | 5.07 | 0.911 | 0.525 |
| 20 | -0.770 | -6.40 | 0.966 | 1.329 |
| 21 | -0.065 | -2.24 | 0.541 | 0.466 |
| 22 | 0.066 | 5.45 | 0.516 | 0.278 |
| 23 | 0.374 | 5.25 | 0.018 | 0.297 |
| 24 | -0.126 | 7.85 | 0.983 | 0.679 |
钻孔观测和模拟温度曲线差异较大的可以分为3种情况:1)观测温度在不同深度均低于模拟温度,如钻孔1和2;2)观测和模拟温度在埋深较浅部分具有较大差异,如钻孔3、10、16、18、22和23;3)观测和模拟温深曲线由于形状差异产生不一致,如钻孔5、7、8、18和20。第一种情况可能受不同的地表温度条件影响,钻孔1和2所处位置海拔高于遂溪气象站海拔,导致实际地表温度低于遂溪站测量值;第二种情况是由于钻孔进入空气或者含水层的热传导性较差,导致地下水热对流作用无法起主导作用[9];第三种情况则可能由地质体的垂向异质性造成,当地下水在水文地质条件差异较大界面流动时,由于流速的变化导致温深曲线形状发生变化[27],此情形下,率定得到的地下水流速为垂向平均流速。
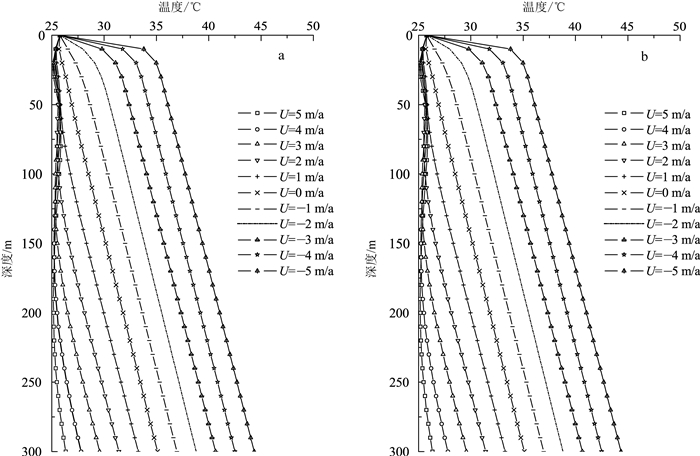
3.3 城市热岛效应对地温影响1961—2016年遂溪站地表温度数据每年增加约0.011 ℃,1954—2016年湛江站地表温度数据每年增加约为0.017 ℃。遂溪气象站位于城市郊区,其地表温度变化可能只受全球气候变暖的影响;湛江气象站位于城市区域,其地表温度变化受全球气候变暖和城市热岛效应的双重影响。气候变化和城市热岛效应通过不同的物理机制[28]造成地表温度升高,通过热传导和热对流作用影响地下温度。本文使用一维非稳定流水-热运移模型,计算遂溪站和湛江站地表温度为边界条件下,不同地下水流速对应的地温分布情况(图 6),分析城市热岛效应对地温的影响。图 6显示:地下水流动对地温分布产生显著影响[2-3]:地下水流速为0时,地表温度变化通过热传导作用向下传播,随深度增加呈指数递减;地下水流速为正值时,地表温度通过热对流运动影响地温分布,造成地下水补给区地温值降低,其年间波动特征的幅度衰减速度则随着地下水流速的增加而减缓,使得地下水补给区温深曲线呈“S”形;地下水流速为负值时,地底深处高温随热对流作用向上传递,造成地下水排泄区地温值升高,其年间波动向下传递过程则受地下水向上流动过程抑制。
|
| U的正值和负值分别表示地下水向下和向上流动。 图 6 遂溪站(a)和湛江站(b)地表温度影响下不同流速对应的地下水温分布图 Fig. 6 Calculated subsurface temperature profiles in 2016 with different groundwater fluxes in Suixi (a) and Zhanjiang (b) station |
|
|
受城市热岛效应的影响,湛江气象站的地表温度高于遂溪气象站,其模拟的地下温度值也高于遂溪。为分析城市热岛效应对地下温度的影响,图 7展示了在不同流速时,湛江站与遂溪站2016年在地表温度影响下的地下水温度差值。总体上来说,城市热岛效应导致地下水补给区和排泄区地下温度升高,湛江站地下温度值平均高于遂溪站约0.96 ℃。城市热岛效应在地下水排泄区增温效应更加明显,且增幅与地下水流速呈正相关变化。城市热岛效应对地下水补给区地温分布影响较为复杂:湛江站与遂溪站地表温度差值随时间呈现周期波动,这种波动特征随地下水入渗影响地温,使得地温差值呈现“S”形曲线;城市化热岛效应对地表温度影响主要发生在2011—2016年(图 3),其对地下温度的影响主要作用于浅层含水层。

|
| 图 7 2016年地表温度影响下湛江站与遂溪站不同流速时地下水温差值图 Fig. 7 Differences of subsurface temperature profiles between Zhanjiang and Suixi station with different groundwater fluxes in 2016 |
|
|
为提高本文提出方法计算地下水流速的精确性,对模型涉及主要参数进行了敏感性分析。其中:地质体热扩散率作为模型中的重要热力学参数,受土壤有机质含量、土壤孔隙度及土壤湿度等因素影响,土壤垂向异质性通过改变土壤热导率和热容量来影响地温分布[27, 29];地表温度变化是模型的上边界温度条件,受地表湿度、气温、光强和地表介质等因素影响,其通过热传导和热对流作用对地温产生扰动。以下对地质体热扩散率和地表温度的敏感性进行分析。
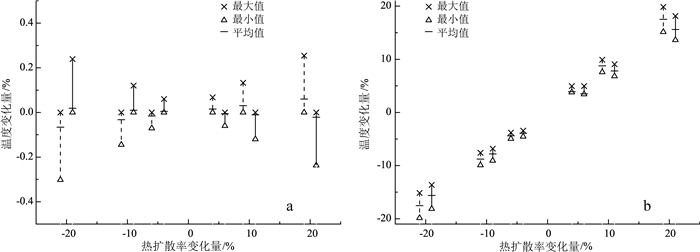
以20.5 m2/a作为模型中地质体热扩散率基准值,同时以遂溪气象站1961—2016年地表温度作为地表温度的基准值,对基准值不同幅度增减情形(-20%, -10%, -5%, 5%, 10%, 20%)的地温分布情况进行计算,选取U=1和-1 m/a情形下结果进行分析,二者分别表示地下水排泄区和补给区。地质体热扩散率敏感性分析结果(图 8a)表明,地质体扩散率在±20%变化时,分别造成补给区和排泄区地下水温值变化量为±0.3%和±0.25%;地表温度敏感性分析结果(图 8b)表明,地表温度在±20%变化时,分别造成补给区和排泄区地下水温值变化为±20%和±18%。由上述结果可知:地质体热扩散率和地表温度对利用地温推算地下水流速结果均具有较大的影响,即使热扩散率仅造成地下水温值变化±0.3%,其对地下水流速计算结果影响也可达到±3.5%(图 7);相较于对热扩散率进行率定,地表温度的准确观测在提高地温推算地下水流速准确性更为重要。因此参数地表温度对地下水补给区地温影响更加明显,在利用观测钻孔地温值计算地下水入渗速率过程中应考虑。
|
| 虚线表示U=1 m/a(排泄区),实线表示U=-1 m/a(补给区)情形。 图 8 地质体热扩撒率(a)和地表温度变化(b)的参数敏感性分析结果 Fig. 8 Sensitivity of subsurface temperature to thermal diffusivity(a) and GST (b) |
|
|
1) 温度示踪法对地表暖化情景下雷州半岛东北部地下水流速进行计算,得到研究区域地下水补给速度为0.066~2.580 m/a,均值为0.796 m/a;地下水排泄速度为0.050~0.770 m/a,均值为0.269 m/a。地下水入渗以研究区域西北部降水和河道渗漏为主,地下水排泄入海主要发生在东海岛、南三岛和硵州岛。温度示踪解析区域地下水流动情况与地下水位分布情况相一致。观测和计算地温数据具有较强相关性(R2>0.50)和较低均方根误差(均值为0.748),表明研究提出方法计算结果具有较强的可信性。
2) 城市热岛效应造成研究区域地表温度增加速率为每年0.006 ℃,造成地下补给区和排泄区温度增加约0.96 ℃。参数敏感性分析结果表明地质体热扩散率和地表温度均对地温计算结果产生较明显的影响,对其准确率定在利用观测钻孔地温值计算地下水流速过程十分重要。
3) 本文提出的地表暖化影响下温度示踪地下水流速的计算方法丰富了地下水流速快速测算手段,但由于地下水热运移过程复杂和相关机理研究不够深入,温度示踪地下水流速研究亟待进一步加强。
| [1] |
吴志伟, 宋汉周. 地下水温度示踪理论与方法研究进展[J]. 水科学进展, 2011, 22(5): 733-740. Wu Zhiwei, Song Hanzhou. Temperature as a Groundwater Tracer:Advances in Theory and Methodology[J]. Advances in Water Science, 2011, 22(5): 733-740. |
| [2] |
Anderson M P. Heat as a Ground Water Tracer[J]. Ground Water, 2005, 43(6): 951-968. DOI:10.1111/gwat.2005.43.issue-6 |
| [3] |
Taniguchi M, Shimada J, Tanaka T, et al. Disturbances of Temperature-Depth Profiles Due to Surface Climate Change and Subsurface Water Flow:1:An Effect of Linear Increase in Surface Temperature Caused by Global Warming and Urbanization in Tokyo, Metropolitan Area, Japan[J]. Water Resource Research, 1999, 35(5): 1507-1517. DOI:10.1029/1999WR900009 |
| [4] |
Taniguchi M, Uemura T, Jago-on K. Combined Effects of Urbanization and Global Warming on Subsurface Temperature in Four Asian Cities[J]. Vadose Zone Journal, 2007, 6: 591-596. DOI:10.2136/vzj2006.0094 |
| [5] |
Anibas C, Fleckenstein J H, Volze N, et al. Transient or Steady-State? Using Vertical Temperature Profiles to Quantify Groundwater-Surface Water Exchange[J]. Hydrological Processes, 2009, 23: 2165-2177. DOI:10.1002/hyp.v23:15 |
| [6] |
马瑞, 董启明, 孙自永, 等. 地表水与地下水相互作用的温度示踪与模拟研究进展[J]. 地质科技情报, 2013, 32(2): 131-137. Ma Rui, Dong Qiming, Sun Ziyong, et al. Using Heat to Trace and Model the Surface Water-Groundwater Interactions:A Review[J]. Geological Science and Technology Information, 2013, 32: 131-137. |
| [7] |
朱静思, 束龙仓, 鲁程鹏. 基于热追踪方法的河道垂向潜流通量的非均质性研究[J]. 水利学报, 2013, 44(7): 818-825. Zhu Jingsi, Shu Longcang, Lu Chengpeng. Study on the Heterogeneity of Vertical Hyporheic Flux Using a Heat Tracing Method[J]. Shuili Xuebao, 2013, 44(7): 818-825. |
| [8] |
李英玉, 赵坚, 吕辉, 等. 河岸带潜流层温度示踪流速计算方法[J]. 水科学进展, 2016, 27(3): 423-429. Li Yingyu, Zhao Jian, Lü Hui, et al. Investigation on Temperature Tracer Method Calculated Flow Rate of Hyporheic Layer in Riparian Zone[J]. Advances in Water Science, 2016, 27(3): 423-429. |
| [9] |
Taniguchi M. Evaluation of Vertical Groundwater Fluxes and Thermal Properties of Aquifers Based on Transient Temperature-Depth Profiles[J]. Water Resources Research, 1993, 29(7): 2021-2026. DOI:10.1029/93WR00541 |
| [10] |
Constantz J, Su G W, Seymour D, et al. Estimation of Hydraulic Conductivity in an Alluvial System Using Temperature[J]. Ground Water, 2004, 42(6/7): 890-902. |
| [11] |
李端有, 陈鹏霄, 王志旺. 温度示踪法渗流监测技术在长江堤防渗流监测中的应用初探[J]. 长江科学院院报, 2000, 17(增刊): 48-51. Li Duanyou, Chen Pengxiao, Wang Zhiwang. Application of Temperature Indication Method in Seepage Monitoring of Yangtze River Levee[J]. Journal of Yangtze River Scientific Research Institute, 2000, 17(Sup.): 48-51. |
| [12] |
董海洲, 陈建生. 利用温度示踪方法探测基坑渗漏[J]. 岩石力学与工程学报, 2004, 23(12): 2085-2090. Dong Haizhou, Chen Jiansheng. Study on Groundwater Leakage of Foundation Pit with Temperature Tracer Method[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(12): 2085-2090. DOI:10.3321/j.issn:1000-6915.2004.12.026 |
| [13] |
王新建, 潘纪顺. 堤坝多集中渗漏通道位置温度探测研究[J]. 岩土工程学报, 2010, 32(11): 1800-1805. Wang Xinjian, Pan Jishun. Location Detection of Concentrated-Leakage Passages in Dam by Groundwater Temperature[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1800-1805. |
| [14] |
Bredehoeft J D, Papadopulos I S. Rates of Vertical Groundwater Movement Estimated from the Earth's Thermal Profile[J]. Water Resource Research, 1965, 1(2): 325-328. DOI:10.1029/WR001i002p00325 |
| [15] |
Taniguchi M, Shimada J, Uemura T. Transient Effects of Surface Temperature and Groundwater Flow on Subsurface Temperature in Kumamoto Plain, Japan[J]. Physics and Chemistry of the Earth, 2003, 28: 477-486. DOI:10.1016/S1474-7065(03)00067-6 |
| [16] |
Taniguchi M, Williamson D R, Peck A J. Disturbances of Temperature-Depth Profiles Due to Surface Climate Change and Subsurface Water Flow:2:An Effect of Step Increase in Surface Temperature Caused by Forest Clearing in Southwest Western Australia[J]. Water Resources Research, 1999, 35(5): 1519-1530. DOI:10.1029/1998WR900010 |
| [17] |
Menberg K, Blum P, Kurylyk B L, et al. Observed Groundwater Temperature Response to Recent Climate Change[J]. Hydrology and Earth System Sciences, 2014, 11(3): 4453-4466. |
| [18] |
Kurylyk B L, Macquarrie K T. A New Analytical Solution for Assessing Climate Change Impacts on Subsurface Temperature[J]. Hydrological Processes, 2014, 28(7): 3161-3172. DOI:10.1002/hyp.v28.7 |
| [19] |
Keshari A K, Koo M. A Numerical Model for Estimating Groundwater Flux from Subsurface Temperature Profiles[J]. Hydrological Processes, 2010, 21(25): 3440-3448. |
| [20] |
吴志伟, 宋汉周. 基于Lu模型的浅部地温场与渗流场耦合研究[J]. 水利学报, 2015, 46(3): 326-333. Wu Zhiwei, Song Hanzhou. Study on Shallow Geothermal Field and Seepage Field Coupling Based on Lu Model[J]. Shuili Xuebao, 2015, 46(3): 326-333. |
| [21] |
Zhou X, Chen M, Liang C. Optimal Schemes of Groundwater Exploitation for Prevention of Seawater Intrusion in the Leizhou Peninsula in Southern China[J]. Environmental Geology, 2003, 43(8): 978-985. DOI:10.1007/s00254-002-0722-9 |
| [22] |
Stallman R W. A Multivariate Statistical Approach to Spatial Representation of Groundwater Contamination Using Hydrochemistry and Microbial Community Profiles[J]. Environmental Science Technology, 2005, 39: 7551-7559. DOI:10.1021/es0502627 |
| [23] |
Stallman R W. Computation of Ground-Water Velocity from Temperature Data, Washington, DC, USA[C]//Ray Bentall. Methods of Collecting and Interpreting Ground-Water Data. Washington: U. S. Government Printing Office, 1963: 36-46.
|
| [24] |
Marquardt D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters[J]. SIAM Journal of Applied Mathematics, 1963, 11(2): 431-441. DOI:10.1137/0111030 |
| [25] |
Smerdon J E, Pollack H N, Cermak V, et al. Daily, Seasonal, and Annual Relationships Between Air and Subsurface Temperatures[J]. Journal of Geophysical Research-Atmospheres, 2006, 111: D07101. |
| [26] |
Hachem S, Duguay C R, Allard M. Comparison of MODIS-Derived Land Surface Temperatures with Near-Surface Soil and Air Temperature Measurements in Continuous Permafrost Terrain[J]. Cryosphere, 2012, 6(1): 51-69. DOI:10.5194/tc-6-51-2012 |
| [27] |
Chen Y C, Chiu H W, Su Y F. Does Urbanization Increase Diurnal Land Surface Temperature Variation? Evidence and Implications[J]. Landscape and Urban Planning, 2017, 157: 247-258. DOI:10.1016/j.landurbplan.2016.06.014 |
| [28] |
Taylor C A, Stefan H G. Shallow Groundwater Temperature Response to Climate Change and Urbanization[J]. Journal of Hydrology, 2009, 375: 601-612. DOI:10.1016/j.jhydrol.2009.07.009 |
| [29] |
赵勇胜, 杨元元, 高鹏龙, 等.多孔介质中热蒸汽的迁移特性及其修复氯苯污染土壤效果[J/OL].吉林大学学报(地球科学版). doi: 10.13278/j.cnki.jjuese.20180047. Zhao Yongsheng, Yang Yuanyuan, Gao Penglong, et al. Transport Characteristics of Steam and Steam Remediatation of Chlorobenzene Contaminated Soil[J/OL]. Journal of Jinlin University(Earth Science Edition). doi: 10.13278/j.cnki.jjuese.20180047. |


