2. 吉林大学建设工程学院, 长春 130026
2. Construction Engineering College, Jilin University, Changchun 130026, China
0 引言
随着地下矿产资源勘探深度越来越大,岩石越来越硬,传统钻进方法的适用性逐渐降低,需要研究新的钻进方法来解决硬岩钻进的技术难题。研究表明,振动有利于碎岩[1-2]。完整致密硬岩的固有频率一般在20 kHz以上,属于超声波范畴。在钻进过程中,对岩石施加与其固有频率相当的超声波振动,岩石内部将快速产生损伤导致振动强度大幅下降,而采用传统的切削钻进技术配合超声波振动进行钻进,可以有效提高硬岩钻进效率[3-4]。
目前人们对低频振动碎岩机理进行了较深入的研究:Davison等[5]给出了岩石的动态损伤累积模型;Whittles等[6]认为随着应变率的增加,需要更高的能量来破碎岩石,即动态单轴抗压强度远高于其静态强度。李夕兵等[7-9]进行了不同轴压下相同动荷载冲击和不同轴压下岩石临界冲击破坏的试验研究,认为:在冲击入射加载条件下,硬岩试件在遵循最大拉应力断裂准则产生层裂的同时,还可能因为损伤和剩余反射波的共同作用产生后续破坏;动载条件下,岩石吸能存在一临界入射应力值,超过该值岩石吸能随应变率的增加而增加;岩石的破碎效果主要取决于加载速率和岩石类型。尹土兵等[10]对砂岩试样进行冲击试验,并通过常规霍普金森杆压缩试验中的能量耗散原理,计算出不同条件下动静组合加载岩石试样的能量耗散规律。
上述研究表明,动静组合加载下,岩石对外界载荷的响应受预压力的影响很大。但上述研究涉及的振动频率较低,而在与硬岩自振频率相当的振动频率下,预压力对岩石强度影响的研究还是空白。因此,本文采用单轴动静组合的加载模式,开展了超声波振动下不同应力条件对岩石单轴抗压强度影响的试验研究,以期为超声波振动辅助碎岩钻进技术提供理论指导。
1 动静组合加载碎岩试验 1.1 试验样品根据岩石常规力学性能测试要求,制作直径40 mm、高80 mm的标准花岗岩试样,并对岩样的两端进行研磨,使不平行度小于0.02 mm。花岗岩的平均单轴抗压强度为94.18 MPa。
1.2 试验装置在特制的ZJS-2000型超声波振动装置上进行试验。该装置如图 1所示,由振动器、电源、支架3部分构成,在支架顶端施加竖向预压力,通过电源驱动振动器施加频率为20 kHz、振幅为40 μm的超声波动载。装置的其他性能为:工作电流小于2 A,功率范围为0~1 600 W,最大预压力600 N。

|
| 图 1 ZJS-2000型超声波振动装置 Fig. 1 ZJS-2000 ultrasonic vibration device |
|
|
在5,10,15 min 3个振动时间下,对花岗岩试样分别施加100,200,300,400和500 N的轴向预压力,依次编号为1—15。岩石是一种含有微孔隙、微裂纹等细观缺陷的复合材料[11-12],为了降低岩石各向异性和非均匀性对试验结果的影响,在每个应力条件下分别进行3组平行试验,以测量单轴抗压强度,并且在试验前对3组平行试验所需全部花岗岩试样的完整性系数进行了测量。不同应力条件下,3组平行试验中试样的平均完整性系数如图 2所示。由测量结果可知,本次试验所用试样的完整性系数相差不大,岩石完整性较为一致。试样经振动后,用WEW-1000D万能试验机进行压裂试验,记录各试样的单轴抗压强度,其结果如表 1所示。

|
| 图 2 各试验组试样的完整性系数平均值 Fig. 2 Average value of intavtness index of the rock of each group |
|
|
| 序号 | 振动时间/min | 预压力/N | 单轴抗压强度/MPa | ||
| 第一组 | 第二组 | 第三组 | |||
| 1 | 5 | 100 | 87.44 | 90.10 | 90.56 |
| 2 | 5 | 200 | 90.11 | 98.93 | 99.52 |
| 3 | 5 | 300 | 79.61 | 84.63 | 85.11 |
| 4 | 5 | 400 | 77.31 | 80.28 | 78.84 |
| 5 | 5 | 500 | 78.37 | 85.89 | 79.54 |
| 6 | 10 | 100 | 94.03 | 91.42 | 92.04 |
| 7 | 10 | 200 | 95.08 | 88.05 | 95.08 |
| 8 | 10 | 300 | 78.11 | 81.52 | 84.71 |
| 9 | 10 | 400 | 76.96 | 76.37 | 76.18 |
| 10 | 10 | 500 | 77.73 | 78.53 | 76.80 |
| 11 | 15 | 100 | 89.64 | 96.71 | 94.16 |
| 12 | 15 | 200 | 95.80 | 95.95 | 88.22 |
| 13 | 15 | 300 | 77.04 | 78.54 | 83.31 |
| 14 | 15 | 400 | 76.50 | 71.78 | 74.81 |
| 15 | 15 | 500 | 76.82 | 78.11 | 76.37 |
由预压力与岩石单轴抗压强度的对应关系(图 3)可知:当预压力ps=100 N和200 N时,试样的单轴抗压强度在花岗岩平均单轴抗压强度附近浮动,随振动时间的增加,试样单轴抗压强度的变化不具规律性;当ps>200 N时,试样的单轴抗压强度明显低于平均抗压强度,图 3a中的各条曲线呈凹型。以振动时间10 min为例:当ps=400 N时,各组试样的单轴抗压强度值分别为76.96,76.37和76.18 MPa;而当ps=300 N和500 N时各组试样的单轴抗压强度值分别为78.11,81.52,84.71 MPa及77.73,78.53,76.80 MPa。静载荷为400 N时各组试样的单轴抗压强度值均小于静载荷为300 N与500 N时各组单轴抗压强度值,说明在静载荷为300~500 N范围内,随着ps增加,试样的单轴抗压强度呈先降低后增高的趋势,存在最小值。整理表 1中的试验数据可知:当ps=300 N,振动时间分别为5, 10和15 min时, 3组试样的单轴抗压强度平均值分别为83.12,81.45和79.63 MPa;当ps=400 N时的单轴抗压强度平均值分别为78.81,76.50和74.36 MPa;当ps=500 N时的单轴抗压强度平均值分别为81.27,77.69和77.1 MPa。显然,保持预压力值不变时,试样单轴抗压强度随振动时间的增加而降低。
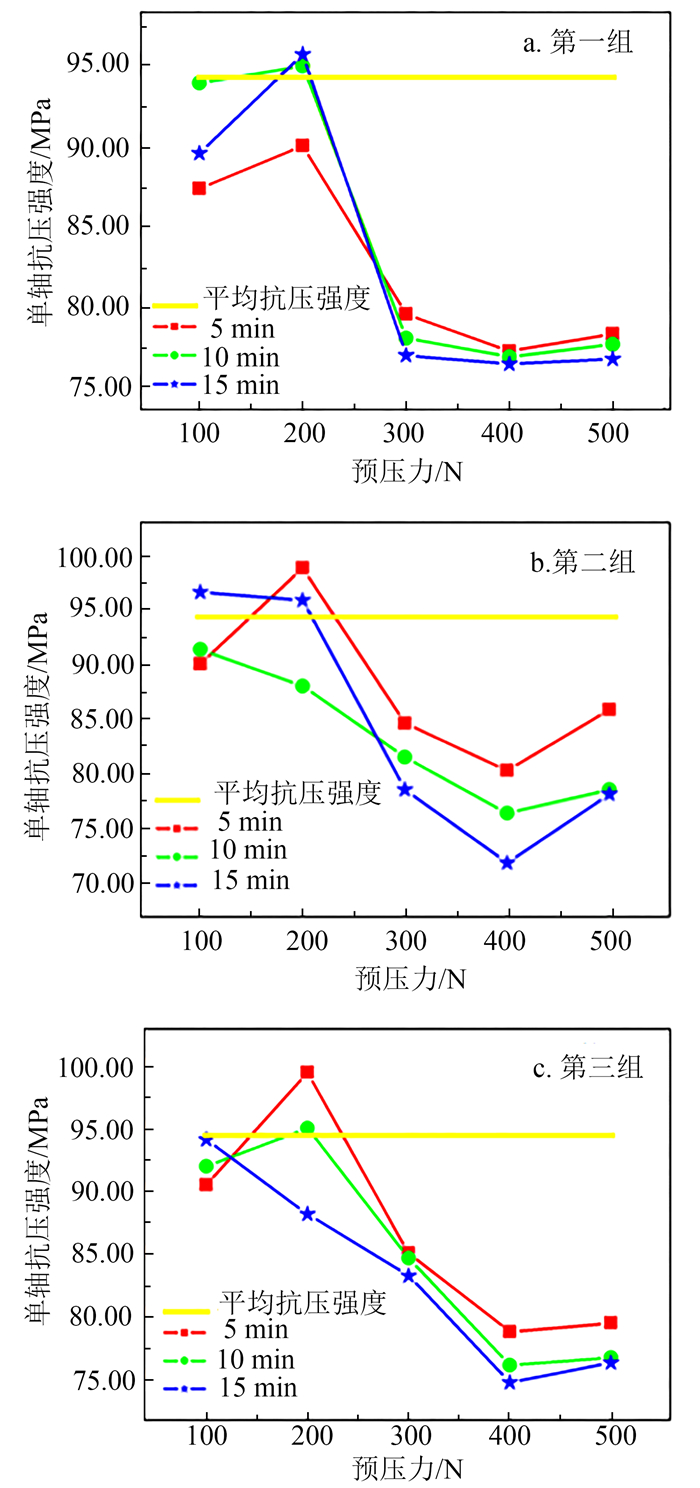
|
| 图 3 不同振动时间条件下预压力与花岗岩抗压强度的响应关系 Fig. 3 Relative of preloading against compressive strength of granite under different conditions of vibration time |
|
|
随着计算机与数字技术的迅速发展,通过数值模拟对岩石破坏机理进行分析已经成为可能[13-14]。试验结果表明,超声波振动下岩石单轴抗压强度随着预压力增加呈先降低后增高的趋势,且存在最优预压力值使岩石单轴抗压强度值最低。鉴于超声波振动辅助碎岩的内在机理为对岩石施加与其固有频率相当的超声波振动,使岩石内部快速产生损伤导致强度大幅下降,初步判断最优预压力产生的原因为岩石固有频率随受力环境的改变而改变。为了验证这一判断,采用有限元分析软件对超声波振动过程进行了数值模拟,包括谐响应分析及模态分析。
2.1 模型建立选用四面体实体单元进行建模,模型为高h=80 mm、半径r=20 mm的半圆柱体,由1个荷载边界、1个约束边界和2个自由边界构成,如图 4所示。研究[15-17]表明,为了提高数值模拟结果的准确性,岩石的非均匀性在模拟的过程中不能被忽略。因此,对所建模型做如下假设:1)假设岩石为非均匀的弹脆性体,其非均匀性仅引起内部各微小单元体密度的不同,令所有单元的密度值满足N(2 950, 5)的正态分布,整个模型的平均密度为2 950 kg/m3;2)由于超声波振动振幅很小,忽略岩石的惯性作用;3)岩石下表面各向位移恒定;4)认为初始情况下加载装置与岩石上表面微微接触,振动过程中不考虑由于接触面摩擦生热引起的岩石物理性质的变化。模型的抗压强度、泊松比及弹性模量以试验试样为标准设置,分别为94.18 MPa, 0.2和55 GPa。
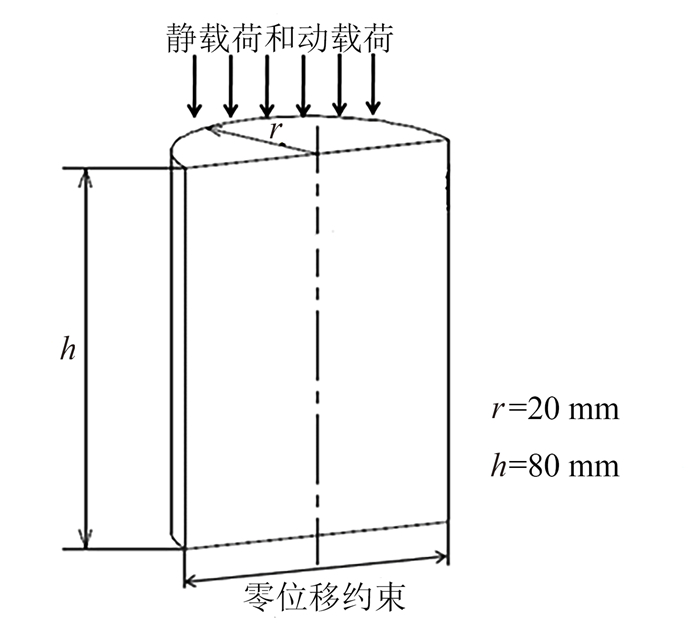
|
| 图 4 数值模拟模型 Fig. 4 Model of numerical simulation |
|
|
根据假设条件,设置约束边界的各向位移为0;在荷载边界上施加动静组合载荷,其加载方程可表示为:
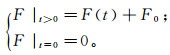 (1)
(1) 式中:F|t>0为振动时刻t荷载边界上施加的总载荷;F0为预压力(静载荷);F(t)为振幅40μm、频率20 kHz的正弦波动载,与实验所用振动器参数一致。
2.2 模拟结果及分析通过模态分析,得到了预压力400 N条件下岩石的一阶、二阶、三阶固有频率分别为:20 246,25 577,30 728 Hz。在模态分析的基础上,对模型进行谐响应分析,得到了预压力400 N条件下,不同岩石内部应力、应变与振动频率的关系曲线,如图 5所示。由模拟结果可知:当振动频率与岩石一阶固有频率相差较大时,振动频率的变化对岩石内部应力、应变影响不明显;随着振动频率逐渐向岩石一阶固有频率靠近,应力、应变迅速增大,振动频率对应力、应变的影响作用越来越明显; 当振动频率与岩石一阶固有频率(20 246 Hz)相同时,应力、应变达到最大值。如图 5中:振动频率为20 246 Hz时岩石内部最大应力与最大应变分别为8.2 MPa和1.8×10-4;而附近任意点振动频率为20 150 Hz时,其内部最大应力与最大应变分别为1.4 MPa和2.9×10-5,可见与最大值相差明显。(由图 5还可看出,一阶固有频率时,内部应力、应变远大于二、三阶时,所以利用这种技术碎岩,只要考虑一阶固有频率即可。故以下均指一阶固有频率。)

|
| 图 5 岩石应力、应变-振动频率曲线 Fig. 5 Curves of stress intensity and strain intensity against frequency of the rock |
|
|
在细观损伤力学中,最经典的局部破裂准则是最大正应力准则:当岩体内部任意点应力满足σ(x, t)>σs时(σs为极限应力,反映岩石的自身特性),裂纹产生。分析模拟结果可知,超声波振动下提高岩石损伤效率的关键在于使岩石共振。研究[18]表明,岩石类脆性材料内部在承受载荷以前已存在裂纹,当岩石共振时,其内部应力、应变迅速增大,根据最大正应力准则,岩石内部微裂纹等细观缺陷产生不可逆的演化过程,进而影响岩石宏观力学性能,表现为岩石强度的降低。
表 2为通过数值模拟模态分析获取的不同受力条件下岩石的固有频率值,预压力与岩石一阶固有频率的关系曲线如图 6所示。可以看出,岩石的一阶固有频率随预压力增大而逐渐增大,增大幅度逐渐降低,预压力-固有频率关系曲线的初始位置为17 113 Hz,低于振动频率。对数值模拟与试验结果进行对比分析,动静组合加载碎岩试验中预压力对岩石强度的影响规律可做如下总结:1)当预压力小于200 N时,岩石固有频率小于振动频率,尽管随着预压力值的增大,岩石固有频率逐渐增大,固有频率与振动频率的差值逐渐减小,但岩石内部原有裂纹处的应力值仍不满足最大正应力准则,岩石的细观损伤程度几乎不变;因此岩石单轴抗压强度在平均强度附近浮动,且该强度随振动时间的增加变化不明显。2)当预压为200~400 N时,频率差值随预压力值的增大而减小,岩石内部原有裂纹处的应力值由于频率差值的减小而急剧增大,满足最大正应力准则,裂纹扩展导致岩石内部损伤程度加剧;因此,岩石单轴抗压强度随预压力增大而降低,且在预压力一定的情况下随振动时间的增加而降低。在预压力为400 N时,频率差值最小,岩石单轴抗压强度达到最低值。3)当预压力>400 N时,岩石固有频率大于振动频率,随着预压力的增大,岩石固有频率继续增大,导致频率差值相应增大,但增大幅度较慢,虽然岩石内部原有裂纹处的应力值逐渐减小,但仍满足最大正应力准则;因此,岩石单轴抗压强度随预压力增大而增大,在预压力一定时,岩石强度随振动时间的增加而降低。
| 预压力/N | 振动频率/Hz | 固有频率/Hz | 频率差/Hz |
| 100 | 20 000 | 17 113 | 2 887 |
| 200 | 20 000 | 18 499 | 1 501 |
| 300 | 20 000 | 19 670 | 330 |
| 400 | 20 000 | 20 246 | 246 |
| 500 | 20 000 | 20 488 | 488 |
| 600 | 20 000 | 20 500 | 500 |
| 700 | 20 000 | 20 599 | 599 |
| 800 | 20 000 | 20 633 | 633 |
| 900 | 20 000 | 20 711 | 711 |

|
| 图 6 岩石固有频率-预压力关系曲线 Fig. 6 Curve of inherent frequency against preloading of the rock |
|
|
1) 超声波振动下, 当岩石内部应力应变满足强度准则时, 其内部微裂纹等细观缺陷产生不可逆的演化过程,使岩石单轴抗压强度降低。当应力条件一定时,岩石强度随振动时间的增加而逐渐降低。
2) 当岩石共振时,其内部应力应变迅速增大,缩小振动频率与岩石固有频率差有利于提高超声波振动碎岩效率。
3) 当超声波振动频率一定时,预压力与岩石单轴抗压强度关系曲线呈凹型,存在最优预压力值使得岩石单轴抗压强度最低,这是由于岩石固有频率随预压力的增大呈对数型增长,使得频率差值先增后减造成的,预压力间接影响岩石单轴抗压强度。
| [1] |
Atalah A. Effect of Rock Trenching Vibrations on Nearby Structures[J]. Journal of Construction Engineering and Management, 2008, 134: 234-241. DOI:10.1061/(ASCE)0733-9364(2008)134:4(234) |
| [2] |
Xu G Y, Yan C B. Numerical Simulation for Influence of Excavation and Blasting Vibration on Stability of Mined-out Area[J]. Journal of Central South University of Technology, 2006, 13: 577-583. DOI:10.1007/s11771-006-0091-8 |
| [3] |
Roussy R. The Development of Sonic Drilling Technology[J]. Geo-Drilling International, 2002, 10: 12-14. |
| [4] |
Oothoudt T. Sonic Drilling:An Environmental Imperative[J]. Geo-Drilling International, 1998, 2: 14-16. |
| [5] |
Davison L, Stevens A L. Continuum Measures of Spall Damage[J]. Journal of Applied Physics, 1972, 43: 988-994. DOI:10.1063/1.1661319 |
| [6] |
Whittles D N, Kingman S, Lowndes I, et al. Laboratory and Numerical Investigation into the Characteristics of Rock Fragmentation[J]. Minerals Engineering, 2006, 19: 1418-1429. DOI:10.1016/j.mineng.2006.02.004 |
| [7] |
Li X B, Zhou Z L, Lok Tat-Seng, et al. Innovative Testing Technique of Rock Subjected to Coupled Static and Dynamic Loads[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(5): 739-748. DOI:10.1016/j.ijrmms.2007.08.013 |
| [8] |
李夕兵, 周子龙, 叶州元, 等. 岩石动静组合加载力学特性研究[J]. 岩石力学与工程学报, 2008, 27(7): 1387-1395. Li Xibing, Zhou Zilong, Ye Zhouyuan, et al. Study of Rock Mechanical Characteristics Under Coupled Static and Dynamic Loads[J]. Journal of Rock Mechanics and Engineering, 2008, 27(7): 1387-1395. DOI:10.3321/j.issn:1000-6915.2008.07.011 |
| [9] |
李夕兵, 宫凤强, 高科, 等. 一维动静组合加载下岩石冲击破坏试验研究[J]. 岩石力学与工程学报, 2010, 29(2): 251-260. Li Xibing, Gong Fengqiang, Gao Ke, et al. Test Study of Impact Failure of Rock Subjected to One Dimensional Coupled Static and Dynamic Loads[J]. Journal of Rock Mechanics and Engineering, 2010, 29(2): 251-260. |
| [10] |
尹土兵, 李夕兵, 叶洲元, 等. 温-压耦合及动力扰动下岩石破碎的能量耗散[J]. 岩石力学与工程报, 2013, 32(6): 1197-1202. Yin Tubing, Li Xibing, Ye Zhouyuan, et al. Energy Dissipation of Rock Fracture Under Thermo-Mechanical Coupling and Dynamic Disturbances[J]. Journal of Rock Mechanics and Engineering, 2013, 32(6): 1197-1202. |
| [11] |
Nikolic M, Ibrahimbegovic A. Rock Mechanics Model Capable of Representing Initial Heterogeneities and Full Set of 3D Failure Mechanisms[J]. Computer Methods in Applied Mechanics and Engineering, 2015, 290: 209-227. DOI:10.1016/j.cma.2015.02.024 |
| [12] |
Zhong J H, Liu S X, Ma Y S, et al. Macro-Fracture Mode and Micro-Fracture Mechanism of Shale[J]. Petroleum Exploration and Development, 2015, 42: 269-276. DOI:10.1016/S1876-3804(15)30016-1 |
| [13] |
Rabczuk T, Bordas S, Zi G. On Three-Dimensional Modelling of Crack Growth Using Partition of Unity Methods[J]. Computers & Structures, 2010, 88(23): 1391-1411. |
| [14] |
Bazant Z P, Caner F C, Carol Ignacio, et al. Microplane Model M4 for Concrete:I:Formulation with Work-Conjugate Deviatoric Stress[J]. Journal of Engineering Mechanics, 2000, 126(9): 944-953. DOI:10.1061/(ASCE)0733-9399(2000)126:9(944) |
| [15] |
张德海, 朱浮声, 邢纪, 等. 岩石类非均质脆性材料破坏过程的数值模拟[J]. 岩石力学与工程学报, 2005, 24(4): 570-574. Zhang Dehai, Zhu Fusheng, Xing Ji, et al. Numerical Simulation of Fracture Propagation of Anisotropic Rock-Like Materials[J]. Journal of Rock Mechanics and Engineering, 2005, 24(4): 570-574. DOI:10.3321/j.issn:1000-6915.2005.04.005 |
| [16] |
Volkov C Д. The Intensity Statistical Theory[M]. Beijing: Science Press, 1965.
|
| [17] |
尹崧宇, 赵大军, 周宇, 等. 超声波振动下非均匀岩石损伤过程数值模拟与试验[J]. 吉林大学学报(地球科学版), 2017, 47(2): 526-533. Yin Songyu, Zhao Dajun, Zhou Yu, et al. Numerical Smulation and Experiment of the Damage Process of Heterogeneous Rock Under Ultrasonic Vibration[J]. Journal of Jilin University(Earth Science Edition), 2017, 47(2): 526-533. |
| [18] |
Chang C S, Wang T K, Sluys L J, et al. Fracture Modeling Using a Micro-Structural Mechanics Approach:I:Theory and Formulation[J]. Engineering Fracture Mechanics, 2002, 69: 1941-1958. DOI:10.1016/S0013-7944(02)00070-X |



