2. 河北地质大学勘查技术与工程学院, 石家庄 050031;
3. 中国地质科学院水文地质环境地质研究所, 石家庄 050061
2. School of Prospecting Technology & Engineering, Hebei GEO University, Shijiazhuang 050031, China;
3. Institute of Hydrogeology and Environmental Geology, Chinese Academy of Geological Science, Shijiazhuang 050061, China
0 引言
Terzaghi[1]假设固结过程中土体参数为常数,得到表征超静孔隙水压力消散和土体变形速率快慢的重要参数——固结系数,并建立了单向固结理论。固结系数不仅反映孔隙水压力的消散,还是描述固结度和计算固结沉降的重要因素,其值的准确判断有利于深入研究沉降机理。在沉降过程中,土体内部孔隙水逐渐排出,土骨架压密,土体发生压缩变形,土的透水性降低,体积压缩系数与渗透系数都减小,因此固结系数在很长一段时间里一直被当作常数。但是,很多专家对此持否定的态度:Duncan[2]和Olson[3]分别在第27届和第31届Terzaghi讲座中明确指出将固结系数视作常数是传统Terzaghi固结理论的不足之一。国内外很多学者在研究固结沉降的过程中也发现固结系数并非常数,而是一个随外荷载变化呈现典型非线性变化的值[4-5]。林鹏等[6]、余闯等[7]通过研究软土在压缩过程中固结系数随应力水平变化的规律,认为固结系数随着有效应力呈非线性变化。
固结系数的确定方法一般采用规范推荐的时间平方根法和时间对数法[8]。这两种方法均根据变形曲线的特点进行近似,所耗费的试验时间较长,并且特征时间点的选取均受到试验人员的主观影响,因此这两种方法只是近似的经验方法。人工智能机器学习方法是一种典型的计算机“自学习”方法,其通过对已有数据监督式学习挖掘数据内部的相互联系,对既有数据训练建立潜在的联系,通过分类判断对其他相似数据进行预测。目前,机器学习方法已经成功应用于计算机、机械、通信、地学等众多领域[9-11];土木工程领域中,其在结构损伤、桥梁检测等方面应用相对较多,而在岩土工程领域的应用则相对较少。国内部分学者采用人工智能算法对固结系数的预测进行了初步尝试,取得了一定的成果[12-16]。
由于人工智能算法对数据质量的要求较高,为了减少数据的离散性,本文首先基于固结系数的定义,通过对传统单向固结仪的改装,得到了可进行单向压缩试验和渗透试验的渗透固结仪[17-18];使用该仪器进行软土固结试验,并计算得到不同压力下的固结系数,将该方法定义为公式法。然后通过与时间平方根法和时间对数法的试验结果对比,验证该方法的正确性和稳定性。最后通过室内基础试验得到的土体指标,确定固结系数的影响因素,分别采用支持向量机(SVM)和BP神经网络(BPNN)两种人工智能算法对固结系数进行预测,并与公式法确定的实测值进行对比。本文通过人工智能算法建立滹沱河某区域的固结系数预测模型,从而方便地与数值软件结合,旨在简化该地区固结沉降的数值计算工作。
1 公式法确定固结系数使用单向固结仪进行室内压缩试验可以得到压缩系数和孔隙比,但无法确定对应压力下的渗透系数,而普通渗透仪得到的渗透系数也不能考虑压力的影响;但是渗透系数显然在不同压力下取值不同[19]。因此,本文通过对WG型单杠杆固结仪进行改装,以构造简单、安装方便和密封良好为原则,得到一款渗透固结仪,示意图如图 1。进行渗透固结试验的大体步骤为:先对土体进行压缩试验,待稳定后,记录相应的土样压缩量;然后打开止水夹,对土样进行变水头渗透试验,量测对应压缩量下的渗流量。
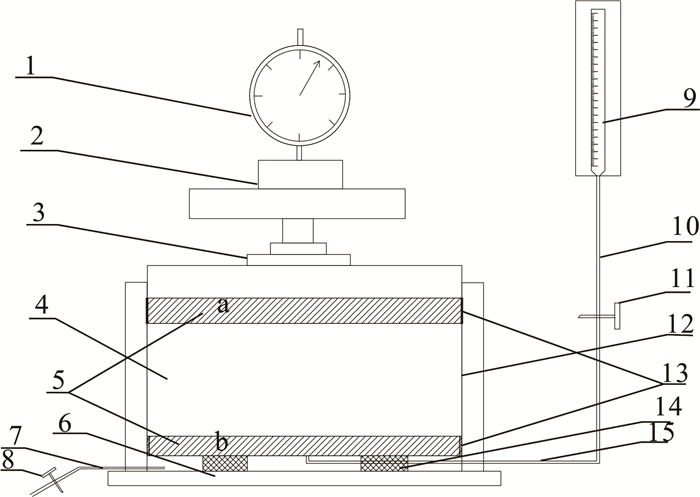
|
| 1.量表;2.加荷系统;3.顶盖;4.土样;5.透水石;6.底座;7.排气管;8.止水夹;9.带刻度蓄水瓶; 10.胶皮管;11.止水夹;12.环刀;13.密封圈;14.垫片;15.进水管。 图 1 改装渗透固结仪的示意图 Fig. 1 Schematic presentation of the modified osmotic oedometer device |
|
|
使用改装的渗透固结仪量测并计算相同试样下的所有参数(压缩系数、渗透系数、孔隙比),根据公式(1)可以直接计算不同压力下固结系数Cv。
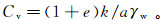 (1)
(1) 式中:e为孔隙比:k为渗透系数:a为竖向压缩系数:γw为水的重度。
因此,改装的渗透固结仪兼顾单向固结仪和渗透仪的优点。
为验证公式法的正确性,对相同土样分别进行不同压力下的渗透固结试验和单向固结试验。分别使用公式法、时间平方根法和时间对数法计算相应固结系数,并将计算结果绘于图 2。由图 2可见,公式法的计算结果与时间对数法拟合的结果较为接近,而时间平方根法拟合值则较二者偏大,这与已有的结论相符[20]。此外,由于时间平方根法和时间对数法中所需的特征固结度时间点都需要通过试验人员的主观判定,因此这两种方法对相同样本计算拟合的结果离散较大。
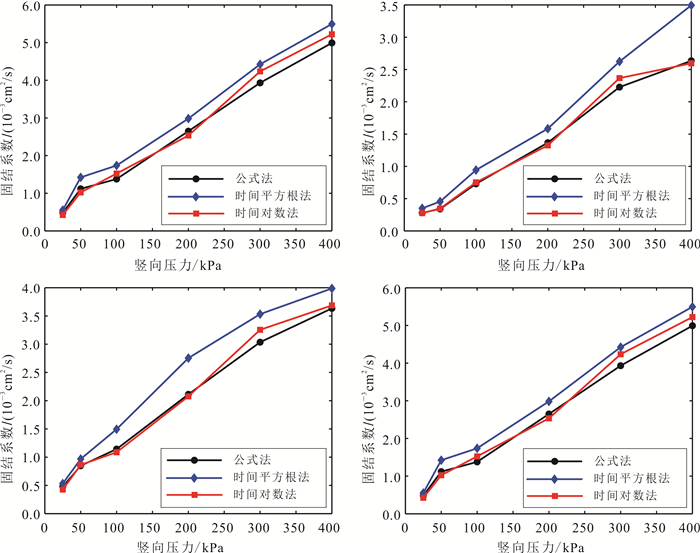
|
| 图 2 不同样本3种计算固结系数方法对比 Fig. 2 Comparison of consolidation coefficient of different samples using three methods |
|
|
邻域粗糙集(NRS)理论是胡清华等[21-22]应用邻域模型对经典粗糙集(RS)理论的一种延拓。NRS方法可直接用于连续数据而无需预先对数据进行离散化,因而其保留了原始数据的重要信息。
给定一个由n个属性描述的分类问题,构建决策系统〈U, A, V, f′〉。其中:U={x1, x2, …, xn}为论域;A为属性集合;V为值域;f′为信息函数,表示样本与属性之间的映射关系。A=C∪D,C为条件属性集,D为分类决策属性集,并且C∩=Ø。对于任意xi∈U,B⊆C(B为条件属性集子集),xi的邻域定义为
 (2)
(2) 式中:δ为满足一定条件的距离函数;xi为固结系数影响因素;δB为属性子集B的距离。
对于非空有限集合U={x1, x2, …, xn}及其上的邻域关系N,∀X⊆U,X在邻域空间的下近似和上近似定义为:
 (3)
(3) 决策属性D将论域U划分为G个等价类,∀B⊆A,决策属性集D关于子集B的上、下近似为
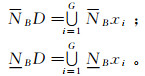
决策系统的近似边界为
 (4)
(4) 邻域决策系统的正域和负域分别为:
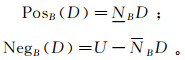
决策属性D对条件属性B的依赖度为
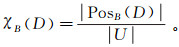 (5)
(5) 式中,若B=Ø,则χB(D)=0。
显然0≤χB(D)≤1,χB(D)反映论域中能被准确分类的样本比例。正域越大,表明决策属性对条件属性的依赖性越强。
在决策系统中,属性重要度定义为条件属性对决策属性的影响程度。假设属性α∈B,则属性α对于决策属性D的重要度为
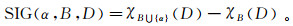 (6)
(6) 通俗的解释为:从条件属性B中删除属性α后,决策属性D对条件属性B依赖度减小的程度。
NRS的约简策略:从空集出发,依次计算全部因素剩余属性的重要度,并将属性重要度最大的因素加入约简集合,直到所有剩余属性的重要度为0;表明加入任何新的属性,该依赖函数均不再发生变化。
2.2 支持向量机理论SVM是Vapnik于1995年根据统计学习理论提出的一种在有限样本下进行机器学习的方法。其通过某种非线性映射将在平面内线性不可分的问题变换到复杂的高维空间中,并在高维空间中建立一个最优分类超平面,从而将平面上的线性不可分问题转化为高维空间中的线性可分问题,同时引入核函数来处理由于维度上升而造成的计算量陡增的问题。
训练样本为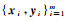
 (7)
(7) 式中:W为可调权值向量;b为偏置值。
寻找最优的分类超平面亦即寻找最优的W和b。引入松弛变量ξ和ξ*,依据结构风险最小化准则,采用ε-SVR模型建立带有约束条件的模型优化函数:
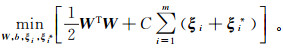
约束条件为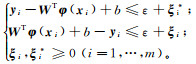
式中:C为惩罚函数;ε为损失函数。
式(7)为一个凸二次优化问题,可采用Lagrange乘子法进行求解。使用二次规划优化算法SMO(sequential minimal optimization)构造得到关于x的预测函数f(x):
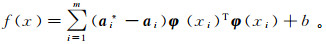 (9)
(9) 式中:f(x)在本文代表固结系数Cv;ai, b为Lagrange乘子和Lagrange系数;ai*为ai的伴随矩阵;m为样本数目。
由于很难直接确定非线性映射φ,因此引入径向基函数(RBF),采用将原始特征的内积平方和等价为映射后的特征内积平方和的方法,间接求解非线性映射,计算不同的f(x)[23]。
3 预测模型建立 3.1 指标选取与因素约简固结系数受到土体参数、固结应力、固结历史等许多因素的共同影响。本文旨在选取易量测指标建立该地区的固结系数模型,从而预测未知点的固结系数。首先对滹沱河某区域的软土取样,制作重塑土样,在改装的渗透固结仪上进行压缩试验和渗透试验,利用公式法计算固结系数。然后对每组样本确定其颗粒级配参数以及土体的物理指标,包括液塑限、含水率、饱和密度和干密度等。
根据NRS的约简策略,分别计算各物理指标对固结系数的重要度,根据得到的权重排序,剔除对固结系数影响较小的因素,保留对固结系数影响较大的因素,达到属性约简目的。
图 3为根据150组样本确定的固结系数重要度。由图 3可见:有效粒径d10、连续粒径d30、限制粒径d60、孔隙比e和压力p比其余指标对固结系数的重要度高,因而选择其作为固结系数的影响因素。不均匀系数Cu和曲率系数Cc是基于d10、d30和d60综合计算后的结果,其容错率更低,因此d10、d30和d60更能从微观上表征固结系数的变化;而含水率w、饱和密度ρd、塑限指数wp和液限指数wL属于土体本身的物理参数,固结系数反映了土体的压硬能力,相比e和p而言,他们对固结系数的影响较小。提取的这5个因素可以分为2类:一类为描述土颗粒自身属性的因素,包括d10、d30和d60,用以表征土体的非均匀性和连续性;另一类为描述土体应力历史的因素,包括e和p,用以表征土体的密实度和应力。根据NRS的筛选,将这5个影响因素作为模型的先验知识,通过支持向量机的“自学习”,挖掘数据的内部联系,建立训练模型,进而预测固结系数。
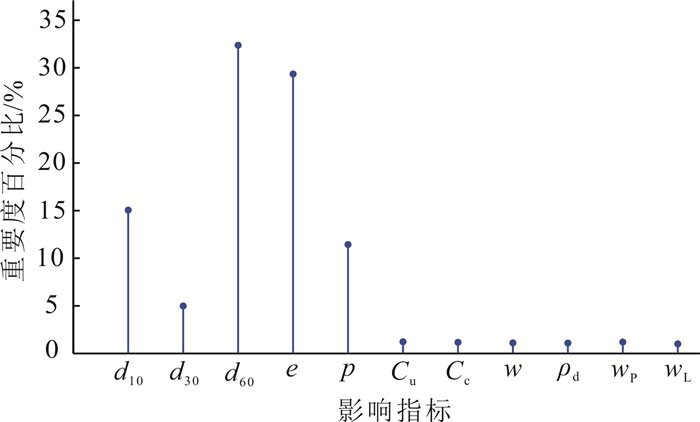
|
| 图 3 各指标对固结系数的重要度百分比 Fig. 3 Importance percentage of consolidation coefficient under various indexes |
|
|
人工智能算法是一种以数据为基础,挖掘数据内部之间隐含信息的方法,因而人工智能算法对数据的“质量”很敏感。在建立预测模型前,应先对数据进行归一化和降维预处理。归一化是为了将数据尽量变换在相同数量级,防止计算过程中出现“大数吃小数”的情况;降维则是为了减少原始数据的冗余信息和各因素之间相关性,防止其影响预测结果的精度,同时避免由于数据量过大而造成的计算复杂问题。
使用主成分分析法(PCA)对原始数据重新整理和归纳,以尽可能多提取有效信息为前提,采用较少的主成分代替5个原始因素,简化分析和解释过程。主成分分析中,提取的每一个主成分均为单一原始因素的线性组合,通常情况下只需要提取包含85%以上信息的前2~3个主成分对数据进行分析就可以满足精度要求[24]。
表 1为对150组样本进行主成分分析后各主成分的特征值和相应的贡献率。由表 1可知:第1主成分的特征值为2.040,方差贡献率为40.798%;第2主成分的特征值为1.455,方差贡献率为29.097%;第3主成分为1.008,方差贡献率为20.163%。累计到第3主成分,方差累计贡献率为90.058%,可见前3个主成分已经包含原始数据90%以上的信息,因此可以用前3个主成分代替原始数据进行分析。
| 主成分 | 初始特征值 | 提取的主成分 | |||||
| 特征值 | 方差贡献率/% | 累计方差贡献率/% | 特征值 | 方差贡献率/% | 累计方差贡献率/% | ||
| 1 | 2.040 | 40.798 | 40.798 | 2.040 | 40.798 | 40.798 | |
| 2 | 1.455 | 29.097 | 69.895 | 1.455 | 29.097 | 69.895 | |
| 3 | 1.008 | 20.163 | 90.058 | 1.008 | 20.163 | 90.058 | |
| 4 | 0.419 | 8.387 | 98.445 | ||||
| 5 | 0.078 | 1.555 | 100.00 | ||||
表 2为因子负荷矩阵,因子负荷矩阵用来计算主成分在各指标下的权重系数。由表 2可知:第1主成分对d10、d30和d60的提取比较充分,表明第1主成分反映与土体自身因素有关的指标;第2主成分对d10、d30、p和e的提取比较充分,其中,d10可以有效反映土体的透水性,e反映土体的密实程度,d10和e在第2主成分中所占权重很大,表明第2主成分反映土体的渗透特性和压缩特性;第3主成分对d10和p的提取比较充分,第3主成分也体现土体的压缩特性和渗透特性,因此第3主成分可看作是对第2主成分的补充。
| 试验指标 | 主成分 | ||
| 1 | 2 | 3 | |
| p | -0.050 | 0.074 | 0.920 |
| d10 | 0.123 | 0.638 | 0.225 |
| d30 | 0.468 | 0.098 | -0.005 |
| d60 | 0.479 | -0.107 | -0.080 |
| e | -0.163 | 0.546 | -0.205 |
采用PCA对原始试验指标进行降维和预处理,不仅剔除了冗余数据,而且降低了数据之间的相关性。在对数据进行处理后,数据之间的相关性进一步降低,彼此独立,从而为后续模型的建立奠定基础。
3.3 模型建立惩罚函数C和RBF核函数参数γ是SVM的待定参数,选取不同的参数会直接影响到SVM的学习效率和模型精度。为了搜索到最优参数组合,采用先大范围大步长粗略搜索、再小范围小步长精确搜索的改进网格搜索法,遍历待定搜索范围内所有的参数组合,做到既覆盖所有范围参数又不遗漏任何一种可能参数,大大降低搜索耗时并使预测模型达到较高的预测精度和稳定性[25]。
笔者基于MATLAB平台,开发并建立了基于改进网格搜索法的固结系数SVM预测模型[26]。该模型核函数为RBF,算法为ε-SVR。随机挑选130组样本作为训练样本,使用改进网格搜索法对SVM的待定参数进行多次重复搜索,通过选取最优结果,确定适用于该区域软土固结系数的SVM模型待定参数为C=3.482、γ=4.287。至此,根据处理后的数据,采用支持向量机建立了该地区的固结系数模型。求解该区域其他地点、未知深度的固结系数,只需要提供相应的影响因素数据,计算机就会根据已经建立的预测模型“自学习”,通过训练数据找寻数据内部的隐含联系,进而计算固结系数。
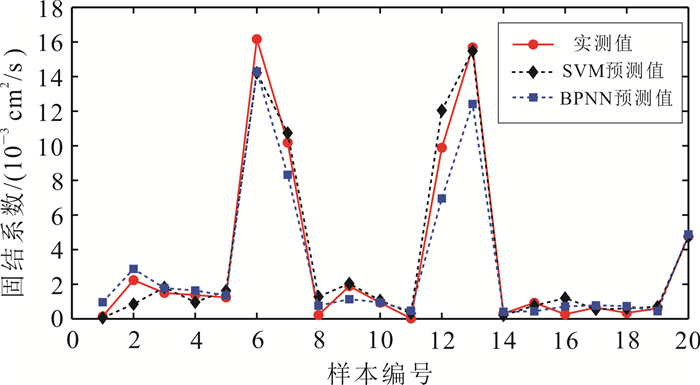
4 预测结果分析根据建立的模型,对20组未知样本进行预测,通过室内试验确定土体的影响因素;采用渗透固结试验的公式法计算相应固结系数,并以此作为实测值。同时,为了增加说服力,本文也采用比较成熟的BPNN算法建立了固结系数模型。BPNN的基本参数:输入层节点数为3,输出层节点数为1,隐含层节点数为10,允许最大训练次数为100,学习率为0.000 1,误差允许限度为1×10-6,经过67次训练。将实测值、SVM预测值和BPNN预测值绘制在图 4中。
|
| 图 4 SVM和BPNN预测值与实测值对比 Fig. 4 Comparison between measured values and predicted values based on SVM and BPNN |
|
|
由图 4可以清楚地看到:SVM模型预测值与实测值的变化趋势较为接近,而BPNN模型预测值与实测值偏差较大,表明SVM的预测效果明显优于BPNN的预测效果。同时,计算这两种方法的均方误差和平方相关系数,以此来对比两种方法,分别列于表 3中。
| 均方误差 | 平方相关系数 | |||
| SVM | BPNN | SVM | BPNN | |
| 8.905 0×10-4 | 0.080 2 | 0.983 5 | 0.890 2 | |
均方误差反映数据的变化程度,其值越小表明实验数据精确度越好;平方相关系数反映数据之间的密切程度,其值越接近1,表明预测值与真值越接近。由表 3可知,SVM的均方误差远远小于BPNN的均方误差,而SVM的平方相关系数比BPNN的平方相关系数提高了约10%, 更接近1;因此,SVM模型的预测精度高于BPNN模型。
其可能产生的原因:BPNN是一种局部搜索的优化方法,容易陷入局部最优解; 此外,BPNN的隐藏层节点需凭经验选取,影响训练的网络精度和容错性。而SVM可以很好地解决上述问题,SVM收敛速度快、精度高,并且其可以根据精确程度和计算速度来自选其待定参数,可控性更好。
5 结论1) 通过对传统固结仪的改装,得到可同时进行渗透试验和压缩试验的渗透固结仪,然后根据公式计算任意压力下的固结系数。与规范推荐的时间平方根法和时间对数法的比较结果表明本文采用的公式法正确可行。另外,公式法得到的计算结果客观,不受主观因素的影响。
2) 采用SVM和BPNN建立固结系数预测模型,进而预测未知点的固结系数。基于结构风险最小化理论建立的SVM固结系数预测模型泛化能力比BPNN预测模型强,因而SVM建立的模型比BPNN所预测的固结系数精度更高、稳定性更好。
3) 固结系数的影响因素不仅与固结应力有关,还与土体自身参数密切相关。本文提出的预测方法简单易行,只需通过室内试验确定相应的土体参数指标作为影响因素,就可以较为准确地预测同一研究区未知点的固结系数。随着计算方法的发展和数值模型的不断更新,通过计算机“自学习”建立概化模型进而预测固结系数的方法,可以方便地与有限单元法、有限差分法等数值计算方法结合,为固结沉降计算开拓新的思路。
| [1] |
Terzaghi K. Theoretical Soil Mechanics[M]. New York: John Wiley and Sons, 1943.
|
| [2] |
Duncan J M. Limitation of Conventional Analysis of Consolidation Settlement[J]. Journal of Geotechnical Engineering Division, ASCE, 1993, 199(9): 1333-1359. |
| [3] |
Olson R E. Settlement of Embankments on Soft Clays[J]. Journal of Geotechnical Engineering, ASCE, 1998, 124(4): 278-288. DOI:10.1061/(ASCE)1090-0241(1998)124:4(278) |
| [4] |
Lowe J, Jonas E, Obrician V. Controlled Gradient Consolidation Test[J]. Journal of the Soil Mechanics and Foundation Engineering Division, ASCE, 1969, 95(Sup.1): 77-97. |
| [5] |
吴义祥. 固结过程中固结系数Cv的变化及其对地面沉降预测的影响[J]. 水文地质工程地质, 1988(2): 47-49. Wu Yixiang. Change of Consolidation Coefficient and Its Influence on Land Subsidence Forecasting[J]. Hydrogeology & Engineering Geology, 1988(2): 47-49. |
| [6] |
林鹏, 许镇鸿, 徐鹏, 等. 软土压缩过程中固结系数的研究[J]. 岩土力学, 2003, 24(1): 106-112. Lin Peng, Xu Zhenhong, Xu Peng, et al. Research on Consolidation Coefficient of Soft Clay Under Compression[J]. Rock and Soil Mechanics, 2003, 24(1): 106-112. DOI:10.3969/j.issn.1000-7598.2003.01.018 |
| [7] |
余闯, 刘松玉. 考虑应力水平的软土固结系数计算与试验研究[J]. 岩土力学, 2004, 25(增刊2): 103-107. Yu Chuang, Liu Songyu. Calculation and Experiment on Consolidation Coefficient for Soft Clay Considering Different Stress Levels[J]. Rock and Soil Mechanics, 2004, 25(Sup.2): 103-107. |
| [8] |
土工试验规程: SL237-1999[S].北京: 中国水利水电出版社, 1999. The Civil Engineering Experiment: SL237-1999[S]. Beijing: China Water & Power Press, 1999. |
| [9] |
卢文喜, 郭家园, 董海彪, 等. 改进的支持向量机方法在矿山地质环境质量评价中的应用[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1511-1519. Lu Wenxi, Guo Jiayuan, Dong Haibiao, et al. Evaluating Mine Geology Environmental Quality Using Improved SVM Method[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(5): 1511-1519. |
| [10] |
张代磊, 黄大年, 张冲. 基于遗传算法优化的BP神经网络在密度界面反演中的应用[J]. 吉林大学学报(地球科学版), 2017, 47(2): 580-588. Zhang Dailei, Huang Danian, Zhang Chong. Application of BP Neural Network Based on Genetic Algorithm in the Inversion of Density Interface[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 580-588. |
| [11] |
王常明, 田书文, 王翊虹, 等. 泥石流危险性评价:模糊c均值聚类-支持向量机法[J]. 吉林大学学报(地球科学版), 2016, 46(4): 1168-1175. Wang Changming, Tian Shuwen, Wang Yihong, et al. Risk Assessment of Debris Flow:A Method of SVM Based on FCM[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(4): 1168-1175. |
| [12] |
许小健, 干洪, 张金轮. 差分进化算法及其在固结系数计算中的应用[J]. 地下空间与工程学报, 2010, 6(5): 958-963, 974. Xu Xiaojian, Gan Hong, Zhang Jinlun. Differential Evolution and Its Application in Computing Consolidation Coefficient[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(5): 958-963, 974. |
| [13] |
包太, 刘新荣. 改进的遗传算法求解固结系数[J]. 土木建筑与环境工程, 2009, 31(1): 23-26. Bao Tai, Liu Xinrong. Consolidation Coefficient Evaluation Using an Improved Genetic Algorithm[J]. Journal of Civil Architectural & Environmental Engineering, 2009, 31(1): 23-26. |
| [14] |
江刚. 遗传算法在固结系数计算中的应用[J]. 土木建筑与环境工程, 2006, 28(1): 71-73. Jiang Gang. Genetic Algorithm for the Consolidation Coefficient Evaluation[J]. Journal of Civil Architectural & Environmental Engineering, 2006, 28(1): 71-73. |
| [15] |
Chen Jiangong, Zhang Yongxing. A Neural Network Method to Evaluate Consolidation Coefficient[J]. Journal of Chongqing University, 2003, 2(1): 1-4. |
| [16] |
Zhu Honghu, Fu Jianping, Dai Fei. Application of BP Neural Networks in the Prediction of Consolidation Coefficient[C]//IEEE. Advances in Computational Tool for Engineering Applications of the International Conference on IEEE, Lebanon: Zouk Mosbeh, 2009: 443-446.
|
| [17] |
师旭超, 汪稔, 胡元育, 等. 渗透固结试验装置的研制[J]. 岩石力学与工程学报, 2004, 23(22): 3891-3895. Shi Xuchao, Wang Ren, Hu Yuanyu, et al. Development of Osmotic Oedometer[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(22): 3891-3895. DOI:10.3321/j.issn:1000-6915.2004.22.028 |
| [18] |
孙丽云, 乐金朝, 刘忠玉, 等. 渗透固结试验装置的改进[J]. 实验力学, 2010, 25(3): 353-358. Sun Liyun, Yue Jinchao, Liu Zhongyu, et al. The Improvement of Osmotic Oedometer[J]. Journal of Experimental Mechanics, 2010, 25(3): 353-358. |
| [19] |
周爱红, 尹超, 袁颖. 基于主成分分析和支持向量机的砂土渗透系数预测模型[J]. 云南大学学报(自然科学版), 2016, 38(5): 742-749. Zhou Aihong, Yin Chao, Yuan Ying. A Permeability Coefficient Prediction Model of Sand Soil Based on Principal Component Analysis and Support Vector Machine[J]. Journal of Yunnan University (Natural Science Edition), 2016, 38(5): 742-749. |
| [20] |
曾巧玲, 张惠明, 陈尊伟, 等. 软黏土固结系数确定方法探讨[J]. 岩土力学, 2010, 31(7): 2083-2110. Zeng Qiaoling, Zhang Huiming, Chen Zunwei, et al. Discussion on Computational Methods for Determining Consolidation Coefficient of Soft Clay[J]. Rock and Soil Mechanics, 2010, 31(7): 2083-2110. DOI:10.3969/j.issn.1000-7598.2010.07.011 |
| [21] |
Hu Qinghua, Yu Daren, Xie Zongxia. Neighborhood Classifiers[J]. Expert Systems with Applications, 2008, 34(2): 866-876. |
| [22] |
胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报, 2008, 19(3): 640-649. Hu Qinghua, Yu Daren, Xie Zongxia. Numerical Attribute Reduction Based on Neighborhood Granulation and Rough Approximation[J]. Journal of Software, 2008, 19(3): 640-649. |
| [23] |
邓乃扬, 田英杰. 数据挖掘中的新方法:支持向量机[M]. 北京: 科学出版社, 2004: 117-122. Deng Naiyang, Tian Yingjie. A New Method in Data Mining:Support Vector Machine[M]. Beijing: Science Press, 2004: 117-122. |
| [24] |
邰淑彩, 孙韫玉, 何娟娟. 应用数理统计[M]. 武汉: 武汉大学出版社: 248-266. Tai Shucai, Sun Yunyu, He Juanjuan. Applied Mathematical Statistics[M]. Wuhan: Wuhan University Press: 248-266. |
| [25] |
张向东, 冯胜洋, 王长江. 基于网格搜索的支持向量机砂土液化预测模型[J]. 应用力学学报, 2011, 28(1): 24-28, 107. Zhang Xiangdong, Feng Shengyang, Wang Changjiang. Support Vector Machine Model for Predicting Sand Liquefaction Based on Grid-Search Method[J]. Chinese Journal of Applied Mechanics, 2011, 28(1): 24-28, 107. |
| [26] |
王小川, 史峰, 郁磊, 等. MATLAB神经网络43个案例分析[M]. 北京: 北京航空航天大学出版社, 2013: 102-119. Wang Xiaochuan, Shi Feng, Yu Lei, et al. 43 Cases Analysis of MATLAB Neural Network[M]. Beijing: Beihang University Press, 2013: 102-119. |



