2. 中国土地勘测规划院数据中心, 北京 100035
2. China Land Surveying and Planning Institute, Beijing 100035, China
0 引言
随着地质研究工作的不断开展,传统的数据处理方法已经无法满足针对高维度、多来源、大容量、异构性数据进行处理和分析的现实需求,如何从大量的地质数据中挖掘出有用信息对于地质工作的进行具有重大意义。近20年来,随着计算机技术的快速发展,作为人工智能领域的一个分支学科,机器学习无论是在理论研究还是实践应用方面都取得了巨大的突破[1]。支持向量机(SVM)和决策树都属于监督学习模型,目前,已有众多学者将其运用于岩性识别问题[2-6]。SVM具有可以从小样本数据中进行学习和模型复杂度可控的优点[7];然而,由于模型的“黑箱”性,无法直接得知输入参数与输出值之间的具体联系[8-9],因此不能对输入特征的重要性进行判断。决策树具有决策能力明显、提取出的规则涉及较少变量和能较好处理非线性问题等优点[10],并且模型自身具有一定的特征选择能力,可以对输入特征的重要性进行度量;但是冗余样本过多会导致树底层决策质量的降低,并伴随过拟合现象的产生[11]。
本文将决策树与支持向量机相结合并用于岩性分类,经过决策树的特征选择,在充分考虑了特征重要性的前提下,将具有强分类能力的特征用于支持向量机,从而提高了分类器的精度与稳定性。
1 最大软间隔支持向量机模型 1.1 模型原理通常情况下支持向量机可以得到全局最优解,并且针对大容量、高维度数据集具有良好的泛化能力,其基本原理如下。定义m×n矩阵X,列向量W、Y。
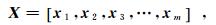 (1)
(1) 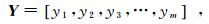 (2)
(2) 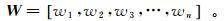 (3)
(3) 式中:X为输入变量即特征变量;xi为列向量[x1,x2,x3,…, xn]T;m为样本数;n为属性特征数;W为与之相应的权重;Y为输出变量即目标变量。
在样本空间中,划分超平面由线性方程定义:
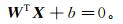 (4)
(4) 式中:法向量W决定了超平面的方向;位移项b决定了超平面与原点之间的距离。定义样本空间中任意点x到超平面的距离为
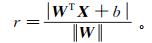 (5)
(5) 对于二分类问题,为了得到良好的分类效果,如果所有样本都得到了正确分类,样本点应满足如下约束条件:
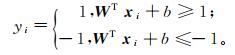 (6)
(6) 定义距离超平面最近并且满足式(6)的训练样本点为支持向量,则两个异类的支持向量距超平面的距离之和定义为
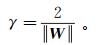 (7)
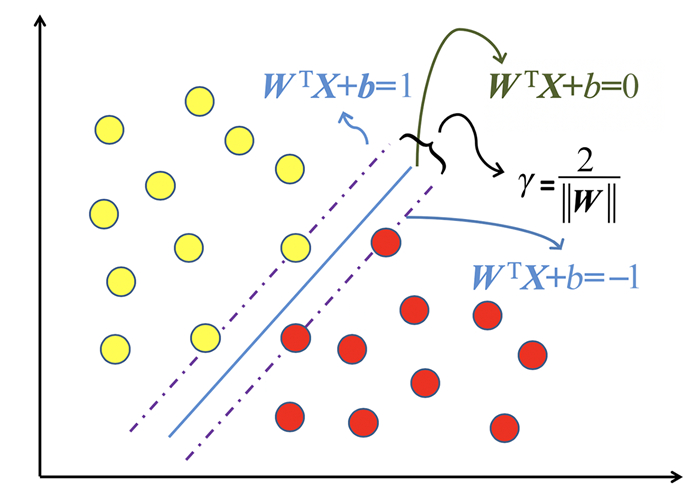
(7) 式中,γ称之为间隔(图 1)。支持向量机算法就是要找到具有最大间隔的超平面,即求出满足式(6)约束的模型参数W,b并使得γ最大:
 (8)
(8)
|
| 图 1 支持向量机模型 Fig. 1 Model of support vector machine |
|
|
显然,为了最大化间隔,仅需最大化||W||-1,等价于最小化||W||2。在此基础上增加松弛因子ξ和正则化参数C:
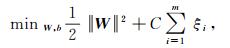
 (9)
(9) 通过对式(9)使用拉格朗日乘数法即可得到对偶问题,从而解出参数,得到最大软间隔的支持向量机模型[12],其中松弛因子ξ为分类误差项。对于错分样本的惩罚程度则通过正则化参数C进行控制。
1.2 核函数对于一般的线性分类器,通常情况下会假设模型的训练样本是线性可分的[13]。然而,对于多源、高维的数据集,原始的样本空间中可能并不存在可以满足分类目标的划分超平面。针对此种情况,支持向量机的优势在于可以通过特定的核函数将样本从原始空间映射到高维特征空间,从而使得样本数据在此高维空间内线性可分[14-17](图 2)。

|
| 图 2 核函数 Fig. 2 Kernel function |
|
|
在求解SVM的过程中,需对式(10)的对偶问题进行求解:
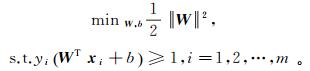 (10)
(10) 令φ(x)为x映射后的特征向量,则式(10)的具体对偶问题为
 (11)
(11) 式中:ai为拉格朗日乘子;yi为样本标签。
求解式(11)涉及到计算φ(xi)Tφ(xj),此为样本xi与xj映射到特征空间之后的内积。在空间维数较高的情况下对其进行直接计算相对困难,因此引入核函数:
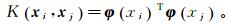 (12)
(12) 即xi与xj在特征空间的内积等于二者在原始空间中核函数的计算结果。因此求解SVM的过程将变为
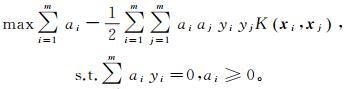 (13)
(13) 实际应用过程中常用的4种核函数如下。
线性核:
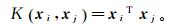 (14)
(14) 多项式核:
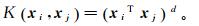 (15)
(15) 式中,d为多项式次数,d≥1。
RBF(radial basis function)核:
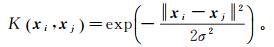 (16)
(16) 式中,σ为带宽, σ>0。
Sigmoid核:
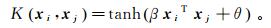 (17)
(17) 式中:β>0;θ < 0。
RBF核函数可变参数少,并且可以将原始空间映射到任意维度,因此应用最为广泛。
2 决策树分类决策树模型是描述对实例进行分类的一种树形结构[1]。模型的学习算法通常是一个递归地选择最优特征并根据该特征对训练数据进行分割的过程。树构建过程往往对应着特征空间的划分。
决策树常用的算法有ID3、C4.5与CART(classification and regression trees),其中ID3算法的核心是在决策树的各结点应用信息增益准则,选取信息增益最大的特征进行分类。由于信息增益最大表征了数据集分类的不确定性减少最多,因此ID3算法构建过程所选择的特征具有更强的分类能力。信息熵(H)与信息增益(G)定义如下:
 (18)
(18) 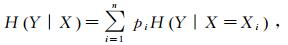 (19)
(19) 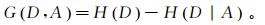 (20)
(20) 式中:X、Y为随机变量;p为随机变量的概率;D为数据集;A为特征;H(D)为集合D的经验熵;H(Y|X)为条件熵;H(D|A)为特征A给定条件下的经验条件熵。
决策树的构建过程如下:首先构建根节点,将所有数据都放入根节点,计算整个数据集的信息熵;然后计算基于每个特征进行子集划分后子集的熵,求得信息增益,将信息增益最大者作为划分空间的最终特征,对数据集进行划分;最后根据每次划分的数据集递归地实现上述过程,直到所有子集被正确分类或者没有可用于分割的特征为止,从而建立决策树。
3 实例验证 3.1 研究区概况本文实验数据来自云南某矿区的钻孔分析数据。根据测井和录井参数资料分析结果,研究区地层的岩石类型主要分为结晶大理岩、褐色泥岩、蚀变花岗岩、角砾岩、褐铁矿化大理岩、破碎带碎裂岩、矽卡岩。矿区的矿床类型为矽卡岩型矿床,主要成矿作用都与区域内花岗岩的产出地点和产出形态有关,因此对矿区内的蚀变花岗岩和矽卡岩进行有效识别对于区块的找矿预测工作具有重要意义。
3.2 样本集选取与特征归一化本文以矿区的223个钻孔分析数据作为学习数据集(表 1),模型的原始输入特征为W、Sn、Mo、Cu、Pb、Zn、Co、Ni、Mn、Sr、Ba、Ag、Cd、Be、As、Sb、Bi共17个化学元素的分析数据,输出为结晶大理岩、褐色泥岩、蚀变花岗岩、角砾岩、褐铁矿化大理岩、破碎带碎裂岩、矽卡岩共7种岩性。
在进行实验之前首先对数据进行预处理,剔除由人为因素或外界因素干扰造成的异常数据,对含有缺失值的数据进行忽略,并将数值进行归一化,从而避免特征量纲差异对预测结果造成的影响。本文选用最大最小化方法将特征归一到[0, 1]:
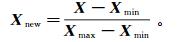
式中:Xnew为归一化后特征;Xmax、Xmin分别为特征的最大值和最小值。
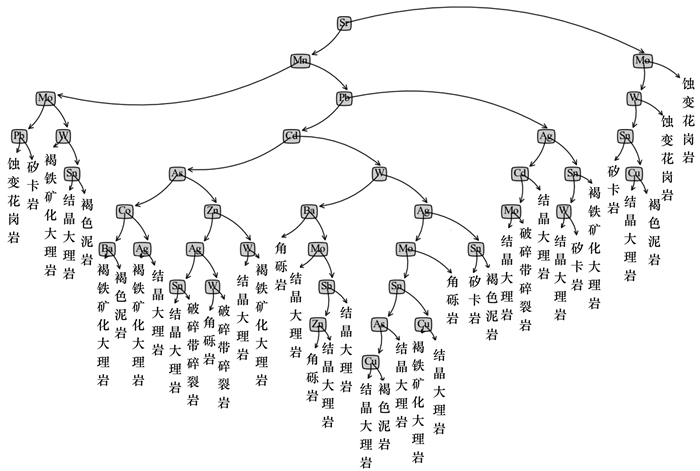
3.3 基于决策树的特征提取特征选择在于选取对训练数据具有更强分类能力的特征,通过适当的特征选择可以提高分类算法的效率和性能。本文用ID3算法对归一化后的数据进行决策树的构建。首先将整个数据集置于根节点,通过信息增益选择最优特征,并根据此特征对数据集进行划分生成子集;然后递归地对子集进行特征选择及划分,直到所有子集被正确分类或者没有可用于分割的特征为止,从而建立决策树(图 3、表 2)。
|
| 图 3 ID3决策树 Fig. 3 ID3 decision tree |
|
|
| 根节点 | Sr |
| 第一层子节点 | Mn,Mo |
| 第二层子节点 | W,Pb,Mo |
| 第三层子节点 | Sn,Ag,Cd,W,Pb |
| 第四层子节点 | Cu,Sn,Cd,W,As |
| 第五层子节点 | W,Mo,Ag,Ba,Zn,Co |
| 第六层子节点 | Sn,Mo,W,Ag,Ba |
| 第七层子节点 | Sn,Sb,W |
| 第八层子节点 | Cu,As,Zn |
| 第九层子节点 | Cu |
| 临近底层叶节点 | Cu,W,Sn,Ag,Ba,Zn |
| 未被选中元素 | Be,Bi,Ni |
由核函数的数学模型可以得知,选取不同的核函数将会得到不同的支持向量机模型[18-20],而正则化参数C的选择控制着模型的最大间隔;因此选择正确的核函数和正则化参数在一定程度上影响着模型最终的泛化能力[21-23]。本文在选择RBF核函数的基础之上,对基于不同核函数参数与正则化参数的模型进行评价,具体参数如下:正则化参数C为1、5、10、15、20;RBF参数r为5、10、20、40、60、80、100、200。
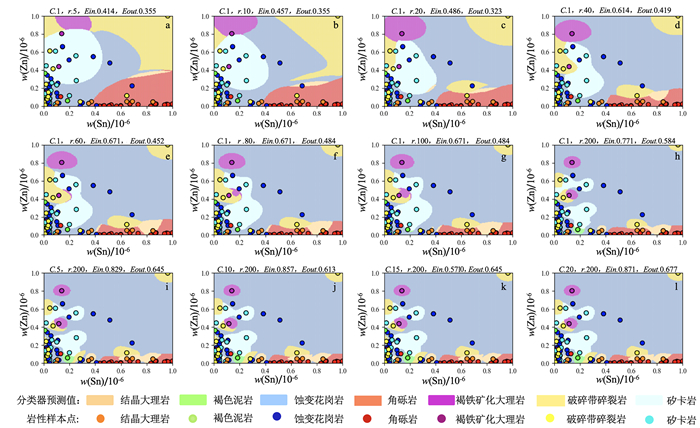
3.5 特征重要性度量为验证经过决策树提取后特征的重要性,分别将位于顶层树节点的特征Sr、Mo、Mn和底层树节点的特征Cu、Sn、Zn用于SVM模型。首先对数据进行随机分割,将75%的数据作为训练集,剩下25%的数据作为测试集。在确保数据完整并且可训练的基础上,将分割后的训练样本集分别送入不同参数配置下的支持向量机模型中进行学习,完成模型的建立。将测试数据集送入已建立的分类预测模型中进行预测,得到的分类预测结果如图 4、图 5、图 6、图 7所示。
|
| Ein.训练集精度;Eout.测试集精度。 图 4 Sn-Zn特征分类 Fig. 4 Sn-Zn feature classification |
|
|
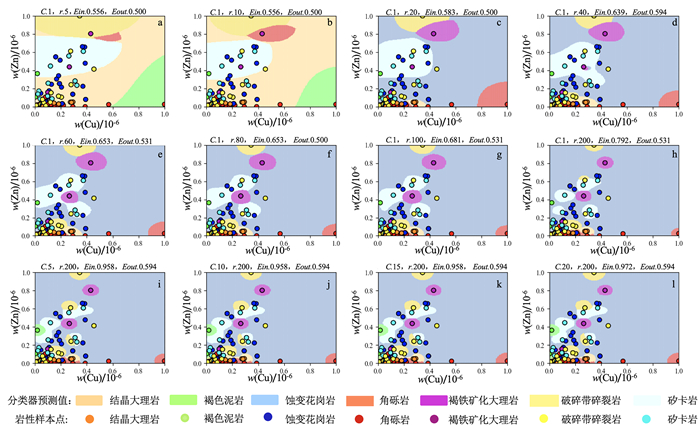
|
| 图 5 Cu-Zn特征分类 Fig. 5 Cu-Zn feature classification |
|
|
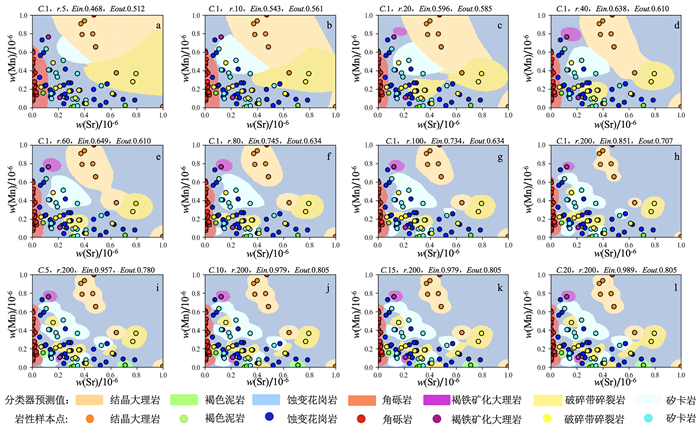
|
| 图 6 Sr-Mn特征分类 Fig. 6 Sr-Mn feature classification |
|
|
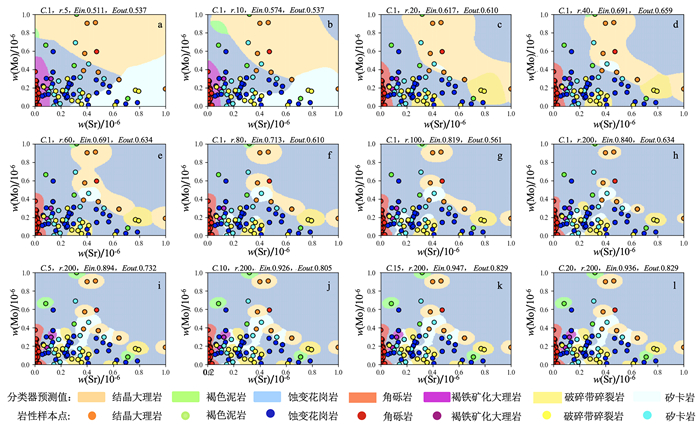
|
| 图 7 Sr-Mo特征分类 Fig. 7 Sr-Mo feature classification |
|
|
依图可得,基于Sr-Mn、Sr-Mo特征的SVM模型分类(图 6、7)精度明显要高于基于Sn-Zn、Cu-Zn特征的SVM模型(图 4、5)。正是由于每次树的递归构建都是基于当前数据集选择最优的特征进行分割,而位于树高层的数据集熵更大,不确定性更高,因此高层节点特征的分类能力要高于低层节点特征,临近叶节点的特征对数据分类的重要性最低。
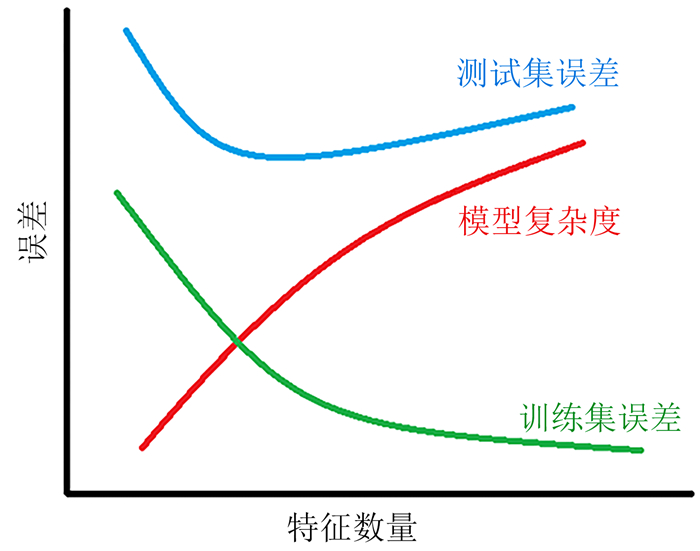
3.6 基于特征提取的SVM模型的岩性分类由于SVM在内部构建的过程中无法得知不同特征对预测结果的影响,因此通常情况下只能将所有特征统一送入模型中进行学习。然而,在模型的建立过程中过多的特征输入会导致模型性能的降低,在预测集上发生过拟合现象(图 8)[24-28]。因此,本文选取位于前五层的非临近底层叶节点:Sr、Mn、Mo、Pb、Cd、As作为最终的输入特征,送入SVM生成分类器进行岩性分类,并与不做特征选择的SVM分类器进行性能对比,结果如表 3所示。
|
| 图 8 特征与模型性能 Fig. 8 Features and model performance |
|
|
| 模型超参数 | 基于不同特征的SVM | 训练集准确度/% | 测试集准确度/% |
| C=1,r=5 | 原始特征SVM | 97.34 | 81.36 |
| 特征提取SVM | 94.73 | 98.76 | |
| C=2,r=5 | 原始特征SVM | 95.78 | 84.61 |
| 特征提取SVM | 94.73 | 96.31 | |
| C=5,r=10 | 原始特征SVM | 100.00 | 69.23 |
| 特征提取SVM | 97.36 | 92.30 | |
| C=5,r=20 | 原始特征SVM | 100.00 | 69.23 |
| 特征提取SVM | 100.00 | 84.61 |
判断一个分类器的性能高低主要考虑其在测试集上的具体表现。由表 3可以得出:不做特征提取,将所有原始特征都作为输入得到的SVM模型更容易发生过拟合现象,具体表现在当参数C>2,r>5时,模型在训练集上的精度高达100%,但在测试集上的分类效果表现较差,仅有69.23%的准确度;比较而言,经过决策树特征提取后的SVM在不同参数配置下的性能更高,并且具有更好的稳定性,在C=5,r=20的参数设置下,模型训练集精度为100%,测试集精度为84.61%,此时模型即使发生过拟合现象,也具有一定的分类能力。
4 结语对覆盖区下伏岩体的有效识别是实现深部找矿突破的关键所在,近年来机器学习理论的发展为岩性识别提供了新的思路。支持向量机属于稀疏核机模型,由于模型参数的确定对应于凸优化问题,因此可以得到全局最优解。本文结合钻孔分析数据将支持向量机模型应用于岩性识别,并使用决策数模型进行特征提取。结果显示,基于特征提取的支持向量机具有更高的精度,可以作为岩性识别的技术参考。
| [1] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012. Li Hang. Statistical Learning Method[M]. Beijing: Tsinghua University Press, 2012. |
| [2] |
于代国, 孙建孟, 王焕增, 等. 测井识别岩性新方法:支持向量机方法[J]. 大庆石油地质与开发, 2005, 24(5): 93-95. Yu Daiguo, Sun Jianmeng, Wang Huanzeng, et al. A New Method of Logging Recognition Lithology:Support Vector Machine Method[J]. Daqing Petroleum Geology and Development, 2005, 24(5): 93-95. DOI:10.3969/j.issn.1000-3754.2005.05.033 |
| [3] |
周继宏, 袁瑞. 基于支持向量机的复杂碎屑岩储层岩性识别[J]. 石油天然气学报, 2012, 34(7): 72-75. Zhou Jihong, Yuan Rui. Lithology Identification of Complex Clastic Rock Reservoirs Based on Support Vector Machine[J]. Journal of Oil and Gas Technolog, 2012, 34(7): 72-75. DOI:10.3969/j.issn.1000-9752.2012.07.014 |
| [4] |
张翔, 肖小玲, 严良俊, 等. 基于模糊支持向量机方法的岩性识别[J]. 石油天然气学报(江汉石油学院学报), 2009, 31(6): 115-118. Zhang Xiang, Xiao Xiaoling, Yan Liangjun, et al. Lithology Identification Based on Fuzzy Support Vector Machine[J]. Journal of Oil and Gas Technolog, 2009, 31(6): 115-118. |
| [5] |
李洪奇, 谭锋奇, 许长福, 等. 基于决策树方法的砾岩油藏岩性识别[J]. 测井技术, 2010, 34(1): 16-21. Li Hongqi, Tan Fengqi, Xu Changfu, et al. Lithology Identification of Conglomerate Reservoir Based on Decision Tree Method[J]. Well Logging Technology, 2010, 34(1): 16-21. DOI:10.3969/j.issn.1004-1338.2010.01.004 |
| [6] |
石广仁. 支持向量机在裂缝预测及含气性评价应用中的优越性[J]. 石油勘探与开发, 2008, 35(5): 589-594. Shi Guangren. Superiorities of Support Vector Machine in Fracture Prediction and Gassinesse Valuation[J]. Petroleum Exploration and Development, 2008, 35(5): 589-594. |
| [7] |
桑吉夫·库尔卡尼, 吉尔伯特·哈曼.统计学习理论基础[M].肖忠祥, 闫效莺, 段沛沛, 等译.北京: 机械工业出版社, 2017. Kulkarni S, Harman G.An Elementary Introduction to Statistical Learining Theory[M].Translated by Xiao Zhongxiang, Yan Xiaoying, Duan Peipei, et al.Beijing: Machinery Industry Press, 2017. |
| [8] |
王建国, 董泽宇, 张文兴, 等. 基于回归树的支持向量机规则提取及应用[J]. 计算机工程与应用, 2017, 53(6): 236-240. Wang Jianguo, Dong Zeyu, Zhang Wenxing, et al. Rule Extraction of Support Vector Machine Based on Regression Tree and Application[J]. Computer Engineering and Applications, 2017, 53(6): 236-240. |
| [9] |
Barakat N, Bradley A P. Rule Extraction from Support Vector Machines:A Review[J]. Neurocomputing, 2010, 74(5): 178-190. |
| [10] |
温小霓, 蔡汝骏. 分类与回归树及其应用研究[J]. 统计与决策, 2007(23): 14-16. Wen Xiaoni, Cai Rujun. Classification and Regression Tree and Its Application Research[J]. Statistics and Decision, 2007(23): 14-16. DOI:10.3969/j.issn.1002-6487.2007.23.006 |
| [11] |
谢益辉. 基于R软件rpart包的分类与回归树应用[J]. 统计与信息论坛, 2007, 22(5): 67-70. Xie Yihui. Classification and Regression Tree Application Based on R Software Rpart Package[J]. Forum on Statistics and Information, 2007, 22(5): 67-70. DOI:10.3969/j.issn.1007-3116.2007.05.013 |
| [12] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 1-415. Zhou Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 1-415. |
| [13] |
范淼, 李超. Python机器学习及实践[M]. 北京: 清华大学出版社, 2016: 1-180. Fan Miao, Li Chao. Python Machine Learning and Practice[M]. Beijing: Tsinghua University Press, 2016: 1-180. |
| [14] |
张冰, 郭智奇, 徐聪, 等. 基于岩石物理模型的页岩储层裂缝属性及各向异性参数反演[J]. 吉林大学学报(地球科学版), 2018, 48(4): 1244-1252. Zhang Bing, Guo Zhiqi, Xu Cong, et al. Fracture Properties and Anisotropic Parameters Inversion of Shales Based on Rock Physics Model[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(4): 1244-1252. |
| [15] |
杨震宇. 基于机器学习的分类算法研究[J]. 科学中国人, 2017, 2: 22-25. Yang Zhenyu. Research on Classification Algorithm Based on Machine Learning[J]. Scientific Chinese, 2017, 2: 22-25. |
| [16] |
丁世飞, 齐丙娟, 谭红艳. 支持向量机理论与算法研究综述[J]. 电子科技大学学报, 2011, 40(1): 2-10. Ding Shifei, Qi Bingjuan, Tan Hongyan. An Overview on Theory and Algorithm of Support Vector Machines[J]. Journal of University of Electronic Science and Technology of China, 2011, 40(1): 2-10. |
| [17] |
冷强奎, 李玉鑑. 使用SVM和二叉树结构的分片线性分类器[J]. 中国科技论文, 2015, 10(2): 164-168. Leng Qiangkui, Li Yujian. A Piecewise Linear Classifier Using SVM and two Forked Tree Structure[J]. China Sciencepaper, 2015, 10(2): 164-168. DOI:10.3969/j.issn.2095-2783.2015.02.010 |
| [18] |
石广仁. 支持向量机在多地质因素分析中的应用[J]. 石油学报, 2008, 29(2): 195-198. Shi Guangren. Application of Support Vector Machine to Multi-Geological-Factor Analysis[J]. Acta Petrolei Sinica, 2008, 29(2): 195-198. DOI:10.3321/j.issn:0253-2697.2008.02.007 |
| [19] |
Janez D, Dale S. Statistical Comparisons of Classifiers over Multiple DataSets[J]. Journal of Machine Learning Research, 2006, 7(1): 1-30. |
| [20] |
Zhang M, Zhou Z. A Review on Multi-Label Learning Algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 |
| [21] |
Yoonkyung L, Yi L, Grace W. Multicategory Support Vector Machines:Theory and Application to the Classification of Microarray Data and Satellite Radiance Data[J]. Journal of the American Statistical Association, 2004, 99: 67-81. DOI:10.1198/016214504000000098 |
| [22] |
Fan R E, Chang K W, Hsieh C J, et al. LIBLINEAR:A Library for Large Linear Classification[J]. Journal of Machine Learning Research, 2008, 9: 1871-1874. |
| [23] |
Shwartz S S, Singer Y, Srebro N, et al. Pegasos:Primal Estimated Sub-Gradient Solver for SVM[J]. Mathematical Programming, 2011, 127(1): 3-30. |
| [24] |
Bouchaffra D, Vitae A, Cheriet M. Machine Learning and Pattern Recognition Models in Change Detection[J]. Pattern Recognition, 2015, 48(3): 613-615. DOI:10.1016/j.patcog.2014.10.019 |
| [25] |
Collins M, Schapire R E, Singer Y. Logistic Regression, Ada Boost and Bregman Distances[J]. Machine Learning, 2002, 48(1): 235-285. |
| [26] |
Canu S, Smola A. Kernel Methods and the Exponential Family[J]. Neurocomputing, 2006, 69(7): 714-720. |
| [27] |
Tsochantaridis I, Joachims T, Hofmann T, et al. Large Margin Methods for Structured and Interdependent Output Variables[J]. Journal of Machine Learning Research, 2005, 1: 1453-1484. |
| [28] |
Chang C C, Lin C J.LIBSVM: A Library for Support Vector Machines[J/OL].ACM Transactions on Intelligent Systems and Technology, 2011, 2(3).http://dx.doi.org/10.1145/1961189.1961199.
|



