0 引言
可控源音频大地电磁法(CSAMT)是在音频大地电磁法(AMT)的基础上发展起来的一种人工源频率域测深方法。20世纪70年代初,加拿大多伦多大学的Strangway教授和他的学生Goldstein提出沿用AMT的测量方式观测人工供电产生的音频电磁场,称这种方法为CSAMT。由于使用人工源[1-2],这种方法克服了天然源观测上的一些困难,被先后应用于深部隐伏金属矿体勘探[3-4]、油气构造勘查[5]、地热和水文工程[6]等方面。目前,普遍应用的均为一维、二维反演技术。近些年,随着计算机技术的飞速发展,三维反演技术开始兴起,出现了共轭梯度法[7-8]、非线性共轭梯度法[9]、有限内存拟牛顿法、高斯牛顿法[10]等三维反演方法。其中,由Broyden等[11-14]在1970年提出并发展起来的基于拟牛顿(BFGS)法的有限内存拟牛顿(L-BFGS)法[15]继承了牛顿法收敛速度快的优点,同时又克服了牛顿法计算量大、产生非下降方向的缺点,在求解无约束优化问题时缩短了计算时间,提高了工作效率。而在求解实际问题时L-BFGS法又具有超线性收敛性和非常好的自校正能力,是最有效的拟牛顿法之一。2006年Avdeeva首先将BFGS法应用到一维大地电磁反演[16],并将这种方法进一步推广到三维反演中[17]。2012年贾定宇等[18]采用L-BFGS方法解决了可控源电磁测深一维反演问题。2013年,刘云鹤等[19]将其应用于3D航空电磁频率域数据反演,对比显示,该方法在反演速度和反演结果的准确性上比非线性共轭梯度法(NLCG)有一定的优势。因此,本文将L-BFGS方法应用到地面可控源电磁勘探三维反演中。不同于赵宁等[15]的研究,在反演过程中,我们采用自适应正则化因子来平衡数据拟合和模型拟合对反演结果的影响。论文首先用理论模型来验证这种方法的准确性和有效性,然后用该方法反演吉林省集安地区采集的可控源电磁数据,并用钻孔验证发现的异常,以证明本文研究方法的有效性和实用性。
1 有限差分法正演三维频率域可控源方法正演计算基于如下异常场满足的微分方程:
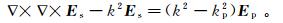 (1)
(1) 式中:kp为背景介质复波数;k为含异常后介质复波数;Ep为背景电场;Es为异常体产生的异常电场[20-21]。
采用虚界面法[22-23],利用直接积分法计算Ep[24]。Es的求解通常采用有限差分法[25-26]、有限元法[27]、积分方程法[28-29],本文采用的是交错网格有限差分法。将三维介质剖分成正六面体单元,即沿x、y、z 3个坐标方向分别用若干个平行的平面以不同的间距将研究区域划分成若干个小的长方体网格单元。式(1)的矢量微分方程可以分解为3个方向上的微分方程,将离散化后的矩阵方程合并,并且进行对称化处理,得到如下的矩阵方程:
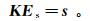 (2)
(2) 式中:K是复系数大型稀疏对称矩阵;s是式(1)右端的源项。采用拟最小残差法(quasi-minimal residual, QMR)求解式(2),求得每个边中点的电场值,再根据法拉第定律微分形式计算磁场分量H。本次研究观测数据选择阻抗Zxy[30],而对于可控源数据有
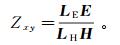
式中:LE、LH分别为空间插值算子;E=Es+Ep。
2 有限内存拟牛顿法反演设正则化目标函数为
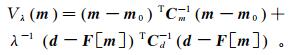 (3)
(3) 式中:m是模型参数向量;d是数据向量;模型Cd是数据方差矩阵;Cm是模型方差函数;F是正演算子;m0是初始模型;λ为自适应正则化因子。当两次反演的拟合差变化小于0.002时,λ=λ/10[31]。
设目标函数二次可微,取目标函数在某已知点xk处的二阶泰勒展开式:
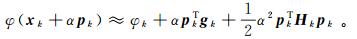 (4)
(4) 式中:α为搜索步长;φk=φ(xk);gk=g(xk)为目标函数的一阶导数;pk表示模型搜索方向;Hk为目标函数的二阶导数,即Hessian矩阵。为了寻找极小化目标函数的搜索方向pk,令
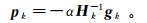 (5)
(5) 则牛顿法的模型更新方式为
 (6)
(6) 利用充分下降条件和曲率条件来约束搜索步长α[32]。在通过式(5)求未知变量的搜索方向pk时,利用了目标函数二阶导数的信息,从而能快速达到局部收敛。但直接求解式(5),需要计算和存储Hessian矩阵H并求其逆,这需要很长的计算时间和较大的存储空间。而拟牛顿法改进了这一缺点,它通过构造一个对称正定矩阵Bk来近似Hessian矩阵Hk,将式(6)写成
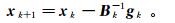 (7)
(7) 为了使Bk合理地逼近Hk,要求其满足
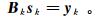 (8)
(8) 式中:sk=xk+1-xk;yk=gk+1-gk。通常是给定一个单位矩阵B0,然后通过修改Bk得到Bk+1。显然,随着迭代的进行,求取矩阵Bk+1将依赖之前反演的各个Bk,从而要求较大的内存来存储Bk。L-BFGS法在上述拟牛顿法的基础上进行了改正,利用BFGS校正公式,由一个对称正定初始矩阵B0∈Rn×n开始,利用下面的校正公式计算得出Hessian矩阵的近似:
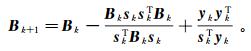 (9)
(9) 式(9)改进了拟牛顿法[1],可以指定一个正整数m,使其只利用最近m次迭代的信息,即使用向量对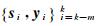
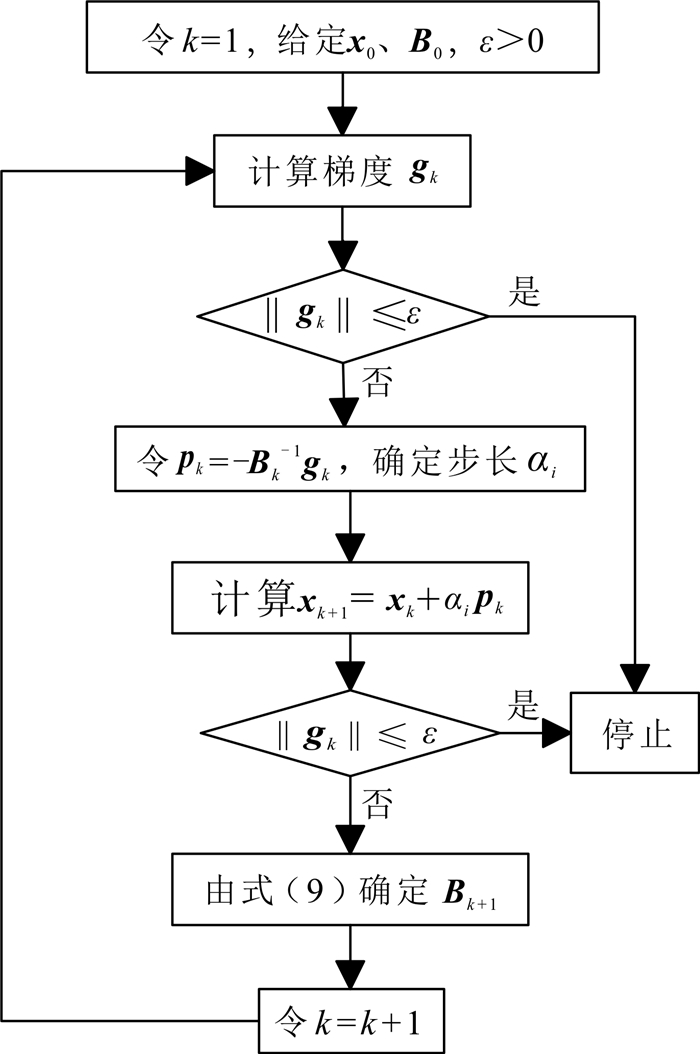
图 1给出了有限内存拟牛顿法用于可控源资料三维反演的流程[19]。从图 1可见首先需要求取梯度gk。而求取gk则需要计算雅可比矩阵,对于三维电磁法,采用伴随正演来求取雅可比矩阵。
|
| 图 1 有限内存拟牛顿法可控源三维反演流程图 Fig. 1 Flow chart of three-dimensional controlled source electromagnetic inversion using L-BFGS |
|
|
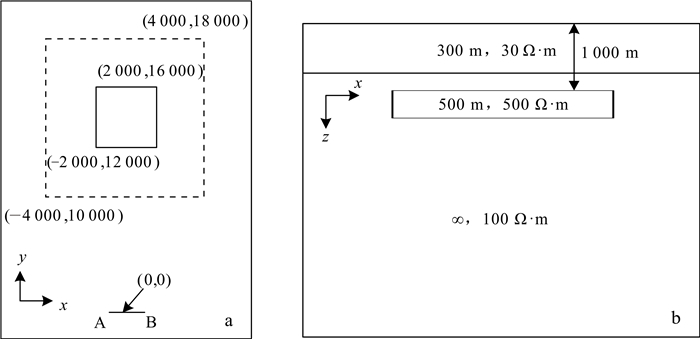
为了验证反演方法的准确性,我们设计了一个两层介质模型,在埋深1 000 m处存在一个规模为4 000 m×4 000 m×500 m、电阻率为500 Ω·m的高阻异常体(图 2)。图 2a中(-4 000, 10 000)×(4 000, 18 000)为测量区域。线距400 m,点距400 m,共441个物理测点。图 2a中AB表示可控源方法观测时使用的发射源,中心点位于(0, 0),源的长度为1 000 m,电流为1 A,发射频率从2-3Hz开始,以倍频增加到213 Hz,共17个频率。观测参数为Zxy的实部和虚部。
|
| a.模型及装置顶视图;b.模型过y=12 000 m的纵断面。 图 2 反演理论模型示意图 Fig. 2 Schematic diagram of the theoretical model for inversion tests |
|
|
本文采用交错网格有限差分法计算了图 2模型的频率响应。模型剖分的网格区域略大于测量范围。x、y和z三个方向被剖分为40×40×30共48 000个网格,x、y方向的网格宽度均为300 m;z方向的网格第一层厚度为25 m,其下各层的厚度按系数1.10递增,总厚度为2 458 m。三维电磁反演存在着关键频率[34-35]。在本例中,关键频率约为2-3、2-2、2-1Hz,其对应的上述装置Zxy响应平面分布模拟结果如图 3所示。从图 3可以看出,Zxy曲线异常响应明显,实部曲线向远离源的方向偏离,虚部向靠近源的方向偏离,且随着频率的增加,异常的幅值增大。
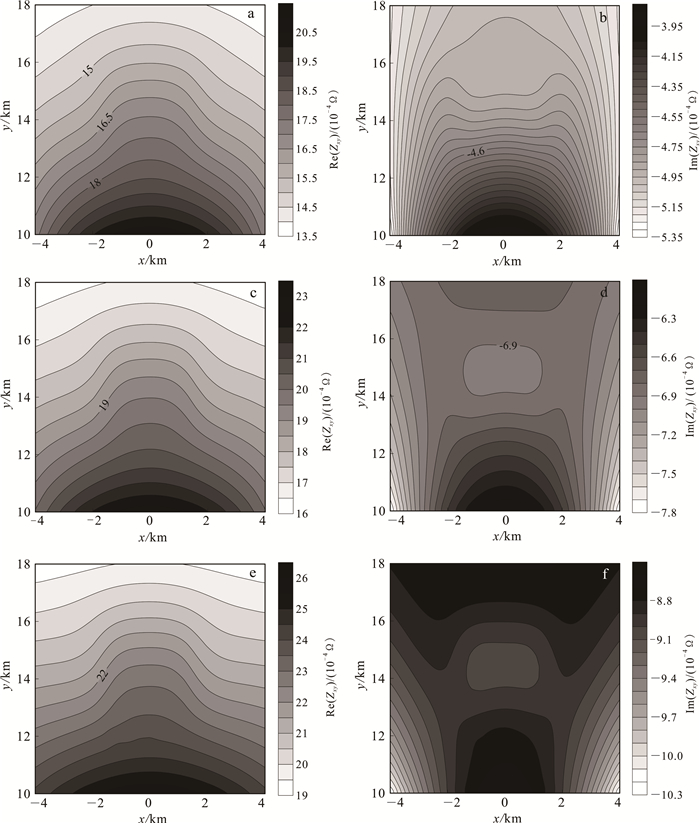
|
| a,b. f=2-3 Hz;c,d. f=2-2 Hz;e,f. f=2-1 Hz。 图 3 不同频率Zxy响应平面等值线图 Fig. 3 Response of Zxy at different frequencies |
|
|
将理论模拟数据的Zxy实部和虚部分别施以5%的高斯噪音后作为观测数据进行反演。初始模型为两层介质模型,第一层介质电阻率为30 Ω·m,厚300 m;第二层介质电阻率为100 Ω·m。文中用于计算背景场的背景模型与初始模型一致,且在反演过程中背景模型不进行更新。反演的网格剖分同正演一致,反演在主频3.6 GHz、内存4.0 GB、处理器为Intel Core i5的个人计算机上进行运算。反演迭代111次,每次迭代4 min,共用时6.2 h。图 4为迭代过程中拟合差(RMS)、自适应正则化因子和模型修正量的变化图。从图 4a可以看出:迭代5次后,拟合差迅速下降到3左右,说明了有限内存拟牛顿法的收敛速度较快;随着迭代次数的增加,拟合差下降速度趋于平缓,最终趋于1。正则化因子则在拟合差趋于平缓后开始降低(图 4b),当两次迭代的拟合差的差值小于0.002时,λ减小为原来的1/10,通过降低模型在目标函数中所占的权重来尽量拟合数据。模型修正量在反演开始时增大速度较快,随着迭代次数的增加,最后也逐渐趋于平稳(图 4c)。
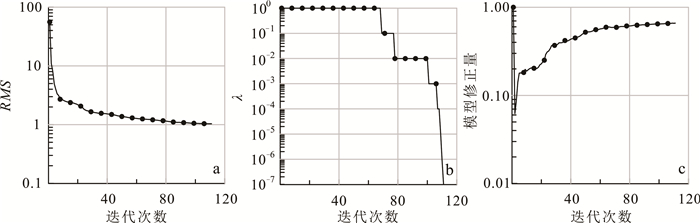
|
| 图 4 加噪模型111次迭代过程中RMS,λ和模型改变量变化曲线 Fig. 4 RMS, λ and mNorm variation with iteration number during 111 iterations of noise-added model |
|
|
图 5为图 2中异常体模型的反演结果。从横切异常体的平面图(图 5a)可看出,异常分布范围与理论异常的平面位置对应。在纵断面图(图 5b、c)上,异常体的大小和在x、y方向的中心位置与理论模型也基本一致,但在z方向上异常体被拉伸,位置偏下,且异常中心电阻率比理论值低。结合模型特点,产生上述现象是由于覆盖层的电阻率较低,电磁波衰减较快,导致深部信号较弱。此外,从本质上,电磁法对高阻异常不灵敏,这造成深部高阻体的分辨能力下降。
为了测试该反演方法对初始模型的依赖性,我们将初始模型改为电阻率为100 Ω·m的均匀半空间模型,再一次进行反演。反演网格与上文一致。观测数据仍为施以5%高斯噪音的Zxy实部和虚部。反演迭代了274次,每次迭代4 min,共用时18.2 h。反演拟合差从146.00下降到1.78,拟合效果较好。反演结果如图 6所示。从图 6中可以明显看出:地下介质为层状结构,浅部为低阻,厚度约200 m,真实模型为300 m,反演结果与真实模型较为接近;深部的高阻异常体与第一次反演结果对比,水平位置也吻合较好,但深度明显向下偏移,电阻率值也更低。将两次反演结果进行对比,可以看出,第一次反演结果要优于第二次,但后者也能与真实模型较好吻合。这说明当初始模型与真实模型不接近时,反演方法仍能反演出真实模型。

|
| a.z=-1 km处平面图;b.y=14 km处x方向剖面图;c.x=0 km处y方向剖面图。 图 6 初始模型为均匀半空间的三维反演电阻率分布图 Fig. 6 3D inversion resistivity distribution with the prior model of half-uniform space |
|
|
为了验证该方法的实用性,本文将其应用到实际数据的处理中。采用的数据为吉林省集安市海关地区钼矿勘查的可控源实测数据,工区位于海关市的西南部。该区晚侏罗世在鸭绿江火山-岩浆岩带中南段形成了火山喷发、岩浆侵入相间出现成带分布的火山-岩浆岩带,这一中生界构造-岩浆岩带多金属成矿带内沿鸭绿江构造金、铅、锌、铜等矿化十分普遍,是主要的找矿远景区段。研究区域附近已经发现几个小型钼矿点[36],至今没有发现大规模的矿床。本次工作期望通过地面可控源电磁勘探,了解矿区的深部电性特征,寻找隐伏矿化富集地段和含钼矿岩体,为深部钻探施工提供依据。工区内布设了5条北西向测线,距离源由远到近依次为1—5线。线距为200 m,点距50 m,共140个测点,电极距离50 m。观测方式采用赤道偶极方式,发射源采用电导线源,位于工区东北部,平行于测线方向,源长为1 km,距离最近的测线约6.9 km。
4.1 区域地质背景在构造上,矿区位于华北地台东部,在辽东台隆太子河—浑江陷褶断束中。鸭绿江断裂在区内通过。
区内出露的地层主要为古元古界集安群临江(岩)组,构成凉水—小古马岭背斜。地层总体走向310°左右,背斜北东翼地层北东倾,倾角20°~40°,背斜南西翼地层南西倾,倾角10°~40°。岩性为片麻岩、含墨黑云变粒岩、浅粒岩。
区内脉岩发育,种类繁多,多数为燕山期,尤以燕山晚期活动更为常见,主要有花岗斑岩、细粒闪长岩、闪长玢岩、石英斑岩等,多呈北东向展布。矿体主要分布在中、酸性脉岩发育区,临江(岩)组中的硅化、绿泥石化、绢云母化、碳酸盐化、黄铁矿化组合及中元古代碱长花岗岩中硅化、绢云母化、黄铁矿化组合中。
区内的鸭绿江断裂始于侏罗纪以前,具有多次继承性活动的特点,它控制了燕山期花岗岩、花岗斑岩、闪长玢岩、长石斑岩侵入体的空间展布及中生代火山喷发,控制了区域内生矿产的分布。同时,还发育北东、北西向断裂构造,它们是区内主要的容矿构造。
4.2 地球物理特征为研究工区不同地层和岩性的电阻率特征,我们搜集了研究区岩石的电阻率信息(表 1)。从结果来看,片麻岩和花岗岩都表现为高阻,蚀变的片麻岩为次高阻,辉钼矿脉为低阻。从表 1中可看出矿脉与围岩电阻率有明显的差异,因此适合开展CSAMT工作。
| 岩石名称 | 含矿性 | 样品数 | 电阻率/(Ω·m) | ||
| 最小值 | 最大值 | 平均值 | |||
| 花岗岩 | 无矿化 | 17 | 62 428 | 2 375 000 | 935 988 |
| 片麻岩 | 无矿化 | 2 | 597 800 | 600 000 | 898 900 |
| 片麻岩 | 蚀变 | 11 | 3 329 | 7 430 | 5 033 |
| 辉钼矿脉 | 浸染状 | 2 | 362 | 388 | 375 |
可控源数据采集频率为2-3~213 Hz,以2的指数倍递增,共17个频率。图 7为典型测点的频率-视电阻率曲线。从图 7可见,工区的电阻率很高,基本在1 000 Ω·m以上。因此,视电阻率从大致512 Hz开始就进入了近区,呈现45°上升。由于干扰和观测误差的存在,在频率-视电阻率曲线上会出现非正常的突跳,如202号测点,频率大于100 Hz时曲线突跳剧烈,只能观察出曲线的大致规律。114号测点数据质量较好,频率-视电阻率曲线平滑。

|
| 图 7 典型测点频率-视电阻率曲线 Fig. 7 Typical sounding curves of stations |
|
|
反演针对阻抗Zxy进行,单位采用实际观测中的常用单位[37],对应的复阻抗频率响应如图 8a所示。由于阻抗的振幅和相位有一定的内在联系[38],我们提出借助Nyquist图对误差数据进行必要的处理[39]。图 8b为对应的Nyquist图,从图中看出曲线从低频到高频逆时针旋转,不符合我们经过大量数值模拟和实际数据得出的其沿顺时针旋转的规律,需要对其进行编辑。图 9为阻抗编辑完成的阻抗数据。
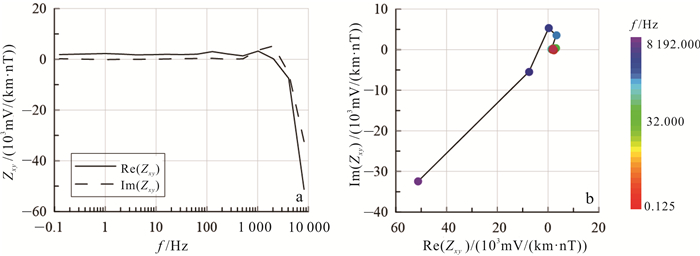
|
| a.阻抗频率响应;b.Nyquist图。 图 8 202号测点阻抗响应 Fig. 8 Raw data of Zxy at station 202 |
|
|
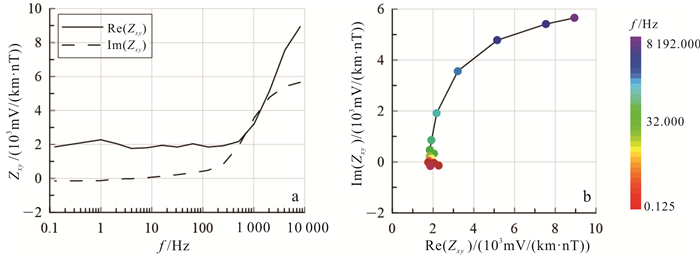
|
| a.阻抗频率响应;b.Nyquist图。 图 9 202号测点编辑后阻抗响应 Fig. 9 Edited data of Zxyat station 202 |
|
|
实际数据在反演之前,需要进行必要的圆滑。由于高频数据质量较差(图 7a),我们只截取0.125~256. 000 Hz频率范围内10个频率的数据。反演数据为阻抗分量Zxy。由于实际数据误差较大,我们将阻抗振幅的5%作为数据误差,让反演更加有效地进行。
反演初始模型参数包括网格大小和初始背景电阻率。网格大小决定了计算的精度,网格越小,计算的精度越高,但计算时间越长。让两个测点中间有两个网格节点,既保证了计算精度,又节约计算时间。如果测点较多,两个测点中间有一个网格节点也可。本次研究点距为50 m,线距200 m,所以将网格大小定为25 m×100 m。z方向的网格大小根据勘探深度的需要进行调整,本文目标深度为1 km,所以第一层厚定为10 m,层厚按照系数1.1依次递增。
初始模型的背景电阻率对反演影响很大。这里根据研究区的地质资料和岩石的地球物理特征,将初始模型的电阻率选为5 000 Ω·m。反演在CPU为3.60 GHz主频的电脑上运算,内存4 Gb。迭代一次7 min,迭代85次,用时650 min。反演拟合差从12.9降到1.53。
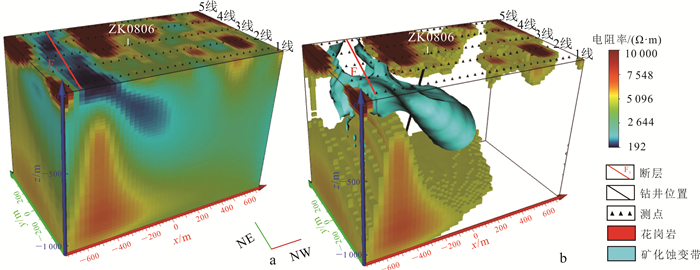
4.5 结果及讨论我们实际感兴趣的是高阻岩体及与之相关的低阻矿化蚀变。图 10为CSAMT三维反演获得的高阻和低阻分布立体图。由图 10可见,电阻率整体以中高阻为主。工区的东部有一条沿北东向延伸的低阻条带,倾向为北西,推测为鸭绿江断裂(图 10中F1所示)。在该断裂的深部有一处高阻带向上隆起,电阻率大约为10 000 Ω·m,推测为花岗斑岩,是与钼矿床成矿有关的岩石。推测成矿过程是经过热液的上涌或侵入,将矿质携带到一定的部位,并导致围岩发生蚀变。蚀变带是找矿的重要标志。
|
| a.三维反演结果电阻率图;b.花岗岩分布及钻井位置图。 图 10 工区反演结果电阻率分布图 Fig. 10 Resistivity distribution of inversion results in the working area |
|
|
研究区内蚀变主要有硅化、绿泥石化、绢云母化、碳酸盐化、黄铁矿化等。由表 1岩石的电性特征可知,矿化蚀变后的岩石表现为中低阻,因此中低阻带可作为找矿标志。为了突出异常的特征,将高阻的岩浆岩和中低阻带单独画出(图 10b)。从图 10b中可以看出,低阻带为一条由下向上延伸的斜条带状,延伸至-500 m左右,倾角约45°。
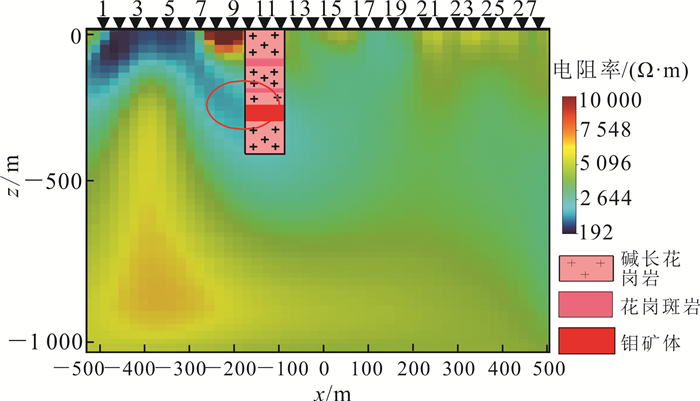
根据花岗岩和低阻带的位置,推测该低阻为矿化蚀变带,并在(-100, 0, 0)处进行钻探验证,图 10b中黑色线为ZK0806钻孔位置及井身空间形态。钻探揭示,在178 m深度上存在厚度90 m的矿化蚀变,蚀变倾向北西,倾角约50°。将钻探剖面与过井三维反演模型的电阻率剖面进行对比(图 11)发现,钻探结果与可控源异常的位置具有非常好的一致性。
|
| 图中叠加了钻探资料对比图,红色条带为钻遇钼矿位置。 图 11 过钻孔的3线剖面反演电阻率分布图 Fig. 11 Inversed resistivity distribution of the 3-profile through borehole |
|
|
本文将有限内存拟牛顿法应用到地面三维可控源电磁勘探中,得出如下认识:
1) 数值模拟结果与理论模型一致,证明了研究方法的准确性和可行性,并且有限内存拟牛顿法收敛速度快,为三维地面可控源电磁反演的实际应用提供了基础。
2) 三维反演结果中推测了一个潜在的钼矿矿脉,并与钻探结果基本一致,证明了文中反演方法的可行性和实用性。
3) 采用可控源方法来探测蚀变钼矿是可行的,可以将其应用到其他类似类型的钼矿探测工作中。
| [1] |
翁爱华, 刘佳音, 贾定宇, 等. 有限长导线源频率测深有限内存拟牛顿一维反演[J]. 吉林大学学报(地球科学版), 2017, 47(2): 597-605. Weng Aihua, Liu Jiayin, Jia Dingyu, et al. 1-D Inversion for Controlled Source Electromagnetic Sounding Using Limited Memory Quasi-Newton Method[J]. Journal of Jilin University (Earth Science Edition), 2017, 47(2): 597-605. |
| [2] |
贲放, 刘云鹤, 黄威, 等. 各向异性介质中的浅海海洋可控源电磁响应特征[J]. 吉林大学学报(地球科学版), 2016, 46(2): 581-593. Ben Fang, Liu Yunhe, Huang Wei, et al. MCSEM Responses for Anisotropic Media in Shallow Water[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 581-593. |
| [3] |
卢鸿飞, 王志福, 王恒, 等. CSAMT测深和重力测量技术在哈密白山钼矿深部找矿和远景评价中的应用[J]. 地球物理学进展, 2013, 28(3): 1547-1556. Lu Hongfei, Wang Zhifu, Wang Heng, et al. The Application of CSAMT and GS on Prospecting and Evalution in Baishan Molybdenum Deposit, Hami, Xinjiang[J]. Progress in Geophysics, 2013, 28(3): 1547-1556. |
| [4] |
王大勇, 李桐林, 高远, 等. CSAMT法和TEM法在铜陵龙虎山地区隐伏矿勘探中的应用[J]. 吉林大学学报(地球科学版), 2009, 39(6): 1134-1140. Wang Dayong, Li Tonglin, Gao Yuan, et al. The Application of CSAMT and TEM to Exploration Buried Deposits in Longhu Mountain Area at Tongling, Anhui Province[J]. Journal of Jilin University (Earth Science Edition), 2009, 39(6): 1134-1140. |
| [5] |
Silva N V D, Morgan J V, Macgregor L, et al. A Finite Element Multifrontal Method for 3D CSEM Modeling in the Frequency Domain[J]. Geophysics, 2012, 77(2): 101-115. DOI:10.1190/geo2010-0398.1 |
| [6] |
张晋.可控源音频大地电磁法在河南省卢氏县水文地质构造调查中应用[D].长春: 吉林大学, 2014. Zhang Jin.The Application of Controlled Source Audio-Frequency Magnetotelluric in Lushi County of Henan Province Hydrology Geological Structure Survey[D].Changchun: Jilin University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10183-1015507565.htm |
| [7] |
吴小平, 徐果明. 利用共轭梯度法的电阻率三维反演研究[J]. 地球物理学报, 2000, 43(3): 420-427. Wu Xiaoping, Xu Guoming. Study On 3-D Resistivity Inversion Using Conjugate Gradient Method[J]. Chinese Journal of Geophysics, 2000, 43(3): 420-427. DOI:10.3321/j.issn:0001-5733.2000.03.016 |
| [8] |
林昌洪, 谭捍东, 舒晴, 等. 可控源音频大地电磁三维共轭梯度反演研究[J]. 地球物理学报, 2012, 55(11): 3829-3838. Lin Changhong, Tan Handong, Shu Qing, et al. Three-Dimensional Conjugate Gradient Inversion of CSAMT Data[J]. Chinese Journal of Geophysics, 2012, 55(11): 3829-3838. DOI:10.6038/j.issn.0001-5733.2012.11.030 |
| [9] |
翁爱华, 刘云鹤, 贾定宇, 等. 地面可控源频率测深三维非线性共轭梯度反演[J]. 地球物理学报, 2012, 55(10): 3506-3515. Weng Aihua, Liu Yunhe, Jia Dingyu, et al. Three-Dimensional Controlled Source Electromagnetic Inversion Using Non-Linear Conjugate Gradients[J]. Chinese Journal of Geophysics, 2012, 55(10): 3506-3515. DOI:10.6038/j.issn.0001-5733.2012.10.034 |
| [10] |
彭荣华, 胡祥云, 韩波. 基于高斯牛顿法的频率域可控源电磁三维反演研究[J]. 地球物理学报, 2016, 59(9): 3470-3481. Peng Ronghua, Hu Xiangyun, Han Bo. 3D Inversion of Frequency-Domain CSEM Data Based on Gauss-Newton Optimization[J]. Chinese Journal of Geophysics, 2016, 59(9): 3470-3481. |
| [11] |
Boyden C G. The Convergence of a Class of Double Rank Minimization Algorithms:The New Algorithm[J]. Journal of the Institute of Mathematics and Applications, 1970, 6: 222-231. DOI:10.1093/imamat/6.3.222 |
| [12] |
Fletcher R. A New Approach to Variable Metric Algorithms[J]. Computer Journal, 1970, 13: 317-322. DOI:10.1093/comjnl/13.3.317 |
| [13] |
Goldfarb D. A Family of Variable Metric Methods Derived by Variational Means[J]. Mathematics of Computation, 1970, 24: 23-26. DOI:10.1090/S0025-5718-1970-0258249-6 |
| [14] |
Shanno D F. Conditioning of Quasi-Newton Methods for Function Minimization[J]. Mathematics of Computation, 1970, 24(111): 647-650. DOI:10.1090/S0025-5718-1970-0274029-X |
| [15] |
赵宁, 王绪本, 秦策, 等. 三维频率域可控源电磁反演研究[J]. 地球物理学报, 2016, 59(1): 330-341. Zhao Ning, Wang Xuben, Qin Ce, et al. 3D Frequency-Domain CSEM Inversion[J]. Chinese Journal of Geophysics, 2016, 59(1): 330-341. |
| [16] |
Avdeeva A D, Avdeev D B.QN Inversion of Large-Scale MT Data[C]//Progress in Electromagnetic Research Symposium.Cambridge: [s.n.], 2006: 210-213.
|
| [17] |
Avdeev D, Avdeeva A. 3D Magnetotelluric Inversion Using a Limited-Memory Quasi-Newton Optimization[J]. Geophysics, 2009, 74(3): F45-F57. DOI:10.1190/1.3114023 |
| [18] |
贾定宇.基于L-BFGS方法的水平电偶极一维反演[D].长春: 吉林大学, 2012. Jia Dingyu.Inversing Horizontal Electromagnetic Dipole Data by L-BFGS Method[D].Changchun: Jilin University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10183-1012367903.htm |
| [19] |
刘云鹤, 殷长春. 三维频率域航空电磁反演研究[J]. 地球物理学报, 2013, 56(12): 4278-4287. Liu Yunhe, Yin Changchun. 3D Inversion for Frequency-Domain HEM Data[J]. Chinese Journal of Geophysics, 2013, 56(12): 4278-4287. DOI:10.6038/cjg20131230 |
| [20] |
Commer M, Newman G A. New Advances in Three-Dimensional Controlled-Source Electromagnetic Inversion[J]. Geophysics Journal International, 2008, 172(2): 513-535. DOI:10.1111/gji.2008.172.issue-2 |
| [21] |
王卫平, 曾昭发, 李静, 等. 频率域航空电磁法地形影响和校正方法[J]. 吉林大学学报(地球科学版), 2015, 45(3): 941-951. Wang Weiping, Zeng Zhaofa, Li Jing, et al. Topographic Effects and Correction for Frequency Airborne Electromagnetic Method[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(3): 941-951. |
| [22] |
Da U C.A Reformalism for Computing Frequency-and Time-Domain EM Responses of a Buried Finite-Loop[C]//SEG Technical Program Expanded Abstracts.[S.l.]: Society of Exploration Geophysicists, 1995: 811-814.
|
| [23] |
刘云鹤, 刘国兴, 翁爱华, 等. 基于二级近似离散复镜像法的低频电磁格林函数计算[J]. 地球物理学报, 2011, 54(4): 1114-1121. Liu Yunhe, Liu Guoxing, Weng Aihua, et al. Calculation of Low-Frequency Electromagnetic Green's Functions Using Two-Level Approximate Discrete Complex Image Method[J]. Chinese Journal of Geophysics, 2011, 54(4): 1114-1121. DOI:10.3969/j.issn.0001-5733.2011.04.027 |
| [24] |
翁爱华, 王雪秋. 利用数值积分提高一维模型电偶源电磁测深响应计算精度[J]. 西北地震学报, 2003, 25(3): 193-197. Weng Aihua, Wang Xueqiu. Utilizing Direct Integration to Enhance Calculation Accuracy of 1D Electromagnetic Response for Current Dipole Source[J]. Northwestern Seismological Journal, 2003, 25(3): 193-197. DOI:10.3969/j.issn.1000-0844.2003.03.001 |
| [25] |
Newman G A, Alumbaugh D L. Frequency-Domain Modelling of Airborne Electromagnetic Responses Using Staggered Finite Differences[J]. Geophysical Prospecting, 1995, 43(8): 1021-1042. DOI:10.1111/gpr.1995.43.issue-8 |
| [26] |
谭捍东, 余钦范, 魏文博. 大地电磁法三维交错采样有限差分数值模拟[J]. 地球物理学报, 2004, 46(5): 705-711. Tan Handong, Yu Qinfan, Wei Wenbo. Magnetote-lluric Three-Dimensional Modeling Using the Staggered-Grid Finite Difference Method[J]. Chinese Journal of Geophysics, 2004, 46(5): 705-711. |
| [27] |
徐志锋, 吴小平. 可控源电磁三维频率域有限元模拟[J]. 地球物理学报, 2010, 53(8): 1931-1939. Xu Zhifeng, Wu Xiaoping. Controlled Source Electromagnetic 3-D Modeling in Frequency Domain by Finite Element Method[J]. Chinese Journal of Geophysics, 2010, 53(8): 1931-1939. DOI:10.3969/j.issn.0001-5733.2010.08.019 |
| [28] |
Wannamaker P E, Hohmann G W, SanFilipo W A. Electromagnetic Modeling of Three-Dimensional Bodies in Layered Earths Using Integral Equations[J]. Geophysics, 1984, 49: 60-74. DOI:10.1190/1.1441562 |
| [29] |
徐凯军, 李桐林, 张辉, 等. 利用积分方程法的大地电磁三维正演[J]. 西北地震学报, 2006, 28(2): 104-107. Xu Kaijun, Li Tonglin, Zhang Hui, et al. Three Dimensional Magnetotelluric Forward Modeling Using Integral Equation[J]. Northwestern Seismological Journal, 2006, 28(2): 104-107. |
| [30] |
翁爱华, 李大俊, 李亚彬, 等. 数据类型对三维地面可控源电磁勘探效果的影响[J]. 地球物理学报, 2015, 58(2): 697-708. Weng Aihua, Li Dajun, Li Yabin, et al. Selecion of Parameter Types in Controlled Source Electromagnetic Method[J]. Chinese Journal of Geophysics, 2015, 58(2): 697-708. |
| [31] |
Kelbert A, Egbert G D, Schultz A. Non-Linear Conjugate Gradient Inversion For Global EM Induction:Resolution Studies[J]. Geophysical Journal of the Royal Astronomical Society, 2008, 173(2): 365-381. DOI:10.1111/gji.2008.173.issue-2 |
| [32] |
Nocedal J, Wright S J. Numerical Optimization[M]. New York: Springer-Verlag, 1999.
|
| [33] |
袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 1997. Yuan Yaxiang, Sun Wenyu. Optimization Theory and Methods[M]. Beijing: Science Press, 1997. |
| [34] |
杨悦, 李亚彬, 翁爱华, 等. 频率选择对三维可控源反演的影响[J]. 地球物理学进展, 2015, 30(2): 829-835. Yang Yue, Li Yabin, Weng Aihua, et al. Effect of the Choice of Frequency on Three-Dimensional Controlled Source Electromagnetic Inversion[J]. Progress in Geophysics, 2015, 30(2): 829-835. |
| [35] |
Grayver A V, Streich R, Ritter O. 3D Inversion and Resolution Analysis of Land-Based CSEM Data from the Ketzin Storage Formation[J]. Geophysics, 2014, 79(2): 820-830. |
| [36] |
王玉波, 刘维英, 张兴全, 等. 集安市矿产资源开发现状及找矿前景分析[J]. 矿产勘查, 2010, 1(增刊1): 83-86. Wang Yubo, Liu Weiying, Zhang Xingquan, et al. Current Situation of Mineral Resources Exploitation and Prospect Analysis in Ji'an City[J]. Mineral Exploration, 2010, 1(Sup.1): 83-86. |
| [37] |
陈乐寿, 王光锷. 大地电磁测深法[M]. 北京: 地质出版社, 1990. Chen Leshou, Wang Guang'e. Magnetotelluric Sounding Method[M]. Beijing: Geological Publishing House, 1990. |
| [38] |
Kaufman A A, Keller G V. Frequency and Transient Sounding[M]. New York: Elsevier Methods in Geochemistry & Geophysics, 1983.
|
| [39] |
Li Dajun, Weng Aihua, Yang Yue, et al. Magnitude-Phase Relationship Behind Controlled-Source Electromagnetic Field Revealed by Nyquist Diagrams[J]. Journal of Environmental and Engineering Geophysics, 2018, 22(1): 365-373. |




