0 引言
不断增长的能源需求迫使我们不断寻找新的石油储量。海洋中蕴藏着大量的油气资源,已成为未来勘探开发的工作重心。海洋可控源电磁法(marine controlled-source electromagnetic method)是利用船只拖曳导线源(导线和电极)进行近海底发射,通过布设在海底成网格状分布的接收机接收电磁响应的勘探方法。
早在20世纪50年代,人们开始从事电磁法在海洋油气勘探中的应用研究。Cagniard[1]最早提出了大地电磁测深法(MT)并探讨了该方法在海洋环境下应用的可能性;Bannister[2]指出利用频率域偶极-偶极装置可以确定海底电阻率;Cox[3]提出使用水平电偶极源作为发射源研究海底地质结构;李桐林等[4]介绍了浅海MT在辽河油田滩海区的应用;Eidesmo等[5]提出SBL(sea bed logging)技术,并对海洋可控源电磁法的探测精度和工作效率进行大幅度改进;Constable等[6]分析了海洋可控源电磁法对不同埋深薄高阻层的灵敏度;Zhao等[7]研究了天然气水合物的频率域电磁响应,并讨论了可控源电磁法在天然气水合物探测中的可行性;Key[8]研究了一维海洋可控源电磁数据的多组分和多频率正、反演;Silva Crepald等[9]提出利用地震CMP(common middle point)方法定性解释海洋可控源电磁响应;Streich等[10]采用累加法计算了有限长导线源的电磁响应。
以往海洋电磁理论研究偏向于各向同性介质模型,然而,海洋沉积地层表现出不同程度的各向异性。Everett等[11]推导了一维水平各向同性(TI)介质频率域可控源电磁响应计算公式,并据此对大洋实测数据进行解释,得出与各向同性模型不同的解释结果;Yin[12]通过对海洋大地电磁(MMT)的研究,总结出任意各向异性海洋大地电磁视电阻率和相位特征;Løseth等[13]推导了任意各向异性介质中的电磁场;Kong等[14]利用有限元法对海洋可控源各向异性电磁响应进行了正演模拟;Newman等[15]利用非线性共轭梯度法实现海洋可控源TI介质电磁数据反演;刘云鹤等[16]分析了发射源姿态变化对海洋电磁观测数据的影响;殷长春等[17]和贲放等[18]对浅海区域各向异性介质的可控源电磁响应特征进行了研究。
本文利用延拓算法实现海洋可控源电磁法一维各向异性模型正演模拟。基于标量势分解的理论引入标量势,进而利用电场和磁场连续性边界条件实现场的向上和向下双向延拓,并在海底将其耦合到发射源上,从而实现电磁场的求解。在验证了算法的精度之后,通过分析海底各向异性的电磁响应特征,我们提出利用极性图的方式定性识别海底电各向异性。希望本文研究可为海洋可控源电磁数据处理与解释提供合适的模型,减少反演多解性。
1 正演算法假设时间因子为eiωt,则似稳态条件下麦克斯韦方程组为:
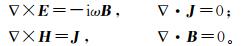 (1)
(1) 式中:E为电场强度;ω为角频率;B为磁感应强度;H为磁场强度;J为总电流密度。J=σE+Je,Je为源电流密度,σ为电导率。任意各向异性介质中的电导率和电阻率可用如下张量矩阵形式表示:
 (2)
(2) 式中,电导率(电阻率)张量是对称正定的,后面的讨论中我们仅采用电阻率张量。Yin[19]指出,式(2)中的电阻率张量可利用对如下主电阻率张量通过3次欧拉旋转获得,即
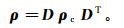
式中:
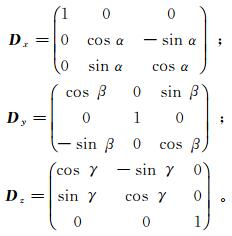
式中:α、β、γ分别表示绕x、y、z轴旋转的旋转角。
假定大地磁导率为真空磁导率μ0,则B=μ0H。由式(1)中电场和磁场的无源性,根据标量势分解理论,引入螺旋管形(toroidal)与极向形(poloidal)标量位,将电磁场[20]表示为
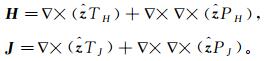 (3)
(3) 式中:TH与TJ为螺旋管形标量位;PH、PJ为极形标量位;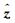
在波数域中,
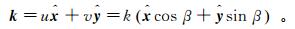
式中:k=|k|为波数;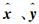
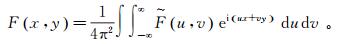 (4)
(4) 式中,波浪线表示波数域中的场或标量位,下同。则
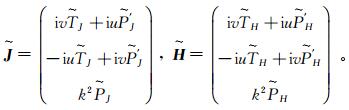 (5)
(5) 式中,撇号表示关于z的导数。
根据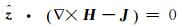

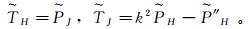 (6)
(6) 将式(5)代入式(1),并结合式(6)可得
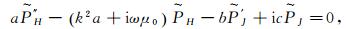 (7)
(7) 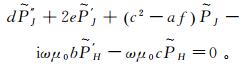 (8)
(8) 其中:
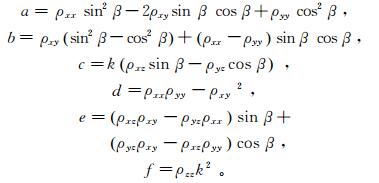
在一维层状介质中,假设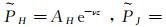
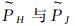
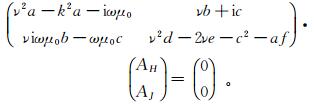 (9)
(9) 由于电磁场的振幅不为0,则式(9)的系数矩阵行列式为0。由此我们可以求解ν[21]。
求得的ν有4个解,分别表示螺旋管形与极向形标量位的上行波与下行波。据式(9)我们可以计算振幅AH与AJ的比值:
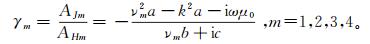
根据电磁场在导电介质表面的连续性,可得标量位满足如下边界条件:
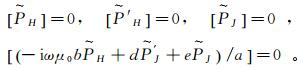
式中,[]表示标量位在界面两侧的变化。此外,由于在发射源附近垂直电流密度与水平磁场发生跳跃,依据文献[12, 20]可得标量位满足如下耦合关系:
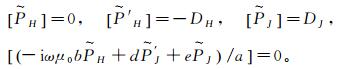
假定构成电偶极发射源的两个电极分别位于rA与rB处,则

式中: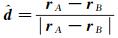
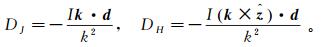
式中: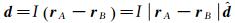
根据文献[23],我们可以计算由2个电偶极源所产生场的阻抗张量Z(上标x与y表示电偶源的方向),即
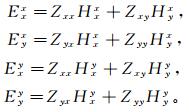
计算可得:
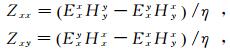
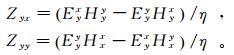
式中,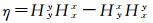
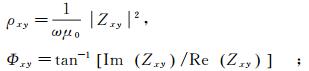 (10)
(10) 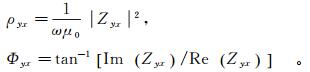 (11)
(11) 在各向异性介质中,上面定义的阻抗张量与各向异性主轴方向有关。为了利用这种相关性有效识别电各向异性,我们将其转换到极坐标系中。假设方位角φ=0时射线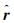
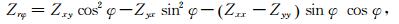 (12)
(12) 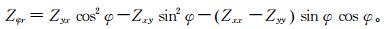 (13)
(13) 理论上,Zrφ等价于由径向电场与切向磁场所定义的阻抗张量,而Zφr等价于由切向电场和径向磁场所定义的阻抗张量。由这些新的张量元素,类似式(10)与式(11)我们可以进一步定义方位视电阻率
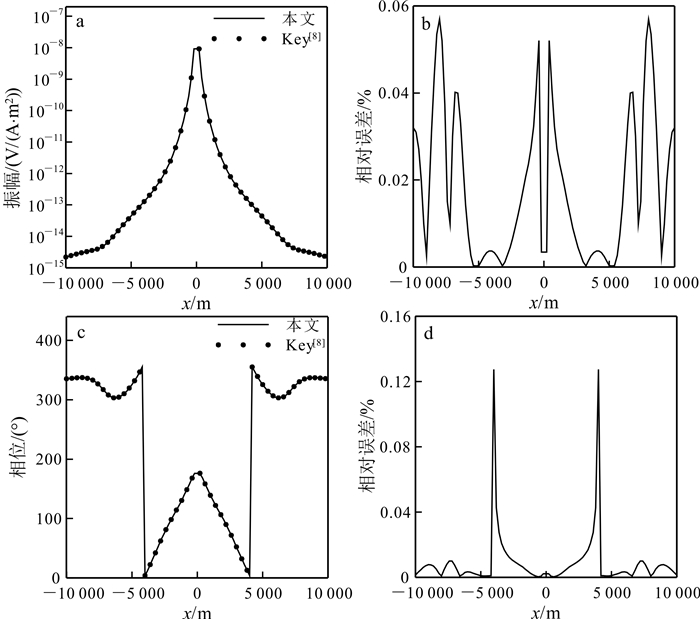
为了验证本文算法的正确性,我们首先选择20个各向同性交互薄层。假设交互层电阻率分别为7.464和0.536 Ω·m,每层厚度为1 m,则根据文献[24]可得到等价各向异性地层的纵向电阻率ρl=1 Ω·m,横向电阻率ρt=4 Ω·m。我们进一步假设海水电阻率为0.3 Ω·m,深度为1 000 m;海底为两层介质,上覆介质为厚度20 m的等价各向异性地层,下方为电阻率1 Ω·m的各向同性基岩。水平电偶极子位于海底上方30 m处,偶极矩为1 A·m,发射频率为0.25 Hz。图 1给出本文等价各向异性模拟算法和Key[8]各向同性模型算法的电磁响应对比结果。从图 1中可以看出,本文计算结果与Key[8]计算结果符合得很好,振幅最大相对误差不超过0.06%,相位最大相对误差不超过0.15%。
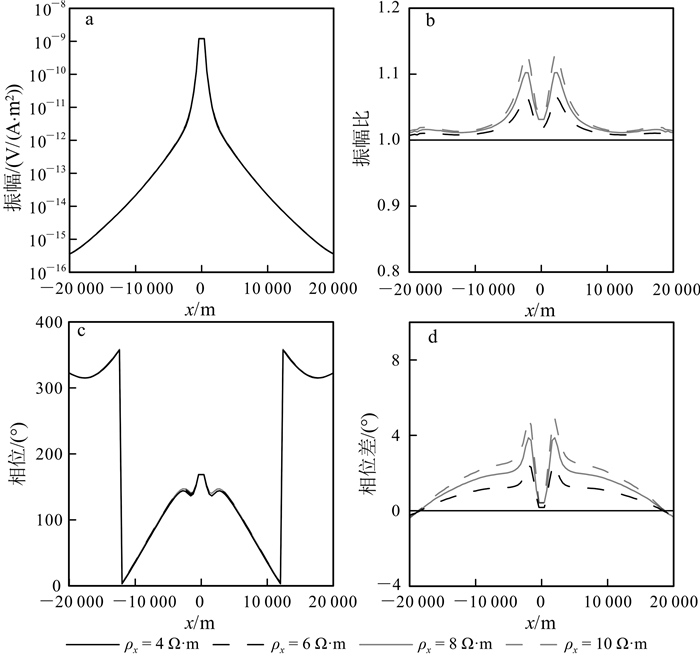
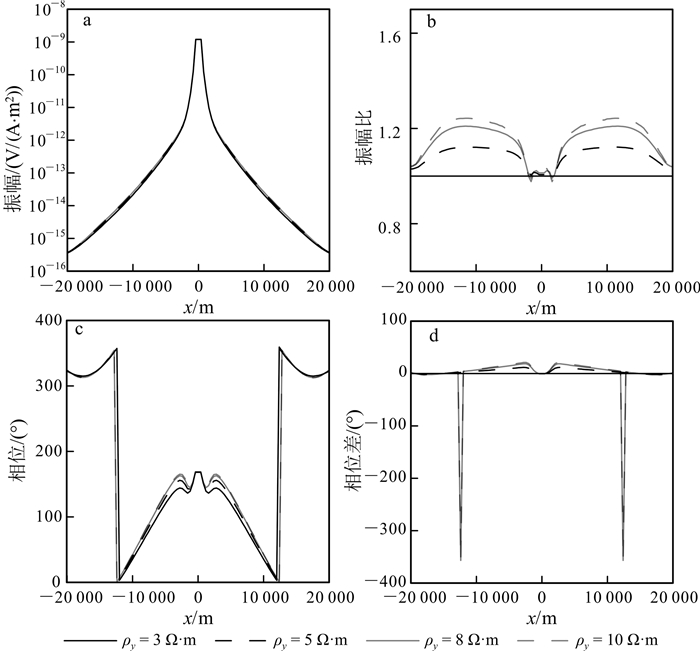
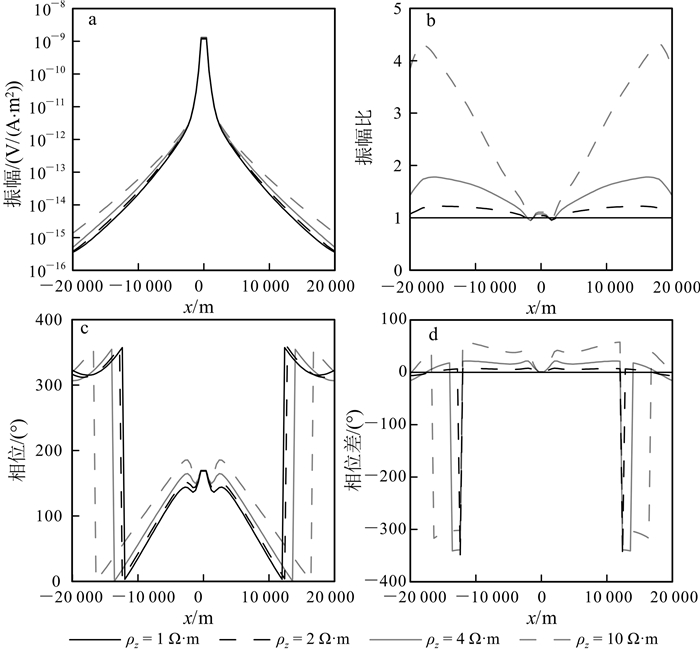
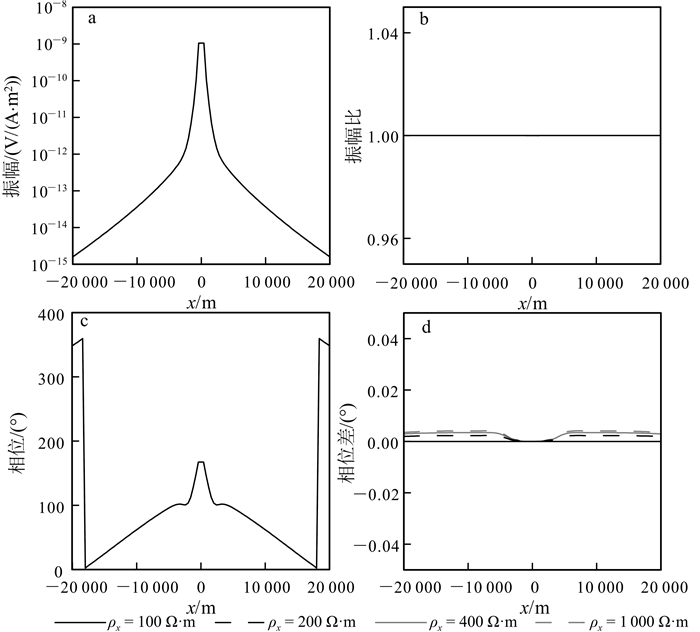
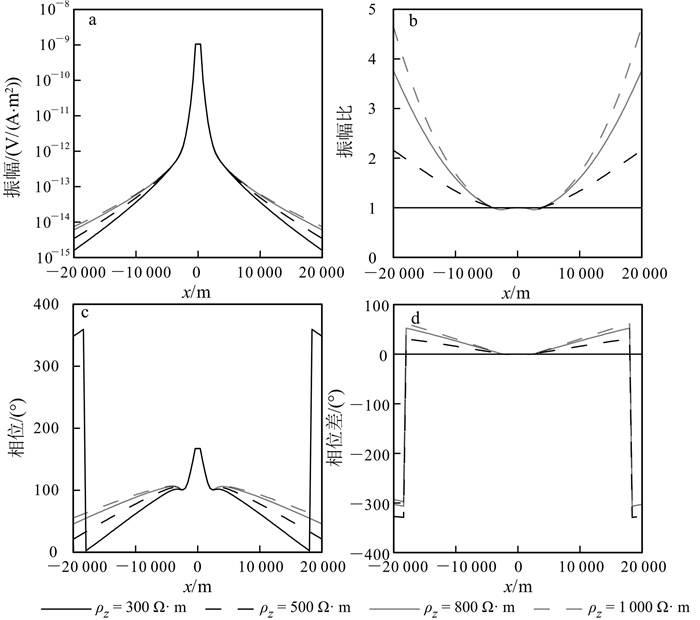
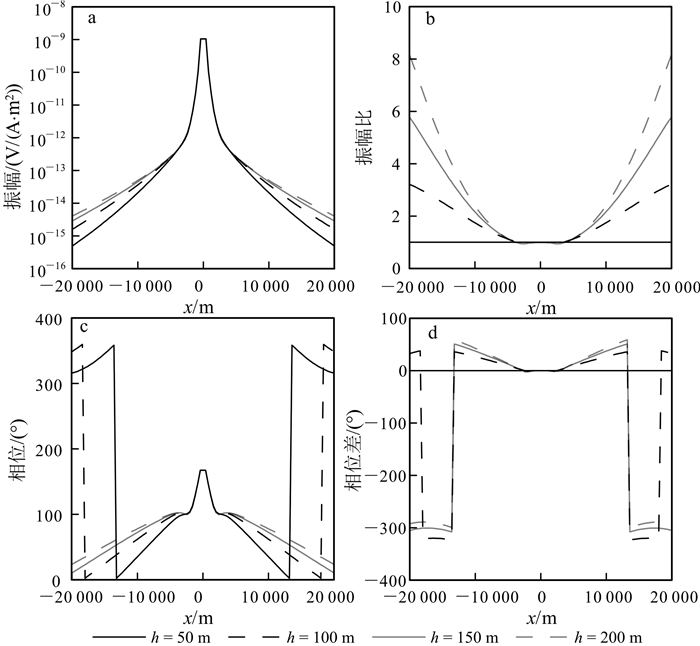
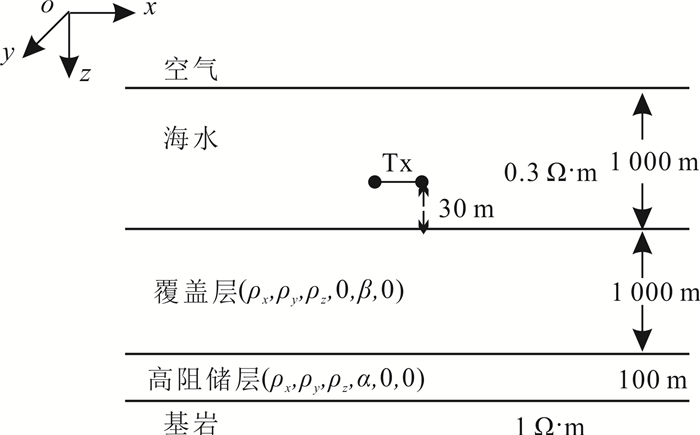
下面我们分析海底各向异性模型的电磁响应特征,并以此为基础进一步研究海底介质各向异性的识别方法。假设的模型如图 2所示。海水层电阻率为0.3 Ω·m,海水深度1 000 m;其下为厚度1 000 m的盖层;盖层下方为厚度100 m的高阻油气层;油气层下为各向同性基岩,电阻率为1 Ω·m。水平电偶极源(Tx)位于海底上方30 m处,偶极矩1 A·m,发射频率为0.25 Hz,接收机位于海底介质中。首先假设高阻层为各向同性,电阻率为100 Ω·m,覆盖层为三轴各向异性(triaxle anisotropy)。我们分析电阻率分别沿x,y和z方向发生变化时的海洋电磁响应特征。
|
| 图 2 海洋可控源电磁地电模型 Fig. 2 Marine CSEM model |
|
|
图 3—5给出了三轴各向异性覆盖层电阻率分别沿x,y,z方向发生变化时的电磁响应。可以看出:1)振幅曲线的中间部分直达波占主导,振幅比值在1左右,相位差接近于0;2)随收发距增加,地层波的影响在振幅和相位曲线上开始体现,地层各向异性影响得到明显反映;3)当振幅比达到极值时,导波的影响开始出现,上覆地层电阻率的变化造成高阻储层内场的激发强度不同,因而导波强度也随上覆地层的各向异性特征发生变化;4)当收发距很大时,振幅比值回归到1,相位差回归到0,说明此时空气波占主导地位。另外,对比图 3—5中的结果发现,覆盖层各向异性对海洋可控源电磁响应的影响显著,覆盖层电阻率沿水平和垂直方向的变化在海洋电磁响应上均有明显反映。这一现象说明可从海洋电磁响应中求解海底覆盖层的各向异性特征。
下面我们研究海底高阻储层各向异性对海洋电磁响应的影响特征。为此,假设覆盖层和基底半空间均为各向同性,电阻率为1 Ω·m,而高阻储层为三轴各向异性,电阻率分别沿x,y,z方向发生变化。图 6—8分别给出了三轴各向异性高阻储层电阻率分别沿x,y,z方向发生变化时的电磁响应。可以看出:虽然海洋可控源电磁对高阻储层十分敏感,但高阻储层水平方向电阻率的变化对海洋电磁响应影响很小,海洋电磁响应只对高阻储层的垂向电阻率敏感。此外,图 9还给出了模型电阻率相同但储层厚度变化时的海洋电磁响应。从图 9可以看出,电场响应明显受储层厚度的影响。上述发现可从物理上给出合理解释。事实上,电磁信号在海底围岩介质中呈现常规的电磁扩散特征,因此介质电阻率沿各方向的变化均可引起电磁响应的变化。然而,由于海底高阻层中电磁信号呈现导波特征,电磁响应仅与介质波导特性(垂向电阻率及厚度)有关。因此,虽然海洋可控源电磁能够有效反映海底高阻层的存在,但仅能有效反映高阻储层垂向电阻率和厚度的变化。
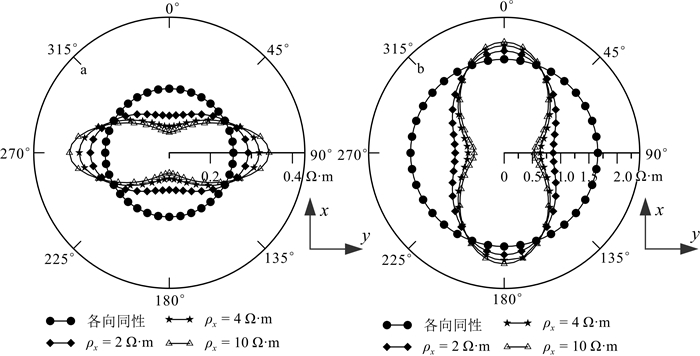
由前节的讨论可知,地层波主要出现在小收发距处,这部分信号携带了覆盖层的信息,若能合理利用就能确定介质的各向异性特征。为此,我们提出一种定性识别各向异性特征的方法——极性图法。假设海水层电阻率为0.3 Ω·m,海水深度1 000 m。其下为厚度1 000 m的直立各向异性盖层,ρy=ρz=1 Ω·m,电阻率在x方向发生变化。高阻储层为各向同性,电阻率为100 Ω·m,各向同性基岩电阻率为1 Ω·m。依据式(12)与式(13)我们得到极坐标下的阻抗张量,进而计算出视电阻率ρφra与ρrφa。
图 10展示了收发距r0=4 000 m时,海底各向异性盖层上视电阻率ρφra与ρrφa的方位分布特征。图 10中从原点到各测点连线的长度表示视电阻率大小,连线的方向表示观测的水平电场或磁场方向;笛卡尔坐标系的x轴沿0°方向,y轴沿90°方向。从图 10可以看出,各向同性模型表面视电阻率ρφra与ρφra的分布均为圆形,说明视电阻率不随观测方向发生变化。相比之下,各向异性覆盖层表面ρrφa和ρφra相互正交,均有效地反映了各向异性电阻率的变化特征。然而,ρrφa呈现各向异性的反常现象(anisotropic paradox),即计算的视电阻率最大值和最小值分别对应于最小和最大主轴电阻率。
|
| 图 10 海底覆盖层x方向电阻率变化时MCSEM视电阻率ρrφa(a)和ρφra(b)极性图 Fig. 10 Polar plots of apparent resistivities ρrφa(a) and ρφra(b) for a three-layer earth under the ocean with an anisotropic overburden whose resistivity changes in x direction |
|
|
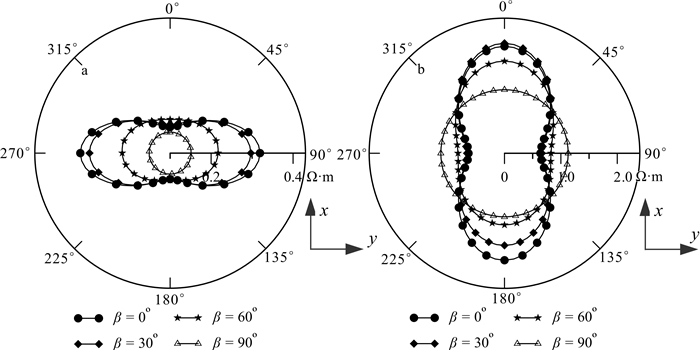
我们再考虑一种更为复杂的各向异性情况:直立各向异性盖层(ρx=4 Ω·m,ρy=ρz=1.0 Ω·m)绕y轴旋转(β分别为0°、30°、60°与90°)。我们计算了对应不同旋转角度时视电阻率ρrφa与ρφra随方位角的变化。由图 11可以看出,海底直立各向异性盖层发生倾斜时,ρrφa与ρφra受倾角影响异常变小,直到β=90°时,异常体呈现水平各向同性,ρrφa与ρφra均为圆形分布。另外,图 11中同样可以看出ρrφa的各向异性的反常现象及ρrφa与ρφra的正交特征。
|
| ρx=4Ω·m, ρy=ρz=1Ω·m。 图 11 倾斜各向异性盖层MCSEM视电阻率ρrφa(图a)与ρφra(图b)极性图 Fig. 11 Polar plots of MCSEM apparent resistivities ρrφa(a) and ρφra(b) for a three-layer earth under the ocean with a diopping anisotropic overburden |
|
|
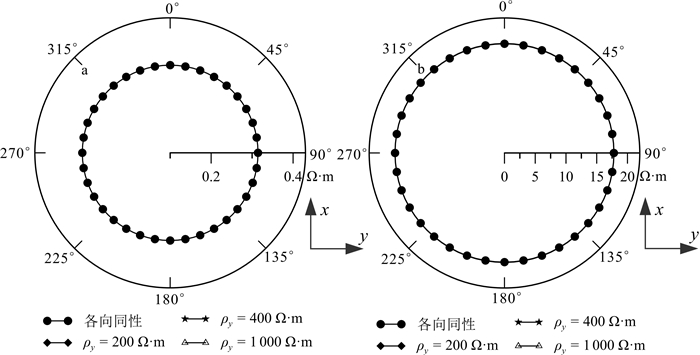
为进一步验证前述关于海洋可控源电磁法对海底介质中高阻储层各向异性识别能力的结论,我们计算了海底含直立各向异性高阻层模型(ρx=ρz=100 Ω·m,ρy=100, 200, 400, 1 000 Ω·m)视电阻率ρrφa与ρφra在海底的分布特征。从图 12可以看出,海底高阻储层各向异性特征难以从极性图上识别。
|
| 图 12 海底介质中含有直立各向异性高阻储层MCSEM视电阻率ρrφa(a)和ρφra(b)极性图(电阻率沿y方向变化) Fig. 12 Polar plots of MCSEM apparent resistivities ρrφa(a) and ρφra(b) for a three-layer earth with an anisotropic reservoir whose resistivity changes in y direction |
|
|
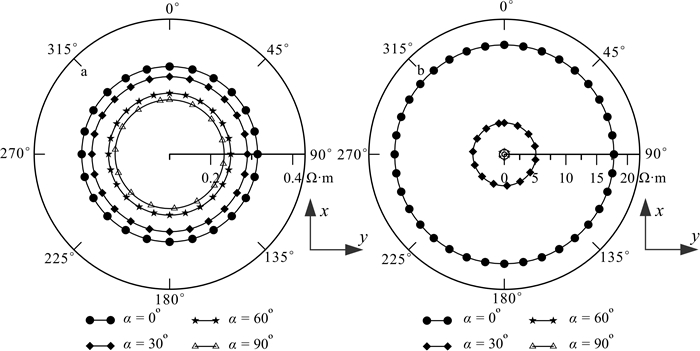
下面我们再考虑直立各向异性高阻层(ρx=ρz=100 Ω·m, ρy=400 Ω·m)绕x轴旋转(α分别为0°、30°、60°和90°)的情况。我们计算了对应不同旋转角度时视电阻率ρrφa与ρφra随方位角的变化。从图 13可以看出,当高阻层为倾斜各向异性时,ρrφa和ρφra幅值均受各向异性倾角的影响,然而从ρrφa和ρφra的分布特征无法识别高阻储层的各向异性特征。结合前述对海底介质含各向异性高阻储层电场响应特征的研究,可得出如下结论:由于电磁场在高阻层中的导波特征,海洋可控源电磁对海底高阻各向异性储层沿水平方向的电性变化不敏感,因此,海底高阻储层的各向异性特征难以识别。
|
| ρy=400Ω·m, ρx=ρz=100Ω·m。 图 13 高阻储层倾斜各向异性时MCSEM视电阻率ρrφa(a)与ρφra(b)极性图 Fig. 13 Polar plots of MCSEM apparent resistivities ρrφa(a) and ρφra(b) for a three-layer earth under the ocean with a dipping anisotropic reservoir |
|
|
本文基于各向异性电磁场理论和场延拓算法对海洋各向异性地层可控源电磁响应进行模拟研究,通过分析海底各向异性介质的电磁响应特征可得出如下结论:
1) 海底覆盖层各向异性特征可以通过极性图的方式进行定性识别,但需要注意各向异性反常现象。当海底介质为水平各向同性时,由于介质电性沿水平方向不发生变化,此时介质中的电磁场在水平面内呈现圆形极化,虽然海洋电磁响应会受各向异性影响,但从极性图上难以识别其各向异性特征。
2) 由于电磁信号在高阻介质中的导波特征,海洋可控源电磁对高阻储层沿水平方向的各向异性不敏感,仅对高阻层的垂向电阻率和厚度变化敏感。
3) 由于各向异性对海洋可控源电磁响应有着明显的影响,考虑到海底良好的沉积环境,地层层理发育,因此在进行海洋电磁数据处理解释时,应充分考虑各向异性的影响。
| [1] |
Cagniard L. Basic Theory of the Magnetotelluric Mehod of Geophysical Prospecting[J]. Geophysics, 1953, 18(3): 605-635. DOI:10.1190/1.1437915 |
| [2] |
Bannister P R. Determination of the Electrical Conduc-tivity of the Sea Bed in Shallow Waters[J]. Geophysics, 1968, 33(6): 995-1003. DOI:10.1190/1.1439993 |
| [3] |
Cox C. Electromagnetic Induction in the Oceans and Inferences on the Constitution of the Earth[J]. Geophysical Surveys, 1980, 4: 137-156. DOI:10.1007/BF01452963 |
| [4] |
李桐林, 林君, 刘福春, 等. 国内外海洋大地电磁测深的发展综述[J]. 国外地质勘探技术, 1998, 4: 1-10. Li Tonglin, Lin Jun, Liu Fuchun, et al. Review on Marine Magnetotellric Techolonogy and Developments[J]. Foreign Geoexploration Techolonogy, 1998, 4: 1-10. |
| [5] |
Eidesmo T, Ellingsrud S, Macgregor L, et al. Sea Bed Logging (SBL), a New Method for Remote and Direct Identification of Hydrocarbon Filled Layers in Deepwater Areas[J]. First Break, 2002, 20(3): 144-152. |
| [6] |
Constable S, Weiss C J. Mapping Thin Resistors and Hydrocarbons with Marine EM Methods:Insights from 1D Modeling[J]. Geophysics, 2006, 71(2): G73-G51. DOI:10.1190/1.2187788 |
| [7] |
Zhao L X, Geng J H, Zhang S Y, et al. 1-D Controlled Source Electromagnetic Forward Modeling for Marine Gas Hydrates Studies[J]. Applied Geophysics, 2008, 5(2): 121-126. DOI:10.1007/s11770-008-0012-8 |
| [8] |
Key K. 1D Inversion of Multicomponent, Multifre-quency Marine CSEM Data:Methodology and Synthetic Studies for Resolving Thin Resistive Layers[J]. Geophysics, 2009, 74(2): F9-F20. DOI:10.1190/1.3058434 |
| [9] |
Silva Crepaldi J L, Pereira Buonora M P, Figueiredo I. Fast Marine CSEM Inversion in the CMP Domain Using Analytical Derivatives[J]. Geophysics, 2011, 76(5): F303-F313. DOI:10.1190/geo2010-0237.1 |
| [10] |
Streich R, Becken M. Electromagnetic Fields Generated by Finite-Length Wire Sources:Comparison with Point Dipole Solutions[J]. Geophysical Prospecting, 2011, 59(2): 361-374. DOI:10.1111/gpr.2011.59.issue-2 |
| [11] |
Everett M E, Constable S. Electric Dipole Fields over an Anisotropic Seafloor:Theory and Application to the Structure of 40Ma Pacific Ocean Lithosphere[J]. Geophysical Journal International, 1999, 136(1): 41-56. DOI:10.1046/j.1365-246X.1999.00725.x |
| [12] |
Yin C. MMT Forward Modeling for a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2006, 71(3): G115-G128. DOI:10.1190/1.2197492 |
| [13] |
Løseth L O, Ursin B. Electromagnetic Fields in Planarly Layered Anisotropic Media[J]. Geophysical Journal International, 2007, 170(1): 44-80. DOI:10.1111/gji.2007.170.issue-1 |
| [14] |
Kong F N, Johnstad S E, Rosten T, et al. A 2.5D Finite-Element-Modeling Difference Method for Marine CSEM Modeling in Stratifief Anisotropic Media[J]. Geophysics, 2008, 73(1): F9-F19. DOI:10.1190/1.2819691 |
| [15] |
Newman G A, CommerM, Carazzone J J. Imaging CSEM Data in the Presence of Electrical Anisotropy[J]. Geophysics, 2010, 75(2): F51-F61. DOI:10.1190/1.3295883 |
| [16] |
刘云鹤, 殷长春, 翁爱华, 等. 海洋可控源电磁法发射源姿态影响研究[J]. 地球物理学报, 2012, 55(8): 2757-2768. Liu Yunhe, Yin Changchun, Weng Aihua, et al. Attitude Effect for Marine CSEM System[J]. Chinese Journal of Geophysics, 2012, 55(8): 2757-2768. |
| [17] |
殷长春, 贲放, 刘云鹤, 等. 三维任意各向异性介质中海洋可控源电磁法正演研究[J]. 地球物理学报, 2014, 57(12): 4110-4122. Yin Changchun, Ben Fang, Liu Yunhe, et al. MCSEM 3D Modeling of Arbitrarily Anisotropy Media[J]. Chinese Journal of Geophysics, 2014, 57(12): 4110-4122. DOI:10.6038/cjg20141222 |
| [18] |
贲放, 刘云鹤, 黄威, 等. 各向异性介质中的浅海海洋可控源电磁响应特征[J]. 吉林大学学报(地球科学版), 2016, 46(2): 581-593. Ben Fang, Liu Yunhe, Huang Wei, et al. MCSEM Response for Anisotropic Media in Shallow Water[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(2): 581-593. |
| [19] |
Yin C. Geoelectrical Inversion for a One-Dimensional Anisotropic Model and Inherent Non-Uniqueness[J]. Geophysical Journal International, 2000, 140(1): 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |
| [20] |
Yin C, Maurer H M. Electromagnetic Induction in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2001, 66(5): 1405-1416. DOI:10.1190/1.1487086 |
| [21] |
Bronstein I N, Semendjajew K. Taschenbuch der Mathematik[M]. Leipzig: Teubner Verlagsgesellschaft and Nauka-Verlag, 1979.
|
| [22] |
Yin C, Zhang P, Cai J. Forward Modeling of Marine DC Resistivity Method for a Layered Anisotropic Earth[J]. Applied Geophysics, 2016, 13(2): 279-287. DOI:10.1007/s11770-016-0560-2 |
| [23] |
Li X, Pedersen L B. The Electromagnetic Response of an Azimuthally Anisotropic Half-Space[J]. Geophy-sics, 1991, 56(9): 1462-1473. |
| [24] |
Yin C, Hodges G.Identification of Electrical Anisotropy from Helicopter EM Data[C]//SAGEEP 2003: Proceedings of the Symposium on the Application of Geophysics to Engineering and Environmental Problems.San Antonio: [s.n.], 2003: 419-431.
|