0 引言
局部重力场精化是物理大地测量学的基本任务之一。近年来,随着科技的发展和测量手段的增多,人类可获取的重力场信息越来越丰富,包括地面/海洋重力测量、航空重力测量、卫星测高等。其中地面重力测量有易测量、精度高、分布灵活和涵盖重力场频域广等优点,被广泛应用于局部重力场建模以及模型精度评估等领域[1]。如何利用地面实测数据建立高精度的局部重力场模型成为当今研究的热点问题。径向基函数(radial basic function)是一种局部重力场的参数化描述,在空间域和频率域都有较好的局部化特征,被广泛用于局部重力场建模[2]。其中包括点质量核径向基函数(point-mass kernel)[3]、径向多极函数(radial multipoles)[4]、泊松小波径向基函数(poisson wavelets)[5]等。点质量核径向基函数由于其结构简单、建模方便等优点得到较为广泛的应用[6-7]。但是当直接利用离散的实测数据进行重力场建模时,设计矩阵严重病态,无法进行稳定求解。所以传统点质量核径向基函数建模过程中需要对实际的离散观测值进行格网化处理, 以消除设计矩阵的病态性,此过程会引入新的误差,而且观测噪声对解的影响会被放大。
针对以上情况,本文试图建立一种直接利用离散数据进行点质量核径向基函数建模的方法,将Tikhonov正则化方法引入到点质量核径向基函数建模过程中,以抑制设计矩阵的病态性。
1 点质量核径向基函数为突出地球重力场的局部化特性,在建模过程中采用“移去-恢复”思想,当不考虑地形、大气等因素的影响时,扰动位全波段信息可以表示为
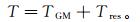 (1)
(1) 式中:TGM为重力场信号的长波部分,可以通过低阶重力场模型进行模拟;Tres为残余扰动位,需要利用残余重力场信息进行逼近。
在利用径向基函数进行建模时,点x处的残余扰动位Tres(x)就可以用基函数Ψ的线性组合进行表示,且该函数在Bjerhanmmar球外部满足调和特性[8]:
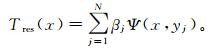 (2)
(2) 式中:βj为径向基函数系数;yj表示第j个径向基函数的位置。径向基函数在极坐标系下的球谐展开式为
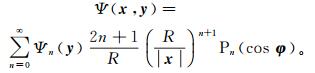 (3)
(3) 式中:|x| < R;|y|>R;Pn为n阶勒让德多项式;φ向量为x与y之间球心角矩;Ψn是n阶勒让德系数;R是Bjerhanmmar球的半径。点质量核的勒让德系数定义为
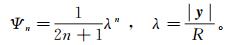 (4)
(4) 联立式(3)、(4)可以得到点质量核径向基函数的球谐展开形式:
 (5)
(5) 式中,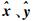
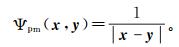 (6)
(6) 联立式(2)和式(6)可得
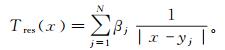 (7)
(7) 利用点质量核径向基函数进行局部重力场建模的关键在于β的确定。根据地表残余重力异常Δg与残余扰动位的关系,可得
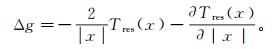 (8)
(8) 结合式(7)和式(8),并写成矩阵形式:
 (9)
(9) 矩阵A可由基函数与计算点的位置信息确定,其矩阵元素Aij可表示为
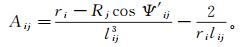 (10)
(10) 式中:ri和Rj分别表示重力异常点和基函数点到地心的距离;Ψ′ij和lij分别为两点的球心角和距离。最后基于最小二乘法可以求得矩阵β。
依据公式(9),在参数β的求解过程中,需要对设计矩阵A做求逆处理。但是离散分布的数据,尤其是多个实测数据分布很密时,就会导致设计矩阵中的多行或者多列参数类似,使设计矩阵的条件数较大,造成方程非适定。所以利用传统径向基函数建模时,一般要求建模数据与径向基函数分布在一定分辨率的格网上,这就保证了设计矩阵求逆过程是非奇异的,从而可以得到稳定、正确的解。
然而由于实际测量过程中的不确定性,很难保证实测数据的均匀分布。在测量环境恶劣的情况下,实测数据的精度很难得到保证。任何格网化实质是一个数据平滑的过程,这种处理方法使得实测数据在一定程度上损失高频信息;而且格网化过程中还会引入格网化误差,这种格网化误差会随着实测点中噪声的增大而增大。
2 Tikhonov正则化当直接利用离散的数据建模时,需要引入正则化方法来消除数据分布不合理造成的矩阵病态性。在多类正则化方法中,Tikhonov正则化方法对先验信息的要求较少,适用于重力场建模过程中的病态性处理[9]。
对公式(9)进行最小二乘求解时引入Tikhonov正则化方法,其正则化准则与正则化解[10]可写成:
 (11)
(11) 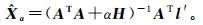 (12)
(12) 式中:l′表示误差方程自由项;Mα(X)为正则化准则参量;
对系数矩阵A做奇异值分解:
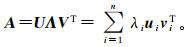 (13)
(13) 式中:U=[u1, u2, …, un]、V=[v1, v2, …, vn],分别为矩阵A的左右奇异值向量,且二者都为正交矩阵;Λ=diag[λ1, λ1,…, λn],并递减分布且大于0。联立式(9)和式(13)可得点质量核径向基函数的正则化谱分析形式:
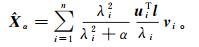 (14)
(14) 为确定最优的正则化系数,引入均方误差MSE:
 (15)
(15) 式中:E为数学期望;σ0为单位权中误差。
观察式(15)可得,合理地选取正则化参数α是MSE取最小值的关键。文献[11]研究发现,通过广义交叉检验(GCV)来确定最佳正则化参数是可行有效的,该函数被定义为
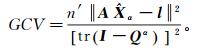 (16)
(16) 式中:Qα是影响矩阵;
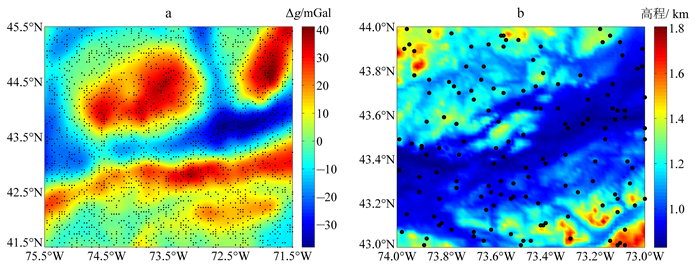
实验区位于美国阿巴拉契亚山脉,地形变化剧烈。以NGA(国家地理空间情报局)公布的EGM2008模型[13]进行模拟实验。将全频域模型计算得到的重力异常值作为实测值用于模型构建,得到的高程异常值作为真值进行模型检核。将截断到180阶的模拟值作为全球背景场,进而得到残余值。试验区内用于建模的残余重力异常信息与用于模型检核的高程分布如图 1所示,其统计信息见表 1。
|
| 图 1 试验区残余重力异常(a)及高程(b) Fig. 1 Residual gravity anomaly(a) and height (b) of experimental area |
|
|
| 试验区信息 | 残余重力异常/mGal | 残余高程异常/m |
| 最小值 | -35.490 0 | -0.578 0 |
| 最大值 | 36.124 1 | 0.296 7 |
| 均值 | 3.007 0 | -0.231 4 |
| 均方差 | 13.609 8 | 0.234 3 |
直接利用传统的点质量核径向基函数建模。即当建模数据呈现如图 1a分布时,利用标靶思路分别循环分辨率和埋深,设定不同参数下的模型结构,统计传统非去奇异方法在不同模型参数情况下的设计矩阵条件数(模型构造参数参考文献[14]),结果见图 2。

|
| 图 2 不同参数下设计矩阵条件数 Fig. 2 Condition numbers of the design matrix under different parameters |
|
|
分析图 2数据,当基函数较多,或者基函数埋深较浅时,设计矩阵A的条件数都大于矩阵的病态临界值1 000;此时求逆过程是一个信号放大的非平稳过程,得到的解是不可靠的,计算结果会引起千米级的偏差,而且解对观测误差极其敏感,即方程的解是不稳定的。
图 2中部分模型结构条件下设计矩阵的条件数虽然小于1 000;但是此时基函数埋深较深,而且基函数分辨率较大,基函数描述的只是残余重力场的中频部分,无法对重力场参量的短波分量进行精细描述,此种模型结构也是不可取的。
3.3 建模精度分析Kriging方法是一种基于局部加权思想的格网化方法,可以有效利用局部点位特征信息,在实际生产中得到广泛应用[15-16]。本节利用Kriging法对实测数据进行格网化处理,并将其作为对比试验。
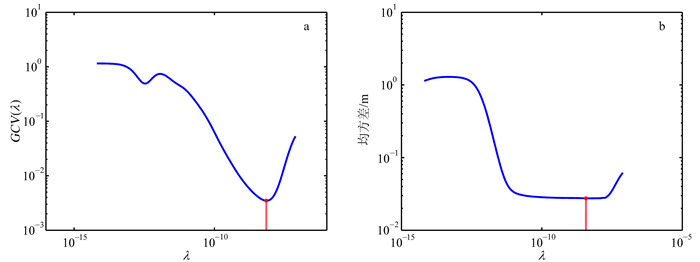
本文将Tikhonov正则化方法引入到点质量核径向基函数建模中,以上述实验数据为基础,模型参数设置为埋深10 km,平面分辨率为6′。统计不同正则化参数下公式(14)中的GCV值,以及相应的建模误差,如图 3所示。
|
| 图 3 不同正则化系数对应GCV值(a)及模型误差(b) Fig. 3 GCV values (a) and model errors (b) under different regularization parameters |
|
|
由图 3a发现:当正则化系数取3.697×10-9时,GCV值达到最小值。此时利用该值进行点质量核径向基函数建模,得到的模型精度最好。这验证了当GCV最小时,确定的正则化系数为最优。图 3b中当正则化系数在最优值的某一个区间内(4.059×10-10~1.750×10-8),模型精度波动小于1 mm。
为研究该区域最佳的基函数网格结构,采用“标靶”思想进行实验,基函数深度变化范围为1~46 km,步长5 km;空间分辨率为6′~33′,步长3′。并利用该区域离散分布的残余高程异常数据进行实验,从而确定最佳的网格设计。
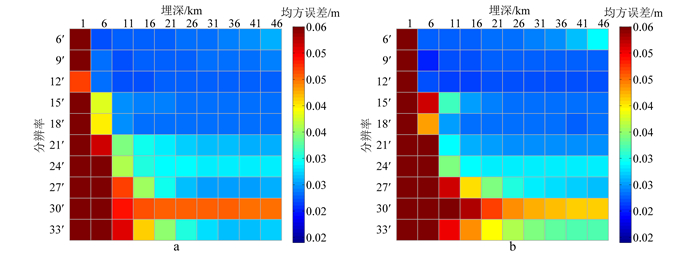
利用传统的格网化方法作为对比试验(格网化方法采用Kriging法),得到不同模型参数下的实验结果见图 4a、表 2,本文提出的正则化方法计算结果见图 4b、表 3,图 5、表 4统计了两种模型在最优结构下检核点的精度。
|
| 图 4 格网化方法(a)与正则化方法(b)均方误差 Fig. 4 Model error based on gridding method (a) and regularization method (b) |
|
|
| m | |||||||||||
| 分辨率 | 埋深/km | ||||||||||
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | ||
| 6′ | 0.115 5 | 0.027 2 | 0.027 4 | 0.027 7 | 0.027 9 | 0.028 1 | 0.028 4 | 0.028 8 | 0.029 4 | 0.030 7 | |
| 9′ | 0.081 5 | 0.028 2 | 0.027 3 | 0.027 6 | 0.027 7 | 0.027 9 | 0.028 1 | 0.028 3 | 0.028 5 | 0.028 9 | |
| 12′ | 0.051 7 | 0.028 2 | 0.026 9 | 0.027 2 | 0.027 4 | 0.027 5 | 0.027 6 | 0.027 7 | 0.027 7 | 0.027 7 | |
| 15′ | 0.081 1 | 0.043 1 | 0.029 3 | 0.029 0 | 0.028 8 | 0.028 6 | 0.028 6 | 0.028 5 | 0.028 5 | 0.028 5 | |
| 18′ | 0.062 1 | 0.044 9 | 0.029 5 | 0.028 2 | 0.028 1 | 0.028 1 | 0.028 2 | 0.028 3 | 0.028 4 | 0.028 5 | |
| 21′ | 0.079 4 | 0.056 3 | 0.038 9 | 0.034 8 | 0.033 3 | 0.032 4 | 0.031 8 | 0.031 3 | 0.031 1 | 0.031 0 | |
| 24′ | 0.078 7 | 0.060 9 | 0.040 8 | 0.035 1 | 0.034 1 | 0.033 8 | 0.033 7 | 0.033 7 | 0.033 7 | 0.033 7 | |
| 27′ | 0.075 2 | 0.067 5 | 0.051 7 | 0.040 7 | 0.034 6 | 0.031 7 | 0.030 5 | 0.030 3 | 0.030 4 | 0.030 8 | |
| 30′ | 0.081 7 | 0.067 2 | 0.053 9 | 0.051 2 | 0.050 9 | 0.050 9 | 0.050 7 | 0.050 5 | 0.050 2 | 0.050 0 | |
| 33′ | 0.071 1 | 0.067 5 | 0.055 9 | 0.046 4 | 0.039 7 | 0.035 4 | 0.032 9 | 0.031 7 | 0.031 5 | 0.031 9 | |
| m | ||||||||||
| 分辨率 | 埋深/km | |||||||||
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | |
| 6′ | 0.137 5 | 0.027 4 | 0.027 6 | 0.027 9 | 0.028 2 | 0.028 5 | 0.029 0 | 0.029 8 | 0.031 3 | 0.034 0 |
| 9′ | 0.082 0 | 0.025 4 | 0.027 2 | 0.027 3 | 0.027 5 | 0.027 6 | 0.027 7 | 0.027 8 | 0.027 8 | 0.027 9 |
| 12′ | 0.082 0 | 0.027 2 | 0.026 1 | 0.026 3 | 0.026 7 | 0.026 9 | 0.027 1 | 0.027 2 | 0.027 2 | 0.027 1 |
| 15′ | 0.082 0 | 0.056 6 | 0.036 6 | 0.030 0 | 0.028 8 | 0.028 5 | 0.028 4 | 0.028 4 | 0.028 5 | 0.028 5 |
| 18′ | 0.082 0 | 0.048 0 | 0.029 9 | 0.028 2 | 0.028 1 | 0.028 1 | 0.028 1 | 0.028 0 | 0.027 9 | 0.028 0 |
| 21′ | 0.082 0 | 0.075 8 | 0.034 2 | 0.031 1 | 0.030 2 | 0.029 8 | 0.029 5 | 0.029 4 | 0.029 4 | 0.029 5 |
| 24′ | 0.082 0 | 0.064 2 | 0.039 4 | 0.034 0 | 0.033 1 | 0.033 2 | 0.033 4 | 0.033 4 | 0.033 4 | 0.033 3 |
| 27′ | 0.082 0 | 0.078 1 | 0.056 7 | 0.045 3 | 0.038 9 | 0.035 4 | 0.033 5 | 0.032 5 | 0.031 9 | 0.031 7 |
| 30′ | 0.082 0 | 0.077 4 | 0.070 7 | 0.057 8 | 0.051 8 | 0.049 0 | 0.047 6 | 0.046 9 | 0.046 5 | 0.046 3 |
| 33′ | 0.082 0 | 0.063 5 | 0.055 3 | 0.048 5 | 0.044 0 | 0.041 1 | 0.039 2 | 0.038 1 | 0.037 5 | 0.037 4 |
|
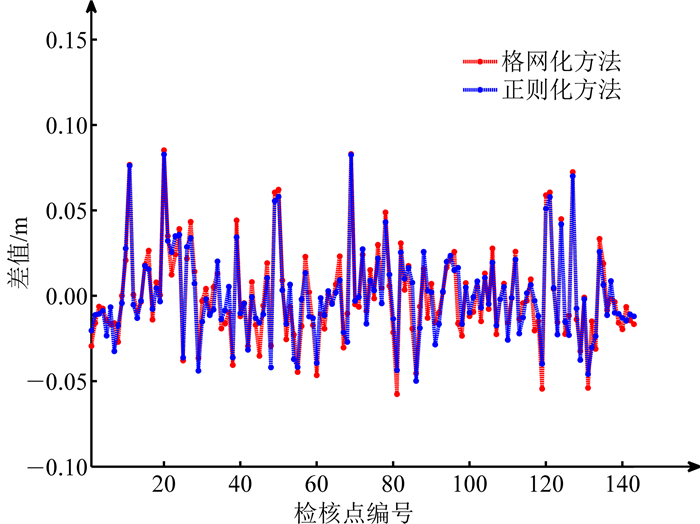
| 图 5 最优模型下两种模型与检核点的差值 Fig. 5 Two methods difference with the checking points for the optimal model structure |
|
|
| m | ||
| 方法 | 格网化方法 | 正则化方法 |
| 最大值 | 0.085 2 | 0.082 8 |
| 最小值 | -0.057 6 | -0.049 8 |
| 均值 | -0.012 9 | 0.011 7 |
| 均方差 | 0.026 1 | 0.025 3 |
上述两种方法的计算结果表明,点质量核径向基函数的逼近精度受到模型埋深以及分辨率的影响(图 4)。当空间分辨率一定时,基函数的建模精度随着埋深的增大呈现出先减小后增大的趋势;这说明当基函数的数量即平面分辨率确定后,埋深较浅(深),模型计算得到的残余高程异常主要贡献波段集中在高(低)频,无法对残余重力场元所在的波段(中高频)进行有效拟合。同时,埋深与基函数解的稳定性存在较强的关联:当埋深较浅时,解的稳定性得到一定的保障,但是当基函数数量较多(较少)时,会存在过度拟合(拟合不足)的问题,使其稳定性降低;反之,埋深过深,分辨率较高,即基函数数量较多会增加基函数的重叠程度,同时,较少的基函数无法对检核结果进行有效逼近,从而导致解的精度和稳定性变差。
从计算结果来看,正则化建模方法与传统的格网化方法之间的差异不大:在标靶实验中,正则化建模方法中最优的模型结构为埋深6 km、空间分辨率9′,此时模型恢复精度达到2.54 cm(表 3);传统格网化方法在深度11 km、埋深12′的条件下精度较好,达到2.69 cm(表 2)。当模型结构严重病态时(埋深过浅、过深;基函数过多、过少),格网化方法的建模精度比正则化方法稍好;在各自最优结构下,两种方法结果精度相当,正则化方法略优(图 5)。
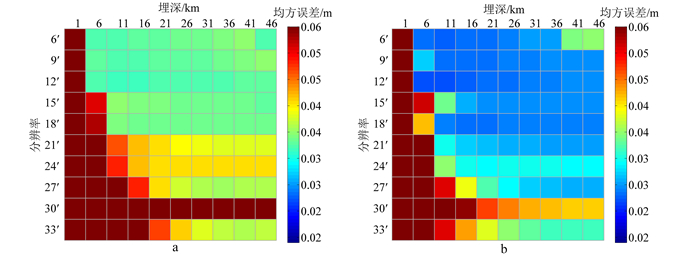
为验证两种方法的抗干扰能力,对原始数据加入系统误差0 mGal、均方差3 mGal的高斯白噪声,统计得到如下实验结果:图 6a、表 5为噪声下格网化方法的建模误差,图 6b、表 6代表噪声下正则化方法的建模精度,统计两种模型在最优结构下的精度分布见图 7、表 6。
|
| 图 6 加入白噪声后格网化法(a)和正则化方法(b)均方误差 Fig. 6 Gridding method (a) and regularization method (b) accuracy with white noise |
|
|
| m | ||||||||||
| 分辨率 | 埋深/km | |||||||||
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | |
| 6′ | 0.155 4 | 0.037 0 | 0.037 4 | 0.037 6 | 0.038 0 | 0.038 3 | 0.038 8 | 0.039 3 | 0.039 6 | 0.037 1 |
| 9′ | 0.121 4 | 0.038 1 | 0.037 1 | 0.037 4 | 0.037 6 | 0.037 9 | 0.038 2 | 0.038 6 | 0.039 1 | 0.039 9 |
| 12′ | 0.070 2 | 0.037 3 | 0.036 4 | 0.036 8 | 0.037 0 | 0.037 2 | 0.037 3 | 0.037 5 | 0.037 7 | 0.038 0 |
| 15′ | 0.105 4 | 0.055 8 | 0.039 5 | 0.039 3 | 0.038 9 | 0.038 7 | 0.038 5 | 0.038 4 | 0.038 3 | 0.038 2 |
| 18′ | 0.080 4 | 0.058 0 | 0.039 4 | 0.038 3 | 0.038 3 | 0.038 3 | 0.038 4 | 0.038 5 | 0.038 6 | 0.038 6 |
| 21′ | 0.104 5 | 0.072 9 | 0.051 4 | 0.047 0 | 0.045 6 | 0.044 6 | 0.043 8 | 0.043 3 | 0.042 9 | 0.042 8 |
| 24′ | 0.102 4 | 0.079 2 | 0.053 5 | 0.046 7 | 0.045 6 | 0.045 5 | 0.045 5 | 0.045 5 | 0.045 5 | 0.045 6 |
| 27′ | 0.096 6 | 0.087 3 | 0.067 2 | 0.053 4 | 0.045 8 | 0.042 2 | 0.040 8 | 0.040 6 | 0.040 8 | 0.041 3 |
| 30′ | 0.106 1 | 0.086 6 | 0.069 7 | 0.067 1 | 0.067 2 | 0.067 4 | 0.067 4 | 0.067 1 | 0.066 8 | 0.066 5 |
| 33′ | 0.091 9 | 0.087 0 | 0.072 3 | 0.060 5 | 0.051 9 | 0.046 3 | 0.043 1 | 0.041 6 | 0.041 3 | 0.041 9 |
| m | ||||||||||
| 分辨率 | 埋深/km | |||||||||
| 1 | 6 | 11 | 16 | 21 | 26 | 31 | 36 | 41 | 46 | |
| 6′ | 0.148 3 | 0.028 0 | 0.027 8 | 0.028 2 | 0.028 4 | 0.028 7 | 0.029 9 | 0.029 9 | 0.039 4 | 0.039 7 |
| 9′ | 0.082 0 | 0.032 3 | 0.028 0 | 0.028 4 | 0.028 6 | 0.028 8 | 0.029 1 | 0.029 3 | 0.029 5 | 0.029 8 |
| 12′ | 0.082 0 | 0.027 2 | 0.027 3 | 0.027 8 | 0.028 0 | 0.028 4 | 0.028 8 | 0.029 1 | 0.029 3 | 0.029 6 |
| 15′ | 0.082 0 | 0.056 6 | 0.038 6 | 0.031 1 | 0.029 7 | 0.029 4 | 0.029 3 | 0.029 4 | 0.029 6 | 0.029 8 |
| 18′ | 0.082 0 | 0.047 1 | 0.028 9 | 0.028 2 | 0.028 6 | 0.028 8 | 0.028 9 | 0.028 8 | 0.028 8 | 0.028 9 |
| 21′ | 0.082 0 | 0.075 7 | 0.034 6 | 0.032 1 | 0.031 3 | 0.030 9 | 0.030 6 | 0.030 4 | 0.030 3 | 0.030 5 |
| 24′ | 0.082 0 | 0.064 6 | 0.040 1 | 0.035 0 | 0.034 3 | 0.034 4 | 0.034 4 | 0.034 4 | 0.034 3 | 0.034 3 |
| 27′ | 0.082 0 | 0.077 9 | 0.055 7 | 0.043 7 | 0.037 5 | 0.034 2 | 0.032 4 | 0.031 5 | 0.031 1 | 0.030 9 |
| 30′ | 0.082 0 | 0.077 2 | 0.071 1 | 0.058 8 | 0.052 3 | 0.049 2 | 0.047 7 | 0.046 9 | 0.046 5 | 0.046 4 |
| 33′ | 0.082 0 | 0.078 5 | 0.055 6 | 0.048 0 | 0.043 2 | 0.040 1 | 0.038 1 | 0.036 9 | 0.036 4 | 0.036 4 |

|
| 图 7 噪声最优模型下两种模型与检核点的差值 Fig. 7 Two methods difference with the checking points for the optimal model structure under noise |
|
|
分析表 5、图 6a统计结果发现,在加入高斯白噪声之后,传统的格网化方法稳定性和精度都明显降低,而且当模型矩阵不稳定时,很小的扰动都会引起待估参数较大的波动。表 6、图 6b结果说明引入正则化方法之后,模型解的稳定性以及精度都显著提高,在相同的噪声水平下,相比于传统格网化建模方法,正则化建模方法的精度并未发生严重的损失;说明正则化方法可以一定程度上控制了观测误差对解的影响,模型结构更加稳定。由图 7、表 7可得,相对于传统的格网化方法,本文提出的正则化方法精度提升了约27.9%。
| m | ||
| 方法 | 格网化方法 | 正则化方法 |
| 最大值 | 0.107 8 | 0.086 5 |
| 最小值 | -0.082 7 | -0.053 9 |
| 均值 | -0.017 3 | 0.010 3 |
| 均方差 | 0.036 5 | 0.026 3 |
本文将Tikhonov正则化引入到点质量核径向基函数建模领域中,使得直接利用离散数据进行局部重力场建模成为可能。总结公式推理及实验结论可得如下结论:
1) 在基础数据无误差的情况下,本文提出的基于Tikhonov正则化方法的点质量核径向基函数方法精度与传统的格网化方法相当;这说明基于此方法直接利用离散点数据进行重力场建模是可行的。
2) 当实测数据被噪声干扰时,本文方法精度未受到大的损失,且建模精度优于传统格网化方法;这说明基于Tikhonov正则化方法的点质量核径向基函数能在一定程度上提高模型的稳定性。
3) 多种径向基函数的求解过程类似,本文所提方法对其他类型径向基函数建模流程具有一定的参考价值。
| [1] |
Moritz H. Advanced Physical Geodesy[M]. London: Abacus Press, 1980.
|
| [2] |
Tenzer R, Klees R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling[J]. Studia Geophysica et Geodaetica, 2008, 52(3): 287-304. DOI:10.1007/s11200-008-0022-2 |
| [3] |
Lehmann R. The Method of Free-Positioned Point Masses:Geoid Studies on the Gulf of Bothnia[J]. Bulletin Géodésique, 1993, 67(1): 31-40. DOI:10.1007/BF00807295 |
| [4] |
Bentel K, Schmidt M, Denby C R. Artifacts in Regional Gravity Representations with Spherical Radial Basis Functions[J]. Journal of Geodetic Science, 2013, 3(3): 173-187. |
| [5] |
吴怿昊, 罗志才, 周波阳. 基于泊松小波径向基函数融合多源数据的局部重力场建模[J]. 地球物理学报, 2016, 59(3): 852-864. Wu Yihao, Luo Zhicai, Zhou Boyang. The Approach of Regional Geoid Refinement Based on Combining Multi-Satellite Altimetry Observations and Heterogeneous Gravity Data Sets[J]. Chinese Journal of Geophysics, 2016, 59(3): 852-864. |
| [6] |
Antunes C, Pail R, Catalāo J. Point Mass Method Applied to the Regional Gravimetric Determination of the Geoid[J]. Studia Geophysica et Geodaetica, 2003, 47(1): 495-509. |
| [7] |
吴星, 张传定, 赵东明. 基于球面边值问题的点质量调和分析方法[J]. 地球物理学报, 2009, 52(12): 2993-3000. Wu Xing, Zhang Chuanding, Zhao Dongming. Point Mass Harmonic Analysis Method Based on Spherical Boundary Value Problem[J]. Chinese Journal of Geophysics, 2009, 52(12): 2993-3000. DOI:10.3969/j.issn.0001-5733.2009.12.008 |
| [8] |
Tenzer R, Klees R. The Choice of the Spherical Radial Basis Functions in Local Gravity Field Modeling[J]. Studia Geophysica et Geodaetica, 2008, 52(3): 287-304. DOI:10.1007/s11200-008-0022-2 |
| [9] |
邹贤才, 李建成. 最小二乘配置方法确定局部大地水准面的研究[J]. 武汉大学学报(信息科学版), 2004, 29(3): 218-222. Zou Xiancai, Li Jiancheng. A Local Geoid Determination Using Least-Squares Collocation[J]. Editorial Board of Geomatics & Information Science of Wuhan University, 2004, 29(3): 218-222. |
| [10] |
欧阳永忠, 邓凯亮, 黄谟涛, 等. 确定大地水准面的Tikhonov最小二乘配置法[J]. 测绘学报, 2012, 41(6): 804-810. Ouyang Yongzhong, Deng Kailiang, Huang Motao, et al. The Tikhonov-Least Squares Collocation Method for Determining Geoid[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(6): 804-810. |
| [11] |
孙中苗.航空重力测量理论、方法及应用研究[D].郑州: 信息工程大学, 2004. Sun Zhongmiao.Theory, Method and Application of Airborne Gravimetry[D].Zhengzhou: Information Engineering University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-90008-2005030005.htm |
| [12] |
沈云中, 许厚泽. 不适定方程正则化算法的谱分解式[J]. 大地测量与地球动力学, 2002, 22(3): 10-14. Shen Yunzhong, Xu Houze. Spectral Decomposition Formula of Regularization Solution for Ill-Posed Equation[J]. Journal of Geodesy & Geodynamics, 2002, 22(3): 10-14. |
| [13] |
Golsorkhi M S. The Development and Evaluation of the Earth Gravitational Model 2008(EGM2008)[J]. Journal of Geophysical Research, 2012, 117(B4): 531-535. |
| [14] |
Claessens S J, Featherstone W E, Barthelmes F. Experiences with Point-Mass Gravity Field Modelling in the Perth Region, Western Australia[J]. Journal of Geophysical Research Space Physics, 2001, 3(2): 342-348. |
| [15] |
李振海, 汪海洪. 重力数据网格化方法比较[J]. 大地测量与地球动力学, 2010, 30(1): 140-144. Li Zhenhai, Wang Haihong. Comparison Among Methods for Gravity Data Gridding[J]. Journal of Geodesy & Geodynamics, 2010, 30(1): 140-144. |
| [16] |
范雕, 李姗姗, 孟书宇, 等. 利用重力异常反演马里亚纳海沟海底地形[J]. 吉林大学学报(地球科学版), 2018, 48(5): 1481-1492. Fan Diao, Li Shanshan, Meng Shuyu, et al. Inversion of Mariana Trench Seabed Terrain Using Gravity Anomalies[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(5): 1481-1492. |


