0 引言
导数换算作为位场数据处理的重要部分,一直以来被广泛应用。导数结果不仅用来圈定局部异常、分离叠加异常,更是其他位场数据处理方法,如边界识别[1]、欧拉反褶积[2]、重力归一化总梯度[3]等方法必须的数据准备;导数的精度直接影响了这些方法的处理效果,从而影响对位场数据的解译。导数换算通常被认为是不稳定的,且阶次越高,导数换算越不稳定[4]。为此许多学者提出了一系列方法,这些方法大致分为三类。第一类为空间域方法,包括近似公式法[5-6]、有限元法[7]、样条函数法[8]等。第二类为波数域方法,包括常规算子法、向上延拓法、补偿圆滑滤波法[9]、正则化方法[4]、迭代法[10]以及正则化法与迭代法相结合的方法[11],其中向上延拓作为低通滤波,可通过上延小距离达到压制噪声的目的,提高导数换算精度。此外,类似于傅里叶变换的方法,如余弦变换法[12-13]、Hartley变换法[14]也被引入到导数计算中,这两种变换法只是减少了计算量,导数精度提高有限。第三类是空间域和波数域相结合的方法,如ISVD(integrated second vertical derivative)法[15],该方法利用空间域求导方法提高了导数精度,拓展了求解位场各阶垂向导数的方法。
Chebyshev滤波器是在一致意义上对理想滤波器的最佳逼近,具有良好的通带和阻带性能,在信号处理上有广泛应用[16]。本文提出Chebyshev低通滤波的位场任意阶导数换算方法,利用径向平均功率谱曲线确定滤波参数,使得该方法操作方便。
1 基本原理 1.1 Chebyshev低通滤波器导数换算在波数域中,位场数据的x、y、z 3个方向任意阶的导数换算公式可表示为
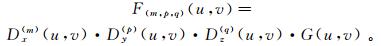 (1)
(1) 式中:G(u, v)和F(m, p, q)(u, v)分别表示位场原异常和其所求导数的波谱;Dx(m)(u, v)=(iu)(m)为x方向m阶导数算子;Dy(p)(u, v)=(iv)(p)为y方向p阶导数算子;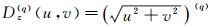
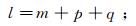 (2)
(2) 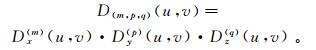 (3)
(3) 则式(1)变为
 (4)
(4) 由前人[4]研究得知,理论导数算子D(m, p, q)(u, v)属于高通滤波器,在导数换算过程中会放大高频噪声;导数阶次l越大,理论导数算子D(m, p, q)(u, v)的放大作用也越强,高频噪声干扰变强,会恶化导数计算结果。因此,需要附加一个低通滤波器来压制高频成分,增强导数换算过程的稳定性,提高求导结果精度。
Chebyshev低通滤波器是基于最佳一致逼近原理设计的一类滤波器。该滤波器在通带内频率响应幅度以等波纹形式波动,在过渡带衰减较快,与理想滤波器的频率响应曲线之间误差最小,能够在很好地保留有用信号的同时滤除无用信号。Chebyshev低通滤波器频率响应HN(ω)的公式为
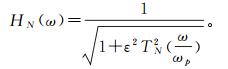 (5)
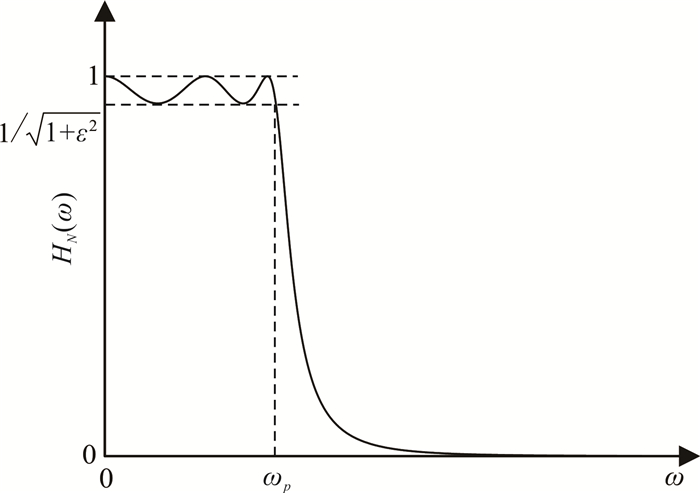
(5) 式中:ε为小于1的正数,表征通带内波纹振幅大小(图 1);N为滤波器阶次;
|
| 图 1 Chebyshev低通滤波器频率响应示意图 Fig. 1 Schematic diagram for the Chebyshev low-pass filter frequency response |
|
|
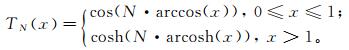 (6)
(6) 因此得到新的求导公式:
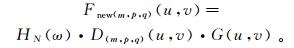 (7)
(7) 将Fnew(m, p, q)(u, v)进行傅里叶反变换,得到所求导数结果。
1.2 Chebyshev低通滤波器频率响应特性及参数选择为了分析Chebyshev低通滤波器的频率响应特性,我们分别计算了式(5)不同ε、N、ωp的频率响应曲线(图 2)。从图中可以看出:1)ε越大,通带的波动越大,会造成通带有用信号的损失加大(图 2a),因此在使用过程中ε取值应偏小,经过大量模型实验,文中选取ε=0.01即可满足计算;2)滤波器阶次N主要影响通带内波动的疏密,也影响过渡带的带宽,N越大,滤波器的衰减越快,N=15时和N=20时频率响应衰减已经差别不大(图 2b),因此文中选取N =15作为滤波参数;3)通带截止频率ωp主要控制滤波器的分频效果,小于ωp的有用成分被保留,大于ωp的高频噪声部分被压制(图 2c),其参数选取的好坏直接关系到导数换算结果的精度,因此,ωp作为本文方法的关键参数需要慎重选择。

|
| a. ε不同,N、ωp相同;b. N不同,ε、ωp相同;c. ωp不同,N、ε相同。 图 2 Chebyshev低通滤波器频率响应 Fig. 2 Frequency response of Chebyshev low-pass filter |
|
|
这里我们借鉴曾小牛等[4]提出的方法来选取截止频率ωp,其原理是通过分析位场异常的径向平均功率谱特征来确定ωp。一般来说位场信号的有用成分大部分保留在中低频部分,与位场异常信号不相关的噪声则表现为高频,在功率谱曲线图上存在一个转折点(ωp位置)将位场异常信号谱和噪声谱大致分开。对于噪声水平大的原始异常,其功率谱曲线的转折点较明显,易于确定截止频率参数;而对于噪声水平小或经过去噪预处理的原始异常,其功率谱曲线的转折点较难寻找,可适当添加高斯白噪声增加异常的噪声水平,从而利于确定ωp。
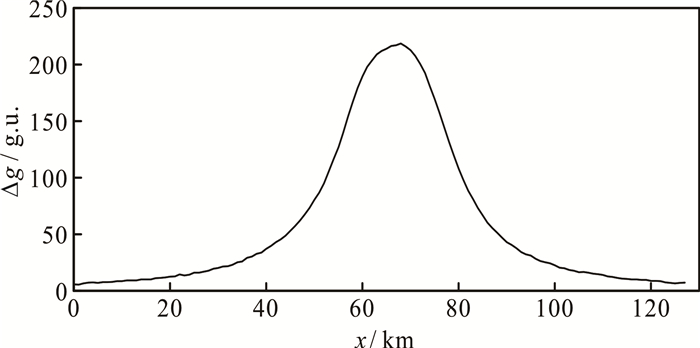
2 模型试验为了验证本文方法的有效性,首先设计了包含4个无限长水平圆柱体的二度体组合模型,模型参数见表 1,测线长127 km,点距为1 km。图 3是该模型体产生的理论重力异常添加均值为0 g.u.①、标准差为0.4 g.u.的高斯噪声之后的重力异常Δg。对该重力异常分别采用常规FFT(fast Fourier transformation)法、向上延拓法、ISVD法和本文方法计算水平一阶导数Δgx(m=1,p=q=0)、垂向一阶导数Δgz(m=p=0,q=1)和垂向二阶导数Δgzz(m=p=0,q=2),所求结果见图 4。为了对比的公平性,各方法均采用相同的扩边模式,并通过计算各方法处理结果与理论值的均方误差(RMSE)来衡量求导结果的好坏,其计算公式为
① g.u.(重力单位)为非法定计量单位,1 g.u. =10-6 m/s2,下同。
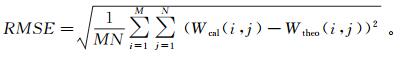 (8)
(8) | 地质体编号 | 圆柱体质心水平坐标/km | 横截面半径/km | 埋深/km | 剩余密度/(g/cm3) |
| 1 | (60,0) | 4.0 | 10.0 | 0.2 |
| 2 | (70,0) | 4.0 | 10.0 | 0.2 |
| 3 | (55,0) | 2.0 | 7.0 | -0.1 |
| 4 | (75,0) | 2.0 | 7.0 | 0.1 |
|
| 图 3 二度体模型含噪声重力异常 Fig. 3 Noisy gravity anomaly of 2D model |
|
|
|
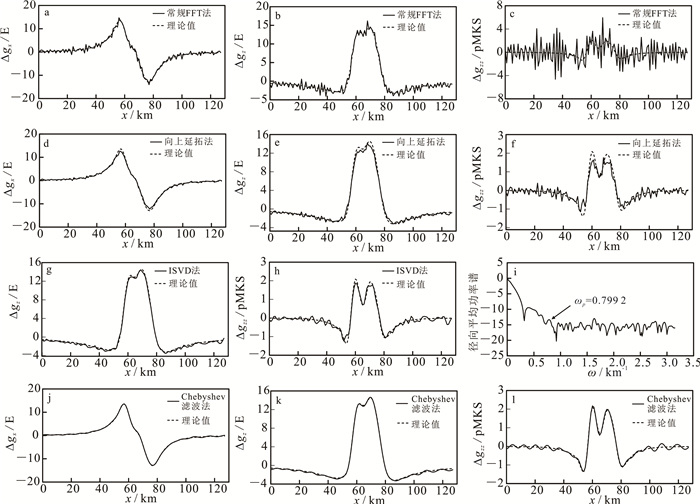
| E(厄缶)为非法定计量单位,1 E=10-9 s-2,下同;1 pMKS=10-12 (m·s2)-1,下同。 图 4 二度体模型求导结果 Fig. 4 Derivatives of 2D model |
|
|
式中:Wcal(i, j)和Wtheo(i, j)分别表示求导结果和导数理论值;M,N为行列计算点数。
图 4a—c为常规FFT法计算的水平一阶、垂向一阶和垂向二阶导数。从图 4a—c中可知,常规FFT法的求导过程对高频噪声没有压制,其求导结果存在明显的振荡,与理论值的均方误差最大(表 2),而且导数阶次越高,计算稳定性越差,求导结果振荡的越强烈,垂向二阶导数(图 4c)已经无法识别出有效异常。图 4d—f为向上延拓法计算的导数,可以看出,在压制高频噪声的同时,异常的幅值也被压制,导致其计算结果精度降低。由于ISVD法只能计算垂向导数,这里我们只计算了垂向一阶导数(图 4g)和垂向二阶导数(图 4h),可以看出,ISVD法由于计算中利用了空间域方法计算水平导数,其求得的垂向导数精度很高,而其垂向二阶导数与理论值的误差较其垂向一阶导数与理论值的误差变大,这是由于ISVD法计算导数需要利用前一阶导数,误差具有累积效应。图 4j—l为Chebyshev滤波法计算的导数,依据图 4i中功率谱确定的滤波截止频率0.779 2,计算得到水平一阶和垂向一阶导数与理论值的差别不大,其均方根误差最小(表 2);垂向二阶导数结果较其他方法计算的结果更接近理论值,只是在边界处有振荡。另外,由于本文方法不同阶次的导数均采用同样的截止频率,且都是以原始异常为基础经一步计算得到,不存在误差的累积;这说明本文方法计算的导数不仅能有效地降低噪声的影响,还能保证计算结果有较其他方法更高的精度。
为了说明截止频率对本文方法导数计算结果的影响,我们选取图 4i中截止频率0.779 2周围的3个截止频率0.5,1.0和1.5对图 3重力异常进行垂向二阶导数计算,其结果见图 5。可以看出,当ωp=0.5时,垂向二阶导数结果较圆滑,主体异常(60 km处)幅值被压制(图 5a);当ωp=1.0时,求导结果与图 4l中结果相近,主体异常处的导数结果计算较好(图 5b);当ωp=1.5时,垂向二阶导数曲线抖动加剧,甚至影响了主体异常(图 5c)。这说明:在截止频率取值接近0.779 2时(如ωp=1.0),导数计算结果既能很好地突出主体异常,又能降低噪声干扰的影响;小于这一截止频率(如ωp=0.5),噪声被压制的同时,有用信号也会损失; 大于这一截止频率(如ωp=1.5),噪声得不到有效压制,影响了整个求导结果。

|
| 图 5 二度体模型Chebyshev滤波法垂向二阶导数结果 Fig. 5 Second vertical derivatives of 2D model using the proposed method |
|
|
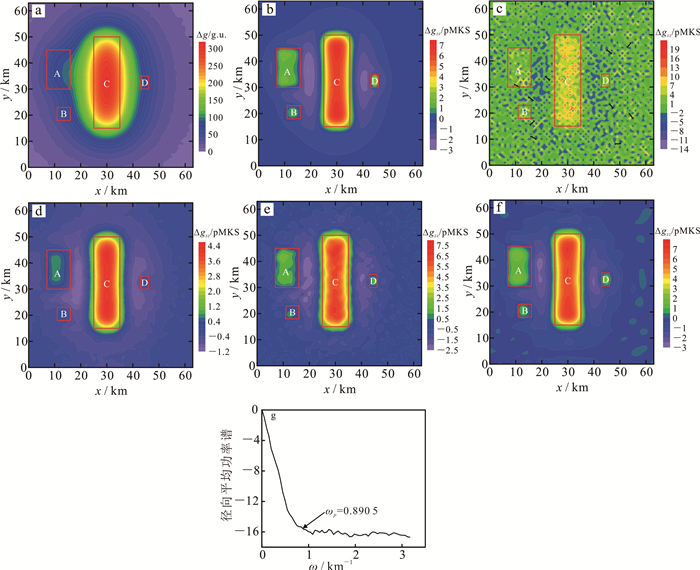
为了进一步检验本文方法的适用性,设计了4个长方体组成的三度体模型,模型参数见表 3。图 6a为模型体重力异常添加了均值为0 g.u.、标准差为0.5 g.u.的高斯噪声后的重力异常,模型体A和C的异常较明显,模型B和D的异常由于幅值小,淹没在模型A和C产生的异常中,无法清晰识别出。碍于篇幅,这里我们仅计算采用上述4种方法的垂向二阶导数。图 6b为理论垂向二阶导数异常。图 6c—f分别为常规FFT法、向上延拓法、ISVD法和Chebyshev滤波法计算的垂向二阶导数图。图 6g为选取截止频率的功率谱曲线图。从图 6可知:常规FFT法对噪声无法有效压制,有用异常信号基本淹没在过大的噪声中,无法有效识别(图 6c);向上延拓法能够很好地压制噪声,但是异常幅值同时也被削弱,模型B和D的异常未能较好地显示出来(图 6d);ISVD法较向上延拓法有了很大进步,不仅对4个模型体的异常均有显示,幅值也与理论异常相近,只是噪声影响还有较大存在,异常曲线受噪声影响存在畸变(图 6e);本文方法选取截止滤波频率0.890 5计算垂向二阶导数,求导结果与理论值的误差仍是最小(表 4),4个模型体均有效识别出,异常幅值与理论值相差无几,噪声干扰得到有效压制,只是在边界处异常存在轻微振荡(图 6f)。这与二度体模型试验效果相似。
| 地质体编号 | 上/下埋深/km | x方向边界位置/km | y方向边界位置/km | 剩余密度/(g/cm3) |
| A | 3/5 | 7/16 | 30/45 | 0.1 |
| B | 3/4 | 11/16 | 18/23 | 0.1 |
| C | 5/13 | 25/35 | 15/50 | 0.3 |
| D | 2/3 | 43/46 | 30/35 | 0.1 |
|
| a.三度体模型含噪声重力异常;b.理论垂向二阶导数;c.常规FFT法垂向二阶导数;d.向上延拓法垂向二阶导数;e. ISVD法垂向二阶导数;f. Chebyshev滤波法垂向二阶导数;g.径向平均功率谱曲线。 图 6 三度体模型重力异常及各方法垂向二阶导数结果图 Fig. 6 Noisy gravity anomaly of 3D model and its second vertical derivatives |
|
|
同样地,为了进一步说明截止频率对三度体重力异常导数换算结果的影响,我们选取截止频率0.5,1.0和1.5对图 6a中的重力异常进行导数计算,其结果见图 7。可以看出:随着截止频率的变大,地质体B和D产生的小异常变得越来越明显,但是噪声的影响也变得越来越大。ωp=1.0(接近0.890 5)时的计算结果平衡了这两种情况,即突出异常的同时,尽量降低了噪声对结果的干扰,这与二度体模型的试验结果一样。两次试验说明了本文方法利用功率谱确定截止频率的做法是可取的。

|
| 图 7 三度体模型Chebyshev滤波法垂向二阶导数结果 Fig. 7 Second vertical derivatives of 3D model using the proposed method |
|
|
综合上述模型试验分析可知,本文方法不仅能够压制噪声的干扰,保证计算的稳定性,还能最大幅度地提高结果的精度,较其他求导方法具有更好的处理效果。
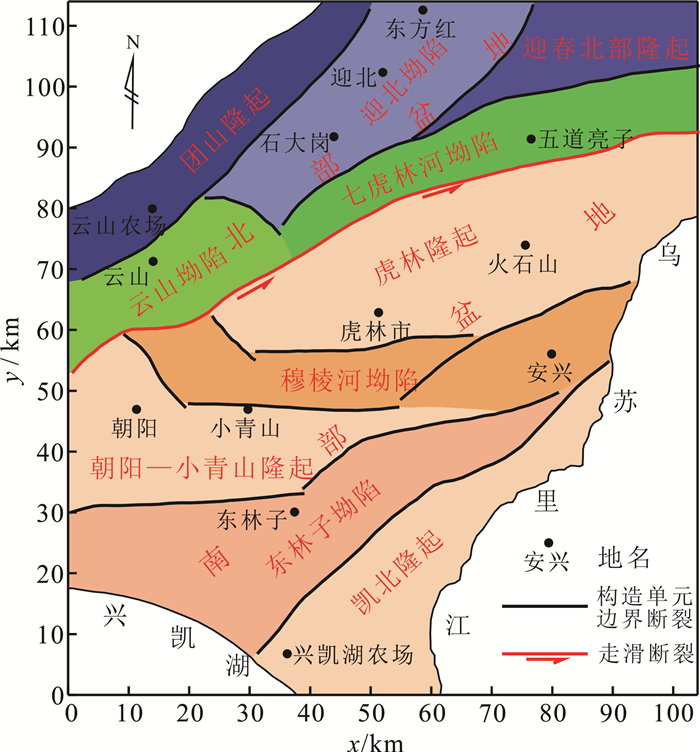
3 实例应用虎林盆地位于黑龙江省东部,地处那丹哈达燕山褶皱带和吉黑华力西褶皱带交界处,是在性质不同构造单元交界带上形成的中、新生代盆地[17]。该盆地内部次级构造单元发育,总体呈NEE向隆、坳相间的条带分布(图 8)[18],是大庆油田外围东带油气勘探的重点区域之一[17-19]。
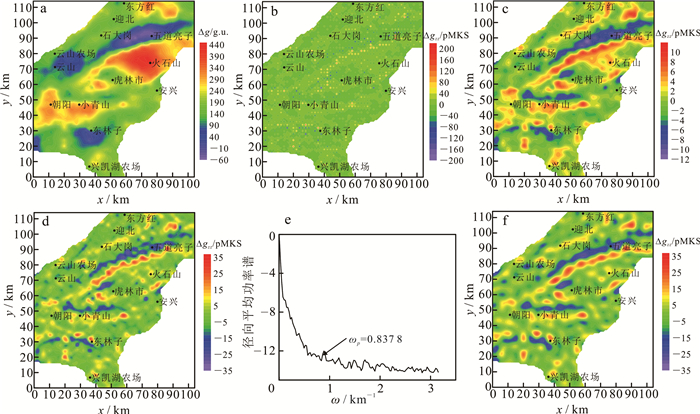
为了验证本文方法计算导数的实用性,我们对虎林盆地布格重力异常进行垂向二阶导数计算,数据网格点距1 km,横纵网格点数105×115。图 9a为虎林盆地布格重力异常,异常总体呈现正异常,从北到南依次分布多个重力极值圈闭,异常分布复杂。其中反映断裂的重力异常标志不仅表现为重力异常梯级带,还表现为等值线同形扭曲以及等值线突然变宽、变窄。图 9b—f为4种方法计算得到的垂向二阶导数图。可以看出:由于实际数据总是包含噪声,常规FFT法(图 9b)计算的导数畸变严重,单点异常多且复杂,不能有效识别出浅部异常;向上延拓法结果(图 9c)能大致展现出该地区的浅部异常特征,但异常幅值衰减严重,弱小异常未能显示出来;ISVD法的导数结果(图 9d)比向上延拓法(图 9c)提供更多浅部异常特征,但噪声影响残存,孤立异常圈闭繁多;本文方法采用0.837 8的截止频率进行计算,其垂向二阶导数结果(图 9f)展现的浅部异常特征清楚明显,异常连续性好。这说明本文方法的计算过程稳定,高频噪声得到了有效压制,所求的导数结果精度更高。
|
| a.原始布格重力异常;b.常规FFT法垂向二阶导数;c.向上延拓法垂向二阶导数;d. ISVD法垂向二阶导数;e.径向平均功率谱曲线;f. Chebyshev滤波法垂向二阶导数。 图 9 虎林盆地布格重力异常及各方法垂向二阶导数结果 Fig. 9 Bouguer gravity anomaly in the Hulin basin and its second vertical derivatives |
|
|
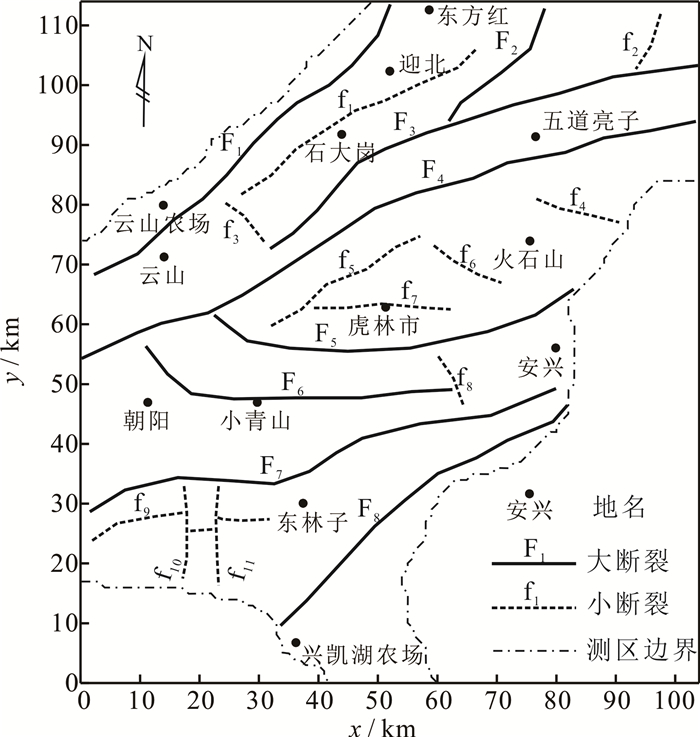
依据本文方法计算出的垂向二阶导数零值线位置(图 9f),我们对虎林盆地进行了断裂划分,划分出了8条大断裂和11条小断裂(图 10)。其中8条大断裂在布格重力异常上表现为重力异常梯级带的形式。对比盆地内的构造单元分布(图 8),这8条大断裂的位置对应盆内的构造单元边界,其中F3和F4为岩石圈断裂,分别对应敦密断裂的南北两支。11条小断裂主要为盆地构造单元内部的断裂,刻画出构造单元内部的精细结构,其位置在文献[19]中均可得到证实。
|
| 图 10 虎林盆地断裂分布图 Fig. 10 Fault distribution map of Hulin basin |
|
|
1) 本文利用Chebyshev低通滤波器与常规波数域导数换算算子相结合的模式,提出了一种新的位场任意阶导数换算方法。通过分析该低通滤波器的滤波特性,并结合异常径向平均功率谱曲线,确定了滤波所需参数的选取方法,避免了人为因素对求导结果的影响。
2) 通过模型试验证明了确定滤波参数的方法是有效的,相比常规FFT法、向上延拓法和ISVD法,Chebyshev滤波法的导数换算过程较稳定,所求导数与理论值的误差最小,具有较高的精度。
3) 在虎林盆地的实际数据处理中,Chebyshev滤波法求得的垂向二阶导数受噪声影响较小,结果较合理,依此划分出的19条断裂均与前人研究结果吻合,说明了该方法有一定的实用价值。
4) Chebyshev滤波法的提出提高了导数换算的精度,为增强后续位场数据处理与解释的准确性提供了良好的保障。
| [1] |
Verduzco B, Fairhead J D, Green C M, et al. New Insights into Magnetic Derivatives for Structural Mapping[J]. Leading Edge, 2012, 23(2): 116-119. |
| [2] |
Guo C C, Xiong S Q, Xue D J, et al. Improved Euler Method for the Interpretation of Potential Data Based on the Ratio of the Vertical First Derivative to Analytic Signal[J]. Applied Geophysics, 2014, 11(3): 331-339. DOI:10.1007/s11770-014-0442-4 |
| [3] |
张凤琴, 张凤旭, 刘财, 等. 利用DCT法计算重力归一化总梯度[J]. 吉林大学学报(地球科学版), 2007, 37(4): 804-808. Zhang Fengqin, Zhang Fengxu, Liu Cai, et al. Using DCT to Calculate Normalized Full Gradient of Gravity Anomalies[J]. Journal of Jilin University (Earth Science Edition), 2007, 37(4): 804-808. |
| [4] |
曾小牛, 李夕海, 贾维敏, 等. 位场各阶垂向导数换算的新正则化方法[J]. 地球物理学报, 2015, 58(4): 1400-1410. Zeng Xiaoniu, Li Xihai, Jia Weimin, et al. A New Regularization Method for Calculating the Vertical Derivatives of the Potential Field[J]. Chinese Journal of Geophysics, 2015, 58(4): 1400-1410. |
| [5] |
Meskó C A. Two-Dimensional Filtering and the Second Derivative Method[J]. Geophysics, 2012, 31(3): 606. |
| [6] |
Agarwal B N P, Lal T. Calculation of the Second Vertical Derivative of Gravity Field[J]. Pure & Applied Geophysics, 1969, 76(1): 5-16. |
| [7] |
徐世浙. 用有限元法计算二维重力场垂直分量及重力位二阶导数[J]. 石油地球物理勘探, 1984, 19(5): 468-476. Xu Shizhe. Calculation of Vertical Component of 2D Gravitational Field and Second Derivative of Gravitational Potential by Finite[J]. Oil Geophysical Prospecting, 1984, 19(5): 468-476. |
| [8] |
汪炳柱. 用样条函数法求重力异常二阶垂向导数和向上延拓计算[J]. 石油地球物理勘探, 1996, 31(3): 415-422. Wang Bingzhu. Computing the Vertical Second Derivative and Upward Continuation of Gravity Anomaly by Spline Function Method[J]. Oil Geophysical Prospecting, 1996, 31(3): 415-422. |
| [9] |
侯重初. 补偿圆滑滤波方法[J]. 石油物探, 1981(2): 27-34. Hou Zhongchu. Filtering of Smooth Compensation[J]. Geophysical Prospecting for Petroleum, 1981(2): 27-34. |
| [10] |
王彦国, 张瑾. 位场高阶导数的波数域迭代法[J]. 物探与化探, 2016, 40(1): 143-147. Wang Yanguo, Zhang Jin. The Iterative Method for Higher-Order Derivative Calculation of Potential Fields in Wave Number Domain[J]. Geophysical & Geochemical Exploration, 2016, 40(1): 143-147. |
| [11] |
杜威, 许家姝, 吴燕冈, 等. 位场垂向高阶导数的Tikhonov正则化迭代法[J]. 吉林大学学报(地球科学版), 2018, 48(2): 394-401. Du Wei, Xu Jiashu, Wu Yangang, et al. Tikhonov Regularization Iteration Method for High-Order Vertical Derivatives of Potential Field[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(2): 394-401. |
| [12] |
张凤旭, 孟令顺, 张凤琴, 等. 重力位谱分析及重力异常导数换算新方法:余弦变换[J]. 地球物理学报, 2006, 49(1): 244-248. Zhang Fengxu, Meng Lingshun, Zhang Fengqin, et al. A New Method for Spectral Analysis of the Potential Field and Conversion of Derivatives of Gravity Anomalies:Cosine Transform[J]. Chinese Journal of Geophysics, 2006, 49(1): 244-248. DOI:10.3321/j.issn:0001-5733.2006.01.031 |
| [13] |
张凤旭, 张凤琴, 孟令顺, 等. 基于离散余弦变换的磁位谱分析及磁异常导数计算方法[J]. 地球物理学报, 2007, 50(1): 297-304. Zhang Fengxu, Zhang Fengqin, Meng Lingshun, et al. Magnetic Potential Spectrum Analysis and Calculating Method of Magnetic Anomaly Derivatives Based on Discrete Cosine Transform[J]. Chinese Journal of Geophysics, 2007, 50(1): 297-304. DOI:10.3321/j.issn:0001-5733.2007.01.037 |
| [14] |
马国庆, 黄大年, 杜晓娟, 等. Hartley变换在位场(重、磁)异常导数计算中的应用[J]. 吉林大学学报(地球科学版), 2014, 44(1): 328-335. Ma Guoqing, Huang Danian, Du Xiaojuan, et al. Hartley Transform in the Application of the Derivatives of Potential Field (Gravity and Magnetic) Data[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(1): 328-335. |
| [15] |
Fedi M, Florio G. A Stable Downward Continuation by Using the ISVD Method[J]. Geophysical Journal of the Royal Astronomical Society, 2002, 151(1): 146-156. DOI:10.1046/j.1365-246X.2002.01767.x |
| [16] |
蒋甫玉, 孟令顺, 张凤旭, 等. Chebyshev逼近滤波器在位场分离中的应用[J]. 物探与化探, 2008, 32(3): 311-315. Jiang Fuyu, Meng Lingshun, Zhang Fengxu, et al. The Application of Chebyshev Approximation Filter to Separating Potential Anomalies[J]. Geophysical & Geochemical Exploration, 2008, 32(3): 311-315. |
| [17] |
张凤旭, 张兴洲, 张凤琴, 等. 黑龙江省虎林盆地单元结构的地质-地球物理研究[J]. 吉林大学学报(地球科学版), 2010, 40(5): 1170-1176. Zhang Fengxu, Zhang Xingzhou, Zhang Fengqin, et al. Study on Geology and Geophysics on Structural Units of Hulin Basin in Heilongjiang Province[J]. Journal of Jilin University (Earth Science Edition), 2010, 40(5): 1170-1176. |
| [18] |
刘志宏, 梅梅, 高军义, 等. 东北东部虎林盆地的构造特征、成盆机制及敦密断裂带北东段的形成时代[J]. 吉林大学学报(地球科学版), 2014, 44(2): 480-489. Liu Zhihong, Mei Mei, Gao Junyi, et al. Structural Features Formation Mechanism of Hulin Basin and Deformation Time of Northeastern Segment of Dunhua-Mishan Fault Zone in Northeast China[J]. Journal of Jilin University (Earth Science Edition), 2014, 44(2): 480-489. |
| [19] |
邰振华, 张凤旭, 刘国兴, 等. 基于差分求导的伪总梯度余弦值法的位场边界检测[J]. 石油地球物理勘探, 2014, 49(4): 807-814. Tai Zhenhua, Zhang Fengxu, Liu Guoxing, et al. Potential Field Edge Detection Based on Difference Derivative with Cosine of Pseudo Total Gradient[J]. Oil Geophysical Prospecting, 2014, 49(4): 807-814. |