2. 山东大学海洋研究院, 山东 青岛 266237
2. Institute of Marine Science and Technology, Shandong University, Qingdao 266237, Shandong, China
0 引言
随着经济社会的发展和人类活动的增加,地下水资源受生活污水、工业排放、农业灌溉等的影响越来越大,许多地区的地下水已经遭受一定程度的污染[1]。科学合理的地下水水质评价有助于正确管理利用地下水资源。
目前,虽然有很多数学评价方法用于地下水水质评价,如单因子评价法[1]、综合指数法[2]、多元统计分析法[3-4]、属性识别法[5]、模糊综合评价法[6-8]、人工神经网络模型[9]、投影寻踪聚类模型[10]等,但这些评价方法都存在不同程度的缺陷。如:评价模型中的指标一般由专家评判选择,易受主观因素影响;为突出各评价指标不同的重要性程度,往往通过主观赋权法或客观赋权法对评价指标赋予权重,赋权过程中易受主观因素或客观数据影响而产生误差;模糊综合评价法、聚类分析模型等许多评价方法需要构建数学函数,函数构造过程中易受人为因素影响,且计算分析时易丢失数据信息,致使评价结果与实际情况之间存在一定的误差。
与其他地下水水质评价方法相比,物元可拓评价模型不仅适用于多指标综合评价问题,而且可通过系统物元变换和结构变换等方式,将不相容问题转化为相容问题[11], 但物元可拓评价模型在评价过程中也存在一定的局限性[12-13]。基于此,笔者对模型构建过程进行改进,先运用层次分析法[14-15]和熵权法[16-17]计算评价指标的综合权重,再从感官、一般化学和毒理学3个方面构建地下水水质综合评价指标体系;并将基于综合权重和改进物元可拓评价模型构建的地下水水质评价模型应用于平度市古岘镇地下水水质评价,与综合评分法、属性识别法的地下水水质评价结果进行比较分析,以检验本文水质模型评价结果的正确性。
1 确定指标综合权重目前,地下水质综合评价过程中指标权重的确定方法可按计算形式的不同分为主观求权法和客观求权法。主观求权法依据专家主观经验及判断对评价指标的权重进行赋值,有层次分析法、环比评分法等;客观求权法根据样本数据反映的信息计算各指标的权重值,包括熵权法、相关系数法等。但这两类方法在计算指标权重值时,都存在明显的缺陷,如:主观求权法计算得到的指标权重值具有绝对主观性,其过度依赖主观判断,缺乏客观数据的分析,相同指标会因研究者主观经验不同而得到许多不同的值;而运用客观求权法确定的指标值具有绝对客观性,缺少主观因素的参与,权重值与实际数据联系密切,易受样本数据中极值的影响,指标权重值极易随样本数据的变化而波动变化,稳定性较差。因此,有必要集成主、客观求权法的优点,即结合基于实际决策问题的主观判断和基于客观数据的理论依据计算评价指标的综合权重,尽量使各指标权重值与实际重要程度相符,提高评价结果的准确性。现在已有一些通过加权组合主观赋权法和客观赋权法来计算评价指标组合权重的求权方法[18-20], 然而到目前为止,主客观权重加权组合方法是否可以同时兼顾主客观求权法的优点还不能确定[21]。本文通过熵权法修正层次分析法计算得到的权重来最终确定地下水质评价指标的综合权重,以提高指标权重的可信度。
层次分析法(AHP)是一种定性与定量相结合的数学分析方法,该法以专家主观评判为主,通过对各层次评价指标的两两重要性程度进行比较计算,为各指标赋予相应的权重。运用AHP赋权,最大的问题就是主观因素过度参与,如比较判断矩阵的构造易受专家主观想法的干扰、判断矩阵一致性检验的标准是一个主观经验值、一致性检验公式中的随机一致性指标也是一个主观经验值;这易使指标权重值具有绝对的主观性。
熵权法是根据样本数据所提供的信息量,计算评价指标变异性大小来确定指标权重值的一种客观求权方法。虽然运用熵权法计算指标权重具有较强的数学理论依据,抛弃了主观因素对权重值的影响,但权重值过度依靠客观数据,评价结果易受样本数据变化和极值的影响,使指标权重值具有绝对的客观性。
如上所述,AHP法注重于主观经验和专业评判,熵权法则偏向于利用客观数据所蕴含的信息,都存在明显的不足。故本文运用AHP法和熵权法计算地下水质评价指标的综合权重,将专家的专业判断和各个数据的信息充分结合,既能反映主观意愿,又能结合客观信息,避免了指标权重的绝对主观性和绝对客观性。通过熵权法修正AHP法计算的权重,最终确定各地下水质评价指标的综合权重,具体计算过程如下:
1) 运用AHP法初步计算地下水质评价体系中第j项指标的权重wj。
2) 利用熵权法修正wj得到指标权重hj,即根据由AHP法构建的比较判断矩阵计算各评价指标的熵权。
3) 确定各项指标的综合权重。
① 计算相对综合权重g。第j项指标相对综合权重gj的计算公式为
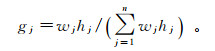 (1)
(1) 式中,n为评价指标的总数量。
② 计算最终综合权重s。最终综合权重即各层次评价指标相对于目标层O的权重,准则层B中各项指标的相对综合权重即为其最终综合权重,指标层C中各项指标的最终综合权重由各指标在该层的相对综合权重与相邻上一层次指标的最终综合权重相乘得到。
由于许多资料中已经对AHP法和熵权法的计算原理、公式做了详细的介绍,这里不再赘述,具体可参考文献[14]—[17]。
2 改进的物元可拓评价模型物元可拓评价模型能够将多目标决策问题转化为单目标决策问题,且定量化地表示评价结果。在评价地下水水质过程中,物元可拓评价模型不仅能够充分考虑到水质的不确定性和水质界限的模糊性,还能反映水质评价结果对于评价等级的贴近程度,分析预测地下水水质的变化趋势。然而,由单一的主观赋权法或客观赋权法计算得到的评价指标权重,极易对评价结果造成误差。因此,将指标的综合权重应用于评价模型,有助于降低评价结果的偏差。
物元可拓评价模型的构造过程一般包括5步:明确物元概念及待评物元矩阵、建立经典域及节域物元矩阵、构造关联函数、计算综合关联度、确定评价等级。然而,评价指标的实际值一旦超过节域范围,将导致物元可拓评价模型的关联函数无法进行计算,所以要对物元可拓评价模型的构造过程进行相应的改进。在明确物元概念及待评物元矩阵、建立经典域和节域物元矩阵后,规格化处理经典域和待评物元矩阵,具体改进过程如下:
1) 规格化处理经典域和待评物元矩阵。将经典域物元矩阵RN中各指标的量值两端和待评物元矩阵R0中的量值都除以节域中各指标取值范围的最大值bip(i=1, 2, …, n),得到和R′N和R′0:
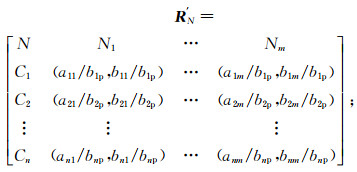 (2)
(2) 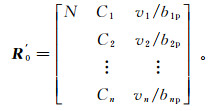 (3)
(3) 式中:N为待评价的对象(本文中为地下水水质等级);Ci(i=1, 2, …, n)为评价对象N的第i个指标;Nj(j=1, 2, …, m)表示评价对象所划分的第j个评价等级;(aij, bij)为第i个指标关于评价等级j的数值范围(i=1, 2, …, n,j=1, 2, …, m);bip(i=1, 2, …, n)为第i个指标取值范围的最大值;vi(i=1, 2, …, n)为待评对象第i个指标的值。
2) 计算处理后的待评物元体关于新的经典域物元矩阵中量值范围的距离Dij:
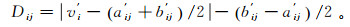 (4)
(4) 式中:a′ij、b′ij(i=1, 2, …, n,j=1, 2, …, m)为矩阵R′N中aij、bij除以bip后的值;v′i为R′0中vi除以bip后的值。
3) 计算关联度并确定评价等级。用Dij代关联度函数,记综合关联度为Kj, 即
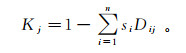 (5)
(5) 式中:si为第i项指标的最终综合权重。取K(j)=max{Kj},则待评物元属于等级j。
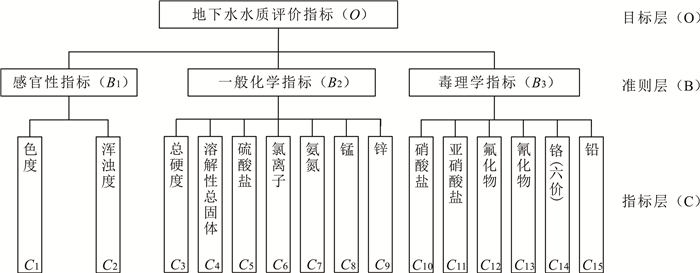
3 建立地下水水质综合评价指标体系本文从感官性、一般化学和毒理学3个方面选取具有代表性的15项常规指标,构建地下水水质综合评价指标体系,如图 1所示。
|
| C4—C15为该物质的质量浓度。 图 1 地下水水质综合评价指标层次结构模型 Fig. 1 Hierarchical structure model of comprehensive evaluation index of groundwater quality |
|
|
参照《地下水质量标准》(GB/T 14848-2017)[22]对地下水水质进行综合评价,各项评价指标Ⅰ—Ⅴ级的分级评价标准如表 1所示。其中,评价指标硝酸盐与亚硝酸盐的质量浓度依据标准规定,以氮计量。
| 等级 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 |
| Ⅰ | ≤5 | ≤3 | ≤150 | ≤300 | ≤50 | ≤50 | ≤0.02 | ≤0.05 | ≤0.05 | ≤2.0 | ≤0.01 | ≤1.0 | ≤0.001 | ≤0.005 | ≤0.005 |
| Ⅱ | ≤5 | ≤3 | ≤300 | ≤500 | ≤150 | ≤150 | ≤0.10 | ≤0.05 | ≤0.50 | ≤5.0 | ≤0.10 | ≤1.0 | ≤0.01 | ≤0.01 | ≤0.005 |
| Ⅲ | ≤15 | ≤3 | ≤450 | ≤1 000 | ≤250 | ≤250 | ≤0.50 | ≤0.10 | ≤1.00 | ≤20.0 | ≤1.00 | ≤1.0 | ≤0.05 | ≤0.05 | ≤0.010 |
| Ⅳ | ≤25 | ≤10 | ≤650 | ≤2 000 | ≤350 | ≤350 | ≤1.50 | ≤1.50 | ≤5.00 | ≤30.0 | ≤4.80 | ≤2.0 | ≤0.10 | ≤0.10 | ≤0.100 |
| Ⅴ | >25 | >10 | >650 | >2 000 | >350 | >350 | >1.50 | >1.50 | >5.00 | >30.0 | >4.80 | >2.0 | >0.10 | >0.10 | >0.100 |
以平度市古岘镇10个监测井的地下水水质实测资料作为研究对象,运用构建的地下水水质评价模型和综合评价指标体系对该地区地下水水质状况进行综合评价,平度市古岘镇各监测井地下水水质综合评价各项指标的实测值如表 2所示。
| 测点 | C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | C9 | C10 | C11 | C12 | C13 | C14 | C15 |
| 1 | 4.7 | 5.1 | 365.5 | 784 | 211.6 | 156.3 | 0.028 | 0.077 | 0.645 | 6.16 | 0.037 2 | 0.552 | 0.047 6 | 0.003 3 | 0.051 9 |
| 2 | 4.2 | 2.4 | 381.4 | 936 | 167.1 | 137.9 | 0.034 | 0.062 | 0.038 | 2.58 | 0.004 8 | 0.615 | 0.002 1 | 0.005 2 | 0.006 9 |
| 3 | 4.1 | 1.5 | 146.7 | 288 | 81.8 | 45.2 | 0.032 | 0.023 | 0.018 | 4.95 | 0.012 9 | 0.736 | 0.000 0 | 0.001 2 | 0.002 3 |
| 4 | 4.6 | 1.7 | 404.4 | 879 | 175.3 | 227.8 | 0.054 | 0.038 | 0.016 | 2.74 | 0.006 8 | 0.825 | 0.003 7 | 0.007 6 | 0.008 8 |
| 5 | 4.2 | 2.8 | 358.2 | 856 | 233.5 | 197.2 | 0.021 | 0.049 | 0.061 | 4.72 | 0.016 3 | 0.684 | 0.001 4 | 0.008 7 | 0.016 6 |
| 6 | 4.8 | 3.4 | 415 | 842 | 171.3 | 233.1 | 0.128 | 0.046 | 0.003 | 17.54 | 0.018 1 | 0.668 | 0.034 1 | 0.004 8 | 0.055 7 |
| 7 | 4.7 | 2.8 | 396.5 | 1 164 | 123.3 | 329.7 | 0.436 | 0.158 | 1.043 | 14.92 | 0.014 8 | 1.353 | 0.061 3 | 0.070 1 | 0.045 9 |
| 8 | 4.3 | 2.2 | 364.8 | 996 | 230.2 | 210.5 | 0.048 | 0.039 | 0.027 | 12.54 | 0.019 8 | 0.697 | 0.004 4 | 0.006 1 | 0.005 4 |
| 9 | 4.3 | 0.5 | 136.8 | 271 | 56.2 | 50.4 | 0.001 | 0.046 | 0.054 | 3.21 | 0.000 6 | 0.385 | 0.000 2 | 0.000 0 | 0.001 7 |
| 10 | 4.5 | 1.2 | 397.4 | 682 | 115.8 | 150.6 | 0 | 0.001 | 0.973 | 5.69 | 0.008 7 | 0.345 | 0.005 8 | 0.006 2 | 0.005 1 |
平度市古岘镇10个监测井的地下水水样采集、检测均由专业人员根据相关标准进行,即表 2中的数据完全能够满足地下水质量评价要求。此外,考虑到《地下水质量标准》(GB/T 14848-2017)[22]中没有对各评价指标第Ⅴ级标准的上限作出明确要求,且在所有待评价水样中未发现严重超标的因子,故本文参考文献[11],在水质评价过程中,去掉第Ⅴ级标准,采用Ⅰ—Ⅳ级评价标准进行计算,既能达到评价要求,又能简化计算过程。
4.1 确定评价指标综合权重依据水质评价模型中确定评价指标综合权重的过程,计算平度市古岘镇地下水水质综合评价中各指标的综合权重。
1) 按照层次分析法的基本原理,并在大量相关文献和专家意见的基础上,构造目标层O对应于准则层B的比较判断矩阵P以及准则层B对应于指标层C的比较判断矩阵P1、P2、P3:

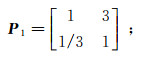


计算矩阵P的最大特征值λmax及所对应的特征向量WP,得λmax=3.009,WP=[0.297 0.164 0.539]T,则AHP一致性指标IC=0.004 5,平均随机一致性指标IR=0.58,一致性比例RC=0.008 < 0.1。由一致性检验公式可知,矩阵P满足一致性要求,故WW=[0.297 0.164 0.539]即为准则层指标B1、B2、B3对目标层O的权重系数。同理,可得指标层C各指标对准则层B的权重系数:W1=[0.75 0.25];W2=[0.172 0.120 0.037 0.066 0.042 0.337 0.226];W3=[0.047 0.035 0.088 0.424 0.230 0.176]。
2) 运用熵权法修正由层次分析法初步计算得到的各评价指标权重。根据熵权法计算各指标的熵值和熵权,可得经熵权法修正后指标B1、B2、B3对目标层O的权重系数H以及指标层C各指标对准则层B的权重系数H1、H2、H3。经计算,H=[0.331 0.331 0.338],H1=[0.5 0.5],H2=[0.136 0.149 0.131 0.169 0.180 0.115 0.120],H3=[0.191 0.157 0.216 0.139 0.144 0.153]。
3) 计算最终综合权重。根据公式(1)计算各层评价指标的相对综合权重,在此基础上,计算各层评价指标相对于目标层O的最终综合权重:准则层B中各项指标的相对综合权重即为其最终综合权重;指标层C中各项指标的最终综合权重由各指标在该层的相对综合权重与相邻上一层次指标的最终综合权重相乘得到。运用层次分析法和熵权法计算各评价指标最终综合权重的结果如表 3所示。
| B | AHP初步计算权重 | 熵权修正指标权重 | 最终权重 | C | AHP初步计算权重 | 熵权修正指标权重 | 综合权重 | 最终综合权重 | ||
| O | B1 | 0.297 | 0.331 | 0.293 | C1 | 0.750 | 0.500 | 0.750 | 0.220 | |
| C2 | 0.250 | 0.500 | 0.250 | 0.073 | ||||||
| C3 | 0.172 | 0.136 | 0.179 | 0.029 | ||||||
| C4 | 0.120 | 0.149 | 0.137 | 0.022 | ||||||
| C5 | 0.037 | 0.131 | 0.037 | 0.006 | ||||||
| B2 | 0.164 | 0.331 | 0.162 | C6 | 0.066 | 0.169 | 0.085 | 0.014 | ||
| C7 | 0.042 | 0.180 | 0.058 | 0.009 | ||||||
| C8 | 0.337 | 0.115 | 0.297 | 0.048 | ||||||
| C9 | 0.226 | 0.120 | 0.207 | 0.034 | ||||||
| C10 | 0.047 | 0.191 | 0.059 | 0.032 | ||||||
| C11 | 0.035 | 0.157 | 0.036 | 0.020 | ||||||
| B3 | 0.539 | 0.338 | 0.545 | C12 | 0.088 | 0.216 | 0.125 | 0.068 | ||
| C13 | 0.424 | 0.139 | 0.386 | 0.210 | ||||||
| C14 | 0.230 | 0.144 | 0.217 | 0.118 | ||||||
| C15 | 0.176 | 0.153 | 0.177 | 0.097 | ||||||
由表 3可知,相对于感官性指标和一般化学指标,毒理学指标在地下水水质评价中较为重要,其权重达0.545。分析整个评价指标体系指标层中15项评价指标的权重可知,评价指标色度、氰化物、铬(六价)、铅是最为重要的4项指标,4项指标权重之和达0.645,其他指标和这4项指标相比,重要性程度较小。
4.2 构造经典域、节域和待评物元矩阵地下水水质等级N,地下水水质综合评价指标C和其特征值V共同构成地下水水质物元。根据表 1中数据构造Ⅰ、Ⅱ、Ⅲ、Ⅳ级分级标准的经典域矩阵RN和节域矩阵RP,并按公式(2)规格化处理经典域矩阵RN,得到新的经典域矩阵R′N:

以1号测点为例,构建待评物元矩阵R1:

依据公式(3)对矩阵R1规格化处理,得到新的待评物元矩阵R′1:

根据公式(4)计算出测点1中15个地下水水质评价指标关于Ⅰ、Ⅱ、Ⅲ、Ⅳ级评价等级的距离,结果为
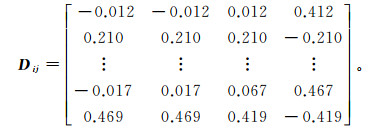
根据公式(19)计算综合关联度Kj,得到KⅠ=0.829 7,KⅡ=0.865 8,KⅢ= 0.962 2,KⅣ=0.854 6。计算K(j)=max{Kj}=0.962 2,可知测点1的地下水水质等级为Ⅲ级。
4.4 评价结果分析按照测点1地下水水质等级的评价过程,计算其余9个测点地下水水质的综合关联度,并依据水质等级评价方法,最终确定各测点地下水质的质量等级(表 4)。同时,为验证和说明基于综合权重和改进物元可拓评价模型的水质评价结果的合理性,运用《地下水质量标准》(GB/T14848—2017)[22]中介绍的综合评分法和属性识别法(各评价指标权重采用上文计算得到的综合权重,置信度取0.7),对10个测点的水质等级进行综合评价,评价结果如表 4所示。
| 测点 | 地下水水质评价等级关联度 | 水质评价等级 | ||||||
| KⅠ | KⅡ | KⅢ | KⅣ | 本文模型 | 综合评分法 | 属性识别法 | ||
| 1 | 0.829 7 | 0.865 8 | 0.962 2 | 0.854 6 | Ⅲ | Ⅳ | Ⅲ | |
| 2 | 0.996 3 | 1.017 2 | 0.987 5 | 0.688 1 | Ⅱ | Ⅱ | Ⅰ | |
| 3 | 1.029 0 | 1.024 2 | 0.958 5 | 0.649 5 | Ⅰ | Ⅰ | Ⅰ | |
| 4 | 0.979 1 | 1.012 5 | 0.995 0 | 0.705 2 | Ⅱ | Ⅱ | Ⅱ | |
| 5 | 0.975 4 | 1.001 0 | 0.981 4 | 0.709 0 | Ⅱ | Ⅳ | Ⅰ | |
| 6 | 0.847 4 | 0.883 8 | 0.992 8 | 0.835 3 | Ⅲ | Ⅳ | Ⅲ | |
| 7 | 0.689 5 | 0.735 7 | 0.904 8 | 0.992 5 | Ⅳ | Ⅳ | Ⅲ | |
| 8 | 0.975 8 | 1.010 6 | 1.002 6 | 0.708 6 | Ⅱ | Ⅱ | Ⅱ | |
| 9 | 1.024 6 | 1.017 5 | 0.953 5 | 0.628 5 | Ⅰ | Ⅰ | Ⅰ | |
| 10 | 0.982 7 | 1.025 2 | 1.005 0 | 0.685 1 | Ⅱ | Ⅱ | Ⅱ | |
分析由本文模型计算得到的古岘镇10个测点处水质评价结果可知,该地区地下水水质较好,水质等级多为Ⅰ级和Ⅱ级,仅测点7的水质较差,为Ⅳ级。根据表 4中的水质评价结果,比较分析本文地下水水质评价模型、综合评分法和属性识别法的水质评价结果。经对比可知,虽然3种方法的水质评价结果基本相同,但在这10个测点处,运用综合评分法得到的水质等级偏低,运用属性识别法得到的水质等级偏高,而本文模型的评价结果或与它们保持一致,或介于两者之间。本文水质评价模型和综合评分法水质评价结果的相同率达70%,仅测点1、5、6的评价结果不同。分析评价结果不同的原因可能是综合评分法在水质评价过程中默认各项指标的重要性程度相同,而本文地下水水质评价模型充分考虑指标之间重要性程度的差异,给各项评价指标赋予不同的权重值。所以,当测点1、5、6中存在运用综合评分法评价得到评分较高的指标,却在本文水质评价模型中所占权重较小时,就导致综合评分法的评价结果比本文地下水水质评价模型的评价结果低出1个等级。
对比本文模型和属性识别法的水质评价结果可知,两种方法的的评价结果相同率也达70%,仅测点2、5、7的地下水水质评价结果存在1个级别的差异。分析评价结果不同的原因可能是属性识别法在利用综合属性测度评价水质等级时,易于丢失部分评价信息和淡化水质界限的模糊性,而本文构建的水质评价模型充分考虑水质的不确定性,能够较为全面地评价水质等级。所以,当运用属性识别法评价水质等级时,有可能造成评价结果比实际情况好,水质等级偏高。
综合以上分析可知,基于综合权重和改进物元可拓法的地下水水质评价模型在评价过程中,既能合理考虑各项评价指标重要性程度的差异,又能充分考虑水质等级的模糊性和不确定性,其结果较综合评分法、属性识别法的水质评价结果更加合理、可信,说明本文构建的地下水水质评价模型能够科学地评价区域地下水水质情况。
5 结论1) 本文从感官性、一般化学和毒理学三方面构建了地下水质综合评价指标体系,并根据熵权法和层次分析法计算了各指标的综合权重。结果表明,指标色度、氰化物、铬(六价)、铅在地下水质评价中占有重要地位,应予以重视。
2) 基于综合权重和改进物元可拓法的水质评价模型既克服了指标权重绝对主观性、绝对客观性的缺陷,又考虑了水质等级的连续性、模糊性和随机性。经分析,其评价结果较常用的综合评分法、属性识别法更加准确合理。
3) 依据最新颁布的《地下水质量标准》(GB/T 14848-2017),运用本文评价模型对平度市古岘镇10个测点的地下水水质进行了综合评价,结果表明,该区地下水水质等级多为Ⅰ级和Ⅱ级,水质较好,可作为该区生活用水和工农业用水。
| [1] |
张兆吉, 费宇红, 郭春艳, 等. 华北平原区域地下水污染评价[J]. 吉林大学学报(地球科学版), 2012, 42(5): 1456-1461. Zhang Zhaoji, Fei Yuhong, Guo Chunyan, et al. Regional Groundwater Contamination Assessment in the North China Plain[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(5): 1456-1461. |
| [2] |
Bhalla G, Swamee P K, Kumar A, et al. Assessment of Groundwater Quality Near Municipal Solid Waste Landfill by an Aggregate Index Method[J]. International Journal of Environmental Sciences, 2012, 2(2): 1492-1503. |
| [3] |
Chapagain S K, Pandey V P, Shrestha S, et al. Assessment of Deep Groundwater Quality in Kathmandu Valley Using Multivariate Statistical Techniques[J]. Water, Air and Soil Pollution, 2010, 210(1/2/3/4): 277-288. |
| [4] |
Kazakis N, Mattas C, Pavlou A, et al. Multivariate Statistical Analysis for the Assessment of Groundwater Quality Under Different Hydrogeological Regimes[J]. Environmental Earth Sciences, 2017, 76(9): 349. DOI:10.1007/s12665-017-6665-y |
| [5] |
余文忠, 唐德善, 陆廷春. 熵权属性识别法在地下水水质评价中的应用[J]. 水电能源科学, 2013, 31(7): 41-43. Yu Wenzhong, Tang Deshan, Lu Tingchun. Application of Attribute Recognition Method Combined with Entropy Theory to Evaluation of Groundwater Quality[J]. Water Resources and Power, 2013, 31(7): 41-43. |
| [6] |
房春生, 孟赫, 单玉书, 等. 基于GIS的吉林省地下水水质模糊评价[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 293-297. Fang Chunsheng, Meng He, Shan Yushu, et al. Fuzzy Comprehensive Evaluation of Groundwater Quality Based on GIS of Jilin Province[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(Sup.1): 293-297. |
| [7] |
Hosseini-Moghari S M, Ebrahimi K, Azarnivand A. Groundwater Quality Assessment with Respect to Fuzzy Water Quality Index (FWQI):An Application of Expert Systems in Environmental Monitoring[J]. Environmental Earth Sciences, 2015, 74(10): 7229-7238. DOI:10.1007/s12665-015-4703-1 |
| [8] |
Kumar N V, Mathew S, Swaminathan G. Multifactorial Fuzzy Approach for the Assessment of Groundwater Quality[J]. Journal of Water Resource and Protection, 2010, 2(6): 597-608. DOI:10.4236/jwarp.2010.26069 |
| [9] |
王冬生, 李世华, 周杏鹏. 基于PSO-RBF神经网络模型的原水水质评价方法及应用[J]. 东南大学学报(自然科学版), 2011, 41(5): 1019-1023. Wang Dongsheng, Li Shihua, Zhou Xingpeng. Assessment Method of Raw Water Quality Basedon PSO-RBF Neural Network Model and Its Application[J]. Journal of Southeast University(Natural Science Edition), 2011, 41(5): 1019-1023. |
| [10] |
肖长来, 危润初, 梁秀娟, 等. 基于投影寻踪聚类模型的龙坑水源地地下水水质评价[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 248-252. Xiao Changlai, Wei Runchu, Liang Xiujuan, et al. Assessment of Water Quality of Groundwater in Longkeng Based on Projection Pursuit Cluster Model[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(Sup.1): 248-252. |
| [11] |
兰双双, 姜纪沂, 王滨. 基于物元可拓法的地下水水质评价:以梨树县平原区浅层地下水为例[J]. 吉林大学学报(地球科学版), 2009, 39(4): 722-727. Lan Shuangshuang, Jiang Jiyi, Wang Bin. Evaluation of Groundwater Quality Based on Matter-Element and Extension Means:Taking Shallow Groundwater of Plain Areas in Lishu for Example[J]. Journal of Jilin University (Earth Science Edition), 2009, 39(4): 722-727. |
| [12] |
韩彰, 陈健, 李经纬, 等. 改进物元可拓法在水闸工程安全综合评估中的应用[J]. 水力发电, 2015, 41(4): 82-85. Han Zhang, Chen Jian, Li Jingwei, et al. Application of Improved Matter-Element Extension Model to Sluice Structure Comprehensive Safety Assessment[J]. Water Power, 2015, 41(4): 82-85. |
| [13] |
汪伦焰, 袁杰, 李娜, 等. 基于物元可拓模型的水生态文明城市建设评价:以许昌市为例[J]. 人民长江, 2016, 47(18): 18-21. Wang Lunyan, Yuan Jie, Li Na, et al. Evaluation of Water Ecological Civilization City Construction Based on Matter-Element Extension Evaluation Model:Case of Xuchang City[J]. Yangtze River, 2016, 47(18): 18-21. |
| [14] |
卢文喜, 李迪, 张蕾, 等. 基于层次分析法的模糊综合评价在水质评价中的应用[J]. 节水灌溉, 2011(3): 43-46. Lu Wenxi, Li Di, Zhang Lei, et al. Application of Fuzzy Comprehensive Evaluation Based on AHP in Water Quality Evaluation[J]. Water Saving Irrigation, 2011(3): 43-46. |
| [15] |
熊德明, 张明峰, 吴陈君, 等. 基于模糊层次分析方法的泥质有效低熟气源岩评价[J]. 吉林大学学报(地球科学版), 2015, 45(6): 1620-1630. Xiong Deming, Zhang Mingfeng, Wu Chenjun, et al. Evaluation Method of Terrestrial Low-Mature Gas Source Rocks by Fuzzy AHP[J]. Journal of Jilin University (Earth Science Edition), 2015, 45(6): 1620-1630. |
| [16] |
宋丽婧, 魏琛, 宋玲梅. 五元系数法-改进熵权法在水质评价中的应用[J]. 南水北调与水利科技, 2015, 13(2): 268-273. Song Lijing, Wei Chen, Song Lingmei. Application of Five-Element Connection Number Method-Improved Entropy Method in Water Quality Evaluation[J]. South-to-North Water Transfers and Water Science & Technology, 2015, 13(2): 268-273. |
| [17] |
马荣, 石建省, 刘继朝. 熵权耦合随机理论在含水层非均质综合指数研究中的应用[J]. 吉林大学学报(地球科学版), 2011, 41(5): 1520-1528. Ma Rong, Shi Jiansheng, Liu Jichao. Application of Entropy Weight and Stochastic Theory to Study the Heterogeneity Synthetic Index of Aquifer[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(5): 1520-1528. |
| [18] |
鲁璐.基于物元可拓模型的土地整理综合效益评价研究[D].武汉: 华中师范大学, 2012. Lu Lu.Study on the Comprehensive Benefits of the Land Consolidation Based on the Matter-Element Extension Model[D].Wuhan: Central China Normal University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10511-1012386365.htm |
| [19] |
石永莲, 严宁珍, 倪九派. 基于模糊贴近度法的白河水质评价[J]. 中国农村水利水电, 2014(9): 47-52. Shi Yonglian, Yan Ningzhen, Ni Jiupai. Water Quality Evaluation of Bai River Based on Fuzzy Nearness[J]. China Rural Water and Hydropower, 2014(9): 47-52. |
| [20] |
吴海泽, 余红, 胡友彪, 等. 区域生态安全的组合权重评价模型[J]. 安全与环境学报, 2015, 15(2): 370-375. Wu Haize, Yu Hong, Hu Youbiao, et al. Research on the Establishment of the Regional Ecological Security Assessment Model by Means of the Combined Weights[J]. Journal of Safety and Environment, 2015, 15(2): 370-375. |
| [21] |
李刚, 李建平, 孙晓蕾, 等. 主客观权重的组合方式及其合理性研究[J]. 管理评论, 2017, 29(12): 17-26+61. Li Gang, Li Jianping, Sun Xiaolei, et al. Research on a Combined Method of Subjective-Objective Weighing and the Its Rationality[J]. Management Review, 2017, 29(12): 17-26+61. |
| [22] |
地下水质量标准: GB/T 14848-2017[S].北京: 中国标准出版社, 2017. Quality Standard for Ground Water: GB/T 14848-2017[S]. Beijing: China Standards Press, 2017. |



