2. 浙江交工钱潮建设有限公司, 杭州 310051
2. Qianchao Construction CO. Ltd. of Zhejiang Communications Construction Group, Hangzhou 310051, China
0 引言
我国滑坡地质灾害频发,工程中针对不同成因的滑坡常采取不同的治理措施。已有研究[1-2]表明,绝大多数滑坡都是直接或间接地由坡内地下水渗流场变化而引发的,因此截排水措施几乎在所有的滑坡治理中都会用到。现有常用的截排水措施包括:地表排水沟、地下排水洞、排水盲沟、水平排水洞等,这些排水措施已经在滑坡防治中得到了较为成熟的应用,但是这些措施都是利用重力势能进行排水,而新近提出的充气截排水技术[3-5]通过在坡体后缘水位线以下充入有压气体,排开土体孔隙水形成非饱和土截水帷幕来达到截渗减排的目的。这一过程涉及到复杂的固、液、气三相耦合效应,而已有的关于充气截排水的研究只考虑了水-气两相流相互作用的的过程。如:康剑伟等[5]在不考虑充气过程中土体变形的条件下,基于水-气二相流理论,模拟了充气阻渗过程;杜丽丽等[6]通过数值模拟耦合气-水两相,探究了渗透系数、充气气压、孔隙率对截排水效果的影响;余文飞等[7]建立了二维长边坡数值模型,探究了充气时坡体内不同阶段水-气二相流具体的运动特征。另外已有的物理模型试验[3, 8]也证明了充气截排水的有效性,并研究了相关的影响因素,但以上研究均未考虑土体骨架可能发生的变形。本文首先通过数值模拟求得充气过程中瞬时非饱和渗流场的解答,再将得到的结果应用到土体应力应变计算中,通过非完全耦合计算分析最终得到充气引起土体变形的规律。
1 水-气运移与土体变形机理分析充气截排水技术的关键在于往坡体后缘冲入有压气体,形成非饱和截水帷幕,从而减少地下水入渗到下游潜在滑坡区。对于非饱和截水帷幕形成过程的研究是十分重要的,这个过程涉及到土体中水-气相互作用并不断发生运移,同时由于孔隙气压力与水压力的作用,在宏观上土体骨架在不同阶段也表现出相应的变形特征。余文飞等[7]结合数值分析结果得到充气截排水过程大致可分为3个阶段,即充气非饱和区形成与扩展阶段、不稳定两相流阶段和充气截排水工作阶段。起初,充气形成的非饱和区在坡体内部地下水位线以下持续扩大,但气体未逸出坡体;紧接着,非饱和区突破坡体地下水位线,使得原本被封存在非饱和区内的有压气体在短时间内快速释放到坡体外,导致非饱和区内气压迅速下降,水-气二相流的平衡被打破,水-气界面的形状和运移处于非稳定状态,但非饱和区范围仍在不断扩大,下游坡体内地下水位由于非饱和区拦截的作用而逐渐降低,截排水效果随时间具有波动性;最后,随着充气的进行,从充气点到坡面形成相对固定的气体逸出通道,坡体内水的渗流路径也重新趋于稳定,此时非饱和区形态处于相对固定状态。以上过程很好地说明了充气截排水的工作机理,但是并没有考虑充气过程中土体的变形。由于向土体中充气,刚开始气压力会对土体有一个托顶的作用使土体发生隆起变形,而当气体逸出后土体又会发生沉降变形。此过程类似于浅层气的形成和释放[9-11]。浅层气作为封闭的压力气体形成后可使地层微量膨胀,气体与土颗粒一起承担上覆的荷重,当气体在一定条件下逸出时就会发生以垂直沉降为主的变形。但当气体在无控制条件下释放时,含气层气压力急剧下降,快速的气流对土体产生冲刷,带走大量的土、砂颗粒,并且会严重扰动含气土层,降低土体强度。因此上述相关研究对于同样要在土层中形成含气非饱和区的充气截排水而言具有很强的借鉴意义。
2 控制方程与模型建立本文先利用岩土软件GEO-STUDIO中的SEEP/W和AIR/W模块耦合,模拟得到坡体充气情况下的瞬时非饱和渗流场;然后将得到的孔压改变导入SIGMA/W模块中的应力-应变计算的每个荷载步,得到相应孔压改变的体积位移变化。上述过程就是非完全耦合分析。相比于完全耦合分析[12],非完全耦合分析可以先获取对非饱和渗流域的完全了解,有助于得到正确的水利边界条件、恰当的材料性质和合适的时间序列,更易于控制且数值上优于同时求解渗流-变形的耦合方程。
2.1 充气时水-气两相运移控制方程根据质量守恒定律,在等温条件下,忽略非饱和土体内的化学、相变等因素的影响,建立同时包含孔隙气压力和孔隙水压力的质量守恒方程。假设水为不可压缩流体,则密度不变,所以其质量守恒方程可以用体积守恒方程(式(1))来表示;而考虑气体可压缩性的质量守恒方程可用式(2)[13]表示。
 (1)
(1) 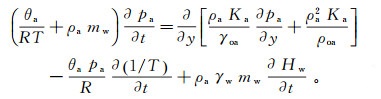 (2)
(2) 式中:mw为土水特征曲线在某一特定孔隙水压力处的斜率;γw为水的重度;t为时间;Kw为随含水率变化而变化的渗透系数;Hw为渗流过程中的总水头;pa为孔隙气压力;Qw为水的单宽流量;θa为空气的单位体积分数;T为温度常数;ρa为气体密度;Ka为随含水率变化而变化的透气系数;γoa为标准状态下气体重度;ρoa为标准状态下气体密度;R为气体常数,对于干燥空气,R=287 J/(kg·K)。
在非饱和土中,基质吸力是由存在于水气交界面的收缩膜而产生的,其值等于孔隙气压力和孔隙水压力之差,且与水的体积分数有着密切的关系,它们之间的关系通过土水特征曲线来反映。本文通过Van Genuchten模型[14]来定义土水特征曲线,见式(3);并在此基础上确定水、气渗透率曲线,见式(4)、(5)。
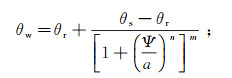 (3)
(3) 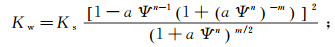 (4)
(4) 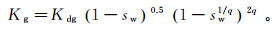 (5)
(5) 式中:θw为水体积分数;θs为饱和水体积分数;θr为残余水体积分数;Ψ为基质吸力;a,n,m均为拟合经验参数,n=1/(1-m);Ks为饱和土的渗透系数;Kg为透气系数;Kdg为干土透气系数;sw为有效饱和度;q为系数,q=2.9。
式(3)—(5)联立质量守恒方程共同构成了描述坡体中水-气二相运移数学模型的控制方程。
2.2 渗流-变形耦合方程本文假设所用土体材料的本构模型为线弹性模型,对于二维问题,非饱和土介质的增量应变-应力关系[15]可以写成
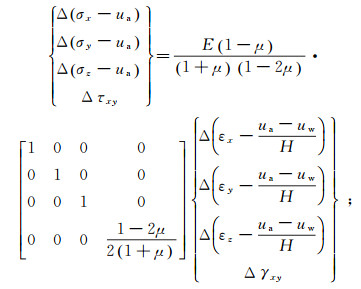 (6)
(6) 式中:σx,σy,σz分别为x,y,z方向正应力;τxy为垂直于x方向沿y方向切应力;εx, εy, εz分别为x,y,z方向正应变;γxy为垂直于x方向沿y方向切应变;ua为孔隙气压力;uw为孔隙水压力; ua-uw为基质吸力;μ为泊松比;E为土的刚度模量,可以是常数或上覆土层有效应力的函数。
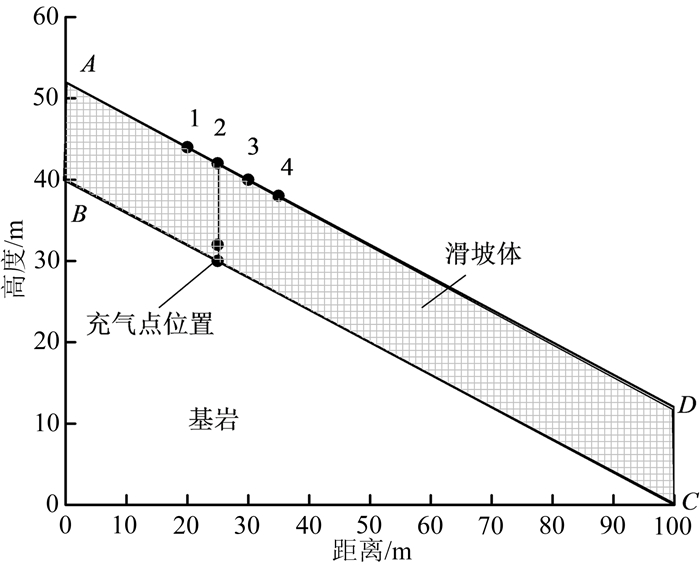
2.3 数值计算模型及参数选取采用二维边坡进行模拟分析,具体模型及网格划分如图 1所示。滑坡体位于基岩上方,滑面位置固定,坡体厚12 m、长100 m、坡度21°。充气点位置坐标为(25,31)。
|
| 图 1 几何模型和网格划分 Fig. 1 Geometric model and mesh generation |
|
|
首先进行水-气二相流的模拟。自然条件下未充气时的边界条件:坡体后缘AB水头为49 m,坡体表面AD为透水透气边界,坡体右侧CD为潜在渗流面边界但不透气,滑面以下基岩面BC设为不透水边界。充气时的边界条件:水相边界条件同上;气相边界条件为,充气位置选取合适的充气气压值,坡体表面AD为透气边界,气压大小等于大气压的值,坡体两侧AB、CD和底部BC为不透气边界。采用粉砂作为模型材料,Van Genuchten模型的拟合参数取值为a=7,n=1.86,m=0.462,非饱和土渗透系数函数和透气系数函数只需给定饱和土的渗透系数Ks和干土的透气系数Kdg即可确定,结合工程地质手册[16]及工程经验,取Kdg=10Ks=3.0×10-3 cm/s,θs=0.352 m3/m3,θr=0.040 m3/m3。之后将水-气二相流模拟结果导入SIGMA/W模块进行计算,假定坡体AB、CD边界只能沿竖向移动,BC边界水平和竖向都固定,选取材料本构模型为线弹性模型,各参数取值如表 2所示。
| 土体材料 | 泊松比 | 材料重度/ (kN/m3) |
内摩擦角 /(°) |
黏聚力 /kPa |
弹性模量 /kPa |
| 粉砂 | 0.334 | 19.7 | 34 | 6 | 12 000 |
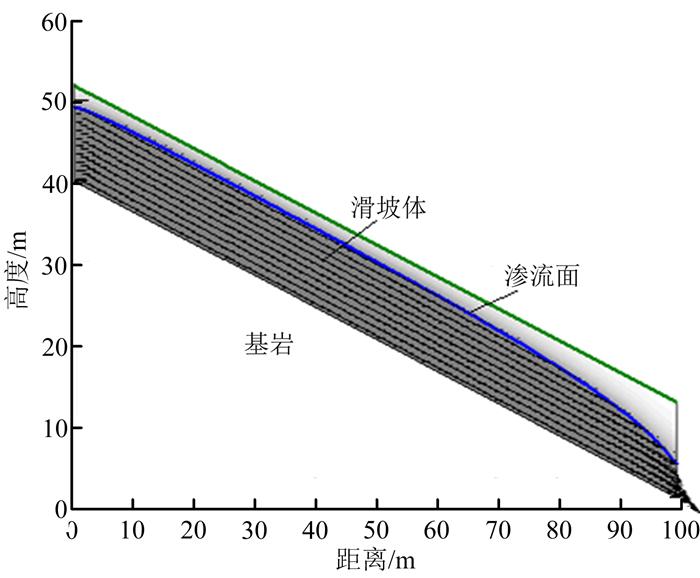
首先进行稳态分析,得到未充气时自然状态下的边坡初始渗流场,结果如图 2所示。
|
| 图 2 自然状态下边坡初始渗流场 Fig. 2 Initial seepage field of slope under natural statement |
|
|
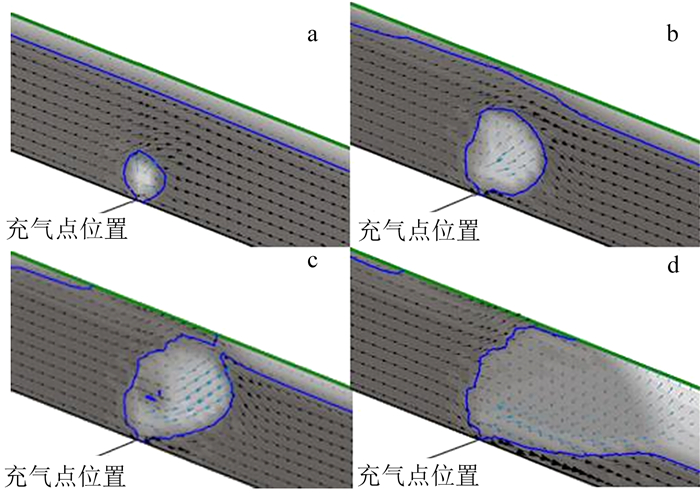
然后计算充气状态下的非饱和瞬态渗流场的变化。图 3所示是当充气压力p=100 kPa时,充气引起的非饱和区形态以及渗流场的变化过程,从阶段1到阶段4,图中颜色越深的区域代表饱和度越大,箭头越大代表流速越大。充气刚开始时,气体排开土体孔隙中的水,非饱和区域范围较小,且离充气点越近的地方饱和度越小,同时水流流动方向发生改变,但坡内地下水位线无明显变化(图 3a);随着充气的进行,非饱和区逐渐扩大,且坡体内的地下水位线有明显的上升,这是由于非饱和区大小达到一定程度后严重阻碍了后缘来水的渗流路径,水流只能向坡面方向流去导致地下水位局部抬升(图 3b);紧接着非饱和区突破地下水位线,与下游水位线以上的非饱和区域连通,气体开始逸出坡体,此时非饱和区气压力迅速降低,水气界面向气相方向运动挤压气体,当气压力增大到一定程度时水气界面又向液相方向运动,非饱和区以此规律不断发展直到达到水气平衡状态,而下游水位由于非饱和区对后缘来水的拦截逐渐下降(图 3c);最后到达稳定状态(图 3d)。
|
| a.阶段1;b.阶段2;c.阶段3;d.阶段4。 图 3 充气压力为100 kPa时非饱和区及渗流场的变化过程 Fig. 3 Change of unsaturated zone and seepage field during aerating when the aerated pressure is 100 kPa |
|
|
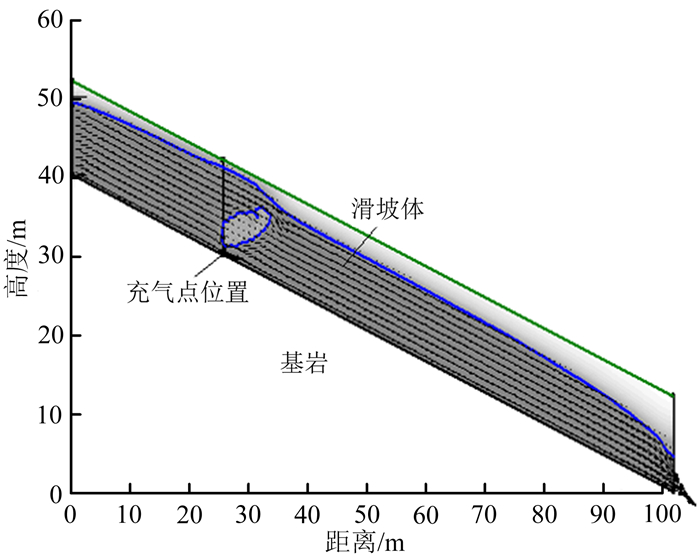
另外,当充气压力较小时,虽然非饱和区不断扩大,但是始终无法突破地下水位线,图 4所示是充气压力p=80 kPa时充气稳定后的渗流场。可以推测气体驱替该气压下所能驱动的部分土体孔隙通道中的水体,使得该区域饱和度下降,且由于土体的封气性,形成一个有明显水气分界面的稳定非饱和区,从而在一定程度上拦截后缘来水。
|
| 图 4 充气压力为80 kPa时的稳定渗流场 Fig. 4 Steady seepage field when the aerated pressure is 80 kPa |
|
|
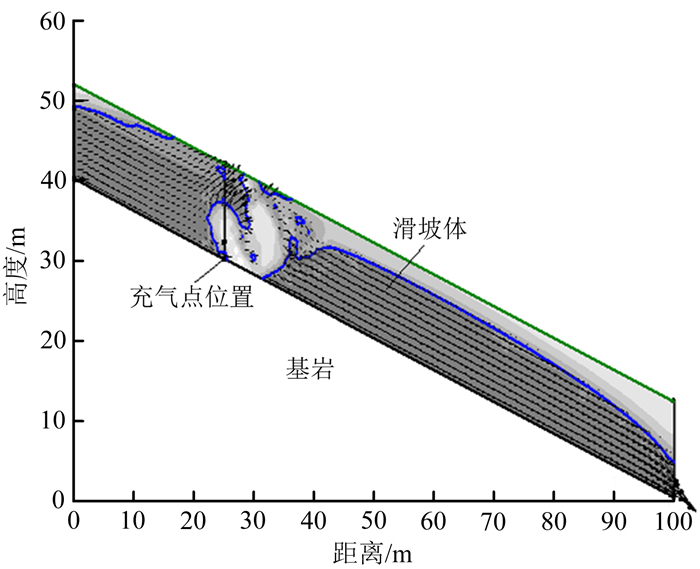
当充气压力过大时,虽然非饱和区从阶段1到阶段4的时间大大缩短,但是由于气压力超过此坡体的进气气压上限值[4],水气运移的平衡已被打破,数值上不再收敛,物理上表现为渗流场紊乱。图 5为充气压力p=120 kPa时某一时刻水气相互作用形成的不稳定紊乱渗流场。
|
| 图 5 充气压力为120 kPa时某一时刻形成的紊乱渗流场 Fig. 5 Unstable seepage field formed at a certian moment when the aerated pressure is 120 kPa |
|
|
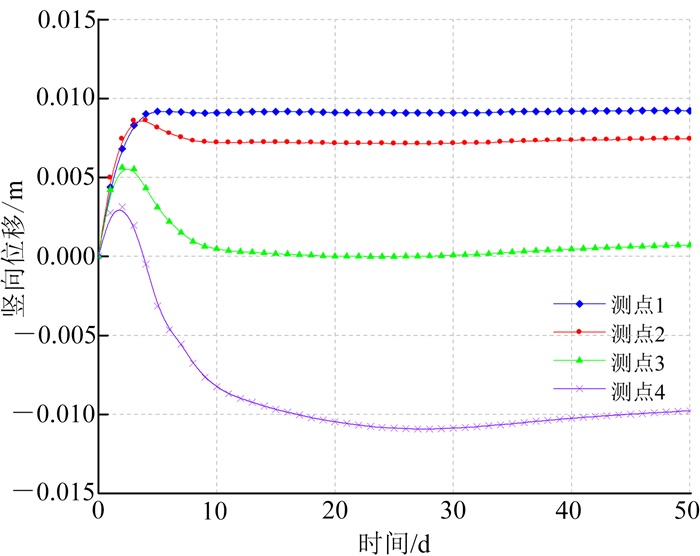
将上述计算得到非饱和渗流场作为已知条件导入到SIGMA/W模块进行变形模拟分析。选取图 1中1(20,44)、2(25,42)、3(30,40)、4(35,38)4个测点,模拟在不同充气压力下各点竖向位移随时间的变化,探究充气压力大小及渗流场变化对坡体变形的影响。在充气压力p=100 kPa的条件下,4个测点的竖向位移随时间的变化如图 6所示。
|
| 图 6 充气压力为100 kPa时测点竖向位移随时间变化曲线 Fig. 6 Vertical displacement versus time curve of each measuring point when the aerated pressure is 100 kPa |
|
|
从图 6可以看出,所有点的竖向位移都随时间先增大后减小,最后趋于稳定。这是因为有压气体排开土体孔隙水形成一个相对封闭的有压非饱和区后会对周围土体有托顶挤压的作用,从而使地表土体发生隆起变形;而当封闭非饱和区与外界联通气体逸出时,地表土体又会发生沉降变形,所以各测点的竖向位移形成了如图 6所示的变化趋势。而充气稳定后其中测点1和2的竖向位移为正,测点3的竖向位移约为0,测点4的竖向位移为负。这是因为测点1和2的位置相对于充气非饱和区偏上,且位于水气交界面的水相一侧,气体压力对上游土体有顶托作用且阻碍其向下游的变形,故其竖向位移为正;测点3和4的位置相对于充气非饱和区偏下,且位于水气交界面的气相一侧,其中测点3受向上托顶的力产生的正向竖向位移与受沿坡向推挤的力产生的负向竖向位移相当,故竖向位移约为0,而测点4在充气稳定后受沿坡向推挤的力产生的负向竖向位移占优势,所以最后竖向位移为负。
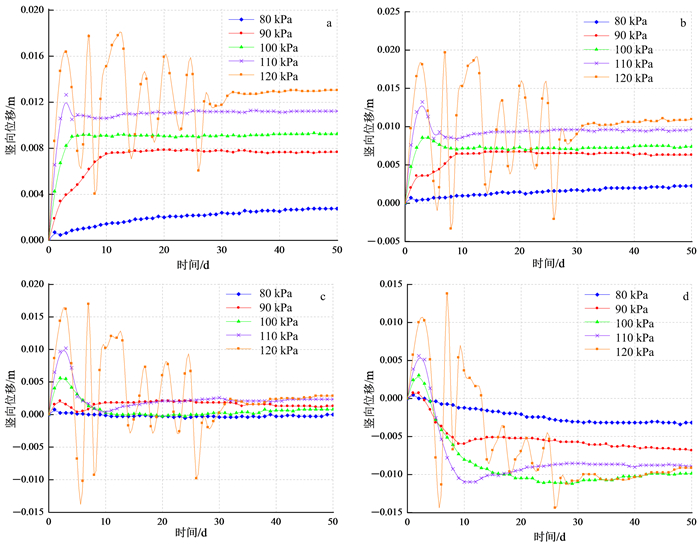
3.3 不同充气压力下各测点位移变化分析为进一步探究充气压力大小对坡体渗流场及土体变形的影响,以及渗流场变化与土体变形之间的联系,选取不同的充气压力进行数值模拟,得到各测点在不同充气压力下竖向位移随时间的变化规律。由图 7a、7b可知,测点1和测点2的在不同充气压力下竖向位移的变化规律类似。当充气压力较小(p≤90 kPa)时,在模拟的时间范围内竖向位移随着充气进行缓慢增大;当充气压力较大(90 kPa < p≤110 kPa)时,竖向位移先增大后减小最后趋于一个相对稳定的值;当充气压力继续增大(p>110 kPa)时,竖向位移开始出现波动的不稳定现象。产生上述不同现象的原因是:充气压力较小时,非饱和区在坡体内不断扩大,气压力缓慢向上托顶上覆土层,但是非饱和区始终不能突破坡体表面;充气压力较大时,非饱和区突破坡体表面前气压力逐渐向上托顶上覆土层,非饱和区突破坡体表面后,气体逸出坡体气压力减小,上覆土层出现沉降;充气压力继续增大超过进气气压上限值时,过大的充气压力会造成渗流场紊乱,同时破坏土体结构,此时气体通过裂隙逸出坡体,非饱和区气压力下降,坡体表面土体发生下陷,而当周围的水重新挤压非饱和区气体,孔隙气压力又开始上升,坡体表面土体发生隆起变形;随后气压增大到一定程度又会逸出导致坡体表面土体发生下陷,如此坡体表面土体竖向位移做类似的上下波动变化,直到最后达到一个相对稳定的状态。
|
| a.测点1;b.测点2;c.测点3;d.测点4。 图 7 不同充气压力下不同测点竖向位移随时间变化 Fig. 7 Vertical displacement versus time curve of the different measuring points under different aerated pressures |
|
|
由图 7c可知,在充气压力p=120 kPa时,测点3的竖向位移呈现无规律的上下波动变化。该测点在不同充气压力下初期竖向位移所能达到的峰值随充气压力的增大而增大,而最后稳定的竖向位移值均较小(y < 0.003 m)。这是因为测点3受向上托顶的力产生的正向竖向位移与受沿坡向推挤的力产生的负向竖向位移相当,故位移较小。由图 7d可知,测点4在充气后期竖向位移都为负值,当充气压力超过100 kPa后,测点最后的竖向位移大小无规律,即位于非饱和区域下游的测点的位移量不一定随充气压力的增大而相应增大,而是具有一定的不确定性。
4 结论1) 在一定且合适的充气压力下,充气非饱和区的形成可分为4个阶段,即充气初始阶段、非饱和区扩大水位抬升阶段、不稳定两相流阶段和非饱和区稳定阶段。而当充气压力较小时,充气形成的非饱和区无法突破坡体表面,仅停留在水位抬升阶段;充气压力过大时,无法形成稳定非饱和区达到截排水工作状态。
2) 在某一特定且合适的充气压力下,坡体表面土体的竖向位移均随时间呈现先增大后减少的规律,与土体中非饱和区的发展具有一定协同性,最后稳定时越靠近坡体上游的土体整体竖向位移越大。
3) 不同充气压力下,偏向充气点上游的坡体表面土体竖向位移随充气压力的增大而增大,偏向充气点下游的坡体表面土体竖向位移的变化规律则不明显。当充气压力过大时,无法形成稳定非饱和区,在土体变形上表现为竖向位移变化无规律。
4) 采用弹性应力-应变关系对充气截排水过程中土体变形的预测基本反映了其变形趋势,具有一定的参考价值,为定量描述非饱和土渗流以及变形的耦合分析问题提供了有效途径。
| [1] |
孙红月, 尚岳全, 龚晓南. 工程措施影响滑坡地下水动态的数值模拟研究[J]. 工程地质学报, 2004, 12(4): 436-440. Sun Hongyue, Shang Yuequan, Gong Xiaonan. Numerical Simulation of Groundwater Seepage Field in Landslide[J]. Journal of Engineering Geology, 2004, 12(4): 436-440. DOI:10.3969/j.issn.1004-9665.2004.04.019 |
| [2] |
张作辰. 滑坡地下水作用研究与防治工程实践[J]. 工程地质学报, 1996, 4(4): 80-85. Zhang Zuochen. Mechanism of Groundwater Effect Landslide Stability and Control Construction[J]. Journal of Engineering Geology, 1996, 4(4): 80-85. |
| [3] |
杜丽丽, 孙红月, 尚岳全, 等. 滑坡应急治理充气截水方法[J]. 岩石力学与工程学报, 2013, 32(增刊2): 3954-3960. Du Lili, Sun Hongyue, Shang Yuequan, et al. Method of Intercepting Water by Filting Soil with Air in Emergency Treatment Engineering of Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(Sup.2): 3954-3960. |
| [4] |
杜丽丽, 孙红月, 尚岳全. 松散堆积土边坡充气排水方法[J]. 吉林大学学报(地球科学版), 2013, 43(3): 877-882. Du Lili, Sun Hongyue, Shang Yuequan. Air-Filled Drainage Method in Loose Accumulation Soil Slope[J]. Journal of Jilin University(Earth Science Edition), 2013, 43(3): 877-882. |
| [5] |
康剑伟, 孙红月, 刘长殿. 一维土柱高压充气阻渗法的数值模拟[J]. 公路工程, 2013, 38(3): 67-71. Kang Jianwei, Sun Hongyue, Liu Changdian. Numerical Simulation of High-Pressure Infiltration Resistance of One-Dimensional Soil Column[J]. Highway Engineering, 2013, 38(3): 67-71. |
| [6] |
杜丽丽, 孙红月, 尚岳全, 等. 充气截排水滑坡治理数值模拟研究[J]. 岩石力学与工程学报, 2014, 33(增刊1): 2628-2634. Du Lili, Sun Hongyue, Shang Yuequan, et al. Simulation of Numericalcontrol of Pneumatic Cut-off Method for Landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Sup.1): 2628-2634. |
| [7] |
余文飞, 孙红月, 尚岳全, 等. 坡体充气过程中气水两相流数值模拟[J]. 岩石力学与工程学报, 2016(增刊2): 3597-3604. Yu Wenfei, Sun Hongyue, Shang Yuequan, et al. Numerical Simulation of Air-Water Two-Phase Flow in Inflatable Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2016(Sup.2): 3597-3604. |
| [8] |
余文飞, 孙红月, 沈佳轶, 等. 降低滑坡地下水位的充气截排水法最佳充气压力研究[J]. 岩石力学与工程学报, 2017, 36(4): 890-897. Yu Wenfei, Sun Hongyue, Shen Jiayi, et al. Research on Optimal Air Filling Pressure for Groundwater Blocking and Draining in Slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(4): 890-897. |
| [9] |
王勇, 孔令伟, 郭爱国, 等. 气体释放速率对浅层气藏中气水运移的影响[J]. 浙江大学学报(工学版), 2010, 44(10): 1883-1889. Wang Yong, Kong Lingwei, Guo Aiguo, et al. Effects of Gas Release Rate on Gas-Water Migration in Shallow Gas Reservoir[J]. Journal of Zhejiang University(Engineering Science), 2010, 44(10): 1883-1889. DOI:10.3785/j.issn.1008-973X.2010.10.007 |
| [10] |
胡新国. 浅层天然气对土体工程的影响[J]. 岩土工程界, 2003, 6(2): 39-41. Hu Xinguo. Influence of Shallow Soil Layer Containing High-Pressure Gas on Soil Body[J]. Chinese Journal of Gectchnical Engineering, 2003, 6(2): 39-41. DOI:10.3969/j.issn.1674-7801.2003.02.037 |
| [11] |
王勇, 孔令伟, 郭爱国. 有控放气措施下含浅层气地层的一维变形分析[J]. 岩土力学, 2011, 32(增刊1): 241-246. Wang Yong, Kong Lingwei, Guo Aiguo. Analysis of One-Dimensional Deformation of Shallow Gassy Stratum Caused by Controlling Gas Release[J]. Rock and Soil Mechanics, 2011, 32(Sup.1): 241-246. |
| [12] |
徐炎兵, 韦昌富, 李幻, 等. 非饱和土渗流与变形耦合问题的有限元分析[J]. 岩土力学, 2009, 30(5): 1490-1496. Xu Yanbing, Wei Changfu, Li Huan, et al. Finite Element Analysis of Coupling Seepage and Deformation in Unsaturated Soils[J]. Rock and Soil Mechanics, 2009, 30(5): 1490-1496. DOI:10.3969/j.issn.1000-7598.2009.05.053 |
| [13] |
Geo-Slope International Ltd. Air Flow Modeling with AIR/W 2007[M]. Calgary: Geo-Slope International Ltd Press, 2008: 117-120.
|
| [14] |
Van Genuchten M T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils[J]. Soil Science Society of America Journal, 1980, 44: 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
| [15] |
Geo-Slope International Ltd. Sigma Modeling with AIR/W 2007[M]. Calgary: Geo-Slope International Ltd Press, 2008: 131-141.
|
| [16] |
常士骠, 张苏民, 项勃, 等. 工程地质手册[M]. 第四版. 北京: 中国建筑工业出版社, 2006: 158-161. Chang Shibiao, Zhang Sumin, Xiang Bo, et al. Engineering Geology Handbook[M]. 4th ed. Beijing: China Architecture and Building Press, 2006: 158-161. |


