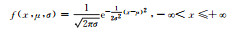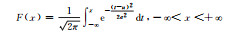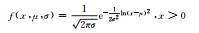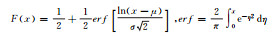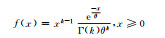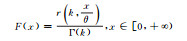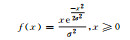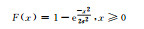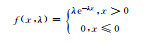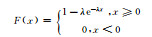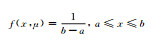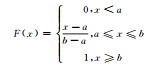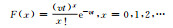0 引言
岩体是由结构面和岩块共同组成的系统,大多数结构面是具有一定方向、尺度与空间分布的不连续面。结构面的五大基本参数包括产状、迹长、形态、间距、张开度,具有这些参数的不连续面随机组合形成岩体结构网络。结构面参数中的迹长反映了结构面规模,产状描述了结构面方向,结构面形态是岩体力学性质和水力学性质研究的基础,间距反映了岩体完整性,张开度用来描述结构面开启性。结构面几何参数是不连续面三维网络模拟以及岩体结构性质统计研究的基础,一般由野外实测而得[1],测量方法分为接触测量和非接触测量。接触测量法主要利用皮尺和罗盘进行结构面信息采集[2],操作简单但低效、不安全。非接触测量法有三维激光扫描仪法和数字近景摄影测量法:三维激光扫描法具有扫描速度快、获取信息量大、节约时间、使用方便等特点,但由于扫描距离和范围有限、成本较高难以达到普及化应用;数字近景摄影测量法具有成本低、容易实现、劳动强度小、拍摄照片可以反复使用等特点,在工程地质作业中受到广泛青睐[3-5]。国内外许多学者进行了数字近景摄影测量的相关研究:Ross-Brown等[6]首次利用摄影测量像片进行了岩体节理走向和迹长的解译;王凤艳等[7]利用数字近景摄影测量技术结合基于空间坐标的结构面几何信息解算模型获取岩体结构面参数信息;胡运海[8]基于数字近景摄影测量技术对北川县擂鼓镇凤凰山进行了滑坡动态监测;高昭良[9]建立了基于数字摄影测量的滑坡监测系统,对滑坡体进行有效监测。
近些年来,大量研究发现岩体结构面具有统计相似性特征,因而开展结构面的间距、规模、张开度、产状等几何参数概率分布的研究。基于摄影测量方法获取岩体结构面参数并研究分布规律,可求出岩体结构面参数理论分布,从而建立岩体结构面参数概率模型,但如何找到合适的概型是比较困难的;采用统计推断和随机数学的方法可以有效解决这个问题[10]。随机变量的概率统计一般有如下分布类型:正态、对数正态、伽马、负指数、泊松、均匀或威尔分布等,参数一般是未知的。常用的假设检验方法有A-D检验法、χ2法、K-S检验法、K检验法、W检验法、C-M检验法、D检验法等;其中K-S检验法具有很强通用性[11-12],国内外诸多学者基于K-S检验法进行了大量相关研究;Massey L. H. [13]进行了K-S检验法的最优拟合研究:Lilliefors H. [14]在均值和方差未知的情况下进行正态分布的K-S假设检验;李勇等[15]基于非参数试验对松塔坝址构造域边界进行识别;陈剑平[16]基于K-S假设检验原理对三峡坝址永久船闸人工岩石高边坡的不连续面观测数据进行了假设检验;马建全等[17]采用K-S检验法对四川省雅安经石棉至泸沽高速公路进行假设验证,确定变量的分布类型。
本文基于数字近景摄影测量理论,以VirtuoZo数字摄影测量站为平台提取结构面特征点的三维坐标,利用Matlab程序实现岩体结构面迹长、产状、间距等信息的快速获取,并基于K-S检验原理对获取的岩体几何参数编程实现概率分布检验,分析参数所服从的分布规律,寻找最优拟合概型,以期为迹长模型估计、连通率计算、岩石质量指标计算及岩体稳定性评价提供基础。
1 方法 1.1 常用概率分布函数根据统计学原理,将样本观测值分成若干区间,制作频率直方图。由频率直方图可以观察观测值分布特征,但频率直方图缺少数学描述,于是给出常见的概率分布函数(表 1)。但哪个函数可以准确地描述观测值概率分布特征,直觉上较难判断,需要进行观测值的假设检验。概率密度函数是假设检验的前提,常用的概率密度函数有正态分布、对数正态分布、伽马分布、瑞利分布、指数分布、均匀分布、泊松分布等(表 1)。
在工程地质问题研究过程中,先估计结构面几何参数服从的分布,再进行假设检验。检验法以χ2检验和K-S检验最为常用,但由于χ2检验受分组影响以及样本数量限制,K-S检验结果更为精确。当样本容量n很大时,K-S检验通过对样本每个点进行检验,得到样本所服从分布的直观判断。
假设H0:F(x)=F0(x),其中,F0(x)是完全已知的连续型分布。考虑一个样本具有n个观测值,首先将样本数据按照从小到大的顺序进行排序,这些数据可以构造一个阶梯状的累积频率函数:
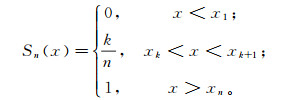 (1)
(1) 式中:x1, x2, …, xn为排序后的样本数据值;1≤k≤ n。
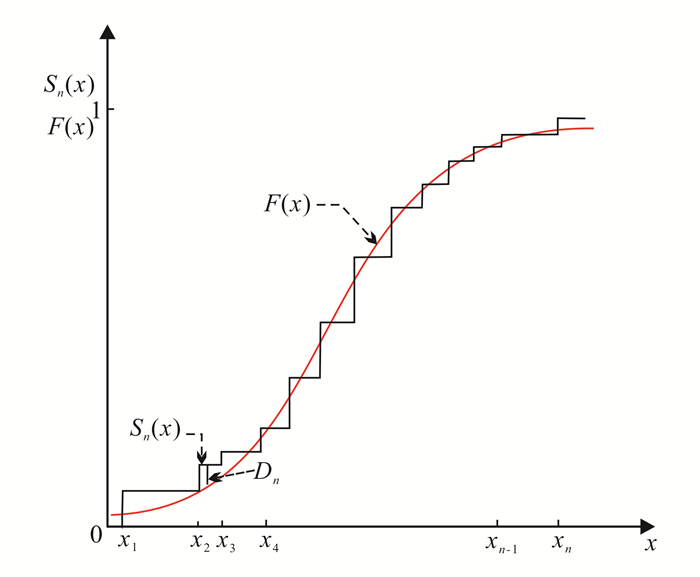
图 1表明了Sn(x)与F(x)的关系。
|
| 图 1 累积频率及其理论分布 Figure 1 Distribution of the cumulative frequency and its theoretical |
|
|
K-S检验中,Sn(x)和F(x)在整个区间范围内的最大差值就是理论模型和观测数据之间差值的度量,即假设检验的统计量,表示为
 (2)
(2) 理论上,Dn的分布取决于n的大小。
给定一个具体的显著性水平α,K-S检验是将公式(2)中的Dn与临界值Dnα进行比较:
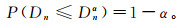 (3)
(3) 式中,P为Dn<Dnα的概率。如果Dn<Dnα,则接受显著水平α下假设的分布类型;否则拒绝此假设分布类型。当n充分大时,Sn(x)与F(x)可以足够接近,它们的统计量会趋向于0,这样的结果是概率为1的必然事件,即
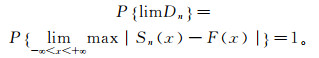 (4)
(4) 因此,当n足够大时可用累积频率函数来代替理论概率分布函数[19-21]。
1.3 最优拟合度当结构面参数的K-S检验结果出现服从多种概率分布情况时,需进一步判别最优概率分布。引入拟合度φ比较各种概率分布与实际情况的接近程度。拟合度是对预测概率模型进行检验并对预测结果与实际发生情况的接近程度进行描述的参数:
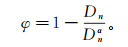 (5)
(5) φ越大,则概率分布模型拟合度越优[22]。
2 工程实例 2.1 研究区概况研究区域位于长春市东南部的净月开发区东升村,地理坐标为125°30′ E、43°48′ N。研究区内存在大量废弃的采石场,边坡开发严重、出露面积较大,需要进行大量岩体随机结构面调查,为边坡稳定性评价提供数据。选择其中一个出露完整的边坡为实验对象(图 2),该边坡长约50 m,高约30 m,走向240°,倾角80°。由于边坡底部有大量积水,地势险峻,很难进行野外人工接触作业;选用近景摄影测量方法可以有效解决野外作业环境险峻、人工测量难以靠近等问题。

|
| 图 2 研究区影像图 Figure 2 Image maps of the research area |
|
|
研究数据是基于数字近景摄影测量技术获取的,分为野外数据和室内数据。野外数据采集主要包括摄影测量时所进行的研究区地面控制测量和建立立体模型的边坡控制点测量;室内数据处理包括立体模型的建立以及结构面信息的提取。
2.2.1 野外数据采集1) 控制测量
整体控制测量:研究区地形起伏较大,山体由于采石被分割成几个分散陡峭的边坡。根据地形特点,分别采用导线测量和三角高程测量进行边坡平面和高程控制,经平差计算得到研究区整体控制测量成果。
边坡控制测量:由于研究区内的边坡底部有大量的积水,边坡面陡峭,不易靠近,采用免棱镜全站仪空间极坐标测量法进行边坡控制测量。野外需要尽可能多地采集易辨识控制点以便内业处理时选用,实际作业时每个坡面上至少选择11个控制点以保证边坡三维模型的精度。
2) 边坡影像获取
采用非量测相机进行边坡摄影,实验使用相机型号为佳能EOS 5D Mark Ⅱ。利用室内三维控制架进行相机标定,获取相机内方位元素及镜头畸变系数;摄影距离根据地形情况确定,摄影基线与边坡走向一致,采用近似正直摄影方式获取边坡立体像对,最后结合相机标定参数校正边坡影像。
2.2.2 室内数据处理基于外业的控制测量成果和校正的边坡立体像对,利用VirtuoZo工作站进行边坡三维模型建立,包括测区建立、相对定向、绝对定向和非水平核线影像生成等环节。所建模型点位测量精度为±0.05 m。基于立体模型,利用VirtuoZo中的IGS (integrated graphic system)模块采集结构面特征点坐标信息并标记属性,再结合结构面参数解算模型获取边坡全景露头大量结构面的迹长、产状、间距等参数。
2.3 结构面参数K-S检验根据文献[22],选取正态、对数正态、指数、伽马、均匀、瑞利、泊松7种分布函数,采用Matlab编制K-S检验程序对SPSS软件中未有的分布类型进行补充并对获取的结构面迹长、产状、间距等结构面参数进行K-S检验。
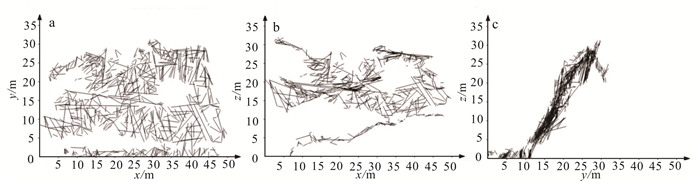
2.3.1 结构面迹长检验以研究区内坡2为例,基于近景摄影测量方法获取坡2结构面几何参数,并将迹线投影至工程坐标系所定义的3个相互垂直投影面上,得到683条迹线的二维分布情况(图 3)。
|
| a. xoy面;b. xoz面;c. yoz面。 图 3 结构面迹线二维分布 Figure 3 Two-dimensional distribution map of structural plane trace |
|
|
对683条二维迹长进行K-S检验,结果如图 4和表 2所示。由图 4可见,二维迹长服从对数正态分布。由表 2可见,P≈Sig,并且,由Ksstat和Z分别计算Dn,得到近似相等的值;可知程序运行结果与SPSS软件验证结果一致。

|
| a. xoy面;b. xoz面;c. yoz面。 图 4 二维迹长K-S检验结果拟合曲线 Figure 4 Fitting curve of two-dimensional trace length by K-S test |
|
|
| 检验数据 | 分布类型 | 参数 | K-S检验 | SPSS软件 | ||||||||
| μ | σ | H | P | Ksstat | Cv | N | Z | Sig | ||||
| xoy面迹长 | 对数正态 | 0.613 | 0.791 | 0 | 0.273 | 0.038 | 0.051 7 | 683 | 0.991 | 0.280 | ||
| xoz面迹长 | 对数正态 | 0.536 | 0.628 | 0 | 0.605 | 0.029 | 0.051 7 | 683 | 0.757 | 0.615 | ||
| yoz面迹长 | 对数正态 | 0.533 | 0.689 | 0 | 0.310 | 0.038 | 0.051 7 | 683 | 0.958 | 0.318 | ||
| 三维迹长 | 对数正态 | 0.485 | 0.606 | 0 | 0.052 | 0.051 | 0.052 0 | 676 | 1.343 | 0.054 | ||
注:H.原假设;P.概率;Ksstat=Dn;Cv=Dnα;N.样本数;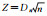 ;Sig.概率。 ;Sig.概率。 |
||||||||||||
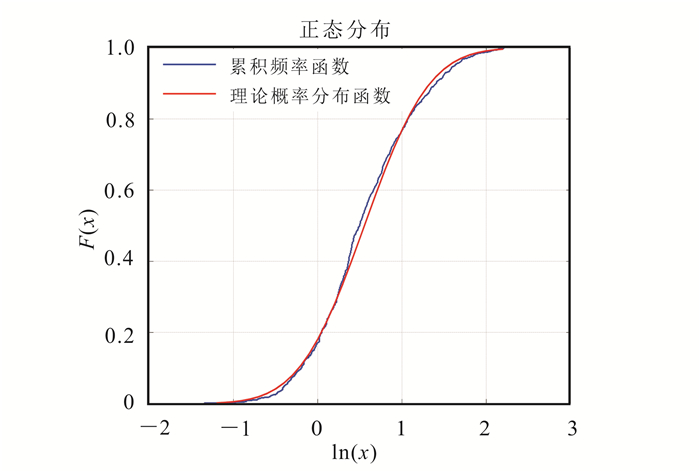
由于迹长分布存在较严重的拖尾情况,将迹长大于10的部分去除后进行K-S检验,此时三维迹长服从对数正态分布规律(图 5,表 2)。
|
| 图 5 三维迹长的K-S检验结果拟合曲线 Figure 5 Fitting graph of three-dimensional trace length by K-S test results |
|
|
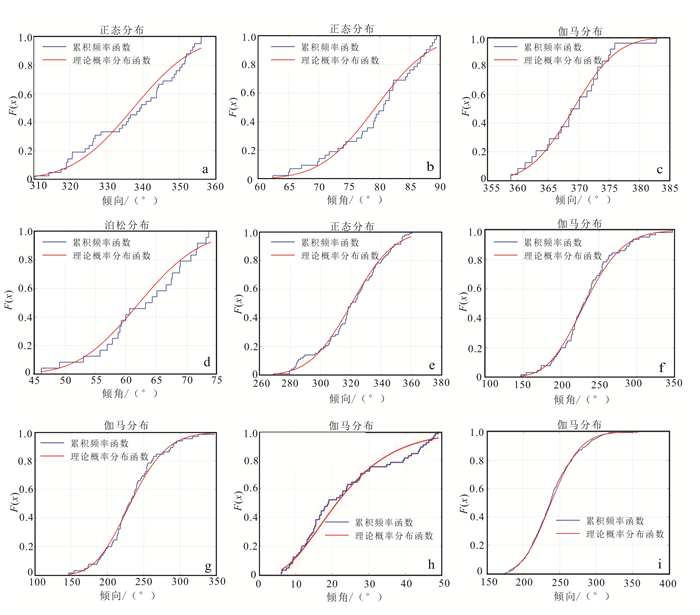
基于目标函数法将产状进行优势分组,共分成5组,对每一组进行检验,发现产状服从正态分布、伽马分布、瑞利分布以及泊松分布(表 3,图 6)。由最优拟合度计算可知产状趋于服从伽马分布规律。同时,第五组倾角不服从任何一种分布。
| 组别 | 迹线数量 | 倾向 | 倾角 | |||||||||||
| 分布 | H | P | Ksstat | Cv | φ | 分布 | H | P | Ksstat | Cv | φ | |||
| 1 | 42 | 正态 | 0 | 0.614 | 0.113 | 0.205 | 0.448 | 正态 | 0 | 0.516 | 0.122 | 0.205 | 0.404 | |
| 伽马 | 0 | 0.563 | 0.118 | 0.205 | 0.425 | 伽马 | 0 | 0.396 | 0.135 | 0.205 | 0.344 | |||
| 泊松 | 0 | 0.360 | 0.139 | 0.205 | 0.324 | |||||||||
| 2 | 24 | 正态 | 0 | 0.996 | 0.079 | 0.709 | 正态 | 0 | 0.923 | 0.106 | 0.269 | 0.606 | ||
| 伽马 | 0 | 0.997 | 0.077 | 0.715 | 伽马 | 0 | 0.866 | 0.116 | 0.269 | 0.569 | ||||
| 泊松 | 0 | 0.955 | 0.099 | 0.269 | 0.633 | |||||||||
| 3 | 92 | 正态 | 0 | 0.801 | 0.066 | 0.140 | 0.531 | 正态 | 0 | 0.710 | 0.071 | 0.140 | 0.490 | |
| 伽马 | 0 | 0.697 | 0.072 | 0.140 | 0.483 | 伽马 | 0 | 0.953 | 0.052 | 0.140 | 0.627 | |||
| 泊松 | 0 | 0.276 | 0.102 | 0.140 | 0.271 | |||||||||
| 4 | 65 | 正态 | 0 | 0.814 | 0.077 | 0.166 | 0.538 | 正态 | 0 | 0.071 | 0.157 | 0.166 | 0.054 | |
| 伽马 | 0 | 0.889 | 0.070 | 0.166 | 0.580 | 伽马 | 0 | 0.482 | 0.102 | 0.166 | 0.387 | |||
| 瑞利 | 0 | 0.228 | 0.127 | 0.166 | 0.235 | |||||||||
| 5 | 320 | 正态 | 0 | 0.052 | 0.062 | 0.063 | 0.016 | |||||||
| 伽马 | 0.322 | 0.044 | 0.063 | 0.302 | ||||||||||
|
| a、b.第一组;c、d.第二组;e、f.第三组;g、h.第四组;i.第五组。 图 6 五组产状K-S检验最优结果拟合曲线 Figure 6 Optimal result fitting curve of five groups by K-S test |
|
|
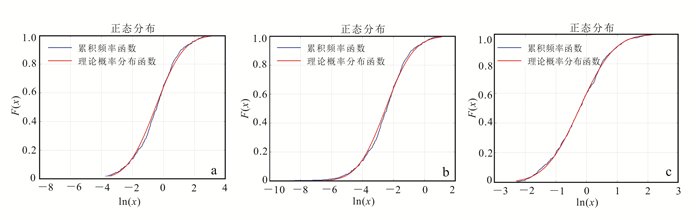
检验xoy、xoz面间距,可知其服从对数正态分布(图 7a、b,表 4)。将yoz面间距数据进行去除极大值和极小值处理(去除间距对数值大于1和小于负1.5的值),处理后的yoz面间距服从对数正态分布(图 7c,表 4)。
|
| a. xoy面间距;b.xoz面间距;c.yoz面间距。 图 7 面间距K-S检验结果拟合曲线 Figure 7 Fitting curve of discontinuities spacing by K-S test |
|
|
| 检验数据 | 分布类型 | 参数 | Matlab程序结果 | |||||
| μ | σ | H | P | Ksstat | Cv | |||
| xoy面间距 | 对数正态 | 1.092 | 1.422 | 0 | 0.116 | 0.051 9 | 0.059 1 | |
| xoz面间距 | 对数正态 | 0.577 | 0.641 | 0 | 0.324 | 0.032 2 | 0.045 9 | |
| yoz面间距 | 对数正态 | 0.868 | 1.139 | 0 | 0.167 | 0.038 3 | 0.046 7 | |
1) 基于数字近景摄影测量原理,利用数字摄影测量工作站VirtuoZo,可建立研究区边坡的高精度立体模型,模型点位测量精度为±0.05 m,结合基于空间坐标的结构面参数解算模型,获取了边坡全景露头大量随机结构面的参数。
2) 经K-S检验知:结构面二维迹长服从对数正态分布;去除极大值后的三维迹长亦服从对数正态分布;分组后的产状服从正态分布、伽马分布、瑞利分布、泊松分布4种分布,由最优拟合度计算可知产状趋向于服从伽马分布规律;二维xoy,xoz面间距服从对数正态分布,经极大值和极小值去除后的yoz面间距亦服从对数正态分布。
3) 基于Matlab编程实现了岩体结构面参数的K-S检验,程序可实现正态、对数正态、指数、伽马、瑞利、均匀、泊松多种分布函数的检验,补充了SPSS软件中不具备的对数正态、伽马、瑞利3种分布函数;同时用SPSS软件中具有的指数、均匀、泊松、正态分布函数验证了程序正确性。该程序还可以进行其他任一变量的概率分布检验。
4) 对于研究中出现的某结构面参数不服从任何一种分布的情况,需要进一步研究。
| [1] |
伍法权. 统计岩体力学原理[M]. 武汉: 中国地质大学出版社, 1993. Wu Faquan. Principles of Statistical Mechanics of Rock Mass[M]. Wuhan: China University of Geosciences Press, 1993. |
| [2] |
张文.基于三维激光扫描技术的岩体结构信息化处理方法及工程应用[D].成都: 成都理工大学, 2011. Zhang Wen. Information Processing Methodon Rock Mass Structure and Its Application in Geological Engineering Based on Three-Dimensional Laser Scanning Technique[D]. Chengdu: Chengdu University of Science and Technology, 2011. http://cdmd.cnki.com.cn/Article/CDMD-10616-1011235815.htm |
| [3] |
范留明, 王中锋, 李宁. 基于近景摄影测量法计算掘进隧洞中切穿顶拱的裂隙面产状[J]. 地球科学与环境学报, 2008, 36(1): 283-285. Fan Liuming, Wang Zhongfeng, Li Ning. Attitude Determination of Joint Running Through Vault Based on Close-Range Photogrammetry in Excavating Tunnel[J]. Journal of Earth Sciences and Environment, 2008, 36(1): 283-285. |
| [4] |
吴志勇, 聂德新, 蔡云, 等. 岩体结构信息的采集处理研究[J]. 中国地质灾害与防治学报, 2003, 14(2): 82-83. Wu Zhiyong, Nie Dexin, Cai Yun, et al. Research of Collecting Information of Rock Mass Structure[J]. The Chinese Journal of Geological Hazard and Control, 2003, 14(2): 82-83. DOI:10.3969/j.issn.1003-8035.2003.02.017 |
| [5] |
李浩, 杜丽丽, 贾晓敏, 等. 基于数码影像的边坡工程地质编录信息系统[J]. 华南理工大学学报(自然科学版), 2008, 36(1): 145-151. Li Hao, Du Lili, Jia Xiaomin, et al. Geologic Logging Information System Based on Digital Image for Slope Engineering[J]. Journal of South China University of Technology (Natural Science Edition), 2008, 36(1): 145-151. DOI:10.3321/j.issn:1000-565X.2008.01.026 |
| [6] |
Ross-Brown D M, Atkinson K B. Terrestrial Photogrammetry in Openpits:1:Descripion and Use of the Phototheodolite in Mine Surveying[J]. Inst Mining & Meteallurgy, 1972, 81: 190-194. |
| [7] |
王凤艳.数字近景摄影测量快速获取岩体裂隙信息的工程应用[D].长春: 吉林大学, 2006. Wang Fengyan. Engineering Application of Rapid Acquiring Rock Mass Fractures Information with Digital Close Range Photogrammetry[D]. Changchun: Jilin University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10183-2006109721.htm |
| [8] |
胡运海.近景摄影测量技术在滑坡监测中的运用: 以北川县擂鼓镇凤凰山滑坡为例[D].成都: 成都理工大学, 2012. Hu Yunhai. The Application of Close-Range Photogrammetry in Landslide Monitoring: Take the Landslide in Phoenix Mountain, Leigu Town, Beichuan County for Example[D]. Chengdu: Chengdu University of Technology, 2012. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2216253 |
| [9] |
高昭良. 基于多基线数字近景摄影测量的滑坡监测系统研究[J]. 城市勘测, 2015(2): 5-8. Gao Zhaoliang. The Research of Landslide Monitoring System Based on Multi-Baseline Digital Close-Range Photogrammetry[J]. Urban Geotechnical Investigation & Surveying, 2015(2): 5-8. DOI:10.3969/j.issn.1672-8262.2015.02.001 |
| [10] |
巩城城, 马凤山, 张亚民, 等. 基于岩体结构面统计与分维数的岩体质量评价及其在矿山工程中的应用[J]. 中国地质灾害与防治学报, 2011, 22(2): 92-98. Gong Chengcheng, Ma Fengshan, Zhang Yamin, et al. Rock Mass Quality Based on Discontinuity Statistics and Fractal Dimension and Its Application in Mining Areas[J]. The Chinese Journal of Geological Hazard and Control, 2011, 22(2): 92-98. DOI:10.3969/j.issn.1003-8035.2011.02.017 |
| [11] |
吴世伟, 叶军. 参数未知的K-S法检验临界值分析[J]. 港工技术, 1990, 4(1): 16-20. Wu Shiwei, Ye Jun. Analysis of Critical Value by K-S Method with Unknown Parameters[J]. Port Engineering Technology, 1990, 4(1): 16-20. |
| [12] |
阮云凯, 陈剑平, 曹琛, 等. K-S检验在裂隙岩体统计均质区划分中的应用[J]. 东北大学学报(自然科学版), 2015, 36(10): 1471-1475. Ruan Yunkai, Chen Jianping, Cao Chen, et al. Application of K-S Test in Structural Homogeneity Dividing of Fractured Rock Mass[J]. Journal of Northeastern University (Natural Science), 2015, 36(10): 1471-1475. |
| [13] |
Mssey L H. The Kolmogornov-Smirnov Test for Goodness of Fit[J]. American Statistical Association, 1951, 46: 68-78. DOI:10.1080/01621459.1951.10500769 |
| [14] |
Lilliefors H. On the Kolmogornov-Smirnov Test for Normality with Mean and Variance Unknown[J]. American Statistical Association, 1967, 62: 399-402. DOI:10.1080/01621459.1967.10482916 |
| [15] |
Li Y Y, Wang Q, Chen J P, et al. Identification of Structural Domain Boundaries at the Songta Dam Site Based on Nonparametric Tests[J]. Rock Mechanics and Mining Sciences, 2014, 70: 177-184. DOI:10.1016/j.ijrmms.2014.04.018 |
| [16] |
陈剑平, 王清, 肖树芳, 等. X2检验假设分布有效性的工程地质应用[J]. 长春地质学院学报, 1996, 26(3): 332-335. Chen Jianping, Wang Qing, Xiao Shufang, et al. An Application of Chi-Square Test Validity of Assumed Distribution in the Engineering Geology[J]. Journal of Changchun University of Earth Sciences, 1996, 26(3): 332-335. |
| [17] |
马建全, 李广杰, 徐佩华, 等. 基于拉丁方抽样及K-S检验的边坡可靠性分析[J]. 岩土力学, 2011, 32(7): 2153-2156. Ma Jianquan, Li Guangjie, Xu Peihua, et al. Reliability Analysis of Slope with Latin Hypercube Sampling and K-S Test[J]. Rock and Soil Mechanics, 2011, 32(7): 2153-2156. DOI:10.3969/j.issn.1000-7598.2011.07.039 |
| [18] |
郭跃华. 概率论与数理统计[M]. 北京: 科学出版社, 2007. Guo Yuehua. Probability Theory and Mathematical Statistics[M]. Beijing: Science Press, 2007. |
| [19] |
Conver W J. A Kolmogorov Goodness of Fit Test for Distributions[J]. American Statistical Association, 1972, 67: 591-596. DOI:10.1080/01621459.1972.10481254 |
| [20] |
朱红兵, 何丽娟. 关于SPSS中单样本K-S检验法进行正态分布等的一致性检验时适用条件的研究[J]. 首都体育学院学报, 2009, 21(4): 466-470. Zhu Hongbing, He Lijuan. A Study on Appropriate Conditions in Consistency Test of Normal Distribution by Single Sample K-S Check in SPSS[J]. Journal of Capital Institute of Physical Education, 2009, 21(4): 466-470. DOI:10.3969/j.issn.1009-783X.2009.04.021 |
| [21] |
陈剑平, 肖树芳, 王清. 随机不连续面三维网络计算机模拟原理[M]. 长春: 东北师范大学出版社, 1995. Chen Jianping, Xiao Shufang, Wang Qing. Principle of Three-Dimensional Network Computer Simulation of Stochastic Discontinuous Plane[M]. Changchun: Northeast Normal University Press, 1995. |
| [22] |
张思俊, 吴世伟. 结构可靠度分析中小子样概型的拟合检验[J]. 水电能源科学, 1989, 6(4): 368-376. Zhang Sijun, Wu Shiwei. Test of Goodness of Fit for Small Sample Distribution in Structural Reliability Analysis[J]. International Journal Hydroelectric Energy, 1989, 6(4): 368-376. |