0 引言
声波测井的全波列资料可以用来评价地层性质[1]。随着人们对孔隙地层中油气的不断开发,非常规油气藏的地位开始变得越来越重要。非常规储层的主要特征是低孔隙度、低渗透率,并且裂隙比较发育,从而这类地层中的体波和模式波会有频散和衰减现象[2]。因此,研究弹性波对孔隙、裂隙介质及油气的响应特征显得十分重要。唐晓明等[3-4]利用含孔隙、裂隙介质弹性波动的统一理论研究了孔隙、裂隙地层的声波测井响应特征,结果表明随着裂隙密度的增加,纵、横波速度出现频散现象,斯通利波、伪瑞利波以及弯曲波的能量衰减和速度频散受裂隙密度的影响,裂隙对声场影响的频率区间由裂隙纵横比控制。Hornby等[5]用平板状裂缝模型研究了斯通利波通过单一裂缝时的传播特性,结果表明裂缝的存在会产生反射斯通利波。随后Tang等[6]用渗透带理论模型研究了斯通利波的传播规律,指出在渗透带地层同样会产生反射斯通利波。由于斯通利波对渗透性地层或者开口裂缝十分敏感,所以斯通利波的相关信息能较好地确定裂缝的位置,评价裂缝带的渗透性,而这种渗透性地层往往是大量油气的储存地点,因此斯通利波对地层的响应特征在很大程度上可以指示油气。潘保芝等[7]利用常规测井资料和电成像测井数据建立了一种识别火成岩储层有效裂缝的方法,可快速识别储层裂缝。黄文新等[8]进一步证明了反射斯通利波和反射率能够用于评估储层渗透率,但未曾使用反射系数等参数对实际井段的阵列声波测井数据进行系统评价。
我们对信号进行傅里叶变换可以得到声波信号在不同性质地层上的频率分布特征,傅里叶变换适用于具有周期性或平稳性的信号,所以在处理具有时变特性的阵列声波测井信号时不免会有一定的局限性。对于非平稳的阵列声波测井信号,我们不仅需要从总体上了解它的频率成分,还需要了解每一时刻信号中所包含的频率成分。希尔伯特黄变换(Hilbert-Huang transform, HHT)可以将信号分解为有限个固有模态函数(intrinsic mode function, IMF),然后对各模态分量进行变换从而得到信号能量在时间尺度上的分布规律,实现信号动力特性的量化提取[9-12]。熊学军等[13]利用经验模态分解(empirical mode decomposition, EMD)方法对海浪观测资料进行了处理,结果表明,各模态在HHT谱中的分布趋势和傅里叶谱中谱线的变化趋势是一致的,第一模态的中心频率与傅里叶频率谱的谱峰频率对应,EMD方法是一种对非线性、非平稳数据处理的有效方法。王祝文等[14-15]基于HHT对阵列声波测井信号进行了时频分析,从HHT幅值谱中得到了边际谱、能量谱和瞬时能量谱,认为HHT谱表现出的相关特征与实际波列中所包含的纵波、横波、斯通利波和伪瑞利波有关,不同HHT谱中的峰值与储集层岩石结构构造可能存在内在联系;但是还没有对它们之间的具体关系进行更深入地分析。
前人大多是对不同结构构造的地层进行理论上的数值模拟,得到的结论和规律都是理想化的,在实际工作中由于地层性质的复杂多变往往会导致最终的结果与理论分析存在一定的偏差。为了加强声波测井理论与实际测井数据之间的联系,从理论分析得到对实际问题实质的理解,进一步弄清楚斯通利波在含气裂缝性地层的响应特征和HHT与地层性质的关系,笔者在前人研究结果的基础上,将中值滤波、傅里叶变换和HHT应用在辽河盆地东部凹陷含气孔、裂隙地层的实测阵列声波测井数据上,研究了裂隙和油气对斯通利波及其反射波和高、低频波的影响,同时分析了HHT处理波列数据的优点和孔、裂隙地层阵列声波信号的时频分布特征。
1 斯通利波波场分离斯通利波是沿井身在流体中传播的压力波。在全波列记录中,斯通利波主要存在于5 kHz以下的低频部分。我们可以用频率域低通滤波器得到所需的低频斯通利波波形;再经过中值滤波,把斯通利波的直达波与反射波分离,就可以利用反射波和直达波进行反射系数、反射能量等参数的求取。
求取反射系数的公式[16]为
 (1)
(1) 式中:D(k)是直达斯通利波的频谱;R(k)是反射斯通利波的频谱。如果D(k)接近0,那么r(k)便会出现极值;为了避免这种情况,可以用下面的公式来代替:
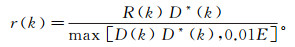 (2)
(2) 式中:D*(k)为D(k)的共轭频谱;E为D(k)D*(k)的峰值。
对直达斯通利波和反射斯通利波进行傅里叶变换,得到频率谱,把每个深度各频率幅值的平方相加,就求得了反射斯通利波和直达斯通利波的能量曲线。
2 希尔伯特黄变换原理 2.1 EMD原理EMD方法的思路是用波动上、下包络的平均值去确定“瞬时平衡位置”,进而提取内在模函数IMF。将原始信号x(t)分解成如下形式[14-15]:
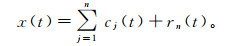 (3)
(3) 式中:cj(t)为第j个固有模态函数;rn(t)为残量,为一个单调函数或小于某个预定值的数。
2.2 HHT和HHT谱计算对于任一固有模态函数c(t),其HHT结果g(t)定义为
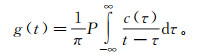 (4)
(4) 式中:P为柯西主值;t为时间变量。
c(t)的解析信号z(t)可定义为
 (5)
(5) 式中,a(t)和θ(t)分别为阵列声波信号x(t)的瞬时振幅和瞬时相位,按下式计算:
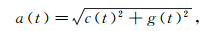 (6)
(6) 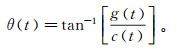 (7)
(7) 由瞬时相位可得到阵列声波信号的瞬时频率ω(t):
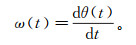 (8)
(8) 可见,经过HHT得到的振幅和频率都是时间的单值函数,它突破了傅里叶变换固定幅值、固定频率的限制和整个信号长度全局量的限制。如果把振幅显示在频率-时间平面上,就可以得到HHT幅值谱H(ω, t)。
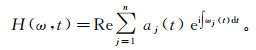 (9)
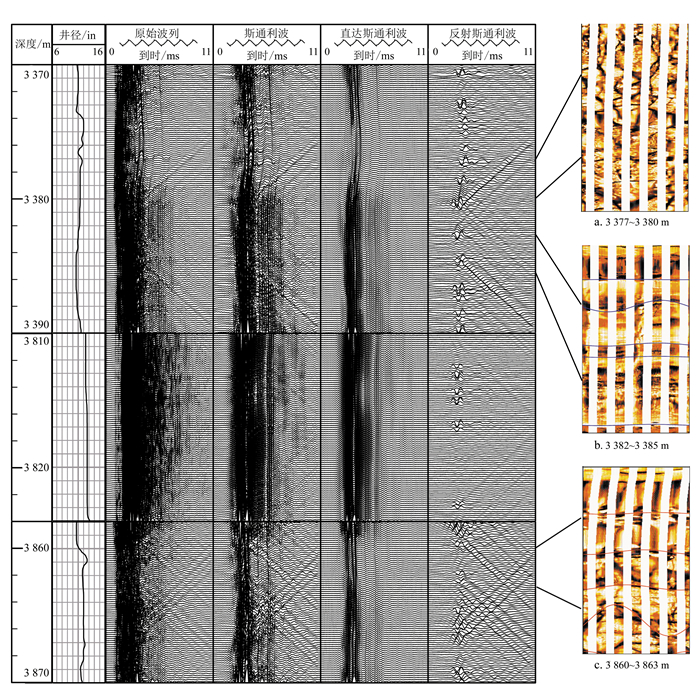
(9) 本文采用的是辽河盆地东部凹陷HXXX井单极子阵列声波数据。由实测资料可知3 800~3 870 m为不含油气地层,3 370~3 390 m为工业油气流井段。图 1原始波列中3 812~3 822 m层段的波列幅值明显高于3 372~3 386 m层段和3 860~3 868 m层段,3 860~3 868 m层段有“V”字型反射斯通利波。对原始波列低通滤波后得到了斯通利波,从图 1中可以看出:3 812~3 822 m斯通利波幅值稳定,基本无反射斯通利波,为致密地层;3 860~3 868 m斯通利波的幅值明显降低,反射斯通利波“V”字型明显,常规测井井径曲线显示非扩径,说明可能有裂隙发育。图 1中的电成像测井图(图 1c)证明了该层为裂隙地层。
|
| 英寸(in)为非法定计量单位,1 in=2.54 cm,下同。 图 1 斯通利波波场分离 Figure 1 Wavefield separation of Stoneley wave |
|
|
3 372~3 386 m层段斯通利波幅值降低,特别是3 372~3 380 m;但是3 372~3 380 m没有明显的反射斯通利波,3 380~3 386 m出现了反射斯通利波,而斯通利波幅值降低不明显。为了解释这一现象,我们给出了图 1右侧的3 372~3 380 m层段和3 380~ 3 386 m层段中部分电成像测井图。
1) 电成像图 1a(3 377~3 380 m)中裂隙非常发育,属于网状裂隙,该段地层被解释为含油气的孔、裂隙地层。该层段没有出现“V”字型反射斯通利波,究其原因可能有2个:1)裂隙的高度发育致使斯通利波能量衰减非常严重,从而使反射斯通利波的显示不明显,甚至完全消失;2)网状裂缝中不同裂缝(波阻抗)界面产生的反射斯通利波难以有效地区分,并且非同相位反射斯通利波的叠加会使信号强度减弱[17]。
2) 电成像图 1b(3 382~3 385 m)中裂隙不明显,而薄互层地层、岩性界面较明显。薄互层地层、岩性界面也会产生反射斯通利波,但对斯通利波能量的影响不大。由于该层段为渗透性孔隙地层,斯通利波能量也会发生衰减并产生相应的反射斯通利波,所以该层段可见到“V”字型反射波并且斯通利波幅值下降。这也说明在实际应用中应注意裂缝与薄互层地层、岩性界面的区别。
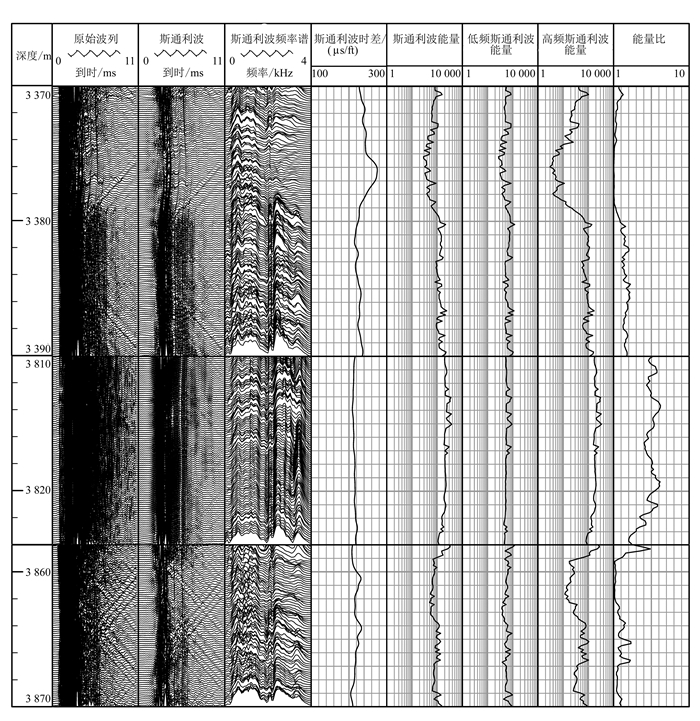
图 2中3 860~3 868 m的裂隙地层相较于3 812~3 822 m的致密地层,3 372~3 380 m的含油气裂隙地层相较于3 380~3 386 m的含油气孔隙地层,它们的斯通利波能量衰减明显。这是由于斯通利波是沿井身在流体中传播的压力波,当井眼穿过裂隙时井内流体进入裂隙,流体相对于骨架振动,在这些地层中产生黏滞扩散,使斯通利波的能量明显衰减。
|
| 英尺(ft)为非法定计量单位,1 ft=0.304 8 m,下同。 图 2 斯通利波综合图 Figure 2 Comprehensive achievement of Stoneley wave |
|
|
如果以2 kHz频率为分界点,我们可以得到“直达的”高频斯通利波(2~4 kHz)和低频斯通利波(0~2 kHz)的能量曲线,其数值代表不同地层斯通利波能量的相对大小(图 2)。在3 812~3 822 m致密地层区间,斯通利波的高频能量明显大于低频能量;3 860~3 868 m裂隙地层高频能量发生了明显衰减,特别是裂隙密集段3 860~3 863 m,但低频斯通利波能量几乎没有变化。此现象说明裂隙地层中斯通利波能量的衰减主要发生在高频段,故会出现主频下降的现象。图 2中的能量比是高频斯通利波能量与低频斯通利波能量的比值。从能量比中不仅可以看出高频、低频斯通利波能量的相对大小,还可以得到高、低频斯通利波能量衰减幅度的信息:3 812~3 822 m致密地层高频斯通利波能量大约是低频斯通利波能量的5倍,3 860~3 868 m裂隙地层能量比的数值明显降低且几乎小于1;说明高频斯通利波的能量衰减严重且已低于低频,可见能量比更直观地反映出了裂隙对于高、低频斯通利波能量的影响。
同样,裂隙对地层性质的改变会使斯通利波产生相对时滞。这是因为井中斯通利波由声脉冲与井壁接触时产生,其同时受到弹性分界面两侧介质性质的影响,地层裂隙的出现改变了地层的性质,降低了地层的体积模量、剪切模量等参数,致使斯通利波的速度下降,从而使波至时间推迟。因此,斯通利波在渗透性地层(裂缝)的能量衰减、主频下降和到时滞后三者之间具有相关性,这种现象在3 372~3 380 m含油气裂隙地层尤其明显。
通过上文的讨论我们知道,3 812~3 822 m为无油气较致密地层,3 380~3 386 m为含油气孔隙储层,基本可以认为油气是这两个层段的唯一差异。图 2含油气储层(3 380~3 386 m)斯通利波的能量相较于不含气地层(3 812~3 822 m)来说是减小的,证明了油气确实会导致斯通利波能量的衰减。同理,我们也可以得到油气会使斯通利波主频下降、到时滞后的结论。这是由于油气的残留会使孔隙流体的流通性和可压缩性变大,斯通利波的衰减和走时滞后现象增强,所以油气和裂隙对斯通利波的影响是相似的,并且裂隙对斯通利波的影响比油气更大一些。从能量比的角度思考,相对于3 812~3 822 m致密地层,3 372~3 380 m含油气裂隙地层的能量比几乎为零,说明高频斯通利波的能量衰减相当严重(裂隙占主要贡献,也有油气的小部分贡献);3 380~3 386 m含油气孔隙地层的能量比虽然较小,但是其值仍然大于1,说明在同样有油气贡献的情况下,渗透性孔隙地层高频斯通利波能量的衰减程度远小于裂隙地层。即能量比接近0时,判断地层为渗透性裂隙地层;能量比较小但有一定数值(略大于1)时,判断地层为渗透性孔隙地层。能量比能反映出高频、低频斯通利波能量各自的衰减程度,故可从另一个侧面衡量渗透性地层的性质。
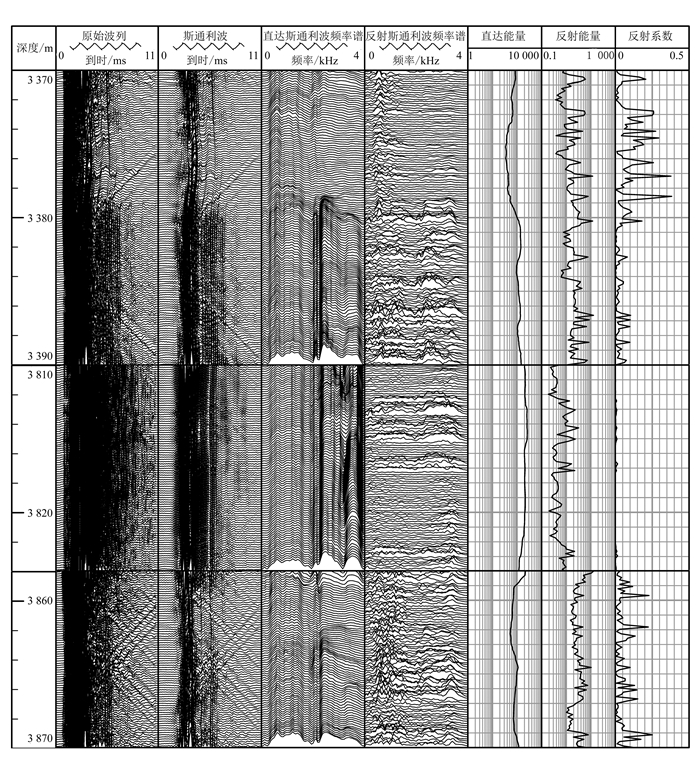
通过对斯通利波进行波场分离,我们可以得到直达波、反射波的一些特征。由式(2)可知,反射系数为反射斯通利波和直达斯通利波主频峰值的比值,可选取直达斯通利波主频峰值位置进行计算,其值与反射斯通利波能量成正比,与直达斯通利波能量成反比。图 3中:3 812~3 822 m致密地层的直达斯通利波能量比较稳定,反射能量很小,故反射系数几乎为零;3 860~3 868 m裂隙地层反射斯通利波能量增强(低频部分增强明显),直达斯通利波能量降低,由式(2)可知该层反射系数变大并出现了峰值,因此反射系数表现为尖锐的峰值一般指示裂缝;3 372~3 380 m层段是典型的含油气孔、裂隙地层,由前文知3 372~3 380 m层段没有出现“V”字型反射斯通利波,原因是高度发育的网状裂缝使非同相位的反射斯通利波相互叠加或者斯通利波能量的严重衰减致使反射波的能量较低,式(2)中分母的衰减程度(直达波的能量)比分子(反射波的能量)要大得多,所以尽管没有“V”字型反射斯通利波的出现,该层段的反射系数还是很大;3 380~3 386 m为含油气孔隙地层,油气层会产生一定的反射波(包括薄互层地层和岩性界面产生的),最重要的是孔隙(渗透性)地层会使斯通利波能量衰减,所以一般含油气孔隙地层也会产生相应的反射系数,但其数值理论上不会很大。延伸到岩性界面和薄互层较多的致密地层,由于致密地层中的斯通利波能量几乎不会发生衰减,即便有反射斯通利波的产生,反射斯通利波能量与直达斯通利波能量量级的差别过大同样会导致反射系数趋近于零;说明只有裂缝产生的反射斯通利波才会形成高值反射系数。因此,反射系数在判断地层的渗透性时有较高的可靠性。
|
| 图 3 直达斯通利波和反射斯通利波对比 Figure 3 Comparison of direct and reflected Stoneley wave |
|
|
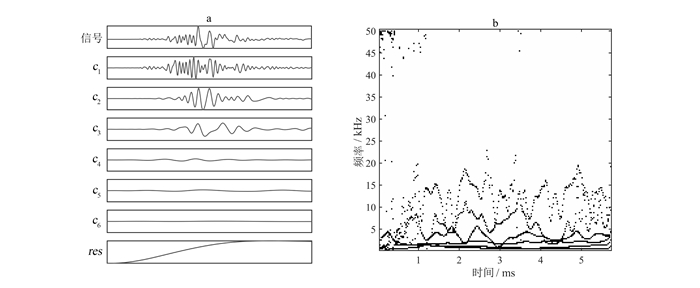
图 4是HXXX井中致密地层阵列声波测井原始波列信号的EMD图和HHT幅值谱。图 4中每个IMF分量都对应着不同的振幅和频率,从上到下逐一减小,并且每个频率不是定值,而是围绕一个中心频率波动。频率高的IMF分量对应原始信号中先到达的纵波和横波,频率低的IMF分量则表示后到达的斯通利波,故IMF分量不仅包含原始信号固有的物理性质,又具有时间上的局域化特征。将每个IMF按照式(4)—(9)进行HHT可以得到波列信号的瞬时振幅和瞬时频率,把各内在模函数的振幅表现在频率-时间二维图上就可以得到三维HHT幅值谱H(ω, t)。致密地层HHT幅值谱能量主要集中在0~5 kHz,低频能量较大,高频能量在整个时间尺度内均有分布,主要集中在500~2 000 μs。
|
| res.信号本身微弱的趋势或仪器的漂零。 图 4 阵列声波信号的IMF分量(a)及HHT幅值谱(b) Figure 4 IMF components (a) and Hilbert-Huang amplitude spectrum(b) of array acoustic logging signal |
|
|
HHT幅值谱直观地显示了原始信号的时频分布特征。如果将HHT幅值谱对时间积分,就可以得到HHT边际谱,边际谱代表每个频率的振幅在整个时间长度的累积和;将振幅的平方对时间积分可得到HHT能量谱;将振幅的平方对频率积分可得到HHT瞬时能量谱,瞬时能量谱与图 1中原始波列给出的信息类似,它提供了阵列声波信号能量随时间变化的规律。
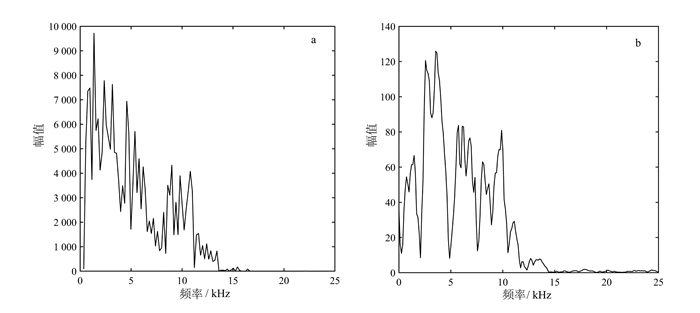
由图 4中HHT幅值谱得到图 5所示的HHT边际谱。HHT和傅里叶变换都能给出原始信号的频率分布。由图 5可知,声波信号的能量主要集中在0~10 kHz,并且0~5 kHz的低频能量大于5~10 kHz的高频能量。这是由于致密地层中各种成分的波都无明显衰减,并且高频纵、横波的能量量级远小于低频的斯通利波,高频的伪瑞利波能量较大,所以致使低频能量比高频能量大,但仍保持在同一个量级上。HHT边际谱把原始信号的频率划分得非常细致,得到的频率分辨率明显优于傅里叶变换谱,并且HHT边际谱对高、低频能量的分级相对合理,即致密地层斯通利波能量较其他波动能量强得多;而在傅里叶变换频率谱中得到的高频能量较大。阵列声波信号的一大特点就是无周期性,边际谱只包含由原波动分解出的具有瞬时频率的各个子波,从而改善了傅里叶变换的假频现象,不仅提高了信号表示的效率,而且能够表示可变的频率,故能更好地反映出原始信号中固有的物理性质。
|
| 图 5 信号的HHT边际谱(a)和傅里叶频率谱(b) Figure 5 HHT marginal spectrum (a) and Fourier transform frequency spectrum (b) of signal |
|
|
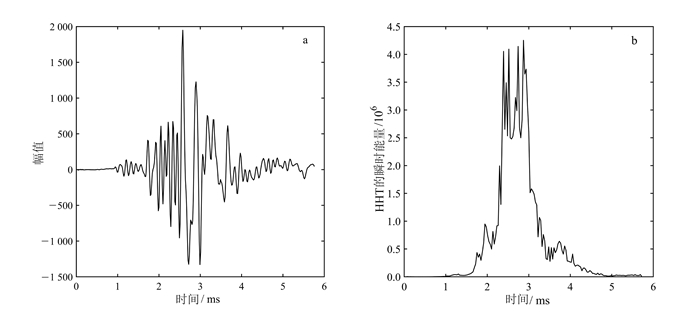
图 6给出了致密地层的HHT瞬时能量谱与原始波列图。HHT瞬时能量谱给出的信息与原始波列图类似,并且突出了能量的集中时间段。由原始波列图可知,斯通利波的到时在2.5 ms左右,与HHT瞬时能量谱2.5 ms能量骤增为峰值完全对应;粗略地看出伪瑞利波在原始波列图波至时间为1.8 ms,对比HHT瞬时能量谱发现与1.8~2.5 ms伪瑞利波能量正好吻合,从而验证了HHT瞬时能量谱的正确性;在0~1.8 ms瞬时能量谱的幅值几乎为零,这是由于纵横波与斯通利波能量量级相差太大而造成的。HHT瞬时能量谱包含了原始波列的一切信息并着重给出了不同时间段的能量信息,还突出了斯通利波、伪瑞利波和纵波、横波的能量分级。由于斯通利波对地层性质的变化非常敏感,故HHT瞬时能量谱能更好地揭示井中声波的传播规律,放大储集层结构的响应特征,特别是孔、裂隙渗透性地层。从上面的叙述中可以看出,HHT谱从不同的方面突出了阵列声波的动力特性,它们与斯通利波和纵波、横波的特征相关联,从而我们可以根据HHT谱的特征对地层属性进行进一步评价。
|
| 图 6 信号的声波信号全波列(a)和HHT瞬时能量谱(b) Figure 6 Full waveform (a) and HHT instantaneous energy spectrum (b) of signal |
|
|
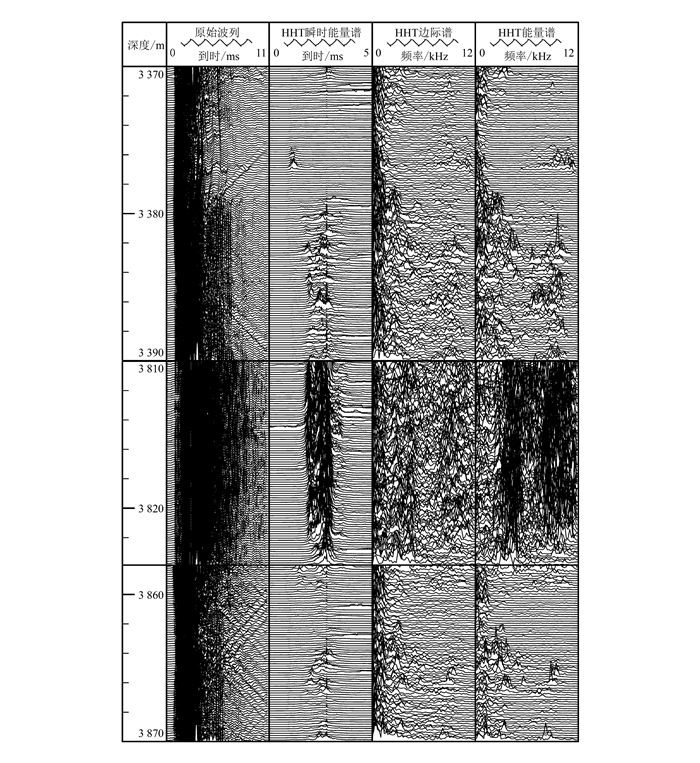
图 7为HXXX井阵列声波测井信号的HHT瞬时能量谱、HHT边际谱和HHT能量谱。3 372~3 380 m和3 860~3 868 m裂隙地层原始波列的幅值比3 810~3 822 m致密地层低。由于原始波列的时间尺度较大,在整个井段不能清晰地看出幅值衰减的具体时间,这个问题在HHT瞬时能量谱中得到了较好的解决。HHT瞬时能量谱中能量具有明显的时间集中特征,集中在1.8~3.0 ms,主要是斯通利波和伪瑞利波的能量。由于纵、横波与斯通利波的能量数量级相差很大,所以在图中显示不明显。在3 860~3 868 m裂隙地层中,整个能量段发生严重衰减。在3 372~3 380 m含油气地层中,网状裂缝的存在导致能量段衰减程度很大。3 380~3 386 m含油气的孔隙地层造成的斯通利波能量衰减在HHT瞬时能量谱中也显示得比较清楚。原始波列中能量衰减不明显的问题在HHT瞬时能量谱中得到了较好的解决,体现了HHT瞬时能量谱的优点。
|
| 图 7 原始数据HHT谱 Figure 7 HHT spectrum of raw data |
|
|
在HHT边际谱和HHT能量谱中,致密地层的波动能量主要集中在0~5和8~12 kHz这两个部分,其中0~5 kHz主要由斯通利波能量组成,8~12 kHz主要代表纵、横波和高频伪瑞利波。3 860~3 868和3 372~3 380 m可明显观测到由油气或裂隙所造成的低频能量衰减(主频降低),其中高频伪瑞利波似乎也发生了严重衰减,而伪瑞利波与地层性质的关系还有待研究。HHT放大了阵列声波信号对地层性质的响应特征,给出的地层性质信息非常丰富。当地层性质(渗透率)发生改变时,阵列声波信号的能量和频率变化在HHT谱上表现得相当明显,这种直观程度明显高于图 2综合多种谱线的分析。
由前文可知,斯通利波对渗透性地层的敏感度非常大,为了进一步说明HHT更能突出斯通利波对含油气裂隙地层的响应特征,我们对斯通利波进行经验模态分解和希尔伯特黄变换。图 8是斯通利波HHT谱。由于滤除了伪瑞利波和纵波、横波,斯通利波HHT谱的能量整体上小于原始波列的HHT谱中的能量。

|
| 图 8 斯通利波HHT谱图 Figure 8 HHT spectrum of Stoneley wave |
|
|
HHT瞬时能量谱能量集中在2.5~3.0 ms,2.5 ms对应着斯通利波的波至时间。在3 812~3 822 m致密地层中斯通利波能量很大,在3 860~3 868 m裂隙地层中斯通利波能量发生严重衰减,到时滞后明显。从图 8中的原始波列图能够看出能量的衰减,但不能看出波至时间的变化,并且能量的衰减特征没有在HHT瞬时能量谱中表现得明显。在3 372~3 380 m含油气裂隙地层中,网状裂缝的存在导致斯通利波衰减程度非常大;3 380~3 386 m含油气孔隙地层造成的斯通利波能量衰减也显示得非常清楚。但是,若直接从图 8中的斯通利波波列图或图 2中的斯通利波能量曲线分析,能量的衰减虽然可见却非常有限,故HHT瞬时能量谱对于粗略地寻找孔、裂隙渗透性地层的效果可能更好。
在HHT边际谱和HHT能量谱中,致密地层的斯通利波能量主要集中在0~5 kHz,这与傅里叶变换得到的频率谱表现一致。在3 860~3 868 m和3 372~3 380 m可明显观测到由裂隙或油气所造成的斯通利波能量衰减,主频下降非常明显。3 380~3 386 m渗透性孔隙地层造成的斯通利波能量衰减和主频下降虽不及裂隙地层程度大,但是相对图 2的斯通利波频率谱明显了很多。从HHT边际谱和HHT能量谱中不仅可以得到斯通利波能量和频率的信息,还可以清晰地看出地层性质变化导致斯通利波能量、频率的变化规律,波的能量、主频和到时的变化特征仅仅在HHT谱上就能全部表示出来,非常简单直观。
5 结论本文应用希尔伯特黄变换对含气孔、裂隙地层的斯通利波进行了处理,以研究斯通利波时频分布特征,可得到以下的结论。
1) 油气和裂隙会引起斯通利波能量衰减、主频下降和到时滞后,三者之间具有相关性。斯通利波的能量衰减主要发生在高频部分。油气对斯通利波的影响程度小于裂隙对斯通利波的影响程度。
2) 能量比(高频与低频斯通利波的比值)接近零时判断地层为渗透性裂隙地层,能量比较小但有一定数值时判断地层为渗透性孔隙地层。
3) 裂隙会使反射斯通利波能量增强、反射系数变大,计算的高值反射系数一般只会出现在裂缝性地层,故利用反射系数评价地层性质的可靠性更高。
4) HHT幅值谱直观地显示了阵列声波测井信号的时频分布。HHT边际谱和HHT能量谱在裂缝性地层清晰地显示出主频能量的大幅度下降;HHT瞬时能量谱表现出裂缝性储层声波能量的衰减规律,同时又可观测到到时滞后。
5) HHT方法是处理时变信号的一种比较适用的方法,它能够从原始信号中分解出若干个具有不同瞬时频率的IMF分量,既保证了原始信号固有的物理性质,又具有时间上的局域化特征。
| [1] |
王桂斋, 胡天跃. 多频声波全波列波形裂缝特征分析及应用[J]. 天然气地球科学, 2014, 25(增刊1): 11-16. Wang Guizhai, Hu Tianyue. Analysis and Application of Multi-Frequency Acoustic Full Waveform Characteristics of Fracture[J]. Natural GasGeoscience, 2014, 25(Sup. 1): 11-16. |
| [2] |
陈雪莲, 唐晓明, 钱玉萍. 含孔隙、裂隙致密介质中多极子声波的传播特征[J]. 地球物理学报, 2014, 57(9): 2961-2970. Chen Xuelian, Tang Xiaoming, Qian Yuping. Propagation Characteristics of Multipole Acoustic Logging in Cracked Porous Tight Formations[J]. Chinese Journal of Geoghysics, 2014, 57(9): 2961-2970. |
| [3] |
唐晓明. 含孔隙、裂隙介质弹性波动的统一理论:理论的推广[J]. 中国科学:地球科学, 2011, 41(6): 784-795. Tang Xiaoming. A Unified Theory for Elastic Wave Propagation Through Porous Media Containing Cracks:An Extension of Biot's Poroelastic Wave Theory[J]. Sci China Earth Sci, 2011, 41(6): 784-795. |
| [4] |
Tang X M, Chen X L, Xu X K. A Cracked Porous Medium Elastic Wave Theory and Its Application to Interpreting Acoustic Data from Tight Formations[J]. Geophysics, 2012, 77(6): D245-D252. DOI:10.1190/geo2012-0091.1 |
| [5] |
Hornby B E, Johnson D L, Winkler K W, et al. Fracture Evaluation Using Reflected Stoneley Wave Arrivals[J]. Geophysics, 1998, 54(10): 1274-1288. |
| [6] |
Tang X M, Cheng C H. Borehole Stoneley Wave Propagation Across Permeable Structures[J]. Geophysical Prospecting, 1993, 41(2): 165-187. DOI:10.1111/gpr.1993.41.issue-2 |
| [7] |
潘保芝, 刘文斌, 张丽华, 等. 一种提高储层裂缝识别准确度的方法[J]. 吉林大学学报(地球科学版), 2018, 48(1): 298-306. Pan Baozhi, Liu Wenbin, Zhang Lihua, et al. A Method for Improving Accuracy of Reservoir Fracture Identification[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(1): 298-306. |
| [8] |
黄文新, 历元彬. 用反射斯通利波确定地层裂缝宽度和渗透率[J]. 江汉石油学院学报, 1994, 16(增刊1): 26-31. Huang Wenxin, Li Yuanbin. Determining Fracture Width and Permeability of a Layer from Reflected Stoneley Wave[J]. Journal of Jianghan Petroleum Institute, 1994, 16(Sup. 1): 26-31. |
| [9] |
Huang N E, Shen Z, Long S R, et al. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis[J]. Proc R Soc Lond A, 1998, 454(A): 903-995. |
| [10] |
Huang N E, Shen Z, Long S R. A New View of Nonlinear Water Waves:The Hilbert spectrum[J]. Annual Review of Fluid Mechanics, 1999, 31(1): 417-457. DOI:10.1146/annurev.fluid.31.1.417 |
| [11] |
刘喜武, 刘洪, 李幼铭, 等. 局域波分解及其在地震信号时频分析中的应用[J]. 地球物理学进展, 2007, 22(2): 365-375. Liu Xiwu, Liu Hong, Li Youming, et al. Local Waves Decomposition and Its Applications to Seismic Signal Time-Frequency Analysis[J]. Progress in Geophysics, 2007, 22(2): 365-375. DOI:10.3969/j.issn.1004-2903.2007.02.006 |
| [12] |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1585-1590. Yang Peijie, Yin Xingyao, Zhang Guangzhi. Seismic Signal Time-Frequency Analysis and Attributes Extraction Based on HHT[J]. Progress in Geophysics, 2007, 22(5): 1585-1590. DOI:10.3969/j.issn.1004-2903.2007.05.037 |
| [13] |
熊学军, 郭炳火, 胡筱敏, 等. EMD方法和Hilbert谱分析法的应用与探讨[J]. 黄渤海海洋, 2002, 20(2): 12-21. Xiong Xuejun, Guo Binghuo, Hu Xiaomin, et al. Application and Discussion of Empirical Mode Decomposition Method and Hilbert Spectral Analysis Method[J]. Journal of Oceanography of Huanghai & Bohai Seas, 2002, 20(2): 12-21. DOI:10.3969/j.issn.1671-6647.2002.02.003 |
| [14] |
王祝文, 刘菁华, 聂春燕. 基于Hilbert-Huang变换的阵列声波测井信号时频分析[J]. 地球科学:中国地质大学学报, 2008, 33(3): 387-392. Wang Zhuwen, Liu Jinghua, Nie Chunyan. Time-Frequency Analysis of Array Acoustic Logging Waveform Signal Based on Hilbert-Huang Transform[J]. Earth Science:Journal of China University of Geosciences, 2008, 33(3): 387-392. |
| [15] |
王祝文, 刘菁华, 聂春燕. Hilbert-Huang变换在提取阵列声波信号动力特性中的应用[J]. 地球物理学进展, 2008, 23(2): 450-455. Wang Zhuwen, Liu Jinghua, Nie Chunyan. Application of Hilbert-Huang Transform in Extracting Dynamic Properties of Array Acoustic Signals[J]. Progress in Geophysics, 2008, 23(2): 450-455. |
| [16] |
余春昊, 李长文. 利用斯通利波信息进行裂缝评价[J]. 测井技术, 1998, 22(4): 273-277. Yu Chunhao, Li Changwen. Application of Stoneley Waves to Fracture Evaluation[J]. WLT, 1998, 22(4): 273-277. |
| [17] |
赵辉, 司马立强, 戴诗华. 斯通利波在储层评价中的应用及认识[J]. 大庆石油地质与开发, 2012, 31(2): 171-174. Zhao Hui, Sima Liqiang, Dai Shihua. Stoneley Wave Method Used in Reservoir Evaluation and Its Understandings[J]. Petroleum Geology and Oilfield Development in Daqing, 2012, 31(2): 171-174. DOI:10.3969/J.ISSN.1000-3754.2012.02.035 |



