0 引言
近年来,深海沉积矿产资源,尤其是以高品质锰结核为代表的多金属结核矿物的发现及深海可燃冰提取技术的进步,加快了人们对深海矿产资源的勘探需求。深海埋藏管线的检测和海底污染物的运移等环境工程问题也越来越受到重视。国际深海勘探领域“圈地运动”蓬勃兴起。由于深海沉积层的电阻率包含了其物理性质的丰富信息,因此开展海洋直流电阻率法研究在海洋矿产探测、海底管线检测和海底污染物运移等方面具有很大的实用价值。海底是非常稳定的环境,上方海水可近似看作电各向同性均匀介质,电极周围环境干扰小并且与海水之间的阻抗小,易于获得很大的供电电流,这在地面直流电阻率法中是很难做到的。除此之外,直流电场空间分布受电阻率的变化影响较大,对海底的高阻油气层和低阻金属矿产识别能力较强。由于目前三维海洋直流电阻率法发表的成果较少,因此开展高精度三维海洋直流电阻率正演模拟研究具有重要理论价值。
制约海洋直流电法发展的一个重要因素是探测方式的效率。20世纪60年代,海洋电阻率法开始用于调查北冰洋大陆架上的永冻层和矿产资源勘探,但当时的接收装置对岩性的区分效果较弱[1];Hakim等[2]在对海底进行填图时提出了两种特殊的布极方式,提高了电阻率法对岩性的识别能力。Rosenberger等[3]设计了一种自由落体式的电阻率海底沉积物原位探测装置,取得了很好的应用效果。Edwards等于1986年引入了深海海底勘探瞬变电磁方法理论,于1987年对该理论进行了完善,并于1988年对二维模型进行了模拟计算的展示[4-6]。但以上的探测方式大多适用于浅海直流电阻率法勘探;在深海探测中,由于海底洋流活动异常活跃且活动规律未知,传统探测方式中放置海底的接收电极往往会造成丢失和测量偏差等问题,严重影响数据的质量。考虑到以上种种原因,基于前人经验,本文引入一种同心扫面深海全拖曳探测方式。即一条船拖着发射电极静止在海平面上,以该船为中心,通过手持GPS仪器提前在海平面布设一系列回形测线,计算并存储测线上每个测点的位置;然后另一条探测船拖曳接收电极,根据GPS仪器导航,沿测线依次记录各测点所接收的电位信息;最后,计算得到拖曳平面内测点的视电阻率信息,通过画图软件展示在平面图上,从而可以形象地观测拖曳平面各个方位的视电阻率。这种探测方式不仅避免了传统探测方式接收电极丢失的风险和测量偏差的难题,还实现了拖曳平面内的多方位探测,通过计算拖曳的平面内各个方位的视电阻率可有效识别海底沉积层电性分布特征,特别是电各向异性信息。
空气层基本不导电,因此在地面直流电阻率法中,地面点源电流向地下呈半球面扩散。而在海洋直流电阻率法中,海水中电流源的发射电流呈球面扩散,且发射电流在空气与海水的分界面处会发生反射,因此海洋直流电法的正演理论与地面直流电法不同,控制方程中需要使用镜像法。葛为中[7-8]对一维层状介质的点源场进行了系统研究,基本上解决了水中一维直流电场的正演模拟问题;并于1998年推导出了一维层状介质水下点电源的电位和视电阻率理论公式,讨论了水底电测深转换函数之间的关系,同时指出水下或水底电阻率法由于电极装置接近沉积层,比水面电阻率法具有更好的探测能力。王自民[9]论述了在水面上进行电阻率测量的方法。黄俊革等[10]利用规则网格有限单元法对水下电阻率进行模拟,指出水下电极深度和水底地形都会对测量结果产生影响,但由于规则网格对地形模拟较差和所选第一类边界条件的局限性,取得的模拟结果精度并不理想。翁爱华等[11]对一维海洋电阻率法进行模拟,详细讨论了深海探测中的影响因素,并指出海洋电阻率法对分辨油气和矿产资源的优越性。在电磁法建模方面:刘长胜等[12]计算了海水为均匀半空间的瞬变电磁响应;李慧[13]计算了浅海瞬变电磁垂直偶极子和中心回线装置的响应曲线;周胜等[14]计算了深海拖曳式瞬变电磁的响应规律。
正演是反演的基础,由于介质各向异性会带来更多的计算参数,因此目前的正反演只考虑了介质的各向同性或简化的电导率各向异性。而深海沉积物是典型的电各向异性分布[15],因此在当前的正反演中往往隐含着一些不可忽略的错误[16]。在三维各向异性正演计算中可以通过加入三维电导率张量来模拟介质在空间中的任意电导率各向异性,从而实现仿真模拟与实际地质模型的完全匹配,保证正演模拟的可信度,提高计算的精确度。对于一些简单的各向异性模型,目前已经得到了均匀半空间倾斜各向异性模型的解析解[17]以及各向异性层状介质的地电响应计算结果[18-21],但三维正演模拟结果发表较少。本文首先提出针对海底矿产勘查的全拖曳式直流电阻率勘查技术。进而从泊松方程出发,以镜像法为基础,结合精度较高的第三类边界条件,通过引入电导率张量求解海洋各向异性环境下直流电法三维正演问题。为了解决源的奇异性问题,本文采取了一次场与二次场分离的方法,一次场从半空间的解析解获得,而二次场采用有限元法求取。对于海底起伏物性界面,本文选用了可以模拟任意形状的非结构网格进行模拟。本文算法与一维半解析解的对比验证了算法的精确性。最后,通过对海底任意各向异性模型的数值模拟证明本文算法的有效性,并验证海洋直流电法对海底各向异性目标体的探测能力。
1 正演理论 1.1 电导率张量对于任意各向异性地下介质,电导率张量σ(σ=ρ-1,ρ为电阻率)可用一个含有6个独立分量的正定对称张量表示,即
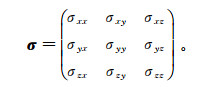 (1)
(1) σ和主轴电导率张量σc之间存在如下关系:
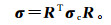 (2)
(2) 式中,R=RxRyRz为欧拉旋转矩阵,具体形式由Yin[22]给出。
1.2 基于二次场的边值问题假设区域Ω中存在一个点电源,由其激发产生的电位u=us+up满足Poisson方程,up和us分别表示一次场电位和由异常体激发的二次电位,海平面处的电位满足Newman边界条件,区域其他边界Γ∞处的电位满足第三类边界条件,则二次场满足的边值条件表示如下[23]:
 (3)
(3) 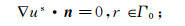 (4)
(4) 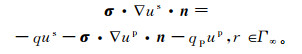 (5)
(5) 其中:
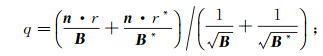 (6)
(6) 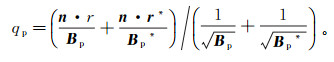 (7)
(7) 而
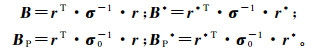
式中:n为边界法向量;σ0是围岩电导率张量;r是网格节点到源的距离;r*是网格节点到镜像法中源对应像位置的距离。
电流强度为I的一次电位的解析解可表示为[19]
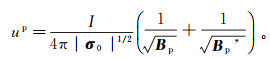 (8)
(8) 在Hilbert函数空间H1(Ω)内取测试函数N,利用Galerkin有限单元法[24]可得
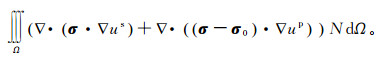 (9)
(9) 我们使用开源代码TetGen[25]将区域Ω剖分成Delaunay四面体网格,利用格林恒等式化简式(9)后代入边界条件,并对二次场在各个单元中进行插值,得到如下线性方程组:
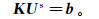 (10)
(10) 式中:K是全局系数矩阵;b是右端源项;Us是待求的二次电位列向量。使用并行直接求解器MUMPS求解大型稀疏线性方程组可得到二次场电位,最后与一次场电位相加即可得到网格节点的总电位。在获得测点的总电位后,考虑到点源在介质中,所以利用镜像法计算公式来计算相应的视电阻率,计算公式为
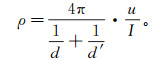 (11)
(11) 式中:d表示真实点源到测点的距离;d′表示点源的镜像到测点的距离;u表示测点的总电位。
1.3 非结构网格局部加密技术直接由Delaunay refinement triangulation生成的非结构化网格可以通过引入加密技术来提高数值解的精度[25-26]。目前的加密技术大体分为全局加密技术和局部加密技术。局部加密技术相对全局加密来说会大大减少计算量,本文采用了局部加密技术中的局部节点加密[27]和局部面积加密。为了提高点源附近的计算精度,我们选择在源附近均匀地增加节点以对源附近的网格进行加密;二次场由于异常体和围岩接触面处的电阻率差异而产生,因此我们在网格生成器中选择限制异常体表面的三角形单元大小,以加密网格、提高二次场的计算精度。
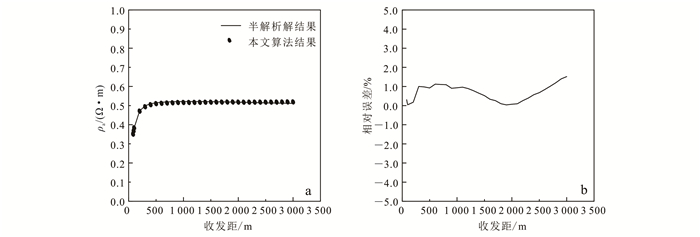
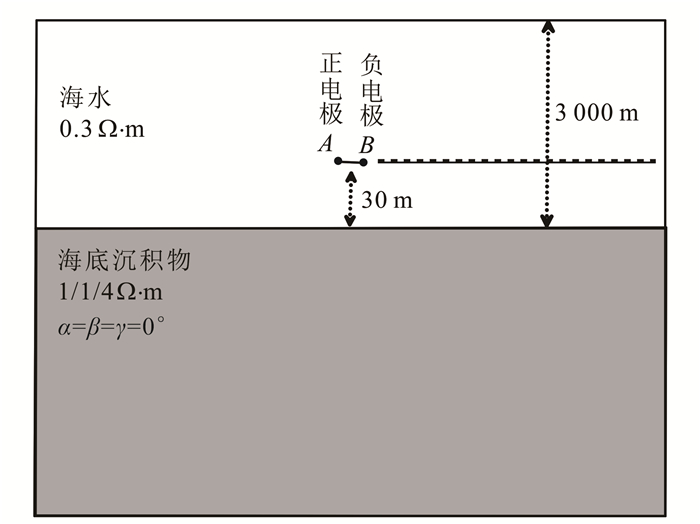
1.4 精度验证本文算例运行平台为:Intel(R) Xeon(R) CPU E5-2667 v3 @ 3.20 GHz 3.20 GHz。我们采用任意各向异性的两层模型(图 1)来验证本文算法精度。第一层海水的电阻率ρ0=0.3 Ω·m,第二层海底沉积物的主轴电阻率及3个欧拉角为:ρx=1 Ω·m,ρy=1 Ω·m,ρz=4 Ω·m,α=0°,β=0°,γ=0°。考虑到现有的层状介质模型结果均采用单极-单极装置,首先假设两个发射点源A、B。坐标分别位于(-0.5,0,0)和(0.5,0,0)处,观测各接收点的电位差并计算视电阻率。图 2给出了本文算法和Yin等[28]半解析解的对比结果。
|
| 图 1 两层海洋各向异性模型 Figure 1 Two-layered anisotropic model for sea |
|
|
由图 2a可知:当发收距较小时,海水电阻率得到很好的反映;随着发收距的增大,海底沉积层的电阻率得到越来越明显的反映。由于受海水的影响较大,图中收发距较大时得到的电阻率是海水和海底沉积层的综合响应。另外,由图 2可以看出,本文算法的结果与半解析解吻合很好,最大相对误差为2%,说明本文算法具有较高的精度。
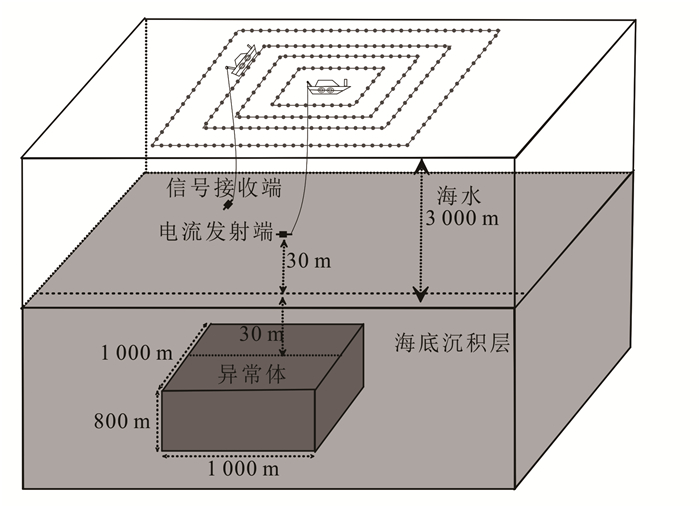
2 算例 2.1 模型建立为研究海底金属矿床及围岩各向异性的电阻率响应特征,我们参考公开发布的海底矿物电学性质和矿藏规模[29],主要依据已有的正演模拟文献选取海底沉积层电阻率[28]。由于深海多金属结核尤其是锰结核以锰钴镍氧化物为主,因此主要参考软锰矿的电阻率范围选取异常体电阻率[14],建立如图 3所示的模型。在10 km×10 km×10 km的模型空间中,建立z轴垂直向下的笛卡尔坐标系,坐标原点位于海平面中心[30]。海水深度为3 000 m,电阻率为0.3 Ω·m,海底沉积物的主轴电阻率为ρ0 x=1 Ω·m,ρ0 y=2 Ω·m,ρ0 z=4 Ω·m,沉积物中金属矿埋深30 m,长宽均为1 000 m,厚度为800 m,主轴电阻率为ρ1 x=0.5 Ω·m,ρ1 y=0.002 5 Ω·m,ρ1 z=0.01 Ω·m。假设电流发射船静止于海平面,下方拖曳着距海底30 m的发射电极,接收船拖曳着距海底30 m的接收电极,并在回形测线上沿测点依次完成测量。我们采用单极-单极装置。
|
| 图 3 三维海洋直流电法模型示意图 Figure 3 3D model for marine DC resistivity modeling |
|
|
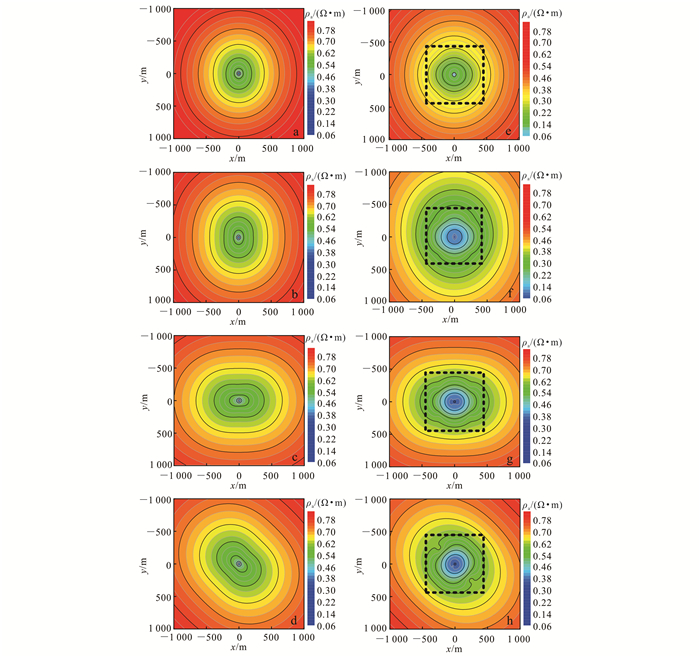
为了研究海底地层和异常体各向异性对视电阻率响应的影响特征,本文针对图 3给出的三维模型计算了各种电各向异性组合模型的视电阻率,结果如图 4所示。为对比,图 4同时展示了各向异性围岩中存在(图 4e、f、g、h)和不存在(图 4a、b、c、d)各向异性异常体时的海底视电阻率响应。
|
| 图中黑色虚线框指示异常体边界。旋转角度分别为:a. α0/β0/γ0=0°/0°/0°;b. α0/β0/γ0=45°/0°/0°;c. α0/β0/γ0=90°/0°/90°;d. α0/β0/γ0=90°/0°/135°;e. α0/β0/γ0=0°/0°/0°,α1/β1/γ1=0°/0°/0°;f. α0/β0/γ0=45°/0°/0°,α1/β1/γ1=0°/0°/0°;g. α0/β0/γ0=90°/0°/90°,α1/β1/γ1=45°/0°/0°;h. α0/β0/γ0=90°/0°/135°,α1/β1/γ1=0°/0°/135°。 图 4 任意各向异性视电阻率分布图 Figure 4 Apparent resistivities' distributions for arbitrarily anisotropies |
|
|
由图 4a可以看出,视电阻率等值线呈椭圆状分布,在实际电阻率小的方向被压缩,在实际电阻率大的方向被拉伸。由于受海水影响较大,视电阻率体现海水与海底沉积层的综合影响。图 4b描述的是当海底沉积层绕x轴旋转45°时的视电阻率分布,此时y轴方向的实际电阻率变大,x轴方向的电阻率不变,因此与图 4a对比,图 4b中沿y方向的视电阻率拉伸更大。图 4c描述的是海底沉积层绕x轴和z轴旋转90°时的视电阻率分布,由于绕x轴旋转90°,图中视电阻率等值线相对于图 4a、b长轴达到了最大拉伸;同时由于地层绕z轴旋转90°,因此视电阻率也相应地绕z轴顺时针旋转了90°。图 4d描述的是当地层绕x轴和z轴分别旋转90°和135°时的视电阻率分布,与图 4c相比,视电阻率等值线很好地反映了地层各向异性特征,极性图方向有效地指示了海底沉积地层的电性主轴方向。由此可见,视电阻率分布可准确地反映出海底沉积层的各向异性分布信息。
图 4e描述的是电各向异性海底沉积层中存在各向异性异常体时的视电阻率分布,与图 4a对比可以发现:受各向异性围岩的影响,异常体边缘处视电阻率等值线出现畸变,异常体内部的视电阻率等值线较好地反映了各向异性异常体的电性分布情况;但由于受围岩影响较大,异常体对应位置的视电阻率等值线在x轴方向的拉伸与y轴方向的压缩并不十分明显。图 4f给出沉积层主轴电阻率绕x轴旋转45°、异常体主轴电阻率不旋转时的视电阻率分布:与图 4b对比可以发现,异常体边缘的等值线出现畸变,由此可大致判断异常体边界位置;与图 4e对比可知,异常体内部的视电阻率等值线在实际电阻率小的方向被拉伸、实际电阻率大的方向被压缩,这是受围岩电阻率影响的结果,可以根据这个现象推测围岩主轴电阻率的旋转方向。图 4g描述的是沉积层主轴电阻率绕x轴和z轴各旋转90°、异常体主轴电阻率绕x轴旋转45°时的视电阻率分布,与图 4c对比发现:由于异常体主轴电阻率绕x轴旋转,导致椭圆等值线的短轴被压缩;由于受围岩的影响,异常体边界处形成了短轴向外凸的花瓣状曲线。图 4h描述的是沉积层主轴电阻率绕x轴和z轴分别旋转90°和135°、异常体主轴电阻率绕z轴旋转135°时的视电阻率分布,与图 4d对比发现:异常体内部等值线与外部围岩的视电阻率椭圆等值线正交,很好地区分异常体和围岩各向异性的差异;异常体边界处受围岩影响,等值线出现畸变。
综合上述,深海直流拖曳装置可以有效地反映海底沉积层和良导矿体的电性分布特征,异常体边界处的视电阻率畸变等值线可以有效地指示异常体边界位置,视电阻率等值线的分布可有效识别围岩和异常体的各向异性特征。
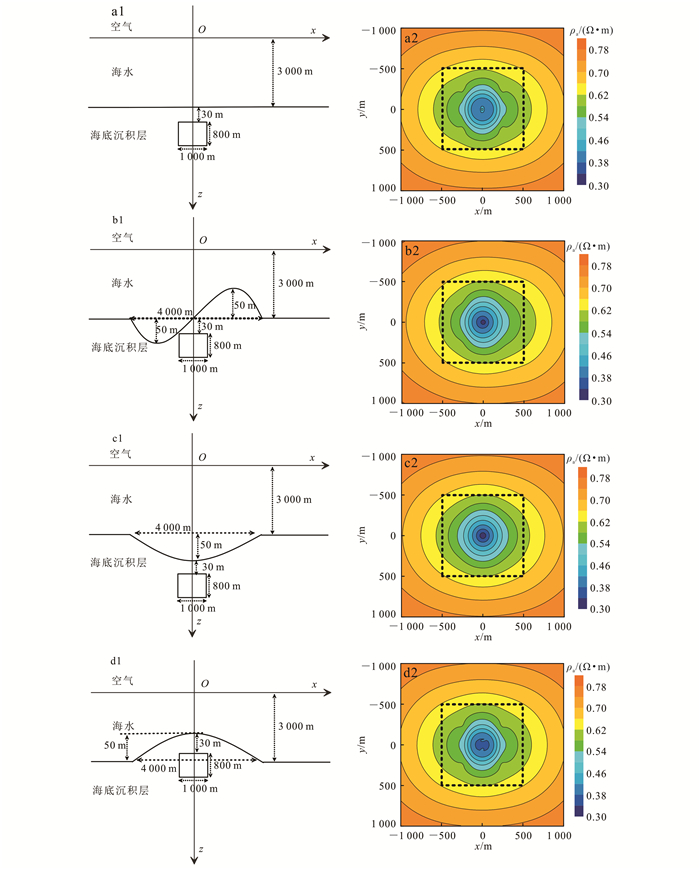
2.3 海底地形对视电阻率的影响深海探测中,由于海底火山运动活跃,海底地形往往高低起伏,对实际探测造成一定影响。为了更好地模拟实际起伏地形的视电阻率响应,我们建立了如图 5所示的不同海底起伏地形模型。图 5a1、b1、c1、d1中的异常体长宽均为1 000 m,厚800 m。图 5a1为海底无地形起伏时的正演模型,异常体上表面距海底30 m;图 5b1为海底同时存在海峰、海谷地形时的正演模型,海峰、海谷宽度均为2 000 m,海峰高50 m,海谷深50 m,矿体位于坐标原点正下方3 030 m;图 5c1为海底存在海谷地形时的正演模型,海谷宽度为4 000 m,深50 m,矿体位于坐标原点正下方3 080 m;图 5d1为海底存在海峰地形时的正演模型,海峰宽度为4 000 m,高50 m,矿体位于坐标原点正下方2 980 m。图 5a2、b2、c2、d2则为a1、b1、c1、d1对应的视电阻率响应图。
图 5a2为海底无地形起伏时各向异性模型的视电阻率响应,主要作为分析含地形起伏时视电阻率变化的参考图件。对比图 5a2、b2、c2、d2可以发现,海峰、海谷地形造成对应于异常体的视电阻率异常不对称、边界被光滑,整体异常由海谷向海峰一侧移动。
3 结论本文基于点源电场的泊松方程,利用非结构节点有限元方法,并采用一次场与二次场分离技术,成功实现了全拖曳式深海直流电阻率三维数值模拟,并通过与半解析解对比验证了算法的精度。通过对任意各向异性模型的数值模拟实验得出如下结论:
1) 全拖曳式深海直流电阻率法可有效勘探海底矿产资源。
2) 本文提出的算法可以有效模拟各向异性海洋沉积层环境中直流电阻率法的视电阻率响应。
3) 即使在海底各向异性环境及海底起伏地形条件下,海底异常体的电性特征(包括各向异性特征)仍然可以得到有效探测和识别。
全拖曳式海洋直流电阻率法探测方式灵活、观测效率高、勘探成本低,可解决传统深海探测的系列技术难题。随着海洋电阻率勘探仪器的发展,可望该技术将在海底矿产资源勘查中发挥越来越重要的作用。
| [1] |
Chevallier M, Lagabrielle R. Prospection Electrique Par Courant Continu en Site Aquatique[J]. Bulletin de Liason des Laboretoires des Ponts et Chaussees, 1991, 171: 57-62. |
| [2] |
Hakim M, Sibony N. Resistivity at Sea:Inversion and Interpretation of Measurements[J]. SEG Technical Program Expanded Abstracts, 1987, 6(1): 94-95. |
| [3] |
Rosenberger A, Weidelt P. Design and Application of a New Free Fall in Situ Resistivity Probe for Marine Deep Water Sediment[J]. Marine Geology, 1999, 160(3/4): 327-337. |
| [4] |
Edwards R N, Chave A D. Atransient Electric Dipole-Dipole Method for Mapping the Conductivity of the Sea Floor[J]. Geophysics, 1986, 51(4): 984-987. DOI:10.1190/1.1442156 |
| [5] |
Cheosman S J, Edwards R N, Chave A D. On the Theory of Sea-Floor Conductivity Mapping Using Transient Electromagnetic System[J]. Geophysics, 1987, 52(2): 204-217. DOI:10.1190/1.1442296 |
| [6] |
Edwards R N. Two-Dimensional Modelling of a Towed In-Line Electric Dipole-Dipole Sea-Floor Electromagnetic System:The Optimum Time Delay or Frequency for Target Resolution[J]. Geophysics, 1988, 53(6): 846-853. DOI:10.1190/1.1442519 |
| [7] |
葛为中. 层状介质点源电场正演解析及其应用[J]. 地球物理学报, 1994, 37(增刊1): 534-541. Ge Weizhong. The Forward Solution of the Electrical Field due to a Point Source in Layered Media and Its Applications[J]. Chinese Journal of Geophysics, 1994, 37(Sup. 1): 534-541. |
| [8] |
葛为中. 水下电测深的理论计算和解释方法[J]. 桂林工学院学报, 1998, 18(2): 172-175. Ge Weizhong. Theoretical Calculation and Interpretation Method of Underwater Electrical Sounding[J]. Journal of Guilin Institute of Technology, 1998, 18(2): 172-175. |
| [9] |
王自民. 水上直流电测深法勘探的应用[J]. 桂林工学院学报, 1997, 17(增刊1): 23-25. Wang Zimin. Application of Water Direct Current Sounding Method[J]. Journal of Guilin Institute of Technology, 1997, 17(Sup. 1): 23-25. |
| [10] |
黄俊革, 阮百尧, 鲍光淑. 水下直流电阻率法数值模拟[J]. 物探化探计算技术, 2004, 26(2): 136-140. Huang Junge, Ruan Baiyao, Bao Guangshu, et al. DC Resistivity Numerical Modelling Underwater[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2004, 26(2): 136-140. DOI:10.3969/j.issn.1001-1749.2004.02.011 |
| [11] |
翁爱华, 祝嗣安. 天然气水合物的近海底直流电测深响应[J]. 石油地球物理勘探, 2010, 45(3): 458-461. Weng Aihua, Zhu Sian. Near Sea-Bottom DC Sounding Response for Gas Hydrate[J]. Oil Geophysical Prospecting, 2010, 45(3): 458-461. |
| [12] |
刘长胜, 林君. 海底表面磁源瞬变响应建模及海水影响分析[J]. 地球物理学报, 2006, 49(6): 1891-1898. Liu Changsheng, Lin Jun. Transient Electromagnetic Response Modelling of Magnetic Source on Seafloor and the Analysis of Eeawater Effect[J]. Chinese Journal of Geophysics, 2006, 49(6): 1891-1898. DOI:10.3321/j.issn:0001-5733.2006.06.039 |
| [13] |
李慧.海洋瞬变响应理论计算及浅海底瞬变电磁探测技术研究[D].长春: 吉林大学, 2006: 27-48. Li Hui. Theoretical Calculation of Marine Transient Electromagnetic Response and Research of Shallow Sea-Sloor Detection Technology[D]. Changchun: Jilin University, 2006: 27-48. http://cdmd.cnki.com.cn/Article/CDMD-10183-2007095251.htm |
| [14] |
周胜, 席振铢, 宋刚, 等. 深海拖曳式瞬变电磁的响应规律[J]. 中南大学学报(自然科学版), 2012, 43(2): 605-610. Zhou Sheng, Xi Zhenzhu, Song Gang, et al. Responses of the Towed Transient Electromagnetic Sounding on Deep Sea[J]. Journal of Central South University (Science and Technology), 2012, 43(2): 605-610. |
| [15] |
何继善, 鲍力知. 海洋电磁法研究的现状和进展[J]. 地球物理学进展, 1999, 14(1): 7-39. He Jishan, Bao Lizhi. Present Situation and Progress of Marine Electromagnetic Research[J]. Progress in Geophysics, 1999, 14(1): 7-39. |
| [16] |
Herwanger J V, Pain C C, Binley A, et al. Aniso-tropic Resistivity Tomography[J]. Geophysical Journal International, 2004, 158(2): 409-425. DOI:10.1111/gji.2004.158.issue-2 |
| [17] |
Habberjam G. Apparent Resistivity, Anisotropy and Strike Measurements[J]. Geophysical Prospecting, 1975, 23(2): 211-247. DOI:10.1111/gpr.1975.23.issue-2 |
| [18] |
Wait J R. Current Flow into a Three-Dimensionally Anisotropic Conductor[J]. Radio Science, 1990, 25(5): 689-694. DOI:10.1029/RS025i005p00689 |
| [19] |
Li P, Uren N. Analytical Solution for the Point Source Potential in an Anisotropic 3-D Half-Sapce:Ι:Two-Horizontal-Layer Case[J]. Mathematical and Computer Modelling, 1997, 26(5): 9-27. DOI:10.1016/S0895-7177(97)00155-6 |
| [20] |
Yin C, Weidelt P. Geoelectrical Fields in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 1999, 64(2): 426-434. DOI:10.1190/1.1444547 |
| [21] |
Yin C, Maurer H M. Electromagnetic Induction in a Layered Earth with Arbitrary Anisotropy[J]. Geophysics, 2001, 66(5): 1405-1416. DOI:10.1190/1.1487086 |
| [22] |
Yin C. Geoelectrical Inversion for a One-Dimensional Anisotropic Model and Inherent Non-Uniqueness[J]. Geophysical Journal International, 2000, 140(1): 11-23. DOI:10.1046/j.1365-246x.2000.00974.x |
| [23] |
金建铭. 电磁场有限元法[M]. 西安: 西安电子科技大学出版社, 2014. Jin Jianming. The Finite Element Method in Electromagnetics[M]. Xi'an: Xidian University Press, 2014. |
| [24] |
任政勇, 汤井田. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟[J]. 地球物理学报, 2009, 52(10): 2627-2634. Ren Zhengyong, Tang Jingtian. 2.5-D DC Resistivity Modeling by Adaptive Finite-Element Method with Unstructured Triangulation[J]. Chinese Journal Geophysics, 2009, 52(10): 2627-2634. DOI:10.3969/j.issn.0001-5733.2009.10.023 |
| [25] |
Hang S. A Quality Tetrahedral Mesh Generator and Three-Dimensional Delaunay Triangulator[D]. Berlin: Weierstrass Institute for Applied Analysis and Stochastic, 2006.
|
| [26] |
Ren Z, Tang J. A Goal-Oriented Adaptive Finite-Element Approach for Multi-Electrode Resistivity System[J]. Geophysical Journal International, 2014, 199(1): 136-145. DOI:10.1093/gji/ggu245 |
| [27] |
Rücker C, Günther T, Spitzer K, et al. Three-Di-mensional Modelling and Inversion of DC Resistivity Data Incorporating Topography:Ι:Modelling[J]. Geophysical Journal International, 2006, 166(2): 495-505. DOI:10.1111/gji.2006.166.issue-2 |
| [28] |
Yin C, Zhang P, Cai J, et al. Forward Modelling of Marine DC Resistivity Method for a Layered Anisotropic Earth[J]. Applied Geophysical, 2016, 13(2): 279-287. DOI:10.1007/s11770-016-0560-2 |
| [29] |
罗婕, 田学达, 魏雪峰, 等. 深海锰结核资源的研究进展[J]. 中国锰业, 2004, 22(4): 6-9. Luo Jie, Tian Xueda, Wei Xuefeng, et al. Advance of Study on the Deep-Sea Manganese Nodule[J]. China's Manganese Industry, 2004, 22(4): 6-9. DOI:10.3969/j.issn.1002-4336.2004.04.002 |
| [30] |
贲放, 刘云鹤, 黄威, 等. 各向异性介质中的浅海海洋可控源电磁响应特征[J]. 吉林大学学报(地球科学版), 2016, 46(2): 581-593. Ben Fang, Liu Yunhe, Huang Wei, et al. MCSEM Response for Anisotropic Media in Shallow Water[J]. Journal of Jilin University (Earth Science Edition), 2016, 46(2): 581-593. |