0 引言
近年来, 因输油管道和储油设施造成的有机化合物泄漏对土壤、地下水的污染越来越严重, 对这一课题的研究和治理工作也得到越来越多的重视。轻质非水相流体(LNAPL)[1]污染物一经泄漏进入地下以后, 主要运移形式为重力下渗和相间运移,即LNAPL在重力作用下在非饱和带土壤中下渗, 同时在毛细力作用下产生横向迁移[2]。当LNAPL到达地下水位以上, 进入饱水度增加的毛细带区域时, 结束向下迁移过程, 以向两侧运移为主[3], 在毛细带内横向扩展开来, 形成漂浮在地下水面上的LNAPL透镜体[4]。
目前国内外对LNAPL迁移的研究, 多是对LNAPL在非饱和带和饱和带中的迁移进行定量研究或者改变一些参数观察其对迁移的影响。Cho等[5]在一个小型的水流单元内研究了无机污染物的指状扩散现象, 发现经染色的污染物在非饱和带内产生指状流, 向下迁移到毛细带后使垂向迁移速率降低了50%。Simmons等[6]以不同密度的CaCl2作为溶质, 观察了其在非饱和带及毛细带的迁移, 结果表明低密度流堆积在地下水面上并产生侧向迁移, 水面起到了屏障作用, 降低了孔隙水流的流速; 中高密度流在毛细带继续以指状流形式向下迁移, 进入到地下水中。国外较早就开始了对形成透镜体的大小形状进行预测的研究。Abdul [7]使用柴油和细砂在模拟柱中进行了一维实验, 结果表明污染物将会在穿透非饱和带后在地下水面表面形成稳定的薄饼状透镜体, 透镜体的上边界是平的。Pantazidou等[8]利用水-油、油-气、水-气各自的两相界面的界面张力以及孔隙孔喉的直径, 给出了一种预测透镜体厚度的方程式,并且认为稳定时NAPL(非水相液体)形成透镜体的上边界并不是直线而是一条曲线。Schroth等[9]用柴油、矿物油, 以及4种不同粒径的砂,利用Pantazidou的预测公式研究了NAPL在非饱和带中迁移达到平衡时形成透镜体的几何结构, 发现在均质介质中, 稳定状态时透镜体形状应该是上边界为一条直线而下边界是条曲线。但是Pantazidou和Schroth的公式中用到的水-油、油-气和水-气的界面张力随LNAPL的不断渗漏和迁移发生变化, 不考虑这一变化则会对结果造成一定的误差。在模拟槽实验甚至实际场地中,实时测定各两相间的界面张力是不现实的。Miller等[10]利用LNAPL和DNAPL(重质非水相液体)透镜体上下边界的压力差,以及自身重力的平衡关系,提出了一种利用进入压力预测最大透镜体厚度的公式,并使用PF-5070代表DNAPL, 柴油代表LNAPL, 分别进行了5组两相流(水-油)实验和4组三相流(水-油-气)实验对污染物在非饱和带中形成的透镜体厚度进行验证;然而在预测最大透镜体厚度的时候, 并没有提出准确确定吸湿脱湿曲线进入压力的方法。
土-水特征曲线(SWCC)描述了土体吸力的和土中吸附的含水率的关系[11]。即含水率越高, 土体吸力越低。土-水特征曲线一般是以空气为非润湿相, 本文中以柴油作为非润湿相, 得出的吸力和含水率的关系, 称为饱和度-压力曲线(S-p曲线)。目前非饱和土的土-水特征曲线的测试方法较多, 包括压力板法、盐溶液法、滤纸法、TDR(时域反射技术)基质吸力测量法、Temple仪法等[12-14];但这些方法往往需要精密的仪器进行大范围的计算, 测量步骤复杂。本文提出了一种较为简单的方法,只需准确测出吸湿脱湿曲线的进入压力即可解决上述问题。即采用砂芯漏斗装置测定中砂和粗砂的油、水间的饱和度-压力曲线[15], 并采用Van Genuchten模型(VG模型)进行拟合, 确定水-油两相吸湿及脱湿进气压力,即可预测透镜体的厚度;并采用模拟实验对预测的透镜体厚度进行了验证。
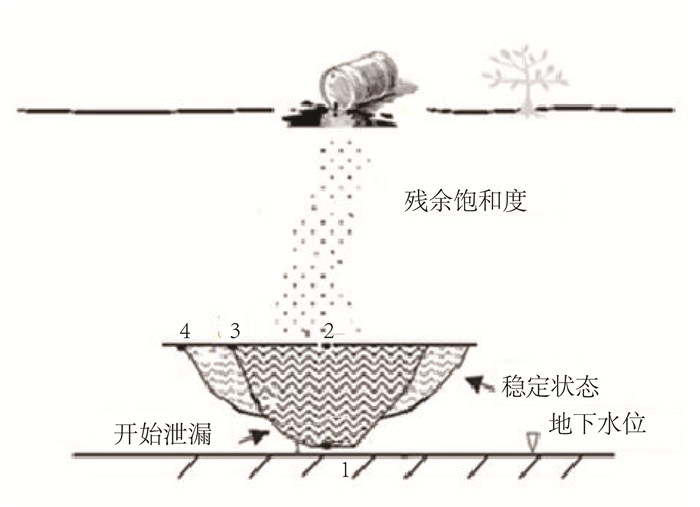
1 材料与方法 1.1 实验原理如图 1所示, LNAPL泄漏进入非饱和带后向下运动并驱替水, 直至LNAPL在毛细带形成稳定的透镜体之前, LNPAL聚集体都是在驱替水, 即整个透镜体中压力都大于脱湿曲线的进入压力(即开始泄露状态点1、2、3处的压力均大于脱湿曲线进入压力); 之后当泄漏源不再泄漏时, 由于驱动力的减小, 在最下面的LNAPL将被水重新驱替, 稳定后点4处的压力应大于脱湿曲线的进入压力, 而点1处的压力小于吸湿曲线的进入压力。即透镜体的下边界上的压力从脱湿曲线的进入压力慢慢变小到吸湿曲线的进入压力, 从而压缩原来的透镜体至稳定状态。根据垂向上的受力平衡, 假定上下界面的面积相同且都为A, 我们可以得出以下公式:

|
| 图 1 LNAPL在非饱和带形成的透镜体厚度预测 Figure 1 Predicting the lens thickness of LNAPL formed in the unsaturated zone |
|
|
从而可以推出透镜体厚度的预测公式:
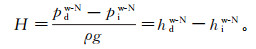 (1)
(1) 式中: H为透镜体厚度; m为透镜体的质量; g为重力加速度; ρ为LNAPL的密度; p为压力水头; h为进入压力水头; 下角标d、i分别代表脱湿、吸湿, 上角标w-N代表水-NAPL相。
这与Miller等[10]的研究相符。
由式(1)可知, 对透镜体厚度的预测可以简化为求出脱湿、吸湿曲线的进入压力水头。即只需采用砂芯漏斗装置测定中砂、粗砂的水-柴油S-p曲线, 即可准确测出吸湿、脱湿曲线的进入压力水头。
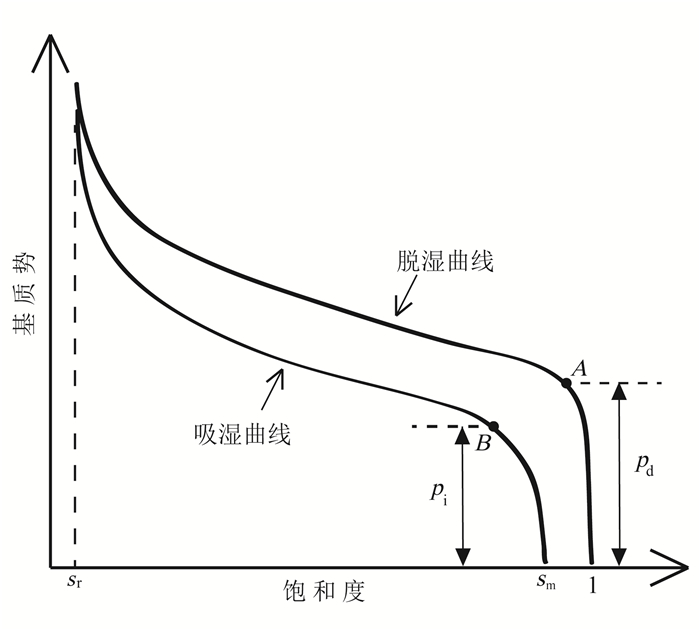
在非饱和土中, 土体在吸湿和脱湿过程中的土-水特征曲线存在滞后作用。具体来说, 在同一吸力下, 土体在脱湿过程中的含水率要大于吸湿过程中的含水率。将其中气相抽象为非润湿相,滞后作用即抽象为水和一种非润湿相(本文中为柴油)S-p曲线的滞后作用。图 2为典型非饱和土-水特征曲线。当脱湿曲线的毛细压力低于pd时, 非润湿相无法驱替出润湿相; 当吸湿曲线的毛细压力达到或低于pi时, 非润湿相变得不连续从而无法在介质中流动。由于吸湿过程中会产生闭合气泡, 因此吸湿曲线的最大饱和度不能达到1。通过实验可以测出S-p曲线并求出pd、pi, 从而预测透镜体厚度。
|
| Sr为残余饱和度;Sm为吸湿曲线能达到的最大饱和度;pd、pi分别为脱湿、吸湿曲线的进入压力。 图 2 非饱和土土-水特征曲线的滞后作用 Figure 2 Hysteresis effect of the soil-water characteristic curve of unsaturated soil |
|
|
实验所用LNAPL为0#柴油, 取自长春市中国石油加油站, 常温下为淡黄色液体, 20 ℃下密度为0.840 g/mL。柴油具有低挥发性、不溶于水的特点, 因而在对LNAPL的研究中经常使用。所用非饱和带介质为中砂和粗砂, 粒径分别为0.25~0.50 mm、0.50~1.00 mm; 含水层所用介质为砾石, 粒径大于1.00 mm。实验使用的柴油先经过染色再注入实验装置, 所用染色剂为苏丹蓝, 溶于油而不溶于水。
1.3 实验方法 1.3.1 S-p曲线实验实验装置如图 3所示, 左边是G3/250 mL的砂芯漏斗, 右边是带有刻度的玻璃管, 中间用橡胶管连接。实验开始前把砂芯漏斗装入体积为V0的水, 再将质量为m0的砂均匀放入漏斗中, 保持水位高于砂的高度。这样能得到完全饱和的土样, 除去多余的水并称量其体积(V1), 从而算出土样的饱和含水率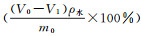

|
| 图 3 S-p曲线实验装置图 Figure 3 Experimental setup of the saturation-pressure curve |
|
|
实验首先在土样上面加入足够量的柴油作为非润湿相; 然后通过降低右边的玻璃管以增加其基质吸力从而使土样开始脱水, 基质吸力可以由玻璃管降低高度得出, 饱和度可以由排出水的体积和饱和含水率求出;一直降低玻璃管高度得到完整的脱湿曲线;达到残余饱和度后, 再升高玻璃管, 降低土样的基质吸力从而使土样开始吸水, 根据玻璃管升高的高度得出基质吸力;再根据不同吸力下的饱和度得到吸湿曲线。
目前常用3种公式来拟合水-土特征曲线:Brooks-Corey模型(BC模型)、VG模型以及Fredlund-Xing模型(FX模型)[16]。BC模型是最早提出的拟合方程, 该数学模型呈现出非光滑或开放式的形式;VG模型是一个平滑的、封闭的数学模型, 该模型能模拟更广的吸力范围, 更有效地拟合实际的土-水特征曲线的形状;FX模型类似于VG模型, 且增加了一个修正因子以表征含水率为0时的吸力值, 但是这样也使得模型更加复杂。在本实验中, 模拟S-p曲线的重点是求出各自的进入压力, 因此对于0含水率的吸力值并没有特别高的要求。综合以上考虑, 本文选择了VG模型。VG模型表达式[17]为
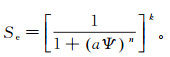 (2)
(2) 式中:Se为有效饱和度, 可以用完全饱和度(Sa=1)、介质饱和度S和残余饱和度Sr来表达(Se=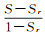
将数据整理, 用ORIGIN软件进行处理, 得出拟合的吸湿脱湿曲线。
1.3.2 模拟槽实验实验使用长为50 cm、高40 cm、宽5 cm的模拟槽。在模拟槽底部先填入2~3 cm厚砾石模拟含水层, 再均匀填入分选好的中砂或粗砂, 每填2~3 cm捣实一次。填完后, 从左侧底部用蠕动泵注入蒸馏水, 保持左侧进水槽水位不变(中砂为3.5 cm, 粗砂为0.8 cm)。由于毛细作用, 在含水层上方会形成一个湿润的毛细带。当毛细带完全形成后, 从上方连续无压力注入已染色的0#柴油, 保持注入速度一定, 每隔一定时间观测记录柴油的迁移情况。透镜体形状稳定后测定LNAPL在毛细带形成稳定透镜体的厚度。
1.3.3 预测结果与实验结果拟合以S-p曲线为基础, 确定出吸湿、脱湿曲线的进入压力, 并计算出预测的透镜体厚度。根据模拟槽实验测量出实际的透镜体厚度。比较预测厚度和实际厚度的差距并分析误差。
2 结果与分析 2.1 S-p曲线根据实验所得基质吸力水头-饱和度的关系, 用ORIGIN软件拟合VG方程, 得出中砂、粗砂吸湿、脱湿曲线(图 4、图 5)。
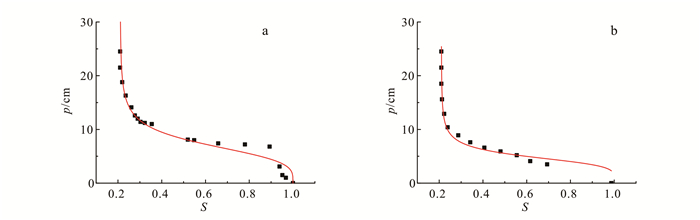
|
| 图 4 中砂脱湿(a)、吸湿曲线(b) Figure 4 Main drainage(a) and wetting(b) curve of medium sand |
|
|
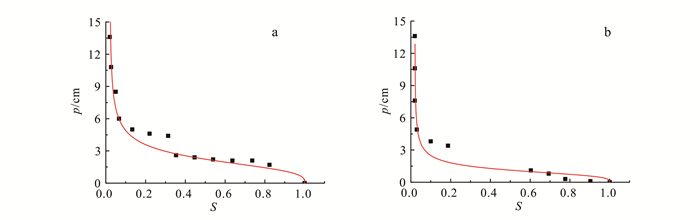
|
| 图 5 粗砂脱湿(a)、吸湿曲线(b) Figure 5 Main drainage(a) and wetting(b) curve of the coarse soil |
|
|
中砂、粗砂实验中各拟合参数如表 1所示。
| 介质 | 曲线 | a/cm-1 | h/cm | k |
| 中砂 | 脱湿曲线 | 0.13 | 7.72 | 6.53 |
| 吸湿曲线 | 0.32 | 3.11 | 2.77 | |
| 粗砂 | 脱湿曲线 | 0.48 | 2.08 | 3.26 |
| 吸湿曲线 | 1.27 | 0.79 | 2.02 |
将脱湿、吸湿曲线的进入压力水头相减, 可以得出中砂、粗砂实验预测的透镜体厚度分别为4.61和1.29 cm。
2.2 模拟槽验证实验结果分别用中砂、粗砂作为均质介质, 模拟非饱和带, 最后得出的透镜体厚度如图 6所示。
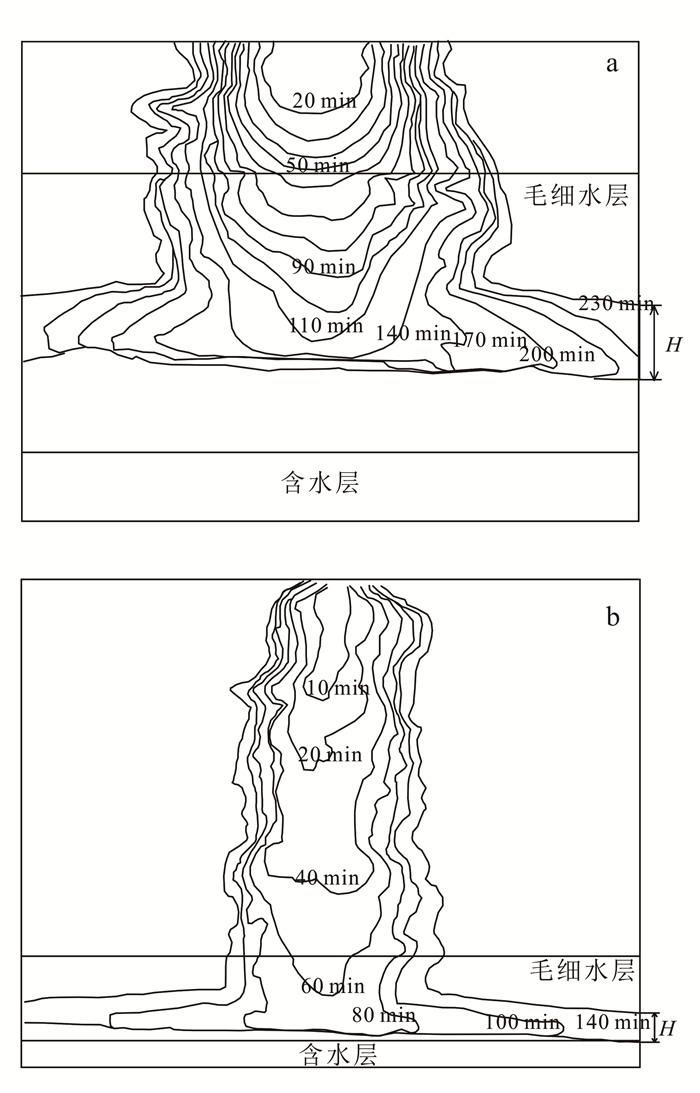
|
|
时间表示柴油随时间的迁移轨迹。 a.H=5.30 cm;b.H=1.50 cm。 图 6 中砂(a)、粗砂(b)实验透镜体厚度 Figure 6 Lens thickness of the medium soil (a)and the coarse soil (b)experiment |
|
|
在中砂模拟槽实验中我们发现:在到达毛细带前和到达毛细上升带而未到达毛细湿润带之间(前90 min),LNAPL湿润锋迁移速率为0.20 cm/min;在到达毛细湿润带之后(90 min后),LNAPL湿润锋迁移速率为0.11 cm/min。柴油锋面迁移速率从上至下越来越小,是因为迁移到毛细带后,柴油多受到一个向上的水-油界面张力作用,阻滞了柴油的迁移,并且随着含水率的增加,介质孔隙被水所占据,油要往下迁移必须穿过剩余的孔隙或者驱替水分,从而导致柴油锋面运移速率随着含水率的增加而减小;柴油到达毛细边缘后,纵向迁移基本停滞,横向迁移迅速发育,并且在水力梯度(5×10-2)的存在下,向右迁移的速率(0.18 cm/min)要比向左迁移的速率(0.15 cm/min)大。经过230 min的迁移, 达到稳定时透镜体厚度为5.30 cm。
在粗砂模拟槽实验中:在到达毛细带前(前40 min),LNAPL湿润锋迁移速率为0.61 cm/min;在到达毛细上升带而未到达毛细湿润带之间(40~60 min),LNAPL湿润锋迁移速率为0.52 cm/min;在到达毛细湿润带之后(60 min后),LNAPL湿润锋迁移速率为0.14 cm/min。与中砂类似,柴油锋面迁移速率从上至下越来越小。柴油到达毛细边缘后,纵向迁移基本停滞,横向迁移迅速发育,粗砂中的水力梯度较小(4×10-3),向右迁移的速率与向左迁移的速率基本一致(都为0.44 cm/min)。经过140 min的迁移, 达到稳定时透镜体厚度为1.50 cm。
2.3 实验结果分析中砂的模拟槽实验实测透镜体厚度为5.30 cm, 用S-p曲线预测的透镜体厚度为4.61 cm, 相对误差为13.0%。粗砂的模拟槽实验实测透镜体厚度为1.50 cm, 用S-p预测的透镜体厚度为1.29 cm, 相对误差为14.0%。在Miller等[10]的实验中,最大误差为16.4%,平均误差为12.2%,因此认为这部分误差是可以接受的。误差的原因是在S-p曲线的实验中, 绘制的两条曲线理论上应该是在完全干燥的情况下的吸湿曲线和完全饱和的情况下的脱湿曲线, 而在实验过程中这种情况很难达到, 实验中的脱湿、吸湿曲线一般是介于完全脱湿、完全吸湿曲线中间的两条曲线, 从而导致预测的透镜体厚度偏小。在实验中可以通过增加一个大于1的校正参数来增加预测准确度。
不同介质中透镜体厚度进行相比较可知, 中砂要远高于粗砂, 这是因为粗砂的孔径大, 孔隙结构疏松, 孔隙连续性强, 饱和状态下能够储存大量水分。但是大孔隙土壤具有较小的基质势, 脱湿状态下水分优先从大孔隙排出, 使得土样在极小的吸力条件下就开始快速失水, 因而具有较低的脱湿进入压力。
3 结论1) 稳定状态的LNAPL透镜体厚度可以采用测定S-p曲线的脱湿曲线和吸湿曲线的进入压力的方法进行预测, 利用S-p曲线预测柴油在中砂及粗砂介质的非饱和带中形成的透镜体厚度分别为4.61 cm和1.29 cm。
2) 通过模拟实验测得实验条件下中砂和粗砂形成的透镜体厚度分别为5.30 cm和1.50 cm, 与利用S-p曲线预测透镜体厚度的相对误差达到了13.0%和14.0%, 这是由于实验中的脱湿与吸湿过程不是在完全干燥的情况下得到的。因此在利用S-p曲线预测透镜体厚度时, 可以采用一个大于1的校正参数来提高准确度。
3) LNAPL在非饱和带形成的透镜体厚度与介质粒径有关, 介质粒径越大, 颗粒之间排列较为松散, 内部具有较多的大孔隙, 从而导致吸湿脱湿进入压力的差别小, 透镜体厚度越小。
| [1] |
Liu Z, Wu H. Pore-Scale Modeling of Immiscible Two-Phase Flow in Complex Porous Media[J]. Applied Thermal Engineering, 2016, 93: 1394-1402. DOI:10.1016/j.applthermaleng.2015.08.099 |
| [2] |
Blunt M J, Bijeljic B, Dong H, et al. Pore-Scale Imaging and Modelling[J]. Advances in Water Resources, 2013, 51(1): 197-216. |
| [3] |
Sleep B E, Sehayek L, Chien C C. A Modeling and Experimental Study of Light Nonaqueous Phase Liquid (LNAPL) Accumulation in Wells and LNAPL Recovery from Wells[J]. Water Resources Research, 2000, 36(12): 3535-3545. DOI:10.1029/2000WR900224 |
| [4] |
Valvatne P H, Piri M, Lopez X, et al. Predictive Pore-Scale Modeling of Single and Multiphase Flow[J]. Transport in Porous Media, 2005, 58(1): 23-41. |
| [5] |
Cho H, De Rooij G H. Pressure Head Distribution During Unstable Flow in Relation to the Formation and Dissipation of Fingers[J]. Hydrology and Earth System Sciences Discussions, 2002, 6(4): 763-771. DOI:10.5194/hess-6-763-2002 |
| [6] |
Simmons C T, Pierini M L, Hutson J L. Laboratory Investigation of Variable-Density Flow and Solute Transport in Unsaturated-Saturated Porous Media[J]. Transport in Porous Media, 2002, 47(2): 215-244. DOI:10.1023/A:1015568724369 |
| [7] |
Abdul A S. Migration of Petroleum Products Through Sandy Hydrogeologic Systems[J]. Groundwater Monitoring & Remediation, 1988, 8(4): 73-73. |
| [8] |
Pantazidou M, Sitar N. Emplacement of Nonaqueous Liquids in the Vadose Zone[J]. Water Resources Research, 1993, 29(3): 705-722. DOI:10.1029/92WR02450 |
| [9] |
Schroth M H, Istok J D, Ahearn S J, et al. Geometry and Position of Light Nonaqueous-Phase Liquid Lenses in Water-Wetted Porous Media[J]. Journal of Contaminant Hydrology, 1995, 19(4): 269-287. DOI:10.1016/0169-7722(95)00023-O |
| [10] |
Miller C D, Durnford D S, Fowler A B. Equilibrium Nonaqueous Phase Liquid Pool Geometry in Coarse Soils with Discrete Textural Interfaces[J]. Journal of Contaminant Hydrology, 2004, 71(1): 239-260. |
| [11] |
Roman S, Soulaine C, Alsaud M A, et al. Particle Velocimetry Analysis of Immiscible Two-Phase Flow in Micromodels[J]. Advances in Water Resources, 2015, 95: 199-211. |
| [12] |
李志清, 李涛, 胡瑞林, 等. 非饱和土土水特征曲线(SWCC)测试与预测[J]. 工程地质学报, 2007, 15(5): 700-707. Li Zhiqing, Li Tao, Hu Ruilin, et al. The Prediction and Examination of the Unsaturated Soil-Water Characteristic Curve[J]. Journal of Engineering Geology, 2007, 15(5): 700-707. DOI:10.3969/j.issn.1004-9665.2007.05.020 |
| [13] |
孙德安, 张俊然, 吕海波. 全吸力范围南阳膨胀土的土-水特征曲线[J]. 岩土力学, 2013, 34(7): 1839-1846. Sun De'an, Zhang Junran, Lü Haibo. Soil-Water Characteristic Curve of Nanyang Expansive Soil in Full Suction Range[J]. Rock and Soil Mechanics, 2013, 34(7): 1839-1846. |
| [14] |
张雪东.土水特征曲线及其在非饱和土力学中应用的基本问题研究[D].北京: 北京交通大学, 2010. Zhang Xuedong. The Research About the Fundamental Problem of the Soil-Water Characteristic Curve Applying on the Soil Mechanics Unsaturated Soils[D]. Beijing: Beijing Jiaotong University, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10004-2010259888.htm |
| [15] |
Sharma R S, Mohamed M H A. An Experimental Investigation of LNAPL Migration in an Unsaturated/Saturated Sand[J]. Engineering Geology, 2003, 70(3): 305-313. |
| [16] |
戚国庆, 黄润秋. 土水特征曲线的通用数学模型研究[J]. 工程地质学报, 2004, 12(2): 182-186. Qi Guoqing, Huang Runqiu. A Universal Mathematical Model of Soil-Water Characteristic Curve[J]. Journal of Engineering Geology, 2004, 12(2): 182-186. DOI:10.3969/j.issn.1004-9665.2004.02.012 |
| [17] |
Van Genuchten. A Closed-Form Equation for Predic-ting the Hydraulic Conductivity of Unsaturated Soils[J]. Soil Science Society of America Journal, 1980, 44: 892-898. DOI:10.2136/sssaj1980.03615995004400050002x |
| [18] |
卢宁, 立科恩. 非饱和土力学[M]. 北京: 高等教育出版社, 2012. Lu Ning, Likos. Unsaturated Soil Mechanics[M]. Beijing: Higher Education Press, 2012. |



